Probabilistic Modelling of Station Locations in Bicycle-Sharing Systems

Abstract

We present a simulation methodology for generating the locations of stations in Bicycle-Sharing Systems. We present several methods that are inspired by the literature on spatial point processes. We evaluate how the artificially generated systems compare to existing systems through a case study involving 11 cities worldwide. The method that is found to perform best is a data-driven approach in which we use a dataset of places of interest in the city to ‘rate’ how attractive city areas are for station placement. The presented methods use only non-proprietary data readily available via the Internet.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Bicycle-Sharing Systems¹ (BSSs) are an increasingly popular phenomenon, as witnessed by the worldwide number of operational systems growing from roughly 350 such systems [7] in 2010 to almost 1,000 at the time of writing [18]. Due to this strong increase, the question of choosing station locations in a new BSS is of increasing relevance to planners, operators, and scientists. A well-studied approach is to optimise some measure of coverage of ‘interesting’ parts of the city. The choice of Geographic Information System (GIS) dataset to identify interesting locations in the target city depends on the context—e.g., residential and commercial area density are of interest to a commuting-oriented BSS, and proximity to landmarks and restaurants to a BSS focussing on tourism and leisure. In the literature, the best station locations are then typically chosen using some form of deterministic optimisation—e.g., the methods implemented in the geographic analysis tool ArcGIS [10] or the optimisation tool suite XPRESS [8]. This approach will typically return a single optimal solution. In some cases, the user is required to manually determine a set of candidate locations beforehand.

In this paper, we will consider the use of stochastic simulation to generate BSS station locations as an alternative to deterministic optimisation. The probabilities informing the simulation procedure are inspired by the literature on spatial point processes. We will discuss the use of two baseline approaches—in particular the Poisson and Ginibre point process—and compare these to a simulation procedure that incorporates GIS information. The main criterion is correspondence to real-world BSSs, including several major systems such as the Bicing BSS in Barcelona. The simulation procedure provides insight into how stations are distributed across space - this can inform models of bicycle movement, provide feedback to operators of existing systems, and aid designers of new systems. Executing this approach several times will result in different outcomes, which is typically more informative to planners than the single solution returned by a deterministic optimisation procedure. After all, the GIS data informing the optimality criterion is itself prone to subjectivity and inaccuracies. Additionally, the approach discussed in this paper only uses non-proprietary data and the programming code for the experiments is written in Java and available upon request.

The outline of this paper is as follows. We begin with a discussion of related work and the data sources used in this paper in Sect. 2. We then fix notation and discuss basic simulation procedures in Sect. 3. In Sect. 4, we zoom in on the various techniques to generate station locations. We present the results of a simulation experiment involving a comparison with real-world BSSs in Sect. 5. Section 6 concludes the paper.

2 Background and Data

Before we present this paper’s specific contributions, we first elaborate on its position within the wider scientific and societal context. We begin with a discussion of the background and the related scientific literature in Sect. 2.1, and discuss the data sources used to generate the results of this paper in Sect. 2.2.

2.1 Background and Related Work

The recent wave of attention for BSSs from the scientific community is largely due to vast amount of data collected by third-generation systems [7]. Third-generation systems combat the theft and vandalism that plagued the previous two generations by employing technologies that allow for bikes and users to be uniquely identified. Data regarding bike availability at stations is collected as a by-product of such systems, and in many cases made available to third-party users, including researchers. One popular research area involves the analysis of bicycle usage patterns [9, 11, 13, 20]. Another area, one that is particularly relevant to his paper, involves the development of algorithms for the positioning of station locations [10, 24]. These algorithms can be validated against real-world systems using the station location coordinates that are often provided alongside bike availability data. In the following we present a brief overview of related work concerning both the evaluation of existing systems in terms of their station locations and the design of new systems.

A comprehensive comparison of 38 BSSs worldwide is presented in [21]. Although some of the metrics considered in [21] correspond to usage patterns, some of the metrics solely deal with the geographic position of the stations - two of these metrics will also be considered in Sect. 5. Another research question involves the clustering of stations with similar usage patterns—case studies include Barcelona [9], London [16], and Paris [4]. Of particular interest to this paper is the question of where to position the stations, given a GIS dataset to identify interesting locations: [10] does this for a proposed system in Madrid. The used GIS datasets include the road network, building usages in terms of population and jobs, ‘transport zones’, and locations of other public transportation hotspots. In [3], a methodology for adding new stations to BSSs is discussed and applied to two BSSs (Washington DC and Hangzhou)—the used GIS datasets here include the Google Places API for identifying Points of Interests (POIs), Location Based Social Network check-in obtained via the Foursquare API, and a demographical dataset. The potential introduction of a BSS in Helsinki, Finland is studied in [15], with a particular focus on open data. A potential BSS in Coimbra, Portugal is studied in [8]. The BSS in New York is studied in [17]; one of the GIS datasets used to identify locations of interest corresponds to taxi GPS transactions. A case study involving data provided by the municipality of Milan is presented in [5]. Naturally, the techniques used to optimise station locations can be applied in many other contexts a well—e.g., placement of defibrillators [22], fire watchtowers [2] or electric taxi charging stations [23]—see also the overview presented in the section on location-allocation models in [10]. For a general overview of location-allocation modelling of bike sharing systems can be found in [24]. Finally, in [12], a methodology for automatically learning patterns in a spatial context is discussed.

2.2 Data

Two main data sources are used in this paper. We use the OpenStreetMap project [14] as a source of geographical information, and use the CityBikes API [1] to obtain data about the locations of bicycle-sharing stations around the world. Both are discussed in more detail below.

OpenStreetMap. OpenStreetMap (OSM) is a project in which users collaborate to create a dataset of roads and places that forms the basis of a non-proprietary map of the world. The database consists of four types of entries: nodes, ways, relations and tags. The nodes are single latitude-longitude coordinates indicating, e.g., points of interest or corners of larger areas. Ways are sequences of nodes, denoting paths and polygons that determine, e.g., the shapes of parks and roads. Relations are ordered lists of nodes, ways and other relations, and are used to denote larger geographic entities such as cycling routes or large motorways. The tags are used to store metadata about the other three data types. A tag can be used to, for example, indicate that a node corresponds to a convenience store or highway traffic lights.

We use the OSM database for two purposes. First of all, we use it to identify places that are unsuited for BSS station placement, as we discuss in Sect. 3.1. A second purpose for the OSM database is that we use it to collect data about places of interest. In particular, we are interested in nodes that are tagged as a ‘shop’ or ‘amenity’. Note that the latter category is relatively broad, and includes park benches among others. Still we use this as a way of identifying locations of interest, as we discuss in greater detail in Sect. 4.4. The idea behind this choice is that those locations indicate areas that are interesting from a leisure-oriented point of view.

CityBikes. To obtain data about the station locations of existing BSSs, we use the API for the website citybik.es. The project behind this website started as an Android app named CityBikes which helped users plan journeys in a BSS by displaying information about station occupancies. The data used by the app has been made available through a publicly-accessible API. Their system features information about BSSs worldwide, although we will only consider a fraction of those in this paper.

3 Preliminaries

This section combines several topics underlying all of the BSS station placement algorithms of Sect. 4. The structure of this section is as follows. In Sect. 3.1, we discuss the choice of a target area given that a city has been selected. We discuss ways to denote and characterise a configuration of BSS station locations—from now on referred to as a topology—in this city in Sect. 3.2, and then discuss a generic simulation procedure for generating a BSS in Sect. 3.3.

3.1 Target Areas and Valid Station Placement Locations

Given a choice of city, the first step in obtaining a BSS topology is determining the target area, i.e., the area within the city in which BSS stations can be placed. Initially, this will be (roughly, considering the approximately ellipsoidal shape of the face of the earth) a rectangle $[\lambda _{\min },\lambda _{\max },\phi _{\min },\phi _{\max }]$ where $\lambda _{\min }$ and $\lambda _{\max }$ are the minimum and maximum longitudes respectively and $\phi _{\min }$ and $\phi _{\max }$ the minimum and maximum latitudes. The choice of target area has an impact of the accuracy of the method—as we discuss below, we discretise space by projecting the (approximate) rectangles spanning the city onto pixels in an image file. Since we are limited by memory constraints, there is a trade-off between the zoom level (i.e., how big the rectangles are—smaller rectangles capture more detail) and the size of the target area. Since we compare simulation procedures to existing BSSs in this paper, we choose the initial target areas to match the bounding boxes of the existing BSS’s station locations, with a margin of 1 km added. If one were interested in designing a BSS for a city that does not currently have one, manual selection of a rectangle as a target area, possibly informed by opening OSM in a web browser, would be the most straightforward approach.

Fig. 1.

Original and filtered versions of the OSM map of the target area in Barcelona. The figure on the far right includes the convex hull spanned by 100 m circles around the stations in the Bicing BSS.

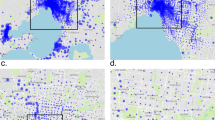
Within a typical initial target area, not all areas will be suited for station placement—particularly bodies of water, parks/forests, and farmland/desert. To identify those areas, we download the pre-generated 256-by-256-pixel tiles used to display OSM maps in a browser. The tiles in the full OSM dataset span the whole world and are generated for each of 20 zoom levels, where level 0 corresponds to capturing the entire face of the planet in a single 256-by-256-pixel tile and each subsequent level zooms in further by a factor 2. Given an initial target area in the form of a rectangle, we first identify the tiles corresponding to this area, and obtain an appropriate zoom level. This is done by specifying a maximum of number of pixels in the final image, and then determining the highest zoom level such that the resulting map still has fewer pixels than the maximum. When this is done, we amalgamate all the needed tiles in a single PNG image file—see Fig. 1a for an example involving the Bicing BSS in Barcelona. Finally, we identify the pixels corresponding to bodies of water in the following way: we identify pixel colours ranges² that tend to correspond to water bodies, then we identify for each pixel whether it falls inside that range, and finally mark a pixel as ‘water’ if there are 8 of those pixels within a circle with a radius of 3 pixels around it. These pixels are marked as blue in the filtered image depicted in Fig. 1b. We apply a similar pictures with green pixels for parks/forests and yellow pixels for desert/farmland. The remaining white pixels are then valid for station placement. An alternative to this approach would be to project the generated station locations onto roads, which would also avoid stations being placed in the middle of a building block. Furthermore, as can be seen in Fig. 2, stations are also sometimes placed in tunnels or on islands (e.g., the Holland Tunnel in New York, and Liberty Island), which is also something that can be avoided. This is currently left as future work as the current filtering procedure is accurate enough for illustrative purposes.

Note that the choice to use the pre-generated tiles means that the image files include place names, which causes some distortions—for example, the names of the hilltops in the top-left corner of Fig. 1a result in small patches of white pixels in the top left corner of Fig. 1b. This could be remedied by rendering the tiles manually using open source software such as, for example, Mapnik³. Again, this is left as future research.

After filtering out the invalid areas, a further refinement would be to exclude areas that are otherwise not part of the target area. For example, the area across the river Besòs in the top-right corner of Fig. 1b is not part of Barcelona but of a neighbouring city (Santa Coloma de Gramenet), and the existing BSS does not cover this area even though its city centre would have a fairly large attractiveness rating (as per Sect. 4.4). Hence, we restrict the target area further by instead considering the convex hull spanned by the 100 m areas around the existing BSS stations (in the discretised pixel map). Without this step, several simulation techniques would do considerably worse, in particular the regular grid of Sect. 4.1 and the Poisson point process of Sect. 4.2.

3.2 Topology and Characteristics

A BSS topology can be characterised in many different ways: here, we only discuss characteristics that are purely spatial. A complete spatial characterisation of a BSS topology with N stations is a set of points

$$ (\mathbf {\gamma }_1,\mathbf {\gamma }_2,\ldots ,\mathbf {\gamma }_N) = \left( (\phi _1,\lambda _1), (\phi _2,\lambda _2), \ldots , (\phi _N,\lambda _N)\right) , $$

where $\phi _i$ is the latitude of station i and $\lambda _i$ its longitude. Since we are mostly interested in these locations as projected onto a map of $I \times J$ pixels (see Sect. 3.1), we will also consider

$$ (\mathbf {c}_1,\mathbf {c}_2,\ldots ,\mathbf {c}_N) = \left( (x_1,y_1), (x_2,y_2), \ldots , (x_N,y_N)\right) $$

where

$$ x_i = \left\lfloor J \frac{\lambda _i - \lambda _{\min }}{\lambda _{\max } - \lambda _{\min }} \right\rfloor \;\text {and}\; y_i = \left\lfloor I \frac{\phi _i - \phi _{\min }}{\phi _{\max } - \phi _{\min }} \right\rfloor $$

We choose the centre point $\mathbf {c}_0 = (x_0, y_0)$ of the BSS to be the point

$$ \left( \frac{1}{N} \sum _{i=1}^N x_i, \frac{1}{N} \sum _{j=1}^N y_j\right) . $$

If an existing topology is not available one can alternatively take $(\lfloor J/2 \rfloor , \lfloor I/2 \rfloor )$.

Given two stations’ latitude/longitude coordinates $\gamma _i = (\phi _i,\lambda _i)$ and $\gamma _j = (\phi _j,\lambda _j)$, the distance between them is given by the Haversine formula, computed as

$$\begin{aligned} d(\mathbf {\gamma _i}, \mathbf {\gamma }_j) = 2 R \arcsin \left( \sqrt{\sin ^2\left( \frac{\varDelta \phi }{2}\right) + \cos (\phi _i) \cos (\phi _j) \sin ^2\left( \frac{\varDelta \lambda }{2}\right) } \right) , \end{aligned}$$

(1)

where $\varDelta \phi = \phi _j - \phi _i$, $\varDelta \lambda = \lambda _j - \lambda _i$, and R is the radius of the earth, i.e., approximately $6\,371$ km.

In Sect. 5, we discuss several more abstract metrics that characterise station topologies, all of which involving the distance between stations. In particular, we will consider the following two measures from [21]:

• $\overline{\delta }$: the average distance over all stations of the distance from a station to its nearest neighbour, given by

  $$ \delta _i = \min _{\begin{array}{c} j \in \{1,\ldots ,N\} \\ j \ne i \end{array}} d(\mathbf {\gamma }_i, \mathbf {\gamma }_j), \text { and} $$

• the compactness ratio: the ratio between the area of the convex hull to that of a circle with the same circumference.

Additionally, we use the following measures:

• $\sigma _\delta$: the standard deviation of the nearest neighbour distances,

• $\bar{t}$: the average edge length in the (Euclidean) minimum spanning tree of all the station locations, and

• $\max _{t}$: the maximum edge length in the (Euclidean) minimum spanning tree of all the station locations.

We consider the minimum spanning tree to identify BSSs that are ‘disconnected’ is the sense that there exist clusters of stations such that the stations within the clusters may be close together but the clusters themselves are far apart—this information is not captured by the nearest-neighbour distance $\delta$.

3.3 Simulation Methodology

As mentioned earlier, we consider a city map consisting of $I \times J$ pixels, with I representing the height of the image file and J the width. The final number N of stations is assumed to be fixed a priori, and equal to the size of the city’s existing BSS in Sect. 5. Each pixel corresponds to a (roughly) rectangular area in the city. The first step of the procedure is to assign to each pixel i, j a probability weight $w_{ij}$, with a higher weight corresponding to a larger probability of being selected. We also define $\forall i \in \{1,\ldots ,I\}, j \in \{1,\ldots ,J\}$, the cumulative weights

We then generate a (pseudo-)random number u on [0, 1) using (for example) Java’s built-in random number generator, and find the first pixel for which $c_{ij} / c_{IJ} > u$. The centre of the rectangle corresponding to this pixel is then selected as the next station’s location. We repeat this procedure until we have N stations, and allow the weights to change depending on the locations of the previously sampled stations. For specific applications, this is not necessarily the most efficient procedure, but its appeal is its generality—we apply this procedure for all procedures except the deterministic procedure of Sect. 4.1. In Sect. 4, we discuss various ways to obtain weights $w_{ij}$. Note that although these processes are typically treated as continuous-space processes in the literature, we evaluate their probabilities on the discrete grid of the pixel map.

4 Topology Generation Models

In this section we discuss the procedure for obtaining station configurations. We discuss four methods: the regular grid (Sect. 4.1), the Poisson point process (Sect. 4.2), the Ginibre point process (Sect. 4.3) and the rating-weighted Poisson process (Sect. 4.4). All procedures except the first can be fully described in terms of the weights $w_{ij}$ that inform the simulation methodology of Sect. 3.3.

4.1 Regular Grid

The idea behind the regular grid is straightforward: we place the stations on a square or hexagonal grid in order to optimise the coverage of the target areas. In principle, this means that each station has 4 or 6 nearest neighbours, with distances $\delta$ usually the same across all stations (this is typically not true due to the presence of invalid areas such as water bodies and parks). Given a choice for a square or hexagonal grid, a BSS topology can be defined uniquely using a single value for $\delta$ if we require that a station must be placed at the centre point $(x_0, y_0)$. The question is then how to choose $\delta$ such that there are N stations in the target area. A complication here is the fact that we want to avoid placing stations in the invalid locations discussed in Sect. 3.1. One possibility is an approach based on bisection: we initialise $\delta _{\max }$ to be some large value (e.g., the length of the diagonal in the bounding box of the target area) and initialise $\delta _{\min } = 0$, then check how many stations are placed within the target area for

$$ \delta = \frac{1}{2} (\delta _{\max } - \delta _{\min }). $$

If this number is too large, we set $\delta _{\max } = \frac{1}{2} (\delta _{\max } - \delta _{\min })$, else set $\delta _{\min } = \frac{1}{2} (\delta _{\max } - \delta _{\min })$ and repeat until the new value of $\delta$ yields exactly N stations. One complication is that if the target area is not convex, N is not monotonously decreasing as a function of $\delta$. Even if we use the convex hull to narrow the target area as displayed in Fig. 1c, the exclusion of invalid areas such as water bodies will often result in non-convexity. Hence, this approach is approximative at best. When this is finished it is possible to add random noise (e.g., Gaussian noise) to make the topology look less artificial (we will not do this in Sect. 5).

4.2 Poisson Point Process

The Poisson point process is the most straightforward simulation procedure—the idea is to draw station locations uniformly within the target area. In terms of the procedure of Sect. 3.3, this amounts to fixing a constant $k > 0$ and setting $w_{ij} \equiv k$ $\forall i \in \{1,\ldots ,I\}, j \in \{1,\ldots ,J\}$. In continuous space, this approach is called the Poisson point process because the ordered sequence of longitudes forms a realisation of a Poisson process conditional on it having N points within the box, and similarly for the latitudes. To avoid stations being drawn outside the target area or in invalid locations (as discussed in Sect. 3.1), we set $w_{ij}$ to zero for each point (i, j) corresponding to such a pixel. This results in a Poisson process that is inhomogeneous across the bounding box. In fact, the two approaches in the remainder of Sect. 4 can also be seen as discrete versions of inhomogeneous Poisson point processes.

4.3 Ginibre Point Process

The origins of the Ginibre point process lie in physics, where it is used to model the locations of particles in a cloud. It has recently been applied in the context of telecommunications systems, namely to model locations of base stations in a cellular network [19]. It can be defined iteratively using the following density (see, e.g., [6]):

$$\begin{aligned} f(\mathbf {z}_k|\mathbf {z}_{k-1}\ldots \mathbf {z}_1) = \frac{1}{k!} \cdot {\frac{1}{\pi } e^{-|\mathbf {z}_k|^2}} \cdot {\prod _{j=1}^{k-1} |\mathbf {z}_k - \mathbf {z}_j|^2} \end{aligned}$$

(2)

Generating a sample $(\mathbf {z}_1,\ldots ,\mathbf {z}_N)$ from the standard Ginibre point process is straightforward: let A and B be $N\times N$ matrices filled with realisations of random variables with a normal distribution with mean 0 and variance $\frac{1}{2}$. Then if $\lambda _1,\ldots ,\lambda _N$ are the eigenvalues of the complex matrix $A+ i B$, then

(3)

is a realisation of the standard Ginibre point process. It is scale-invariant: multiplying the points of a standard Ginibre point process by a constant yields a Ginibre point process generated by normally distributed random variables with a different variance. Again, we do not want stations to be placed in rivers or farmland. Our approach is to use (2) to inform the weights $w_{ij}$, setting $w_{ij}$ to zero for invalid pixels. An alternative approach would be to draw, using (3), a topology of size larger than N, and try to find a scale such that N stations are within the target area and in valid areas. However, this approach does not fit into our general methodology. Note that the procedure based on (2) can be computationally expensive compared to one based on (3) as the weights have to be recomputed each time a station is drawn. This is done efficiently by multiplying the elements of the current matrix by a factor that depends on the distance between each pixel and the station location sampled in the current iteration.

4.4 Rating-Weighted Scheme

The idea behind this approach is to incorporate geographical information into the weights. This is done in the following way. We use a matrix $\rho _{ij}$ to denote the attractiveness of pixel (i, j)—this is initially set to 0. We then download a list of amenities and shops in the target area from the OSM website as discussed in Sect. 2.2. This is followed by going through this list and increasing $\rho _{ij}$ by 5 if the Euclidean distance between the location of the element of the list and the centre of the rectangle corresponding to pixel i, j is smaller than 50 m—if this distance is between 50 and 200 m we increase $\rho _{ij}$ by 2, and if it is between 200 and 1000 m we increase $\rho _{ij}$ by 1. Of course, this is but one of many ways to incorporate the information in the list of places.

Additionally, inspired by the Ginibre point process we will also discourage stations being placed within close proximity of each other. Given that n station locations have already been drawn, let $\gamma _{ij}$ be the latitude-longitude coordinate corresponding to the centre of pixel (i, j)—we then set

$$ w_{ij} = \rho _{ij} \prod _{k = 1}^n\left( 1 - \exp \left( \frac{-(d(\mathbf {\gamma }_{ij}, \mathbf {\gamma }_{k}))^2}{\sigma }\right) \right) . $$

Like the Ginibre approach, this approach can be computationally expensive: the rating needs to be computed for each pixel, and if we want to let the rating depend on the locations of the stations sampled thus far (to avoid clustering), we need to recompute it after each successful sample. Efficiency can be improved by aggregating pixels, or by using an estimate of $\rho _{\max }$ rather than the exact value.

5 Analysis and Results

In this section we will provide an overview of simulation experiments done using the methodology presented earlier. The case study will feature a selection of 11 cities. The difference between the methods and the real systems will be illustrated using several metrics, to be discussed below.

We begin with an overview of the characteristics discussed in Sect. 3.2 for a number of cities, presented in Table 1. We have made a selection from the close to 400 BSSs available on the citybik.es website, based on a number of basic metrics. First of all, the BSSs of Barcelona, Paris, London, and New York were considered because of their (large) size. Furthermore, the New York BSS has the interesting property that the station density is much higher in Manhattan and Brooklyn than in New Jersey. Brussels has a very compact BSS, whereas Nice is much more strip-like, as evidenced by the high and low compactness ratios respectively. Melbourne has a very disconnected BSS, with several southern stations that are very far away from the others, as evidenced by its large value for $\max _{t}$, the largest edge length in the minimum spanning tree. Finally, we also include Dublin, Glasgow, Pisa and Tel Aviv.

In general, there is some degree of variety in terms of the inter-spacing, as evidenced by $\bar{\delta }$ and $\bar{t}$, which are strongly correlated. For example, the average distance to the nearest other station is twice as high in Brussels as it is in London and Paris. There are also considerable differences between the ratios of $\sigma _{\delta }$ to $\bar{\delta }$, and indication of the standard deviation relative to the mean. For Brussels this ratio is very low (about $\frac{1}{3}$), and much higher for Nice (about $\frac{2}{3}$), meaning that the stations are more evenly spread out in Brussels than they are in Nice. This is also evident if one compares Fig. 2a–b.

Table 1. Comparison of the systems under consideration in terms of the characteristics discussed in Sect. 3.2.

In Tables 2 and 3, we compare the performance of the topology generation methods in terms of the degree to which their results match the real systems across a range of simulation experiments. In particular, this is done using two different metrics: the coverage overlap and the mean absolute difference. The former metric (the coverage overlap) is calculated as follows: given a city, a coverage radius D, and a topology generation method, we apply the following procedure in each simulation run: we create an image such that each pixel corresponding to an area within D meters of a generated BSS station is marked as ‘covered’ (e.g., by colouring it pink as in Fig. 2). We also do that for the original BSS, and then check for how many pixels within the target area (the convex hull mentioned earlier, minus the invalid areas) the original and generated BSS give the same result. This is divided by the total number of pixels in this target area to give an overlap score. A comparison in terms of this metric is done in Table 2, for a radius D of 200 m.

For the latter metric (the mean absolute difference), we compute a coverage ‘score’ for each pixel based on how many stations are in its vicinity. In particular, each station adds a score of 5 to all pixels whose centre is at most 50 m away from it, a score of 2 to all pixels between 50 and 200 m and a score of 1 to all pixels between 200 m and 1 km. The metric is then computed as the absolute difference between the scores for the real system and the generated one, averaged over all pixels (again restricted to the target area). The results in terms of this metric are displayed in Table 3.

In both tables, the numbers are the averages of 10 of such scores, ${\pm }1.96 {\times }$ the standard deviation of the estimator, which gives a rough indication of the accuracy of the estimates in terms of a (rough) 95% confidence interval. Note that high scores are desirable for the coverage overlaps, whereas low values are desirable for the mean absolute differences. The methods which yielded the best results for a given city have been made bold in both tables.

Table 2. Comparison of the topology generation methodologies in terms of coverage overlap as discussed in Sect. 5. High values indicate a large overlap—the best-performing methods are marked in bold for each city.

Table 3. Comparison of the topology generation methodologies in terms of the mean absolute difference as discussed in Sect. 5. Low values indicate a small difference—the best-performing methods are marked in bold for each city.

Fig. 2.

Left to right: Nice, Brussels, New York. Top to bottom: real system, regular grid (without noise), Poisson, Ginibre, rating-weighted.

For the 200 m coverage overlaps, the rating-weighted scheme is nearly always the best choice, with Barcelona, Dublin, and Pisa the only exceptions. One possible explanation for the low overlap in Dublin is that its BSS is more commuting- than leisure-oriented. The regular grid does fairly well in all cases. For the mean absolute difference, the rating-weighted method is the best choice in all cases, although in many cases (e.g., Melbourne and Pisa) the difference between the regular grid and the rating-weighted scheme is small. The rating-weighted scheme is particularly good in cities where the BSS stations are more unevenly distributed across the city, like New York and Nice. The rating-based scheme also does reasonably well for London, Paris and Tel Aviv. It should be noted that there is still substantial room for parameter tuning for some methods (particularly Ginibre).

6 Conclusions

In this paper, we have introduced a new approach for generating station topologies. Of the four methods proposed, the one whose generated topologies matched the existing systems in the best manner was the data-driven approach, in which areas of the city were ‘rated’ according to popularity.

In future work, we are planning to compare the simulation results to ‘optimal’ results obtained by the deterministic optimisation methods discussed in Sect. 2.1, e.g., the ones presented in [10]. We are also planning to consider a broader variety of rating methods: e.g., closeness to railway stations for a commuting-oriented BSS, or greater weight to landmarks for a tourism-oriented system. Additionally, we hope to link our methodology to bike movement models: classifying stations in terms of their typical usage behaviour (e.g., during peak hours or weekends) based on their location. The programming code used for the experiments will be posted online in the near future. Finally, there are some minor adjustments mentioned in the texts: e.g., generating bespoke OSM tiles using Mapnik, or projecting station locations onto roads.