An Erlang-Coxian-Based Method for Modeling Accelerated Life Testing Data

Abstract

Accelerated life testing (ALT) can be used to expedite failures of a product for predicting the product’s reliability under the normal operating conditions. The resulting ALT data are often modeled by a probability distribution along with a life-stress relationship. However, if the selected probability distribution cannot adequately describe the underlying failure process, the resulting reliability prediction would be misleading. It would be quite valuable if the distribution providing an adequate fit to the ALT data can be determined automatically. This chapter provides a new analytical method to assist reliability engineers in this regard. Essentially, this method uses Erlang-Coxian (EC) distributions, which belong to a particular subset of phase-type distributions, to characterize ALT data. Such distributions are quite efficient for approximating many non-negative distributions, such as Weibull, lognormal and gamma. The advantage of this method is that the best fit to the ALT data can be obtained by gradually changing the model structure, i.e., the number of phases of the associated continuous-time Markov chain (CTMC). To facilitate the implementation of this method, two statistical inference approaches are provided. First, a mathematical programming approach is formulated to simultaneously match the moments of the EC-based ALT model to the empirical moments at the corresponding test stress levels. This approach resolves the feasibility issue of the method of moments. In addition, the maximum likelihood estimation approach is presented, which can easily handle different types of censoring in ALT. Both approaches are accompanied with a stopping criterion for determining the number of phases of the resulting CTMC. Moreover, nonparametric bootstrap method is used to construct the pointwise confidence interval for the resulting reliability estimates. Numerical examples for constant-stress ALT with Type-I and multiple censoring schemes are provided to illustrate the capability of the method in modeling ALT data.

1 Introduction

As technology advances, new products can be made quite reliable. For such a product, it is difficult, if not impossible, to observe failures in a short time period under the product’s normal operating conditions. Accelerated life testing (ALT) has been widely used in industry as a viable tool for estimating the long-term reliability of such a product. The basic idea of ALT is to expose some units of the product to harsher-than-normal operating conditions to expedite failures. Based on the resulting failure time data due to acceleration, a statistical model is developed and used to extrapolate the product’s long-term reliability under the normal operating conditions.

Nonparametric methods are practical choices for estimating the reliability of a product without assuming the underlying failure time distribution. The most popular ones are the Kaplan-Meier estimator and Breslow estimator [21]. However, it is difficult to extend these methods for developing ALT models which require the inclusion of various life-stress relationships for extrapolation in time and stresses. As a result, the most popular methods in modeling ALT data are to develop parametric models based on specified probability distributions with stress-dependent parameters. Such methods, if properly applied, are quite efficient, and the related statistical inference procedures, such as maximum likelihood estimation (MLE) and least squares estimation (LSE), have been extensively studied and made available to practitioners [9, 21, 23, 37].

Accelerated failure time (AFT) models are probably the most widely used parametric ALT models. Mathematically, an AFT model for the cumulative distribution function (Cdf) $F\left( {t;Z} \right)$ of failure time under a constant stress Z can be expressed as [3]:

$$ F\left( {t;Z} \right) = 1 - R\left( {t;Z} \right) = F_{0} (r(Z;\underline{\theta } )t), $$

(11.1)

where $R\left( {\text{t; Z}} \right)$ is the corresponding reliability function, $F_{0} ( \cdot )$ is the baseline Cdf, and $r(Z;\underline{\theta } )$ is a deterministic function of Z. The model can also be expressed in terms of the corresponding hazard function as:

$$ h\left( {t;Z} \right) = h_{0} (r(Z;\underline{\theta } )t)r(Z;\underline{\theta } ), $$

(11.2)

where $h_{0} ( \cdot )$ is the corresponding baseline hazard function.

When using AFT models for reliability prediction, practitioners often face the challenge of choosing a probability distribution that provides an adequate fit to the collected ALT data. To determine the best model from several candidates, the likelihood values or residual plots (e.g., Cox-Snell residuals) of these ALT models can be considered. For relevant methods of goodness-of-fit tests, readers are referred to Bagdonavičius and Nikulin [3]. Regarding more general ALT models, Elsayed et al. [11] proposed the extended linear hazard regression model that is capable of modeling various ALT data and includes many ALT models as special cases. However, all these methods require the baseline Cdf’s (or equivalently the baseline hazard functions) to be pre-specified. To assist engineers in modeling ALT data, a generic method using a collection of versatile distributions would be desirable for a wide range of engineering applications. It would be more attractive if the distribution providing the best fit to the ALT data can be determined adaptively.

Because the versatility of phase-type (PH) distributions naturally meets broad requirements for parametric modeling of failure time data, we propose a generic method using a specific and yet flexible subset of PH distributions, called Erlang-Coxian (EC) distributions [28], to model ALT data. Both mathematical programming and MLE approaches are developed for statistical inference. The contribution of this generic method to the body of ALT literature is twofold. First, the use of EC distributions relaxes strong assumptions about the underlying failure time distributions in developing AFT models. Moreover, the method is able to achieve the best fit to the ALT data under a stopping criterion by adaptively adjusting the number of phases of the associated continuous-time Markov chain (CTMC).

The remainder of this chapter is organized as follows. Section 11.2 briefly reviews the literature on ALT models and PH distributions. Section 11.3 introduces the EC distributions and provides the mathematical formulation of the proposed EC-based ALT model. The mathematical programming and MLE approaches to the estimation of model parameters are presented in Sect. 11.4. Two simulation examples and a case study are provided in Sect. 11.5 to illustrate the capability of the EC-based ALT model for modeling ALT data. Finally, Sect. 11.6 concludes this chapter.

2 Literature Review

Among various probability distributions, the exponential distribution has been widely used in modeling ALT data. Typical examples include the models developed by Lawless and Singhal [16], Bai et al. [5], Bai and Chung [4], and Xiong [36]. The obvious limitation of the exponential distribution is that it can only be used for products with constant failure rates. To predict the reliability of a product with time-dependent failure rate, Nelson [22], Meeker [20], Bhattacharyya and Soejoeti [6], and Tang et al. [34] considered the Weibull distribution and different stress loadings used in ALT experiments. Moreover, Kielpinski and Nelson [15] developed ALT models based on the lognormal distribution and studied the optimum test plans. Doksum and Hóyland [7], and Onar and Padgett [27] used the inverse Gaussian distribution as the underlying distribution for ALT data. For testing of hypotheses for different distributions and thorough literature reviews of ALT models, readers are referred to Sethuraman and Singpurwalla [33], Escobar and Meeker [12], and Elsayed [10]. Despite these guidelines, choosing adequate distributions to fit ALT data is still a challenging task faced by engineers, and sometimes the underlying distributions are quite complex or even unknown.

It would be useful if a collection of probability distributions can be used to approximate those popular or even complex distributions arbitrarily closely so that choosing adequate distributions for ALT analysis can be circumvented. Indeed, PH distributions are quite versatile, which can be used for this purpose. Van Der Heijden [35] derived the lower and upper bounds on the third moment of a positive random variable when the squared coefficient of variation is between 0.5 and 1, and characterized the two-phase Coxian distributions that correspond to these bounds. Asmussen et al. [2] studied MLE for fitting PH distributions. An extended expectation-maximization (EM) algorithm was developed to minimize the information divergence in the density approximation case. Olsson [26] developed an EM algorithm to estimate the parameters of a PH distribution with fixed order from right-censored and interval-censored data. Riska et al. [30] developed a method to efficiently fit a long-tailed data set by partitioning the data set and fitting each partition into a hyperexponential distribution using an EM algorithm. Osogami and Harchol-Balter [28] provided closed-form solutions for mapping general distributions to quasi-minimal PH distributions (EC distributions) by matching their first three moments. In the field of reliability engineering, PH distributions have been used in modeling repairable systems. Sericola [32] proposed an algorithm to compute the interval availability of a system where a two-state semi-Markov process was used to model the system. An exponential distribution and a PH distribution were assumed for the operational and nonoperational state, respectively. Perez-Ocon and Montoro-Cazorla [29] studied the transient behavior of a system with operational and repair times following PH distributions. Moreover, Ruiz-Castro et al. [31] studied the availability and conditional failure probabilities for different types of failures of a multi-component system subject to internal and external repairable (or non-repairable) failures where the corresponding random times follow PH distributions.

The brief literature review indicates that PH distributions have not been used in modeling ALT data. To the best of our knowledge, this chapter demonstrates, for the first time, the potential of using PH distributions for ALT data analysis. Although the proposed model is developed based on a specific PH distribution, the concept and statistical estimation methods can be naturally extended to other types of PH models.

3 Mathematical Formulation of an EC-Based ALT Model

A PH distribution describes the time to absorption of a CTMC defined on a finite-state space [1]. Figure 11.1 shows two examples, where the time until absorption to the respective absorbing state in each CTMC can be characterized by a PH distribution. Essentially, such a CTMC with the specific structure can be described by an infinitesimal generator matrix:

Fig. 11.1

CTMCs whose absorption times define two different phase-type distributions

$$ {\mathbf{Q}} = \left[ {\begin{array}{*{20}c} 0 & {\mathbf{0}} \\ {\varvec{S}^{0} } & \varvec{S} \\ \end{array} } \right], $$

(11.3)

where S is the subgenerator matrix consisting of the transition rates among transient states and the ones for transitions into the absorbing state, and $\varvec{S}^{0} = - \varvec{S}1$ in which ${\mathbf{1}} = (1,1, \ldots ,1)^{'}$ is a column vector of 1’s of appropriate dimensions.

Let T be the time to absorption of a k-phase CTMC and ${\varvec{\uppi}} = (\pi_{1} ,\pi_{{\mathbf{2}}} , \ldots ,\pi_{k} )$ be the initial distribution of the CTMC. The Cdf of T can be expressed as:

$$ F\left( t \right) = 1 - R(t) = 1 - {\varvec{\uppi}}\;\exp \left\{ {\text{t}\varvec{S}} \right\}{\mathbf{1}},\quad t \ge 0 $$

(11.4)

where $\exp \left\{ {t\varvec{S}} \right\}$ is matrix exponential defined as:

$$ \exp \left\{ {t\varvec{S}} \right\} = \mathop \sum \limits_{k = 0}^{\infty } \frac{1}{k!}(t\varvec{S})^{k} . $$

(11.5)

The corresponding probability density function (pdf) is:

$$ f\left( t \right) = {\varvec{\uppi}}\, \text{exp}\left\{ {t\varvec{S}} \right\}\varvec{ S}^{{\mathbf{0}}} ,t \ge 0$$

(11.6)

and the hazard function is given by:

$$ h\left( t \right) = f(t)/(1 - F(t)) = {\varvec{\uppi}}\exp \{ t\varvec{S}\} \varvec{S}^{0} /({\varvec{\uppi}}\exp \{ t\varvec{S}\} 1), t{ \ge }0. $$

(11.7)

In addition, the lth moment of the distribution can be expressed as:

$$ E[T^{l} ] = ( - 1)^{l} l!{\varvec{\uppi}}\,\varvec{S}^{ - l} {\mathbf{1}}. $$

(11.8)

For examples, the CTMC in Fig. 11.1a results in a three-phase Erlang distribution $E(3,\lambda )$ with:

$$ {\varvec{\uppi}} = (\uppi_{1} ,0,0)\;{\text{and}}\;\varvec{S} = \left[ {\begin{array}{*{20}c} { - \lambda } \\ 0 \\ 0 \\ \end{array} \begin{array}{*{20}c} \lambda \\ { - \lambda } \\ 0 \\ \end{array} \begin{array}{*{20}c} 0 \\ \lambda \\ { - \lambda } \\ \end{array} } \right], $$

and the one in Fig. 11.1b gives a three-phase Coxian distribution $C(\lambda_{1} ,\lambda_{2} ,\lambda_{3} ,p_{1} ,p_{2} )$ with:

$$ {\varvec{\uppi}} = (\uppi_{1} ,0,0)\;{\text{and}}\;\varvec{S} = \left[ {\begin{array}{*{20}c} { - \lambda_{1} } \\ 0 \\ 0 \\ \end{array} \begin{array}{*{20}c} { p_{1} \lambda_{1} } \\ { - \lambda_{2} } \\ 0 \\ \end{array} \begin{array}{*{20}c} 0 \\ { p_{2} \lambda_{2} } \\ { - \lambda_{3} } \\ \end{array} } \right], $$

where $0 < p_{i} \le 1$, $i = 1,2$.

One of the most attractive properties of PH distributions is that the set of PH distributions is dense in the set of nonnegative distributions [24]. In other words, in theory, any nonnegative distribution can be approximated arbitrarily closely by a PH distribution. The only limitation is that PH distributions are light-tailed, thus may not be used as effective models for heavy-tailed distributions. Among different subsets of PH distributions, Erlang distributions and Coxian distributions are probably the most popular ones. They have been extensively studied in queueing theory and widely used in healthcare such as survival analysis and modeling the length of stay of patients in a hospital [18, 19].

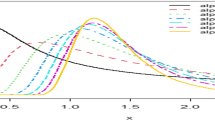
An important aspect of mapping a general distribution to a PH distribution is to select the type and the number of phases of the corresponding CTMC. For example, for a data set (see Fig. 11.2a) generated from the Weibull(η = 1200, β = 1.5) distribution, a three-phase Erlang distribution $E(3,\widehat{\lambda } = 0.0026344)$ can be obtained through an MLE approach, and the corresponding log-likelihood value is 76.91. A three-phase Coxian:

Fig. 11.2

Example for Weibull (η = 1200, β = 1.5)

$$ C(\widehat{\lambda }_{1} = 0.00176, \widehat{\lambda }_{2} = 0.00176, \widehat{\lambda }_{3} = 41.20788, \widehat{p}_{1} = 1, \widehat{p}_{2} = 1) $$

can also be obtained with log-likelihood value of 77.79. Obviously, the three-phase Coxian distribution, which turns out to be a hypoexponential distribution, provides a better fit (see Fig. 11.2b).

Before addressing the proposed EC-based ALT model, we first introduce the following definitions regarding the determination of a subset of PH distributions under certain estimation accuracy requirements [28].

Definition 1

Let $E\text{[X}^{l} ]$ be the lth moment of random variable X with distribution G. The normalized lth moment $m_{l}^{G}$ of X for l = 2,3 is defined as: $m_{2}^{G} = \frac{{E[X^{2} ]}}{{(E[X])^{2} }}$ and $m_{3}^{G} = \frac{{E[X^{3} ]}}{{E\left[ X \right]E[X^{2} ]}}$.

Definition 2

A distribution G is well represented by a distribution F if F and G agree on their first three moments. PH ₃ refers to the distributions that are well represented by a PH distribution.

It is well known that a distribution G is in PH ₃ if and only if its normalized moments satisfy $m_{3}^{G} > m_{2}^{G} \text{ > }1$ [14]. Since any nonnegative random variable with distribution G satisfies $m_{3}^{G} { \ge }m_{2}^{G} { \ge }1$, almost all such distributions are in PH ₃.

Osogami and Harchol-Balter [28] introduced EC distributions that are quite efficient for approximating PH ₃ distributions. Figure 11.3 shows the CTMC for a k-phase EC distribution ($k{ \ge }3$), which consists of an Erlang $E(k - 2,\lambda_{1} )$ with k-2 phases and a two-phase Coxian $C(\lambda_{2} ,\lambda_{3} ,p_{c} )$, for which:

Fig. 11.3

CTMC whose absorption time defines a k-phase EC distribution

$$ {\varvec{\uppi}} = (\underbrace {{{\varvec{\uppi}}_{1} ,0, \ldots ,0}}_{{}})\;{\text{and}}\,\varvec{S} = \left[ {\begin{array}{*{20}c} { - \lambda_{1} } & {\lambda_{1} } & 0 & {} & \cdots & {} & 0 \\ 0 & { - \lambda_{1} } & {\lambda_{1} } & 0 & {} & 0 & {} \\ \vdots & 0 & { - \lambda_{1} } & \ddots & \ddots & {} & \vdots \\ {} & {} & 0 & \ddots & {\lambda_{1} } & 0 & {} \\ \vdots & {} & {} & \ddots & { - \lambda_{1} } & {\lambda_{1} } & 0 \\ {} & 0 & {} & {} & 0 & { - \lambda_{2} } & {p_{c} \lambda_{2} } \\ 0 & \cdots & {} & \cdots & {} & 0 & { - \lambda_{3} } \\ \end{array} } \right]. $$

(11.9)

The idea of creating an EC distribution is that a two-phase Coxian distribution can well represent any distribution that has high second and third moments while an Erlang distribution has only two free parameters and has the least normalized second moment among all the PH distributions with a fixed number of phases. Therefore, such a k-phase EC distribution can represent probability distributions in a wide range of variability using only a small number of phases. This is quite important in developing an ALT model, which needs additional parameters for quantifying the life-stress relationship.

Following Eqs. (11.1) and (11.4), the proposed EC-based ALT model (essentially an AFT model) for a product’s failure time under stress level Z can be expressed as:

$$ F\left( {t;Z} \right) = F_{0} \left( {r\left( {Z;\underline{\theta } } \right)t} \right) = 1 - {\varvec{\uppi}}\;\exp \left\{ {r\left( {Z;\underline{\theta } } \right)t\varvec{S}} \right\}{\mathbf{1}},\quad t \ge 0, $$

(11.10)

where $\varvec{S}$ is given in Eq. (11.9), and ${\varvec{\uppi}}$ is set to be $(1,0, \ldots ,0)$ throughout this chapter.

The corresponding pdf is given by:

$$ f\left( {t;Z} \right) = r\left( {Z;\underline{\theta } } \right){\varvec{\uppi}}\;{ \exp }\left\{ {r\left( {Z;\underline{\theta } } \right)t\,\varvec{S}} \right\}\;\varvec{S}^{{\mathbf{0}}} ,\quad t \ge 0, $$

(11.11)

and the hazard function is:

$$ h\left( {t;Z} \right) = r\left( {Z;\underline{\theta } } \right){\varvec{\uppi}}\;\exp \{ r\left( {Z;\underline{\theta } } \right)t\varvec{S}\} \varvec{S}^{0} /({\varvec{\uppi}}\exp \{ r\left( {Z;\underline{\theta } } \right)t\varvec{S}\} {\mathbf{1}}),\quad t \ge 0. $$

(11.12)

In addition, the corresponding lth moment under stress level Z can be expressed as:

$$ E[T_{Z}^{l} ] = \left( { - 1} \right)^{l} \left( {r(Z;\underline{\theta } )} \right)^{ - l} l!{\varvec{\uppi}}\,\varvec{S}^{ - l} {\mathbf{1}}. $$

(11.13)

To use such an EC-based ALT model in practice, it is necessary to determine the number of phases of the EC distribution adaptively based on the collected ALT data and estimate all the parameters. Effective solutions to these issues will make the proposed model more flexible in fitting ALT data than existing parametric models.

4 Statistical Inference Methods

This section addresses two statistical inference methods for estimating the parameters $\underline{\Theta } = [\lambda_{1} ,\lambda_{2} ,\lambda_{3} ,p_{c} ,\underline{\theta } ]$ of an EC-based ALT model. In particular, a constant-stress ALT experiment with Type-I censoring is considered. Let $\tau_{i}$ be the censoring time under stress level $Z_{i}$, $i = 1,2, \ldots ,m$, $n_{i}$ be the total number of units tested under $Z_{i}$, $t_{ij}$ be the recorded failure/censoring time of unit j tested under $Z_{i}$.

4.1 Use of Mathematical Programming

For complete ALT data, the lth empirical moment of failure times under stress level $Z_{i}$ can be calculated by: $M_{l}^{i} = (1/n_{i} )\sum\nolimits_{j = 1}^{{n_{i} }} {t_{ij}^{l} }$. For the case of Type-I censoring, the corresponding empirical moments can be calculated using the idea of data augmentation [25]:

$$ M_{l}^{i} = \frac{1}{{n_{i} }}\left[ {\sum\limits_{j = 1}^{{n_{i} }} {\left( {\delta_{ij}^{{[0,\tau_{i} ]}} t_{ij}^{l} + (1 - \delta_{ij}^{{[0,\tau_{i} ]}} )\left( {\tau_{i} + \int_{0}^{\infty } {\frac{{1 - F(x + \tau_{i} ;Z_{i} )}}{{1 - F(\tau_{i} ;Z_{i} )}}dx} } \right)^{l} } \right)} } \right], $$

(11.14)

where,

$\updelta_{ij}^{{[0,\tau_{i} ]}} = \{ 1,\;{\text{if}}\;t_{ij} < \tau_{i} ;0,\;{\text{otherwise}}\}$, $\int_{0}^{\infty } {\left[ {1 - F(x + \tau_{i} ;Z_{i} )} \right]/\left[ {1 - F(\tau_{i} ;Z_{i} )} \right]dx}$ is the mean residual life of a unit tested under $Z_{i}$ and censored at time $\tau_{i}$, and $F( \bullet ;Z_{i} )$ is given by Eq. (11.10).

The traditional method of moments set several population moments equal to the corresponding empirical moments and solve those equations simultaneously for the model parameters. To overcome the feasibility issue of this method by allowing deviations, the mathematical formulation for determining the matching EC-based ALT model with the least number of phases (i.e., k) can be expressed as a mathematical programming problem (P₁):

$$ \begin{array}{*{20}l} { ( {\text{P}}_{ 1} )} & {\mathop {\hbox{min} }\limits_{k} }\qquad\qquad\qquad k & {} & {} \\ { ( {\text{SP}}_{ 1} )} & {\begin{array}{*{20}c} { \hbox{min} } \\ {\underline{\theta } ,\lambda_{1} ,\lambda_{2} ,\lambda_{3} ,p_{c} } \\ {\{ s_{i,l} ,\varepsilon_{i,l} \} ,i \in \{ 1, \ldots ,M\} ,l \in \{ 1,2,3\} } \\ \end{array} } \quad {g_{k} = \sum\limits_{i = 1}^{M} {\sum\limits_{l = 1}^{3} {\left( {\omega_{i,l}^{(1)} s_{i,l} + \omega_{i,l}^{(2)} \varepsilon_{i,l} } \right)} } } & {} & {} \\ {} & {{\text{Subject}}\;{\text{to}}} & {} & {} & {} \\ {} & {\frac{{ - (r(Z_{i} ;\underline{\theta } ))^{ - 1} 1!\varvec{\pi S}^{ - 1} {\mathbf{1}} - M_{1}^{i} }}{{M_{1}^{i} }} = \varepsilon_{i,1} - s_{i,1} ,} \quad {\text{for}} \qquad {i = 1, \ldots ,m,} & { [ 1 {\text{st}}\;{\text{moment]}}} \\ {} & {\frac{{(r(Z_{i} ;\underline{\theta } ))^{ - 2} 2!\varvec{\pi S}^{ - 2} {\mathbf{1}} - M_{2}^{i} }}{{M_{2}^{i} }} = \varepsilon_{i,2} - s_{i,2} ,} \,\,\quad {\text{for}} \qquad {i = 1, \ldots ,m,} & { [ 2 {\text{nd}}\;{\text{moment]}}} \\ {} & {\frac{{ - (r(Z_{i} ;\underline{\theta } ))^{ - 3} 3!\varvec{\pi S}^{ - 3} {\mathbf{1}} - M_{3}^{i} }}{{M_{3}^{i} }} = \varepsilon_{i,3} - s_{i,3} ,} \quad {\text{for}} \qquad {i = 1, \ldots ,m,} & { [ 3 {\text{rd}}\;{\text{moment]}}} \\ {} & {\varepsilon_{i,1} \ge 0,\varepsilon_{i,2} \ge 0,\varepsilon_{i,3} \ge 0,} \quad\qquad\,\, {\text{for}} \qquad {i = 1, \ldots ,m,} & {} \\ {} & {s_{i,1} \ge 0,s_{i,2} \ge 0,s_{i,3} \ge 0,} \qquad\quad\,\,\, {\text{for}} \qquad {i = 1, \ldots ,m,} & {} \\ {} & {\lambda_{1} \ge 0,\lambda_{2} \ge 0,\lambda_{3} \ge 0,p_{c} \ge 0,} & {} & {} & {}\\ {} & {{\text{Subject}}\;{\text{to}}} & {} & {}& {} \\ {} & \qquad\qquad {g_{k} \le \widetilde{\rm E},} & {} & {} \\ {} & \qquad\qquad {k \in \{ 3,4, \ldots \} ,} & {} & {} \\ \end{array} $$

(11.15)

where $\varepsilon_{i,l}$ is the “excess” variable in the lth moment for stress level $Z_{i}$, $s_{i,l}$ is the corresponding slack variable, $\omega_{i,l}^{(1)}$ and $\omega_{i,l}^{(2)}$ are the weights assigned to the deviation from the lth moment (the conceived importance of the deviation), and $\tilde{\rm E}$ is the pre-specified overall tolerance.

This mathematical programming problem consists of two stages. For a given value of k, a sub-problem SP₁ is solved to obtain the minimal value of $g_{k}$, which corresponds to the best matching EC-based ALT model with the k phases. The procedure is continued until the first value of k and the corresponding EC-based ALT model are found, which satisfies the overall tolerance constraint. Note that the size of matrix $\varvec{S}$ increases as the value of k increases, which only increases the number of phases in Erlang E(k-2, λ ₁) without increasing the number of parameters. Despite the simplicity in terms of formulation, the challenge of using this approach is that extensive computational effort is required in finding the solution that satisfies those nonlinear constraints. Moreover, this approach may not result in the desirable optimality properties of MLE.

4.2 Use of MLE Approach

The MLE approach has been widely used in modeling ALT because of its capability of handling different types of censoring. In particular, for ALT data with Type-I censoring, the log-likelihood function lnL can be expressed as:

$$ \begin{aligned} ln\,L(\underline{\Theta } & = \left[ {\lambda_{1} ,\lambda_{2} ,\lambda_{3} ,p_{c} ,\underline{\theta } } \right]) \\ & = \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{{n_{i} }} \left[ {\updelta_{ij}^{{\left[ {0,\tau_{i} } \right]}} \;{ \ln }\left( {f\left( {t_{ij} ;Z_{i} } \right)} \right) + (1 -\updelta_{ij}^{{[0,\tau_{i} ]}} )\,{ \ln }\left( {1 - F(t_{ij} ;Z_{i} )} \right)} \right] \\ & = \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{{n_{i} }}\updelta_{ij}^{{\left[ {0,\tau_{i} } \right]}} \,{ \ln }\left( {r\left( {Z_{i} ;\underline{\theta } } \right){\varvec{\uppi}}\, { \exp }\left\{ {r\left( {Z_{i} ;\underline{\theta } } \right)t_{ij} \varvec{S}} \right\}\varvec{ S}^{{\mathbf{0}}} } \right) \\ & \quad +\, (1 -\updelta_{ij}^{{[0,\tau_{i} ]}} )\,{ \ln }\left( {{\varvec{\uppi}}\, { \exp }\left\{ {r\left( {Z_{i} ;\underline{\theta } } \right)t_{ij} \varvec{S}} \right\}\mathbf{1}} \right) \\ \end{aligned} $$

(11.16)

For a case with random censoring, the log-likelihood function can be obtained by replacing $\updelta_{ij}^{{[0,\tau_{i} ]}}$ by $\updelta_{ij} = \{ 1,\;{\text{if}}\;t_{ij} {\text{is}}\;{\text{a}}\;{\text{failure}}\;{\text{time}};0,\;{\text{otherwise}}\}$ for each $t_{ij}$. The MLEs of the model parameters can be obtained by maximizing the log-likelihood function. In practice, different optimization algorithms, such as Quasi-Newton and Nelder-Mead algorithms, can be used.

A practical issue is to determine the number of phases in the EC-based ALT model. For such model selection problems under the framework of MLE, the Akaike Information Criterion (AIC) has been widely used. The AIC for an EC-based ALT model can be expressed as:

$$ AIC = 2q - 2lnL(\lambda_{1} ,\lambda_{2} ,\lambda_{3} ,p_{c} ,\underline{\theta } ), $$

(11.17)

where $q$ is the number of parameters which is the same for EC-based ALT models with different numbers of phases when the number of parameters in $\underline{\theta }$ is fixed. As a result, using AIC in determining the best EC-based ALT model is equivalent to comparing the log-likelihood values of those candidate models. Note that the likelihood-ratio test is widely used for testing nested models, which is not appropriate in determining the number of phases in EC-based ALT models because different EC-based ALT models with different numbers of phases essentially have the same number of parameters.

4.3 Method for Constructing Confidence Intervals

To quantify the uncertainty in parameter estimates $\underline{{\hat{\Theta }}}$ and the consequent reliability estimates, a nonparametric bootstrap method is proposed to construct the interested confidence intervals. This is a sample-reuse method, which can be used when no efficient alternatives are both tractable and sufficiently accurate. For EC-based ALT models, this may be the case.

In this chapter, the bootstrap procedure is used to construct pointwise confidence intervals for reliability function (or Cdf). This procedure is developed based on the method described by Efron and Tibshirani [8]. The detailed steps are as follows:

• 1. Each sample (say bootstrap sample j) consisting of n _i data points for each stress level Z _i is obtained by sampling, with replacement, from the original ALT data.

• 2. Parameters $\underline{{\hat{\Theta }}}$ are estimated based on each bootstrap sample. For the mathematical programming approach, the new bootstrap estimates $\underline{{\hat{\Theta }}}_{j}$ are calculated by solving the sub-problem SP₁ in Eq. (11.15). For the MLE approach, $\underline{{\hat{\Theta }}}_{j}$ is obtained by maximizing Eq. (11.16).

• 3. Compute the corresponding reliability function using Eq. (11.10), given the bootstrap estimate $\underline{{\hat{\Theta }}}$

• 4. Repeat Steps 1–3 for B (say 5000) times to obtain a set of reliability estimates at time t as:

  $$ \{ \widehat{{R_{1} }}(t),\widehat{{R_{2} }}(t), \cdots ,\widehat{{R_{B} }}(t)\} . $$

• 5. Sort the set in increasing order for each desired time to give:

  $$ \{ \widehat{{R_{[1]} }}(t),\widehat{{R_{[2]} }}(t), \cdots ,\widehat{{R_{[B]} }}(t)\} . $$

• 6. Determine the lower and upper bounds of pointwise 100(1-α)% confidence interval for reliability function as:

  $$ [\widehat{{R_{[v]} }}(t),\widehat{{R_{[u]} }}(t)], $$

  where $v = \left[ {\alpha B/2} \right]^{ + }$ and $u = \left[ {(1 - \alpha /2)B} \right]^{ + }$.

5 Numerical Examples

In this section, we provide three examples to illustrate the capability of EC-based ALT models in analyzing ALT data. In the first two examples, complete and Type-I censored ALT data are simulated respectively from two popular parametric ALT models: (1) Inverse-Power-Law-Weibull model, and (2) Arrhenius-Lognormal model. The corresponding EC-based ALT models are developed using the mathematical programming method, and their estimation accuracy is studied. Afterwards, a case study is presented to demonstrate the use of the proposed EC-based ALT model and MLE method in predicting the reliability of a type of miniature lamps under the use condition based on randomly censored ALT data.

5.1 Complete Data from an Inverse-Power-Law-Weibull ALT Model

In the first example, a set of ALT data is generated from an inverse-power-law-Weibull ALT model with Cdf: $F(t;Z_{i} ) = 1 - \exp ( - (t/\eta (Z_{i} ))^{\beta } )$, where the shape parameter $\beta = 1.5$ and the scale parameter depends on stress level $Z_{i}$ in the form of $\eta (Z_{i} ) = 1200Z_{i}^{ - 2}$. This ALT model is a special case of AFT model. Three stress levels (m = 3): $Z_{1} = 1$, $Z_{2} = 2$, and $Z_{3} = 3$, are considered in the hypothetic ALT experiment. At each stress level, ten units are tested to failure resulting in complete ALT data. Table 11.1 shows the data and the empirical moments. Figure 11.4a shows the empirical Cdf’s for the simulated data and the Cdf’s of the presumed ALT model for visual comparison. One can see that the empirical Cdf’s significantly differ from the Cdf’s of the presumed ALT model because of the randomness and small sample size of the ALT experiment. Without assuming a Weibull-based ALT model, it is more reasonable to develop an ALT model in a generic way that matches the ALT data as much as possible.

Table 11.1 ALT data generated from F(t;Z _i ) = 1 − exp (-(t/(1200Z ⁻² _i ))^1.5)

Fig. 11.4

4 Plots for ALT data generated from: F(t; Z _i ) = 1 – exp (−t(/(1200Z ⁻² _i ))^1.5)

To estimate the model parameters of the EC-based ALT model through the mathematical programming method, we solve the nonlinear programming problem P₁, where i = 1, 2, 3, and the corresponding empirical moments:

$$ M_{l}^{i} = (1/n_{i} )\sum\limits_{j = 1}^{{n_{i} }} {t_{ij}^{l} } ,\;l = 1,\,2,\,3, $$

calculated for the ith stress level are given in the last three columns of Table 11.1, the weights assigned to the deviation from the lth moment are:

$$ \begin{aligned} \omega_{1,1}^{(1)} & = \omega_{2,1}^{(1)} = \omega_{3,1}^{(1)} = \omega_{1,1}^{(2)} = \omega_{2,1}^{(2)} = \omega_{3,1}^{(2)} = 1, \\ \omega_{1,2}^{(1)} & = \omega_{2,2}^{(1)} = \omega_{3,2}^{(1)} = \omega_{1,2}^{(2)} = \omega_{2,2}^{(2)} = \omega_{3,2}^{(2)} = 0.5, \\ \omega_{1,3}^{(1)} & = \omega_{2,3}^{(1)} = \omega_{3,3}^{(1)} = \omega_{1,3}^{(2)} = \omega_{2,3}^{(2)} = \omega_{3,3}^{(2)} = 0.25, \\ \end{aligned} $$

respectively, and the tolerance level $\widetilde{\rm E}$ is set to be 0.35. Moreover, the life-stress relationship is assumed to be $r\left( {Z_{i} ;\underline{\theta } = [\alpha_{0} ,\alpha_{1} ]} \right) = \alpha_{0} Z_{i}^{{\alpha_{1} }}$. Solving this problem using the interior-point algorithm yields parameter estimates:

$$ \left[ {\widehat{{\lambda_{1} }},\widehat{{\lambda_{2} }},\widehat{{\lambda_{3} }},\widehat{{p_{c} }},\widehat{{\alpha_{0} }},\widehat{{\alpha_{1} }}} \right] = \left[ {41.520,41.657,41.504,0.584,0.0000969,2.443} \right], $$

for which k = 5 and $g_{5}^{*} = 0.3394 < \tilde{\rm E}$. The deviations of the resulting EC-based ALT model in the first three moments under different stress levels are given in Table 11.2. Each percentage error is calculated by: (moment of the EC-based ALT model - empirical moment)/empirical moment. One can see that the mathematical programming method provides quite accurate moment matching results. Figure 11.4b compares the empirical Cdf’s for the simulated data and the Cdf’s estimated using the EC-based ALT model. It is clear that the Cdf estimates match the empirical Cdf’s very well. To quantify the estimation uncertainty, the 95% confidence intervals of the Cdf’s estimated using the EC-based ALT model (see Fig. 11.5) are also calculated using the bootstrap method addressed in Sect. 11.4.3.

Table 11.2 Deviations of the EC-based ALT model from the first three empirical moments

Fig. 11.5

Cdf estimates using the EC-based model and 95% bootstrap confidence intervals

5.2 Type-I Censored Data from an Arrhenius-Lognormal ALT Model

A set of censored ALT data is generated from an Arrhenius-lognormal ALT model $F(t;Z_{i} ) =\Phi \left( {(\ln t - u(Z_{i} ))/\sigma } \right)$, where $\sigma = 1.5$ and the location parameter $u$ depends on stress level $Z_{i}$ in the form of $u(Z_{i} ) = \ln (50) + 5/Z_{i}$. Again, three stress levels: $Z_{1} = 1$, $Z_{2} = 2$, and $Z_{3} = 3$ are considered with ten units for each level. The censoring times at these stress levels are 80000, 6000, and 3000, respectively. Table 11.3 shows the simulated ALT data.

Table 11.3 Censored ALT data generated from $F(t;Z_{i} ) =\Phi \left( {(\ln \,t - \,\ln (50) - 5/Z_{i} )/1.5} \right)$

To develop an EC-based ALT model using the mathematical programming method, the weights assigned to the deviation from the lth empirical moment are again set to be:

$$ \begin{aligned} \omega_{1,1}^{(1)} & = \omega_{2,1}^{(1)} = \omega_{3,1}^{(1)} = \omega_{1,1}^{(2)} = \omega_{2,1}^{(2)} = \omega_{3,1}^{(2)} = 1, \\ \omega_{1,2}^{(1)} & = \omega_{2,2}^{(1)} = \omega_{3,2}^{(1)} = \omega_{1,2}^{(2)} = \omega_{2,2}^{(2)} = \omega_{3,2}^{(2)} = 0.5, \\ \omega_{1,3}^{(1)} & = \omega_{2,3}^{(1)} = \omega_{3,3}^{(1)} = \omega_{1,3}^{(2)} = \omega_{2,3}^{(2)} = \omega_{3,3}^{(2)} = 0.25, \\ \end{aligned} $$

respectively, and the tolerance level $\tilde{\rm E}$ is set to be 0.95, which is determined through trial and error. Moreover, the life-stress relationship is assumed to be $r\left( {Z_{i} ;\underline{\theta } = [\alpha_{0} ,\alpha_{1} ]} \right) = \alpha_{0} \exp ( - \alpha_{1} Z_{i}^{ - 1} )$. Unlike in the first example, the empirical moments in this example cannot be calculated directly from the data. Instead, Eq. (11.14) needs to be used, which depends on the model parameters to be estimated. By solving the corresponding nonlinear programming problem similar to Eq. (11.15), the parameters of the EC-based ALT model are estimated as: $[\widehat{{\lambda_{1} }},\widehat{{\lambda_{2} }},\widehat{{\lambda_{3} }},\widehat{{p_{c} }},\widehat{{\alpha_{0} }},\widehat{{\alpha_{1} }}] = \left[ {15.798,209.5,1799.7,0.382,0.0013,5.895} \right]$ for which k = 5 and $g_{7}^{*} = 0.9357 < \tilde{\rm E}$. Table 11.4 shows the empirical moments calculated using Eq. (11.14) for the three stress levels and the deviations of the resulting EC-based ALT model in the corresponding moments. One can see that the deviations are well balanced across different stress levels as well as the corresponding moments.

Table 11.4 Deviations of the EC-based ALT model from the first three empirical moments

5.3 Case Study

ALT has been widely used in evaluating the reliability of microelectronics [13, 38]. In this section, the ALT data reported by Liao and Elsayed [17] is used to illustrate the use of the proposed ALT model in practice. The purpose of this ALT experiment is to estimate the reliability of a type of miniature lamps under the use condition: 2 V. The highest operating voltage of the lamp is 5 V. It is well known that the coil temperature of an incandescent lamp during operation is mainly due to the electric current.

Three constant voltage levels were utilized in the experiment: 5, 3.5, and 2 V. Table 11.5 gives the observed failure times and censoring times under the three stress levels. It is worth pointing out that the test under 3.5 V was randomly censored and the one under 2 V was Type-I censored. To avoid making an assumption on the underlying distribution, such as Weibull and Lognormal, we use the proposed EC-based ALT model to predict the reliability of this type of miniature lamps.

Table 11.5 ALT data of miniature lamps [17]

To facilitate data analysis, we standardize the stress levels by defining $Z_{i} = [V_{i} - V_{0} ]/[V_{H} - V_{0} ]$, where $V_{0} = 2$ V and $V_{H} = 5$ V. As a result, we have: $Z_{1} = 1$, $Z_{2} = 0.5$, and $Z_{3} = 0$. The life-stress relationship is assumed to be characterized by:

$$ r\left( {Z_{i} ;\underline{\theta } } \right) = \exp (\alpha_{0} Z_{i}^{{\alpha_{1} }} ). $$

(11.18)

Because the data set contains different types of censoring times, we use the MLE method introduced in Sect. 11.4.2 for statistical inference. Table 11.6 shows the MLEs of parameters for different EC-based ALT models with different numbers of phases. By comparing the log-likelihood values, the EC-based ALT model with k = 7 phases is selected after balancing the prediction accuracy and the complexity of the models

Table 11.6 MLEs of parameters for different EC-based ALT models with different numbers of phases (k)

Figure 11.6 illustrates the statistical fittings of the resulting EC-based ALT model for the three test stress levels. The empirical Cdf (ecdf using Kaplan-Meier method) of the lamp under each voltage level is presented in Fig. 11.6a. Compared to the corresponding empirical Cdf’s, this model exhibits satisfactory prediction capability. This can also be verified by examining the Cox-Snell residual plot presented in Fig. 11.6b, where the residuals can be easily tested against the exponential distribution with mean of one (the straight line with slope of one going through the origin). Figure 11.7 shows the predicted reliability function, pdf and hazard rate of the lamp under the normal operating condition. The corresponding 95% bootstrap confidence interval for reliability function is also presented. The mean-time-to-failure can be easily obtained as 2397.2 h by setting l = 1 in Eq. (11.13).

Fig. 11.6

Illustration of statistical fittings of the resulting model

Fig. 11.7

Predicted reliability function with 95% confidence intervals, pdf, and hazard rate under 2 V using the resulting EC-based ALT model

6 Concluding Remarks

This chapter introduces a generic method for modeling ALT data using EC distributions, which belong to an important subset of PH distributions. Without assuming other particular probability distributions for failure times, such as extreme-value distributions, lognormal distribution, and gamma distributions, this method leads to an EC-based ALT model which can well represent the underlying failure time distribution that may be difficult to verify or even unknown. To automatically determine the model structure, both a mathematical programming approach and an MLE approach are developed for adaptively determining the number of phases and estimating the model parameters. The numerical examples demonstrate that the proposed generic method indeed provides practitioners, particularly in the area of microelectronics, with a convenient statistical tool for modeling ALT data. To the best of our knowledge, this is the first attempt to demonstrate the potential of using PH distributions in ALT data analysis.