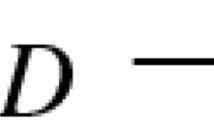Morphisms to Brauer–Severi Varieties, with Applications to Del Pezzo Surfaces

Abstract

We classify morphisms from proper varieties to Brauer–Severi varieties, which generalizes the classical correspondence between morphisms to projective space and globally generated invertible sheaves. As an application, we study del Pezzo surfaces of large degree with a view towards Brauer–Severi varieties, and recover classical results on rational points, the Hasse principle, and weak approximation.

1 Introduction

1.1 Overview

The goal of this article is the study of morphisms $X\rightarrow P$ from a proper variety X over a field k to a Brauer–Severi variety P over k, i.e., P is isomorphic to projective space over the algebraic closure $\overline{k}$ of k, but not necessarily over k. If X has a k-rational point, then so has P, and then, P is isomorphic to projective space already over k. In this case, there exists a well-known description of morphisms $X\rightarrow P$ in terms of globally generated invertible sheaves on X. However, if X has no k-rational point, then we establish in this article a correspondence between globally generated classes of $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$, whose obstruction to coming from an invertible sheaf on X is measured by some class $\beta$ in the Brauer group $\mathrm{Br}(k)$, and morphisms to Brauer–Severi varieties of class $\beta$ over k.

As an application of this correspondence, we study del Pezzo surfaces over k in terms of Brauer–Severi varieties, and recover many known results about their geometry and their arithmetic. If k is a global field, then we obtain applications concerning the Hasse principle and weak approximation. Our approach has the advantage of being elementary, self-contained, and that we sometimes obtain natural reasons for the existence of k-rational points.

1.2 Morphisms to Brauer–Severi Varieties

Let X be a proper variety over a field k, and let $\overline{k}$ be the algebraic closure of k. When studying invertible sheaves on X, there are inclusions and equalities of abelian groups

$$ \mathrm{Pic }(X) \,\subseteq \, \mathrm{Pic }_{(X/k)({{\acute{\mathrm{e}}{\mathrm{t}}}})}(k) \,=\, \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)\,\subseteq \, \mathrm{Pic }(X_{\overline{k}}). $$

On the left (resp. right), we have invertible sheaves on X (resp. $X_{\overline{k}}$) up to isomorphism, whereas in the middle, we have sections of the sheafified relative Picard functor over k (with respect to the étale and fppf topology, respectively). Moreover, the first inclusion is part of an exact sequence

$$ 0\,\rightarrow \,\mathrm{Pic }(X) \,\rightarrow \, \mathrm{Pic }_{(X/k)({{\acute{\mathrm{e}}{\mathrm{t}}}})}(k)\,\mathop {\longrightarrow }\limits ^{\delta }\,\mathrm{Br}(k), $$

where $\mathrm{Br}(k)$ denotes the Brauer group of the field k, and we refer to Remark 3.3 for explicit descriptions of $\delta$. If X has a k-rational point, then $\delta$ is the zero map, i.e., the first inclusion is a bijection.

By definition, a Brauer–Severi variety is a variety P over k, such that $P_{\overline{k}}\cong {{\mathbb P}}_{\overline{k}}^N$ for some N, i.e., P is a twisted form of projective space. Associated to P, there exists a Brauer class $[P]\in \mathrm{Br}(k)$ and by a theorem of Châtelet, P is trivial, i.e., isomorphic to projective space over k, if and only if $[P]=0$. This is also equivalent to P having a k-rational point. In any case, we have a class $\mathcal{O}_P(1)\in \mathrm{Pic }_{(P/k)(\mathrm{fppf})}(k)$, in general not arising from an invertible sheaf on P, which becomes isomorphic to $\mathcal{O}_{{{\mathbb P}}^N}(1)$ over $\overline{k}$, see Definition 2.17.

In this article, we extend the notion of a linear system to classes in $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ that do not necessarily come from invertible sheaves. More precisely, we extend the notions of being globally generated, ample, and very ample to such classes, see Definition 3.1. Then, we set up a dictionary between globally generated classes in $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ and morphisms from X to Brauer–Severi varieties over k. In case X has a k-rational point, then we recover the well-known correspondence between globally generated invertible sheaves and morphisms to projective space. Here is an easy version of our correspondence and we refer to Theorem 3.4 and Remark 3.5 for details.

Theorem 1.1

Let X be a proper variety over a field k.

• (1) Let $\varphi :X\rightarrow P$ be a morphism to a Brauer–Severi variety P over k. If we set $\mathcal{L}:=\varphi ^*\mathcal{O}_P(1)\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$, then $\mathcal{L}$ is a globally generated class and

  $$ \delta (\mathcal{L}) \,=\, [P] \,\in \mathrm{Br}(k). $$

• (2) If $\mathcal{L}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ is globally generated, then $\mathcal{{L}}\otimes _k\overline{k}$ corresponds to a unique invertible sheaf $\mathcal{M}$ on $X_{\overline{k}}$ and the morphism associated to the complete linear system $|\mathcal{M}|$ descends to a morphism over k

  $$ |\mathcal{L}|\,:\,X \,\rightarrow \, P, $$

  where P is a Brauer–Severi variety over k with $\delta (\mathcal{L})=[P]$.

We note that our result is inspired by a geometric construction of Brauer–Severi varieties of Grothendieck, see [21, Sect. 5.4], and it seems that it is known to the experts. As immediate corollaries, we recover two classical theorems about Brauer–Severi varieties due to Châtelet and Kang, see Corollaries 3.6 and 3.8.

1.3 Del Pezzo Surfaces

In the second part, we apply this machinery to the geometry and arithmetic of del Pezzo surfaces over arbitrary ground fields. I would like to stress that most, if not all, of the results of this second part are well-known. To the best of my knowledge, I have tried to give the original references. However, my organization of the material and the hopefully more geometric approach to del Pezzo surfaces via morphisms to Brauer–Severi varieties is new.

By definition, a del Pezzo surface is a smooth and proper surface X over a field k, whose anti-canonical invertible sheaf $\omega _X^{-1}$ is ample. The degree of a del Pezzo surface is the self-intersection number of $\omega _X$. The classification of del Pezzo surfaces over $\overline{k}$ is well-known: The degree d satisfies $1\le d\le 9$, and they are isomorphic either to ${{\mathbb P}}^1\times {{\mathbb P}}^1$ or to the blow-up of ${{\mathbb P}}^2$ in $(9-d)$ points in general position.

As an application of Theorem 1.1, we obtain the following.

• (1) If $d=8$ and $X_{\overline{k}}\cong {{\mathbb P}}^1_{\overline{k}}\times {{\mathbb P}}^1_{\overline{k}}$, then there exists an embedding

  $$\begin{array}{ccccc} |-\frac{1}{2}K_X|&:&X&{\hookrightarrow }&P \end{array} $$

  into a Brauer–Severi threefold P. Moreover, X is either isomorphic to a product of two Brauer–Severi curves or to a quadratic twist of the self-product of a Brauer–Severi curve. We refer to Theorem 5.1 and Proposition 5.2 for details.

• (2) If $d\ge 7$ and $X_{\overline{k}}\not \cong {{\mathbb P}}^1_{\overline{k}}\times {{\mathbb P}}^1_{\overline{k}}$, then there exists a birational morphism

  $$\begin{array}{ccccc} f&:&X\rightarrow & {} P \end{array} $$

  to a Brauer–Severi surface P over k that is the blow-up in a closed and zero-dimensional subscheme of length $(9-d)$ over k. We refer to Theorem 6.1 for details.

• (3) If $d=6$, then there exist two finite field extensions $k\subseteq K$ and $k\subseteq L$ with [K : k]|2 and [L : k]|3 such that there exists a birational morphism $f:X\rightarrow P$ to a Brauer–Severi surface P over k that is the blow-up in a closed and zero-dimensional subscheme of length 3 over k if and only $k=K$. On the other hand, there exists a birational morphism $X\rightarrow Y$ onto a degree 8 del Pezzo surface Y of product type if and only if $k=L$. We refer to Theorem 7.1 for details.

• (4) For partial results if $d\le 5$, as well as birationality criteria for when a del Pezzo surface is birationally equivalent to a Brauer–Severi surface, we refer to Sect. 8.

As further applications, we recover well-known results about rationality, unirationality, existence of k-rational points, Galois cohomology, the Hasse principle, and weak approximation for del Pezzo surfaces.

Notations and Conventions

In this article, k denotes an arbitrary field, $\overline{k}$ (resp. $k^\mathrm{sep}$) its algebraic (resp. separable) closure, and $G_k=\mathrm{Gal}(k^\mathrm{sep}/k)$ its absolute Galois group. By a variety over k we mean a scheme X that is of finite type, separated, and geometrically integral over k. If K is a field extension of k, then we define $X_K:=X\times _{{\mathrm{Spec}\,}k}{\mathrm{Spec}\,}K$.

2 Picard Functors and Brauer Groups

This section, we recall a couple of definitions and general results about the various relative Picard functors, about Brauer groups of fields and schemes, as well as Brauer–Severi varieties.

2.1 Relative Picard Functors

Let us first recall a couple of generalities about the several Picard functors. Our main references are [22, 23], as well as the surveys [3, Chap. 8] and [30].

For a scheme X, we define its Picard group $\mathrm{Pic }(X)$ to be the abelian group of invertible sheaves on X modulo isomorphism. If $f:X\rightarrow S$ is a separated morphism of finite type over a Noetherian base scheme S, then we define the absolute Picard functor to be the functor that associates to each Noetherian $T\rightarrow S$ the abelian group $\mathrm{Pic }_X(T):=\mathrm{Pic }(X_T)$, where $X_T:=X\times _ST$. Now, as explained, for example in [30, Sect. 9.2], the absolute Picard functor is a separated presheaf for the Zariski, étale, and the fppf topologies, but it is never a sheaf for the Zariski topology. In particular, the absolute Picard functor is never representable by a scheme or by an algebraic space. This leads to the introduction of the relative Picard functor $\mathrm{Pic }_{X/S}$ by setting $\mathrm{Pic }_{X/S}(T):=\mathrm{Pic }(X_T)/\mathrm{Pic }(T)$, and then, we have the associated sheaves for the Zariski, étale, and fppf topologies

$$ \mathrm{Pic }_{(X/S)(\mathrm{zar})}, \quad \mathrm{Pic }_{(X/S)({\acute{\mathrm{e}}{\mathrm{t}}})}, \quad \text{ and } \quad \mathrm{Pic }_{(X/S)(\mathrm{fppf})}. $$

In many important cases, these sheaves are representable by schemes or algebraic spaces over S. For our purposes, it suffices to work with the sheaves so that we will not address representability questions here, but refer the interested reader to [3, Chap. 8.2] and [30, Chap. 9.4] instead. Having introduced these sheaves, let us recall the following easy facts, see, for example, [30, Exercise 9.2.3].

Proposition 2.1

Let $X\rightarrow S$ be a scheme that is separated and of finite type over a Noetherian scheme S. Let L be a field with a morphism ${\mathrm{Spec}\,}L\rightarrow S$.

• (1) Then, the following natural maps are isomorphisms:

  $$ \mathrm{Pic }_X(L)\,\mathop {\longrightarrow }\limits ^{\cong }\,\mathrm{Pic }_{X/S}(L)\,\mathop {\longrightarrow }\limits ^{\cong }\,\mathrm{Pic }_{(X/S)(\mathrm{zar})}(L). $$

• (2) If L is algebraically closed, then also the following natural maps are isomorphisms:

  $$ \mathrm{Pic }_X(L)\,\mathop {\longrightarrow }\limits ^{\cong }\,\mathrm{Pic }_{(X/S)({\acute{\mathrm{e}}{\mathrm{t}}})}(L)\,\mathop {\longrightarrow }\limits ^{\cong }\,\mathrm{Pic }_{(X/S)(\mathrm{fppf})}(L). $$

It is important to note that if L is not algebraically closed, then the natural map $\mathrm{Pic }_X(L)\rightarrow \mathrm{Pic }_{(X/S)({\acute{\mathrm{e}}{\mathrm{t}}})}(L)$ is usually not an isomorphism, i.e., not every section of $\mathrm{Pic }_{(X/S)({\acute{\mathrm{e}}{\mathrm{t}}})}$ over L arises from an invertible sheaf on $X_L$. The following example, taken from [30, Exercise 9.2.4], is crucial to everything that follows and illustrates this.

Example 2.2

Let X be the smooth plane conic over ${{\mathbb R}}$ defined by

$$ X\,:=\,\{\, x_0^2+x_1^2+x_2^2=0 \,\} \,\subset \,{{\mathbb P}}^2_{{{\mathbb R}}}. $$

Then, X is not isomorphic to ${{\mathbb P}}^1_{{\mathbb R}}$ since $X({{\mathbb R}})=\emptyset$, but there exists an isomorphism $X_{{\mathbb C}}\rightarrow {{\mathbb P}}^1_{{\mathbb C}}$. In particular, X is an example of a non-trivial Brauer–Severi variety (see Definition 2.14).

Next, if $x\in X$ is a closed point, then $\kappa (x)\cong {{\mathbb C}}$, that is, x is a zero-cycle of degree 2. Moreover, $\mathcal{O}_X(x)$ generates $\mathrm{Pic }_X({{\mathbb R}})$, for if there was an invertible sheaf of odd degree on X, then there would exist an invertible sheaf of degree 1 on X and then, Riemann–Roch would imply $X({{\mathbb R}})\ne \emptyset$, a contradiction.

On the other hand, x splits on $X_{{\mathbb C}}$ into two closed points, say $x_1$ and $x_2$. Since $\mathcal{O}_{X_{{\mathbb C}}}(x_1)$ and $\mathcal{O}_{X_{{\mathbb C}}}(x_2)$ are isomorphic as invertible sheaves on $X_{{\mathbb C}}$, it follows that $\mathcal{O}_{X_{{\mathbb C}}}(x_1)$ descends from a class in $\mathrm{Pic }_{(X/{{\mathbb R}})({\acute{\mathrm{e}}{\mathrm{t}}})}({{\mathbb C}})$ to a class in $\mathrm{Pic }_{(X/{{\mathbb R}})({\acute{\mathrm{e}}{\mathrm{t}}})}({{\mathbb R}})$.

These observations show that the natural map $\mathrm{Pic }_X({{\mathbb R}})\rightarrow \mathrm{Pic }_{(X/{{\mathbb R}})({\acute{\mathrm{e}}{\mathrm{t}}})}({{\mathbb R}})$ is not surjective.

In this example, we have $X({{\mathbb R}})=\emptyset$, i.e., the structure morphism $X\rightarrow {\mathrm{Spec}\,}{{\mathbb R}}$ has no section. Quite generally, we have the following comparison theorem for the several relative Picard functors, and refer, for example, to [30, Theorem 9.2.5] for details and proofs.

Theorem 2.3

(Grothendieck) Let $f:X\rightarrow S$ be a scheme that is separated and of finite type over a Noetherian scheme S, and assume that $\mathcal{O}_S\mathop {\longrightarrow }\limits ^{\cong }f_*\mathcal{O}_X$ holds universally.

• (1) Then, the natural maps

  $$ \mathrm{Pic }_{X/S} \,{\hookrightarrow }\, \mathrm{Pic }_{(X/S)(\mathrm{zar})} \,{\hookrightarrow }\, \mathrm{Pic }_{(X/S)({\acute{\mathrm{e}}{\mathrm{t}}})} \,{\hookrightarrow }\, \mathrm{Pic }_{(X/S)(\mathrm{fppf})} $$

  are injections.

• (2) If f has a section, then all three maps are isomorphisms. If f has a section locally in the Zariski topology, then the latter two maps are isomorphisms, and if f has a section locally in the étale topology, then the last map is an isomorphism.

To understand the obstruction to realizing a section of $\mathrm{Pic }_{(X/S)({{\acute{\mathrm{e}}{\mathrm{t}}}})}$ or $\mathrm{Pic }_{(X/S)(\mathrm{fppf})}$ over S by an invertible sheaf on X in case there is no section of $X\rightarrow S$, we recall the following definition.

Definition 2.4

For a scheme T, the étale cohomology group ${H_{{\acute{\mathrm{e}}{\mathrm{t}}}}^{{2}}}(T,{{\mathbb G}}_m)$ is called the cohomological Brauer group, and is denoted $\mathrm{Br}'(T)$. The set of sheaves of Azumaya algebras on T modulo Brauer equivalence also forms a group, the Brauer group of T, and is denoted $\mathrm{Br}(T)$.

We will not discuss sheaves of Azumaya algebras on schemes in the sequel, but only remark that these generalize central simple algebras over fields (see Sect. 2.3 for the latter), and refer the interested reader to [20] and [37, Chap. IV] for details and references, as well as to [41] for a survey.

Using that ${{\mathbb G}}_m$ is a smooth group scheme, Grothendieck [21] showed that the natural map ${H_{{\acute{\mathrm{e}}{\mathrm{t}}}}^{{2}}}(T,{{\mathbb G}}_m)\rightarrow H^2_{\mathrm{fppf}}(T,{{\mathbb G}}_m)$ is an isomorphism, i.e., it does not matter whether the cohomological Brauer group $\mathrm{Br}'(T)$ is defined with respect to the étale or the fppf topology. Next, there exists a natural injective group homomorphism $\mathrm{Br}(T)\rightarrow \mathrm{Br}'(T)$, whose image is contained in the torsion subgroup of $\mathrm{Br}'(T)$. If T is the spectrum of a field k, then this injection is even an isomorphism, i.e., $\mathrm{Br}(k)=\mathrm{Br}'(k)$, see, for example, [18, 21], and [37, Chap. IV] for details and references.

The connection between Brauer groups, Proposition 2.1, and Theorem 2.3 is as follows, see, for example [3, Chap. 8.1] or [30, Sect. 9.2].

Proposition 2.5

Let $f:X\rightarrow S$ be a scheme that is separated and of finite type over a Noetherian scheme S, and assume that $\mathcal{O}_S\mathop {\longrightarrow }\limits ^{\cong }f_*\mathcal{O}_X$ holds universally. Then, for each S-scheme T there exists a canonical exact sequence

$$ 0\,\rightarrow \,\mathrm{Pic }(T)\,\rightarrow \,\mathrm{Pic }(X_T)\,\rightarrow \,\mathrm{Pic }_{(X/S)(\mathrm{fppf})}(T)\,\mathop {\longrightarrow }\limits ^{\delta }\,\mathrm{Br}'(T)\,\rightarrow \,\mathrm{Br}'(X_T)\,. $$

If f has a section, then $\delta$ is the zero-map.$\square$

2.2 Varieties and the Amitsur Subgroup

By our conventions above, a variety over a field k is a scheme X that is of finite type, separated, and geometrically integral over k. In this situation, the conditions of Proposition 2.5 are fulfilled, as the following remark shows.

Remark 2.6

If X is a proper variety over a field k, then

• (1) the structure morphism $f:X\rightarrow {\mathrm{Spec}\,}k$ is separated, of finite type, and $\mathcal{O}_{{\mathrm{Spec}\,}k}\cong f_*\mathcal{O}_X$ holds universally.

• (2) The morphism f has sections locally in the étale topology (see, for example, [18, Appendix A]).

• (3) Since the base scheme is a field k, we have $\mathrm{Br}(k)=\mathrm{Br}'(k)$.

In Remark 3.3, we will give an explicit description of $\delta$ in this case.

In Example 2.2, the obstruction to representing the class of $\mathcal{L}:=\varphi ^*\mathcal{O}_{{{\mathbb P}}^1_{{\mathbb C}}}(1)$ in $\mathrm{Pic }_{(X/{{\mathbb R}})(\mathrm{fppf})}({{\mathbb R}})$ by an invertible sheaf on X can be explained via $\delta$, which maps $\mathcal L$ to the non-zero element of $\mathrm{Br}({{\mathbb R}})\cong {{\mathbb Z}}/2{{\mathbb Z}}$. In terms of Azumaya algebras (since the base is ${\mathrm{Spec}\,}{{\mathbb R}}$, these are central simple ${{\mathbb R}}$-algebras), this Brauer class corresponds the ${{\mathbb R}}$-algebra ${{\mathbb H}}$ of quaternions, but we will not pursue this point of view in the sequel.

Proposition 2.7

Let X be a proper variety over a field k. Then, there exist natural isomorphisms of abelian groups

$$ \mathrm{Pic }_{X/k}(k^\mathrm{sep})^{G_k} \,\mathop {\longrightarrow }\limits ^{\cong }\, \mathrm{Pic }_{(X/k)({{\acute{\mathrm{e}}{\mathrm{t}}}})}(k) \,\mathop {\longrightarrow }\limits ^{\cong }\, \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k), $$

where the ${-}^{G_k}$ denotes Galois invariants.

Proof The first isomorphism follows from Galois theory and sheaf axioms and the second isomorphism follows from Theorem 2.3 and Remark 2.6.$\square$

The Brauer group $\mathrm{Br}(k)$ of a field k is an abelian torsion group, see, for example, [18, Corollary 4.4.8]. Motivated by Proposition 2.5, we introduce the following subgroup of $\mathrm{Br}(k)$ that measures the deviation between $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ and $\mathrm{Pic }(X)$.

Definition 2.8

Let X be a proper variety over a field k. Then, the Amitsur subgroup of X in $\mathrm{Br}(k)$ is the subgroup

$$ \mathrm{Am}(X) \,:=\, \delta (\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k))\,\subseteq \,\mathrm{Br}(k). $$

By the previous remarks, it is an abelian torsion group.

The following lemma gives bounds for the order of torsion in $\mathrm{Am}(X)$.

Lemma 2.9

Let X be a proper variety over a field k. If there exists a closed point on X, whose residue field is of degree n over k, then every element of $\mathrm{Am}(X)$ has an order dividing n.

Proof Let $x\in X$ be a closed point, say, with residue field K / k that is of degree n over k. Since $X_K$ has a K-rational point, the map $\delta$ of $X_K$ is identically zero by Proposition 2.5. Thus, we have an inclusion $\mathrm{Am}(X) \subseteq \mathrm{Br}(K|k):=\ker (\mathrm{Br}(k)\rightarrow \mathrm{Br}(K))$, where $\mathrm{Br}(k)\rightarrow \mathrm{Br}(K)$ is the restriction homomorphism.

If K is separable over k, then $\mathrm{Br}(K|k)$ is contained in the n-torsion of $\mathrm{Br}(k)$, which follows from the fact that the composition of restriction and corestriction is multiplication by n, see [18, Proposition 4.2.10].

If K is a purely inseparable extension of k, generated by $p^r$-th roots, then $\mathrm{Br}(K|k)$ is $p^r$-torsion (which yields even stronger bounds on the torsion than claimed), see for example, Hochschild’s Theorem [18, Theorem 9.1.1] for an explicit description for this group.

In general, we can factor the extension K / k into a separable and a purely inseparable extension, and by combining the previous two special cases, the statement follows. $\square$

Using Proposition 2.5, we can give two alternative definitions of $\mathrm{Am}(X)$. In fact, the birational invariance of this group for Brauer–Severi varieties is a classical result of Amitsur, probably known to Châtelet and Witt in some form or another, see also Theorem 2.19 below.

Proposition 2.10

Let X be a smooth and proper variety over k. Then,

$$ \mathrm{Am}(X)\,=\, \ker \left( \mathrm{Br}(k)\,\rightarrow \,\mathrm{Br}'(X)\right) \,=\,\ker \left( \mathrm{Br}(k)\,\rightarrow \,\mathrm{Br}(k(X))\right) . $$

In particular, $\mathrm{Am}(X)$ is a birational invariant of smooth and proper varieties over k.

Proof The first equality follows from the exact sequence of Proposition 2.5. Since X is smooth over k, the natural map $\mathrm{Br}'(X)\rightarrow \mathrm{Br}(k(X))$ is injective, see, for example, [37, Example III.2.22], and then, the second equality follows. From this last description, it is clear that $\mathrm{Am}(X)$ is a birational invariant. $\square$

Remark 2.11

In [10, Sect. 5], the kernel of $\mathrm{Br}(k)\rightarrow \mathrm{Br}(k(X))$ was denoted $\mathrm{Br}(k(X)/k)$. Thus, if X is smooth and proper over k, then this latter group coincides with $\mathrm{Am}(X)$. However, this group should not be confused with $\mathrm{Br}(k(X))/\mathrm{Br}(k)$, which is related to another important birational invariant that we will introduce in Sect. 4.2.

If X has a k-rational point, then $\mathrm{Am}(X)=0$ by Proposition 2.5. On the other hand, there exist proper varieties X with trivial Amitsur subgroup without k-rational points (some degree 8 del Pezzo surfaces of product type with $\rho =1$ provide examples, see Corollary 5.4). Let us recall that a zero-cycle on X is a formal finite sum $\sum _i n_i Z_i$, where the $n_i\in {{\mathbb Z}}$ and where the $Z_i$ are closed points of X. It is called effective if $n_i\ge 0$ for all i. The degree is defined to be $\deg (Z):=\sum _i n_i[\kappa (Z_i):k]$, where $\kappa (Z_i)$ denotes the residue field of the point $Z_i$.

Corollary 2.12

Let X be a proper variety over a field k. If there exists a zero cycle of degree 1 on X, then $\mathrm{Am}(X)=0$. $\square$

If X is a projective variety over k, then $\mathrm{Pic }_{(X/k)({{\acute{\mathrm{e}}{\mathrm{t}}}})}$ and $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}$ are representable by a group scheme $\mathrm{Pic }_{X/k}$ over k, the Picard scheme. The connected component of the identity is denoted $\mathrm{Pic }_{X/k}^0$, and the quotient

$$ {\mathrm{NS}}_{X/k}(\overline{k}) \,:=\, \mathrm{Pic }_{X_{\overline{k}}/\overline{k}}(\overline{k}) \,/\, \mathrm{Pic }^0_{X_{\overline{k}}/\overline{k}}(\overline{k}), $$

the Néron–Severi group, is a finitely generated abelian group, whose rank is denoted $\rho (X_{\overline{k}})$. We refer to [3, Sect. 8.4] for further discussion. Moreover, if X is smooth over k, then $\mathrm{Pic }_{X/k}^0$ is of dimension $\frac{1}{2}b_1(X)$, where $b_1$ denotes the first $\ell$-adic Betti number.

Lemma 2.13

Let X be a smooth and projective variety over a field k with $b_1(X)=0$. Then, $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ is a finitely generated abelian group,

$$ \mathrm{rank}\,\mathrm{Pic }(X)\,=\,\mathrm{rank}\,\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k) \,\le \,\rho (X_{\overline{k}}), $$

and $\mathrm{Am}(X)$ is a finite abelian group.

Proof If $b_1(X)=0$, then, by the previous discussion, $\mathrm{Pic }(X_{\overline{k}})$ is a finitely generated abelian group of rank $\rho (X_{\overline{k}})$. Since $\mathrm{Pic }(X)$ and $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ are contained in $\mathrm{Pic }(X_{\overline{k}})$, they are also finitely generated of rank at most $\rho (X_{\overline{k}})$. Since $\mathrm{Am}(X)=\delta (\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k))$ is a torsion subgroup of $\mathrm{Br}(k)$, Proposition 2.5 implies the stated equality of ranks. Moreover, being torsion and a finitely generated abelian group, $\mathrm{Am}(X)$ is finite. $\square$

2.3 Brauer–Severi Varieties

Next, we recall a couple of results about Brauer–Severi varieties, and refer the interested reader to [18, Chap. 5] and the surveys [27, 41] for details, proofs, and further references.

Definition 2.14

A Brauer–Severi variety over a field k is a proper variety P over k, such that there exists a finite field extension K of k and an isomorphism $P_K\cong {{\mathbb P}}_K^n$ over K.

In case P is of dimension one (resp. two, resp. three), we will also refer to it as a Brauer–Severi curve (resp. Brauer–Severi surface, resp. Brauer–Severi threefold). Any field extension K of k such that $P_K$ is isomorphic to projective space over K is called a splitting field for P, and P is said to split over K. By a theorem of Châtelet, a Brauer–Severi variety P over k is trivial, i.e., splits over k, i.e., is k-isomorphic to projective space over k, if and only if it possesses a k-rational point. Since a geometrically integral variety over a field k always has points over $k^\mathrm{sep}$, it follows that a Brauer–Severi variety can be split over a finite and separable extension of k, which we may also assume to be Galois if we want.

For a finite field extension K of k that is Galois with Galois group G, the set of all Brauer–Severi varieties of dimension n over k that split over K, can be interpreted as the set of all G-twisted forms of ${{\mathbb P}}^n_K$, which is in bijection to the cohomology group $H^1(G,\mathrm{Aut}({{\mathbb P}}^n_K))$. Using $\mathrm{Aut}({{\mathbb P}}^n)\cong \mathrm{PGL}_{n+1}$, and taking cohomology in the short exact sequence

$$ 1\,\rightarrow \,{{\mathbb G}}_m\,\rightarrow \,\mathrm{GL}_{n+1}\,\rightarrow \,\mathrm{PGL}_{n+1}\,\rightarrow \,1, $$

the boundary map associates to the class of a Brauer–Severi variety P of dimension n in $H^1(G,\mathrm{PGL}_{n+1}(K))$ a class in

$$ \mathrm{Br}(K|k) \,:=\, \ker \left( \mathrm{Br}(k)\rightarrow \mathrm{Br}(K)\right) \,=\,\ker \left( {H_{{\acute{\mathrm{e}}{\mathrm{t}}}}^{{2}}}(k,{{\mathbb G}}_m) \rightarrow {H_{{\acute{\mathrm{e}}{\mathrm{t}}}}^{{2}}}(K,{{\mathbb G}}_m) \right) . $$

Taking the limit over all finite Galois extensions of k, we obtain for every Brauer–Severi variety P over k a class $[P]\in \mathrm{Br}(k)$. This cohomology class is torsion and its order is called the period of P, denoted $\mathrm{per}(P)$. By a theorem of Châtelet, a Brauer–Severi variety is trivial if and only if the class $[P]\in \mathrm{Br}(k)$ is zero, i.e., if and only if $\mathrm{per}(P)=1$. We will say that two Brauer–Severi varieties over k are Brauer equivalent if their associated classes in $\mathrm{Br}(k)$ are the same.

To say more about Brauer classes associated to Brauer–Severi varieties, we will shortly digress on non-commutative k-algebras, and refer to [18, Sect. 2] and [26] for details: We recall that a central simple k-algebra is a k-algebra A, whose center is equal to k (i.e., A is central), and whose only two-sided ideals are (0) and A (i.e., A is simple). If A is moreover finite-dimensional over k, then by theorems of Noether, Köthe, and Wedderburn, there exists a finite and separable field extension $k\subseteq K$ that splits A, i.e., $A\otimes _kK\cong \mathrm{Mat}_{n\times n}(K)$. In particular, the dimension of A over k is always a square, and we set the degree of A to be $\mathrm{deg}(A):=\sqrt{\dim _k(A)}$. Two central simple k-algebras $A_1$ and $A_2$ are said to be Brauer equivalent if there exist integers $a_1,a_2\ge 1$ such that $A_1\otimes _k\mathrm{Mat}_{a_1\times a_1}(k)\cong A_2\otimes _k\mathrm{Mat}_{a_2\times a_2}(k)$.

The connection between central simple algebras and Brauer–Severi varieties is the following dictionary, see [18, Theorem 2.4.3].

Theorem 2.15

Let $k\subseteq K$ be a field extension that is Galois with Galois group G. Then, there is a natural bijection of sets between

• (1) Brauer–Severi varieties of dimension n over k that split over K,

• (2) $H^1(G, \mathrm{PGL}_{n+1}(K))$, and

• (3) central simple k-algebras of degree $n+1$ over k that split over K.

Under this bijection, Brauer equivalence of (1) and (3) coincide.

We also recall that a division algebra is a k-algebra in which every non-zero element has a two-sided multiplicative inverse. For example, field extensions of k are division algebras, and a non-commutative example is provided by the quaternions over ${{\mathbb R}}$. Given a simple and finite-dimensional k-algebra A, a theorem of Wedderburn states that there exists a unique division algebra D over k and a unique integer $m\ge 1$ and an isomorphism of k-algebras $A\cong \mathrm{Mat}_{m\times m}(D)$, see [18, Theorem 2.1.3].

Corollary 2.16

If two Brauer–Severi varieties over k of the same dimension are Brauer equivalent, then they are isomorphic as schemes over k.

Proof By Theorem 2.15, it suffices to show that two Brauer equivalent central simple k-algebras $A_1$, $A_2$ of the same dimension are isomorphic. By Wedderburn’s theorem, there exist division algebras $D_i$ and integers $m_i\ge 1$ such that $A_i\cong \mathrm{Mat}_{m_i\times m_i}(D_i)$ for $i=1,2$. By definition of Brauer-equivalence, there exist integers $a_i\ge 1$ and an isomorphism of k-algebras

$$ A_1\otimes _k\mathrm{Mat}_{a_1\times a_1}(k) \,\cong \, A_2\otimes _k\mathrm{Mat}_{a_2\times a_2}(k). $$

Together with the k-algebras isomorphisms

$$ \begin{array}{lcl} A_i\otimes _k\mathrm{Mat}_{a_i\times a_i}(k) &{}\cong &{} \mathrm{Mat}_{m_i\times m_i}(D_i)\otimes _k\mathrm{Mat}_{a_1\times a_1}(k) \\ &{}\cong &{} \mathrm{Mat}_{a_im_i\times a_im_i}(D_i) \end{array} $$

and the uniqueness part in Wedderburn’s theorem, we conclude $D_1\cong D_2$, as well as $a_1=a_2$, whence $A_1\cong A_2$, see also [18, Remark 2.4.7]. $\square$

For Brauer–Severi varieties over k that are of different dimension, we refer to Châtelet’s theorem (Corollary 3.8) below. On the other hand, for Brauer–Severi varieties over k that are of the same dimension, Amitsur conjectured that they are birationally equivalent if and only if their classes generate the same cyclic subgroup of $\mathrm{Br}(k)$, see also Remark 2.20.

For projective space, the degree map $\deg :\mathrm{Pic }({{\mathbb P}}^n_k)\rightarrow {{\mathbb Z}}$, which sends $\mathcal{O}_{{{\mathbb P}}^n_k}(1)$ to 1, is an isomorphism. Thus, if P is a Brauer–Severi variety over k and $G_k:=\mathrm{Gal}(k^\mathrm{sep}/k)$, then there are isomorphisms

$$\begin{array}{lclcl} \mathrm{Pic }_{(P/k)(\mathrm{fppf})}(k) &{}\cong &{} \mathrm{Pic }_{(P/k)}(k^\mathrm{sep})^{G_k} &{}\cong &{}\mathrm{Pic }_{(P/k)}(k^\mathrm{sep}) \\ &{}\cong &{} \mathrm{Pic }({{\mathbb P}}^{\dim (P)}_{k^\mathrm{sep}}) &{}\mathop {\longrightarrow }\limits ^{\mathrm{deg}}&{} {{\mathbb Z}}. \end{array}$$

The first isomorphism is Proposition 2.7, and the second follows from the fact that the $G_k$-action must send the unique ample generator of $\mathrm{Pic }_{(P/k)}(k^\mathrm{sep})$ to an ample generator, showing that $G_k$ acts trivially. The third isomorphism follows from the fact that P splits over a separable extension.

Definition 2.17

For a Brauer–Severi variety P over k, we denote the unique ample generator of $\mathrm{Pic }_{(P/k)(\mathrm{fppf})}(k)$ by $\mathcal{O}_P(1)$.

We stress that $\mathcal{O}_P(1)$ is a class in $\mathrm{Pic }_{(P/k)(\mathrm{fppf})}(k)$ that usually does not come from an invertible sheaf on P - in fact this happens if and only if P is a trivial Brauer–Severi variety, i.e., split over k. For a Brauer–Severi variety, the short exact sequence from Proposition 2.5 becomes the following.

Theorem 2.18

(Lichtenbaum) Let P be a Brauer–Severi variety over k. Then, there exists an exact sequence

$$ 0\,\rightarrow \, \mathrm{Pic }(P) \,\rightarrow \, \underbrace{\mathrm{Pic }_{(P/k)(\mathrm{fppf})}(k)}_{\cong \,{{\mathbb Z}}} \,\mathop {\longrightarrow }\limits ^{\delta }\, \mathrm{Br}(k) \,\rightarrow \,\mathrm{Br}(k(P))\,. $$

More precisely, we have

$$\begin{aligned} \delta (\mathcal{O}_P(1))= & {} [P], \quad \text{ and } \\ \mathrm{Pic }(P)= & {} \mathcal{O}_P(\mathrm{per}(P))\cdot {{\mathbb Z}}. \end{aligned}$$

Since $\omega _P\cong \mathcal{O}_P(-\dim (P)-1)$, the period $\mathrm{per}(P)$ divides $\dim (P)+1$.

Again, we refer to [18, Theorem 5.4.5] for details and proofs. Using Proposition 2.10, we immediately obtain the following classical result of Amitsur [1] as corollary.

Theorem 2.19

(Amitsur) If P is a Brauer–Severi variety over k, then $\mathrm{Am}(P)\cong {{\mathbb Z}}/\mathrm{per}(P){{\mathbb Z}}$. If two Brauer–Severi varieties are birationally equivalent over k, then the have the same Amitsur subgroups inside $\mathrm{Br}(k)$ and in particular, the same period. $\square$

Remark 2.20

In general, it is not true that two Brauer–Severi varieties of the same dimension and the same Amitsur subgroup are isomorphic. We refer to Remark 7.2 for an example arising from a Cremona transformation of Brauer–Severi surfaces. However, Amitsur asked whether two Brauer–Severi varieties of the same dimension with the same Amitsur subgroup are birationally equivalent.

In our applications to del Pezzo surfaces below, we will only need the following easy and probably well-known corollary.

Corollary 2.21

Let P be a Brauer–Severi variety over k. If there exists a zero-cycle on P, whose degree is prime to $(\dim (P)+1)$, then P is is trivial.

Proof Since $\mathrm{Am}(P)\cong {{\mathbb Z}}/\mathrm{per}(P){{\mathbb Z}}$ and its order divides $(\dim (P)+1)$, Lemma 2.9 and the assumptions imply $\mathrm{Am}(P)=0$. Thus, $\mathrm{per}(P)=1$, and then, P is trivial. $\square$

We end this section by mentioning another important invariant of a Brauer–Severi variety P over k, namely, its index, denoted $\mathrm{ind}(P)$. We refer to [18, Chap. 4.5] for the precise definition and note that it is equal to the smallest degree of a finite separable field extension K / k such that $P_K$ is trivial, as well as to the greatest common divisor of the degrees of all finite separable field extensions K / k such that $P_K$ is trivial. By a theorem of Brauer, the period divides the index, and they have the same prime factors, see [18, Proposition 4.5.13].

3 Morphisms to Brauer–Severi Varieties

This section contains Theorem 3.4, the main observation of this article that describes morphisms from a proper variety X over a field k to Brauer–Severi varieties in terms of classes in of $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$. We start by extending classical notions for invertible sheaves to such classes, and then, use these notions to phrase and prove Theorem 3.4. As immediate corollaries, we obtain two classical results of Kang and Châtelet on the geometry of Brauer–Severi varieties.

3.1 Splitting Fields, Globally Generated and Ample Classes

Before coming to the main result of this section, we introduce the following.

Definition 3.1

Let X be a proper variety over k and $\mathcal{L}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$.

• (1) A splitting field for $\mathcal L$ is a field extension K / k such that $\mathcal{L}\otimes _kK$ lies in $\mathrm{Pic }(X_K)$, i.e., arises from an invertible sheaf on $X_K$.

• (2) The class $\mathcal L$ is called globally generated (resp. ample, resp. very ample) if there exists a splitting field K for $\mathcal{L}$ such that $\mathcal{L}\otimes _kK$ is globally generated (resp. ample, resp. very ample) as an invertible sheaf on $X_K$.

From the short exact sequence in Proposition 2.5, it follows that if K is a splitting field for the class $\mathcal{L}$, then there exists precisely one invertible sheaf on $X_K$ up to isomorphism that corresponds to this class. The following lemma shows that these notions are independent of the choice of a splitting field of the class $\mathcal L$.

Lemma 3.2

Let X be a proper variety over k and $\mathcal{L}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$.

• (1) There exists a splitting field for $\mathcal L$ that is a finite and separable extension k, and it can also chosen to be Galois over k.

• (2) Let K and $K'$ be splitting fields for $\mathcal{L}$. Then $\mathcal{L}\otimes _k K\in \mathrm{Pic }(X_K)$ is globally generated (resp. ample, resp. very ample) if and only if $\mathcal{L}\otimes _k K'\in \mathrm{Pic }(X_{K'})$ is globally generated (resp. ample, resp. very ample).

Proof To simplify notation in this proof, we set $\mathcal{L}_K:=\mathcal{L}\otimes _k K$.

Let K be a finite and separable extension of k, such that $\delta (\mathcal{L})\in \mathrm{Br}(k)$ lies in $\mathrm{Br}(K|k)$, where $\delta$ is as in Proposition 2.5. Then, $\delta (\mathcal{L}_K)=0$, i.e., $\mathcal{L}_K$ comes from an invertible sheaf on $X_K$. In particular, K is a splitting field for $\mathcal L$, which is a finite and separable extension of k. Passing to the Galois closure of K / k, we obtain a splitting field for $\mathcal L$ that is a finite Galois extension of k. This establishes claim (1).

Claim (2) is a well-known application of flat base change, but let us recall the arguments for the reader’s convenience: By choosing a field extension of k that contains both K and $K'$, we reduce to the case $k\subseteq K\subseteq K'$. We have $H^0(X_K,\mathcal{L}_K)\otimes _K K'\cong H^0(X_{K'},\mathcal{L}_{K'})$ by flat base change for cohomology, from which it is easy to see that $\mathcal{L}_K$ is globally generated if and only if $\mathcal{L}_{K'}$ is so. Next, if $\mathcal{L}_K$ is very ample, then its global sections give rise to a closed immersion $X_K\rightarrow {{\mathbb P}}^n_K$ for some n. After base change to $K'$, we obtain a closed embedding $X_{K'}\rightarrow {{\mathbb P}}^n_{K'}$ which corresponds to the global sections of $\mathcal{L}_{K'}$, and so, also $\mathcal{L}_{K'}$ is very ample. Conversely, if $\mathcal{L}_{K'}$ is very ample, then it is globally generated, and thus, $\mathcal{L}_K$ is globally generated by what we just established, and thus, gives rise to a morphism $\varphi _K:X_K\rightarrow {{\mathbb P}}^n_K$. By assumption and flat base change, $\varphi _{K'}$ is a closed embedding, and thus, $\varphi _K$ is a closed embedding, and $\mathcal{L}_K$ is very ample. From this, it also follows that $\mathcal{L}_K$ is ample if and only if $\mathcal{L}_{K'}$ is. $\square$

Remark 3.3

Let X be a proper variety over k and let

$$ \begin{array}{ccccc} \delta&:&\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)&{\longrightarrow }&\mathrm{Br}(k) \end{array} $$

be as in Proposition 2.5. We are now in a position to describe $\delta$ explicitly.

• (1) First, and more abstractly: given a class $\mathcal{L}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$, we can choose a splitting field K that is a finite extension k. Thus, ${\mathrm{Spec}\,}K\rightarrow {\mathrm{Spec}\,}k$ is an fppf cover, the class $\mathcal{L}\otimes _k K$ comes with an fppf descent datum, and it arises from an invertible sheaf $\mathcal{M}$ on $X_K$. The crucial point is that the descent datum is for a class in $\mathrm{Pic }(X_K)$, where isomorphism classes of invertible sheaves are identified. In order to turn this into a descent datum for the invertible sheaf $\mathcal M$, we have to choose isomorphisms, which are only unique up to a ${{\mathbb G}}_m=\mathrm{Aut}(\mathcal{M})$-action, and we obtain a ${{\mathbb G}}_m$-gerbe that is of class $\delta (\mathcal{L})\in H^2_{\mathrm{fppf}}({\mathrm{Spec}\,}k,{{\mathbb G}}_m)=\mathrm{Br}(k)$. This gerbe is neutral if and only if $\delta (\mathcal{L})=0$. This is equivalent to being able to extend the descent datum for the class $\mathcal{L}\otimes _k K$ to a descent datum for the invertible sheaf $\mathcal{M}$.

• (2) Second, and more concretely: given a class $\mathcal{L}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$, we can choose a splitting field K that is a finite Galois extension of k, say with Galois group G. Thus, the class ${\mathcal{{L}}}\otimes _k K$ arises from an invertible sheaf $\mathcal M$ on $X_K$ and lies in $\mathrm{Pic }_X(K)^G$ and we can choose isomorphisms

  $$ \imath _g \,:\, g^*\mathcal{M} \,\mathop {\longrightarrow }\limits ^{\cong }\, \mathcal{M}, $$

  which are unique up to a ${{\mathbb G}}_m$-action. In particular, they may fail to form a Galois descent datum for $\mathcal M$, and the failure of turning $\{\imath _g\}_{g\in G}$ into a Galois descent datum for $\mathcal M$ gives rise to a cohomology class $\delta (\mathcal{L})\in {H_{{\acute{\mathrm{e}}{\mathrm{t}}}}^{{2}}}({\mathrm{Spec}\,}k,{{\mathbb G}}_m)=\mathrm{Br}(k)$. More precisely, this class lies in the subgroup $\mathrm{Br}(K|k)$ of $\mathrm{Br}(k)$.

The following is an analog for Brauer–Severi varieties of the classical correspondence between morphisms to projective space and globally generated invertible sheaves as explained, for example, in [24, Theorem II.7.1], see also Remark 3.5 below.

Theorem 3.4

Let X be a proper variety over a field k.

• (1) Let $\varphi :X\rightarrow P$ be a morphism to a Brauer–Severi variety P over k, and consider the induced homomorphism of abelian groups

  $$ \begin{array}{ccccc} \varphi ^*&:&\mathrm{Pic }_{(P/k)(\mathrm{fppf})}(k)\rightarrow & {} \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k). \end{array} $$

  Then, $\mathcal{L}:=\varphi ^*\mathcal{O}_P(1)$ is a globally generated class with

  $$ \begin{array}{ccc} \delta (\mathcal{L}) \,=\, [P]\in & {} \mathrm{Br}(k), \end{array} $$

  where $\delta$ is as in Proposition 2.5. If $\varphi$ is a closed immersion, then $\mathcal L$ is very ample.

• (2) Let $\mathcal{L}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ be a globally generated class. If K is a splitting field, then the morphism to projective space over K associated to the complete linear system $|\mathcal{L}\otimes _kK|$ descends to morphism over k

  $$ \begin{array}{ccccc} |\mathcal{L}|&:&X\rightarrow & {} P, \end{array} $$

  where P is a Brauer–Severi variety over k with $\delta (\mathcal{L})=[P]$. If $\mathcal{L}$ is very ample, then $|\mathcal{L}|$ is a closed immersion.

Proof Let $\varphi :X\rightarrow P$ and $\mathcal L$ be as in (1). Then, we have $\delta (\mathcal{L})=\delta (\mathcal{O}_P(1))=[P]\in \mathrm{Br}(k)$, where the first equality follows from functoriality of the exact sequence in Proposition 2.5, and the second from Theorem 2.18. Let K be a splitting field for $\mathcal L$, and let $\mathcal M$ be the invertible sheaf corresponding to $\mathcal{L}\otimes _k K$ on $X_K$. Being an invertible sheaf, we have $\delta (\mathcal{M})=0\in \mathrm{Br}(K)$, which implies that the morphism $\varphi _K:X_K\rightarrow P_K$ maps to a Brauer–Severi variety of class $[P_K]=\delta (\mathcal{M})=0$, i.e., $P_K\cong {{\mathbb P}}_K^n$. By definition and base change, we obtain $\mathcal{M}\cong \varphi _K^*(\mathcal{O}_{{{\mathbb P}}_K^n}(1))$. Thus, $\mathcal M$ is globally generated (as an invertible sheaf), which implies that $\mathcal{L}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ is globally generated in the sense of Definition 3.1. Moreover, if $\varphi$ is a closed immersion, then so is $\varphi _K$, which implies that $\mathcal{M}\in \mathrm{Pic }(X_K)$ is very ample (as an invertible sheaf), and thus, $\mathcal{L}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ is very ample in the sense of Definition 3.1. This establishes claim (1).

To establish claim (2), let $\mathcal{L}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf)}}(k)$ be globally generated. By Lemma 3.2, there exists a splitting field $K'$ for $\mathcal{L}$ that is a finite Galois extension of k, say with Galois group G. Thus, $\mathcal{L}\otimes _kK'$ corresponds to an invertible sheaf $\mathcal{M}$ on $X_{K'}$, whose isomorphism class lies in $\mathrm{Pic }_{X}(K')^G$, see Proposition 2.7.

If $f:X\rightarrow {\mathrm{Spec}\,}k$ is the structure morphism, then $(f_{K'})_*\mathcal{M}$ is a finite-dimensional $K'$-vector space. By our assumptions on global generation we obtain a morphism over $K'$

$$ |\mathcal{M}| \,:\,X_{K'} \,\rightarrow \, {{\mathbb P}}((f_{K'})_*\mathcal{M}). $$

As explained in Remark 3.3.(2), there exist isomorphisms $\{\imath _g:g^*\mathcal{M}\rightarrow \mathcal{M}\}_{g\in G}$ that are unique up to a ${{\mathbb G}}_m$-action. In particular, we obtain a well-defined G-action on ${{\mathbb P}}((f_{K'})_*\mathcal{M})$, and the morphism defined by $|\mathcal{M}|$ is G-equivariant. Taking the quotient by G, we obtain a morphism over k

$$ |\mathcal{L}|\,:\,X\rightarrow P. $$

Since $P_K$ is isomorphic to ${{\mathbb P}}((f_{K'})_*\mathcal{M})$, we see that P is a Brauer–Severi variety over k and, as observed by Grothendieck in [21, Sect. 5.4], we have $\delta (\mathcal{L})=[P]$ in $\mathrm{Br}(k)$.

Finally, let K be an arbitrary splitting field for $\mathcal{L}$. Let $\varphi :X\rightarrow P$ be the previously constructed morphism and choose an extension field $\Omega$ of k that contains K and $K'$. Then, $\mathcal{L}\otimes _k\Omega$ is an invertible sheaf on $X_\Omega$, globally generated by Lemma 3.2, and, since $k\subseteq K'\subseteq \Omega$, the morphism associated to $|\mathcal{L}\otimes _k\Omega |$ is equal to $\varphi _\Omega =(\varphi _{K'})_\Omega :X_\Omega \rightarrow P_\Omega$. Since K is a splitting field for $\mathcal{L}$, it is also a splitting field for $P_{K}$ (see the argument in the proof of claim (1)), and in particular, $P_{K'}$ is a trivial Brauer–Severi variety. We have $\mathcal{L}\otimes _k\Omega \cong \varphi _\Omega ^*\mathcal{O}_{P_\Omega }(1)$, from which we deduce $\mathcal{L}\otimes _k K\cong \varphi _{K}^*\mathcal{O}_{P_{K}}(1)$, as well as that $\varphi _{K}$ is the morphism associated to $|\mathcal{L}\otimes _k K|$. In particular, the morphism associated to $|\mathcal{L}\otimes _k K|$ descends to $\varphi :X\rightarrow P$, where P is a Brauer–Severi variety of class $\delta (\mathcal{L})$. This establishes claim (2). $\square$

Remark 3.5

Let us note the following.

• (1) The construction of a Brauer–Severi variety over k from a globally generated class in $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ (in our terminology) is due to Grothendieck in [21, Sect. 5.4].

• (2) In Theorem 3.4.(2), we only considered complete linear systems. We leave it to the reader to show the following generalization: Given a class $\mathcal{L}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$, a splitting field K that is finite and Galois over k with Galois group G, and $V\subseteq H^0(X_K,\mathcal{L}\otimes _kK)$ a G-stable K-linear subspace, whose global sections generate $\mathcal{L}\otimes _kK$, we can descend the morphism $X_K\rightarrow {{\mathbb P}}(V)$ to a morphism $X\rightarrow P'$, where $P'$ is a Brauer–Severi variety over k of class $[P']=\delta (\mathcal{L})\in \mathrm{Br}(k)$.

• (3) If X in Theorem 3.4 has a k-rational point, i.e., $X(k)\ne \emptyset$, then we recover the well-known correspondence between morphisms to projective space and globally generated invertible sheaves:

  • (a) Then, $\delta \equiv 0$ and every class in $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ comes from an invertible sheaf on X by Proposition 2.5,

  • (b) and since every morphism $\varphi :X\rightarrow P$ gives rise to a k-rational point on P, i.e., P is a trivial Brauer–Severi variety.

3.2 Two Classical Results on Brauer–Severi Varieties

As our first corollary and application, we recover the following theorem of Kang [29], see also [18, Theorem 5.2.2], which is a Brauer–Severi variety analog of Veronese embeddings of projective spaces.

Corollary 3.6

(Kang) Let P be a Brauer–Severi variety of period $\mathrm{per}(P)$ over k. Then, the class of $\mathcal{O}_{P}(\mathrm{per}(P))$ arises from a very ample invertible sheaf on P and gives rise to an embedding

$$ |\mathcal{O}_P(\mathrm{per}(P))| \,:\, P \,\rightarrow \, {{\mathbb P}}^N_k, \quad \text{ where } \quad N\,=\, \left( {\begin{array}{c}\dim (P)+\mathrm{per}(P)\\ \mathrm{per}(P)\end{array}}\right) . $$

After base change to a splitting field K of P, this embedding becomes the $\mathrm{per}(P)$-uple Veronese embedding of ${{\mathbb P}}^{\dim (P)}_K$ into ${{\mathbb P}}^N_K$.

Proof

If $n\ge 1$, then $\mathcal{O}_P(n)$ is very ample in the sense of Definition 3.1, and thus, defines an embedding into a Brauer–Severi variety $P'$ over k. Over a splitting field of P, this embedding becomes the n-uple Veronese embedding. Since $\delta (\mathcal{O}_P(1))=[P]\in \mathrm{Br}(k)$ and this element of order $\mathrm{per}(P)$, we see that if $\mathrm{per}(P)$ divides n, then $\mathcal{O}_P(n)$ is an invertible sheaf on P and $P'$ is a trivial Brauer–Severi variety. $\square$

Example 3.7

Let X be a smooth and proper variety of dimension one over k. If $\omega _X^{-1}$ is ample, then it is a curve of genus $g(X)=h^0(X,\omega _X)=0$. Thus, X is isomorphic to ${{\mathbb P}}^1$ over $\overline{k}$, i.e., X is a Brauer–Severi curve. There exists a unique class $\mathcal{{L}}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ with $\mathcal{{L}}^{\otimes 2}\cong \omega _X^{-1}$, and it gives rise to an isomorphism $|\mathcal{{L}}|:X\rightarrow P$, where P is a Brauer–Severi curve with $\delta (\mathcal{{L}})=[P]\in \mathrm{Br}(k)$. Moreover, $\mathcal{{L}}^{\otimes 2}\cong \omega _X^{-1}$ is an invertible sheaf on X that defines an embedding $|\omega _X^{-1}|:X\rightarrow {{\mathbb P}}^2_k$ as a plane conic.

A subvariety $X\subseteq P$ of a Brauer–Severi variety P over k is called twisted linear if $X_{\overline{k}}$ is a linear subspace of $P_{\overline{k}}$. As second application, we recover the following theorem of Châtelet, see [18, Sect. 5.3], and it follows from a Brauer–Severi variety analog of Segre embeddings of products of projective spaces.

Corollary 3.8

(Châtelet) Let $P_1$ and $P_2$ be two Brauer–Severi varieties over k of dimension $d_1$ and $d_2$, respectively.

• (1) If $P_1$ is a twisted linear subvariety of $P_2$, then $[P_1]=[P_2]\in \mathrm{Br}(k)$.

• (2) If $[P_1]=[P_2]\in \mathrm{Br}(k)$, then there exists a Brauer–Severi variety P over k, such that $P_1$ and $P_2$ can be embedded as twisted-linear subvarieties into P.

Proof If $\varphi :P_1{\hookrightarrow }P_2$ is a twisted-linear subvariety, then $\varphi ^*\mathcal{O}_{P_2}(1)=\mathcal{O}_{P_1}(1)\in \mathrm{Pic }_{(P_1/k)(\mathrm{fppf})}(k)$. We find $[P_1]=\delta (\mathcal{O}_{P_1}(1))=\delta (\mathcal{O}_{P_2}(1))=[P_2]$ by functoriality of the exact sequence of Proposition 2.5, and (1) follows.

Next, we show (2). By Theorem 3.4, there exists an embedding $\varphi$ of $P_1\times {{\mathbb P}}_k^{d_2}$ into a Brauer–Severi variety P of dimension $N:=(d_1+1)(d_2+1)-1=d_1d_2+d_1+d_2$ over k associated to the class $\mathcal{O}_{P_1}(1)\boxtimes \mathcal{O}_{{{\mathbb P}}_k^{d_2}}(1)$. Over a splitting field of $P_1$, this embedding becomes the Segre embedding of ${{\mathbb P}}^{d_1}\times {{\mathbb P}}^{d_2}$ into ${{\mathbb P}}^N$. If x is a k-rational point of ${{\mathbb P}}_k^{d_2}$, then $\varphi (P_1\times \{x\})$ realizes $P_1$ as twisted-linear subvariety of P and we have $[P]=[P_1]\in \mathrm{Br}(k)$ by claim (1). Similarly, we obtain an embedding of $P_2$ as twisted-linear subvariety into a Brauer–Severi variety $P'$ of dimension N over k of class $[P']=[P_2]\in \mathrm{Br}(k)$. Since $[P]=[P']\in \mathrm{Br}(k)$ and $\dim (P)=\dim (P')$, we find $P\cong P'$ by Corollary 2.16 and (2) follows. $\square$

4 Del Pezzo Surfaces

For the remainder of this article, we study del Pezzo surfaces with a view towards Brauer–Severi varieties. Most, if not all, results of these sections are known in some form or another to the experts. However, our more geometric approach, as well as some of the proofs, are new.

Let us first recall some classical results about del Pezzo surfaces, and refer the reader to [35, Chap. IV] or the surveys [7, 41, 47] for details, proofs, and references. For more results about the classification of geometrically rational surfaces, see [25, 34].

Definition 4.1

A del Pezzo surface is a smooth and proper variety X of dimension two over a field k such that $\omega _X^{-1}$ is ample. The degree of a del Pezzo surface is the self-intersection number of $\omega _X$.

In arbitrary dimension, smooth and proper varieties X over k with ample $\omega _X^{-1}$ are called Fano varieties. As discussed in Example 3.7, Fano varieties of dimension one over k are the same as Brauer–Severi curves over k.

4.1 Geometry

The degree d of a del Pezzo surface X over a field k satisfies $1\le d\le 9$. Set $\overline{X}:=X_{\overline{k}}$. We will say that X is of product type if

$$ \begin{array}{ccc} \overline{X}\cong & {} {{\mathbb P}}^1_{\overline{k}}\times {{\mathbb P}}^1_{\overline{k}}, \end{array} $$

in which case we have $d=8$. If X is not of product type, then there exists a birational morphism

$$ \begin{array}{ccccc} \overline{f}&:&\overline{X}\rightarrow & {} {{\mathbb P}}^2_{\overline{k}} \end{array} $$

that is a blow-up of $(9-d)$ closed points $P_1,...,P_{9-d}$ in general position, i.e., no 3 of them lie on a line, no 6 of them lie on a conic, and there is no cubic through all these points having a double point in one of them. In particular, if $d=9$, then $\overline{f}$ is an isomorphism and X is a Brauer–Severi surface over k.

4.2 Arithmetic

By the previous discussion and Lemma 2.13, the Néron–Severi rank of a del Pezzo surface X of degree d over k satisfies

$$ 1\,\le \,\rho (X)\,:=\, \mathrm{rank}\,\mathrm{Pic }(X)\,=\,\mathrm{rank}\,\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k) \,\le \,10-d, $$

and $\rho (X_{\overline{k}})=10-d$.

The following result about geometrically rational surfaces allows using methods from Galois theory even if the ground field k is not perfect. This result is particularly useful in proofs, see also the discussion in [47, Sect. 1.4]. In particular, it applies to del Pezzo surfaces.

Theorem 4.2

(Coombes$+\varepsilon$) Let X be a smooth and proper variety over k such that $X_{\overline{k}}$ is birational to ${{\mathbb P}}^2_{\overline{k}}$. Then,

• (1) $X_{k^\mathrm{sep}}$ is birationally equivalent to ${{\mathbb P}}^2_{k^\mathrm{sep}}$ via a sequence of blow-ups in points in $k^\mathrm{sep}$-rational points and their inverses.

• (2) The natural map $\mathrm{Pic }_X(k^\mathrm{sep})\rightarrow \mathrm{Pic }_X({\overline{k}})$ is an isomorphism.

Proof Assertion (1) is the main result of [11]. Clearly, assertion (2) holds for projective space over any field. Next, let Y be a variety that is smooth and proper over $k^\mathrm{sep}$, $\widetilde{Y}\rightarrow Y$ be the blow-up of a $k^\mathrm{sep}$-rational point, and let $E\subset \widetilde{Y}$ be the exceptional divisor. Then, $\mathrm{Pic }_{\widetilde{Y}}(K)=\mathrm{Pic }_Y(K)\oplus {{\mathbb Z}}\cdot E$ for $K=k^\mathrm{sep}$, as well as for $K=\overline{k}$. Using (1) and these two observations, assertion (2) follows. $\square$

We will also need the following useful observation, due to Lang [33] and Nishimura [39], which implies that having a k-rational point is a birational invariant of smooth and proper varieties over k. We refer to [47, Sect. 1.2] for details and proof.

Lemma 4.3

(Lang–Nishimura) Let $X\dashrightarrow Y$ be a rational map of varieties over k, such that X is smooth over k, and such that Y is proper over k. If X has a k-rational point, then so has Y.$\square$

Moreover, we have already seen that a Brauer–Severi variety P over k is isomorphic to projective space over k if and only if P has a k-rational point, and we refer the interested reader to [14] for an algorithm to decide whether a Brauer–Severi surface has a k-rational point. In Definition 2.8, we defined the Amitsur group and showed its birational invariance in Proposition 2.10. Using Iskovskih’s classification [25] of geometrically rational surfaces, we obtain the following list and refer to [10, Proposition 5.2] for details and proof.

Theorem 4.4

(Colliot-Thélène–Karpenko–Merkurjev) Let X be a smooth and proper variety over a perfect field k such that $X_{\overline{k}}$ is birationally equivalent to ${{\mathbb P}}^2_{\overline{k}}$. Then, $\mathrm{Am}(X)$ is one of the following groups

$$ 0, \quad {{\mathbb Z}}/2{{\mathbb Z}}, \quad ({{\mathbb Z}}/2{{\mathbb Z}})^2, \quad \text{ and } \quad {{\mathbb Z}}/3{{\mathbb Z}}. $$

We will see explicit examples of all these groups arising as Amitsur groups of del Pezzo surfaces in the next sections.

We now introduce another important invariant. Namely, if $G_k$ denotes the absolute Galois group of k, and $H\subseteq G_k$ is a closed subgroup, then we consider for a smooth and projective variety X over k the group cohomology

$$ H^1\left( H,\, \mathrm{Pic }_{X/k}({k^\mathrm{sep}})\right) , $$

which is an abelian torsion group. If $b_1(X)=0$, then $\mathrm{Pic }_{X/k}(k^\mathrm{sep})$ is finitely generated by Lemma 2.13 and then, $H^1(H,\, \mathrm{Pic }_{X/k}({k^\mathrm{sep}}))$ is a finite abelian group. Moreover, if $X_{k^\mathrm{sep}}$ is a rational surface, then $\mathrm{Br}'(X_{k^\mathrm{sep}})=0$ (see, for example, [35, Theorem 42.8] or [36]) and an appropriate Hochschild–Serre spectral sequence yields an exact sequence

$$ 0\,\rightarrow \,\mathrm{Br}'(X)/\mathrm{Br}(k)\,\mathop {\longrightarrow }\limits ^{\alpha }\, H^1\left( G_k,\, \mathrm{Pic }_{X/k}({k^\mathrm{sep}})\right) \,\rightarrow \, H^3(G_k,(k^\mathrm{sep})^\times ). $$

Moreover, if k is a global field, then the term on the right is zero by a theorem of Tate (see, for example, [38, Chap. VIII.3]), thus, $\alpha$ is an isomorphism, and we obtain an interpretation of this cohomology group in terms of Brauer groups, see [47, Sect. 3.4].

Lemma 4.5

If P is a Brauer–Severi variety over k, then

$$ H^1\left( H,\, \mathrm{Pic }_{P/k}({k^\mathrm{sep}})\right) \,=\,0 $$

for all closed subgroups $H\subseteq G_k$.

Proof Since $\mathrm{Pic }_{P/k}({k^\mathrm{sep}})\cong {{\mathbb Z}}\cdot \mathcal{O}_P(1)$ and since $G_k$ acts trivially on the class $\mathcal{O}_P(1)$, the desired $H^1$ is isomorphic to $\mathrm{Hom}(H,{{\mathbb Z}})$, see [4, Chap. III.1, Exercise 2], for example. This is zero since H is a profinite group and the homomorphisms to ${{\mathbb Z}}$ are required to be continuous. $\square$

In Proposition 2.10, we established birational invariance of $\mathrm{Am}(X)$. The following result of Manin [35, Sect. 1 of the Appendix] shows that also the above group cohomology groups are a birational invariants.

Theorem 4.6

(Manin) For every closed subgroup $H\subseteq G_k$, the group

$$ H^1\left( H,\, \mathrm{Pic }_{X/k}({k^\mathrm{sep}})\right) $$

is a birational invariant of smooth and projective varieties over k. $\square$

Remark 4.7

Every birational map between smooth and projective surfaces can be factored into a sequence of blow-ups in closed points, see [35, Chap. III]. Using this, one can give very explicit proofs of Proposition 2.10 and Theorem 4.6 in dimension 2. (For such a proof of Theorem 4.6 in dimension 2, see the proof of [35, Theorem 29.1].)

4.3 Hasse Principle and Weak Approximation

For a global field K, i.e., a finite extension of ${{\mathbb Q}}$ or of ${{\mathbb F}}_p(t)$, we denote by $\Omega _K$ the set of its places, including the infinite ones if K is of characteristic zero. A class $\mathcal{{C}}$ of varieties over K satisfies

• (1) the Hasse principle, if for every $X\in \mathcal{{C}}$ we have $X(K)\ne \emptyset$ if and only if $X(K_\nu )\ne \emptyset$ for all $\nu \in \Omega _K$. Moreover, $\mathcal{{C}}$ satisfies

• (2) weak approximation, if the diagonal embedding

  $$ X(K) \rightarrow \prod _{\nu \in \Omega _K} X(K_\nu ) $$

  is dense for the product of the $\nu$-adic topologies.

If $\mathcal{{C}}$ satisfies weak approximation, then it obviously also satisfies the Hasse principle, but the converse need not hold. For example, Brauer–Severi varieties over K satisfy the Hasse principle by a theorem of Châtelet [5], as well as weak approximation. However, both properties may fail for del Pezzo surfaces over K, and we refer to [47] for an introduction to this topic. We end this section by noting that the obstruction to a class $\mathrm{Pic }_{(X/K)(\mathrm{fppf})}(K)$ coming from $\mathrm{Pic }_X(K)$ satisfies the Hasse principle.

Lemma 4.8

Let X a proper variety over a global field K and let $\mathcal{{L}}\in \mathrm{Pic }_{(X/K)(\mathrm{fppf})}(K)$. Then, the following are equivalent

• (1) $0=\delta (\mathcal{L})\in \mathrm{Br}(K)$, and

• (2) $0=\delta (\mathcal{{L}}\otimes _K K_\nu )\in \mathrm{Br}(K_\nu ) \text{ for } \text{ all } \nu \in \Omega _K$.

Proof A class in $\mathrm{Br}(K)$ is zero if and only if its image in $\mathrm{Br}(K_\nu )$ is zero for all $\nu \in \Omega _K$ by the Hasse principle for the Brauer group. From this, and functoriality of the exact sequence from Proposition 2.5, the assertion follows. $\square$

For example, if $X(K_\nu )\ne \emptyset$ for all $\nu \in \Omega _X$, then $\delta$ is the zero map by Proposition 2.5 and this lemma. In this case, every class in $\mathrm{Pic }_{(X/K)(\mathrm{fppf})}(K)$ comes from an invertible sheaf on X.

5 Del Pezzo Surfaces of Product Type

In this section, we classify degree 8 del Pezzo surfaces of product type over k, i.e., surfaces X over k with $X_{\overline{k}}\cong {{\mathbb P}}^1_{\overline{k}}\times {{\mathbb P}}^1_{\overline{k}}$, in terms of Brauer–Severi varieties.

First, for ${{\mathbb P}}^1_k\times {{\mathbb P}}^1_k$, the anti-canonical embedding can be written as composition of Veronese- and Segre-maps as follows

$$ \begin{array}{ccccccc} |-K_{{{\mathbb P}}^1_k\times {{\mathbb P}}^1_k}|&:&{{\mathbb P}}^1_k\times {{\mathbb P}}^1_k&\mathop {\longrightarrow }\limits ^{\nu _2\times \nu _2}&{{\mathbb P}}^2_k\times {{\mathbb P}}^2_k&\mathop {\longrightarrow }\limits ^{\sigma }&{{\mathbb P}}^8_k\,. \end{array} $$

Next, the invertible sheaf $\omega _{{{\mathbb P}}^1_k\times {{\mathbb P}}^1_k}^{-1}$ is uniquely 2-divisible in the Picard group, and we obtain an embedding as a smooth quadric

$$ \begin{array}{ccccc} |{\scriptstyle -\frac{1}{2}}K_{{{\mathbb P}}^1_k\times {{\mathbb P}}^1_k}|&:&{{\mathbb P}}^1_k\times {{\mathbb P}}^1_k&\mathop {\longrightarrow }\limits ^{\sigma }&{{\mathbb P}}^3_k\,. \end{array} $$

Now, let X be a degree 8 del Pezzo surface of product type over k. Then, the anti-canonical linear system yields an embedding of X as a surface of degree 8 into ${{\mathbb P}}^8_k$. However, the “half-anti-canonical linear system” exists in general only as a morphism to a Brauer–Severi threefold as the following result shows.

Theorem 5.1

Let X be a degree 8 del Pezzo surface of product type over a field k. Then, there exist a unique class $\mathcal{L}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ with $\mathcal{L}^{\otimes 2}\cong \omega _X^{-1}$ and an embedding

$$\begin{array}{ccccc} |\mathcal{{L}}|&:&X&{\hookrightarrow }&P \end{array} $$

into a Brauer–Severi threefold P over k with Brauer class

$$\begin{array}{ccc} \delta (\mathcal{L}) \,=\, [P]\in & {} \mathrm{Br}(k), \end{array} $$

and such that $X_{\overline{k}}$ is a smooth quadric in $P_{\overline{k}}\cong {{\mathbb P}}^3_{\overline{k}}$. Moreover, X is rational if and only if X has a k-rational point. In this case, we have $P\cong {{\mathbb P}}^3_k$.

Proof To simplify notation, set $L:=k^\mathrm{sep}$. We have $X(L)\ne \emptyset$, for example, by [18, Proposition A.1.1], as well as $\mathrm{Pic }(X_L)\cong \mathrm{Pic }(X_{\overline{k}})\cong {{\mathbb Z}}^2$ by Theorem 4.2. The classes (1, 0) and (0, 1) of $\mathrm{Pic }(X_L)$ give rise to two morphisms $X_L\rightarrow {{\mathbb P}}^1_L$, and we obtain an isomorphism $X_L\cong {{\mathbb P}}^1_L\times {{\mathbb P}}^1_L$. By abuse of notation, we re-define $\overline{X}$ to be $X_L$. Next, the absolute Galois group $G_k$ acts trivially on the canonical class $(-2,-2)$, and thus, the $G_k$-action on ${{\mathbb Z}}(1,1)\subset {{\mathbb Z}}^2$ is trivial. By Proposition 2.7, we have $\mathrm{Pic }_{X/k}(K)^{G_k}\cong \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$, and, since $(1,1)\in {{\mathbb Z}}^2$ is $G_k$-invariant, the unique invertible sheaf $\mathcal{{L}}$ on $\overline{X}$ with $\mathcal{{L}}^{\otimes 2}\cong \omega _{\overline{X}}^{-1}$ descends to a class in $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$. Over L, the class $\mathcal{{L}}$ is very ample and defines an embedding of $\overline{X}$ as smooth quadric surface into ${{\mathbb P}}^3_L$. Thus, by Theorem 3.4, we obtain an embedding $|\mathcal{{L}}|:X{\hookrightarrow }P$, where P is a Brauer–Severi threefold over k with $\delta (\mathcal{{L}})=[P]\in \mathrm{Br}(k)$.

Finally, if X is rational, then it has a k-rational point, and then, also P has a k-rational point, i.e., $P\cong {{\mathbb P}}^3_k$. Conversely, if there exists a k-rational point $x\in X$, then X is a quadric in ${{\mathbb P}}^3_k$, and projection away from x induces a birational map $X\dashrightarrow {{\mathbb P}}^2_k$. $\square$

Next, we establish an explicit classification of degree 8 del Pezzo surfaces of product type in terms of the Néron–Severi rank $\rho$ and Brauer–Severi curves. To simplify notation in the sequel, let us recall the definition of contracted products. If a finite group G acts on a scheme X from the right and it acts on a scheme Y from the left and all schemes and actions are over ${\mathrm{Spec}\,}k$ for some field k, then we denote the quotient of $X\times _{{\mathrm{Spec}\,}k} Y$ by the diagonal G-action defined by $(x,y)\mapsto (xg,g^{-1}y)$ for all $g\in G$ by

$$ X\wedge ^G Y \,:=\, (X\times _{{\mathrm{Spec}\,}k} Y)/G. $$

We refer to [19, Chap. III.1.3] for details and applications.

Proposition 5.2

Let X and $X\subset P$ be as in Theorem 5.1.

• (1) if $\rho (X)=2$, then

  $$\begin{array}{ccc} X\cong & {} P'\times P'', \end{array} $$

  where $P'$ and $P''$ are Brauer–Severi curves over k, whose Brauer classes satisfy $[P]=[P']+[P'']\in \mathrm{Br}(k)$. In particular, $P\cong {{\mathbb P}}^3_k$ if and only if $P'\cong P''$.

• (2) If $\rho (X)=1$, then there exist a Brauer–Severi curve $P'$ over k and a finite Galois extension K / k with Galois group $H:={{\mathbb Z}}/2{{\mathbb Z}}$, such that X arises as twisted self-product

  $$\begin{array}{ccccc} X\cong & {} (P'\times P')_K/H= & {} {\mathrm{Spec}\,}K\wedge ^H (P'\times P'), \end{array} $$

  where the H-action permutes the factors of $P'_K\times P'_K$. Moreover, $P\cong {{\mathbb P}}^3_k$ and $P'$ is a hyperplane section of $X\subset {{\mathbb P}}^3_k$.

Proof

We keep the notations and assumptions from the proof of Theorem 5.1. The $G_k$-action fixes the class (1, 1). Since the $G_k$-action preserves the intersection pairing on $\mathrm{Pic }_{X/k}(k^\mathrm{sep})$, it follows that $G_k$ acts on ${{\mathbb Z}}(1,-1)$ either trivially, or by sign changes. We have $\rho (X)=2$ in the first case, and $\rho (X)=1$ in the latter.

First, assume that $\rho (X)=2$. By Theorem 3.4, the classes (1, 0) and (0, 1) give rise to morphisms to Brauer–Severi curves $X\rightarrow P'$ and $X\rightarrow P''$ of class $[P']=\delta ((1,0))$ and $[P'']=\delta ((0,1))$ in $\mathrm{Br}(k)$, respectively. Thus, we obtain a morphism $X\rightarrow P'\times P''$, which is an isomorphism because it is an isomorphism over $k^\mathrm{sep}$. Since $\delta$ is a homomorphism, we find $[P]=\delta (\mathcal{{L}})=\delta ((1,1))=\delta ((1,0))+\delta ((0,1))=[P']+[P'']$. Using that $P'$ and $P''$ are of period 2, we find that $P\cong {{\mathbb P}}^3_k$ if and only if $[P]=0$, i.e., if and only if $[P']=[P'']$. By Corollary 2.16, the latter is equivalent to $P'\cong P''$.

Second, assume that $\rho (X)=1$. Then, the $G_k$-action permutes (0, 1) and (1, 0), i.e., it permutes the factors of ${{\mathbb P}}^1_{k^\mathrm{sep}}\times {{\mathbb P}}^1_{k^\mathrm{sep}}$. Thus, there exists a unique quadratic Galois extension K / k, such that $\mathrm{Gal}(k^\mathrm{sep}/K)$ acts trivially on $\mathrm{Pic }_{X/k}(k^\mathrm{sep})$ and by the previous analysis we have $X_K:=Q''\times Q'''$ for two Brauer–Severi curves $Q''$, $Q'''$ over K. Using these and the $H:=\mathrm{Gal}(K/k)$-action, we obtain a H-stable diagonal embedding $Q'\subset X_K$ of a Brauer–Severi curve over K, and then, the two projections induce isomorphisms $Q'\cong Q''$ and $Q'\cong Q'''$ over K. Taking the quotient by H, we obtain a Brauer–Severi curve $P':=Q'/H\subset X$ over k. Clearly, $P'_K\cong Q'$ and we obtain the description of X as twisted self-product. On X, the curve $P'$ is a section of the class (1, 1), which implies that this class comes from an invertible sheaf, and thus, $0=\delta ((1,1))\in \mathrm{Br}(k)$ by Proposition 2.5. Since $\delta ((1,1))=[P]$, we conclude $P\cong {{\mathbb P}}^3_k$. $\square$

Remark 5.3

In the case of quadrics in ${{\mathbb P}}^3$, similar results were already established in [9]. A related, but somewhat different view on degree 8 del Pezzo surfaces of product type was taken in (the proof of) [10, Proposition 5.2]: If X is such a surface, then there exists a quadratic Galois extension K / k and a Brauer–Severi curve C over K, such that $X\cong \mathrm{Res}_{K/k}C$, where $\mathrm{Res}_{K/k}$ denotes Weil restriction, see also [41].

Corollary 5.4

Let X be as in Theorem 5.1. Then,

$$ H^1\left( H,\, \mathrm{Pic }_{X/k}({k^\mathrm{sep}})\right) \,=\,0 $$

for all closed subgroups $H\subseteq G_k$, and

$$ \mathrm{Am}(X) \,\cong \, \left\{ \begin{array}{ll} 0 &{} \text{ if } \, \rho =1 \, \text{ or } \text{ if } \, X\cong {{\mathbb P}}^1_k\times {{\mathbb P}}^1_k,\\ ({{\mathbb Z}}/2{{\mathbb Z}})^2 &{} \text{ if } \, \rho =2 \, \text{ and } \, {{\mathbb P}}^1_k\not \cong P'\not \cong P''\not \cong {{\mathbb P}}^1_k,\\ ({{\mathbb Z}}/2{{\mathbb Z}}) &{} \text{ in } \text{ the } \text{ remaining } \, \rho =2\text{-cases. } \end{array} \right. $$

Proof Set $H^1(H):=H^1(H,\, \mathrm{Pic }_{X/k}({k^\mathrm{sep}}))$. If $\rho =2$, then the $G_k$-action on $\mathrm{Pic }_{X/k}(k^\mathrm{sep})$ is trivial, and we find $H^1(H)=0$ as in the proof of Lemma 4.5. Moreover, $\mathrm{Am}(X)$ is generated by $\delta ((0,1)$ and $\delta ((1,0))$, i.e., by $[P']$ and $[P'']$ in $\mathrm{Br}(k)$. From this, the assertions on $\mathrm{Am}(X)$ follow in case $\rho =2$.

If $\rho =1$, then there exists an isomorphism $\mathrm{Pic }_{X/k}(k^\mathrm{sep})\cong {{\mathbb Z}}^2$, such that the $G_k$-action factors through a surjective homomorphism $G_k\rightarrow {{\mathbb Z}}/2{{\mathbb Z}}$ and acts on ${{\mathbb Z}}^2$ via $(a,b)\mapsto (b,a)$. In particular, we find $H^1({{\mathbb Z}}/2{{\mathbb Z}},{{\mathbb Z}}^2)=0$ with respect to this action, see, for example, [4, Chap. III.1, Example 2]. From this, we deduce $H^1(H)=0$ using inflation maps. Moreover, $\mathrm{Am}(X)$ is generated by $\delta ((1,1))$, which is zero, since (1, 1) is the class of an invertible sheaf. $\square$

Corollary 5.5

If X is as in Theorem 5.1, then the following are equivalent

• (1) X is birationally equivalent to a Brauer–Severi surface,

• (2) X is rational,

• (3) X has a k-rational point, and

• (4) X is isomorphic to

  $$ X\,\cong \,{{\mathbb P}}^1_k\times {{\mathbb P}}^1_k \quad \text{ or } \text{ to } \quad X\,\cong \,{\mathrm{Spec}\,}K\wedge ({{\mathbb P}}^1_k\times {{\mathbb P}}^1_k). $$

Proof The implications $(2)\Rightarrow (1)$ and $(2)\Rightarrow (3)$ are trivial, and we established $(3)\Rightarrow (2)$ in Theorem 5.1. Moreover, if X is birationally equivalent to a Brauer–Severi surface P, then $\mathrm{Am}(P)=\mathrm{Am}(X)$ is cyclic of order 1 or 3 by Lemma 4.5 and Theorem 4.6. Together with Corollary 5.4, we conclude $\mathrm{Am}(P)=\mathrm{Am}(X)=0$, i.e., $P\cong {{\mathbb P}}^2_k$, which establishes $(1)\Rightarrow (2)$.

Since $(4)\Rightarrow (3)$ is trivial, it remains to establish $(3)\Rightarrow (4)$. Thus, we assume $X(k)\ne \emptyset$. If $\rho =2$, then $X\cong P'\times P''$ and both Brauer–Severi curves $P'$ and $P''$ have k-rational points, i.e., $X\cong {{\mathbb P}}^1_k\times {{\mathbb P}}^1_k$. If $\rho =1$, we have an embedding $X\subset {{\mathbb P}}^3_k$ and $X\cong {\mathrm{Spec}\,}K\wedge (P'\times P')$. Since $X(k)\ne \emptyset$, we have $X(K)\ne \emptyset$, which yields $P'(K)\ne \emptyset$, and thus $P'_K\cong {{\mathbb P}}^1_K$. A k-rational point on X gives rise to a K-rational and $\mathrm{Gal}(K/k)$-stable point on $X_K\cong {{\mathbb P}}^1_K\times {{\mathbb P}}^1_K$. In particular, this point lies on some diagonal ${{\mathbb P}}^1_K\subset X_K$, and thus, lies on some diagonal $P''\subseteq X$ with $X\cong {\mathrm{Spec}\,}K\wedge (P''\times P'')$. Since $P''(k)\ne \emptyset$, we find $P''\cong {{\mathbb P}}^1_k$. $\square$

We refer to Sect. 6.1 for more applications of these results to the arithmetic and geometry of these surfaces.

6 Del Pezzo Surfaces of Large Degree

Let X be a del Pezzo surface of degree d over a field k that is not of product type. Then, there exists a birational morphism

$$ \begin{array}{ccccc} \overline{f}&:&\overline{X}\rightarrow & {} {{\mathbb P}}^2_{\overline{k}} \end{array} $$

that is a blow-up in $(9-d)$ closed points $P_1,...,P_{9-d}$ in general position. We set $H:=\overline{f}^*\mathcal{O}_{{{\mathbb P}}^2_{\overline{k}}}(1)$ and let $E_i:=\overline{f}^{-1}(P_i)$ be the exceptional divisors of $\overline{f}$. Then, there exists an isomorphism of abelian groups

$$ \begin{array}{ccc} \mathrm{Pic }(\overline{X})\cong & {} {{\mathbb Z}}H\,\oplus \,\bigoplus _{i=1}^{9-d}\,{{\mathbb Z}}E_i. \end{array} $$

The $(-1)$-curves of $\overline{X}$ consist of the $E_i$, of preimages under $\overline{f}$ of lines through two distinct points $P_i$, of preimages under $\overline{f}$ of quadrics through five distinct points $P_i$, etc., and we refer to [35, Theorem 26.2] for details. Let $K_{\overline{X}}$ be the canonical divisor class of $\overline{X}$, and let $\widetilde{E}$ be the sum of all $(-1)$-curves on $\overline{X}$. We leave it to the reader to verify the following table.

d	class of $\widetilde{E}$ in $\mathrm{Pic }(\overline{X})$			relations
9	0			3H	$=$	$-K_{\overline{X}}$
8			$E_1$	3H	$=$	$-K_{\overline{X}}$	+	$\widetilde{E}$
7	H			H	$=$			$\widetilde{E}$
6	3H	−	$\sum _{i=1}^3E_i$	0	$=$	$-K_{\overline{X}}$	-	$\widetilde{E}$
5	6H	−	$2\sum _{i=1}^4E_i$	0	$=$	$-2K_{\overline{X}}$	-	$\widetilde{E}$
4	12H	−	$4\sum _{i=1}^5E_i$	0	$=$	$-4K_{\overline{X}}$	-	$\widetilde{E}$
3	27H	−	$9\sum _{i=1}^6E_i$	0	$=$	$-9K_{\overline{X}}$	-	$\widetilde{E}$
2	84H	−	$28\sum _{i=1}^7E_i$	0	$=$	$-28K_{\overline{X}}$	-	$\widetilde{E}$
1	720H	−	$240\sum _{i=1}^8E_i$	0	$=$	$-240 K_{\overline{X}}$	-	$\widetilde{E}$

Together with Theorem 3.4, we obtain the following result.

Theorem 6.1

Let X be a del Pezzo surface of degree $d\ge 7$ over a field k that is not of product type. Then, $\overline{f}$ descends to a birational morphism

$$ f : X\rightarrow P $$

to a Brauer–Severi surface P over k, where

$$ \delta (H) \,=\, [P] \,\in \,\mathrm{Br}(k) \quad \text{ and } \quad \mathrm{Am}(X)\,\cong \,{{\mathbb Z}}/\mathrm{per}(P){{\mathbb Z}}. $$

Moreover, X is rational if and only if $P\cong {{\mathbb P}}^2_k$. This is equivalent to X having a k-rational point.

Proof

By Theorem 4.2, the invertible sheaf H on $X_{\overline{k}}$ defining $\overline{f}$ already lies in $\mathrm{Pic }_X({k^\mathrm{sep}})$, i.e., $\overline{f}$ descends to $k^\mathrm{sep}$, and by abuse of notation, we re-define $\overline{X}$ to be $X_{k^\mathrm{sep}}$. Clearly, the canonical divisor class $K_{\overline{X}}$ is $G_k$-invariant, and since $G_k$ permutes the $(-1)$-curves of $\overline{X}$, also the class of $\widetilde{E}$ is $G_k$-invariant. In particular, $K_{\overline{X}}$ and $\widetilde{E}$ define classes in $\mathrm{Pic }_{X/k}(k^\mathrm{sep})^{G_k}\cong \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$. If $d\ge 7$, then the above table shows that there exist positive multiples of H that are integral linear combinations of $K_{\overline{X}}$ and $\widetilde{E}$. Thus, $H\in \mathrm{Pic }_{X/k}(k^\mathrm{sep})$ descends to a class in $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$. By Theorem 3.4, $\overline{f}$ descends to a birational morphism $f:X\rightarrow P$, where P is a Brauer–Severi surface of class $\delta (H)\in \mathrm{Br}(k)$. The assertion on $\mathrm{Am}(X)$ follows from Proposition 2.10 and Theorem 2.19.

If X has a k-rational point, then so has P, and then $P\cong {{\mathbb P}}^2_k$. Since f is a birational morphism, $P\cong {{\mathbb P}}^2_k$ implies that X is rational. And if X is rational, then it has a k-rational point by Lemma 4.3. $\square$

As an immediate consequence, we obtain rationality and the existence of k-rational points in some cases.

Corollary 6.2

Let X be as in Theorem 6.1. If $d\in \{7,8\}$, then X has a k-rational point and $\overline{f}$ descends to a birational morphism $f:X\rightarrow {{\mathbb P}}^2_k$.

Proof

By Theorem 6.1, there exists a birational morphism $X\rightarrow P$ that is a blow-up in a closed subscheme $Z\subset P$ of length $(9-d)$. By Corollary 2.21, we have $P\cong {{\mathbb P}}^2_k$ if 3 and $(9-d)$ are coprime. In particular, we have $X(k)\ne \emptyset$ in these cases by Theorem 6.1 and Lemma 4.3. $\square$

Since a del Pezzo surface of degree 9 is a Brauer–Severi surface, it has rational points if and only if it is trivial. In particular, Corollary 6.2 does not hold for $d=9$.

6.1 Applications to Arithmetic Geometry

We now give a couple of applications of the just established results. Again, we stress that most if not all of these applications are well-known, and merely illustrate the usefulness of studying varieties via Brauer–Severi varieties.

Corollary 6.3

If X is a del Pezzo surface of degree $\ge 7$ over k, then

$$\begin{array}{ccc} H^1\left( H,\, \mathrm{Pic }_{X/k}({k^\mathrm{sep}})\right)= & {} 0. \end{array} $$

for all closed subgroups $H\subseteq G_k$

Proof If X is not of product type, then it is birationally equivalent to a Brauer–Severi surface P by Theorem 6.1, and then the statement follows from Theorem 4.6 and Lemma 4.5. If X is of product type, then this is Corollary 5.4. $\square$

For the next application, let us recall that a surface is called rational if it is birationally equivalent to ${{\mathbb P}}^2_k$, and that it is called unirational if there exists a dominant and rational map from ${{\mathbb P}}^2_k$ onto it. The following result is a special case of [35, Theorem 29.4].

Corollary 6.4

Let X be a del Pezzo surface of degree ${\ge }7$ over a field k. Then, the following are equivalent:

• (1) X is rational,

• (2) X is unirational, and

• (3) X has a k-rational point.

Proof Clearly, we have $(1)\Rightarrow (2)\Rightarrow (3)$, whereas $(3)\Rightarrow (1)$ follows from Corollary 5.5 and Theorem 6.1. $\square$

This leads us to the question whether a del Pezzo surface necessarily has a k-rational point. Over finite fields, this is true and follows from the Weil conjectures, which we will recall in Theorem 8.1 below. By a theorem of Wedderburn, finite fields have trivial Brauer groups, and thus, the following corollary gives existence of k-rational points for more general fields.

Corollary 6.5

Let X be a del Pezzo surface of degree ${\ge }7$ over a field k with $\mathrm{Br}(k)=0$. Then, X has a k-rational point, and thus, is rational.

Proof

If X is not of product type, then there exists a birational morphism $f:X\rightarrow P$ to a Brauer–Severi surface by Theorem 6.1. Since $\mathrm{Br}(k)=0$, we have $P\cong {{\mathbb P}}^2_k$, and Theorem 6.1 gives $X(k)\ne \emptyset$.

Thus, let X be of product type. By Proposition 5.2, X is a product of Brauer–Severi curves ($\rho =2$), or contains at least a Brauer–Severi curve ($\rho =1$). Since $\mathrm{Br}(k)=0$, all Brauer–Severi curves are isomorphic to ${{\mathbb P}}^1_k$, and thus, contain k-rational points. In particular, we find $X(k)\ne \emptyset$. $\square$

In Sect. 4.3, we discussed the Hasse principle and weak approximation for varieties over global fields. Here, we establish the following.

Corollary 6.6

Del Pezzo surfaces of degree ${\ge }7$ over global fields satisfy weak approximation and the Hasse principle.

Proof

If X is not of product type, then it is birationally equivalent to a Brauer–Severi surface by Theorem 6.1, and since the two claimed properties are preserved under birational maps and hold for Brauer–Severi varieties, the assertion follows in this case.

If X is of product type, then there are two cases by Proposition 5.2. If $\rho =2$, then X is a product of two Brauer–Severi curves, and we conclude as before.

Thus, we may assume $\rho =1$. Let us first establish the Hasse principle: there exists a quadratic Galois extension L / K, such that $\rho (X_L)=2$. From $X(K_\nu )\ne \emptyset$ for all $\nu \in \Omega _K$, we find $X_{L_\mu }\cong {{\mathbb P}}^1_{L_\mu }\times {{\mathbb P}}^1_{L_\mu }$ for all $\mu \in \Omega _L$, and thus, $X_L\cong {{\mathbb P}}^1_L\times {{\mathbb P}}^1_L$ by the Hasse principle for Brauer–Severi curves. As in the proof of Corollary 5.5, we exhibit X as twisted self-product of ${{\mathbb P}}^1_k$, which has a k-rational point and establishes the Hasse principle. Thus, to establish weak approximation, we may assume that X has a k-rational point. But then, X is rational by Corollary 5.5, and since weak approximation is a birational invariant, the assertion follows. $\square$

7 Del Pezzo Surfaces of Degree 6

In the previous sections, we have seen a close connection between Brauer–Severi varieties and del Pezzo surfaces of degree ${\ge }7$. In this section, we discuss del Pezzo surfaces of degree 6, which are not so directly linked to Brauer–Severi varieties.

For the geometry and the arithmetic of these surfaces, we refer the interested reader to [6, 35], and the survey [47, Sect. 2.4]. We keep the notation introduced in Sect. 6: If X is a degree 6 del Pezzo surface over a field k, then there exists a blow-up $f_{\overline{k}}:\overline{X}\rightarrow {{\mathbb P}}^2_{\overline{k}}$ in three points in general position with exceptional $(-1)$-curves $E_1$, $E_2$, and $E_3$. Then, there are six $(-1)$-curves on X, namely the three exceptional curves $E_i$, $i=1,2,3$ of $\overline{f}$, as well as the three curves $E_i':=H-E_j-E_k$, $i=1,2,3$ where $\{j,k\}=\{1,2,3\}\backslash \{i\}$ and where $H=\overline{f}^*\mathcal{O}_{{{\mathbb P}}^2}(1)$ as in Sect. 6. These curves intersect in a hexagon as follows.

The absolute Galois group $G_k$ acts on these six $(-1)$-curves on $X_{k^\mathrm{sep}}$, and associated to this action, we have following field extensions of k.

• (1) Since $G_k$ acts on the two sets $\{E_1,E_2,E_3\}$ and $\{E_1',E_2',E_3'\}$, there is a group homomorphism

  $$ \varphi _1\,:\,G_k\,\rightarrow \,S_2\,\cong \,{{\mathbb Z}}/2{{\mathbb Z}}. $$

  The fixed field of either of the two sets is a finite separable extension $k\subseteq K$ with [K : k]|2, and $k\ne K$ if and only if $\varphi _1$ is surjective.

• (2) Since $G_k$ acts on the three sets $\{E_i,E_i'\}$, $i=1,2,3$, there is a group homomorphism

  $$ \varphi _2\,:\,G_k\,\rightarrow \,S_3. $$

  There exists a finite separable extension $k\subseteq L$ with [L : k]|3, unique up to conjugation in $k^\mathrm{sep}$, over which at least one of these three sets is defined. We have $k\ne L$ if and only if 3 divides the order of $\varphi _2(G_k)$. Next, there exists a finite and separable extension $L\subseteq M$ with [M : L]|2, over which all three sets are defined.

Combining $\varphi _1$ and $\varphi _2$, we obtain a group homomorphism

$$ G_k\,\mathop {\longrightarrow }\limits ^{\varphi _1\times \varphi _2}\, {{\mathbb Z}}/2{{\mathbb Z}}\times S_3\,\cong \,D_{2\cdot 6}, $$

where $D_{2\cdot 6}$ denotes the dihedral group of order 12, i.e., the automorphism group of the hexagon. Using these field extensions, we obtain the following classification, which uses and slightly extends a classical result of Manin from [35] in case (3).

Theorem 7.1

Let X be a del Pezzo surface of degree 6 over a field k.

• (1) The morphism $\overline{f}$ descends to a birational morphism

  $$ f\,:\,X\,\rightarrow \,P $$

  to a Brauer–Severi surface P if and only if $k=K$. In this case, $\rho (X)\ge 2$ and $\mathrm{Am}(X)=\mathrm{Am}(P)$.

• (2) There exists a birational morphism $X\rightarrow Y$ onto a degree 8 del Pezzo surface Y of product type if and only if $k=L$. In this case,

  $$\begin{array}{c|ccc} &{} \rho (X) &{} Y \\ \hline k\ne M &{} 3 &{} {\mathrm{Spec}\,}M\wedge ({{\mathbb P}}^1_k\times {{\mathbb P}}^1_k) \\ k=M &{} 4 &{} {{\mathbb P}}^1_k\times {{\mathbb P}}^1_k \end{array}$$

  X has a k-rational point, and $\mathrm{Am}(X)=0$.

• (3) If $k\ne K$ and $k\ne L$, then $\rho (X)=1$, $\mathrm{Am}(X)=0$, and the following are equivalent.

  • (a) X is birationally equivalent to a Brauer–Severi surface,

  • (b) X is birationally equivalent to a product of two Brauer–Severi curves,

  • (c) X is rational, and

  • (d) X has a k-rational point.

Proof Let us first show (1). If $k=K$, then $F:=E_1+E_2+E_3$ descends to a class in $\mathrm{Pic }(X_{k^\mathrm{sep}})^{G_k}=\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ and we find $\rho (X)\ge 2$. Thus, also $H=\frac{1}{3}(-K_X+F)$ descends to a class in $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$, and by Theorem 3.4, we obtain a birational morphism $|H|:X\rightarrow P$ to a Brauer–Severi surface, which coincides with $\overline{f}$ over $\overline{k}$. Conversely, if $\overline{f}$ descends to a birational morphism $f:X\rightarrow P$, then the exceptional divisor of f is of class F or $E'_1+E_2'+E_3'$, and we find $k=K$. Moreover, we have $\mathrm{Am}(X)=\mathrm{Am}(P)$ by Theorem 4.6.

If $k=L$, then, say $E_1+E_1'$, descends to a class in $\mathrm{Pic }(X_{k^\mathrm{sep}})^{G_k}$. Moreover, we find that the classes $\frac{1}{2}(-K_X+E_1+E_1')=\,2H-E_2-E_3$ as well as $\frac{1}{2}(-K_X-E_1-E_1')\,=\, H-E_1$, and thus, the classes H, $E_1$, and $E_1'=H-E_2-E_3$ lie in $\mathrm{Pic }(X_{k^\mathrm{sep}})^{G_k}$. The $G_k$-action is trivial on H and $E_1$, whereas it is either trivial on the set $\{E_2,E_3\}$ (if $k=M$) or permutes the two (if $k\ne M$). Since the class of $E_1$ is $G_k$-invariant and there is a unique effective divisor in this linear system, we find that ${{\mathbb P}}^1_k\cong E_1\subset X$. In particular, X has a k-rational point and $\mathrm{Am}(X)=0$. Using Theorem 3.4 and the fact that X has a k-rational point, we obtain a birational morphism

$$ |\frac{1}{2}(-K_X+E_1+E_1')|\,:\, X\rightarrow Y\subset {{\mathbb P}}^3_k $$

onto a smooth quadric Y with a k-rational point. In particular, Y is a degree 8 del Pezzo surface of product type. Over $k^\mathrm{sep}$, this morphism contracts $E_1$ and $E_1'$ and thus, we find

$$ \mathrm{Pic }(Y_{k^\mathrm{sep}}) \,\cong \, \left( {{\mathbb Z}}H\oplus \bigoplus _{i=1}^3{{\mathbb Z}}E_i\right) / \langle E_1, E_1' \rangle \,\cong \,{{\mathbb Z}}\overline{E}_2 \oplus {{\mathbb Z}}\overline{E}_3. $$

The $G_k$-action on it is either trivial ($k=M$) or permutes the two summands ($k\ne M$). Using $Y(k)\ne \emptyset$ and Corollary 5.5, we find $\rho (X)=4$ and $Y\cong {{\mathbb P}}^1_k\times {{\mathbb P}}^1_k$ in the first case, and $\rho (X)=3$ and $Y\cong {\mathrm{Spec}\,}M\wedge ({{\mathbb P}}^1_k\times {{\mathbb P}}^1_k)$ in the latter. Conversely, if there exists a birational morphism $X\rightarrow Y$ onto a degree 8 del Pezzo surface of product type, then the exceptional divisor is of class $E_i+E_i'$ for some i, and thus, $k=L$. This establishes (2).

Finally, assume that $k\ne K$ and $k\ne L$. Then, $\varphi _1$ is surjective, and $\varphi _2(G_k)$ contains all 3-cycles of $S_3$. From this, it is not difficult to see that $\mathrm{Pic }(X_{\overline{k}})^{G_k}$ is of rank 1 and generated by the class of $K_X$. Since this latter class is an invertible sheaf, we find $\mathrm{Am}(X)=0$. Thus, if X is birationally equivalent to a Brauer–Severi surface P, then $\mathrm{Am}(X)=0$ together with Lemma 4.5 and Theorem 4.6 implies that $P\cong {{\mathbb P}}^2_k$. Similarly, if X is birationally equivalent to the product $P'\times P''$ of two Brauer–Severi curves, then $P'\cong P''\cong {{\mathbb P}}^1_k$. From this, we obtain the implications $(a)\Leftrightarrow (b)\Leftrightarrow (c)\Rightarrow (d)$. The implication $(d)\Rightarrow (c)$ is due to Manin [35, Theorem 29.4]. $\square$

Remark 7.2

In case (1) of the above theorem it is important to note that P need not be unique, but that $\mathrm{Am}(P)$ is well-defined. More precisely, if we set $F:=E_1+E_2+E_3$ and $F'=E_1'+E_2'+E_3'$, then Theorem 3.4 provides us with two morphisms to Brauer–Severi surfaces $P_1$ and $P_2$

$$ \begin{array}{lclcc} |H| &{}=&{} |\frac{1}{3}(-K_X+F)| &{}:&{} X \,\rightarrow \, P_1 \\ |H'| &{}:=&{}|\frac{1}{3}(-K_X+F')| &{}:&{} X\,\rightarrow \, P_2\\ \end{array} $$

Since $H+H'=-K_X$ and $\delta (K_X)=0$, we find

$$ [P_1]\,=\,\delta (H)\,=\,\delta (-K_X-H')\,=\,-\delta (H')\,=\,-[P_2]\,\in \,\mathrm{Br}(k), $$

and thus, $P_1\cong P_2$ if and only if both are isomorphic to ${{\mathbb P}}^2_k$. On the other hand, $P_1$ and $P_2$ are birationally equivalent, since we have birational morphisms

$$ P_1\,\mathop {\longleftarrow }\limits ^{|H|}\,X\,\mathop {\longrightarrow }\limits ^{|H'|} P_2\,. $$

Over $\overline{k}$, this becomes the blow-up of three closed points Z followed by the blow-down of the three $(-1)$-curves that are the strict transforms of lines through any two of the points in Z. This is an example of a Cremona transformation.

We remark that a surface of case (3) and without k-rational points is neither birationally equivalent to a Brauer–Severi surface nor to the product of two Brauer–Severi curves. For finer and more detailed classification results for degree 6 del Pezzo surfaces, we refer the interested reader to [2, 10, 13]. Finally, the sum $\widetilde{E}$ of all $(-1)$-curves on $X_{k^\mathrm{sep}}$ is a $G_k$-invariant divisor, and thus, descends to a curve on X. By [35, Theorem 30.3.1], the complement $X\backslash \widetilde{E}$ is isomorphic to a torsor under a two-dimensional torus over k, which can be used to study the arithmetic and geometry of these surfaces, see also [43].

8 Del Pezzo Surfaces of Small Degree

For the remainder of this article, our results will be less complete and less self-contained. We will circle around questions of birationality of a del Pezzo surface X of degree ${\le }5$ to Brauer–Severi surfaces, and about descending the morphism $\overline{f}:\overline{X}\rightarrow {{\mathbb P}}^2_{\overline{k}}$ to k.

8.1 Birationality to Brauer–Severi Surfaces

Let $k={{\mathbb F}}_q$ be a finite field of characteristic p, and let X be a smooth and projective surface over k such that $X_{\overline{k}}$ is birationally equivalent to ${{\mathbb P}}^2$. Then, it follows from the Weil conjectures (in this case already a theorem of Weil himself) that the number of k-rational points is congruent to 1 modulo q, see [35, Chap. IV.27]. In particular, we obtain that

Theorem 8.1

(Weil) If X is a del Pezzo surface over a finite field ${{\mathbb F}}_q$, then X has a ${{\mathbb F}}_q$-rational point.

Since $\mathrm{Br}({{\mathbb F}}_q)=0$ by a theorem of Wedderburn, there are no non-trivial Brauer–Severi varieties over ${{\mathbb F}}_q$.

Remark 8.2

Let X be a del Pezzo surface of degree ${\ge }5$ over a field k. Manin [35, Theorem 29.4] showed that X is rational if and only if it contains a k-rational point. Even if X has no k-rational point, Manin [35, Theorem 29.3] showed that

$$ H^1\left( H,\,\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k^\mathrm{sep})\right) \,=\,0 $$

for all closed subgroups $H\subseteq G_k$. We refer to [8, Théorème 2.B.1] for a general principle explaining this vanishing of cohomology.

In this section, we give a partial generalization to birational maps to Brauer–Severi surfaces.

Lemma 8.3

Let X be a degree d del Pezzo surface over k. Then,

• (1) There exists an effective zero-cycle Z of degree d on X. If $d\ne 2$ or if $\mathrm{char}(k)\ne 2$, then there exists such a zero-cycle Z, whose closed points have residue fields that are separable over k.

• (2) The abelian group $\mathrm{Am}(X)$ is finite and every element has an order dividing d.

Proof If $d\ge 3$, then $\omega _X^{-1}$ is very ample, and $|\omega _X^{-1}|$ embeds X as a surface of degree d into ${{\mathbb P}}^d_k$. Intersecting X with a linear subspace of codimension 2, we obtain an effective zero-cycle Z of degree d on X. The closed points of Z have automatically separable residue fields if k is finite. Otherwise, k is infinite, and then, the intersection with a generic linear subspace of codimension 2 yields a Z that is smooth over k by [28, Théorème I.6.3]. Thus, in any case, we obtain a Z, whose closed points have residue fields that are separable over k. If $d=2$, then $|\omega _X^{-1}|$ defines a double cover $X\rightarrow {{\mathbb P}}^2_k$, and the pre-image of a k-rational point yields an effective zero-cycle Z of degree 2 on X. If $\mathrm{char}(k)\ne 2$, then residue fields of closed points of Z are separable over k. If $d=1$, then $|-K_X|$ has a unique-base point, and in particular, X has a k-rational point. This establishes (1). Since $b_1(X)=0$, the group $\mathrm{Am}(X)$ is finite by Lemma 2.13. Then, assertion (2) follows from Lemma 2.9. $\square$

Corollary 8.4

Let X be a del Pezzo surface of degree d over a field k.

• (1) If $d\in \{1,2,4,5,7,8\}$ and X is birationally equivalent to a Brauer–Severi surface P, then $P\cong {{\mathbb P}}^2_k$ and X has a k-rational point.

• (2) If $d\in \{1,3,5,7,9\}$ and X is birationally equivalent to a product $P'\times P''$ of two Brauer–Severi curves, then $P'\cong P''\cong {{\mathbb P}}^1_k$ and X has a k-rational point.

Proof Let X and d be as in (1). Then, every element of $\mathrm{Am}(X)$ is of order dividing d by Lemma 8.3, but also of order dividing 3 by Theorems 2.18 and 4.6. By our assumptions on d, we find $\mathrm{Am}(P)=0$, and thus, $P\cong {{\mathbb P}}^2_k$. Since the latter has a k-rational point, so has X by Lemma 4.3. This shows (1). The proof of (2) is similar and we leave it to the reader. $\square$

Combining this with a result of Coray [12], we obtain the following.

Theorem 8.5

Let X be a del Pezzo surface of degree $d\in \{5,7,8\}$ over a perfect field k. Then, the following are equivalent

• (1) There exists a dominant and rational map $P\dashrightarrow X$ from a Brauer–Severi surface P over k,

• (2) X is birationally equivalent to a Brauer–Severi surface,

• (3) X is rational, and

• (4) X has a k-rational point.

Proof The implications $(3)\Rightarrow (2)\Rightarrow (1)$ are trivial.

Let $\varphi :P\dashrightarrow X$ be as in (1). By Lemma 8.3, there exists a zero-cycle of degree 9 on P, and another one of degree d on X. Using $\varphi$, we obtain a zero-cycle of degree dividing 9 on X. By assumption, d is coprime to 9, and thus, there exists a zero-cycle of degree 1 on X. By [12], this implies that X has a k-rational point and establishes $(1)\Rightarrow (4)$.

The implication $(4)\Rightarrow (3)$ is a result of Manin [35, Theorem 29.4]. $\square$

Now, if a del Pezzo surface X over a field k is birationally equivalent to a Brauer–Severi surface, then $H^1(H,\mathrm{Pic }_{X/k}(k^\mathrm{sep}))=0$ for all closed subgroups $H\subseteq G_k$ by Theorem 4.6. Moreover, this vanishing holds for all del Pezzo surfaces of degree ${\ge }5$, see Remark 8.2. However, for del Pezzo surfaces of degree ${\le }4$, these cohomology groups may be non-zero, see [35, Sect. 31], [32, 45, 46]. In particular, del Pezzo surfaces of degree ${\le }4$ are in general not birationally equivalent to Brauer–Severi surfaces.

For further information concerning geometrically rational surfaces, unirationality, central simple algebras, and connections with cohomological dimension, we refer the interested reader to [10].

8.2 Del Pezzo Surfaces of Degree 5

In order to decide whether a birational map $f_{\overline{k}}:X_{\overline{k}}\rightarrow {{\mathbb P}}^2_{\overline{k}}$ as in Sect. 6 descends to k for a degree 5 del Pezzo surface X over k, we introduce the following notion.

Definition 8.6

Let X be a del Pezzo surface over a field k. A conic on X is a geometrically integral curve C on X with $C^2=0$ and $-K_X\cdot C=2$. An element $\mathcal{{L}}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ is called a conic class if $\mathcal{{L}}\otimes _k\overline{k}\cong \mathcal{O}_{X_{\overline{k}}}(\overline{C})$ for some conic $\overline{C}$ on $X_{\overline{k}}$.

The following is an analogue of Theorem 6.1 for degree 5 del Pezzo surfaces.

Theorem 8.7

Let X be a del Pezzo surface of degree 5 over a field k. Then, the following are equivalent:

• (1) There exists a birational morphism $f:X\rightarrow P$ to a Brauer–Severi surface, such that $f_{\overline{k}}$ is the blow-up of 4 points in general position.

• (2) There exists a birational morphism $f:X\rightarrow {{\mathbb P}}^2_k$, such that $f_{\overline{k}}$ is the blow-up of 4 points in general position.

• (3) There exists a class $F\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ such that

  $$ F_{\overline{k}} \,\cong \, \mathcal{O}_{\overline{X}}(E_1+E_2+E_3+E_4), $$

  where the $E_i$ are disjoint $(-1)$-curves on $\overline{X}$.

• (4) There exists a conic class in $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$.

If these equivalent conditions hold, then X has a k-rational point.

Proof If f is as in (1), then X has a k-rational point by Corollary 8.4. Thus, $P\cong {{\mathbb P}}^2_k$, and we obtain $(1)\Rightarrow (2)$.

If f is as in (2), then the exceptional divisor of f is a class F as stated in (3), and we obtain $(2)\Rightarrow (3)$.

If f is as in (3), then, using Theorem 3.4, there exists a birational morphism $|\frac{1}{3}(-K_X-F)|:X\rightarrow P$ to a Brauer–Severi surface P as in (1), which establishes $(3)\Rightarrow (1)$.

If f is as in (2), let $Z\subset {{\mathbb P}}^2_k$ be the degree 4 cycle blown up by f. Then $f^*(\mathcal{O}_{{{\mathbb P}}^2_k}(2)(-Z))$, i.e., the pullback of the pencil of conics through Z, is a conic class on X and establishes $(2)\Rightarrow (4)$.

Finally, if C is a conic class on X, then, using Theorem 3.4, there exists a birational morphism $|-K_X+C|:X\rightarrow P$ to a Brauer–Severi surface P as in (1), which establishes $(4)\Rightarrow (1)$. $\square$

Remark 8.8

By theorems of Enriques, Swinnerton-Dyer, Skorobogatov, Shepherd-Barron, Kollár, and Hassett (see [47, Theorem 2.5] for precise references and overview), a degree 5 del Pezzo X over a field k always has a k-rational point. Thus, X is rational by [35, Theorem 29.4], and we have

$$ \mathrm{Am}(X)=0, \quad \text{ as } \text{ well } \text{ as } \quad H^1(H,\mathrm{Pic }_{X/k}(k^\mathrm{sep}))=0 $$

for every closed subgroup $H\subseteq G_k$ by Corollary 2.12, Theorem 4.6, and Lemma 4.5.

8.3 Del Pezzo Surfaces of Degree 4

A classical theorem of Manin [35, Theorem 29.4] states that a del Pezzo surface of degree 4 over a sufficiently large field k is unirational if and only if it contains a k-rational point. Here, we have the following analogue in our setting.

Proposition 8.9

Let X be a del Pezzo surface of degree 4 over a perfect field k. Then, the following are equivalent

• (1) There exists a dominant rational map $P\dashrightarrow X$ from a Brauer–Severi surface P over k.

• (2) X is unirational,

• (3) X has a k-rational point,

Proof The implications $(2)\Rightarrow (1)$ is trivial and $(2)\Rightarrow (3)$ is Lemma 4.3.

The implication $(3)\Rightarrow (2)$ is shown in [35, Theorem 29.4] and [35, Theorem 30.1] if k has at least 23 elements and in [31, Theorem 2.1] and [40, Proposition 5.19] in the remaining cases.

To show $(1)\Rightarrow (3)$, we argue as in the proof of the implication $(1)\Rightarrow (4)$ of Theorem 8.5 by first exhibiting a degree 1 zero-cycle on X, and then, using [12] to deduce the existence of a k-rational point on X. We leave the details to the reader. $\square$

If a field k is finite or perfect of characteristic 2, then a degree 4 del Pezzo surface over k always has a k-rational point, see [35, Theorem 27.1] and [16]. In this case, we also have $\mathrm{Am}(X)=0$. From Lemma 8.3, we infer that $\mathrm{Am}(X)$ is at most 4-torsion for degree 4 del Pezzo surfaces. For the possibilities of $H^1(G_k,\mathrm{Pic }_{X/k}(k^\mathrm{sep}))$, see [45].

The following is an analog of Theorem 6.1 for degree 4 del Pezzo surfaces.

Theorem 8.10

Let X be a del Pezzo surface of degree 4 over a field k. Then, the following are equivalent:

• (1) There exists a birational morphism $f:X\rightarrow P$ to a Brauer–Severi surface, such that $f_{\overline{k}}$ is the blow-up of 5 points in general position.

• (2) There exists a birational morphism $f:X\rightarrow {{\mathbb P}}^2_k$, such that $f_{\overline{k}}$ is the blow-up of 5 points in general position.

• (3) There exists a curve ${{\mathbb P}}^1_k\cong E\subset X$ with $E^2=-1$.

• (4) There exists a class $E\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ with $E^2=K_X\cdot E=-1$.

If these equivalent conditions hold, then X has a k-rational point.

Proof The implication $(2)\Rightarrow (1)$ is trivial. If f is as in (1), then X has a k-rational point by Corollary 8.4. Thus, $P\cong {{\mathbb P}}^2_k$, and we obtain $(1)\Rightarrow (2)$.

If f is as in (2), let $Z\subset {{\mathbb P}}^2_k$ be the degree 5 cycle blown up by f. Then $f^*(\mathcal{O}_{{{\mathbb P}}^2_k}(2)(-Z))$, i.e., the pullback of the class of the unique conic through Z, is a class E as stated in (4) on X and establishes $(2)\Rightarrow (4)$.

If E is a class as in (4), then, using Theorem 3.4, there exists a birational morphism $|-K_X-E|:X\rightarrow P$ to a Brauer–Severi surface P as in (1), which establishes $(4)\Rightarrow (1)$.

The implication $(3)\Rightarrow (4)$ is trivial, and if E is a class as in (4), then there exists a unique section of the associated invertible sheaf on $k^\mathrm{sep}$. This is necessarily $G_k$-invariant, thus, descends to a curve on X, and establishes $(4)\Rightarrow (3)$. $\square$

Remark 8.11

In [44], Skorobogatov called del Pezzo surfaces of degree 4 that satisfy condition (3) above quasi-split.

Before proceeding, let us recall a couple of classical results on the geometry of degree 4 del Pezzo surfaces, and refer the interested reader to [44] and [15, Chap. 8.6] for details. The anti-canonical linear system embeds X as a complete intersection of two quadrics in ${{\mathbb P}}^4_k$, i.e., X is given by $Q_0=Q_1=0$, where $Q_0$ and $Q_1$ are two quadratic forms in five variables over k. The degeneracy locus of this pencil of quadrics

$$ \mathrm{Deg}_X \,:=\, \left\{ \,\det (t_0Q_0+t_1Q_1)\,=\,0 \,\right\} \,\subset \, {{\mathbb P}}^1_k\,=\,{\mathrm{Proj}}\,k[t_0,t_1] $$

is a zero-dimensional subscheme, which is étale and of length 5 over k. Over $\overline{k}$, its points correspond to the singular quadrics containing X, all of which are cones over smooth quadric surfaces. Let $\nu _2:{{\mathbb P}}^1_k\rightarrow {{\mathbb P}}^2_k$ be the 2-uple Veronese embedding and set

$$ Z := \nu _2(\mathrm{Deg}_X)\,\subset \,C:=\nu _2({{\mathbb P}}^1_k)\,\subset \,{{\mathbb P}}^2_k. $$

If X contains a k-rational $(-1)$-curve, i.e., if X is quasi-split, then X is the blow-up of ${{\mathbb P}}^2_k$ in Z, see Theorem 8.10 and [44, Theorem 2.3].

Proposition 8.12

Let X be a del Pezzo surface of degree 4 over a field k of characteristic $\ne 2$ with at least 5 elements. Then, the following are equivalent:

• (1) The degeneracy scheme $\mathrm{Deg}_X$ has a k-rational point.

• (2) There exists a finite morphism $\psi :X\rightarrow S$ of degree 2, where S is a del Pezzo surface of degree 8 of product type.

Moreover, if $\psi$ is as in (2), then S is isomorphic to a quadric in ${{\mathbb P}}^3_k$.

Proof To show $(1)\Rightarrow (2)$, assume that $\mathrm{Deg}_X$ has a k-rational point. Thus, there exists degenerate quadric Q with $X\subset Q\subset {{\mathbb P}}^4_k$. As explained in the proof of [15, Theorem 8.6.8], Q is a cone over a smooth quadric surface, and the projection away from its vertex ${{\mathbb P}}^4_k\dashrightarrow {{\mathbb P}}^3_k$ induces a morphism $X\rightarrow {{\mathbb P}}^3_k$ that is finite of degree 2 onto a smooth quadric surface S. In particular, S is a del Pezzo surface of degree 8 of product type.

To show $(2)\Rightarrow (1)$, let $\psi :X\rightarrow S$ be as in the statement. Then, we have a short exact sequence (which even splits since $\mathrm{char}(k)\ne 2$)

$$ 0\,\rightarrow \,\mathcal{O}_S\,\rightarrow \,\psi _*\mathcal{O}_X\,\rightarrow \,{\mathcal{{L}}}^{-1}\,\rightarrow \,0, $$

where $\mathcal{{L}}$ is an invertible sheaf on S, which is of type (1, 1) on $S_{\overline{k}}\cong {{\mathbb P}}^1_{\overline{k}}\times {{\mathbb P}}^1_{\overline{k}}$. In particular, $|\mathcal{{L}}|$ defines an embedding $\imath :S\rightarrow {{\mathbb P}}^3_k$ as a quadric, and establishes the final assertion. Now, $\imath \circ \psi$ arises from a 4-dimensional subspace V inside the linear system $(\imath \circ \psi )^*\mathcal{O}_{{{\mathbb P}}^3_k}(1)\cong \omega _X^{-1}$. Thus, $\imath \circ \psi$ is the composition of the anti-canonical embedding $X\rightarrow {{\mathbb P}}^4_k$, followed by a projection ${{\mathbb P}}^4_k\dashrightarrow {{\mathbb P}}^3_k$. As explained in the proof of [15, Theorem 8.6.8], such a projection induces a degree 2 morphism onto a quadric if and only if the point of projection is the vertex of a singular quadric in ${{\mathbb P}}^4_k$ containing X. In particular, this vertex and the corresponding quadric are defined over k, giving rise to a k-rational point of $\mathrm{Deg}_X$. $\square$

In order to refine Proposition 8.12, we will use conic classes as introduced in Definition 8.6.

Proposition 8.13

Let X be a del Pezzo surface of degree 4 over a field k. Then, the following are equivalent:

• (1) There exists a conic class in $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$.

• (2) There exists a finite morphism $\psi :X\rightarrow P'\times P''$ of degree 2, where $P'$ and $P''$ are a Brauer–Severi curves over k.

Moreover, if $\psi$ is as in (2), then $P'\cong P''$.

Proof Let $\mathcal{{L}}\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ be a conic class. By Theorem 3.4, there exist morphisms $|{\mathcal{{L}}}|:X\rightarrow P'$ and $|\omega _X^{-1}\otimes \mathcal{{L}}^{-1}|:X\rightarrow P''$, where $P'$ and $P''$ are Brauer–Severi curves over k. Combining them, we obtain a finite morphism $X\rightarrow P'\times P''$ of degree 2. As in the proof of $(2)\Rightarrow (1)$ of Proposition 8.12 we find that $P'\times P''$ embeds into ${{\mathbb P}}^3$, and thus, $0=[{{\mathbb P}}^3_k]=[P']+[P'']\in \mathrm{Br}(k)$ by Proposition 5.2. This implies $[P']=[P'']$ since these classes are 2-torsion, and thus, $P'\cong P''$ by Corollary 2.16. This establishes $(1)\Rightarrow (2)$.

Conversely, let $\psi :X\rightarrow P'\times P''$ be as in (2). Then, $\psi ^*(\mathcal{O}_{P'}(1)\boxtimes \mathcal{O}_{P''}(1))$ is a conic class, and (1) follows. $\square$

8.4 Del Pezzo Surfaces of Degree 3

For these surfaces, we have the following analogue of Theorem 6.1.

Theorem 8.14

Let X be a del Pezzo surface of degree 3 over a field k. Then, the following are equivalent:

• (1) There exists a birational morphism $f:X\rightarrow P$ to a Brauer–Severi surface, such that $f_{\overline{k}}$ is the blow-up of 6 points in general position.

• (2) There exists a class $F\in \mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)$ such that

  $$ F_{\overline{k}} \,\cong \, \mathcal{O}_{\overline{X}}(E_1+E_2+E_3+E_4+E_5+E_6), $$

  where the $E_i$ are disjoint $(-1)$-curves on $\overline{X}$.

Proof The proof is analogous to that of Theorem 8.7, and we leave the details to the reader. $\square$

Note that if the equivalent conditions of this theorem are fulfilled, then X is not minimal. But the converse does not hold in general: If Y is a unirational, but not rational del Pezzo surface of degree 4 over k, and $y\in Y$ is a k-rational point not lying on an exceptional curve, then the blow-up $X\rightarrow Y$ in y is a non-minimal degree 3 del Pezzo surface over k with k-rational points that is not birationally equivalent to a Brauer–Severi surface over k.

By [35, Theorem 28.1], a degree 3 del Pezzo surface X is minimal if and only if $\rho (X)=1$, i.e., $\mathrm{Pic }_{(X/k)(\mathrm{fppf})}(k)={{\mathbb Z}}\cdot \omega _X$. In this case, we have $\mathrm{Am}(X)=0$. In particular, if such a surface is birationally equivalent to a Brauer–Severi surface P, then $P\cong {{\mathbb P}}^2_k$ by Proposition 2.10 and Theorem 2.19. In particular, X is rational and has a k-rational point in this case.

8.5 Del Pezzo Surfaces of Degree 2

Arguing as in the proof of Theorem 8.5, it follows that if there exists a dominant and rational map $P\dashrightarrow X$ from a Brauer–Severi surface P onto a degree 2 del Pezzo surface over a perfect field k, then X has a k-rational point, and thus $\mathrm{Am}(X)=0$. In particular, if X is birationally equivalent to a Brauer–Severi surface, then it is rational, see also Corollary 8.4.

By work of Manin [35, Theorem 29.4], a degree 2 del Pezzo surface over a field k is unirational if it has a k-rational point not lying on an exceptional curve. Together with non-trivial refinements of [17, 42], such surfaces over finite fields are always unirational.

By Lemma 8.3, we have that $\mathrm{Am}(X)$ is at most 2-torsion for degree 2 del Pezzo surfaces. For the possibilities of $H^1(G_k,\mathrm{Pic }_{X/k}(k^\mathrm{sep}))$, as well as further information concerning arithmetic questions, we refer to [32].

8.6 Del Pezzo Surfaces of Degree 1

If X is a del Pezzo surface of degree 1, then it has a k-rational point, namely the unique base point of $|-K_X|$. Thus, we have $\mathrm{Am}(X)=0$, and there are no morphisms or rational maps to non-trivial Brauer–Severi varieties.