An Efficient Gaussian Kernel Based Fuzzy-Rough Set Approach for Feature Selection

Abstract

Fuzzy-rough set based feature selection is highly useful for reducing data dimensionality of a hybrid decision system, but the reduct computation is computationally expensive. Gaussian kernel based fuzzy rough sets merges kernel method to fuzzy-rough sets for efficient feature selection. This works aims at improving the computational performance of existing reduct computation approach in Gaussian kernel based fuzzy rough sets by incorporation of vectorized (matrix, sub-matrix) operations. The proposed approach was extensively compared by experimentation with the existing approach and also with a fuzzy rough set based reduct approaches available in Rough set R package. Results establish the relevance of proposed modifications.

1 Introduction

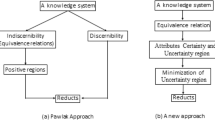
Rough Set Theory(RST), introduced by Prof. Pawlak [10] in 1980s, is very useful for classification and analysis of imprecise, uncertain or incomplete information and knowledge. The fundamental concept behind RST is the approximation space of a concept represented as the set. The process of knowledge discovery in a given decision system primarily consists of reduct computation (or feature selection) as the preprocessing step for dimensionality reduction. The features which are not a part of the reduct can be removed from the dataset with minimum information loss.

Feature Selection of a dataset with categorical attributes can be carried out by RST, but feature selection of a dataset with real-valued attributes is not possible through the classical RST. For handling this situation the fuzzy-rough set model is used. The Fuzzy Rough Set Theory (FRST) was introduced by Dubois and Prade [4] in 1990s and extended by several researchers [3, 7, 12]. Many reduct computation approaches were developed using FRST. They are categorized into fuzzy discretization based [1, 6] and fuzzy similarity relation based [5, 7, 15, 15]. In [7], it is established that fuzzy similarity relation based reduct computation are more efficient.

Recently an extension to fuzzy rough set model, named as Gaussian Kernel-based fuzzy rough set (GK-FRS) model, by adopting a Gaussian kernel function fuzzy similarity relation was introduced by Hu et al. [5]. The GK-FRS models combine the advantages of kernel methods with fuzzy rough sets. A sequential forward selection (SFS) based reduct computation approach was also proposed [18] based on GK-FRS. In 2015, GK-FRS was adopted to systems with various type of attributes (real-valued, categorical, boolean, set, interval based) with the concept of hybrid distance by Zeng et al. [18]. FRSA-NFS-HIS algorithm was introduced in [18] based on the extended GK-FRS model.

The computation complexity of fuzzy rough set based reduct algorithm is much higher than classical rough set based reduct algorithms [14]. The reason being, in later approaches computation, is based on the granules (equivalence classes), but fuzzy rough set based reduct computation inevitably involved object based computations. The existing approaches do not attempt any possibility of imposing granular or sub-granular aspect in fuzzy rough set based reduct computations. The aim of this paper is to improve the computational performance of FRSA-NFS-HIS algorithm by bringing an aspect of granular/sub-granular computations. This study brings out the importance of modeling fuzzy rough set reduct computation using matrix, sub-matrix based vectorized operations in the efficient vector-based environment such as Matlab and R. Our proposed Modified FRSA-NFS-HIS (MFRSA-NFS-HIS) algorithm was implemented in R environment, and extensive comparative analysis with existing approaches is reported in this paper.

This paper is organized as follows. Section 2 gives the theoretical background. Section 3 discusses the Gaussian Kernel-based Fuzzy-Rough Sets and FRSA-NFS-HIS. In Sect. 4 Proposed MFRSA-NFS-HIS Algorithm is detailed. Section 5 describes Experiments, Results and Analysis of these different approaches. The paper is concluded with Sect. 6.

2 Theoretical Background

2.1 Rough Set Theory

Rough Set Theory is a useful tool to discover data dependency and to reduce the number of attributes contain in the dataset using data alone requiring no additional information. Let DS = (U, A $\cup \{d\}$) is a decision system, where d is a decision attribute and $d \notin A$, U is nonempty set of finite objects and A is a nonempty finite set of conditional attributes such that $a: U\rightarrow V_a$ for every $a \in$ A. $V_a$ is the set of domain values of attribute ’a’. For any R $\subseteq$ A, there is an associated equivalence relation, called as indiscernible relation IND(R),

$$\begin{aligned} IND(R) = \{(x,y)\in U^2 | (\forall a \in R)(a(x) = a(y))\} \end{aligned}$$

(1)

The equivalence relation partitions the universe into a family of disjoint subsets, called equivalence classes. The equivalence class including x is denoted by $[x] _R$ and the set of equivalance classes induced by IND(R) is denoted by U/IND(R) or U/R in short.

Let X be a concept (X $\subseteq$ U) and approximations to X are defined using U/R. The lower and the upper approximations of X are defined respectively as follows:

$$\begin{aligned} \underline{R}X= & {} \{x\in U | [x]_R \subseteq X\}; \end{aligned}$$

(2)

$$\begin{aligned} \overline{R}X= & {} \{x\in U | [x]_R \cap X \ne \phi \}; \end{aligned}$$

(3)

The pair $<\underline{R}X, \overline{R}X>$ is called a rough set when $\underline{R}X \ne \overline{R}X$.

Let R and Q be sets of attributes inducing equivalence relations over U, then the positive regions can be defined as:

$$\begin{aligned} POS_R(Q) = \bigcup _{X\in U/Q} \underline{R}X \end{aligned}$$

(4)

The positive region $POS_{R}(Q)$ contains all the objects of the universe U that can be classified into different classes of U/Q using the information of attribute set R. The dependency or gamma ($\gamma$) is calculated as:

$$\begin{aligned} \gamma _R(\{d\}) = \frac{|POS_R(\{d\})|}{|U|} \end{aligned}$$

(5)

2.2 Fuzzy-Rough Sets

The classical Rough Set Theory cannot deal with real-valued data and the fuzzy-rough set is a solution to that problem as it can efficiently deal with real-valued data without resorting to discretization. Let R is a fuzzy relation and decision system DS =(U, A $\cup$ {d}) where U is a non-empty set of objects and A is a set of conditional attributes, a $\in$ A be a quantitative(real-valued) attribute. For measurement of the approximate similarity between two objects for a quantitative attributes, fuzzy similarity relations are used. Few example of the fuzzy similarity relation are [7]:

$$\begin{aligned} (1)\quad \mu _{R _a}(x,y)= & {} 1 - \frac{|a(x)-a(y)|}{|a _{max}-a _{min}|} \end{aligned}$$

(6)

$$\begin{aligned} (2)\quad \mu _{R _a}(x,y)= & {} exp\left( -\frac{(a(x)-a(y))^2}{2\sigma _a^2}\right) \end{aligned}$$

(7)

$$\begin{aligned} (3)\quad \mu _{R _a}(x,y)= & {} max\left( min\left( \frac{a(y)-a(x)+\sigma _a}{\sigma _a}, \frac{a(x)-a(y)+\sigma _a}{\sigma _a}\right) ,0\right) \end{aligned}$$

(8)

where $\sigma _a$ denotes the standard deviation of a. If attribute a $\in$ A is qualitative (nominal) then R$_a$(x,y) = 1 for a(x) = a(y) and R$_a$(x,y) = 0 for a(x) $\ne$ a(y). The similarity relation is extended to a set of attributes A by

$$\begin{aligned} R_A(x,y) = \mathfrak {I}(R_{a\in A}(x,y)) \end{aligned}$$

(9)

where $\mathfrak {I}$ represent a t-norm.

The lower and upper approximations are defined based on fuzzy similarity relations. The fuzzy R-lower and R-upper approximations are defined in Radzikowska-Kerry’s fuzzy rough set model [3, 12] as:

$$\begin{aligned} \underline{R}A(y)= & {} inf _{x\in X} \mathbb {I} (R(x,y), A(x)) \end{aligned}$$

(10)

$$\begin{aligned} \overline{R}A(y)= & {} sup _{x\in X} \mathfrak {I}(R(x,y), A(x)) \end{aligned}$$

(11)

where for all y in U, $\mathbb {I}$ is the implicator and $\mathfrak {I}$ is the t-norm. The pair $<\underline{R}A, \overline{R}A>$ is called a fuzzy-rough set.

3 Gaussian Kernel Based Fuzzy-Rough Sets

The kernel methods and rough set are crucial domains for machine learning and pattern recognization. The kernel methods map the data into a higher dimensional feature space while rough set granulates the universe with the use of relations. Hu et al. [5] used the benefits of both and made a Gaussian kernel based fuzzy rough set approach for reduct computation. The content of this section is already discussed in the literature [5, 18]. For the completeness of the paper, we give a summary of the original content.

3.1 Hybrid Decision System (HDS) and Hybrid Distance (HD)

A HDS can be written as $(U, A \cup \{d\}, V, f)$, where U is the set of objects, $A = A^r \cup A^c \cup A^b,$ $A^r$ is the real-valued attribute set, $A^c$ is the categorical attribute set and $A^b$ is the boolean attribute set. {d} denotes a decision attribute. $A^r \cap A^c = \phi ,$ $A^r \cap A^b = \phi ,$ and $A \cap \{d\} = \phi$.

In HDS, there may be different types of attributes. To construct the distance among the objects, different distance measurement functions are used based on attribute type in literature [18]. The Hybrid Distance(HD) for a Hybrid Decision System (HDS) based on different types of attributes is defined as:

$$\begin{aligned} HD_B(x, y) = \sqrt{\sum _{a\in B} d^2(a(x), a(y))} \end{aligned}$$

(12)

where B is the set of conditional attributes of the HDS, and

$$\begin{aligned} d(a(x),a(y)) = {\left\{ \begin{array}{ll} vdm(a(x),a(y)), &{} \text {a is a categorical attribute}\\ vdr(a(x),a(y)), &{} \text {a is a real-valued attribute}\\ vdb(a(x),a(y)), &{} \text {a is a boolean attribute}\\ \end{array}\right. } \end{aligned}$$

(13)

3.2 Gaussian Kernel

In the literature Hu et al. [5] uses gaussian kernel function for computing the fuzzy similarity relation between the objects. The gaussian kernel function is defined as:

$$\begin{aligned} k(x_i, x_j) = exp\left( - \frac{||x_i - x_j||^2}{2\delta ^2} \right) \end{aligned}$$

(14)

where $||x_i - x_j||$ is the distance between the objects and $\delta$ is the kernel parameter. $\delta$ plays an important role in controlling the granularity of approximation. In [18], $||x_i - x_j||$ was taken as $HD(x_i,x_j)$ for generalised the GK-FRS to HDS.

3.3 Dependency Computation

$R_G^B$ denotes Gaussian kernel based fuzzy similarity relation where HD is computed over B $\subseteq$ A. Based on Proposition 3 in [18], $R_G^{\{a\}\cup \{b\}}$ can be computed using $R_G^{\{a\}}, R_G^{\{b\}}$ by,

$$\begin{aligned} R_G^{\{a\}\cup \{b\}}(x, y) = R_G^{\{a\}}(x,y) \times R_G^{\{b\}}(x,y)\quad \forall x,y \in U \end{aligned}$$

(15)

It is essential to find the fuzzy lower and upper approximation for calculating the dependency of the attributes. This approximation is calculated from the fuzzy similarity relation $R_G$.

Proposition 1

[18]. The formula for calculating the fuzzy lower and upper approximation is defined as:

$$\begin{aligned} \underline{R_G}d_i(x)&= \sqrt{1-\left( sup_{y\notin d_i} R_G(x,y)\right) ^2} \end{aligned}$$

(16)

$$\begin{aligned} \overline{R_G}d_i(x)&= sup_{y\in d_i} R_G(x,y) \end{aligned}$$

(17)

where $\forall d_i \in U/\{d\}$.

The universe U is divided into different granules U/{d} = {$d_1, d_2,...,d_l$}. The fuzzy positive regions of decision attribute ({d}) concerning B are defined as:

$$\begin{aligned} POS_{B}(\{d\}) = \bigcup _{i=1}^l \underline{R_G^B}d_i. \end{aligned}$$

(18)

The dependency of the attribute or a set of attributes is defined as follows:

$$\begin{aligned} \gamma _B(\{d\}) = \frac{|POS_B(\{d\})|}{|U|} = \frac{|\bigcup _{i=1}^l \underline{R_G^B} d_i|}{|U|} \end{aligned}$$

(19)

where $\bigcup _{i=1}^l \underline{R_G^B} d_i = \sum _i \sum _{x\in d_i} \underline{R_G^B} d_i(x)$.

3.4 The FRSA-NFS-HIS Algorithm

The FRSA-NFS-HIS algorithm uses SFS control strategy for reduct computation. This Algorithm starts with an empty reduct set R. In every iteration an attribute $a\in A-R$ is added to R based on the criteria of giving maximum gamma gain ($\gamma _{R\cup \{a\}}(\{d\}) - \gamma _R(\{d\})$). The end condition is determined by a parameter $\epsilon$ (a very small value near to zero and is a user control parameter). The algorithm completes execution and returns R when no available attributes $a\in A-R$ gives a gamma gain exceeding epsilon ($\epsilon$).

4 Proposed MFRSA-NFS-HIS Algorithm

This section describes the proposed MFRSA-NFS-HIS algorithm by incorporating vectorized operation in the FRSA-NFS-HIS algorithm.

4.1 Vectorization in FRSA-NFS-HIS Algorithm

All fuzzy similarity relation based fuzzy rough set reduct computation involves object based computation. Starting with the computation of fuzzy similarity relation for each conditional attributes, computation of fuzzy lower approximation involves object-wise computation. Hence the implementation involves several nested looping structures over the space of objects (U). Computing environments such as R, Matlab have excellent support for matrix and sub-matrix based operation. Vectorization is the process of modeling the computation involving nested loops into matrix, sub-matrix based operations. It is established [16] that the same computation through vectorization can result in significant performance gain over implementation using loops.

The first important computation involved in FRSA-NFS-HIS algorithm is the calculation of fuzzy silmilarity relation for individual conditional attributes. This requires computation of appropriate distance function between a pair of objects requiring two loops. These are translated as matrix based operation by replication of attribute column |U| times resulting in $|U | \times |U |$ matrix and finding matrix based distance computation with its transpose and applying gaussian kernel function on the resulting matrix. The fuzzy similarity relation computation between a set of attributes is computed by element-wise multiplication of individual similarity matrices by using Eq. 15.

The most frequent computation in FRSA-NFS-HIS algorithm is the computation of gamma using Algorithm 1 which computes fuzzy dependency using Eq. 19. Improving the computation efficiency of Algorithm 1 has an immense impact on the overall performance of MFRSA-NFS-HIS algorithm.

The Algorithm 1 calculates lower approximation of each concept using all the objects. For an example, let U/{d} = {$d_1, d_2, d_3$}, $d_1 = \{x_1,x_2,x_3,x_8\},$ $d_2 = \{x_4, x_5\},$ and $d_3 = \{x_6, x_7\}$.

$\underline{R_G}d_1(x_1) = \sqrt{1 - \left( sup_{y\notin d_1} R_G(x_1, y)\right) ^2} = \sqrt{1 - \left( sup\{R_G(x_1,x_4),R_G(x_1,x_5),R_G(x_1,x_6),R_G(x_1,x_7)\}\right) ^2}$ But when we calculating lower approximation for the object $x_4$ which is belong to the different decision class ($x_4 \in U-d_i$)

$\underline{R_G}d_1(x_4) = \sqrt{1 - \left( sup\{R_G(x_4,x_4),R_G(x_4,x_5),R_G(x_4,x_6),R_G(x_4,x_7),R_G(x_4,x_9),\}\right) ^2}$

and as the value of $R_G(x_4,x_4) = 1$, the total value becomes zero. It means all the objects which do not belong to the same decision class contribute zero in gamma calculation.

The proposed algorithm IDGKA (Algorithm 2) computes gamma using only the objects which are belonging to the same decision class. The IDGKA algorithm does not use the objects which are belonging to a different decision class. For computing gamma, the IDGKA algorithm uses all the objects only once for any number of decision classes. So, the Algorithm 2 reduces $|U-d_i|$ iterations for each decision class ($d_i$) and executes only $|d_i|$ times for each decision class (concept). The computation of the proposed Algorithm 2 involves sub-matrix based operation described below.

$POS_G^B$ is a zero vector of size |U| representing a fuzzy positive region membership of each object. The actual membership is incrementally assigned by considering each decision concept objects in(line no 3 to 5 of Algorithm 2) iteration. For a decision concept $d_i$ the row-wise maximum are computed on sub-matrix $R_G^B(d_i, U-d_i)$ and the positive region membership for $d_i$ objects is computed as a vector operation using Eq. 16. Finally, in line number 6 $\gamma _B(\{d\})$ is computed through a summation of the $POS_G^B$ vector. Hence all the required computation of DGKA are vectorized in IDGKA using submatrix and vector operations.

4.2 Overcoming $\epsilon$-Parameter Dependency

In SFS based reduct computation algorithm based on classical rough sets, the possibility of occurrence of a trivial ambiguous situation is identified in [14]. In such situation, no available attributes are resulting any gamma gain leading to sub reduct computation instead of reduct computation. The end condition of FRSA-NFS-HIS can result in a similar situation wherein no available attributes give a gamma gain exceeding $\epsilon$ but has a possibility for an increase in gamma if proceeded to future iterations. Such situation results in sub reduct computation in FRSA-NFS-HIS algorithm. To overcome this we have modified the end condition as $\gamma _R == \gamma _A$. This will incur computation overhead for $\gamma _A$ computation but is required for having proper end condition.

The resulting MFRSA-NFS-HIS algorithm is given in Algorithm 3.

5 Experiments, Results and Analysis

The experiments are conducted on Intel (R) i5 CPU, Clock Speed 2.66 GHz, 4 GB of RAM, Ubuntu 14.04, 64 bit OS and R Studio, Version 0.99.447. In this work, we have used benchmark datasets for performing the experiments. The datasets are described in Table 1. All the datasets are from UCI Machine Learning Repository [8]. The proposed MFRSA-NFS-HIS algorithm is implemented in R environment.

Table 1. Description of datasets

Table 2. Comparison with FRSA-NFS-HIS and MFRSA-NFS-HIS algorithms with respect to computational time (in seconds) and reduct size

5.1 Comparative Experiments with FRSA-NFS-HIS Algorithm

The experiments are performed on proposed feature selection (MFRSA-NFS-HIS) algorithm. The results obtained are compared with the result of the existing FRSA-NFS-HIS algorithm reported in [18] for all the datasets in Table 1. In [18], the results of the FRSA-NFS-HIS algorithm is reported in Fig. 1, where results are varying, and we take the lower bound of the results for comparing the result with MFRSA-NFS-HIS algorithm. The Table 2 shows the comparison of the results of FRSA-NFS-HIS and MFRSA-NFS-HIS algorithm.

Analysis of Results. The comparison of the results of existing feature selection approach and proposed feature selection approach is given in Table 2. From the Table 2, it is observed that the proposed approach takes less time than existing approach for all the datasets in Table 1 and the computation gain of the algorithm MFRSA-NFS-HIS is varying from 97 % to 99 %. The size of the reduct is almost same for both the approaches. The size of the reduct in a few datasets is higher in MFRSA-NFS-HIS due to the modification of the end condition determined by $\gamma _A$.

5.2 Comparative Experiments with L-FRFS and B-FRFS Algorithms

The feature selection algorithm Fuzzy Lower Approximation based FS (L-FRFS) and Fuzzy Boundary Approximation based FS (B-FRFS) are proposed by Jensen et al. [7] which are implemented in Rough Set package in R environment [13]. The proposed algorithm MFRSA-NFS-HIS also implemented in R environment using the vectorized operations [16]. For executing the L-FRFS and B-FRFS algorithms, we used Lukasiewicz t-norm, Lukasiewicz implicator, and fuzzy similarity measure defined in Eq. 8. The comparison of results of the algorithm L-FRFS, B-FRFS with MFRSA-NFS-HIS are given in Table 3.

Table 3. Comparison of algorithm L-FRFS and B-FRFS available in R package with MFRSA-NFS-HIS algorithms with respect to computational time (in seconds) and reduct size

The computation time of the algorithms L-FRFS and B-FRFS reported in the literature [7], and the results of Rough Set R package executed on the above mentioned system is significantly different. This may be primarily due to the hardware configuration used in [7]. But the details of the hardware configurations are not specified in [7]. So, for the completeness of comparative analysis, we have executed MFRSA-NFS-HIS on the datasets used in [7] and the results are summarized in Table 4.

Table 4. Comparison of algorithm L-FRFS and B-FRFS reported in the literature [7] with MFRSA-NFS-HIS algorithms with respect to computational time (in seconds) and reduct size

Analysis of Results. From the analysis of the results, it is observed that the reduct computation algorithm MFRSA-NFS-HIS takes comparatively lesser computation time than the algorithms L-FRFS and B-FRFS which is available in Rough Set package in R platform. The last column of the Table 3 depicts the computational gain percentage obtained by MFRSA-NFS-HIS over L-FRFS and B-FRFS algorithm respectively. The computation gain with respect to L-FRFS and B-FRFS is more than 95 %.

From the analysis of the results reported in the literature for the algorithm L-FRFS and B-FRFS, it is observed that the computation gain of MFRSA-NFS-HIS algorithm with respect to algorithm L-FRFS and B-FRFS is more than 84 % for all datasets from Table 4 except the Ionosphere dataset in which a gain percentage 46 % with L-FRFS is obtained. The reduct size of MFRSA-NFS-HIS is also much higher than FRFS algorithms. This is primarily due to the difference in Ionosphere dataset size used in [7] and in our experiments. From the comparison of the results of R package and results reported in the literature with MFRSA-NFS-HIS it is observed that the proposed MFRSA-NFS-HIS algorithm achieves a significant computational gain over the existing methods.

6 Conclusion

In this paper, improvements for FRSA-NFS-HIS algorithm are proposed by incorporation of vectorized operation as MFRSA-NFS-HIS algorithm. The proposed MFRSA-NFS-HIS algorithm has a significant improvement on computation time over the existing method. The size of the reduct computed by MFRSA-NFS-HIS algorithm are almost same as FRSA-NFS-HIS. We have also compared the MFRSA-NFS-HIS with L-FRFS and B-FRFS algorithms available in R package and obtained significant computational gains. The obtained results establish the relevance and role of vectorization in fuzzy rough reduct computation. The proposed approach facilitates model construction in HDS by giving relevant reduced feature set in an effective manner. In future distributed/parallel algorithm for MFRSA-NFS-HIS will be investigated for feasible fuzzy rough reduct computation in Big data scenario.