Keywords

1 Introduction

For modern digital computer, faster Arithmetic Logic Unit (ALU) circuit design is essential where portable computers have become as small as the size of palm limitation. This had been possible over the decades due to the revolution that took place in the area of Very Large Scale Integration (VLSI) design.

Various circuits are designed for the purpose of arithmetic computation towards some specific directions such as fast binary adder with conditional carry generator [1], carry save adder [2], self-time carry look ahead adder [3], a spanning tree carry look-ahead adder [4], low voltage full adder [5], recursive mechanism on a parallel self-time adder [6], fast two’s complement VLSI adder [7] etc. Further, Quantum dot Cellular Automata (QCA) which is the transistor less computational model and is expected to provide high density nanotechnology implementations of various Complementary Metal Oxide Semiconductor (CMOS) circuits are found in [8]. Also some theoretical studies are done in [9] for the arithmetic addition and subtraction functions of logarithmic number system. But all the designed circuits are combinational in nature and complexity is dependent on the use of number of logic gates and associated delays. Integral Value Transformation (IVT) is designed in 2009 [10] in discrete field of mathematics which operates on strings of any base. Also, Carry Value Transformation (CVT) which is a special case of IVT and Exclusive OR (XOR) are the two most important transformations operating on bits of strings, recently found many of their applications [11–15]. CVT and XOR transformations have been observed to provide addition of two positive integers for any base of number system [12, 13].

For the large scale cellular automata (CA) experiments, Cellular Automata Machines (CAMs) become very special compared to any kind of computing machine [16]. The first version of CAM machine is CAM-6 which is produced commercially 20 years back and various CAMs are now available for all the research communities. In CVT-XOR paradigm, CAM is used for the addition of two non-negative integers where internal circuit is designed using AND and XOR gates with carry bit shifting logic. It has been easily seen from the theory of CVT-XOR convergence behavior that CVT-XOR using CAMs can perform better than any other circuit. This is because the CAM used here operates on clock cycle only (without any gate delays) [14]. Along with this multi number CVT-XOR theory is developed and proposed to offer a parallel model for multi number addition using CAM which can be implemented for VLSI design [13]. As hardware complexity for addition or subtraction is same, it is highly needed for the extension of CVT-XOR operations over the integer domain including both positive and negative integers. This is the main agenda of this paper.

The addition of two non-negative integers (Say X and Y) is exactly equal to their CVT and XOR operations sum i.e. X + Y = CVT (X, Y) + XOR (X, Y). And using CVT and XOR operations in recursive manner the maximum number of steps to get CVT = 0 is n+1 where n = MAX (X, Y) number of bits in binary [12]. So in CVT-XOR paradigm, we have to check/concentrate on CVT part which is to be zero to get for both the addition or subtraction result on XOR part. Therefore understanding the dynamics of integer pair with regards to convergence behaviour is an important task in this regard. And the convergence behavior of integer pair is interdependent on bits representing the integer pair.

For example (Fig. 1), let there be a positive integer N = 14. There are 15 integer pairs as (X, Y) whose pair sum is 14 = (X + Y). Now in this paradigm we can easily visualize the nature-inspired tree data structure. If we draw the CVT-XOR convergence tree [17] whose nodes are represented by integer pairs where first part is CVT value and second part is XOR value and root is with CVT = 0 and XOR = X + Y. As can be seen from the following figure, among the 15 integer pairs, seven integer pairs are ((10, 4), (12, 2), (4, 10), (8, 6), (14, 0), (6, 8), (2, 12)) which take one iteration to get CVT = 0 and similarly seven integer pairs are ((7, 7)..., (1, 13)) which take two iterations to get CVT=0 and for one integer pair (0, 14) is taking zero iteration. Clearly, it can be seen that the integer 14 is with binary 4 bits and all the integer pairs involving 14 get at least one 4 bits number except the pair (7, 7) which needs 3 bits. So we are able to get sum on XOR part most of the cases in lesser number of iterations.

Fig. 1.
figure 1

Nature inspired tree data structure for the non-negative integer 14 and pairs (whose sum is 14) are converging towards (0, 14).

Full size image

The paper is organized as follows: Sect. 2 discusses the modified definition of CVT and XOR operations. In Sect. 3, various cases of CVT-XOR properties towards their convergence behaviour to capture the subtraction operation are proposed. Section 4 deals with the complexity and performance analysis of subtraction operation. Lastly, Sect. 5 concludes the paper.

2 Modified Definition of CVT and XOR Operations for Integer Domain

Let A and B are two integers and their signed binary representation be \(A=a_{s}a_{n}...a_{1}\) and \(B=b_{s}b_{n}...b_{1}\) respectively where \(a_{s}\) and \(b_{s}\) are the two sign bits in Most Significant Bit (MSB) position. The CVT of A and B is \(a_{s}\wedge b_{s}a_{n}\wedge b_{n}...a_{1}\wedge b_{1}0\) and XOR of A and B is \(a_{s}\bigoplus b_{s}a_{n}\bigoplus b_{n}...a_{1}\bigoplus b_{1}\). It is to be noted that ith column bits of two integers with ANDing operation is saved in \((i+1)\)th column for CVT calculation with 0 padded in Least Significant Bit (LSB) position. In this binary notation the negative integer is always represented in 2’s complement form. Now three cases can happen for sign bits of two integers: (i) if \(a_{s}=b_{s}=1\), then CVT is negative and obviously XOR is positive, (ii) if sign bits are complement to each other i.e. \(a_{s}=1\) and \(b_{s}=0\) or \(a_{s}=0\) and \(b_{s}=1\), then CVT is positive and XOR is negative and (iii) if \(a_{s}=b_{s}=0\), then both the CVT and XOR are positive.

Illustration 1: An example is shown in Table 1 taking one negative number A = −6 (1010) and one positive number B = 12 (1100) and one extra bit (MSB) considering for sign bit. All the most significant bits are the sign bits respectively. The CVT of above two numbers is +16 and XOR is −10. Therefore, with regards to the additive property of CVT and XOR operations [12], here 12 − 6 = 6 is equal to 16 − 10 = 6.

Table 1. CVT and XOR operations for one negative integer (−6) and one positive integer (12).
Full size table

3 Convergence Behaviour of CVT and XOR Operations for Various Cases of Integer Pairs

Previously in [12] for any two non-negative integers A and B, \(A + B=CVT (A, B) + XOR (A, B)\) and maximum number of iterations leading to CVT = 0 or XOR = 0 is \(n+1\) are proved where n is the number of significant bits of bigger number. Here we are dealing with integer domain and observe different cases of CVT and XOR operations targeted mainly for capturing subtraction operation. The convergence behavior of different cases of integer pairs are shown in different figures where CVT and XOR values are considered as x and y coordinates respectively. We start with any (CVT, XOR) integer pair as initial quadrant in the figure and traversing into the next (CVT, XOR) integer pair after calculating and so on serially one after another until CVT value becomes 0. Thus the final result of addition/subtraction can be found on the y axis except the non-converging case of CVT-XOR operations.

3.1 Both the Integers A and B Are Positive

Various properties are already discussed and some of them are in the form of important theorems [11–13].

3.2 Both the Integers A and B Are Negative

Lemma 1

CVT and XOR will be negative and positive respectively after the first iteration, but from the second iteration onwards, CVT will always be positive and XOR will always be negative.

Proof: Let \(A=a_{s}a_{n}...a_{1}\) and \(B=b_{s}b_{n}...b_{1}\) be the signed binary representation where the MSB are \(a_{s}\) and \(b_{s}\). As A and B are negative integers therefore \(a_{s}=b_{s}=1\). So CVT of two negative integers is negative and XOR is positive after the first iteration. But from the second iteration onwards MSB is always 0 for CVT and 1 for XOR operation, so XOR will always be negative and CVT will always be positive and this would continue.

Illustration 2: Convergence behavior of three (negative, negative) integer pairs are shown in Fig. 2 using state transition diagram: \((a) (-14, -14) \rightarrow (-28, 0) \rightarrow (0, -28),\) \( (b)(-1, -6)\rightarrow (-12, 5)\rightarrow (8,-15) \rightarrow (0, -7)\), and \((c) (-3, -11)\rightarrow (-22, 8)\rightarrow (16, -30) \rightarrow (0, -14).\) CVT patterns for all negative-negative integer pairs (0, 0), (0, −1)...(−16, −16) are shown in Table 2 where from −1 to −16 with regards to rows and columns, a beautiful pattern is conserved having exactly same 1st, 3rd and 4th quadrants.

Fig. 2.
figure 2

State transition diagram of three integer pairs: (a) (−14, −14), (b) (−1, −6), and (c) (−3, −11).

Full size image
Table 2. CVT pattern for negative-negative integer pairs.
Full size table

Lemma 2

For any two negative integers A and B, \(| CVT (A, B) | \ge |CVT (A, A)|\) where \(| A | \ge | B|\).

Proof: Let \(A=a_{s}a_{n}...a_{1}\) and \(B=b_{s}b_{n}...b_{1}\) be the signed binary representation where \(|A |\ge |B|\). As MSB is 1 for both the integers, therefore MSB of both CVT (A, B) and CVT (A, A) are 1. Hence the result can be seen very easily.

Illustration 3: CVT(−3, −2) = CVT(101, 110) = 1000 which is −8 and CVT(−3, −3) = CVT(101, 101) = 1010 which is −6.

Lemma 3

\(|CVT (A, B) |\ge [MAX (|A |, |B |) \times 2]\).

Proof: \(CVT (A, A)=a_{s}\wedge a_{s}a_{n}\wedge a_{n}...a_{1}\wedge a_{1}\) = \(a_{s} a_{n}...a_{1}0\). The place values of \(CVT (a_{i}, a_{i})\) is 2 times the place values of sign binary bits of A i.e. \(CVT (A, A) = |2\times A|\). Now \(CVT (A, B) \ge CVT (A, A)\) for any \(|A |\ge |B|\) (Lemma 2). So \(|CVT (A, B) |\ge [MAX (|A |, |B |) \times 2]\).

3.3 The Integer A is Negative and the Integer B is Positive

Property 1

\(CVT(A, B) \le 2 \times B\).

Examples: \(CVT (-1, 11) = 22\), \(CVT (-4, 11) = 16 < 22\), \(CVT (-7, 2) = 0 < 4\).

When \({\varvec{|A| > |B|}}\) i.e. the Magnitude of the Negative Integer is Bigger.

In this case CVT will always converge. For the proof, similar arguments can be seen from [12].

Illustration 4: Convergence behavior of two integer pairs (one negative and another positive) are shown in Fig. 3 using state transition diagram: \((a) (-17, 11) \rightarrow (22, -28) \rightarrow (8, -14) \rightarrow (0, -6),\) \( (b)(-1, -6)\rightarrow (-12, 5)\rightarrow (8,-15) \rightarrow (0, -7)\) and \((c) (-9, 1)\rightarrow (2, -10)\rightarrow (4, -12) \rightarrow (8, -16) \rightarrow (0,-8).\) CVT patterns for all negative-positive integer pairs (0, 0),(−1, 0)...(−16, 16) are shown in Table 3. Here 2nd, 3rd and 4th quadrants are exactly same.

Table 3. CVT pattern for negative-positive integer pairs.
Full size table

Lemma 4

If \(B = |A |-1\), then their CVT = 0 and XOR = −1.

Proof: The binary representation of A and B are complement to each other when A is negative and \(B = |A |-1\). So their CVT becomes 0. As \(A + B = CVT (A, B) + XOR (A, B)\) and their CVT is 0, XOR = −1.

For e.g. Let A = −3 (1 0 1) and B = 2 (0 1 0). We can observe that signed binary representation of A and B are complement to each other. So clearly their CVT will be 0 (0000) and XOR will be −1 (111).

Fig. 3.
figure 3

State transition diagram of three integer pairs: (a) (−17, 11), (b) (−8, 7), and (c) (−9, 1).

Full size image

Lemma 5

XOR will never be 0.

Proof: Here A is negative and B is positive so their sign bits are 1 and 0 respectively and hence XOR (1, 0) = 1. Therefore, XOR will never be 0.

When \({\varvec{|A| < |B|}}\) i.e. the Magnitude of the Negative Integer is Smaller.

Lemma 6

CVT will always increase and never converge to 0.

Proof: Let the signed binary representation of \(A=a_{s}a_{n}...a_{1}\) and \(B=b_{s}b_{n}...b_{1}\). As A is negative and B is positive, \(a_{s}=1\) and \(b_{s}=0\). So \(XOR(a_{s}, b_{s}) =1.\) Here we are considering that \(|A |< |B |\), so \(A + B >0\) \(\Longrightarrow CVT + XOR >0\) (\(A + B=CVT(A,B)+XOR(A,B)\)). But XOR is negative, so CVT will be positive which is greater than the XOR value. Therefore, CVT can never converge to 0.

Illustration 5: Convergence behavior of two integer pairs (positive integer magnitude is bigger) are shown in Fig. 4 using state transition diagram: \((a) (17, -11) \rightarrow (34, -28) \rightarrow (64, -58)...\) \( (b)(2, -1)\rightarrow (4, -3)\rightarrow (8,-7) \rightarrow (16, -15) \rightarrow (32, -31)\rightarrow (64,-58)...\).

Lemma 7

XOR will never be 0.

Proof: Same as Lemma 5.

When \({\varvec{|A| =|B|}}\) i.e. the Magnitude of the Negative and Positive Integer is equal.

Lemma 8

CVT will never converge to 0.

Fig. 4.
figure 4

State transition diagram of two integer pairs: (a) (17, −11) and (b) (2, −1).

Full size image

Proof: We know that XOR is negative. Here \(|A| = |B|\), so \(A + B=0\) \(\Longrightarrow \) \( CVT+XOR = 0\), but XOR is a negative integer, so CVT must be a positive integer with magnitude = \(|XOR|\). Therefore CVT will never converge to 0.

Lemma 9

In the first iteration (A, B) will be (2, −2) when \(|A|= |B|\) is an odd integer.

Proof: For equal odd integers with opposite sign, their signed binary representation is complement to each other except their LSB. So their CVT is of the form in binary 00...10 which is decimal 2 and XOR is of the form in binary 11...10 which is decimal −2.

It is to be noted that the convergence behaviour for \(|A| = |B|\) is same as the previous case (Fig. 4). In all the cases it may be noted that a straight line is found starting with any random integer pair that signifies the same addition/subtraction result happening on the same straight line and having the final destination on the y axis.

4 Performance Analysis and General Circuit Diagram for CVT-XOR Operations

We have seen that the negative-negative integer pair on successive CVT-XOR operations is converging to CVT = 0. Therefore, result of addition/subtraction is stored in XOR part as in [14]. Similar is the case for negative-positive integer pair where magnitude of negative integer is bigger (Sect. 3.3, when the magnitude of negative integer is bigger), therefore expected result of addition/subtraction is negative and is also converging; we are able to get the result from XOR part. On the other hand, positive-negative integer pair where negative integer is smaller, result of addition is positive (Sect. 3.3, when the magnitude of negative integer is smaller). This is a case which is non-converging. The CVT part is increasing infinitely keeping addition/subtraction result same, thereby increasing the number of bits in binary to represent them. But in practical scenario, hardware register slots (say width w) are fixed which can store finite number of bits for each integer including the sign bit. Therefore, when CVT-XOR operations are performing we have to concentrate only for fixed number of bits. Doing so we can ultimately find that for both the cases CVT is converging and subtraction/addition result can be found in XOR part. It has been seen that given an n bit integer, we have to consider \(n+1\) bits by padding zeros in MSB position for the positive integer. Here we are dealing with general form for all integers and negative integer is represented in 2’s complement form, we have to deal with \(n+2\) bits including sign bit for maximum of n bit integer in our paradigm. We have to pad at least two extra bits 0’s in MSB for positive integer and 1’s in MSB for negative integer. Below Table 4 shows two examples when \(|A |\le |B |\) (Sect. 3.3, when the magnitude of negative integer is smaller or equal to positive integer) for (14, −11) and (2, −2) as initial pairs where CVT is not converging theoretically, but in practical scenario by fixing the bit numbers it can be seen that CVT is converging and XOR part is giving the expected result after maximum of \(n+1\) iterations. Here we obtained the result for (14, −11) pair in 4th iteration and for (2,−2) pair in 3rd iteration. Iteration numbers can vary depending on the integer pairs and their binary representation.

Table 4. Repetitive CVT and XOR operations for one 4 bits (14, −11) and one 2 bits (2,−2) integer pairs to get their subtraction result.
Full size table
Fig. 5.
figure 5

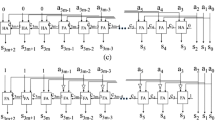
Proposed CAM circuit diagram in simplified form for CVT-XOR operations in general as discussed in [14]

Full size image

Therefore, the time complexity in general for getting the CVT part having all zeros and XOR part holding expected result is of the order of n i.e. O (n) where maximum is n+1 and minimum is 1 is same as [14]. Figure 5 shows the previous CAM circuit from [14], with redrawing to get easy understanding how CVT-XOR operation is performing in parallel and recursive manner. We have seen that we have to consider extra two bits in general. So with 5 slots circuit (Fig. 5) which can performed the addition/subtraction result for 3 bit integer pairs. Given any two integers, binary representation of one integer is stored in CVT part right (LSB) to left (MSB) X1...X5 and another integer is stored in XOR part right (LSB) to left (MSB) Y1...Y5. X1 is connected to voltage ground zero. Therefore, once the operation is started from the second iteration onwards X1 is always holding binary zero. Once all the positions of CVT part become zeros, XOR part gives the expected result. If MSB of XOR part is binary 0 number is positive, and if MSB of XOR part is binary 1 number is negative, in this case we have to take 2’s complement of the number.

Looking back the descriptions of CVT-XOR tree in the introduction, we do the experiment from positive integer 8 to 14 and results of average height can be seen from 2.7, 1.9, 1.72, 1.25, 2.07, 1.05, and 1.4 respectively. It may be remarked that when the number of bits are increasing signifying the larger pairs the average heights are significantly less. On repeating the experiments with random selection up-to 10 bit integer pairs, we find that average iterations is under 3.5 to reach the root of the CVT-XOR tree.

5 Conclusion

In this paper, we have proved that CVT-XOR paradigm is valid for all integers. It has been seen that main property \(A + B=CVT (A, B) + XOR (A, B)\) is also valid for all integers i.e. both for the negative and positive. We thoroughly discussed the convergence behaviour of all types of integer pairs. Some of the related important theorems are proved and shown for the integer pairs in different cases. When initial integer pairs are taken from 1st and 3rd quadrant, CVT of the pair converge to 0 after maximum of \(n+1\) steps; where n is the number of significant bits required for representing bigger integer including sign bit. On the other hand, when initial integer pairs are taken from 2nd and 4th quadrant, their CVT converges to 0 as usual when final result becomes negative. But if the final result becomes zero or positive, CVT goes on increasing keeping their sum result invariant. But under practical scenario, it has been seen that their summation result can be observed in the XOR register after \(w=n+1\) steps. Thus this CVT-XOR paradigm is naturally amenable to VLSI circuit design for faster arithmetic computation.