Abstract
The first step of the development of the idea of intuitionistic fuzziness (see [1]), was related to introducing an intuitionistic fuzzy interpretation of the classical (standard) modal operators “necessity” and “possibility” (see, e.g., [2,3,4,5]). In the period 1988–1993, we defined eight new operators, extending the first two ones. In the end of last and in the beginning of this century, a lot of new operators were introduced. Here, we discuss the most interesting ones of them and study their basic properties.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
The first step of the development of the idea of intuitionistic fuzziness (see [1]), was related to introducing an intuitionistic fuzzy interpretation of the classical (standard) modal operators “necessity” and “possibility” (see, e.g., [2,3,4,5]). In the period 1988–1993, we defined eight new operators, extending the first two ones. In the end of last and in the beginning of this century, a lot of new operators were introduced. Here, we discuss the most interesting ones of them and study their basic properties.
3.1 Intuitionistic Fuzzy Classical Modal Operators
For the formula A for which \(V(A) = \langle a, b\rangle \), where \(a, b \in [0, 1]\) and \(a + b \le 1\), following [1], we define the two modal operators “necessity” and “possibility”:

respectively.
It is suitable to define the evaluation function V so that:

Two different geometrical interpretations of both operators are given in Figs. 3.1, 3.2, 3.3 and 3.4, respectively.
It is obvious, that if p is a tautology, then,  and \(\diamondsuit \,\, p\) are also tautologies. Moreover,
and \(\diamondsuit \,\, p\) are also tautologies. Moreover,

where relation \(``\le \text {''}\) is defined as in (1.1.9).
Let everywhere below:
where \(a, b, c, d, e, f \in [0, 1], a + b \le 1, c + d \le 1, e + f \le 1\).
Here, some of the most important assertions, related to the two classical (standard) modal operators, are formulated and proved for the intuitionistic fuzzy case.
First, following [1], we see that the basic properties of the (standard) modal operators in their intuitionistic fuzzy interpretations for every formula A are:



In classical modal logic, expressions




are (in some sense) equivalent. In the intuitionistic fuzzy case, similarly with De Morgan’s Laws, the situation is different.
Theorem 3.1.1
For every formula A,
-
(a)
expression (3.1.1) is a tautology and an IFT for negations \(\lnot _{1}, \lnot _{2}, \lnot _{6}, \lnot _{8}, \lnot _{13}, \lnot _{14},\) \(\lnot _{35}, \ldots , \lnot _{38}, \lnot _{40}, \lnot _{42}, \ldots , \lnot _{46}, \lnot _{48}, \lnot _{50}, \lnot _{53},\)
-
(b)
expression (3.1.2) is a tautology and an IFT for negations \(\lnot _{1}, \lnot _{8}, \lnot _{53},\)
-
(c)
expression (3.1.3) is a tautology and an IFT for negations \(\lnot _{1}, \lnot _{3}, \ldots , \lnot _{6}, \lnot _{11}, \lnot _{14},\) \(\lnot _{35}, \ldots , \lnot _{37}, \lnot _{39}, \lnot _{41}, \ldots , \lnot _{45}, \lnot _{47}, \lnot _{49}, \lnot _{50}, \lnot _{51},\)
-
(d)
expression (3.1.4) is a tautology and an IFT for negations \(\lnot _{1}, \lnot _{3}, \lnot _{4}\).
This is the first case, when a given expression is a tautology in all cases when it is an IFT. As we saw in the two previous chapters, only small number of IFTs are tautologies.
Theorem 3.1.2
For every formula A, each of the expressions


is
-
(a)
a tautology for implications \(\rightarrow _{2}\),\(\rightarrow _{3}\), \( \rightarrow _{5}\),\(\rightarrow _{8}\),\(\rightarrow _{11}\),\(\rightarrow _{14}\),\(\rightarrow _{15}\), \(\rightarrow _{20}\), \(\rightarrow _{23}\),\(\rightarrow _{24}\), \(\rightarrow _{27}\), \(\rightarrow _{31}\), \(\rightarrow _{32}\), \(\rightarrow _{34}\), \(\rightarrow _{37}\), \(\rightarrow _{40}\), \(\rightarrow _{42}\), \(\rightarrow _{47}\), \(\rightarrow _{48}\), \(\rightarrow _{49}\), \(\rightarrow _{52}\),\(\rightarrow _{55}\), \(\rightarrow _{57}\), \(\rightarrow _{62}\), \(\rightarrow _{63}\), \(\rightarrow _{65}\), \(\rightarrow _{68}\), \(\rightarrow _{69}\), \(\rightarrow _{74}\), \(\rightarrow _{77}\), \(\rightarrow _{79}\), \(\rightarrow _{83}\), \(\rightarrow _{84}\), \(\rightarrow _{88}\), \(\rightarrow _{92}\), \(\rightarrow _{93}\), \(\rightarrow _{97}\), \(\rightarrow _{176},\ldots ,\rightarrow _{185}\),
-
(b)
an IFT for implications \(\rightarrow _{1},\ldots ,\rightarrow _{9},\rightarrow _{11},\ldots ,\rightarrow _{15},\rightarrow _{17},\rightarrow _{18},\rightarrow _{20},\ldots ,\rightarrow _{24},\) \(\rightarrow _{27},\ldots ,\rightarrow _{38},\rightarrow _{40},\rightarrow _{42},\rightarrow _{44},\ldots ,\rightarrow _{53},\rightarrow _{55},\rightarrow _{57},\rightarrow _{59},\ldots ,\rightarrow _{66},\) \(\rightarrow _{68},\rightarrow _{69},\rightarrow _{71},\rightarrow _{72},\rightarrow _{74},\ldots ,\rightarrow _{77},\rightarrow _{79},\ldots ,\rightarrow _{85},\rightarrow _{88},\ldots ,\) \(\rightarrow _{94},\rightarrow _{97},\ldots ,\rightarrow _{139},\rightarrow _{141},\rightarrow _{146},\ldots ,\rightarrow _{170},\rightarrow _{176},\ldots ,\rightarrow _{185}\).
Theorem 3.1.3
For every two formulas A and B, each of the equalities

holds for the disjunction and conjunction, defined by (1.1.4) and (1.1.5).
Open Problem 12 Which other disjunctions and conjunctions, existing of which is discussed in Sect. 1.7, satisfy (3.1.5) and (3.1.6)?
Theorem 3.1.4
For every two formulas A and B, each of the expressions

is
-
(a)
a tautology for implications \(\rightarrow _{2},\rightarrow _{3},\rightarrow _{5},\rightarrow _{8},\rightarrow _{11},\rightarrow _{14},\rightarrow _{15},\rightarrow _{20},\rightarrow _{23},\,\rightarrow _{24},\,\rightarrow _{27},\,\rightarrow _{31},\,\rightarrow _{32},\,\rightarrow _{34},\,\rightarrow _{37},\rightarrow _{40},\,\rightarrow _{42},\,\,\rightarrow _{47},\ldots ,\rightarrow _{49},\,\,\rightarrow _{52}, \rightarrow _{55},\,\rightarrow _{57},\,\rightarrow _{62},\,\rightarrow _{63},\,\rightarrow _{65},\,\rightarrow _{68},\,\rightarrow _{69},\,\rightarrow _{74},\rightarrow _{77},\,\rightarrow _{79},\rightarrow _{83},\rightarrow _{84},\rightarrow _{88},\rightarrow _{92},\rightarrow _{93},\rightarrow _{97},\rightarrow _{176},\ldots ,\rightarrow _{185}\),
-
(b)
an IFT for implications \(\rightarrow _{1},\ldots ,\rightarrow _{9},\rightarrow _{11},\ldots ,\rightarrow _{15},\rightarrow _{17},\rightarrow _{18},\rightarrow _{20},\ldots ,\rightarrow _{24},\rightarrow _{27},\ldots ,\rightarrow _{38},\rightarrow _{40},\rightarrow _{42},\rightarrow _{44},\ldots ,\rightarrow _{53},\,\rightarrow _{55},\,\rightarrow _{57},\,\rightarrow _{59},\ldots ,\rightarrow _{66},\rightarrow _{68},\rightarrow _{69},\rightarrow _{71},\rightarrow _{72},\rightarrow _{74},\ldots ,\rightarrow _{77},\,\rightarrow _{79},\ldots ,\rightarrow _{85},\,\rightarrow _{88},\ldots ,\rightarrow _{94},\,\rightarrow _{97},\ldots ,\rightarrow _{139},\rightarrow _{141},\rightarrow _{146},\ldots ,\rightarrow _{170},\rightarrow _{176},\ldots ,\rightarrow _{185}\).
Theorem 3.1.5
For every two formulas A and B, the expression

is
-
(a)
a tautology for implications \(\rightarrow _{2},\rightarrow _{3},\rightarrow _{5},\rightarrow _{8},\,\rightarrow _{11},\,\rightarrow _{14},\,\rightarrow _{20},\,\rightarrow _{24},\rightarrow _{25},\,\rightarrow _{27},\,\rightarrow _{29},\,\rightarrow _{47},\ldots ,\rightarrow _{49},\,\rightarrow _{52},\,\rightarrow _{55},\,\rightarrow _{57},\,\rightarrow _{58},\,\rightarrow _{60},\,\rightarrow _{69},\,\rightarrow _{77},\rightarrow _{79},\rightarrow _{81},\rightarrow _{92},\rightarrow _{93},\rightarrow _{97},\rightarrow _{99},\rightarrow _{177},\rightarrow _{179},\rightarrow _{181},\rightarrow _{182},\rightarrow _{184}\),
-
(b)
an IFT for implications \(\rightarrow _{1},\ldots ,\rightarrow _{9},\rightarrow _{11},\ldots ,\rightarrow _{14},\rightarrow _{17},\rightarrow _{18},\rightarrow _{20},\rightarrow _{21},\,\rightarrow _{24},\,\rightarrow _{25},\,\rightarrow _{27},\ldots ,\rightarrow _{29},\rightarrow _{46},\ldots ,\rightarrow _{53},\rightarrow _{55},\rightarrow _{57},\ldots ,\rightarrow _{61},\rightarrow _{64},\rightarrow _{66},\,\rightarrow _{69},\,\rightarrow _{71},\,\rightarrow _{72},\rightarrow _{75},\ldots ,\rightarrow _{77},\rightarrow _{79},\ldots ,\rightarrow _{81},\rightarrow _{91},\ldots ,\rightarrow _{94},\rightarrow _{97},\ldots ,\rightarrow _{102},\rightarrow _{108},\ldots ,\rightarrow _{113},\rightarrow _{118},\rightarrow _{120},\ldots ,\rightarrow _{128},\,\rightarrow _{134},\ldots ,\rightarrow _{137},\,\rightarrow _{139},\rightarrow _{141},\,\,\rightarrow _{147},\,\,\rightarrow _{149},\,\ldots ,\rightarrow _{154},\,\,\rightarrow _{156},\,\,\rightarrow _{158},\ldots ,\rightarrow _{162},\,\,\rightarrow _{165},\,\ldots ,\,\rightarrow _{167},\rightarrow _{169},\rightarrow _{177},\rightarrow _{179},\rightarrow _{181},\rightarrow _{182},\rightarrow _{184}\).
Proof
(a) Let, for example, the implication be considered in the variant \(\rightarrow _{11}\). Then,

This completes the proof. \(\square \)
Theorem 3.1.6
For every two formulas A and B, the expression

is
-
(a)
a tautology for implications \(\rightarrow _{2},\rightarrow _{3},\rightarrow _{8},\rightarrow _{11},\rightarrow _{14},\rightarrow _{15},\rightarrow _{20},\rightarrow _{24},\rightarrow _{25},\,\rightarrow _{27},\,\rightarrow _{29},\,\rightarrow _{47},\,\rightarrow _{48},\,\rightarrow _{52},\,\rightarrow _{55},\,\rightarrow _{57},\rightarrow _{58},\rightarrow _{60},\rightarrow _{77},\rightarrow _{79},\rightarrow _{81},\rightarrow _{92},\rightarrow _{97},\rightarrow _{99},\rightarrow _{177},\rightarrow _{179}\),
-
(b)
an IFT for implications \(\rightarrow _{1},\ldots ,\rightarrow _{9},\rightarrow _{11},\ldots ,\rightarrow _{15},\rightarrow _{17},\rightarrow _{18},\rightarrow _{20},\rightarrow _{21},\rightarrow _{24},\rightarrow _{25},\rightarrow _{27},\ldots ,\rightarrow _{29},\rightarrow _{46},\ldots ,\rightarrow _{53},\,\rightarrow _{55},\,\rightarrow _{57},\ldots ,\rightarrow _{61},\,\rightarrow _{64},\rightarrow _{66},\rightarrow _{69},\rightarrow _{71},\ldots ,\,\rightarrow _{73},\,\rightarrow _{75},\ldots ,\rightarrow _{77},\,\rightarrow _{79},\ldots ,\,\rightarrow _{81},\,\rightarrow _{91},\ldots ,\,\rightarrow _{94},\rightarrow _{96},\,\,\ldots ,\,\,\rightarrow _{102},\,\,\rightarrow _{106},\,\,\ldots ,\,\,\rightarrow _{113},\,\,\rightarrow _{118},\,\,\ldots ,\,\rightarrow _{128},\,\,\rightarrow _{134},\,\ldots ,\,\,\rightarrow _{138},\rightarrow _{151},\rightarrow _{158},\rightarrow _{161},\rightarrow _{166},\rightarrow _{167},\rightarrow _{169},\rightarrow _{177},\rightarrow _{179},\rightarrow _{181},\rightarrow _{182},\rightarrow _{184}\).
Theorem 3.1.7
For every two formulas A and B, the expression

is
-
(a)
a tautology for implications \(\rightarrow _{3},\rightarrow _{5},\rightarrow _{11},\rightarrow _{14},\rightarrow _{20},\rightarrow _{25},\rightarrow _{27},\rightarrow _{29},\rightarrow _{48},\rightarrow _{49},\rightarrow _{57},\rightarrow _{58},\rightarrow _{60},\rightarrow _{77},\rightarrow _{79},\rightarrow _{81},\rightarrow _{97},\rightarrow _{99},\rightarrow _{181},\rightarrow _{182},\rightarrow _{184}\),
-
(b)
an IFT for implications \(\rightarrow _{1},\rightarrow _{3},\ldots ,\rightarrow _{7},\rightarrow _{9},\rightarrow _{11},\ldots , \rightarrow _{14},\rightarrow _{17},\rightarrow _{18},\rightarrow _{20},\rightarrow _{21},\rightarrow _{25},\rightarrow _{27},\ldots ,\rightarrow _{29},\rightarrow _{46},\rightarrow _{48},\ldots ,\rightarrow _{51},\rightarrow _{53},\rightarrow _{57},\rightarrow _{58},\rightarrow _{60},\rightarrow _{61},\rightarrow _{64},\,\rightarrow _{66},\,\rightarrow _{71},\,\rightarrow _{72},\,\rightarrow _{75},\ldots ,\rightarrow _{77},\rightarrow _{79},\ldots ,\rightarrow _{81},\rightarrow _{91},\ldots ,\rightarrow _{94},\rightarrow _{97},\ldots ,\rightarrow _{102},\,\rightarrow _{107},\,\ldots ,\rightarrow _{113},\rightarrow _{118},\rightarrow _{120},\ldots ,\rightarrow _{122},\rightarrow _{124},\ldots ,\rightarrow _{128},\rightarrow _{134},\ldots ,\rightarrow _{137},\rightarrow _{151},\rightarrow _{158},\rightarrow _{161},\rightarrow _{166},\rightarrow _{167},\rightarrow _{169},\rightarrow _{181},\rightarrow _{182},\rightarrow _{184}\).
An interesting open problem here is the following.
Open Problem 13 Determine for which pair of implications \((\rightarrow _i, \rightarrow _j)\) and for every two formulas A and B, the following equality is valid:

We remind that for each evaluation function V and for each formula A such that \(V(x) = \langle a, b \rangle ,A\) is “intuitionistic fuzzy sure” (IF-sure), iff \(a \ge 0.5 \ge b\).
Let for the variable x, for which \(V(x) = \langle a, b \rangle \), it is valid that

(see Fig. 3.5).
Following and extending [6], we give the following theorem.
Theorem 3.1.8
(Locality of intuitionistic fuzzy sure) For every formula A, if  and \(A( \diamondsuit \, x)\) are IF-sure, then, for every y, for which
and \(A( \diamondsuit \, x)\) are IF-sure, then, for every y, for which

A(y) is IF-sure.
Proof
Let

We shall prove the assertion by induction on the complexity of the formula A. Let A be a variable, i.e., \(A(x) = x\). Then,

and from (3.1.7) it follows that
i.e., A(y) is IF-sure.
Let \(A = P \wedge Q\), where for P and Q the assertion is valid. Then,
For \(A = P \vee Q\), the check is similar.
Let \(A(x) = \forall z P(x,z)\), where the assertion is valid for P(x, z). For every y, for which (3.1.7) is valid, and for every z:
by assumption. Then,
For \(A(x) = \exists z P(x,z)\) the assertion is proved analogically.
Let  , where the assertion is valid for P(x). Then, we obtain directly, that
, where the assertion is valid for P(x). Then, we obtain directly, that
When \(A(x) = \diamondsuit \, P(x)\) the assertion is proved analogically. \(\square \)
Corollary 3.1.1
(Locality of intuitionistic fuzzy truth) For every formula A, if  and \(A( \diamondsuit \, x)\) are tautologies, then, for every y, for which (3.1.7) is valid, A(y) is a tautology.
and \(A( \diamondsuit \, x)\) are tautologies, then, for every y, for which (3.1.7) is valid, A(y) is a tautology.
The case of IFTs is more complicated.
It can be established that if A and B are IFTs, then, \(A \wedge B\) is not necessarily an IFT. For example, let \(p \vee \lnot p\) and \(q \vee \lnot q\) for different propositions p and q be IFTs, then
Nevertheless, the form
is not always an IFT. Take e.g.:
Then,
but
A Conjunctive Normal Form (CNF) A is of the sort \(D_{1} \wedge \dots \wedge D_{m}\), where \(D_{i} = l_{i,1} \vee \dots \vee l_{i,k_{i}}\) is a clause of literals. A literal is either a propositional variable (e.g., p) or a negated variable (in the same case – \(\lnot p\)). The literals p and \(\lnot p\) are called opposite. Two clauses C and D are called connected if they contain a common variable occurring in opposite literals (e.g., p in C and \(\lnot p\) in D).
Lemma 3.1.1
A clause C is an IFT if and only if it is a classical two-valued tautology iff C contains a pair of opposite literals.
Lemma 3.1.2
A conjunction of two literals C and D, which are IFTs, is an IFT iff they are connected.
Proof
If C and D are IFTs and are connected, then, \(C \wedge D\) is an IFT. Consider an arbitrary V. Let \(C = p \vee A\), \(D = \lnot p \vee B\), where \(V(A) = \langle a, b\rangle ,V(B) = \langle c, d\rangle \) and let \(V(p) = \langle \mu , \nu \rangle \). Then,
and from
and
it follows that \(C \wedge D\) is an IFT.
Let C and D be two IFT clauses. Let us define the following evaluation function W: For variables p which occur in both positive and negative literals in C let \(W(p) = \langle 0.2, 0.2\rangle \). For a variable q that appears in both the positive and the negative forms in D: \(W(q) = \langle 0.4, 0.4\rangle \). Note that the sets of such variables are disjoint. For variables which occur positively in C or D, let W be \(\langle 0.2, 0.4\rangle \) and for variables occurring negatively in C or \(D - \langle 0.4, 0.2\rangle \). It is a simple check which shows that \(W(C \wedge D) = \langle 0.2, 0.4\rangle \). Thus, the conjunction of C and D is not an IFT. \(\square \)
A CNF A is called totally connected if every pair of clauses C, D in it is connected.
Lemma 3.1.3
A CNF A is an IFT iff all clauses in it are IFTs and A is totally connected.
Proof
Assume that all clauses of A are IFTs and that A is totally connected. If we assume that for a some evaluation function W:
is such that \(\mu < \nu \), then, it can be easily seen that there is a pair of clauses C and D of A such that \(C \wedge D\) is already not an IFT (due to W) – but this is impossible by Lemma 3.1.2. In the opposite direction: if at least two clauses in A are not connected, then their conjunction will not be an IFT, hence, A will not be an IFT either. \(\square \)
Theorem 3.1.9
(Locality of IFT) For every connected formula A, if  and \(A( \diamondsuit \, x)\) are IFTs, then, for every y, for which (3.1.7) is valid, A(y) is an IFT.
and \(A( \diamondsuit \, x)\) are IFTs, then, for every y, for which (3.1.7) is valid, A(y) is an IFT.
Proof
The proof is similar to the proof of Theorem 3.1.8, but in the case when formula A is a conjunction of two connected formulas, we use Lemma 3.1.2 \(\square \)
Now, we discuss the basic relations between the quantifiers \(\forall \) and \(\exists \) and the two modal operators  and \(\diamondsuit \,\).
and \(\diamondsuit \,\).
The equalities from [7], Sect. 1.6 can be transformed for both modal operators and both quantifiers, as follows.
Theorem 3.1.10
Let A be a formula and x be a variable. Then,
-
(a)
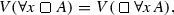
-
(b)
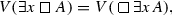
-
(c)
\( V( \forall x \diamondsuit \, A) = V( \diamondsuit \forall xA), \)
-
(d)
\( V( \exists x \diamondsuit \, A) = V( \diamondsuit \exists xA).\)
Proof
Let us check the validity of (a):

Equalities (b)–(d) are proved analogically. \(\square \)
Theorem 3.1.11
Let A be a formula and x be a variable. Then,
-
(a)
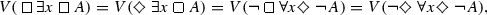
-
(b)
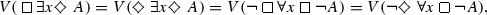
-
(c)
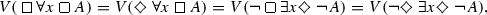
-
(d)
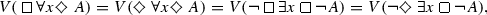
-
(e)
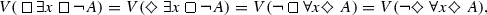
-
(f)
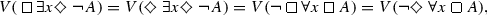
-
(g)
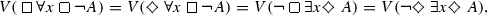
-
(h)

Proof
Let us check the validity of (a)



Equalities (b)–(h) are proved analogically. \(\square \)
Let for a fixed formula A and for a variable x:








Having in mind Theorem 3.1.11, we can prove the following theorem.
Theorem 3.1.12
Let A be a formula and x be a variable. Then,
-
(a)
if \(P \in S(A)\) and \(Q \in T(A)\), then, \(V(P) \le V( \exists xA) \le V(Q)\),
-
(b)
if \(P \in U(A)\) and \(Q \in V(A)\), then, \(V(P) \le V( \forall xA) \le V(Q)\),
-
(c)
if \(P \in W(A)\) and \(Q \in X(A)\), then, \(V(P) \le V( \forall xA) \le V(Q)\),
-
(d)
if \(P \in Y(A)\) and \(Q \in Z(A)\), then, \(V(P) \le V( \exists xA) \le V(Q)\),
where \(V(X) \le V(Y)\) for the formulas X and Y if and only if \(\mu (X) \le \mu (Y)\) and \(\nu (X) \ge \nu (Y)\).
Finally, following [8], we discuss another modal operator, without an analogue in modal logic.
For the formula A, for which \(V(A) = \langle a, b\rangle \), where \(a, b \in [0, 1]\) and \(a + b \le 1\), we define the new modal operator “\( \bigcirc \)” by:
Obviously, the pair \(\langle \frac{a}{a+b}, \frac{b}{a+b} \rangle \) is an intuitionistic fuzzy pair and more particularly – a fuzzy pair, because
The new operator has the following more interesting properties.
Theorem 3.1.13
For every formula A:
-
(a)
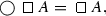
-
(b)
\(\bigcirc \, \diamondsuit \,\,A = \diamondsuit \,\,A,\)
-
(c)
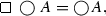
-
(d)
\(\diamondsuit \,\, \bigcirc A = \bigcirc A,\)
-
(e)
\(\bigcirc \, \bigcirc A = \bigcirc A.\)
Proof
(e) For formula A we obtain:
This completes the proof. The rest assertions in (a)–(d) are proved analogically. \(\square \)
Theorem 3.1.14
For every formula A:
-
(a)
Only negation \(\lnot _1\) satisfies equality
$$ \lnot \bigcirc \lnot A = \bigcirc A,$$ -
(b)
Only negations \(\lnot _1, \lnot _2, \lnot _{11}, \lnot _{18}, \lnot _{53}\) satisfy equality
$$ \lnot \bigcirc A = \bigcirc \lnot A.$$
Theorem 3.1.15
For every two formulas A and B and for the disjunction and conjunction defined by (1.1.4) and (1.1.5):
Proof
Let A and B be two formulas, so that \(V(A) = \langle a, b \rangle , V(B) = \langle c, d \rangle , a, b, c, d \in [0, 1]\) and \(a + b \le 1, c + d \le 1.\) Then,
and
First, we prove the validity of the following inequality. For every three real numbers \(a, b, c \in [0, 1]\), if \(a \ge c\), then:
Obviously, the inequality is valid in the form of an equality, when \(a = c\). Let \(a > c\). Then, sequentially, we obtain:
i.e., (3.1.6) is valid.
Now, we check the validity of inequality
Let
If \(a \ge c\), then, we obtain:
If \(\frac{a}{a + b} \ge \frac{c}{c + d}\), then,
If \(\frac{a}{a + b} \le \frac{c}{c + d}\), then, from (3.1.6),
Let \(a < c\). Then,
If \(\frac{a}{a + b} \ge \frac{c}{c + d}\), then, from (1), we obtain
If \(\frac{a}{a + b} \le \frac{c}{c + d}\), then,
In the same way, we can prove that
i.e., the first inequality is checked.
The second inequality in the theorem, as well as the Theorem 3.1.16 are proved by analogy. \(\square \)
Theorem 3.1.16
For every predicate P:
3.2 Extensions of the Intuitionistic Fuzzy Modal Operators
In this section, we introduce the first group of extended intuitionistic fuzzy modal operators.
First, by analogy with the IFS-operators from [7, 9], in the period 1988–1993, we define eight new modal operators.
Let A be a fixed formula for which \(V(A) = \langle a, b \rangle \) and \(\alpha , \beta , \gamma , \delta ,\varepsilon , \eta \in [0,1]\).
We define operators \(D_{\alpha },F_{\alpha ,\beta }\), \(G_{\alpha ,\beta },H_{\alpha ,\beta }\), \(H_{\alpha ,\beta }^{*},J_{\alpha ,\beta },J_{\alpha ,\beta }^{*}\) and \(X_{ \alpha ,\beta ,\gamma ,\delta ,\varepsilon , \eta }\) by:
for
In [10], it was mentioned that the third condition (3.2.3) was omitted in [7, 9]. It was introduced to the definition in [10], because without it, e.g., for constant \(U^* = \langle 0, 0 \rangle \) we obtain
which is impossible.
Obviously,


where r is an arbitrary real number in [0, 1].
Let us define for every formula A:
To every formula A, the evaluation function V assigns for \(D_{\alpha } (A)\) a point from the segment between  and \(V(\diamondsuit \, A)\) depending on the value of the argument \(\alpha \in [0,1]\) (see Fig. 3.6). As in the case of some of the above operations, this construction needs auxiliary elements which are shown in Fig. 3.6.
and \(V(\diamondsuit \, A)\) depending on the value of the argument \(\alpha \in [0,1]\) (see Fig. 3.6). As in the case of some of the above operations, this construction needs auxiliary elements which are shown in Fig. 3.6.
To every formula A, the evaluation function V assigns for \(F_{\alpha ,\beta } (A)\) a point from the triangle with vertices  and \(V(\diamondsuit \, A)\), depending on the value of the arguments \(\alpha , \beta \in [0,1]\) for which \(\alpha +\beta \le 1\) (see Fig. 3.7).
and \(V(\diamondsuit \, A)\), depending on the value of the arguments \(\alpha , \beta \in [0,1]\) for which \(\alpha +\beta \le 1\) (see Fig. 3.7).
To every formula A, the evaluation function V assigns for \(G_{\alpha ,\beta } (A)\) a point in the rectangle whose vertices are the point V(A) and points with coordinates, \(\langle pr_{1} V(A), 0 \rangle , \langle 0, pr_{2} V(A) \rangle \) and \(\langle 0,0\rangle \), where \(pr_{i}p\) is the i-th projection \((i = 1,2)\) (see Fig. 3.8).
To every formula A, the evaluation function V assigns for \(K_{\alpha ,\beta } (A)\) a point \(V(H_{\alpha ,\beta }(A))\) from the rectangle whose vertices are the points with coordinates \(\langle 0, pr_{2}V(A) \rangle \) and  and vertices
and vertices  and V(A), depending on the value of the parameters \(\alpha ,\beta \in [0,1]\) (see Fig. 3.9).
and V(A), depending on the value of the parameters \(\alpha ,\beta \in [0,1]\) (see Fig. 3.9).
To every formula A, the evaluation function V assigns for \(J_{\alpha ,\beta } (A)\) a point \(V(J_{\alpha ,\beta }(A))\) from the rectangle whose vertices are the points with coordinates \(\langle pr_{1}V(\diamondsuit \,\,A),\) \(0 \rangle ,\) \(\langle pr_{1}V(A), 0 \rangle \) and vertices V(A) and \(V(\diamondsuit \, A)\), depending on the value of the parameters \(\alpha , \beta \in [0,1]\) (see Fig. 3.10).
To every formula A, the evaluation function V assigns for \(H^*_{\alpha ,\beta } (A)\) a point \(V(H_{\alpha ,\beta }^{*}(A))\) from the trapezoid with vertices with coordinates \(\langle 0, pr_{2}V(A) \rangle \) and \(\langle 0, 1 \rangle \) and vertices  and V(A), depending on the value of the parameters \(\alpha ,\beta \in [0,1]\) (see Fig. 3.11).
and V(A), depending on the value of the parameters \(\alpha ,\beta \in [0,1]\) (see Fig. 3.11).
To every formula A, the evaluation function V assigns for \(J^*_{\alpha ,\beta } (A)\) a point \(V(J_{\alpha ,\beta }^{*} (A))\) from the trapezoid with vertices with coordinates \(\langle 1, 0 \rangle \) and \(\langle pr_{1}V(A), 0 \rangle \) and vertices V(A) and \(V(\diamondsuit \, A)\), depending on the value of the parameters \(\alpha ,\beta \in [0,1]\) (see Fig. 3.12).
Below, we formulate and prove assertions, that by the moment have been checked only for some intuitionistic fuzzy implications and negation, which gives rise to the following important open problem for solving in future.
Open Problem 14 Check these assertions for all the remaining implications and negations.
Theorem 3.2.1
If formula A is a tautology, then:
-
(a)
for every two \(\alpha , \beta \in [0,1]:\) \(D_{\alpha } (A),F_{\alpha ,\beta } (A)\), for \(\alpha + \beta \le 1,J_{\alpha ,\beta }(A)\) and \(J_{\alpha ,\beta }^{*} (A)\) are tautologies,
-
(b)
\(G_{\alpha ,\beta } (A),H_{\alpha ,\beta } (A),H_{\alpha ,\beta }^{*} (A)\), are IFTs,
-
(c)
for every \(\alpha , \varepsilon , \eta \) so that \(\alpha \ge \varepsilon (1 - \eta ),X_{\alpha ,\beta ,\gamma ,\delta ,\varepsilon ,\eta } (A)\) is an IFT.
Proof
(b) From \(V(A) = \langle 1, 0\rangle \) it follows that
i.e., \(G_{\alpha ,\beta } (A),H_{\alpha ,\beta } (A)\) and \(H_{\alpha ,\beta }^{*} (A)\) are IFTs. The other cases are proved by analogy. \(\square \)
Theorem 3.2.2
If formula A is an IFT, then:
-
(a)
for \(\alpha \ge 0.5\) \(D_{\alpha } (A)\) is an IFT,
-
(b)
for \(\alpha \ge \beta \) and \(\alpha + \beta \le 1\) \(F_{\alpha ,\beta } (A)\) is an IFT,
-
(c)
for \(\alpha \ge \beta \) \(G_{\alpha ,\beta } (A)\) is an IFT,
-
(d)
\(J_{\alpha ,\beta } (A),J_{\alpha ,\beta }^{*} (A)\) are IFTs,
-
(e)
for \(\alpha \ge \delta ,\beta \ge \varepsilon ,\eta \ge \gamma \) \(X_{ \alpha ,\beta ,\gamma ,\delta ,\varepsilon ,\eta } (A)\) is an IFT.
It can be easily seen that for every \(a, b,\alpha ,\beta ,\gamma ,\delta , \varepsilon ,\) \(\eta \) \(\in [0,1]\) and \(a + b \le 1\), if
then
are IFTs. For example,
i.e., \(F_{\alpha ,\beta } (\langle a, b\rangle ) \rightarrow _{11} \langle a, b\rangle \) is an IFT.
On the other hand, we can see that there are cases in which for the different implications, different conditions must hold for the validity of some expression. The following two assertions serve as examples.
Theorem 3.2.3
For every \(a,b,\alpha ,\beta ,\gamma ,\delta ,\varepsilon ,\eta ,\alpha ',\beta ',\gamma ', \delta ', \varepsilon ', \eta ' \in [0,1]\) and \(a + b \le 1\), if \(O \in \lbrace D, F, G,H, H^{*}, J, J^{*} \rbrace \), then:
-
(a)
\(O_{\alpha ,\beta } (\langle a, b\rangle ) \rightarrow _{11} O_{\alpha ',\beta '} (\langle a, b\rangle )\) is a tautology for \(\alpha \le \alpha '\),
-
(b)
\(X_{\alpha ,\beta ,\gamma ,\delta ,\varepsilon ,\eta } (\langle a, b\rangle ) \rightarrow _{11} X_{\alpha ',\beta ',\gamma ',\delta ', \varepsilon ', \eta '} (\langle a, b\rangle )\) is a tautology for \(\alpha \le \alpha ',\beta \le \beta '\) and \(\beta \gamma \ge \beta ' \gamma '\).
Proof
(b) Let \(\alpha \le \alpha ',\beta \le \beta '\) and \(\beta . \gamma \ge \beta '. \gamma '\). Then,
because
and therefore, \(\mathrm{sg}(\alpha a + \beta (1 - a - \gamma b) - ( \alpha ' a + \beta ' (1 - a - \gamma ' b)) = 0.\) The other cases are proved similarly. \(\square \)
Theorem 3.2.4
For every \(a, b, \alpha , \beta , \gamma , \delta , \varepsilon , \eta , \alpha ', \beta ', \gamma ', \delta ', \varepsilon ', \eta ' \in [0,1]\) and \(a + b \le 1\), if \(O \in \lbrace D, F, G, H, H^{*}, J, J^{*} \rbrace \), then
-
(a)
\(O_{\alpha ,\beta } ( \langle a, b \rangle ) \rightarrow _4 O_{\alpha ',\beta '} ( \langle a, b \rangle )\) is an IFT for \(\alpha \le \alpha '\) or \(\beta \ge \beta '\),
-
(b)
\(X_{\alpha ,\beta ,\gamma ,\delta ,\varepsilon , \eta } ( \langle a, b \rangle ) \rightarrow _4 X_{\alpha ',\beta ',\gamma ',\delta ',\varepsilon ', \eta '} ( \langle a, b \rangle )\) is an IFT for \(\alpha \le \alpha ',\beta \le \beta '\) and \(\gamma \ge \gamma '\) or for \(\delta \ge \delta ',\varepsilon \ge \varepsilon '\) and \(\eta \le \eta '\).
Open Problem 15 Which other implications satisfy Theorems 3.2.3 and 3.2.4?
There are properties that, probably, are specific for \(\lnot _1\). For example, the following assertion is valid for \(\lnot _1\), but for \(0 < \varepsilon \le \eta \le 1\) it is not valid for \(\lnot _{45,\varepsilon ,\eta }\) (by definition, \(\lnot _1\) coincides with \(\lnot _{45,0,0}\)).
Theorem 3.2.5
For every \(a, b, \alpha , \beta \in [0,1]\) and \(a + b \le 1\):
-
(a)
\(V(F_{\alpha ,\beta } ( \langle a, b \rangle )) = V(\lnot _1 F_{\beta ,\alpha } ( \lnot _1\langle a, b \rangle ))\), for \(\alpha + \beta \le 1\),
-
(b)
\(V(G_{\alpha ,\beta } ( \langle a, b \rangle )) = V(\lnot _1 G_{\beta ,\alpha } ( \lnot _1\langle a, b \rangle )),\)
-
(c)
\(V(H_{\alpha ,\beta } ( \langle a, b \rangle )) = V(\lnot _1 J_{\beta ,\alpha } ( \lnot _1\langle a, b \rangle )),\)
-
(d)
\(V(J_{\alpha ,\beta } ( \langle a, b \rangle )) = V(\lnot _1 H_{\beta ,\alpha } ( \lnot _1\langle a, b \rangle )),\)
-
(e)
\(V(H^*_{\alpha ,\beta } ( \langle a, b \rangle )) = V(\lnot _1 J^*_{\beta ,\alpha } ( \lnot _1\langle a, b \rangle )),\)
-
(f)
\(V(J^*_{\alpha ,\beta } ( \langle a, b \rangle )) = V(\lnot _1 H^*_{\beta ,\alpha } ( \lnot _1\langle a, b \rangle )).\)
Open Problem 16 Which other negations satisfy Theorems 3.2.5?
Let for every two formulas A and B: \(A \leftarrow B\) iff \(B \rightarrow A\).
Theorem 3.2.6
For every two formulas A and B, for every two real numbers \(\alpha , \beta \in [0,1]\) and for implication \(\rightarrow _4\):
-
(a)
\(F_{\alpha ,\beta } (A \wedge B) \rightarrow _4 F_{\alpha ,\beta } (A) \wedge F_{\alpha ,\beta } (B)\), for \(\alpha + \beta \le 1\),
-
(b)
\(F_{\alpha ,\beta } (A \vee B) \leftarrow _4 F_{\alpha ,\beta } (A) \vee F_{\alpha ,\beta } (B)\), for \(\alpha + \beta \le 1\),
-
(c)
\(G_{\alpha ,\beta } (A \wedge B) = G_{\alpha ,\beta } (A) \wedge G_{\alpha ,\beta } (B),\)
-
(d)
\(G_{\alpha ,\beta } (A \vee B) = G_{\alpha ,\beta } (A) \vee G_{\alpha ,\beta } (B),\)
-
(e)
\(H_{\alpha ,\beta } (A \wedge B) \rightarrow _4 H_{\alpha ,\beta } (A) \wedge H_{\alpha ,\beta } (B),\)
-
(f)
\(H_{\alpha ,\beta } (A \vee B) \leftarrow _4 H_{\alpha ,\beta } (A) \vee H_{\alpha ,\beta } (B),\)
-
(g)
\(J_{\alpha ,\beta } (A \wedge B) \leftarrow _4 H_{\alpha ,\beta } (A) \wedge H_{\alpha ,\beta } (B),\)
-
(h)
\(H_{\alpha ,\beta } (A \vee B) \rightarrow _4 H_{\alpha ,\beta } (A) \vee H_{\alpha ,\beta } (B),\)
-
(i)
\(H_{\alpha ,\beta }^{*} (A \wedge B) \rightarrow _4 H_{\alpha ,\beta }^{*} (A) \wedge H_{\alpha ,\beta }^{*} (B),\)
-
(j)
\(H_{\alpha ,\beta }^{*} (A \vee B) \leftarrow _4 H_{\alpha ,\beta }^{*} (A) \vee H_{\alpha ,\beta }^{*} (B),\)
-
(k)
\(J_{\alpha ,\beta }^{*} (A \wedge B) \leftarrow _4 H_{\alpha ,\beta }^{*} (A) \wedge H_{\alpha ,\beta }^{*} (B),\)
-
(l)
\(H_{\alpha ,\beta }^{*} (A \vee B) \rightarrow _4 H_{\alpha ,\beta }^{*} (A) \vee H_{\alpha ,\beta }^{*} (B) \)
are IFTs.
Proof
(a) For the formulas A and B:
and
i.e.,
is an IFT.
Formulas (b)–(l) are checked by analogy. \(\square \)
Open Problem 17 Which other conjunctions and disjunctions (whenever be defined, following the ideas from Sect. 1.7) have similar properties?
Theorem 3.2.7
For every predicate A, and for every \(\alpha , \beta \in [0, 1]\), such that \(\alpha + \beta \le 1\):
-
(a)
\(V(\exists x F_{\alpha ,\beta } (P(x))) \le V(F_{\alpha ,\beta } \exists x P(x))\),
-
(b)
\(V(\forall x F_{\alpha ,\beta } (P(x))) \ge V(F_{\alpha ,\beta } \forall x P(x)).\)
Corollary 3.2.1
For every predicate A, and for every \(\alpha , \beta \in [0, 1]\), such that \(\alpha + \beta \le 1\):
-
(a)
\(V(\exists x D_{\alpha } (P(x))) \le V(D_{\alpha } \exists x P(x))\),
-
(b)
\(V(\forall x D_{\alpha } (P(x))) \ge V(D_{\alpha } \forall x P(x)).\)
Theorem 3.2.8
For every formula A and for every \(\alpha \), \(\beta ,\gamma ,\delta \in [0,1]\) such that \(\alpha +\beta \le 1\) and \(\gamma +\delta \le 1\):
Proof
Let for \(\alpha ,\beta ,\gamma ,\delta \in [0,1]\): \(\alpha + \beta \le 1\) and \(\gamma + \delta \le 1\). Let \(V(A) = \langle a, b \rangle \). Then,
This completes the proof. \(\square \)
Corollary 3.2.2
For every predicate A, and for every \(\alpha \in [0, 1]\):
-
(a)
\( V(D_{\alpha } (D_{\beta } (A))) = V(D_{\beta } (A)), \)
-
(b)
\( V(D_{\alpha } (F_{\beta ,\gamma } (A))) = V(D_{\alpha +\beta -\alpha \beta -\alpha \gamma } (A))\), for \(\beta + \gamma \le 1,\)
-
(c)
\( V(F_{\alpha ,\beta } (D_{\gamma } (A))) = V(D_{\gamma } (A)).\)
Theorem 3.2.9
For every formula A and for every \(\alpha \), \(\beta ,\gamma ,\delta \in [0,1]\):
Theorem 3.2.10
For every formula A and for every \(\alpha \), \(\beta \in [0,1]\):
-
(a)
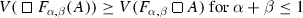 ,
, -
(b)
\(V(\diamondsuit \,\,F_{\alpha ,\beta } (A)) \le V(F_{\alpha , \beta } \diamondsuit \,\,A)\) for \(\alpha +\beta \le 1\),
-
(c)
 ,
, -
(d)
\(V(\diamondsuit \,\,G_{\alpha ,\beta } (A)) \ge V(G_{\alpha , \beta } \diamondsuit \,\,A)\),
-
(e)
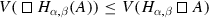 ,
, -
(f)
\(V(\diamondsuit \,\,H_{\alpha ,\beta } (A)) \ge V(H_{\alpha , \beta } \diamondsuit \,\,A)\),
-
(g)
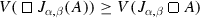 ,
, -
(h)
\(V(\diamondsuit \,\,J_{\alpha ,\beta } (A)) \le V(J_{\alpha , \beta } \diamondsuit \,\,A)\),
-
(i)
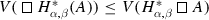 ,
, -
(j)
\(V(\diamondsuit \,\,J^*_{\alpha ,\beta } (A)) \ge V(J^*_{\alpha , \beta } \diamondsuit \,\,A)\).
Theorem 3.2.11
For every A and for every \(\alpha ,\beta \), \(\gamma ,\delta \in [0,1]\):
Theorem 3.2.12
For every formula A and for every \(\alpha \), \(\beta \in [0,1]\):
-
(a)
\(V(H_{\alpha ,\beta } (G_{\gamma ,\delta } (A))) \le V(G_{\gamma ,\delta } (H_{\alpha ,\beta }\) (A))),
-
(b)
\(V(J_{\alpha ,\beta } (G_{\gamma ,\delta } (A))) \le V(G_{\gamma ,\delta } (J_{\alpha ,\beta }\) (A))),
-
(c)
\(V(H_{\alpha ,\beta }^{*} (G_{\gamma ,\delta } (A))) \le V(G_{\gamma ,\delta } (H_{\alpha ,\beta }^{*}\) (A))),
-
(d)
\(V(J_{\alpha ,\beta }^{*} (G_{\gamma ,\delta } (A))) \le V(G_{\gamma ,\delta } (J_{\alpha ,\beta }^{*}\) (A))).
Theorem 3.2.13
Let A be a formula and x be a variable. Then, for every \(\alpha , \beta \in [0,1]\):
We finish with an assertion for the operator X, following [11].
Theorem 3.2.14
For every two IFPs \(\langle \mu , \nu \rangle \) and \(\langle \rho , \sigma \rangle \), there are real numbers \(a, b, c, d, e, f \in [0,1]\) satisfying (3.2.1)–(3.2.3), such that
Proof
Let \(\mu , \nu , \rho , \sigma \in [0, 1]\), such that \(\mu + \nu \le 1, \rho + \sigma \le 1.\) We search for \(a, b, c, d, e, f \in [0,1]\) that satisfy (3.2.1)–(3.2.3) and for which
i.e.,
We discuss nine cases.
- Case 1.:
-
\(\pi = \mu = 0\). Then, \(\nu = 1\). We put
$$a = c = e = f = 0, \ b = \rho , \ d = \sigma .$$Then, conditions (3.2.1)–(3.2.3) are valid and
$$ X_{0,\rho ,0,\sigma ,0,0}(\langle \mu , \nu , \rangle ) = \langle 0 + \rho (1 - 0 - 0 \times 1), \sigma \times 1 + 0(1 - 0 \times \mu - 1) \rangle = \langle \rho , \sigma \rangle .$$ - Case 2.:
-
\(\pi = \nu = 0\). Then, \(\mu = 1\). We put
$$a = \rho , \ b = c = d = f = 0, \ e = \sigma .$$Then, conditions (3.2.1)–(3.2.3) are valid and
$$ X_{\rho ,0,0,0,\sigma ,0}(\langle \mu , \nu , \rangle ) = \langle \rho + 0 \times (1 - 0 \times 1 - 0), 0 + \sigma (1 - 0 \times 1 - 1) \rangle = \langle \rho , \sigma \rangle .$$When \(\pi = 0\) and \(\mu , \nu > 0\), there are three (sub)cases. It is important to mention that now \(\mu , \nu < 1.\)
- Case 3.:
-
\(\rho > \mu \). Then, from \(\pi = 0\) it follows that \(\mu = 1 - \nu \), and hence \(\sigma \le 1 - \rho < 1 - \mu = \nu .\) So, we put
$$a = 1, \ b = \frac{\rho - \mu }{1 - \mu }, c = e = f = 0, \ d = \frac{\sigma }{\nu }.$$Then, conditions (3.2.1)–(3.2.3) are valid and
$$ X_{1,\frac{\rho - \mu }{1 - \mu },0,\frac{\sigma }{\nu },0,0}(\langle \mu , \nu , \rangle ) = \left\langle \mu + \frac{\rho - \mu }{1 - \mu }(1 - \mu ), \frac{\sigma }{\nu }\nu \right\rangle = \langle \rho , \sigma \rangle .$$ - Case 4.:
-
\(\sigma > \nu \). Then, from \(\pi = 0\) it follows again that \(\mu = 1 - \nu \), and hence \(\rho \le 1 - \sigma < 1 - \nu = \mu .\) So, we put
$$a = \frac{\rho }{\mu }, \ b = c = f = 0, \ d = 1, e = \frac{\sigma - \nu }{1 - \nu }.$$Then, conditions (3.2.1)–(3.2.3) are valid and
$$ X_{\frac{\rho }{\mu },0,0,1,\frac{\sigma - \nu }{1 - \nu },0,0}(\langle \mu , \nu , \rangle ) = \left\langle \frac{\rho }{\mu }\mu + 0, \nu + \frac{\sigma - \nu }{1 - \nu }(1 - \nu ) \right\rangle = \langle \rho , \sigma \rangle .$$ - Case 5.:
-
\(\rho \le \mu \) and \(\sigma \le \nu \). Then, we put
$$a = \frac{\rho }{\mu }, \ b = c = e = f = 0, \ d = \frac{\sigma }{\nu }.$$Then, conditions (3.2.1)–(3.2.3) are valid and
$$ X_{\frac{\rho }{\mu },0,0,\frac{\sigma }{\nu },0,0}(\langle \mu , \nu , \rangle ) = \left\langle \frac{\rho }{\mu }\mu + 0, \frac{\sigma }{\nu }\nu + 0 \right\rangle = \langle \rho , \sigma \rangle .$$When \(\pi > 0\), then, \(\mu , \nu < 1\).
- Case 6.:
-
\(\rho > \mu \) and \(\sigma > \nu \). Then, we put
$$a = c = d = f = 1, \ b = \frac{\rho - \mu }{\pi }, \ e = \frac{\sigma - \nu }{\pi }.$$Then, conditions (3.2.1)–(3.2.3) are valid, because:
$$ a + e - e.f = 1 + e - e = 1 \le 1,$$$$ b + d - b.c = d = \frac{\sigma - \nu }{\pi } \le 1,$$$$ b + e = \frac{\rho - \mu }{\pi } + \frac{\sigma - \nu }{\pi } = \frac{\rho + \sigma - \mu - \nu }{\pi } \le 1.$$All other checks are done in a similar way. Now,
$$ X_{1,\frac{\rho - \mu }{\pi },1,1,\frac{\sigma - \nu }{\pi },1}(\langle \mu , \nu , \rangle ) = \left\langle \mu + \frac{\rho - \mu }{\pi }\pi , \nu + \frac{\sigma - \nu }{\pi }\pi \right\rangle = \langle \rho , \sigma \rangle .$$ - Case 7.:
-
\(\rho > \mu \) and \(\sigma \le \nu .\) Then, as in Case 3, we put
$$a = 1, \ b = \frac{\rho - \mu }{1 - \mu }, c = e = f = 0, \ d = \frac{\sigma }{\nu }.$$Then, conditions (3.2.1)–(3.2.3) are valid and
$$ X_{1,\frac{\rho - \mu }{1 - \mu },0,\frac{\sigma }{\nu },0,0}(\langle \mu , \nu , \rangle ) = \left\langle \mu + \frac{\rho - \mu }{1 - \mu }(1 - \mu ), \frac{\sigma }{\nu }\nu \right\rangle = \langle \rho , \sigma \rangle .$$ - Case 8.:
-
\(\rho \le \mu \) and \(\sigma > \nu \). Then, as in point 4, we put
$$a = \frac{\rho }{\mu }, \ b = c = f = 0, \ d = 1, e = \frac{\sigma - \nu }{1 - \nu }.$$Then, conditions (3.2.1)–(3.2.3) are valid and
$$ X_{\frac{\rho }{\mu },0,0,1,\frac{\sigma - \nu }{1 - \nu },0,0}(\langle \mu , \nu , \rangle ) = \left\langle \frac{\rho }{\mu }\mu + 0, \nu + \frac{\sigma - \nu }{1 - \nu }(1 - \nu ) \right\rangle = \langle \rho , \sigma \rangle .$$ - Case 9.:
-
\(\rho \le \mu \) and \(\sigma \le \nu \). Then, as in Case 5, we put
$$a = \frac{\rho }{\mu }, \ b = c = e = f = 0, \ d = \frac{\sigma }{\nu }.$$Then, conditions (3.2.1)–(3.2.3) are valid and
$$ X_{\frac{\rho }{\mu },0,0,\frac{\sigma }{\nu },0,0}(\langle \mu , \nu , \rangle ) = \left\langle \frac{\rho }{\mu }\mu + 0, \frac{\sigma }{\nu }\nu + 0 \right\rangle = \langle \rho , \sigma \rangle .$$
Therefore, the theorem is proved. \(\square \)
A modification of the above theorem is the following theorem.
Theorem 3.2.15
For every two formulas A, B there exists an operator \(Y \in \lbrace F_{\alpha ,\beta },G_{\alpha ,\beta },H_{\alpha ,\beta },H_{\alpha ,\beta }^{*},J_{\alpha ,\beta },J_{\alpha ,\beta }^{*} \rbrace \) and there exist real numbers \(\alpha , \beta \in [0,1]\) such that
Proof
Let everywhere \(V(A) = \langle a, b\rangle \) and \(V(B) = \langle c, d \rangle \), where \(a, b, c, d \in [0,1]\) and \(a + b \le 1\) and \(c + d \le 1\).
The following 9 cases are possible for a, b, c and d.
\(\begin{array}{rclcl} \text {Case 1.} &{}&{}a = c &{}&{} \text {Then, for } Y:\\ &{}&{} \text {and } &{}&{} \text {if } Y = F, \text { then, } \alpha = \beta = 0;\\ &{}&{}b = d &{}&{} \text {if }Y = G, \text { then, } \alpha = \beta = 1;\\ &{}&{}&{}&{} \text {if } Y = H \text {or } Y = H^{*}, \text { then, } \alpha = 1 \text { and } \beta = 0;\\ &{}&{}&{}&{} \text {if } Y = J \text {or } Y=J^{*} \text { then, } \alpha = 0 \text { and } \beta = 1. \end{array}\)
\(\begin{array}{rclcl} \text {Case 2.} &{}&{} a> c &{}&{} \text {Then, } Y = F \text { and } \alpha =\begin{array}{c} {a-c}\\ \hline {1-c-d} \end{array} \text { and } \beta = 0 \\ &{}&{} \text {and } &{}&{} \text {(we shall note that } 1 - c - d > 1 - a - b \ge 0) \\ &{}&{} b = d &{}&{} \text {or } Y = J \text {or } Y = J^{*}, \text { and } \alpha \text { has the above}\\ &{}&{}&{}&{} \text {form and } \beta = 1. \end{array}\)
\(\begin{array}{rclcl} \text {Case 3.} &{}&{} a < c &{}&{} \text {Then, } Y = G \text { and } \alpha = \begin{array}{c} {a}\\ \hline {c} \end{array} \text { and } \beta = 1 \text { (we note} \\ &{}&{}\text {and } &{}&{} that c > a \ge 0) \\ &{}&{} b = d &{}&{} \text {or } Y = J \text { or } Y = J^{*}, \text { and } \alpha \text { has the above} \\ &{}&{}&{}&{} \text {form and } \beta = 0. \end{array}\)
\(\begin{array}{rclcl} \text {Case 4.}&{}&{} a = c &{}&{} Then, Y = F \text { and } \alpha = 0 \text { and } \beta = \begin{array}{c} {b-d}\\ \hline {1-c-d} \end{array} \\ &{}&{} \text {and } &{}&{} \text {(we note that } 1 - c - d> 1 - a - b \ge 0) \\ &{}&{} b > d &{}&{} \text {or } Y = H \text { or } Y = H^{*}, \text { and } \alpha = 1 \text { and } \beta \text { has} \\ &{}&{}&{}&{} \text {the above form}. \end{array}\)
\(\begin{array}{rclcl} \text {Case 5.}&{}&{} a> c &{}&{} \text {Then, } Y = F \text { and } \alpha =\begin{array}{c} {a-c}\\ \hline {1 - c - d} \end{array} \text { and} \\ &{}&{} \text {and } &{}&{} \beta = \begin{array}{c} {b-d}\\ \hline {1-c-d} \end{array} \text { (we note that } \\ &{}&{} b> d &{}&{} 1-c-d >1-a-b \ge 0) \end{array}\)
\(\begin{array}{rclcl} \text {Case 6.}&{}&{} a< c &{}&{} \text {Then, there are two subcases:}\\ &{}&{}\text { and }&{}&{}\\ &{}&{}b> d. &{}&{}\\ &{}6.1.&{} &{}&{} if\; b \le 1 - c, \text { then, } Y = H \text { and } \alpha =\begin{array}{c} {a}\\ \hline {c} \end{array} \text { and }\\ &{}&{}&{}&{} \beta = \begin{array}{c} {b - d}\\ \hline {1 - c - d} \end{array} \\ &{}&{}&{}&{} \text {or } Y = H^{*} \text { and } \alpha =\begin{array}{c} {a}\\ \hline {c} \end{array} \text { and } \beta =\begin{array}{c} {b-d}\\ \hline {1-a-d} \end{array}\\ &{}&{}&{}&{} \text {(we note that } 1-a-d>1-c-d \ge b-d> 0\\ &{}&{}&{}&{} \text { and } c> a \ge 0) \\ &{}6.2. &{} &{}&{}if\; b> 1 - c, \text { then, } Y = H^{*} \text { and } \alpha =\begin{array}{c} {a}\\ \hline {c} \end{array} \text { and}\\ &{}&{}&{}&{} \beta =\begin{array}{c} {b-d}\\ \hline {1-a-d} \end{array} \text { (we note that } 1 - a - d \ge b - d> 0\\ &{}&{}&{}&{} \text { and } c > a \ge 0) \end{array}\)
\(\begin{array}{rclcl} \text {Case 7.}&{}&{} a = c &{}&{} \text {Then, } Y = G \text { and } \alpha = 1 \text { and } \beta = \begin{array}{c} {b}\\ \hline {d} \end{array} \text { (we note}\\ &{}&{}\text { and } &{} &{}\text { that }d > b \ge 0) \\ &{}&{} b < d.&{}&{}\\ &{}&{}&{}&{} \text {or } Y = J \text { or } Y = H^{*}, \text { and } \alpha = 0 \text { and } \beta \text { has the above form.} \end{array}\)
\(\begin{array}{rclcl} \text {Case 8.} &{}&{} a> c &{}&{} \text {Then, there are two subcases: }\\ &{}&{}\text { and } &{}&{}\\ &{}&{} b< d.&{}&{}\\ &{}8.1. &{} &{}&{} if a \le 1 - d, \text { then, } Y = J \text { and } \alpha =\begin{array}{c} {a-c}\\ \hline {1-c-d} \end{array} \text { and }\\ &{}&{}&{}&{} \beta = \begin{array}{c} {b}\\ \hline {d} \end{array} \\ &{}&{}&{}&{} \text {or } Y = J^{*} \text { and } \alpha =\begin{array}{c} {a-c}\\ \hline {1-b-c} \end{array} \text { and } \beta =\begin{array}{c} {b}\\ \hline {d} \end{array} \text { (we }\\ &{}&{}&{}&{}\text { note that } 1 - c - b> 1 - c - d \ge a - c> 0\\ &{}&{}&{}&{}\text { and } d> b \ge 0)\\ &{}8.2.&{} &{}&{} if a> 1 - d, \text { then, } Y = J^{*} \text { and } \alpha =\begin{array}{c} {a-c}\\ \hline {1-b-c} \end{array}\\ &{}&{}&{}&{} \text { and }\beta = \begin{array}{c} {b}\\ \hline {d} \end{array} \text { (we note that } 1-c-b \ge a-c> 0 \\ &{}&{}&{}&{} \text { and } d> b \ge 0)\\ \text {Case 9.}&{}&{} a< c &{}&{} \text {Then, } Y = G \text { and } \alpha = \begin{array}{c} {a}\\ \hline {c} \end{array} \text { and } \beta =\begin{array}{c} {b}\\ \hline {d} \end{array} \text { (we shall }\\ &{}&{}\text { and } &{}&{} \text { note that } c> a \ge 0 \text { and } d > b \ge 0).\\ &{}&{} b < d. &{}&{} \\ \end{array}\)
This completes the proof. \(\square \)
3.3 Second Type of Intuitionistic Fuzzy Modal Operators
In this section, following [7, 9, 12,13,14,15,16,17], several different modal-like operators of second type are defined and the consequences of their generalizations are discussed. We formulate the properties of these operators which hold for them but do not hold for their extensions.
The following two operators of modal type are similar to the operators in Sect. 3.1. Let for formula A: \(V(A) = \langle \mu , \nu \rangle \). Then ,


All of their properties are valid for their first extensions. For a given real number \(\alpha \in [0, 1]\) and formula A,


Obviously,
For every formula A,


Therefore, the new operators “ ” and “
” and “ ” are generalizations of
” are generalizations of  and
and  , respectively. Their geometrical interpretations are given in Figs. 3.13 and 3.14, respectively.
, respectively. Their geometrical interpretations are given in Figs. 3.13 and 3.14, respectively.
For every formula A, for every \(\alpha \in [0, 1]\):
-
(a)
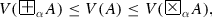
-
(b)
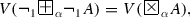
-
(c)
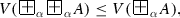
-
(d)
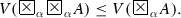
For every formula A, and for every two real numbers \(\alpha , \beta \in [0, 1]\),
-
(a)
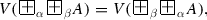
-
(b)
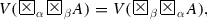
-
(c)
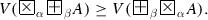
For every formula A, and for every three real numbers \(\alpha , \beta , \gamma \in [0, 1]\),
-
(a)
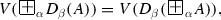
-
(b)
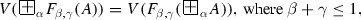
-
(c)
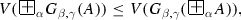
-
(d)
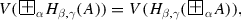
-
(e)
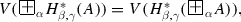
-
(f)
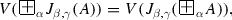
-
(g)
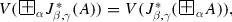
-
(h)
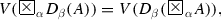
-
(i)
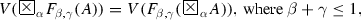
-
(j)
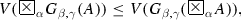
-
(k)
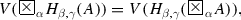
-
(l)
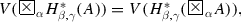
-
(m)
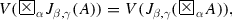
-
(n)
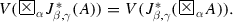
The second extension was introduced in [17] by K. Dencheva. She extended the last two operators to the forms:


where \(\alpha , \beta , \alpha + \beta \in [0, 1]\).
Obviously, for every formula A,




For every formula A, and for every \(\alpha , \beta , \alpha + \beta \in [0, 1]\),
-
(a)
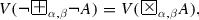
-
(b)
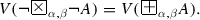
For every formula A, and for every \(\alpha , \beta \in [0, 1]\), each of the inequalities
-
(a)
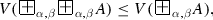
-
(b)
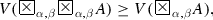
is valid if and only if \(\alpha + \beta = 1\).
For every formula A, and for every \(\alpha \in [0, 1]\),

For every formula A, and for every \(\alpha , \beta , \gamma , \delta \in [0, 1]\) such that \(\alpha + \beta , \gamma + \delta \in [0, 1]\),

Now, the third extension of the above operators is as follows:


where \(\alpha , \beta , \gamma \in [0, 1]\) and \(\max (\alpha , \beta ) + \gamma \le 1\).
Obviously, for every formula A,






For every formula A, and for every \(\alpha , \beta , \gamma \in [0, 1]\) for which \(\max (\alpha , \beta ) + \gamma \le 1\),
-
(a)
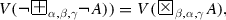
-
(b)
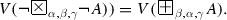
For every formula A, and for every \(\alpha , \beta , \gamma \in [0, 1]\) for which \(\max (\alpha , \beta ) + \gamma \le 1\),
-
(a)
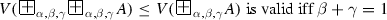 ,
, -
(b)
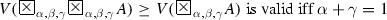 .
.
For every formula A, and for every \(\alpha , \beta , \alpha + \beta \in [0, 1]\),

For every formula A, and for every \(\alpha , \beta , \gamma \in [0, 1]\) for which \(\max (\alpha ,\beta ) + \gamma \le 1\), the four properties
-
(a)
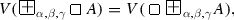
-
(b)
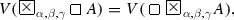
-
(c)
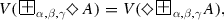
-
(d)
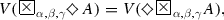
are valid iff \(\alpha = \beta \) and \(\alpha + \gamma = 1\).
For every two formulas A and B, and for every \(\alpha , \beta , \gamma \in [0, 1]\) for which \(\max (\alpha , \beta ) + \gamma \le 1\),
-
(a)

-
(b)
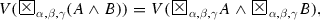
-
(c)
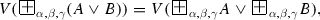
-
(d)
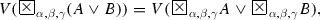
For every predicate A, and for every \(\alpha , \beta , \gamma \in [0, 1]\) for which \(\max (\alpha , \beta ) + \gamma \le 1\),
-
(a)
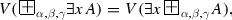
-
(b)
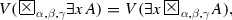
-
(c)
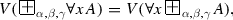
-
(d)

A natural extension of the last two operators is the operator

where \(\alpha , \beta , \gamma , \delta \in [0, 1]\) and \(\max (\alpha , \beta ) + \gamma + \delta \le 1\).
It is the fourth type of operator from the currently discussed group.
Obviously, for every formula A,








For every formula A, and for every \(\alpha , \beta , \gamma , \delta \in [0, 1]\) for which \(\max (\alpha , \beta ) + \gamma + \delta \le 1\):
-
(a)
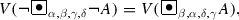
-
(b)
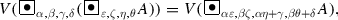
-
(c)
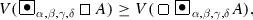
-
(d)
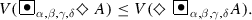
For every pair of formulas A and B, and for every \(\alpha , \beta , \gamma , \delta \in [0, 1]\) for which \(\max (\alpha ,\beta ) + \gamma + \delta \le 1\),
-
(a)
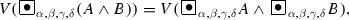
-
(b)
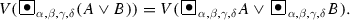
In [18], G. Çuvalcioǧlu introduced the operator \(E_{\alpha ,\beta }\) by
where \(\alpha , \beta \in [0, 1]\), and he studied some of its properties. Obviously,

For every predicate A, and for every \(\alpha , \beta , \gamma , \delta \in [0, 1]\) for which \(\max (\alpha ,\beta ) + \gamma + \delta \le 1\),
-
(a)
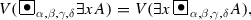
-
(b)
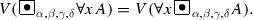
A new (potentially final?) extension of the above operators is the operator

where \(\alpha , \beta , \gamma , \delta , \varepsilon , \zeta \in [0, 1]\) and
Assume that in the particular cases when \(\alpha - \zeta > -\varepsilon , \beta = \delta = 0\) and \(\delta - \zeta < \beta , \gamma = \varepsilon = 0\), the inequalities
hold. Obviously, for every IFS A,










For every formula A, and for every \(\alpha , \beta , \gamma , \delta , \varepsilon , \zeta \in [0, 1]\) for which (3.3.12) and (3.3.13) are valid, the equality

holds.
For every formula A, and for every \(\alpha _1, \beta _1, \gamma _1, \delta _1, \varepsilon _1, \zeta _1, \alpha _2, \beta _2,\) \(\gamma _2,\) \(\delta _2,\varepsilon _2, \zeta _2 \in [0, 1]\) for which conditions that are similar to (3.3.12) and (3.3.13) are valid, the equality


holds.
It must be noted that the equalities

and

which are valid for operator  .
.
Open Problem 18 Check the validity of the above formulas for the case of all intuitionistic fuzzy conjunctions, disjunctions, implications and negations.
Following [9], we formulate and prove the following:
Theorem 3.3.1
Operators \(X_{a,b,c,d,e,f}\) and  are equivalent.
are equivalent.
Proof
Let \(a, b, c, d, e, f \in [0,1]\) and satisfy (6.24) and (6.25). Let
Also, let
Then,
and
(from (3.3.12)).
Thus, we obtain

Conversely, let \(\alpha , \beta , \gamma , \delta , \varepsilon , \zeta \in [0, 1]\) and satisfy (3.3.12) and (3.3.13). From (3.3.13) it follows that for \(\alpha = \beta = \delta = \zeta = 0: \ \varepsilon \le \gamma \), while for \(\alpha = \beta = \gamma = \varepsilon = 0: \ \zeta \le \delta \); from (3.3.12) it follows that for \(\beta = \delta = \varepsilon = \zeta = 0: \ \alpha + \gamma \le 1\), while for \(\alpha = \gamma = \varepsilon = \zeta = 0: \ \beta + \delta \le 1\). Then, let
Let
Then, we obtain,
(from (3.3.12)).
Then, we obtain

Therefore, the two operators are equivalent.
Finally, we construct Fig. 3.15 in which
denotes that operator X represents operator Y, while the converse is not valid, and
denotes that each of the operators represents the other.
Following [19], we introduce the following new operator from modal type, that is a modification of the above discussed operators. It has the form
where \(\alpha , \beta , \gamma , \delta \in [0, 1]\) and \(\alpha + \beta \le 1, \gamma + \delta \le 1\).
First, we check that the new operator generates an intuitionistic fuzzy pair. Indeed,
and
Second, it is easy to see that
Theorem 3.3.2
For every formula A, for every four real numbers \(\alpha , \beta , \gamma , \delta \in [0, 1]\) such that \(\alpha + \beta \le 1, \gamma + \delta \le 1\) and for negation \(\lnot _1\),
Proof
We obtain sequentially that
This completes the proof. \(\square \)
Theorem 3.3.3
For every two formulas A and B an for every four real numbers \(\alpha , \beta , \gamma , \delta \in [0, 1]\) such that \(\alpha + \beta \le 1, \gamma + \delta \le 1\),
-
(a)
\(V(\otimes _{\alpha ,\beta ,\gamma ,\delta } (A \vee B)) = V(\otimes _{\alpha ,\beta ,\gamma ,\delta } A \vee \otimes _{\alpha ,\beta ,\gamma ,\delta }B),\)
-
(b)
\(V(\otimes _{\alpha ,\beta ,\gamma ,\delta } (A \wedge B)) = V(\otimes _{\alpha ,\beta ,\gamma ,\delta } A \wedge \otimes _{\alpha ,\beta ,\gamma ,\delta }B).\)
Proof
For (a), first, we obtain that
Second, we obtain that
Let
Now, for a, c, b, d we must study the following four cases.
- Case 1.:
-
\(a \ge c, b \ge d\):
$$X = \max (\alpha a + \gamma b, \alpha c + \gamma d) - \alpha a - \gamma d$$$$\ge \alpha a + \gamma b - \alpha a - \gamma d \ge 0 $$ - Case 2.:
-
\(a \ge c, b < d\):
$$X = \max (\alpha a + \gamma b, \alpha c + \gamma d) - \alpha a - \gamma b \ge 0 $$ - Case 3.:
-
\(a < c, b \ge d\):
$$X = \max (\alpha a + \gamma b, \alpha c + \gamma d) - \alpha c - \gamma d \ge 0 $$ - Case 4.:
-
\(a< c, b < d\):
$$X = \max (\alpha a + \gamma b, \alpha c + \gamma d) - \alpha c) - \gamma b $$$$\ge \alpha c + \gamma d - \alpha c) - \gamma b \ge 0 $$
Assertion (b) is proved analogously. \(\square \)
The proofs of the next assertion follow by analogy.
Theorem 3.3.4
For every formula A and for every four real numbers \(\alpha , \beta , \gamma , \delta \in [0, 1]\) such that \(\alpha + \beta \le 1, \gamma + \delta \le 1\):
-
(a)
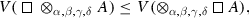
-
(b)
\(V(\otimes _{\alpha ,\beta ,\gamma ,\delta } \diamondsuit \,\,A) \le V(\diamondsuit \,\,\otimes _{\alpha ,\beta ,\gamma ,\delta } A).\)
Theorem 3.3.5
Let A be a formula, such that \(V(A) = \langle \mu , \nu \rangle \) and let \(a, b, c, d, e, f, g, h \in [0, 1]\), so that \(a + b, c + d, e + f, g + h \in [0, 1]\). Then,
Proof
Let formula A and the real numbers a, b, c, d, e, f, g, h satisfy the conditions for operator \(\otimes \). Then
Therefore, (3.3.14) is valid. \(\square \)
Theorem 3.3.6
Let A be a formula, such that \(V(A) = \langle \mu , \nu \rangle \) and let \(a, d, e, h \in (0, 1],b, c, f, g \in (0, 1]\), so that \(a + b, c + d, e + f, g + h \in [0, 1]\) and
Then,
Proof
Let formula A and the real numbers a, b, c, d, e, f, g, h satisfy the conditions of the theorem. First, we see, that from (3.3.15) and (3.3.16) it follows:
But, by the above conditions, \(f, g > 0.\) Therefore,
i.e.,
Now,
Therefore, (3.3.17) is valid. \(\square \)
Theorem 3.3.7
Let A be a formula, \(\alpha , \beta , \gamma , \delta \in [0, 1]\), so that \(\alpha + \beta , \gamma + \delta \in [0, 1],a, b, c, d, e, f \in [0,1]\) so that \(a + e - e.f \le 1,\) \( b + d - b.c \le 1\) and \(b + e \le 1.\) Then,
-
(a)

-
(b)
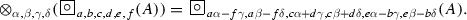
The following two open problems are interesting:
Open Problem 19 Can operator \(\otimes _{\alpha ,\beta ,\gamma ,\delta }\) be represented by the extended modal operators?
Open Problem 20 Can operator \(\otimes _{\alpha ,\beta ,\gamma ,\delta }\) be used for representation of some types of modal operators?
3.4 Intuitionistic Fuzzy Level Operators
Following [9], here we introduce the following two intuitionistic fuzzy level operators for each formula A with evaluation \(V(A) = \langle a, b \rangle \):
We must note, that for every formula A
and
Theorem 3.4.1
For every formula A and for every \(\alpha , \beta ,\gamma ,\delta \) \(\in [0,1]\), such that \(\alpha + \beta \le 1\), \(\gamma + \delta \le 1\):
-
(a)
\( {V(\lnot P_{\alpha ,\beta }(\lnot A))} = V(Q_{\beta , \alpha } (A));\)
-
(b)
\( V(P_{\alpha ,\beta } (Q_{\gamma ,\delta } (A))) = V(Q_{\max (\alpha ,\gamma ),\min (\beta ,\delta )} (P_{\alpha ,\beta } (A)));\)
-
(c)
\(V(Q_{\alpha ,\beta } (P_{\gamma ,\delta } (A))) = V(P_{\min (\alpha ,\gamma ),\max (\beta ,\delta )} (Q_{\alpha ,\beta } (A)));\)
-
(d)
\(V(P_{\alpha ,\beta } (P_{\gamma ,\delta } (A))) = V(P_{\max (\alpha ,\gamma ),\min (\beta ,\delta )} (A));\)
-
(e)
\(V(Q_{\alpha ,\beta } (Q_{\gamma ,\delta } (A))) = V(Q_{\min (\alpha ,\gamma ),\max (\beta ,\delta )} (A)).\)
Proof
(b) Let A be a formula. Then,
This completes the proof. \(\square \)
Theorem 3.4.2
For every two formulas A and B, and for every \(\alpha , \beta \in [0,1]\), such that \(\alpha + \beta \le 1\):
-
(a)
\(V(P_{\alpha ,\beta }(A \wedge B)) = V(P_{\alpha ,\beta } (A)) \wedge V(P_{\alpha ,\beta } (B)),\)
-
(b)
\(V(P_{\alpha ,\beta }(A \vee B)) = V(P_{\alpha ,\beta } (A)) \vee V(P_{\alpha ,\beta } (B)),\)
-
(c)
\(V(Q_{\alpha ,\beta }(A \wedge B)) = V(Q_{\alpha ,\beta } (A)) \wedge V(Q_{\alpha ,\beta } (B)),\)
-
(d)
\(V(Q_{\alpha ,\beta }(A \vee B)) = V(Q_{\alpha ,\beta } (A)) \vee V(Q_{\alpha ,\beta } (B)).\)
Proof
(a) Let A and B be two formulas. Then,
This completes the proof. \(\square \)
Theorem 3.4.3
Let A be a formula and x be a variable. Then, for every \(\alpha , \beta \in [0,1]\), such that \(\alpha + \beta \le 1\):
Proof
(a) Let A be a formula. Then,
This completes the proof. Assertion (b) is proved by analogy. \(\square \)
3.5 Pseudo-fixed Points of the Intuitionistic Fuzzy Operators and Quantifiers
Let \(\mathcal{S}\) be a set of propositions (or more general, formulas) and let \(V: \mathcal{S} \rightarrow [0,1] \times [0,1]\), be defined for every \(A \in \mathcal{S}\) as in Sect. 1.1.
Let for operator Y and for IFP \(\langle a, b \rangle \):
Then, we call that the IFP is a fixed point for operator Y. But, when operator Y is defined over elements of \(\mathcal{S}\), i.e., when for formula A
then we will call that A is a pseudo-fixed point for operator Y. In this case, the equality
holds (see [20]).
Obviously, if (3.5.1) is valid for IFP \(V(A) = \langle a, b \rangle \), then, \(\langle a, b \rangle \) is a fixed point for operator Y.
Below, we determine all pseudo-fixed points of all quantifiers and operators, defined in Chaps. 2 and 3.
Theorem 3.5.1
For all \(\alpha ,\beta \in [0,1]\) the pseudo-fixed point(s) of:
-
(a)
\(\exists \) are all elements \(A \in S\) for which \(V(A) = \langle 1, 0 \rangle ,\)
-
(b)
\(\forall \) are all elements \(A \in S\) for which \(V(A) = \langle 0, 1 \rangle ,\)
-
(c)
\(\exists _{\mu }\) are all elements \(A \in S\) for which
$$\mu (A) = \sup _{x \in \mathcal{S}} \mu (x)$$and in the more general case, all elements \(A \in S\) for which \(V(A) = \langle 1, 0 \rangle ,\)
-
(d)
\(\exists _{\nu }\) are all elements \(A \in S\) for which
$$\nu (A) = \inf _{x \in \mathcal{S}} \nu (x)$$and in the more general case, all elements \(A \in S\) for which \(V(A) \in [0, 1] \times \{ 0 \},\)
-
(e)
\(\forall _{\mu }\) are all elements \(A \in S\) for which
$$\mu (A) = \inf _{x \in \mathcal{S}} \mu (x)$$and in the more general case, all elements \(A \in S\) for which \(V(A) \in \{ 0 \} \times [0, 1],\)
-
(f)
\(\forall _{\nu }\) are all elements \(A \in S\) for which
$$\nu (A) = \sup _{x \in \mathcal{S}} \nu (x)$$and in the more general case, all elements \(A \in S\) for which \(V(A) = \langle 0, 1 \rangle ,\)
-
(g)
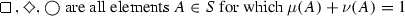 ,
, -
(h)
\(D_{\alpha }\) are all elements \(A \in S\) for which \(\mu (A) + \nu (A) = 1\),
-
(i)
\(F_{\alpha ,\beta }\) are all elements \(A \in S\) for which \(\mu (A) + \nu (A) = 1\) and \(\alpha + \beta \le 1\),
-
(j)
\(G_{\alpha ,\beta }\) are all elements \(A \in S\) for which \(\mu (A) = \nu (A) = 0\),
-
(k)
\(H_{\alpha ,\beta },H_{\alpha ,\beta }^{*}\) are all elements \(A \in S\) for which \(\mu (A) = 0\) and \(\nu (A) = 1\),
-
(l)
\(J_{\alpha ,\beta }, J_{\alpha ,\beta }^{*}\) are all elements \(A \in S\) for which \(\mu (A) = 1\) and \(\nu (A) = 0\),
-
(m)
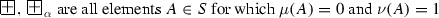 ,
, -
(n)
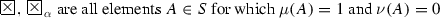 ,
, -
(o)
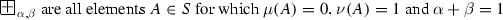 ,
, -
(p)
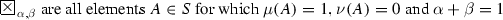 ,
, -
(q)
\(P_{\alpha ,\beta }\) are all elements \(A \in S\) for which \(\alpha \le \mu (A) = 1\) and \(0 \le \nu (A) \le \beta \),
-
(r)
\(Q_{\alpha ,\beta }\) are all elements \(A \in S\) for which \(0 \le \mu (A) = \alpha \) and \(\beta \le \nu (A) \le 1\).
References
Atanassov K. Intuitionistic fuzzy sets, VII ITKR’s Session; 1983 (Deposed in Central Sci. - Techn. Library of Bulg. Acad. of Sci., 1697/84) (in Bulg.), Reprinted: Int J Bioautomation. 2016;2(S1):S1–S6.
Blackburn P, van Bentham J, Wolter F. Modal logic. Amsterdam: North Holland; 2006.
Feys R. Modal logics. Paris: Gauthier-Villars; 1965.
Fitting M, Mendelsohn R. First order modal logic. Dordrecht: Kluwer; 1998.
Mints G. A short introduction to modal logic. Chicago: University of Chicago Press; 1992.
Atanassov K. Elements of intuitionistic fuzzy logics. Part II: Intuitionistic fuzzy modal logics. Adv Stud Contemp Math. 2002;5(1):1–13.
Atanassov K. Intuitionistic fuzzy sets. Heidelberg: Springer; 1999.
Atanassov K. A new topological operator over intuitionistic fuzzy sets. Notes on Intuitionistic Fuzzy Sets. 2015;21(3):90–2.
Atanassov K. On intuitionistic fuzzy sets theory. Berlin: Springer; 2012.
Atanassov K. A short remark on intuitionistic fuzzy operators \(X_{a, b, c, d, e, f}\) and \(x_{a, b, c, d, e, f}\). Notes on Intuitionistic Fuzzy Sets. 2013;19(1):54–6.
Atanassov K. A property of the intuitionistic fuzzy modal logic operator \(X_{a, b, c, d, e, f}\). Notes on Intuitionistic Fuzzy Sets. 2015;21(1):1–5.
Atanassov K. Some operators on intuitionistic fuzzy sets. In: Kacprzyk J, Atanassov K, editors. Proceedings of the First International Conference on Intuitionistic Fuzzy Sets. Sofia, Oct 18-19, 1997; Notes on Intuitionistic Fuzzy Sets. 1997;3(4):28–33. http://ifigenia.org/wiki/issue:nifs/3/4/28-33.
Atanassov K. On one type of intuitionistic fuzzy modal operators. Notes on Intuitionistic Fuzzy Sets. 2005;11(5):24–28. http://ifigenia.org/wiki/issue:nifs/11/5/24-28.
Atanassov K. The most general form of one type of intuitionistic fuzzy modal operators. Notes on Intuitionistic Fuzzy Sets. 2006;12(2):36–38. http://ifigenia.org/wiki/issue:nifs/12/2/36-38.
Atanassov K. Some properties of the operators from one type of intuitionistic fuzzy modal operators. Adv Stud Contemp Math. 2007;15(1):13–20.
Atanassov K. The most general form of one type of intuitionistic fuzzy modal operators. Part 2. Notes on Intuitionistic Fuzzy Sets. 2008;14(1):27–32. http://ifigenia.org/wiki/issue:nifs/14/1/27-32.
Dencheva K. Extension of intuitionistic fuzzy modal operators
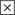 and
and 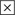 . Proceedings of the Second Int. IEEE Symposium: Intelligent Systems, Varna, June 22–24, vol. 3; 2004. p. 21–22.
. Proceedings of the Second Int. IEEE Symposium: Intelligent Systems, Varna, June 22–24, vol. 3; 2004. p. 21–22.Çuvalcioǧlu G. Some properties of \(E_{\alpha ,\beta }\) operator. Adv Stud Contemp Math. 2007;14(2):305–310.
Atanassov K, Çuvalcioǧlu G, Atanassova V. A new modal operator over intuitionistic fuzzy sets. Notes on Intuitionistic Fuzzy Sets. 2014;20(5):1–8.
Atanassov, K. On Pseudo-fixed Points of the Intuitionistic Fuzzy Quantifiers and Operators, Proceedings of the 8th European Symposium on Computational Intelligence and Mathematics, Sofia, Bulgaria, 5–8 October 2016:66–76.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Atanassov, K.T. (2017). Intuitionistic Fuzzy Modal Logics. In: Intuitionistic Fuzzy Logics. Studies in Fuzziness and Soft Computing, vol 351. Springer, Cham. https://doi.org/10.1007/978-3-319-48953-7_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-48953-7_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-48952-0
Online ISBN: 978-3-319-48953-7
eBook Packages: EngineeringEngineering (R0)












 and
and 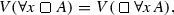
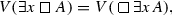
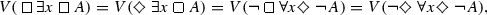
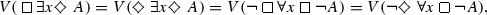
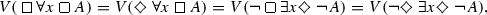
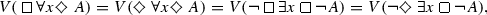
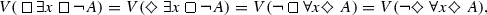
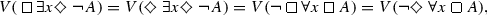
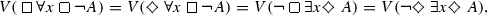

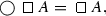
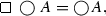







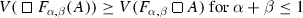 ,
, ,
,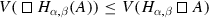 ,
,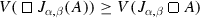 ,
,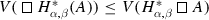 ,
,



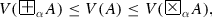
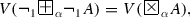
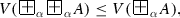
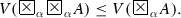
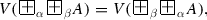
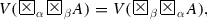
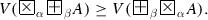
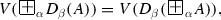
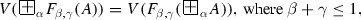
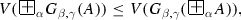
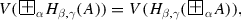
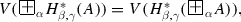
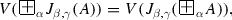
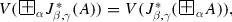
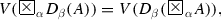
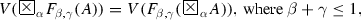
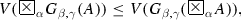
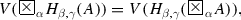
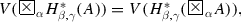
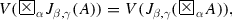
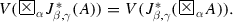
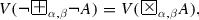
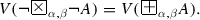
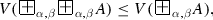
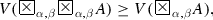
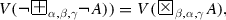
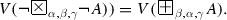
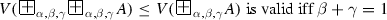 ,
,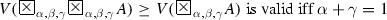 .
.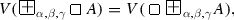
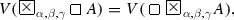
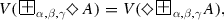
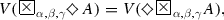

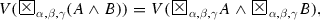
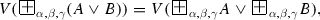
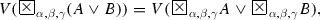
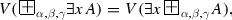
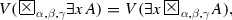
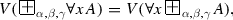

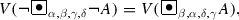
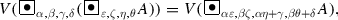
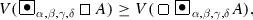
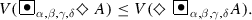
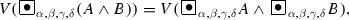
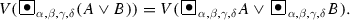
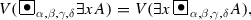
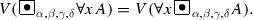

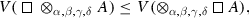

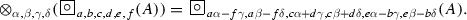
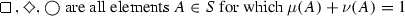 ,
,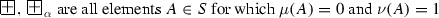 ,
,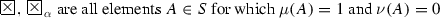 ,
,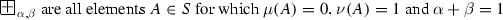 ,
,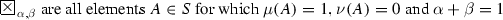 ,
, and
and  . Proceedings of the Second Int. IEEE Symposium: Intelligent Systems, Varna, June 22–24, vol. 3; 2004. p. 21–22.
. Proceedings of the Second Int. IEEE Symposium: Intelligent Systems, Varna, June 22–24, vol. 3; 2004. p. 21–22.