Adaptive Backstepping Control Using Combined Direct and Indirect $\sigma$–Modification Adaptation

Abstract

In this paper, by using the dynamic surface control technique, an adaptive backstepping controller using combined direct and indirect $\sigma$-modification adaptation is proposed for a class of parametric strict-feedback systems. In this approach, a $\sigma$-modification parameter adaptation law that combines direct and indirect update laws is proposed. At first, the $x$-swapping identifier with a gradient-type update law is presented for a class of parametric strict-feedback nonlinear systems. Next, the main steps of the controller design for a class of nonlinear systems in parametric strict-feedback form are described. The closed-loop error dynamics is shown to be globally stable by using the Lyapunov stability approach. Finally, simulation results for a single-link flexible-joint robot manipulator are given to illustrate the tracking performance of the proposed adaptive control scheme.

1 Introduction

Backstepping has been a powerful method for synthesizing adaptive controllers for the class of nonlinear systems with linearly parameterized uncertainties [1]. The uncertainties are assumed to be linear in the unknown constant parameters [2]. The adaptive backstepping control techniques have been found to be particularly useful for controlling parametric strict-feedback nonlinear systems [3], which achieve boundedness of the closed-loop states and convergence of the tracking error to zero. However, adaptive backstepping control can result in overparametrization and adaptation laws differentiations [3], a significant drawback that can be eliminated by introducing tuning functions [4]. For nonlinear systems with parametric lower-triangular form, several adaptive approaches were also presented in [5].

Though, backstepping technique has become one of the most popular design methods for a large class of single-input single-output (SISO) nonlinear systems [3, 5]. A drawback in the traditional backstepping technique is the problem of ‘‘explosion of complexity’’ [2, 6, 7]. That is, the complexity of the controller grows drastically as the system order increases [1]. This problem is caused by the repeated differentiations of certain nonlinear functions such as virtual controls [2, 6, 7]. In [6], a procedure to deal with this problem for the non-adaptive case has been presented for a class of strict-feedback nonlinear systems, and it is called dynamic surface control (DSC). This problem is eliminated by introducing a first-order filtering of the synthetic virtual control input at each step of the traditional backstepping approach [1, 6–8]. In [2], authors are extending this technique to the adaptive control approach and it is called adaptive dynamic surface control.

The methodology proposed in this paper is an extension of the ideas presented in [9–11] for the adaptive backstepping design. This paper presents a new approach that combines direct and indirect $\sigma$-modification adaptation mechanism for adaptive backstepping control of parametric strict-feedback nonlinear systems. In fact, the tracking error based parameter adaptation law of the direct adaptive backstepping control with DSC [2, 11] will be combined with an identification error based parameter adaptation law of the indirect adaptive backstepping control [5, 11–14]. The combined adaptive law is introduced in order to achieve better parameter estimation and hence better tracking performance. The stability analysis of the closed-loop system is performed by using the Lyapunov stability theorem.

This paper is organized as follows. In Sect. 2, the identification based $x$-swapping is provided. The combined direct/indirect adaptive backstepping control with DSC is presented in Sect. 3. The stability analysis of the closed-loop system is given in Sect. 4. In Sect. 5, numerical example for a single-link flexible-joint robot manipulator is used to demonstrate the effectiveness of the proposed approach. Conclusion is contained in Sect. 6.

2 Identification Based x-Swapping

The goal of a swapping filter is to transform a dynamic parametric model into a static form, such that standard parameter estimation algorithms can be used. The term swapping describes the fact that the order of the transfer function describing the dynamics and the time varying parameter error $\tilde{\theta }$ is exchanged [14]. Two types of swapping schemes are presented in [5, 12–14], the z-swapping-based identifier derived from the tracking error model and the $x$-swapping-based identifier derived from the state dynamics [14]. Each of these two swapping-based identifiers allows application of gradient and least squares update laws. In this paper we use the gradient update law. To illustrate the $x$-swapping-based identifier procedure, we consider the following nonlinear system in parametric $x$-model [5, 12–14]

$$ \dot{x}_{i} = f_{i} \left( {x,u} \right) + F_{i}^{T} \left( {x,u} \right)\theta_{i} $$

(1)

where

$$ \begin{aligned} & \left\{ {\begin{array}{*{20}l} {f_{i} \left( {x,u} \right)\; = x_{i + 1} ,i = 1, \cdots ,n - 1} \hfill \\ {f_{n} \left( {x,u} \right)\, = u} \hfill \\ \end{array} } \right. \\ & F_{i}^{T} \left( {x,u} \right) = \varphi_{i}^{T} \left( {\bar{x}_{i} } \right),\bar{x}_{i} = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & \cdots & {x_{i} } \\ \end{array} } \right]^{T} ,i = 1, \cdots ,n \\ \end{aligned} $$

(2)

$\theta_{i} \in {\mathbf{\mathbb{R}}}^{{p_{i} }}$.

Then, we introduce the following two filters

$$ \dot{\Omega }_{0i} = A_{i} \left( {x,t} \right)\left( {\Omega _{0i} + x_{i} } \right) - f_{i} \left( {x,u} \right),\Omega _{0i} \in {\mathbf{\mathbb{R}}} $$

(3)

$$ \dot{\Omega }_{i}^{T} = A_{i} \left( {x,t} \right) {\Omega }_{i}^{T} + F_{i}^{T} \left( {x,u} \right), {\Omega }_{i} \in {\mathbf{\mathbb{R}}}^{{p_{i} }} $$

(4)

where, $i = 1, \cdots ,n$, and $A_{i} \left( {x,t} \right) < 0$ is a negative definite matrix for each $x$ continuous in $t$. We define the estimation error vector as

$$ e_{i} = x_{i} +\Omega _{0i} -\Omega _{i}^{T} \hat{\theta }_{i} ,e_{i} \in {\mathbf{\mathbb{R}}} $$

(5)

with $\hat{\theta }_{i}$ the estimate of $\theta_{i}$ and let

$$ \tilde{e}_{i} = x_{i} +\Omega _{0i} -\Omega _{i}^{T} \theta_{i} ,\tilde{e}_{i} \in {\mathbf{\mathbb{R}}} $$

(6)

Then, we obtain

$$ e_{i} =\Omega _{i}^{T} \tilde{\theta }_{i} + \tilde{e}_{i} $$

(7)

The error signal $\tilde{e}_{i}$ satisfies

$$ \dot{\tilde{e}}_{i} = \dot{x}_{i} + \dot{\Omega }_{0i} - \dot{\Omega }_{i}^{T} \theta_{i} = A_{i} \left( {x,t} \right)\tilde{e}_{i} $$

(8)

To guarantee boundedness of $\Omega _{i}$ when $F_{i} \left( {x,u} \right)$ grows unbounded, a particular choice of $A_{i} \left( {x,t} \right)$ is made [5, 14]

$$ A_{i} \left( {x,t} \right) = A_{0i} - \lambda_{i} F_{i}^{T} \left( {x,u} \right)F_{i} \left( {x,u} \right)P_{i} $$

(9)

where $\lambda_{i} > 0$ and $A_{0i}$ is an arbitrary constant matrix satisfying

$$ P_{i} A_{0i} + A_{0i}^{T} P_{i} = - I,P_{i} = P_{i}^{T} > 0 $$

(10)

The update law for $\hat{\theta }_{i}$ employs the estimation error $e_{i}$ and the filtered regressor $\Omega _{i}$. The gradient update law is given by

$$ \dot{\hat{\theta }}_{i} = {\Gamma}_{i} \frac{{{\Omega}_{i} e_{i} }}{{1 + \nu_{i} {\text{tr}}\left\{ {{\Omega}_{i}^{T} {\Omega}_{i} } \right\}}},{\Gamma}_{i} = {\Gamma}_{i}^{T} > 0,\nu_{i} \ge 0 $$

(11)

where, $i = 1, \cdots ,n$.

To establish the identifier properties, let $\left[ {0,t_{f} } \right)$ be the maximal interval of existence of solutions of (1), the $x$-swapping filters (3) and (4), and the gradient update law (11). Then for $\nu_{i} \ge 0$ the following properties hold [5, 12–14]

• (i) $\tilde{\theta }_{i} \in L_{\infty } \left[ {0,t_{f} } \right)$

• (ii) $e_{i} \in L_{2} \left[ {0,t_{f} } \right) \cap L_{\infty } \left[ {0,t_{f} } \right)$

• (iii) $\dot{\hat{\theta }}_{i} \in L_{2} \left[ {0,t_{f} } \right) \cap L_{\infty } \left[ {0,t_{f} } \right)$

We consider the following Lyapunov function

$$ V_{i} = \frac{1}{2}\tilde{\theta }_{i}^{T} {\Gamma}_{i}^{ - 1} \tilde{\theta }_{i} + \tilde{e}_{i}^{T} P_{i} \tilde{e}_{i} $$

(12)

Along of Eqs. (8) and (11), the derivative of the Lyapunov function (12) is

$$ \begin{aligned} \dot{V}_{i} & = \tilde{\theta }_{i}^{T} {\Gamma}_{i}^{ - 1} \dot{\tilde{\theta }}_{i} + \dot{\tilde{e}}_{i}^{T} P_{i} \tilde{e}_{i} + \tilde{e}_{i}^{T} P_{i} \dot{\tilde{e}}_{i} \\ & = \tilde{\theta }_{i}^{T} {\Gamma}_{i}^{ - 1} \dot{\tilde{\theta }}_{i} + \tilde{e}_{i}^{T} A_{i}^{T} \left( {x,t} \right)P_{i} \tilde{e}_{i} + \tilde{e}_{i}^{T} P_{i} A_{i} \left( {x,t} \right)\tilde{e}_{i} \\ & \le - \tilde{\theta }_{i}^{T} {\Gamma}_{i}^{ - 1} \dot{\hat{\theta }}_{i} - \tilde{e}_{i}^{T} \tilde{e}_{i} = - \frac{{\tilde{\theta }_{i}^{T}\Omega _{i} e_{i} }}{{1 + \nu_{i} {\text{tr}}\left\{ {\Omega _{i}^{T}\Omega _{i} } \right\}}} - \tilde{e}_{i}^{T} \tilde{e}_{i} \\ & { = } - \frac{{e_{i}^{T} e_{i} }}{{1 + \nu_{i} {\text{tr}}\left\{ {\Omega _{i}^{T}\Omega _{i} } \right\}}} + \frac{{e_{i}^{T} }}{{1 + \nu_{i} {\text{tr}}\left\{ {\Omega _{i}^{T}\Omega _{i} } \right\}}}\tilde{e}_{i} - \tilde{e}_{i}^{T} \tilde{e}_{i} \\ & \le - \frac{3}{4}\frac{{e_{i}^{T} e_{i} }}{{1 + \nu_{i} {\text{tr}}\left\{ {\Omega _{i}^{T}\Omega _{i} } \right\}}} - \frac{1}{4}\frac{{e_{i}^{T} e_{i} }}{{\left( {1 + \nu_{i} {\text{tr}}\left\{ {\Omega _{i}^{T}\Omega _{i} } \right\}} \right)^{2} }} + \frac{{e_{i}^{T} }}{{1 + \nu_{i} {\text{tr}}\left\{ {\Omega _{i}^{T}\Omega _{i} } \right\}}}\tilde{e}_{i} - \tilde{e}_{i}^{T} \tilde{e}_{i} \\ & { = } - \frac{3}{4}\frac{{e_{i}^{T} e_{i} }}{{1 + \nu_{i} {\text{tr}}\left\{ {\Omega _{i}^{T}\Omega _{i} } \right\}}} - \left( {\frac{{e_{i} }}{{2\left( {1 + \nu_{i} {\text{tr}}\left\{ {\Omega _{i}^{T}\Omega _{i} } \right\}} \right)}} - \tilde{e}_{i} } \right)^{T} \left( {\frac{{e_{i} }}{{2\left( {1 + \nu_{i} {\text{tr}}\left\{ {\Omega _{i}^{T}\Omega _{i} } \right\}} \right)}} - \tilde{e}_{i} } \right) \\ & \le - \frac{3}{4}\frac{{e_{i}^{T} e_{i} }}{{1 + \nu_{i} {\text{tr}}\left\{ {\Omega _{i}^{T}\Omega _{i} } \right\}}},i = 1, \cdots ,n \\ \end{aligned} $$

(13)

Since $\dot{V}_{i}$ is negative semi-definite, one has $\tilde{\theta }_{i} \in L_{\infty } \left[ {0,t_{f} } \right)$. From $e_{i} =\Omega _{i}^{T} \tilde{\theta }_{i} + \tilde{e}_{i}$ and the boundedness of $\Omega _{i}$, one concludes that $e_{i}$ and $\dot{\tilde{\theta }}_{i} \in L_{2} \left[ {0,t_{f} } \right) \cap L_{\infty } \left[ {0,t_{f} } \right)$.

3 Direct/Indirect Adaptive Backstepping Control with DSC

In the direct/indirect adaptive backstepping control with DSC procedure, the control law and the parameter estimation are not separated. In this paper, the parameter update law for $\hat{\theta }_{i}$ combine gradient-type update laws based on the $x$-swapping identifier and tracking error based update laws. The control objective is to achieve the asymptotic tracking of a reference signal $y_{r}$ by $x_{1}$. The reference signal $y_{r}$ and its derivatives $\dot{y}_{r} , \ldots ,y_{r}^{\left( n \right)}$ are assumed piecewise continuous and bounded. In the following, we describe the main steps of the controller design for the nonlinear system in parametric strict-feedback form

$$ \begin{aligned} \dot{x}_{1} & = x_{2} + \varphi_{1}^{T} (x_{1} )\theta_{1} \\ \dot{x}_{i} & = x_{i + 1} + \varphi_{i}^{T} (\bar{x}_{i} )\theta_{i} ,i = 2, \cdots ,n - 1 \\ \dot{x}_{n} & = u + \varphi_{n}^{T} (x)\theta_{n} \\ \end{aligned} $$

(14)

where, $x = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & \cdots & {x_{n} } \\ \end{array} } \right]^{T} \in {\mathbf{\mathbb{R}}}^{n}$ and $u \in {\mathbf{\mathbb{R}}}$ are the state variables vector and the input of the system, respectively. $\theta_{i} \in {\mathbf{\mathbb{R}}}^{{p_{i} }}$ are unknown constant parameter vectors, $\bar{x}_{i} = \left[ {\begin{array}{*{20}c} {x_{2} } & {x_{3} } & \cdots & {x_{i} } \\ \end{array} } \right]^{T}$. The nonlinear functions $\varphi_{i}^{T} (\bar{x}_{i} ):{\mathbf{\mathbb{R}}}^{i} \to {\mathbf{\mathbb{R}}}^{{p_{i} }}$ are known.

Step $1\left( {i = 1} \right)$

The first surface is defined by $S_{1} = x_{1} - x_{1d}$, and its time derivative is given by

$$ \dot{S}_{1} = \dot{x}_{1} - \dot{x}_{1d} = x_{2} + \varphi_{1}^{T} (x_{1} )\theta_{1} - \dot{x}_{1d} $$

(15)

we choose $\bar{x}_{2}$ to drive $S_{1}$ towards zero with

$$ \bar{x}_{2} = - \varphi_{1}^{T} (x_{1} )\hat{\theta }_{1} + \dot{x}_{1d} - K_{1} S_{1} $$

(16)

we pass $\bar{x}_{2}$ through a first order filter, with time constant $\tau_{2}$, to obtain $x_{2d}$

$$ \tau_{2} \dot{x}_{2d} + x_{2d} = \bar{x}_{2} ,x_{2d} \left( 0 \right) = \bar{x}_{2} \left( 0 \right) $$

(17)

$$ \dot{x}_{2d} = \frac{1}{{\tau_{2} }}\left( { - x_{2d} - \varphi_{1}^{T} (x_{1} )\hat{\theta }_{1} + \dot{x}_{1d} - K_{1} S_{1} } \right) $$

(18)

Step $i\left( {i = 2, \cdots ,n - 1} \right)$

The $i^{th}$ surface is defined by $S_{i} = x_{i} - x_{id}$, and its time derivative is given by

$$ \dot{S}_{i} = \dot{x}_{i} - \dot{x}_{id} = x_{i + 1} + \varphi_{i}^{T} (\bar{x}_{i} )\theta_{i} - \dot{x}_{id} $$

(19)

we choose $\bar{x}_{i + 1}$ to drive $S_{i}$ towards zero with

$$ \bar{x}_{i + 1} = - \varphi_{i}^{T} (\bar{x}_{i} )\hat{\theta }_{i} + \dot{x}_{id} - K_{i} S_{i} $$

(20)

we pass $\bar{x}_{i + 1}$ through a first order filter, with time constant $\tau_{i + 1}$, to obtain $x_{i + 1d}$

$$ \tau_{i + 1} \dot{x}_{i + 1d} + x_{i + 1d} = \bar{x}_{i + 1} ,x_{i + 1d} \left( 0 \right) = \bar{x}_{i + 1} \left( 0 \right) $$

(21)

$$ \dot{x}_{i + 1d} = \frac{1}{{\tau_{i + 1} }}\left( { - x_{i + 1d} - \varphi_{i}^{T} (\bar{x}_{i} )\hat{\theta }_{i} + \dot{x}_{id} - K_{i} S_{i} } \right) $$

(22)

Step $n$

The $n^{th}$ surface is defined by $S_{n} = x_{n} - x_{nd}$, and its time derivative is given by

$$ \dot{S}_{n} = \dot{x}_{n} - \dot{x}_{nd} = u + \varphi_{n}^{T} (x)\theta_{n} - \dot{x}_{nd} $$

(23)

we choose the control input $u$ to drive $S_{n}$ towards zero with

$$ u = - \varphi_{n}^{T} (x)\hat{\theta }_{n} + \dot{x}_{nd} - K_{n} S_{n} $$

(24)

The update laws (direct part) for the parameter estimates are given by [2, 11]

$$ \begin{aligned} \dot{\hat{\theta }}_{1} = & \,\, \bar{{\Gamma }}_{1} S_{1} \varphi_{1} (x_{1} ) \\ \dot{\hat{\theta }}_{i} = & \,\, \bar{{\Gamma }}_{i} S_{i} \varphi_{i} (\bar{x}_{i} ), i = 2, \cdots ,n - 1 \\ \dot{\hat{\theta }}_{n} = & \,\, \bar{{\Gamma }}_{n} S_{n} \varphi_{n} (x) \\ \end{aligned} $$

(25)

where, $\bar{{\Gamma }}_{i} > 0\left( {i = 1, \cdots ,n} \right)$ are design parameters that can be adjusted for the rate of convergence of the parameter estimates.

Let us introduce the following two filters

$$ \dot{\Omega }_{0i} = A_{i} \left( {x,t} \right)\left( {\Omega _{0i} + x_{i} } \right) - f_{i} \left( {x,u} \right),\Omega _{0i} \in {\mathbf{\mathbb{R}}} $$

(26)

$$ \dot{\Omega }_{i}^{T} = A_{i} \left( {x,t} \right)\Omega _{i}^{T} + F_{i}^{T} \left( {x,u} \right),\Omega _{i} \in {\mathbf{\mathbb{R}}}^{{p_{i} }} $$

(27)

where, $i = 1, \cdots ,n$, and

$$ A_{i} \left( {x,t} \right) = A_{0i} - \lambda_{i} F_{i}^{T} \left( {x,u} \right)F_{i} \left( {x,u} \right)P_{i} $$

(28)

where $\lambda_{i} > 0$ and $A_{0i}$ is an arbitrary constant matrix satisfying

$$ P_{i} A_{0i} + A_{0i}^{T} P_{i} = - I,P_{i} = P_{i}^{T} > 0 $$

(29)

The gradient update law (indirect part) is given by [5, 11–14]

$$ \dot{\hat{\theta }}_{i} = {\Gamma}_{i} \frac{{\Omega _{i} e_{i} }}{{1 + \nu_{i} {\text{tr}}\left\{ {\Omega _{i}^{T}\Omega _{i} } \right\}}},{\Gamma}_{i} = {\Gamma}_{i}^{T} > 0,\nu_{i} \ge 0 $$

(30)

where, $i = 1, \cdots ,n$ and $e_{i} = x_{i} +\Omega _{0i} -\Omega _{i}^{T} \hat{\theta }_{i} ,e_{i} \in {\mathbf{\mathbb{R}}}$.

Now we propose the following combined direct and indirect $\sigma$-modification adaptation law [11]

$$ \dot{\hat{\theta }}_{i} = \bar{{\Gamma }}_{i} S_{i} \varphi_{i} (\bar{x}_{i} ) - \bar{{\Gamma }}_{i} \sigma_{i} \left( {\hat{\theta }_{i} - \bar{\theta }_{i} } \right), \bar{{\Gamma }}_{i} > 0 $$

(31)

where, $i = 1, \cdots ,n$, $\sigma_{i}$ is a small positive constant, $\bar{{\Gamma }}_{i}$ is a positive definite constant matrix and $\bar{\theta }_{i}$ is computed with the gradient method as follows

$$ \dot{\bar{\theta }}_{i} = {\Gamma }_{i} \frac{{\Omega _{i} e_{i} }}{{1 + \nu_{i} {\text{tr}}\left\{ {\Omega _{i}^{T}\Omega _{i} } \right\}}},{\Gamma }_{i} = {\Gamma }_{i}^{T} > 0,\nu_{i} \ge 0 $$

(32)

where, ${\Gamma }_{i}$ is a positive definite constant matrix and $e_{i} = x_{i} +\Omega _{0i} -\Omega _{i}^{T} \bar{\theta }_{i} ,e_{i} \in {\mathbf{\mathbb{R}}}$.

4 Stability Analysis

We define the boundary layer error as [2, 11, 15]

$$ y_{i} = x_{id} - \bar{x}_{i} ,i = 2, \cdots ,n $$

(33)

and the parameter estimate errors as

$$ \tilde{\theta }_{i} = \theta_{i} - \hat{\theta }_{i} ,i = 1,2, \cdots ,n $$

(34)

Then the closed-loop dynamics can be expressed in terms of the surfaces $S_{i}$, the boundary layer errors $y_{i}$, and the parameter estimate errors $\tilde{\theta }_{i}$.

The dynamics of the surfaces are expressed, for $i = 1$, as

$$ \begin{aligned} \dot{S}_{1} & = \dot{x}_{1} - \dot{x}_{1d} = x_{2} + \varphi_{1}^{T} (x_{1} )\theta_{1} - \dot{x}_{1d} \; \\ & = S_{2} + x_{2d} + \varphi_{1}^{T} (x_{1} )\theta_{1} - \dot{x}_{1d} \\ & = S_{2} + y_{2} + \bar{x}_{2} + \varphi_{1}^{T} (x_{1} )\theta_{1} - \dot{x}_{1d} \\ & = S_{2} + y_{2} - K_{1} S_{1} + \varphi_{1}^{T} (x_{1} )\tilde{\theta }_{1} \\ \end{aligned} $$

(35)

For $i = 2, \cdots ,n - 1$

$$ \begin{aligned} \dot{S}_{i} & = \dot{x}_{i} - \dot{x}_{id} = x_{i + 1} + \varphi_{i}^{T} (\bar{x}_{i} )\theta_{i} - \dot{x}_{id} \\ & = S_{i + 1} + x_{i + 1d} + \varphi_{i}^{T} (\bar{x}_{i} )\theta_{i} - \dot{x}_{id} \\ & = S_{i + 1} + y_{i + 1} + \bar{x}_{i + 1} + \varphi_{i}^{T} (\bar{x}_{i} )\theta_{i} - \dot{x}_{id} \\ & = S_{i + 1} + y_{i + 1} - K_{i} S_{i} + \varphi_{i}^{T} (\bar{x}_{i} )\tilde{\theta }_{i} \\ \end{aligned} $$

(36)

For $i = n$

$$ \dot{S}_{n} = \dot{x}_{n} - \dot{x}_{nd} = u + \varphi_{n}^{T} (x)\theta_{n} - \dot{x}_{nd} = - K_{n} S_{n} + \varphi_{n}^{T} (x)\tilde{\theta }_{n} $$

(37)

The dynamics of the boundary layer errors $y_{i}$ are expressed, for $i = 2$, as

$$ \begin{aligned} \dot{y}_{2} & = \dot{x}_{2d} - \dot{\bar{x}}_{2} = \frac{1}{{\tau_{2} }}\left( { - x_{2d} - \varphi_{1}^{T} (x_{1} )\hat{\theta }_{1} + \dot{x}_{1d} - K_{1} S_{1} } \right) - \dot{\bar{x}}_{2} \\ & = \frac{1}{{\tau_{2} }}\left( { - x_{2d} + \bar{x}_{2} } \right) - \dot{\bar{x}}_{2} = \frac{1}{{\tau_{2} }}\left( { - y_{2} - \bar{x}_{2} + \bar{x}_{2} } \right) - \dot{\bar{x}}_{2} = - \frac{1}{{\tau_{2} }}y_{2} - \dot{\bar{x}}_{2} \\ \end{aligned} $$

(38)

For $i = 3, \cdots ,n$

$$ \begin{aligned} \dot{y}_{i} & = \dot{x}_{id} - \dot{\bar{x}}_{i} = \frac{1}{{\tau_{i} }}\left( { - x_{id} - \varphi_{i - 1}^{T} (\bar{x}_{i - 1} )\hat{\theta }_{i - 1} + \dot{x}_{i - 1d} - K_{i - 1} S_{i - 1} } \right) - \dot{\bar{x}}_{i} \\ & = \frac{1}{{\tau_{i} }}\left( { - x_{id} + \bar{x}_{i} } \right) - \dot{\bar{x}}_{i} = \frac{1}{{\tau_{i} }}\left( { - y_{i} - \bar{x}_{i} + \bar{x}_{i} } \right) - \dot{\bar{x}}_{i} = - \frac{1}{{\tau_{i} }}y_{i} - \dot{\bar{x}}_{i} \\ \end{aligned} $$

(39)

Let us consider the following Lyapunov function

$$ V = \sum\limits_{i = 1}^{n} {V_{is} } + \sum\limits_{i = 2}^{n} {V_{iy} } + \sum\limits_{i = 1}^{n} {V_{i} } $$

(40)

where

$$ V_{is} = \frac{1}{2}S_{i}^{2} ,V_{iy} = \frac{1}{2}y_{i}^{2} ,V_{i} = \frac{1}{2}\tilde{\theta }_{i}^{T} \bar{{\Gamma }}_{i}^{ - 1} \tilde{\theta }_{i} $$

(41)

Then, one has

$$ \begin{aligned} \dot{V}_{is} & = S_{i} \dot{S}_{i} { = }S_{i} S_{i + 1} + S_{i} y_{i + 1} - K_{i} S_{i}^{2} + S_{i} \varphi_{i}^{T} (\bar{x}_{i} )\tilde{\theta }_{i} \, \\ & \le \left| {S_{i} } \right|\left| {S_{i + 1} } \right| + \left| {S_{i} } \right|\left| {y_{i + 1} } \right| - K_{i} S_{i}^{2} + S_{i} \varphi_{i}^{T} (\bar{x}_{i} )\tilde{\theta }_{i} \\ & \le \left( {1 - K_{i} } \right)S_{i}^{2} + \frac{1}{2}S_{i + 1}^{2} + \frac{1}{2}y_{i + 1}^{2} + S_{i} \varphi_{i}^{T} (\bar{x}_{i} )\tilde{\theta }_{i} ,i = 1, \cdots ,n - 1 \\ \end{aligned} $$

(42)

$$ \dot{V}_{ns} = S_{n} \dot{S}_{n} { = } - K_{n} S_{n}^{2} + S_{n} \varphi_{n}^{T} (x)\tilde{\theta }_{n} \le - K_{n} S_{n}^{2} + S_{n} \varphi_{n}^{T} (x)\tilde{\theta }_{n} \, $$

(43)

We assume that, $\left| {y_{i} \dot{\bar{x}}_{i} } \right| \le M_{1i} y_{i}^{2} + M_{2i} S_{i}^{2} + \delta_{i}^{2}$, where, $M_{1i}$ and $M_{2i}$ are positive constants, and $\delta_{i}$ are bounded functions, then, we can write

$$ \begin{aligned} \dot{V}_{iy} & = y_{i} \dot{y}_{i} = - \frac{1}{{\tau_{i} }}y_{i}^{2} + y_{i} \dot{\bar{x}}_{i} \le - \frac{1}{{\tau_{i} }}y_{i}^{2} + \left| {y_{i} \dot{\bar{x}}_{i} } \right| \, \\ & \le - \frac{1}{{\tau_{i} }}y_{i}^{2} + M_{1i} y_{i}^{2} + M_{2i} S_{i}^{2} + \delta_{i}^{2} ,i = 2, \cdots ,n \\ \end{aligned} $$

(44)

$$ \begin{aligned} \dot{V}_{i} & = \tilde{\theta }_{i}^{T} \bar{{\Gamma }}_{i}^{ - 1} \dot{\tilde{\theta }}_{i} = - \tilde{\theta }_{i}^{T} \bar{{\Gamma }}_{i}^{ - 1} \dot{\hat{\theta }}_{i} \\ & = - \tilde{\theta }_{i}^{T} \bar{{\Gamma }}_{i}^{ - 1} \left( {\bar{{\Gamma }}_{i} S_{i} \varphi_{i} (\bar{x}_{i} ) - \bar{{\Gamma }}_{i} \sigma_{i} \left( {\hat{\theta }_{i} - \bar{\theta }_{i} } \right)} \right) \\ & = - \tilde{\theta }_{i}^{T} S_{i} \varphi_{i} (\bar{x}_{i} ) + \tilde{\theta }_{i}^{T} \sigma_{i} \left( {\hat{\theta }_{i} - \bar{\theta }_{i} } \right), i = 1, \cdots ,n \\ \end{aligned} $$

(45)

One has: $\theta_{i} - \bar{\theta }_{i}$ is bounded, thus: $e_{{\theta_{i} }} = \theta_{i} - \bar{\theta }_{i}$ is bounded, $\bar{\theta }_{i} = \theta_{i} - e_{{\theta_{i} }}$ and $\tilde{\theta }_{i} = \theta_{i} - \hat{\theta }_{i}$.

$$ \begin{aligned} \dot{V}_{i} & = - \tilde{\theta }_{i}^{T} S_{i} \varphi_{i} (\bar{x}_{i} ) + \tilde{\theta }_{i}^{T} \sigma_{i} \left( {\hat{\theta }_{i} - \theta_{i} + e_{{\theta_{i} }} } \right) \\ & = - \tilde{\theta }_{i}^{T} S_{i} \varphi_{i} (\bar{x}_{i} ) - \sigma_{i} \tilde{\theta }_{i}^{T} \tilde{\theta }_{i} + \sigma_{i} \tilde{\theta }_{i}^{T} e_{{\theta_{i} }} \\ & \le - \tilde{\theta }_{i}^{T} S_{i} \varphi_{i} (\bar{x}_{i} ) - \sigma_{i} \tilde{\theta }_{i}^{T} \tilde{\theta }_{i} + \frac{{\sigma_{i} }}{2}\tilde{\theta }_{i}^{T} \tilde{\theta }_{i} + \frac{{\sigma_{i} }}{2}e_{{\theta_{i} }}^{T} e_{{\theta_{i} }} \\ & \le - \tilde{\theta }_{i}^{T} S_{i} \varphi_{i} (\bar{x}_{i} ) - \frac{{\sigma_{i} }}{2}\tilde{\theta }_{i}^{T} \tilde{\theta }_{i} + \frac{{\sigma_{i} }}{2}e_{{\theta_{i} }}^{T} e_{{\theta_{i} }} \\ \end{aligned} $$

(46)

$$ \begin{aligned} \dot{V} = & \sum\limits_{i = 1}^{n} {\dot{V}_{is} } + \sum\limits_{i = 2}^{n} {\dot{V}_{iy} + \sum\limits_{i = 1}^{n} {\dot{V}_{i} } } \\ \le & \sum\limits_{i = 1}^{n - 1} {\left[ {\left( {1 - K_{i} } \right)S_{i}^{2} + \frac{1}{2}S_{i + 1}^{2} + \frac{1}{2}y_{i + 1}^{2} + S_{i} \varphi_{i}^{T} (\bar{x}_{i} )\tilde{\theta }_{i} } \right] - K_{n} S_{n}^{2} } + S_{n} \varphi_{n}^{T} (x)\tilde{\theta }_{n} \\ + & \sum\limits_{i = 2}^{n} {\left( { - \frac{1}{{\tau_{i} }}y_{i}^{2} + M_{1i} y_{i}^{2} + M_{2i} S_{i}^{2} + \delta_{i}^{2} } \right)} - \sum\limits_{i = 1}^{n} {\tilde{\theta }_{i}^{T} S_{i} \varphi_{i} (\bar{x}_{i} )} - \sum\limits_{i = 1}^{n} {\frac{{\sigma_{i} }}{2}\tilde{\theta }_{i}^{T} \tilde{\theta }_{i} } + \sum\limits_{i = 1}^{n} {\frac{{\sigma_{i} }}{2}e_{{\theta_{i} }}^{T} e_{{\theta_{i} }} } \\ \le & - \left( {K_{1} - 1} \right)S_{1}^{2} - \sum\limits_{i = 2}^{n - 1} {\left( {K_{i} - M_{2i} - \frac{3}{2}} \right)S_{i}^{2} - \left( {K_{n} - M_{2n} - \frac{1}{2}} \right)S_{n}^{2} } - \sum\limits_{i = 2}^{n} {\left( {\frac{1}{{\tau_{i} }} - \frac{1}{2} - M_{1i} } \right)} y_{i}^{2} \\ + & \sum\limits_{i = 2}^{n} {\delta_{i}^{2} } - \sum\limits_{i = 1}^{n} {\frac{{\sigma_{i} }}{2}\tilde{\theta }_{i}^{T} \tilde{\theta }_{i} } + \sum\limits_{i = 1}^{n} {\frac{{\sigma_{i} }}{2}e_{{\theta_{i} }}^{T} e_{{\theta_{i} }} } \\ \end{aligned} $$

(47)

If we assume that, $\delta_{i} \in L_{\infty }$, $e_{{\theta_{i} }} \in L_{\infty }$, $K_{1} > 1$, $K_{i} > M_{2i} + \frac{3}{2}$, $K_{n} > M_{2n} + \frac{1}{2}$ and $\frac{1}{{\tau_{i} }} > \frac{1}{2} + M_{1i}$, we obtain the boundedness of all signals $S_{i}$, $y_{i}$ and $\tilde{\theta }_{i}$. Moreover, the surface $S_{i}$ can be made arbitrarily small by adjusting the design parameters $K_{i}$.

5 Numerical Example

Consider the single-link flexible-joint robot shown in Fig. 1. The dynamic model of this robot is given as follow [16, 17]

Fig. 1.

Single link flexible joint robot.

$$ \begin{aligned} & J_{1} {\ddot q}_{1} + MgL \sin \left( {q_{1} } \right) + K\left( {q_{1} - q_{2} } \right) = 0 \\ & J_{2} {\ddot q}_{2} - K\left( {q_{1} - q_{2} } \right) = u \\ \end{aligned} $$

(48)

where $u$ is the input torque. $J_{1}$ and $J_{2}$ are the inertias of the link and the motor respectively. $M$ is the link mass. $g$ is the gravity. $L$ is the link length. $K$ is the stiffness. $q_{1}$ and $q_{2}$ are the angular positions of the link and the motor shaft, respectively.

Let the state variables defined as follows: $x_{1} = q_{1}$, $x_{2} = \dot{q}_{1}$, $x_{3} = q_{2}$ and $x_{4} = \dot{q}_{2}$, and its dynamic model becomes

$$ \begin{aligned} \dot{x}_{1} & = x_{2} \\ \dot{x}_{2} & = f_{1} \left( {x_{1} ,x_{3} } \right) + g_{1} x_{3} \\ \dot{x}_{3} & = x_{4} \\ \dot{x}_{4} & = f_{2} \left( {x_{1} ,x_{3} } \right) + g_{2} u \\ \end{aligned} $$

(49)

with

$$ \begin{aligned} f_{1} \left( {x_{1} ,x_{3} } \right) = & - \frac{MgL}{{J_{1} }}\sin \left( {x_{1} } \right) - \frac{K}{{J_{1} }}x_{1} ,g_{1} = \frac{K}{{J_{1} }} \\ f_{2} \left( {x_{1} ,x_{3} } \right) = & \frac{K}{{J_{2} }}\left( {x_{1} - x_{3} } \right),g_{2} = \frac{1}{{J_{2} }} \\ \end{aligned} $$

(50)

The single-link flexible-joint robot model used in this paper is given by (49) where the parameter values are given in Table 1 [17].

Table 1. Single-link flexible-joint robot model parameters.

For the numerical simulation, the unknown parameter $\theta_{1}$ of the system is selected as $\theta_{1} = MgL$. Our objective is to force the output of the system to follow the reference trajectory given by: $y_{d} = 0.1\sin \left( t \right)$.

We choose $\bar{x}_{2}$, $\bar{x}_{3}$ and $\bar{x}_{4}$ to drive $S_{1}$, $S_{2}$ and $S_{3}$ towards zero with

$$ \bar{x}_{2} = \dot{x}_{1d} - K_{1} S_{1} = \tau_{2} \dot{x}_{2d} + x_{2d} ,x_{2d} \left( 0 \right) = \bar{x}_{2} \left( 0 \right) $$

(51)

$$ \dot{x}_{2d} = \frac{1}{{\tau_{2} }}\left( { - x_{2d} + \dot{x}_{1d} - K_{1} S_{1} } \right) $$

(52)

$$ \bar{x}_{3} = \frac{1}{{g_{1} }}\left( {\frac{{\hat{\theta }_{1} }}{{J_{1} }}\sin \left( {x_{1} } \right) + \frac{K}{{J_{1} }}x_{1} + \dot{x}_{2d} - K_{2} S_{2} } \right) = \tau_{3} \dot{x}_{3d} + x_{3d} ,x_{3d} \left( 0 \right) = \bar{x}_{3} \left( 0 \right) $$

(53)

$$ \dot{x}_{3d} = \frac{1}{{\tau_{3} }}\left( { - x_{3d} + \frac{1}{{g_{1} }}\left( {\frac{{\hat{\theta }_{1} }}{{J_{1} }}\sin \left( {x_{1} } \right) + \frac{K}{{J_{1} }}x_{1} + \dot{x}_{2d} - K_{2} S_{2} } \right)} \right) $$

(54)

$$ \bar{x}_{4} = \dot{x}_{3d} - K_{3} S_{3} = \tau_{4} \dot{x}_{4d} + x_{4d} ,x_{4d} \left( 0 \right) = \bar{x}_{4} \left( 0 \right) $$

(55)

$$ \dot{x}_{4d} = \frac{1}{{\tau_{4} }}\left( { - x_{4d} + \dot{x}_{3d} - K_{3} S_{3} } \right) $$

(56)

We choose the control $u$ to drive $S_{4}$ towards zero with

$$ u = \frac{1}{{g_{2} }}\left( { - \frac{K}{{J_{2} }}\left( {x_{1} - x_{3} } \right) + \dot{x}_{4d} - K_{4} S_{4} } \right) $$

(57)

For the swapping-based identifier we use the following filters

$$ \dot{{\Omega}}_{0} = \left( { - \frac{1}{2} - \lambda \left( { - \frac{{\sin \left( {x_{1} } \right)}}{{J_{1} }}} \right)^{2} } \right)\left( {\Omega _{0} + x_{2} } \right) + \frac{K}{{J_{1} }}x_{1} - g_{1} x_{3} $$

(58)

$$ \dot{{\Omega}}^{T} = \left( { - \frac{1}{2} - \lambda \left( { - \frac{{\sin \left( {x_{1} } \right)}}{{J_{1} }}} \right)^{2} } \right)\Omega ^{T} - \frac{{\sin \left( {x_{1} } \right)}}{{J_{1} }} $$

(59)

The combined direct and indirect $\sigma$-modification adaptation law is given by

$$ \dot{\hat{\theta }}_{1} = - \frac{{\bar{{\Gamma }}}}{{J_{1} }}S_{2} \sin \left( {x_{1} } \right) - \bar{{\Gamma }}\sigma \left( {\hat{\theta }_{1} - \bar{\theta }} \right), \bar{{\Gamma }} > 0 $$

(60)

where, $\bar{\theta }$ is computed with the gradient method as

$$ \dot{\bar{\theta }} = {\Gamma } \frac{{\Omega e}}{{1 + \nu {\text{tr}}\left\{ {\Omega ^{T}\Omega } \right\}}},{\Gamma } = {\Gamma }^{T} > 0,\nu \ge 0. $$

(61)

where, $e = x_{2} +\Omega _{0} -\Omega ^{T} \bar{\theta }$.

The selected initial conditions are: $x\left( 0 \right) = \left[ {\begin{array}{*{20}c} {0.1} & 0 & {0.1 + \frac{MgL}{K}\sin \left( {0.1} \right)} & 0 \\ \end{array} } \right]^{T}$, $\hat{\theta }_{1} \left( 0 \right) = \bar{\theta }\left( 0 \right) = 0$ and $\Omega _{0} \left( 0 \right) =\Omega ^{T} \left( 0 \right) = 0$. The design parameters are selected as follows: $K_{1} = 1$, $K_{2} = 80$, $K_{3} = 10$, $K_{4} = 100$, $\bar{\Gamma} = 15,$ $\sigma = 0.5$, ${\Gamma} = 20,$ $\tau_{2} = \tau_{3} = \tau_{4} = 0.009$ and $\lambda = \nu = 0.1$.

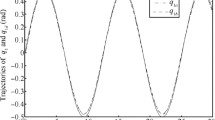
Numerical simulation results are shown in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11. Figures 2, 3, 4 and 5 show actual and desired trajectories of the angular position and velocity of the link and the motor shaft. Figures 6, 7, 8 and 9 show the trajectories of the surfaces. Figure 10 shows the trajectory of the control input signal $u$. Figure 11 shows the trajectory of the estimated parameter $\hat{\theta }_{1}$. From these results, we observe that the actual trajectories converge towards the desired trajectories, and that the errors converge to zero and the estimated parameter $\hat{\theta }_{1}$ converge towards $\theta_{1}$. We can see that the results show that the proposed method has good tracking performance.

Fig. 2.

Angular position of the link: actual x ₁ (“$-$”) and desired x _1d (“$- {\kern 1pt} -$”).

Fig. 3.

Angular velocity of the link: actual x ₂ (“$-$”) and desired x _2d (“$- {\kern 1pt} -$”).

Fig. 4.

Angular position of the motor shaft: actual x ₃ (“$-$”) and desired x _3d (“$- {\kern 1pt} -$”).

Fig. 5.

Angular velocity of the motor shaft: actual x ₄ (“$-$”) and desired x _4d (“$- {\kern 1pt} -$”).

Fig. 6.

Surface S ₁ .

Fig. 7.

Surface S ₂ .

Fig. 8.

Surface S ₃ .

Fig. 9.

Surface S ₄ .

Fig. 10.

Control input u.

Fig. 11.

Estimated parameter $\hat{\theta }_{1}$.

6 Conclusion

In this paper, adaptive backstepping control using combined direct and indirect $\sigma$-modification adaptation based gradient update law is designed using the DSC technique for a class of parametric strict-feedback nonlinear systems. The proposed approach eliminates the problem of explosion of complexity of the traditional backstepping approach. Stability analysis shows that the uniform ultimate boundedness of all signals in the closed-loop system can be guaranteed, and the tracking error can be made arbitrarily small by adjusting the control design parameters. Numerical simulation results demonstrate the effectiveness of the proposed approach.