Finding Disjoint Paths on Edge-Colored Graphs: A Multivariate Complexity Analysis

Abstract

The problem of finding the maximum number of vertex-disjoint uni-color paths in an edge-colored graph (MaxCDP) has been recently introduced in literature, motivated by applications in social network analysis. In this paper we investigate how the complexity of the problem depends on graph parameters (distance from disjoint paths and size of vertex cover), and that is not FPT-approximable. Moreover, we introduce a new variant of the problem, called MaxCDDP, whose goal is to find the maximum number of vertex-disjoint and color-disjoint uni-color paths. We extend some of the results of MaxCDP to this new variant, and we prove that unlike MaxCDP, MaxCDDP is already hard on graphs at distance two from disjoint paths.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The analysis of social networks and social media has introduced several interesting problems from an algorithmic point of view. Social networks are usually viewed as graphs, where vertices represent the elements of the network, and edges represent a binary relation between the represented elements. One of the most relevant properties to analyze social network is the vertex connectivity of two given vertices. Indeed, a relevant property of social networks is how information flows from one vertex to the other, and vertex connectivity is considered as a measure of the information flow. Furthermore, two relevant structural properties of a social network, group cohesiveness and centrality, can be identified via vertex connectivity [8, 12]. Vertex connectivity has been widely investigated in graph theory; Menger’s theorem shows that vertex connectivity is equivalent to the maximum number of disjoint paths between two given vertices.

Usually social networks analyses focus on a single type of relation. However, due to the availability of several social networks, a natural goal is to integrate the information into a single network. Wu [13] introduced a model to consider multi-relational social networks, where different kinds of relations are considered. In the proposed model colors are associated with edges of the graph to distinguish different kinds of relations. Given such an edge-colored graph, a natural combinatorial problem to compute vertex connectivity introduced in [13], called Maximum Colored Disjoint Paths (MaxCDP), asks for the maximum number of vertex-disjoint paths consisting of edges of the same colors (also called uni-color paths) in the input graph.

The complexity of MaxCDP has been investigated in [3, 13]. MaxCDP is polynomial time solvable when the input graph contains exactly one color, while it is NP-hard when the edges of the graph are associated with at least two colors. On general instance, MaxCDP is shown to be not approximable with factor $O(n^{d})$, where n is the number of vertices of the input graph, for any constant $0<d<1$, and W[1]-hard if the parameter if the number of paths in the solution [3]. Moreover, MaxCDP is approximable within factor q, where q is the number of colors of the edges of the input graph, but not approximable within factor $2 - \epsilon$, for any $\epsilon > 0$, when q is a fixed constant. Moreover, in [13] it is considered a variant of the problem where the length of the paths in the solution are (upper) bounded by an integer $l \geqslant 1$, as in many real social networks the diameter of the graph is bounded by a constant and we are interesting in short paths connecting two vertices. When $l \geqslant 4$ MaxCDP is NP-hard, while it is polynomial time solvable for $l < 4$ [13]. The bounded length variant of the problem is approximable within factor $(l-1)/2 + \epsilon$ [13], and it is fixed-parameter tractable for the combined parameter number of paths in the solution and l [3]. Moreover, this variant does not admit a polynomial kernel unless $NP \subseteq coNP/Poly$, as it follows from the results in [7].

In this paper, we further investigate the complexity of MaxCDP and of a related problem that we introduce, called MaxCDDP, whose goal is to find the maximum number of vertex-disjoint and color-disjoint (that is having different colors) uni-color paths. The color disjointness of paths can be interesting to characterize how different relations in a network connects two vertices. In this case, we are not interested to have more paths of a single color, but rather to compute the maximum number of color-disjoint paths between two vertices. We study how the complexity of MaxCDP and MaxCDDP depends on several parameters, in the spirit of a multivariate complexity analysis [9]. As described in the previous paragraph, it has already been studied how the complexity of MaxCDP depends on different constraints (number of colors of each edge, maximum length of a path). We believe that it is interesting to take into account the structure of the input graph when studying the complexity of these two problems, since real-life networks exhibit properties that leads to graphs with a specific structure. For example, it is widely believed that social networks have a “small-world phenomenon” property, and thus information on the structure of the corresponding graphs can be derived. Moreover, such a study is also of theoretical interest, since it helps to better understand the complexity of the two problems.

First, we investigate how the complexity of the two problems depends on two graph parameters: distance from disjoint paths and size of vertex cover. In Sect. 3 we show that on graphs at distance bounded by a constant from disjoint paths MaxCDP admits a polynomial-time algorithm, whereas MaxCDDP is NP-hard. Then, in Sect. 4 we show that MaxCDP is fixed-parameter tractable when parameterized by the size of the vertex cover of the input graph. In Sect. 5 we consider the parameterized complexity of the bounded length version of MaxCDDP, where the parameters are the number of vertex and color-disjoint paths of a solution and the maximum length of a path, and we extend the FPT algorithm for MaxCDP to MaxCDDP. Finally, we show in Sect. 6 that both problems are not $\rho$-approximable in FPT time, for any function $\rho$.

2 Definitions

In this section we present some definitions as well as the formal definition of the two combinatorial problems we are interested in. First, notice that in this paper, we will consider undirected graphs. Given a graph $G=(V,E)$ and a vertex $v \in V$, we denote by N(v) the vertex adjacent to v in G. Consider a set of colors $C=\{c_1,\dots , c_q \}$, where q represents cardinality of C. A C-edge-colored graph (or simply an edge-colored graph when the set of colors is clear from the context) is defined as $G=(V,E,f_C)$, where V denotes the set of vertices of G and E denotes the set of edges, and $f_C: E \rightarrow 2^{C}$ is a coloring of each edge with a set of colors in $C=\{c_1,\dots , c_q \}$. In the paper, we denote by n the size of V and by m the size of E.

A path $\pi$ in G is said to be colored by $c_j \in C$ if all the edges of $\pi$ are colored by $c_j$. A path $\pi$ in G is called a uni-color path if there is a color $c_j \in C$ such that all the edges of $\pi$ are colored by $c_j$.

Given two vertices $x,y \in V$, an xy-path is a path between vertices x and y. Two paths $\pi '$ and $\pi ''$ are internally disjoint (or, simply, disjoint) if they do not share any internal vertex, while a set P of paths is internally disjoint if the paths in P are pairwise internally disjoint. Two uni-color paths $\pi '$ and $\pi ''$ are color disjoint if they are disjoint and they have different colors.

Next, we introduce the formal definitions of the problems we deal with.

We will consider a variant of the two problems where the length of the paths in the solution is (upper) bounded by an integer $l \geqslant 1$, that is we are interested only in paths bounded by l. These variants will be denoted by l-MaxCDP and l-MaxCDDP.

Notice that in the versions of these problems parameterized by the natural parameter, we are also given an integer $k>0$ and we look whether there exists at least k (color) disjoint uni-color st-paths.

A parameterized problem (I, k) is said fixed-parameter tractable (or in the class FPT) with respect to a parameter k if it can be solved in $f(k)\cdot |I|^c$ time (in fpt-time), where f is any computable function and c is a constant. The class XP contains problems solvable in time $|I|^{f(k)}$, where f is an unrestricted function. We defer the reader to the recent monographs of Downey and Fellows or Cygan et al. for additional information around parameterized complexity [5, 6].

The natural notion of parameterized approximation was introduced quite recently (see the survey of Marx for an overview [10]). Informally, it aims at giving more time than polynomiality to achieve better approximation ratio. We give the definition of fpt cost $\rho$-approximation algorithm, as in Sect. 6 we will rule out the existence of such an algorithm for MaxCDP and MaxCDDP. This is a weaker notion than fpt-approximation, but notice that we will prove negative result (which will thus be stronger).

An NP-optimization problem Q is a tuple $(\mathcal{I}, Sol, val, goal)$, where $\mathcal{I}$ is the set of instances, Sol(I) is the set of feasible solutions for instance I, val(I, S) is the value of a feasible solution S of I, and goal is either max or min.

Definition 1

(fpt cost $\rho$ -approximation algorithm, Chen et al. [4]). Let Q be an optimization problem and $\rho :\mathbb {N}\rightarrow \mathbb {R}$ be a function such that $\rho (k) \geqslant 1$ for every $k\geqslant 1$ and $k \cdot \rho (k)$ is nondecreasing (when goal = min) or $\frac{k}{\rho (k)}$ is unbounded and nondecreasing (when goal = max). A decision algorithm $\mathcal{A}$ is an fpt cost $\rho$ -approximation algorithm for Q (when $\rho$ satisfies the previous conditions) if for every instance I of Q and integer k, with $Sol(I)\ne \emptyset$, its output satisfies the following conditions:

• 1. If $opt(I) > k$ (when goal = min) or $opt(I) < k$ (when goal = max), then $\mathcal{A}$ rejects (I, k).

• 2. If $k\geqslant opt(I) \cdot \rho (opt(I))$ (when goal = min) or $k\leqslant \frac{opt(I)}{\rho (opt(I))}$ (when goal = max), then $\mathcal{A}$ accepts (I, k).

Moreover the running time of $\mathcal{A}$ on input (I, k) is $f(k) \cdot |I|^{O(1)}$. If such a decision algorithm $\mathcal{A}$ exists then Q is called fpt cost $\rho$-approximable.

3 Complexity of MaxCDDP and MaxCDP on Graphs at Bounded Distance from Disjoint Paths

In this section we consider the complexity of MaxCDP and MaxCDDP on graphs having distance bounded by a constant from disjoint paths. The distance to disjoint paths is the minimum number of vertices to remove to make the graph a set of disjoint paths.

We show that MaxCDDP is NP-hard for graphs at distance two from disjoint paths, while MaxCDDP is polynomial time solvable when the input graph has distance bounded by a constant from disjoint paths.

3.1 Complexity of MaxCDDP on Graphs at Distance Two from Disjoint Paths

In this section, we show that if the input graph G has distance two from a set of disjoint path, then MaxCDDP is NP-hard.

We give a reduction from Maximum Independent Set on Cubic graphs (MaxISC)¹. We recall the definition of MaxISC:

We build a graph $G=(V,E,f_C)$ from $G_I=(V_I,E_I)$ by defining a gadget $GV_i$ for each vertex $v_i \in V_I$, and connecting the gadget to vertices s and t.

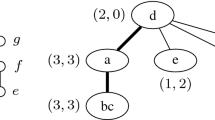
Given $v_i \in V_I$, define a gadget $GV_i$ consisting of a set $V_i$ of 4 vertices (see Fig. 1): $V_i = \{ v'_i, v'_{i,j}: v_i \in V_I, 1 \leqslant j \leqslant 3 \}$.

Moreover, define the set C of colors as follows: $C = \{ c_i : v_i \in V_I \} \cup \{ c_{i,j}: \{ v_i,v_j \} \in E_I \}$.

We assume that, given a vertex $v_i$, the vertices adjacent to $v_i$ (that is the vertices in $N(v_i)$) are ordered, i.e. if $v_j,v_h,v_z \in N(v_i)$ with $1 \leqslant j \leqslant h \leqslant z$, then $v_j$ is the first vertex adjacent to $v_i$, $v_h$ is the second and $v_z$ is the third.

We define the edges of G be means of the following paths:

• a path colored $c_i$ that consists of s, $v'_i$, $v'_{i,1}$, $v'_{i,2}$, $v'_{i,3}$, t, with $1 \leqslant i \leqslant |V_I|$

• if, according to the ordering, $v_j$ is the p-th vertex incident on $v_i$, $1 \leqslant p \leqslant 3$, then there exists a path colored $c_{i,j}$ that passes through s, $v'_{i,p}$, t

Fig. 1.

Gadget $GV_i$ associated with vertex $v_i \in V_I$. Vertices $v_j$, $v_h$, $v_z$ are three vertices of $V_I$, with $N(v_i)=\{ v_j, v_h, v_z \}$ and $j< h < z$. $v_j$ is the first vertex adjacent to $v_i$ in $G_I$ and thus there exists a path in G colored by $c_{i,j}$ that passes through s, $v'_{i,1}$, t; $v_h$ is the second vertex adjacent to $v_i$ in $G_I$ (hence there exists a path in G colored by $c_{i,h}$ that passes through s, $v'_{i,2}$, t); $v_z$ is the third vertex adjacent to $v_i$ in $G_I$ (hence there exists a path in G colored by $c_{i,z}$ that passes through s, $v'_{i,3}$, t).

First, we prove that the graph G has distance two from disjoint paths.

Lemma 2

Given a cubic graph $G_I$, let G be the corresponding graph input of MaxCDDP. Then G has distance two from disjoint paths.

Proof

After the removal of s and t, the paths left in the resulting graph are the paths colored by $c_i$, with $1 \leqslant i \leqslant |V_I|$, that pass through $v'_i$, $v'_{i,1}$, $v'_{i,2}$, $v'_{i,3}$. Since these paths are pairwise vertex disjoint, the lemma holds.    $\square$

Next, we prove the main results of the reduction.

Lemma 3

Let $G_I$ be a cubic graph and G be the corresponding graph input of MaxCDDP. Given an independent set $V'_I$ of $G_I$, then we can compute in polynomial time $|E|+|V'_I|$ disjoint uni-color color paths in G.

Proof

Consider an independent set $V'_I \subseteq V_I$ of $G_I$, we define a set $\mathcal {P}$ of uni-color disjoint paths as follows. $\mathcal {P}$ contains a path $s,v'_i, v'_{i,1}, v'_{i,2}, v'_{i,3}, t$ colored by $c_i$, for each $v_i \in V'_I$. Moreover, for each $\{ v_i,v_j \} \in E_I$, assume w.l.o.g. that $v_i \in V_I \setminus V'_I$ and that $v_j$ is the h-th vertex, $1 \leqslant h \leqslant 3$, adjacent to $v_i$. Then $\mathcal {P}$ contains the path $s, v'_{i,h}, t$ colored by $c_{i,j}$. Notice that these paths, since $V'_I$ is an independent set, are by construction color disjoint.    $\square$

Lemma 4

Let $G_I$ be a cubic graph and G be the corresponding graph input of MaxCDDP. Given $|E|+t$ color disjoint uni-color paths in G, we can compute in polynomial time an independent set of size t for $G_I$.

Proof

Consider a solution $\mathcal {P}$ of the instance of MaxCDDP consisting of $|E|+t$ color disjoint uni-color paths. First, we can assume that $\mathcal {P}$ contains, for each color $c_{i,j}$, a path colored by $c_{i,j}$. Assume this is not the case. Then, we can replace a path colored by $c_i$ or a path colored by $c_j$ with a path $p'$ colored by $c_{i,j}$ that passes through the vertices of gadget $VG_i$ or $VG_j$, without decreasing the number of path in $\mathcal {P}$. Moreover, notice that by replacing a path color $c_i$ with $p'$, the set $\mathcal {P}$ still contains color disjoint uni-color paths.

Now, starting from $\mathcal {P}$, we can compute an independent set $V'_I$ as follows. If $\mathcal {P}$ contains a path $s,v'_i, v'_{i,1}, v'_{i,2}, v'_{i,3}, t$ colored by $c_i$, then $v_i \in V'_I$. Notice that $V'_I$ is an independent set, since, if $v_i$, $v_j$, with $\{ v_i,v_j \} \in E$, are both in $V'_I$, this implies that there is no $c_{i,j}$-path in $\mathcal {P}$, contradicting our assumption.    $\square$

Hence, we can prove the NP-hardness of MaxCDDP on graphs at distance two from disjoint paths.

Theorem 5

MaxCDDP is NP-hard, even if the graph G has distance two from disjoint paths.

Proof

MaxISC is NP-hard [1]. Hence Lemmas 2, 3 and 4 imply that MaxCDDP is NP-hard, even if the graph G has distance two from disjoint paths.    $\square$

The previous result implies that MaxCDDP cannot be solved in $n^{f(k)}$ time unless P = NP (it is not in the class XP), where k is the distance to disjoint paths of G, but also for “stronger” parameters like pathwidth or treewidth [9]

3.2 A Polynomial-Time Algorithm for MaxCDP on Graphs at Constant Distance from Disjoint Paths

In this section, we show that, contrary to MaxCDDP, MaxCDP is polynomial-time solvable when the input graph G has distance bounded by a constant d from a set $\mathcal {P}$ of disjoint paths (that is, it is in the class XP for the parameter distance to disjoint paths).

Next, we present the algorithm. Notice that we assume that a set $X \subseteq V$ is given, such that after the removal of $X \cup \{s,t\}$ the resulting graph consists of a set $\mathcal {P}$ of disjoint paths². We assume that X and $\mathcal {P}$ are defined so that $s,t \notin X$ and that no path in $\mathcal {P}$ contains s and t. Denote by $V(\mathcal {P})$ the set of vertices that belong to a path of $\mathcal {P}$, it holds $V= V(\mathcal {P}) \cup X \cup \{s,t\}$.

Since G has distance d, where $d>0$ is constant, from the set of disjoint paths $\mathcal {P}$, it follows that $|X|\leqslant d$. Let $\mathcal {P'} = \{p_1, \dots , p_b \}$, with $1 \leqslant i \leqslant b \leqslant d$, such that $V(\mathcal {P'}) \subseteq V$ is the set of paths of an optimal solution of MaxCDP such that $p_i$ contains a non-empty subset of X.

The algorithm computes each $p_i$, with $1 \leqslant i \leqslant b$, by iterating through subpaths of size at most d in $\mathcal {P}$ and a subset of X. More precisely, $p_i$ is computed as follows. Each path $p_i$ contains at most $d+1$ disjoint subpaths that belong to paths in $\mathcal {P}$, that are connected through a subset of at most d vertices of X. In time $O(n^{2(d+1)})$, we compute the at most $d+1$ disjoint subpaths $p_x[j_1,j_2]$ of $P_x \in \mathcal {P}$ that belong to $p_i$; in time $O(2^d)$ we compute the subset $X_i \subseteq X$ that belong to each $p_i$. Let $V_i=V(p_i) \cup X_i$, that is the set of vertices that belong to $p_i$ and to subset $X_i$. Notice that the subsets $V_i$, with $1 \leqslant i \leqslant b$, are computed so that they are pairwise disjoint.

The algorithm computes in polynomial time if there exists a uni-color path from s to t that passes through the vertices $V_i$. If for each i with $1 \leqslant i \leqslant b$ such a path exists, then the algorithm computes the maximum number of uni-color disjoint paths in the subgraph $G'$ of G induced by $V' = V \setminus \bigcup _{i=1}^{b} V_i$. Notice that, since $V' \cap X = \emptyset$, it follows that, if we remove s and t from $V'$, $G'$ consists of a set of disjoint paths $\{p'_1, \dots , p'_r\}$. The maximum number of uni-color disjoint paths in the subgraph $G'$ can be computed in polynomial time, as shown in the following lemma.

Lemma 6

Let $G=(V,E,f_c)$ be an edge colored graph such that $V^* = V \setminus \{ s,t \}$ induces a set of disjoint paths. Then MaxCDP on G can be solved in polynomial time.

Proof

Let $P = \{ p'_1, \dots , p'_r \}$ be the set of disjoint paths induced by $V^*$. Since there is no st-path in G containing a vertex of $p'_i$ and a vertex of $p'_j$, with $i \ne j$, we compute a solution of MaxCDP independently on each path $p'_i$. Let $\mathcal {P}_i$ be the set of uni-color st-paths that contains only vertices of $p'_i$. For each i with $1 \leqslant i \leqslant r$, we compute a shortest uni-color st-path p that contains only vertices of $p'_i$, we add it to $\mathcal {P}_i$, and we remove the vertices of p from $p'_i$. We iterate this procedure, until there exists no st-path that contains only vertices of $p'_i$.

We claim that $\mathcal {P}_i$ is a set of uni-color st-paths of maximum size. Consider a shortest path p added to $\mathcal {P}_i$. Let x be the vertex of p adjacent to s and y be the vertex of p adjacent to t. Notice that each vertex in p, except for x and y, is not connected to s or t, otherwise p would not be a shortest path between s and t. Now, assume that there is an optimal solution $\mathcal {Q}$ of MaxCDP that does not contain p and that, moreover, contains an st-path that passes through some vertex of p, otherwise we can add p to $\mathcal {Q}$ and $\mathcal {Q}$ would not be optimal. Then by construction, since P is a set of disjoint paths, $\mathcal {Q}$ must contain a path $p'$ that contains p as a subpath. But then we can replace $p'$ with p in $\mathcal {Q}$, without decreasing the size of the optimal solution.    $\square$

Now, we give the main result of this section.

Theorem 7

MaxCDP is in XP when the distance to disjoint paths is bounded by a constant.

Proof

Notice that for each i with $1 \leqslant i \leqslant b \leqslant d$, we compute the set $V_i$ in time $O(2^d n^{2(d+1)})$; hence the d disjoint sets $V_1,\dots , V_b$ are computed in time $O(2^{d^2} n^{2d(d+1)})$. Since the existence of a uni-color path that passes through the vertices $V_i$ can be computed in polynomial time and since by Lemma 6 we compute in polynomial time the maximum number of uni-color disjoint paths in the subgraph $G'$, the theorem holds.    $\square$

4 FPT Algorithm Parameterized by Vertex Cover for MaxCDP

In this section, we will show that MaxCDP is FPT when parameterized by the size of the vertex cover of the input graph.

Theorem 8

MaxCDP is in FPT when parameterized by the size of the vertex cover of the input graph.

Proof

First, consider uni-color paths of length three s, v, t, for some $v \in V$. Uni-color path of length three are greedily added to a solution of MaxCDP. Since any solution of MaxCDP contains at most one uni-color path that passes through v, it follows that there exists an optimal solution of MaxCDP that contains path s, v, t. Hence, we add such path to our solution $\mathcal {P}$, and we remove vertex v from G.

Let $V'$ be a vertex cover of the resulting graph $G=(V,E,f_C)$, $|V'|=k$ (which can be computed in FPT-time). Since in G there is no uni-color path of length three connecting s and t, the following property holds. Consider a uni-color path p of G, then p either consists of vertices in $V'$ or each vertex of $V \setminus V'$ that belongs to p is adjacent in p to vertices of $V' \cup \{ s \} \cup \{ t \}$. This is true since $V'$ is a vertex cover (and thus $V \setminus V'$ is an independent set in G).

A consequence of this property is that each uni-color path has length at most 2k. Moreover, there can be at most k uni-color paths in a solution (since each path must contain a vertex of $V'$ and $|V'| \leqslant k$). Since both the number of paths and the length of paths are bounded by k and MaxCDP is known to be in FPT w.r.t. the combination of these two parameters [3], the claimed result follows.    $\square$

This algorithm does not easily extend to MaxCDDP. The main difference between MaxCDDP and MaxCDP, when considering as parameter the vertex cover of the input graph, is that in the latter we can safely add a uni-color path s, v, t of length three to a solution, while in the former we are not allowed to do it. Consider for example the uni-color path s, v, t of length three colored by c; if this path belongs to a solution of MaxCDDP, it prevents any other uni-color path $p'$ that passes through v (colored by some color $c'$), but also any path $p''$ colored by c (that does not pass through v) to be part of the solution. So, by adding the path s, v, t to the solution we are computing, we may get a suboptimal solution, since by removing p and by adding $p'$ and $p''$, we possibly compute a larger set of disjoint color uni-color paths.

5 A Fixed-Parameter Algorithm for l-MaxCDDP

In this section, we give a fixed-parameter algorithm for l-MaxCDDP, the length-bounded version of MaxCDDP, parameterized by the number k of uni-color color disjoint st-paths of a solution. Notice that MaxCDDP is W[1]-hard when parameterized by k, as the reduction that prove the W[1]-hardness of MaxCDP parameterized by k consists of paths having distinct colors [3].

Next, we present a parameterized algorithm based on the color coding technique [2]. The algorithm is inspired by the one for MaxCDP [3]. However, in this case we must combine two different labelings, one to label the vertices that belong to a uni-color path, one to label the color associated with a uni-color path of MaxCDDP.

First, we introduce the definition of perfect hash function on which our algorithm is based. A family F of hash functions from a set U (the vertex set in the traditional applications of color coding) to the set $\{l_1, \ldots , l_k\}$ of labels is k-perfect if, for each subset $U'$ of U with $|U'| = k$, there exists a hash function $f \in F$ such that f assigns a distinct label to each element of $U'$. Function f is called a labelling function.

Let $f_v \in F_V$ be a labelling function that assigns to each vertex $v \in V \setminus \{ s,t \}$ a label $f_v(v) \in L_v=\{ 1_v, \dots , h_v \}$, where $h_v=|L_v| \leqslant l k$.

Consider a second labelling function $f_c \in F_C$ that assigns to each color $c \in C$ a label $f_c(v) \in L_c=\{ 1_c, \dots , h_c \}$, where $h_c=|L_c| \leqslant k$.

By the property of perfect hash functions, we assume that each vertex that belongs to a solution of MaxCDDP is assigned a distinct label by $f_v$ and that each color d, such that there exists a uni-color path of MaxCDDP colored by d, is associated with distinct label $f_c$.

A simple path p in G is perfect for a set $L_v$ of labels assigned to V if and only if for each vertex v of p, with $v \notin \{s,t\}$, $f_v(v) \in L_v$, and for each pair of distinct vertices u, v of p, $f_v(u) \ne f_v(v)$. A set $\{ p_1, \ldots , p_k \}$ of uni-color paths is perfect for the set $L_v$ and $L_c$ of labels if and only if: (1) there exists a partition $\{ L_{v,1}, \ldots , L_{v,k} \}$ of $L_v$ such that each $p_i$ is perfect for $L_i$; (2) each path $p_i$, with $1 \leqslant i \leqslant k$, is colored by $c \in C$ associated with a distinct label in $L_c$. We combine two dynamic-programming recurrences to compute, given the labelling functions $f_v$ and $f_c$, whether there exists a set of perfect uni-color paths in G.

First, consider the function $S[L'_v, u, \lambda ]$, with $L'_v \subseteq L_v$, $u \in V$ and $\lambda \in C$. $S[L'_v, u, \lambda ]=1$ if and only if there exists a path from s to vertex $u\ne t$, such that the path is perfect for $L'_v$ and p is colored by $\lambda$.

We consider a second function $\varPi [L'_v, M,z]$, with $L'_v \subseteq L_v$ and $M \subseteq L_c$, $0 \leqslant z \leqslant k$. $\varPi [L'_v, M,z] =1$ if and only if there exist a set of labels $L'_v \subseteq L_v$ and a set of labels $M \subseteq L_c$, such that there exists a set of z uni-color paths perfect for $L'_v$ and M.

$S[L'_v, u, \lambda ]$ is defined as follows (we recall that $\uplus$ represents the disjoint union operator). In the base case, when $u=s$, $S[L'_v, u, \lambda ] = 1$ if $L'_v= \emptyset$, otherwise (when $L'_v \ne \emptyset$), $S[L'_v, u, \lambda ] = 0$.

When $u \ne s$:

$$ S[L'_v, u, \lambda ] = \max _{w \in N(u)} \big \{ S[L''_v, w, \lambda ] \mid L'_v = L''_v \uplus \{f_v(u)\} \wedge \{w,u\} \text { is colored by } \lambda \} $$

Next, we give the recurrence, $\varPi [L'_v,M,z]$. In the base case, that is when $z=0$, then $\varPi [L'_v,M,0]=1$ if $L'_v = \emptyset$ and $M = \emptyset$, else $\varPi [L'_v,M,0]=0$. Recall that l is the bound on the length of each path, $L'_v \subseteq L_v$, $M \subseteq C$ and $0 \leqslant z \leqslant k$, $\varPi [L'_v,M,z]$ is defined as follows:

$$\begin{aligned} \varPi [L'_v,M,z] = {\left\{ \begin{array}{ll} \begin{aligned} \!\max \big \{ &{}\varPi [L''_v,M \setminus \{ f_c(\lambda ) \},z-1] \ \wedge \ S[L^*_v, u, \lambda ] \mid \\ &{} \ L'_v = L''_v \uplus L^*_v \wedge \ |L^*| \leqslant l-1 \ \wedge \ \lambda \in C \wedge f_c(\lambda ) \in M \ \wedge \ \\ &{} \ \{u, t\}\in E \text { is colored by } \lambda \big \} \end{aligned} &{} \end{array}\right. } \end{aligned}$$

(1)

Next, we prove the correctness of the two recurrences.

Lemma 9

Given a labelling $f_v$ of the vertices of G, a color $\lambda \in C$, a vertex u and a set $L'_v \subseteq L_v$, there exists a simple path p in G from s to u perfect for $L'_v$ if and only if $S[L'_v, u, \lambda ]=1$.

Proof

We prove the lemma by induction on the length of the path p. First, we consider the base case, that is $u=s$. Since s is not associated with a label in $L_v$, it holds $S[L'_v, u, \lambda ]=1$ if and only if $L'_v= \emptyset$.

Consider now the general case and assume that there exists a path p in G perfect for $L'_v$ such that p is colored by $\lambda$. Consider the last vertex u of p, and let w be the vertex adjacent to u in p. By induction hypothesis, it follows that $S[L''_v, w, \lambda ]=1$, where $L'_v=L''_v \uplus \{f_v(u) \}$. By the definition of the recurrence, then $S[L'_v, u, \lambda ]=1$.

Assume that $S[L'_v, u, \lambda ]=1$. By the definition of the recurrence it holds that $S[L''_v, w, \lambda ]=1$, where $L'_v=L''_v \uplus \{f_v(u) \}$ and there is an edge $\{ u,w \} \in E$ colored by $\lambda$. By induction hypothesis, since $S[L''_v, w, \lambda ]=1$, there exists a path $p'$ from s to w perfect for $L''_v$ such that $p'$ is colored by $\lambda$. Since $\{ u,w \} \in E$ is colored by $\lambda$, it follows that there exists a simple path p in G from s to u perfect for $L'_v$.    $\square$

Lemma 10

Given a labelling $f_v$ of the vertices of G and a labelling $f_c$ of the set C of colors, a set $L'_v \subseteq L_v$, a set $M \subseteq L_c$, and integer z with $0 \leqslant z \leqslant k$, there exists a set $\{ p_1, \ldots , p_z \}$ of uni-color paths which is perfect for $L'_v$ and M if and only if $\varPi [L'_v,M,z]=1$.

Proof

We prove the lemma by induction on the number of uni-color paths. First, we consider the base case, that is $z=0$. Then there is no uni-color path perfect for $L'_v = \emptyset$ and $M= \emptyset$ if and only if $\varPi [\emptyset ,\emptyset ,0]=1$.

Consider now that there exist z disjoint color uni-color paths. Consider one of such paths, denoted by p, which is colored by $\lambda$ and whose vertices are associated with set of labels $L^*_v$ and such that the vertex of p adjacent to t is u, hence $\{ u,t \} \in E$ is colored by $\lambda$. Then, by Lemma 9 $S[L^*_v, u, \lambda ]=1$. Moreover, by induction hypothesis it holds $\varPi [L''_v,M \setminus \{ f_c(\lambda ) \},z-1]=1$, where $L'_v = L^*_v \uplus L''_v$ and $f_c(\lambda ) \in M$. Hence, by the definition of the recurrence for $\varPi$, it holds $\varPi [L'_v,M,z]=1$.

Consider the case that $\varPi [L'_v,M,z]=1$. By the definition of function $\varPi$, it follows that there exists a color $\lambda \in C$, with $f_c(\lambda ) \in M$, and a set of labels $L^*_v \subseteq L_v$, such that $\varPi [L''_v,M \setminus \{ f_c(\lambda ) \},z-1]=1$, where $L'_v = L''_v \uplus L^*_v$, and $S[L^*_v, u, \lambda ]=1$. By induction hypothesis, since $\varPi [L''_v,M \setminus \{ f_c(\lambda ) \},z-1]=1$, there exists a set $P'$ of $z-1$ paths perfect for the sets $L''_V$ and $M \setminus \{ f_c(\lambda ) \}$. By Lemma 9 there exists a path $p'$ from s to u colorful for $L''_v$ and that has color $\lambda$. Moreover, since $\varPi [L'_v,M,z]=1$, $\{ u,t \} \in E$ is colored by $\lambda$. By the property of labelling $f_c$, no path of $P'$ has label $f_c(\lambda )$, hence $P' \cup p$ is perfect for $L'_v$ and M.    $\square$

We can now state the main result.

Theorem 11

l-MaxCDDP can be solved in time $2^{O(l k)}poly(n)$.

Proof

An optimal solution of l-MaxCDDP consisting of k color disjoint paths exists if and only if $\varPi [L_v,M,k]=1$. The correctness of the recurrence to compute $\varPi$ follows from Lemma 10. Now, we discuss the time complexity to compute $\varPi [L'_v,M,z]$ and $S[L'_v, u, \lambda ]$. First, consider $S[L'_v, u, \lambda ]$. It consists of $2^{l k} n q$ entries and each entry can be computed in time O(n), as we consider each vertex $w \in N(u)$.

Now, consider $\varPi [L'_v,M,z]$. It consists of $2^{k(l+1)} k$ entries. In order to compute $\varPi [L'_v,M,z]$, at most $2^{kl} k$ entries must be considered, since $\varPi [L^*_v,M\setminus \{f_c(v)\},z-1]$ is considered, where we have $2^{kl}$ subsets $L^*_v \subseteq L'_v$ and k labels $f_c(v)$. Given two labelling functions $f_v$ and $f_c$, the time complexity to compute the entries $\varPi [L'_v,M,z]$ is $O(2^{k(2l+1)} k n)$. By the property of color-coding [2], a function $f_v \in F_v$ and a function $f_v \in F_v$ can be computed in time $2^{O(l k)}poly(n)$ and $2^{O(k)}poly(n)$, respectively, hence in time $2^{O(l k)}poly(n)$.    $\square$

6 FPT Inapproximation

Since MaxCDP and MaxCDDP are hard to approximate in poly-time and do not admit fixed-parameterized algorithm for parameter number of paths, it is worth to investigate approximation in FPT time, i.e. find approximate solution with additional time. Unfortunately, in this section, we show that both MaxCDP and MaxCDDP do not admit an FPT cost $\rho$-approximation, for any function $\rho$ of the optimum, unless FPT = W[1]. We will show the result by giving a reduction from the Threshold Set problem. Marx [11] showed that the Threshold Set problem does not admit a fpt cost $\rho$-approximation, for any function $\rho$ of the optimum, unless FPT = W[1].

First, we introduce the definition of the Threshold Set problem.

The cost of a solution of Threshold Set is denoted by |T|. Notice that this problem can be seen as a generalization of the Independent Set problem; indeed, for a graph $G=(V,E)$, we can define $U = V$, $\mathcal {S}= E$ and $w(S) = 1$ for every set $S \in \mathcal {S}$.

We will reduce Threshold Set to MaxCDP in polynomial time such that there is a “one-to-one” correspondence between the solutions of the two problem, therefore the inapproximability result transfers to MaxCDP, and then to MaxCDDP. The reduction is inspired by the one in [3], that shows inapproximability in polynomial time and W[1]-hardness of MaxCDP.

First, we design the reduction for the MaxCDP problem. Notice that we assume that we are given an ordering over the sets in $\mathcal {S}$ (i.e. $S_i< S_j, i<j$). Consider an instance $(U,\mathcal {S},w)$ of Threshold Set, we define a corresponding instance $(G=(V,E,f_C), s, t)$ of MaxCDP. The set V of vertices is defined as follows:

$$ V = \{s, t\} \cup \{ s_i | i \in [|U|]\} \cup \{S_i^j | i \in [|\mathcal {S}|], 1 \leqslant j \leqslant w(S_i) \} $$

The set of colors C is defined as follows: $C=\{ c_i: i \in U \}$.

Now, we define the set E of edges.

• for all $i \in [|U|]$, define an edge $\{s,s_i \}$ colored by $c_i$ and an edge $\{s_i, S_q^j\}$ colored by $c_i$, for all $1 \leqslant j \leqslant w(S_q)$, where q is the smallest index of a set $S_q \in \mathcal {S}$ such that $i \in S_q$,

• from each $S_q^j$, define an edge $\{ S_q^j, S_{q'}^{j'}\}$ colored by $c_i$, for all $1 \leqslant j' \leqslant w(S_{q'})$, such that $i \in S_q$, $i \in S_{q'}$, $q' > q$ and, for each $q<l<q'$, it holds $i \notin S_l$,

• from each $S_q^j$, define an edge $\{ S_q^j,t \}$ colored by $c_i$, where $i \in S_q$ and for each $q' > q$ with $S_{q'} \in \mathcal {S}$, .

See Fig. 2 for an example. Now, we prove the main properties of the reduction.

Fig. 2.

Sample construction of an instance of MaxCDP from an instance of Threshold Set with $\mathcal {S}= \{\{1,2,3\}, \{1,4\}, \{2,3,4\} \}, w(S_1) = 2, w(S_2)=1, w(S_3)=2$. A solution for this instance of Threshold Set could be $T' = \{1,2\}$, and we drawn with dark edges the corresponding disjoint paths for MaxCDP.

Lemma 12

Given an instance $(U,\mathcal {S},w)$ of Threshold Set, let $(G=(V,E,f_C), s, t)$ be the corresponding instance of MaxCDP. Then, given a solution $T'$ of Threshold Set on instance $(U,\mathcal {S},w)$, we can compute in polynomial time a set of $|T'|$ disjoint uni-color paths in $(G=(V,E,f_C), s, t)$.

Proof

Consider a solution $T'$ of Threshold Set on instance $(U,\mathcal {S},w)$, and define a set P of $|T'|$ disjoint uni-color paths in $(G=(V,E,f_C), s, t)$ as follows. For each $i \in T'$, define a uni-color path p colored by $c_i$ that starts in s, passes through $s_i$, and for each $S_q \in \mathcal {S}$, if i is the j-th element of $T'$ in $S_q$, $1 \leqslant j \leqslant w(S_q)$, passes through vertex $S_q^j$. It follows that the path defined are disjoints, as at most one element can be the j-th element of $T'$ in $S_q$ and $|T' \cap S_q| \leqslant w(S_q)$.    $\square$

Lemma 13

Given an instance $(U,\mathcal {S},w)$ of Threshold Set, let $(G=(V,E,f_C), s, t)$ be the corresponding instance of MaxCDP. Then, given a set of q disjoint uni-color paths in $(G=(V,E,f_C), s, t)$, we can compute in polynomial time a solution of size q of Threshold Set on instance $(U,\mathcal {S},w)$.

Proof

Consider a set P of disjoint uni-color paths in $(G=(V,E,f_C), s, t)$. First, we claim that each path in P has a distinct color. Indeed, the paths in P must be disjoint and, by construction, for each color $c_i$ each path must pass trough vertex $s_i$.

Now, starting from P, we define a solution $T'$ of of Threshold Set on instance $(U,\mathcal {S},w)$. For each path $p \in P$ colored by $c_i$, elements $u_i$ belongs to $T'$. We show that $T'$ is a a solution of Threshold Set on instance $(U,\mathcal {S},w)$.

Consider a set $S_i \in \mathcal {S}$, then there exists a most $w(S_i)$ elements in $T'$. Indeed, notice that, by construction, there exists at most $w(S_i)$ vertices $S_i^j$, hence by construction there exist at most $w(S_i)$ paths in P that passes through vertices of $S_i^j$, hence at most $w(S_i)$ elements in $T'$ belong to $S_i$. As a consequence $T'$ is a feasible solution of Threshold Set on instance (U, S, w). By construction, $|T'|=q$.    $\square$

Theorem 14

MaxCDP and MaxCDDP cannot be approximated in FPT-time within any function $\rho$ of the optimum, unless FPT = W[1].

Proof

The theorem holds for MaxCDP since Threshold Set cannot be approximated within any function $\rho$ of the optimum, unless FPT = W[1] [11], and from the properties of the polynomial time reduction proved in Lemmas 12 and 13.

For MaxCDDP, it holds from the fact that in the described reduction all the paths have a distinct color.    $\square$

7 Conclusion

In this paper, we continued the complexity analysis of MaxCDP and deepen the hardness analysis according to the structure of the input graph. We also introduced a new variant, called MaxCDDP, asking for a solution with vertex and disjoint colors.

In the future, we would like to further deepen the analysis on the the structural complexity of MaxCDP and MaxCDDP. For example is MaxCDP in XP when the parameter if the size of the Feedback Vertex Set of the input graph? Is MaxCDP FPT when the parameter if the distance to disjoint paths of the input graph? We would also like to improve the running time of our algorithms and to match them with some lower bounds under widely believed assumptions in order to have a fine-grained complexity analysis of these problems.