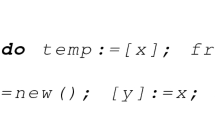Using Unified Model Checking to Verify Heaps

Abstract

This paper addresses the problem of verifying heap evolution properties of pointer programs. To this end, a new unified model checking approach with MSVL (Modeling, Simulation and Verification Language) and PPTL$^{\tiny \text{ SL }}$ is presented. The former is an executable subset of PTL (Projection Temporal Logic) while the latter is an extension of PPTL (Propositional Projection Temporal Logic) with separation logic. MSVL is used to model pointer programs, and PPTL$^{\tiny \text{ SL }}$ to specify heap evolution properties. In addition, we implement a prototype in order to demonstrate our approach.

This research is supported by the National Natural Science Foundation of China Grant Nos. 61133001, 61322202, 61420106004, and 91418201.

1 Introduction

Pointers are indispensable in real-world programs or applications. Reasoning about pointer programs is quite challenging since pointer usage is often complex and flexible. Potential bugs encountered in pointer programs such as null pointer dereference, memory leaks, or shape destruction are due to the nature of pointers. The problem is more serious for concurrent programs since we need to consider all possible execution sequences of processes. Alias analysis, as the name implies, is a point-to analysis which naively checks whether pointers can be aliased. Shape analysis is another form of pointer analysis that attempts to discover the possible shapes of heap structures. It aims to prove that these structures are not misused or corrupted.

Reynolds [1] proposes a famous Hoare-style logic known as separation logic which has received much attention. For the last decade, many works extend separation logic to do automated assertion checking [2] and shape analysis [3] in real-world applications. PTL (Pointer Assertion Logic) is a notation for expressing assertions about the heap structures of imperative languages. PALE (PAL Engine) is a complete implementation of PAL that encodes both programs and partial assertions as formulas in monadic second-order logic. However, loop invariants have to be manually provided so that it is not fully automatic.

In this paper we intend to apply the model checking framework to verify heap evolution properties. As the property-specification language we use a variant of temporal logic namely PPTL$^{\tiny \text{ SL }}$ [4]. PPTL$^{\tiny \text{ SL }}$ is a two-dimensional (spatial and temporal) logic by extending PPTL (Propositional Projection Temporal Logic) [5] with a decidable fragment of separation logic. For the program part, our method makes use of a temporal logic programming language, which is an executable subset of PTL (Projection Temporal Logic), called MSVL (Modeling, Simulation and Verification Language) [6], to model heap programs. PPTL$^{\tiny \text{ SL }}$ can be translated (preserving satisfiability) into a strict subset of PTL. Specifications and models lie in the same logic framework, hence the name unified model checking. The previous unified model checking approach [7] cannot verify heap evolution properties. We extend the approach in [7] by replacing PPTL with the more expressive specification language PPTL$^{\tiny \text{ SL }}$ such that heap evolution properties can be verified, and also the corresponding model checking approach is developed in this paper.

The work in [8] studies the problem of establishing temporal properties, including liveness properties of Java programs with evolving heaps. A specification language Evolution Temporal Logic (ETL) is defined which is a first-order linear temporal logic with transitive closure. ETL mainly focuses on describing behaviors of large granularity heap objects and high-level threads. Navigation Temporal Logic (NTL) [9] extends LTL with pointer assertions on single-reference structures including primitives for the birth and death of entities. The abstracted model checking algorithm for NTL is a non-trivial extension of the tableau based algorithm for LTL, which can be applied for both sequential and concurrent pointer programs. The major disadvantage of the approach of [9] is that it can only verify programs manipulating singly-linked lists. In [10], Rieger presents an abstraction and verification framework for pointer programs operating on unbounded heaps. In his work, two abstraction techniques are introduced, one is for singly-linked structures and the other employs context-free hyperedge replacement graph grammars to model more general heap structures. A two-dimensional (time and space) logic named maLTL is developed in [11] by combining temporal logic LTL and CTL, which is suitable to deal with pointers and heap management in the context of C programs. Since both dimensions of maLTL are realized by temporal logics that makes the difference between the two dimensions unclear.

2 Projection Temporal Logic

Let Var be a countable set of typed variables consisting of static and dynamic variables, and Prop a countable set of propositions. $\mathbb {B}$ represents the boolean domain $\{true, false\}$, and $\mathbb {D}$ denotes the data domain. The terms e and formulas Q of PTL are given by the following grammar:

where $q \in Prop$ is a proposition, $x \in Var$ a variable, and fun a function of arity n and Pred is a predicate of arity n.

A state s is defined to be a pair $(I_{v},I_{p})$ of state interpretations $I_{v}$ and $I_{p}$, $I_{v} \, : \, Var \rightarrow \mathbb {D} \cup \{nil\}, I_{p} \, : \, Prop \rightarrow \mathbb {B}$. An interval $\sigma = \langle s_{0},s_{1},\ldots \rangle$ is a non-empty sequence of states, finite or infinite. The length of $\sigma$, denoted by $|\sigma |$, is $\omega$ if $\sigma$ is infinite, otherwise it is the number of states minus one. To have a uniform notation for both finite and infinite intervals, we will use extended integers as indices. That is, we consider the set $N_{0}$ of non-negative integers, and define $N_{\omega }=N_{0} \cup \{\omega \}$, and extend the comparison operators, $=$, <, $\le$, to $N_{\omega }$ by considering $\omega =\omega$, and for all $i \in N_{0}$, $i < \omega$. Moreover, we define $\preceq$ as $\le - \{(\omega ,\omega )\}$. With such a notation, $\sigma _{(i .. j)}(0 \le i \preceq j \le |\sigma |)$ denotes the sub-interval $\langle s_{i},\ldots ,s_{j} \rangle$ and $\sigma ^{(k)}(0 \le k \preceq |\sigma |)$ denotes the suffix interval $\langle s_{k},\ldots ,s_{|\sigma |} \rangle$ of $\sigma$. The concatenation of $\sigma$ with another interval $\sigma '$ is denoted by $\sigma \cdot \sigma '$. Further, let $\sigma = \langle s_{k},\ldots ,s_{|\sigma |} \rangle$ be an interval and $r_{1},\ldots ,r_{h}$ be integers $(h \ge 1)$ such that $0 \le r_{1} \le r_{2} \le \cdots \le r_{h} \preceq |\sigma |$. The projection of $\sigma$ onto $r_{1},\ldots ,r_{h}$ is the interval, $\sigma \downarrow (r_{1},\ldots ,r_{h}) = \langle s_{t_{1}}, \ldots , s_{t_{l}} \rangle$, where $t_{1},\ldots ,t_{l}$ is obtained from $r_{1},\ldots ,r_{h}$ by deleting all duplicates.

An interpretation for a PTL formula is a triple $\mathcal {I} = (\sigma , k, j)$ where $\sigma = \langle s_{0},s_{1},\ldots \rangle$ is an interval, k a non-negative integer and j an integer or $\omega$ such that $k \preceq j \le |\sigma |$. We write $(\sigma ,k,j) \models Q$ to mean that a formula Q is interpreted over a sub-interval $\sigma _{(k .. j)}$ of $\sigma$ with the current state being $s_{k}$. The notation $s_{k}=(I^{k}_{v},I^{k}_{p})$ indexed by k represents the k-th state of an interval $\sigma$. The semantics of terms and PTL formulas are defined by:

A formula Q is satisfied over an interval $\sigma$, written $\sigma \models Q$, if $(\sigma ,0,|\sigma |) \models Q$ holds. Also we have the following derived formulas:

$$\begin{aligned} \varepsilon&\overset{\text {def}}{=} \lnot \bigcirc true&more&\overset{\text {def}}{=} \lnot \varepsilon&Q_{1};Q_{2}&\overset{\text {def}}{=} (Q_{1},Q_{2}) \,prj\, \varepsilon&Q^{+}&\overset{\text {def}}{=} Q ; Q^{*} \\ \lozenge Q&\overset{\text {def}}{=} true ; Q&\square Q&\overset{\text {def}}{=} \lnot \lozenge \lnot Q&len(n)&\overset{\text {def}}{=} \bigcirc len(n-1)&skip&\overset{\text {def}}{=} len(1) \end{aligned}$$

where $\varepsilon$ (or len(0)) denotes an interval with zero length, “; ” and “$^{+}(^{*})$” are used to describe sequential and loop properties respectively.

3 Modeling, Simulation and Verification Language

MSVL is an executable temporal logic with framing technique which is recently extended with function calls [12] and groups of types such as basic data types, pointer types and struct types [13]. Thus it is capable of modeling pointer programs. The arithmetic and boolean expressions of MSVL can be defined as:

Some useful elementary statements of MSVL can be inductively defined as follows. A convenient way to execute MSVL programs is to transform them into their equivalent normal forms (Definition 1).

Definition 1 (Normal Form of MSVL)

An MSVL program Q is in normal form if , where $Q_{f_{j}}$ is a general MSVL program, whereas $Q_{e_{i}}$ and $Q_{c_{j}}$ are true or all are state formulas of the form: $(x_{1}=e_{1}) \wedge \cdots \wedge (x_{m}=e_{m}) \wedge \overset{\cdot }{q_{x_{1}}} \wedge \cdots \wedge \overset{\cdot }{q_{x_{m}}}$. $\overset{\cdot }{q}$ denotes either q or $\lnot q$.

The normal form divides the formula into two parts: the present part and the future part. A key conclusion is that any MSVL program can be reduced to its normal form [5, 6]. Therefore, we can use an incremental way to execute MSVL programs based on normal form.

Theorem 1

Any MSVL program Q can be reduced to its normal form.

Using normal form of MSVL as a basis, a graph can be constructed, namely Normal Form Graph (NFG) [5, 6], by recursively progressing the future part of a normal form, which explicitly illustrates the state space of an MSVL program.

3.1 Examples of MSVL Programs Manipulating Pointers

Producer-consumer program. Consider the producer-consumer problem encoded in MSVL below. The producer process and the consumer process share a buffer which is realized as a global singly-linked list. The producer repeatedly generates new items by allocating new memory heap cells, and adds them to the tail x of the buffer, whereas the consumer removes items from the head y of the buffer and disposes them.

The parallel operator “||” in MSVL considers the true concurrency semantics of programs. In order to simulate the interleaving semantics of the two concurrent processes, the await statement is employed to force a process to sleep when the waiting condition is false, otherwise the process will continue to execute.

4 The Two-Dimensional Logic PPTL$^{\tiny \text{ SL }}$

Previously, we integrate a decidable fragment of separation logic (referred to as SL) with PPTL to obtain a two-dimensional logic. The logic, referred to as PPTL$^{\tiny \text{ SL }}$ [4], allows us to express heap evolution properties. We assume a countable set PVar of variables with pointer type, and a finite set Loc of memory locations. $PVal=Loc \cup \{null\}$ denotes the set of pointer values which are either locations or null. The syntax of PPTL$^{\tiny \text{ SL }}$ formulas P is defined by the grammar:

$$\begin{aligned} e&{:}\!:= null \mid l \mid x \qquad \phi {:}\!:= e_{1}=e_{2} \mid e_{0} \mapsto \{ e_{1},\ldots ,e_{n} \} \mid \lnot \phi \mid \phi _{1} \vee \phi _{2} \mid \phi _{1} {{\#}} \phi _{2} \mid \exists x : \phi \nonumber \\ P&{:}\!:= \phi \mid \lnot P \mid P_{1} \vee P_{2} \mid {\bigcirc }P \mid (P_{1},\ldots ,P_{m}) \, prj \, P \mid P^{*} \end{aligned}$$

$l \in Loc$, $x \in PVar$, $\phi$ represents SL formulas, and P PPTL$^{\tiny \text{ SL }}$ formulas. Formula $e_{0} \mapsto \{ e_{1},\ldots ,e_{n} \}$ denotes that $e_{0}$ points to $e_{1},\ldots ,e_{n}$, where $e_{0}$ represents an address in the heap and $e_{1},\ldots ,e_{n}$ the consecutive values held in that address. The formula $\phi _{1} {{\#}} \phi _{2}$ specifies properties holding respectively for disjoint portions of the current heap, one makes $\phi _{1}$ true and the other makes $\phi _{2}$ true. The temporal operators as well as their semantics are taken from PTL.

We refer to a pair $(I_{s},I_{h})$ as a memory state, $I_{s} \, : \, PVar \rightharpoonup PVal, I_{h} \, : \, Loc \rightharpoonup {\bigcup }^{n}_{i=1} PVal^{i}$, where $I_{s}$ represents a stack and $I_{h}$ a heap. $I_{s}$ serves as valuations of pointer variables and $I_{h}$ as valuations of heap cells. We write dom(f) to denote the domain of mapping f. Given two mappings $f_{1}$ and $f_{2}$, the notation $f_{1} \perp f_{2}$ means that $f_{1}$ and $f_{2}$ have disjoint domains. Moreover, we use $f_{1} \cdot f_{2}$ to denote the union of $f_{1}$ and $f_{2}$. The semantics of SL formulas is given by:

$$\begin{aligned}&(I_{s},I_{h})[null] = null \qquad (I_{s},I_{h})[l] = l \qquad (I_{s},I_{h})[x] = I_{h}(x) \\&\varvec{I_{s},I_{h} \models _{{}_{SL}} e_{1}=e_{2}} \text{ iff } (I_{s},I_{h})[e_{1}] = (I_{s},I_{h})[e_{2}]. \quad \varvec{I_{s},I_{h} \models _{{}_{SL}} \lnot \phi } \text{ iff } I_{s},I_{h} \not \models _{{}_{SL}} \phi . \\&\varvec{I_{s},I_{h} \models _{_{SL}} e_{0} \mapsto \{ e_{1},\ldots ,e_{n} \}} \text{ iff } dom(I_{h})=\{(I_{s},I_{h})[e_{0}]\} \text{ and } I_{h}((I_{s},I_{h})[e_{0}]) = \\&((I_{s},I_{h})[e_{1}],\ldots ,(I_{s},I_{h})[e_{n}]). \quad \varvec{I_{s},I_{h} \models _{{}_{SL}} \phi _{1} \vee \phi _{2}} \text{ iff } I_{s},I_{h} \models _{_{SL}} \phi _{1} \text{ or } I_{s},I_{h} \models _{{}_{SL}} \phi _{2}. \end{aligned}$$

$$\begin{aligned}&\varvec{I_{s},I_{h} \models _{{}_{SL}} \phi _{1} {{\#}} \phi _{2}} \text{ iff } \exists I_{h_{1}}, I_{h_{2}} : I_{h_{1}} \perp I_{h_{2}} \text{ and } I_{h} = I_{h_{1}} \cdot I_{h_{2}} \text{ and } I_{s},I_{h_{1}} \models _{{}_{SL}} \phi _{1} \\&\text{ and } I_{s},I_{h_{2}} \models _{{}_{SL}} \phi _{2}. \quad \varvec{I_{s},I_{h} \models _{{}_{SL}} \exists x : \phi } \text{ iff } \exists v \in PVal \text{ such } \text{ that } I_{s}[x \rightarrow v], I_{h} \models _{{}_{SL}} \phi . \end{aligned}$$

The semantics of P is similar to that of Q since the only difference is their state formulas (formulas without temporal operators). Therefore, we only give the interpretation of state formulas, i.e., $\varvec{\mathcal {I} \models \phi } \text { iff } I^{k}_{s},I^{k}_{h} \models _{_{SL}} \phi$. We abusively use the notation $\mathcal {I} \models P$, and in this case P is interpreted over an interval of memory states.

SL can describe various heap structures, we present the following derived formulas expressed in SL which are related to singly-linked lists.

$$\begin{aligned}&e \mapsto \{-_{1},\ldots ,-_{n}\} \overset{\text{ def }}{=} \exists x_{1}, \ldots , x_{n} : e \mapsto \{x_{1}, \ldots , x_{n}\} {{\#}} true \\&e \hookrightarrow \{{-,\ldots ,-}\} \overset{\text{ def }}{=} e \mapsto \{{-,\ldots ,-}\} {{\#}} true \quad alloc(e, n) \overset{\text{ def }}{=} e \hookrightarrow \{-_{1},\ldots ,-_{n}\} \\&alloc(e) \! \overset{\text{ def }}{=} \! \bigvee \!{}_{i=1}^{n} alloc(e, i) \quad emp \overset{\text{ def }}{=} \lnot \exists x : alloc(x) \quad \sharp e \! \ge \! n \! \overset{\text{ def }}{=} \! \#\!{}_{i=1}^{n} (\exists x_{i} : x_{i} \! \hookrightarrow \! \{e\}) \\&e_{1} \overset{\circlearrowleft }{\longrightarrow } e_{2} \overset{\text{ def }}{=} alloc(e_{1}, 1) \wedge (e_{2} \ne e_{1} \rightarrow \lnot alloc(e_{2}, 1) \wedge \sharp e_{1}=0) \wedge (\forall x : x \ne e_{2} \rightarrow \\&(\sharp x=1 \rightarrow alloc(x, 1))) \wedge (\forall x : x \ne null \rightarrow \sharp x \le 1) \wedge (\forall x : alloc(x) \rightarrow alloc(x,1)) \\&ls(e_{1},e_{2}) \overset{\text{ def }}{=} e_{1} \overset{\circlearrowleft }{\longrightarrow } e_{2} \wedge \lnot (e_{1} \overset{\circlearrowleft }{\longrightarrow } e_{2} {{\#}} \lnot emp) \\&e_{1} \rightarrow ^{+} e_{2} \overset{\text{ def }}{=} ls(e_{1}, e_{2}) {{\#}} true \quad e_{1} \rightarrow ^{*} e_{2} \overset{\text{ def }}{=} e_{1}=e_{2} \vee e_{1} \rightarrow ^{+} e_{2} \end{aligned}$$

Here, $ls(e_{1},e_{2})$ describes a list segment starting from the location $e_{1}$ to $e_{2}$, $e_{1} \rightarrow ^{+} e_{2}$ and $e_{1} \rightarrow ^{*} e_{2}$ mean that $e_{2}$ is reachable from $e_{1}$ via certain pointer links. emp denotes an empty heap, and alloc(e) indicates the address e is allocated in the current heap. Formulas describing other heap structures can also be derived.

4.1 Specify Heap Evolution Properties

For the producer-consumer program with a shared list, some interesting heap evolution properties can be specified by PPTL$^{\tiny \text{ SL }}$:

• (1) Absence of memory leaks, i.e., any item can be reached by certain variable during the execution of the program: $\square (\forall z: alloc(z) \rightarrow (x \rightarrow ^{*} z \vee y \rightarrow ^{*} z \vee t \rightarrow ^{*} z \vee r \rightarrow ^{*} z))$.

• (2) The tail of the list is never deleted nor disconnected from the head: $\bigcirc ^{2} \square (alloc(x) \wedge y \rightarrow ^{*} x)$.

• (3) Shape integrity of the buffer, i.e., the shape of the buffer is repeatedly formed as a linked list within every five time units: $\bigcirc ^{2} ((len(5) \wedge \lozenge ls(y,null))^{+})$.

In [4], we have proved that PPTL$^{\tiny \text{ SL }}$ is decidable by an equisatisfiable translation. The key idea is that all the formulas expressing heaps in SL are reduced into the first-order theory. Since the model of first-order set has no heap ingredient, we use extra variables to simulate it. Let H denote a vector of n tuples of pointer variables, i.e., $H = ((H_{1,1}, \ldots , H_{1,m_{1}}), \ldots , (H_{n,1}, \ldots , H_{n,m_{n}}))$. The translations $f(\phi ,H)$ and F(P, H) generate an equisatisfiable state formula $\phi '$ to $\phi$ and an equisatisfiable temporal formula $P'$ to P respectively. Both $\phi '$ and $P'$ belong to PTL. The detailed definitions of f and F can be found in [4]. Analogous to MSVL, by using a very similar approach, we can construct a graph structure (also called NFG) that explicitly characterizes the model for any reduced PPTL$^{\tiny \text{ SL }}$ formula. The detailed proofs are given in [4], here we only give a brief summary.

Theorem 2

PPTL$^{\tiny \text{ SL }}$ is decidable, and its complexity is the same as PPTL, i.e., non-elementary.

5 Model Checking with MSVL and PPTL$^{\tiny \text{ SL }}$

Our model checking approach is similar to the traditional automata-based model checking except that ours is based on NFG. The starting point is a pointer program modeled by an MSVL program M, and a PPTL$^{\tiny \text{ SL }}$ formula P that formalizes the desired heap evolution property on M.

In general, the model checking procedure in this framework first creates the NFG $G_{M}$ of an MSVL program and the NFG $G_{\lnot P}$ of the negation of the input PPTL$^{\tiny \text{ SL }}$ formula, then constructs the product G of the two NFGs. The nodes (edges) of G are conjunctions of nodes (edges) in $G_{M}$ and $G_{\lnot P}$. If there exist a valid path in G, a counterexample is found, otherwise M satisfies P.

Fig. 1.

Tool architecture.

We have developed a unified model checking tool (prototype) based on the approach presented in this paper. As shown Fig. 1, the tool structure consists of three essential modules: MSV, PPTL$^{\tiny \text{ SL }}$ solver and unified model checker. An MSVL program M is feeded into MSV, and a property P is given to the PPTL$^{\tiny \text{ SL }}$ solver. MSV constructs the NFG of M and PPTL$^{\tiny \text{ SL }}$ solver builds the NFG of $\lnot P$. The Model checker does not try to build the complete production of the two NFGs in practice. Instead, it works in “on the fly” manner and tries to find one valid path as early as possible. The SMT solver Z3 is called when checking whether an edge in the product NFG is satisfied or not. We have successfully verified the producer-consumer program with respect to the corresponding heap evolution properties mentioned in Sect. 4.

6 Conclusion

In this paper, we propose a unified model checking approach with MSVL and PPTL$^{\tiny \text{ SL }}$. We can apply this approach to verify heap evolution properties of pointer programs, including both safety and liveness properties on heap structures. Since PPTL$^{\tiny \text{ SL }}$ is able to be reduced to a subset of PTL so that programs and properties both belong to the same logic framework which makes the verification more convenient. We have developed a model checking tool that exploits the SMT solver Z3 as the verification engine. In the future, more case studies on various heap structures in addition to singly-linked structures will be carried out.