The Mixed Evacuation Problem

Abstract

A dynamic network introduced by Ford and Fulkerson is a directed graph with capacities and transit times on its arcs. The quickest transshipment problem is one of the most fundamental problems in dynamic networks. In this problem, we are given sources and sinks. Then, the goal of this problem is to find a minimum time limit such that we can send exactly the right amount of flow from sources to sinks. In this paper, we introduce a variant of this problem called the mixed evacuation problem. This problem models an emergent situation in which people can evacuate on foot or by car. The goal is to organize such a mixed evacuation so that an efficient evacuation can be achieved. In this paper, we study this problem from the theoretical and practical viewpoints. In the first part, we prove the polynomial-time solvability of this problem in the case where the number of sources and sinks is not large, and also prove the polynomial-time solvability and computational hardness of its variants with integer constraints. In the second part, we apply our model to the case study of Minabe town in Wakayama prefecture, Japan.

This research was the result of the joint research with CSIS, the University of Tokyo (No. 573) and used the following data: Digital Road Map Database extended version 2013 provided by Sumitomo Electric Industries, Ltd and Zmap TOWN II 2008/09 Shapefile Wakayama prefecture provided by Zenrin Co. Ltd.

Y. Higashikawa, N. Katoh and A. Takizawa—This work was partially supported by JSPS Grant-in-Aid for Scientific Research(A) (25240004).

N. Kamiyama—This work was supported by JST, PRESTO.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The coastal area facing the Pacific Ocean in Japan ranging from Shizuoka prefecture to Miyazaki prefecture has a high risk of a tsunami. In particular, it is predicted that Nankai Trough Earthquake will occur with 70 % probability within thirty years, and it will trigger a tsunami of the huge size which will quickly arrive at the coast (see, e.g., [1]). Based on several assumptions and estimated data, Wakayama prefecture recently designated several areas in which it is difficult for all people in the area to evacuate to safety places such as tsunami evacuation buildings before a tsunami arrives when Nankai Trough Earthquake occurs. For example, it is predicted that in Kushimoto town located at the south end of the main land of Japan, a tsunami arrives at earliest within ten minutes. One of assumptions the prefecture used is that the evacuation is done only by walking. In principle, it used to be not allowed to use cars for evacuation because the usage of cars in such an emergent situation may block evacuation of pedestrians which was observed at the time of Tohoku-Pacific Ocean Earthquake. However, if it is allowed to use cars and the smooth evacuation by car is organized, then the evacuation completion time may be shortened. The aim of this paper is to propose a mathematical model for making such a good “mixed” evacuation plan.

In this paper, we use a dynamic network flow introduced by Ford and Fulkerson [2, 3] for modeling such a mixed evacuation. A dynamic network is a directed graph with capacities and transit times on its arcs. The quickest transshipment problem is one of the most fundamental problems in dynamic networks. In this problem, we are given a dynamic network with several sources and sinks. Furthermore, we are given a supply for each source and a demand for each sink. Then, the goal of this problem is to find the minimum time limit such that we can send exactly the right amount of flow from sources to sinks. Hoppe and Tardos [4] proved that this problem can be solved in polynomial time. In this paper, we introduce a variant of the quickest transshipment problem called the mixed evacuation problem. This problem models an emergent situation in which people can evacuate on foot or by car. The goal of this problem is to organize such a mixed evacuation so that an efficient evacuation can be achieved. In the first part of this paper, we study the mixed evacuation problem from the theoretical viewpoint. First we prove that if the number of sources and sinks is at most $C \log _2 n$ (n is the number of vertices) for some constant C, then mixed evacuation problem can be solved in polynomial time (Sect. 3). In addition, we consider variants of the mixed evacuation problem with integer constraints (Sect. 4). In the second part of this paper, we study the mixed evacuation problem from the practical viewpoint. In this part, we apply our model to the case study in Japan (Sect. 5). More precisely, we apply our model for Minabe town in Wakayama prefecture, which was designated as a city in which safe evacuation from a tsunami is difficult when Nankai Trough Earthquake occurs.

Let $\mathbb {R}$, $\mathbb {R}_+$, $\mathbb {Z}$, $\mathbb {Z}_+$, and $\mathbb {Z}_-$ be the sets of reals, non-negative reals, integers, non-negative integers, and non-positive integers, respectively. For each finite set U, each vector x in $\mathbb {R}^U$, and each subset W of U, we define $x(W) := \sum _{u \in W}x(u)$. Furthermore, for each finite set U and each pair of vectors x, y in $\mathbb {R}^U$, we define $\langle x,y \rangle := \sum _{u \in U}x(u)y(u)$.

2 Preliminaries

The Mixed Evacuation problem is defined as follows. We are given a directed graph $D=(V,A)$ and two disjoint subsets S, T of V. Define $n := |V|$. The subset S (resp., T) is the set of source vertices (resp., sink vertices) in V. We assume that no arc in A enters (resp., leaves) a vertex in S (resp., T). In addition, we are given an arc capacity vector c in $\mathbb {Z}_+^A$, a supply vector b in $\mathbb {Z}_+^S$, a sink capacity vector u in $\mathbb {Z}_-^T$, transit time vectors $\tau _1, \tau _2$ in $\mathbb {Z}_+^A$, and fluid coefficients $q_1,q_2$ in $\mathbb {Z}_+$. In our application, $\tau _1$ represents the speed of walking, and $q_1$ represents the number of people that can walk in the one unit of the arc capacity. The values $\tau _2, q_2$ represent the information for cars. Lastly, we are given a time limit $\mathrm{\Theta }$ in $\mathbb {Z}_+$. Define $[\mathrm{\Theta }] := \{0,1,\ldots , \mathrm{\Theta }\}$.

For each integer i in $\{1,2\}$, each function $f :A \times [\mathrm{\Theta }] \rightarrow \mathbb {R}_+$, each vertex v in V, and each integer $\theta$ in $[\mathrm{\Theta }]$, we define

$$\begin{aligned} \partial _if(v, \theta ) := \sum _{a \in \delta (v;A)}\sum _{t = 0}^{\theta } f(a,t) - \sum _{a \in \varrho (v;A)}\sum _{t = 0}^{\theta - \tau _i(a)} f(a,t), \end{aligned}$$

where $\delta (v;A)$ (resp., $\varrho (v;A)$) represents the set of arcs in A leaving (resp., entering) v. A vector d in $\mathbb {R}^{S \cup T}$ is called an allocation, if $d(v) \ge 0$ for every vertex v in S and $d(v) \le 0$ for every vertex v in T. For each integer i in $\{1,2\}$, each allocation d in $\mathbb {R}^{S \cup T}$, and each vector w in $\mathbb {R}^A_+$, d is said to be (i, w)-feasible, if there exists a function $f :A \times [\mathrm{\Theta }] \rightarrow \mathbb {R}_+$ satisfying the following conditions.

• (D1) Let a and $\theta$ be an arc in A and an integer in $[\mathrm{\Theta }]$, respectively.

  • - If $\theta \le \mathrm{\Theta } - \tau _i(a)$, then $f(a, \theta ) \le q_i \cdot w(a)$.

  • - If $\theta > \mathrm{\Theta } - \tau _i(a)$, then $f(a, \theta ) = 0$.

• (D2) Let v and $\theta$ be a vertex in V and an integer in $[\mathrm{\Theta }]$, respectively.

  • - If $v \in V\!\setminus \!(S \cup T)$, then $\partial _if(v,\mathrm{\theta }) \le 0$.

  • - If $v \in S$ (resp., T), then $\partial _if(v,\mathrm{\theta }) \le d(v)$ (resp., $\partial _if(v,\mathrm{\theta }) \ge d(v)$).

• (D3) Let v be a vertex in V.

  • - If $v \in V\!\setminus \!(S \cup T)$, then $\partial _if(v,\mathrm{\Theta }) = 0$.

  • - If $v \in S$, then $\partial _if(v,\mathrm{\mathrm{\Theta }}) = d(v)$.

For each integer i in $\{1,2\}$ and each vector w in $\mathbb {R}^A_+$, let $\mathcal {F}_i(w)$ be the set of (i, w)-feasible allocations in $\mathbb {R}^{S \cup T}$. An assignment is a tuple $(d_1,d_2,w_1,w_2)$ such that $d_1,d_2$ are allocations in $\mathbb {R}^{S \cup T}$ and $w_1,w_2 \in \mathbb {R}^A_+$. Furthermore, an assignment $(d_1,d_2,w_1,w_2)$ is said to be feasible, if it satisfies the following conditions.  

(F1):

For every vertex v in S (resp., T), $d_1(v) + d_2(v) = b(v)$ (resp., $\ge u(v)$).

(F2):

For every arc a in A, we have $w_1(a) + w_2(a) \le c(a)$.

(F3):

We have $d_1 \in \mathcal {F}_1(w_1)$ and $d_2 \in \mathcal {F}_2(w_2)$.

 

The goal of Mixed Evacuation (me for short) is to decide whether there exists a feasible assignment. Notice that we can straightforwardly formulate me as a linear programming problem (in Sect. 5, we use an algorithm based on the linear programming). However, since the input size of $\mathrm{\Theta }$ is $\log _2 \mathrm{\Theta }$, its size is not bounded by a polynomial in the input size of me.

3 Mixed Evacuation with Few Sources and Sinks

In this section, we prove that if $|S \cup T| \le C \log _2 n$ for some constant C, then me can be solved in polynomial time. Assume that we are given an integer i in $\{1,2\}$, a vector w in $\mathbb {R}_+^A$, and a subset X of $S \cup T$. Define $\mathbf{D}_i^w(X)$ as the set of functions $f :A\times [\mathrm{\Theta }] \rightarrow \mathbb {R}_+$ satisfying (D1) and the following conditions.

• (D4) Let v and $\theta$ be a vertex in V and an integer in $[\mathrm{\Theta }]$, respectively.

  • - If $v \in V\!\setminus \!X$, then $\partial _if(v,\theta ) \le 0$.

  • - If $v \in X$, then $\partial _if(v,\theta ) \ge 0$.

• (D5) For every vertex v in $V\!\setminus \!(S \cup T)$, we have $\partial _if(v, \mathrm{\Theta }) = 0$.

Recall that no arc in A enters (resp., leaves) a vertex in S (resp., T). Thus, for every function f in $\mathbf{D}_i^w(X)$ and every vertex v in $(S\!\setminus \!X) \cup (T \cap X)$, we have $\partial _if(v, \mathrm{\Theta }) = 0$. Furthermore, we define a function $o_i^w :2^{S \cup T} \rightarrow \mathbb {R}_+$ by

$$\begin{aligned} o_i^w(X) := \max \Big \{\sum _{v \in X}\partial _if(v,\mathrm{\Theta }) \ \Big | \ f \in \mathbf{D}_i^w(X)\Big \}. \end{aligned}$$

Theorem 1

(Klinz [4, Theorem 5.1]). Assume that we are given an integer i in $\{1,2\}$, an allocation d in $\mathbb {R}^{S\cup T}$, and a vector w in $\mathbb {R}_+^A$. Then, $d \in \mathcal {F}_i(w)$ if and only if $d(X) \le o_i^w(X)$ for every subset X of $S \cup T$.

For each pair of vertices s in S and t in T, we denote by a(t, s) an arc from t to s. Define $E := A \cup \{a(t,s) \mid s \in S, t \in T\}$. Furthermore, we define H as the directed graph with the vertex set V and the arc set E. Then, for each integer i in $\{1,2\}$, each vector w in $\mathbb {R}_+^A$, each subset X of $S \cup T$, and each vector $\xi$ in $\mathbb {R}^E_+$, $\xi$ is called a feasible static flow with respect to i, w, and X, if it satisfies the following conditions (S1), (S2), and (S3).  

(S1):

For every arc a in A, we have $\xi (a) \le {q_i \cdot w(a)}$.

(S2):

For every pair of vertices s in S and t in T, if at least one of $s \in S\!\setminus \!X$ and $t \in X$ holds, then $\xi (a(t,s)) = 0$.

(S3):

For every vertex v in V, we have $\xi (\delta (v;E)) = \xi (\varrho (v;E))$.

  For each integer i in $\{1,2\}$, each vector w in $\mathbb {R}_+^A$, and each subset X of $S \cup T$, we denote by $\mathbf{S}_i^w(X)$ the set of feasible static flows with respect to i, w, and X. In addition, for each integer i in $\{1,2\}$, we define a vector $k_i$ in $\mathbb {R}^E$ as follows. For each arc a in $E\!\setminus \!A$ (resp., A), we define $k_i(a):= \mathrm{\Theta } + 1$ (resp., $-\tau _i(a)$).

Theorem 2

(Ford and Fulkerson [2, 3]). For every integer i in $\{1,2\}$, every vector w in $\mathbb {R}_+^A$, and every subset X of $S \cup T$, $o_i^w(X)$ is equal to the optimal objective value of the problem of maximizing $\langle k_i, \xi \rangle$ such that $\xi \in \mathbf{S}_i^w(X)$.

Define $\mathcal {P}$ as the set of assignments $(d_1, d_2, w_1, w_2)$ such that it satisfies (F2) and (F3), and the following condition.  

(F1$^+$):

For every vertex v in S (resp., T), $d_1(v) + d_2(v) \le b(v)$ (resp., $\ge u(v))$.

  Let $\mathsf{P1}$ be the problem of maximizing $d_1(S) + d_2(S)$ such that $(d_1,d_2, w_1,w_2) \in \mathcal {P}$. If the optimal objective value of P1 is equal to b(S), then we can conclude that there exists a feasible assignment. Otherwise, we can conclude that there exists no feasible assignment. This observation implies that if we can formulate P1 by a linear programming problem whose size is bounded by a polynomial in the size of me, then the polynomial-time solvability of me follows from the polynomial-time solvability of the linear programming problem [5]. Theorems 1, 2 imply that P1 can be formulated as follows. Define a vector $b^{\circ }$ in $\mathbb {R}^{S\cup T}$ by $b^{\circ }(v) := b(v)$ for each vertex v in S and $b^{\circ }(v) := 0$ for each vertex v in T. Define a vector $u^{\circ }$ in $\mathbb {R}^{S\cup T}$ by $u^{\circ }(v) := 0$ for each vertex v in S and $u^{\circ }(v) := u(v)$ for each vertex v in T.

$$\begin{aligned} \begin{array}{cl} \text{ Maximize } \ \ &{} \ d_1(S) + d_2(S) \\ \text{ subject } \text{ to } \ \ \ &{} \ d_1(v) \ge 0, \ d_2(v) \ge 0 \ \ \ \ (v \in S) \\ &{} \ d_1(v) \le 0, \ d_2(v) \le 0 \ \ \ \ (v \in T) \\ &{} \ u^{\circ }(v) \le d_1(v) + d_2(v) \le b^{\circ }(v) \ \ \ \ (v \in S \cup T) \\ &{} \ \langle k_i, \xi _{i,X} \rangle \ge d_i(X) \ \ \ \ (i \in \{1,2\}, X \subseteq S \cup T) \\ &{} \ \xi _{i,X} \in \mathbf{S}_i^{w_i}(X) \ \ \ \ (i \in \{1,2\}, X \subseteq S \cup T) \\ &{} \ w_1(a) + w_2(a) \le c(a) \ \ \ \ (a \in A) \\ &{} \ d_1, d_2 \in \mathbb {R}^{S \cup T}, \ w_1, w_2 \in \mathbb {R}_+^A. \end{array} \end{aligned}$$

If $|S \cup T| \le C \log _2 n$ for some constant C, then it is not difficult to see that the size of this linear programming problem is bounded by a polynomial of the input size of me. This completes the proof.

4 Mixed Evacuation with Integer Constraints

4.1 Integral Arc Capacities, Supplies, and Sink Capacities

Here we consider Integral Mixed Evacuation (ime for short). This problem is a variant of me in which a feasible assignment $(d_1,d_2,w_1, w_2)$ must satisfy that $d_1,d_2 \in \mathbb {Z}^{S \cup T}$ and $w_1,w_2 \in \mathbb {Z}_+^A$. We prove the NP-completeness of ime by reduction from Disjoint Paths with Different Costs [6] (dpdc for short) defined as follows. In what follows, we do not distinguish a simple directed path in a directed graph and the set of arcs contained in this directed path. We are given a directed graph $G = (N,L)$, a source vertex $v^+$ in N, and a sink vertex $v^-$ in N. Furthermore, we are given cost vectors $\ell _1, \ell _2$ in $\mathbb {Z}_+^L$ and a non-negative integer h in $\mathbb {Z}_+$. The goal of dpdc is to decide whether there exist arc-disjoint simple directed paths $P_1,P_2$ from $v^+$ to $v^-$ such that $\ell _1(P_1) + \ell _2(P_2) \le h$.

Theorem 3

(Li, McCormick, and Simchi-Levi [6]). The problem dpdc is NP-complete even if $h=0$ and $\ell _i(a) \in \{0,1\}$ for every integer i in $\{1,2\}$ and every arc a in L.¹

For proving the fact that ime is in $\mathbf{NP}$, we need the following theorems. For each finite set U and each function $g :2^U \rightarrow \mathbb {R}$, g is said to be submodular, if $g(X) + g(Y) \ge g(X \cup Y) + g(X \cap Y)$ for every pair of subsets X, Y of U.

Theorem 4

(E.g., [7, 8]). Assume that we are given a finite set U and a submodular function $g:2^U \rightarrow \mathbb {R}$. Then, we can find a subset X of U minimizing g(X) among all subsets of U in time bounded by a polynomial in |U| and $\mathsf{EO}$, where $\mathsf{EO}$ is the time required to compute g(X) for a subset X of U.

Theorem 5

(Hoppe and Tardos [4]). For every integer i in $\{1,2\}$ and every vector w in $\mathbb {R}_+^A$, the function $o_i^w$ is a submodular function.

Theorem 6

(E.g., [9]). For every integer i in $\{1,2\}$ and every subset X of $S \cup T$, we can compute $o_i^{w_i}(X)$ in polynomial time.

Assume that we are given an integer i in $\{1,2\}$, an allocation d in $\mathbb {R}^{S \cup T}$, and a vector w in $\mathbb {R}_+^A$. Then, Theorem 1 implies that $d \in \mathcal {F}_i(w)$ if and only if $o_i^w(X) - d(X) \ge 0$ for a subset X of $S\cup T$ minimizing $o_i^w(X) - d(X)$ among all subsets of $S \cup T$. Thus, since Theorem 5 implies that $o_i^w - d$ is submodular, Theorems 4, 6 imply that we can check whether $d \in \mathcal {F}_i(w)$ in polynomial time.²

Theorem 7

The problem ime is NP-complete.

Proof

Theorems 1, 4, 5, and 6 imply that ime is in NP. We prove that ime is NP-complete by reduction from dpdc. Assume that we are given an instance of dpdc such that $h=0$ and $\ell _i(a) \in \{0,1\}$ for every integer i in $\{1,2\}$ and every arc a in L. Then, we construct an instance of ime as follows. Define $V := N \cup \{s^{*}\}$, where $s^{*}$ is a new vertex. Define $A := L \cup \{a_1,a_2\}$, where $a_1$ and $a_2$ are new arcs from $s^{*}$ to $v^+$. Define $S := \{s^{*}\}$ and $T := \{v^-\}$. Define $c(a) := 1$ for each arc a in A. For each arc a in A, we define

$$\begin{aligned} \tau _1(a) := {\left\{ \begin{array}{ll} \ell _1(a) &{} \text{ if } a \in L \\ 0 &{} \text{ if } a = a_1 \\ 1 &{} \text{ if } a = a_2 \end{array}\right. } \ \ \ \ \ \ \ \tau _2(a) := {\left\{ \begin{array}{ll} \ell _2(a) &{} \text{ if } a \in L \\ 1 &{} \text{ if } a = a_1 \\ 0 &{} \text{ if } a = a_2. \end{array}\right. } \end{aligned}$$

Define $b(s^{*}) := 2$ and $u(v^-) := -2$. Define $q_1 := 1$, $q_2 := 1$, and $\mathrm{\Theta } := 0$.

Assume that there are arc-disjoint simple directed paths $P_1,P_2$ in G from $v^+$ to $v^-$ such that $\ell _1(P_1) + \ell _2(P_2) \le 0$. Since $\ell _i(a) \ge 0$ for every integer i in $\{1,2\}$ and every arc a in L, we have $\ell _1(P_1) = \ell _2(P_2) = 0$. For each integer i in $\{1,2\}$, we define a directed path $P^+_i$ in D as the directed path obtained by adding $a_i$ to $P_i$. Since $P_1$ and $P_2$ are arc-disjoint, $P_1^+$ and $P^+_2$ are arc-disjoint. Furthermore, for every integer i in $\{1,2\}$, since $\ell _i(P_i) = 0$ and $\tau _i(a_i) = 0$, we have $\tau _i(P_i^+) = 0$. For each integer i in $\{1,2\}$, we define $d_i(s^{*}) := 1$ and $d_i(v^-) := -1$. In addition, for each integer i in $\{1,2\}$, we define a vector $w_i$ in $\mathbb {Z}^A_+$ as follows. If $a \in P_i^+$, then we define $w_i(a) := 1$. Otherwise, we define $w_i(a) := 0$. Since $P_1^+$ and $P_2^+$ are arc-disjoint, $w_1(a) + w_2(a) \le 1 = c(a)$ for every arc a in A. Thus, $(d_1,d_2,w_1,w_2)$ is a feasible assignment.

Next we assume that there exists a feasible assignment $(d_1,d_2,w_1,w_2)$ such that $d_1, d_2 \in \mathbb {Z}^{S \cup T}$ and $w_1,w_2 \in \mathbb {Z}_+^A$. Since $\tau _1(a_2) = \tau _2(a_1) = 1$, $c(a_1) = c(a_2) = 1$, and $\mathrm{\Theta }=0$, we have $d_1(s^{*}) = d_2(s^{*}) = 1$. Since $c(a) =1$ for every arc a in A, we have $w_1(a), w_2(a) \in \{0,1\}$ and at most one of $w_1(a)$ and $w_2(a)$ is equal to 1 for every arc a in A. For each integer i in $\{1,2\}$, we denote by $L_i$ the sets of arcs a in A such that $w_i(a) = 1$. Then, $L_1$ and $L_2$ are disjoint. For every integer i in $\{1,2\}$, since $d_i(s^{*}) = 1$ and $\mathrm{\Theta } = 0$, $L_i$ contains a simple directed path $L_i^{\prime }$ from $s^{*}$ to $v^-$ such that $\tau _i(L_i^{\prime }) = 0$ as a subset. Furthermore, for every integer i in $\{1,2\}$, the definition of $\tau _i$, we have $a_i \in L_i^{\prime }$. For each integer i in $\{1,2\}$, let $P_i$ be the directed path obtained by removing $a_i$ from $L_i^{\prime }$. Then, for every integer i in $\{1,2\}$, we have $\ell _i(P_i) = 0$. This completes the proof.    $\square$

4.2 Integral Supplies and Sink Capacities

Here we consider problems of finding an integral allocation of supplies and sink capacities. We consider Integral Mixed Evacuation with Arc Capacities (imeac for short) defined as follows. We are given vectors $w_1,w_2 \in \mathbb {Z}_+^A$ such that $w_1(a) + w_2(a) \le c(a)$ for every arc a in A. Then, the goal is to decide whether there exists a feasible assignment $(d_1,d_2,w_1,w_2)$ such that $d_1,d_2 \in \mathbb {Z}^{S \cup T}$. We prove that imeac can be solved in polynomial time. In the rest of this section, we define $o_i := o_i^{w_i}$ for each integer i in $\{1,2\}$. For each finite set U, each function $g :2^U \rightarrow \mathbb {R}$, and each pair of subsets $P_1,P_2$ of $\mathbb {R}^U$, we define $\mathrm{P}(g) := \{x \in \mathbb {R}^U \mid x(X) \le g(X) \ (\forall X \subseteq U)\}$ and $P_1 + P_2 := \{x + y \mid x \in P_1, \, y \in P_2\}$. Then, Theorem 1 implies that imeac can be formulated as the following problem P2.

$$\begin{aligned} \begin{array}{cl} \text{ Maximize } \ \ &{} \ d_1(S) + d_2(S) \\ \text{ subject } \text{ to } \ \ \ &{} \ d_1(v) \ge 0, \ d_2(v) \ge 0 \ \ \ \ (v \in S) \\ &{} \ d_1(v) \le 0, \ d_2(v) \le 0 \ \ \ \ (v \in T) \\ &{} \ u^{\circ }(v) \le d_1(v) + d_2(v) \le b^{\circ }(v) \ \ \ \ (v \in S \cup T) \\ &{} \ d_1 \in \mathrm{P}(o_1), \ d_2 \in \mathrm{P}(o_2), \ d_1, d_2 \in \mathbb {Z}^{S \cup T}. \end{array} \end{aligned}$$

If the optimal objective value is equal to b(S), then we can conclude that there exists a desired assignment. Otherwise, there exists no such an assignment.

Assume that we are given an integer i in $\{1,2\}$. Define $o_i^- :2^{S \cup T} \rightarrow \mathbb {R}_+$ by setting $o_i^-(X)$ to be the minimum value of $o_i(Y)$ over all subsets Y of X such that $X \cap S \subseteq Y$. Let X be a subset of $S \cup T$. Define a function $o_{i,X} :2^{X\!\setminus \!S} \rightarrow \mathbb {R}$ by setting $o_{i,X}(Y) := o_i(Y \cup (X \cap S)) - o_i(X\cap S)$. It is not difficult to see that $o_{i,X}$ is submodular and $o_i^-(X) = \min \{o_{i,X}(Y) \mid Y \subseteq X\!\setminus \!S\} + o_i(X\cap S)$. That is, we can evaluate $o_i^-(X)$ by evaluating the value of $o_i$ and using the algorithm for submodular function minimization. It is known [10, Eq. (3.10)] that $o_i^-$ is a submodular function. Furthermore, it is known [10, Theorem 3.3] that $\mathrm{P}(o_i^-)$ is equal to the set of vectors d in $\mathrm{P}(o_i)$ such that $d(v) \le 0$ for every vertex v in T. Thus, P2 is equivalent to the following problem.

$$\begin{aligned} \begin{array}{cl} \text{ Maximize } \ \ &{} \ d_1(S) + d_2(S) \\ \text{ subject } \text{ to } \ \ \ &{} \ d_1(v) \ge 0, \ d_2(v) \ge 0 \ \ \ \ (v \in S) \\ &{} \ u^{\circ }(v) \le d_1(v) + d_2(v) \le b^{\circ }(v) \ \ \ \ (v \in S \cup T) \\ &{} \ d_1 \in \mathrm{P}(o_1^-), \ d_2 \in \mathrm{P}(o_2^-), \ d_1, d_2 \in \mathbb {Z}^{S \cup T}. \end{array} \end{aligned}$$

We consider the following problem P3.

$$\begin{aligned} \begin{array}{cl} \text{ Maximize } \ \ &{} \ d_1(S) + d_2(S) \\ \text{ subject } \text{ to } \ \ \ &{} \ u^{\circ }(v) \le d_1(v) + d_2(v) \le b^{\circ }(v) \ \ \ \ (v \in S \cup T) \\ &{} \ d_1 \in \mathrm{P}(o_1^-), \ d_2 \in \mathrm{P}(o_2^-), \ d_1, d_2 \in \mathbb {Z}^{S \cup T}. \end{array} \end{aligned}$$

Lemma 1

The optimal objective values of P2 and P3 are the same.

Proof

For each optimal solution $(d_1,d_2)$ of P3, we define $\gamma (d_1,d_2)$ as the number of pairs (i, v) of an integer i in $\{1,2\}$ and a vertex v in S such that $d_i(v) < 0$. Let $(d_1,d_2)$ be an optimal solution of P3 minimizing $\gamma (d_1,d_2)$ among all optimal solutions of P3. If $\gamma (d_1,d_2) = 0$, then since P3 is a relaxation problem of P2, $(d_1,d_2)$ is clearly an optimal solution of P2, and thus the proof is done. Assume that $\gamma (d_1,d_2) \ge 1$. Let (i, v) be a pair of an integer i in $\{1,2\}$ and a vertex v in S such that $d_i(v) < 0$. We assume that $i = 1$ (we can treat the case of $i = 2$ in the same way). For proving this lemma by contradiction, we prove that there exists an optimal solution $(d^{\prime }_1,d^{\prime }_2)$ of P3 such that $\gamma (d_1,d_2) > \gamma (d^{\prime }_1,d^{\prime }_2)$. This contradicts the definition of $(d_1,d_2)$, and thus this completes the proof.

Define vectors $d^{\prime }_1,d^{\prime }_2$ in $\mathbb {Z}^{S \cup T}$ as follows. Define $d^{\prime }_1(v^{\prime }) := d_1(v^{\prime })$ and $d^{\prime }_2(v^{\prime }) := d_2(v^{\prime })$ for each vertex $v^{\prime }$ in $(S \cup T)\!\setminus \!\{v\}$. Furthermore, define $d^{\prime }_1(v) := 0$ and $d^{\prime }_2(v) := \min \{d_2(v), b(v)\}$. We first prove that $d_1(v) + d_2(v) \le d^{\prime }_1(v) + d^{\prime }_2(v)$. If $d^{\prime }_2(v) = d_2(v)$, then since $d_1(v) < 0$, this clearly holds. If $d_2(v) = b(v)$, then since $d_1(v) + d_2(v) \le b(v)$, this clearly holds. This implies that the objective value of $(d^{\prime }_1,d^{\prime }_2)$ is no less than that of $(d_1,d_2)$. Thus, what remains is to prove that $(d^{\prime }_1,d^{\prime }_2)$ is a feasible solution of P3. The above inequality implies that $(d^{\prime }_1,d^{\prime }_2)$ satisfies the first constraint of P3. In addition, $d^{\prime }_2$ clearly belongs to $\mathrm{P}(o^-_2)$. Thus, it suffices to prove that $d^{\prime }_1 \in \mathrm{P}(o_1^-)$. Assume that this does not hold. Then, there exists a subset of X of $S \cup T$ such that $v \in X$ and $o_1^-(X) - d_1(X) < -d_1(v)$. Since it is not difficult to see that $o_1(Y\!\setminus \!\{v\}) \le o_1(Y)$ for every subset Y of X such that $X \cap S \subseteq Y$, $o_1^-(X\!\setminus \!\{v\}) \le o_1^-(X)$. Thus, $o^-_1(X\!\setminus \!\{v\}) < d_1(X\!\setminus \!\{v\})$, which contradicts that $d_1 \in \mathrm{P}(o_1^-)$. This completes the proof.    $\square$

Lemma 2

For every integer i in $\{1,2\}$ and every subset X of $S \cup T$, we have $o_i(X) \in \mathbb {Z}$, which implies that $o_i^-(X) \in \mathbb {Z}$.

Proof

This lemma follows from Theorem 2 and [11, Theorem 12.8].    $\square$

Theorem 8

(E.g., [11, Corollary 46.2c]). Assume that we are given a finite set U and submodular functions $\sigma , \pi :2^U \rightarrow \mathbb {Z}$ such that $\sigma (\emptyset ) = \pi (\emptyset ) = 0$. Then, we have $(\mathrm{P}(\sigma ) \cap \mathbb {Z}^U) + (\mathrm{P}(\pi ) \cap \mathbb {Z}^U) = (\mathrm{P}(\sigma ) + \mathrm{P}(\pi )) \cap \mathbb {Z}^U$.³

Lemmas 1, 2 and Theorem 8 imply that P2 is equivalent to the following problem.

$$\begin{aligned} \begin{array}{cl} \text{ Maximize } \ \ &{} \ d(S) \\ \text{ subject } \text{ to } \ \ &{} \ u^{\circ }(v) \le d(v) \le b^{\circ }(v) \ \ \ \ (v \in S \cup T) \\ &{} \ d \in \mathrm{P}(o_1^-) + \mathrm{P}(o_2^-), \ d \in \mathbb {Z}^{S \cup T}. \end{array} \end{aligned}$$

Theorem 9

(E.g., [11, Theorem 44.6]). Assume that we are given a finite set U and submodular functions $\sigma , \pi :2^U \rightarrow \mathbb {Z}$ such that $\sigma (\emptyset ) = \pi (\emptyset ) = 0$. Then, we have $\mathrm{P}(\sigma ) + \mathrm{P}(\pi ) = \mathrm{P}(\sigma + \pi )$.⁴

Theorem 9 implies that P2 is equivalent to the following problem.

$$\begin{aligned} \begin{array}{cl} \text{ Maximize } \ \ &{} \ d(S) \\ \text{ subject } \text{ to } \ \ &{} \ u^{\circ }(v) \le d(v) \le b^{\circ }(v) \ \ \ \ (v \in S \cup T) \\ &{} \ d \in \mathrm{P}(o_1^- + o_2^-), \ d \in \mathbb {Z}^{S \cup T}. \end{array} \end{aligned}$$

We consider the following relaxation problem LP2 of P2.

$$\begin{aligned} \begin{array}{cl} \text{ Maximize } \ \ &{} \ d(S) \\ \text{ subject } \text{ to } \ \ &{} \ u^{\circ }(v) \le d(v) \le b^{\circ }(v) \ \ \ \ (v \in S \cup T) \\ &{} \ d \in \mathrm{P}(o_1^- + o_2^-). \end{array} \end{aligned}$$

Lemma 3

The optimal objective values of P2 and LP2 are the same.

Proof

Since $o_1^-,o_2^-$ are submodular functions, $o_1^- + o_2^-$ is a submodular function. Furthermore, Lemma 2 implies that $o_1^-(X) + o_2^-(X) \in \mathbb {Z}$ for every subset X of $S \cup T$. Thus, this lemma follows from [11, Corollary 44.3c] (i.e., the box-total dual integrality of the constraints corresponding to $\mathrm{P}(o_1^- + o_2^-)$).    $\square$

Theorem 10

The problem imeac can be solved in polynomial time.

Proof

In the same way as the algorithm described after Theorem 6, we can check in polynomial time whether $d \in \mathrm{P}(o_1^- + o_2^-)$ for a given vector d in $\mathbb {R}^{S \cup T}$ by minimizing the submodular function $o_1^- + o_2^- - d$. In addition, we can check in polynomial time whether a given vector d in $\mathbb {R}^{S \cup T}$ satisfies the first constraint of LP2. Thus, we can solve the separation problem for LP2 by using Theorem 4 in polynomial time (if $d \notin \mathrm{P}(o_1^- + o_2^-)$, then a separating hyperplane can be obtained from a minimizer of $o_1^- + o_2^- -d$). This implies that we can solve imeac in polynomial time by using the results of [12] (see also [13, Theorem 6.36]).    $\square$

4.3 Unsplittable Supplies and Sink Capacities

Here we consider the following variant of imeac called Unsplittable Mixed Evacuation with Arc Capacities (umeac for short). In this problem, we are given vectors $w_1,w_2 \in \mathbb {Z}_+^A$ such that $w_1(a) + w_2(a) \le c(a)$ for every arc a in A. The goal is to decide whether there exists a feasible assignment $(d_1,d_2,w_1,w_2)$ such that $d_1(v),d_2(v) \in \{0,b(v)\}$ for every vertex v in S and $d_1(v),d_2(v) \in \{0,u(v)\}$ for every vertex v in T. In what follows, we prove that umeac is NP-complete. Notice that if $|S \cup T| \le C \log _2 n$ for some constant C, then it follows from Theorems 1, 4, 5, and 6 that umeac can be solved in polynomial time by enumerating all subsets of $S\cup T$. We will prove the NP-completeness of umeac by reduction from Partition. In this problem, we are given a finite set I and a vector $\pi$ in $\mathbb {Z}_+^I$ such that $\pi (I)$ is even. Then, the goal is to decide whether there exists a subset J of I such that $\pi (J) = \pi (I\!\setminus \!J)$. It is well known [14] that Partition is NP-complete.

Theorem 11

The problem umeac is NP-complete.

Proof

In the same ways as the proof of Theorem 7, we can prove that umeac is in NP. We prove that the NP-completeness of umeac by reduction from Partition. Assume that we are given an instance of Partition, and then we construct an instance of umeac as follows. Define $V := \{v_i \mid i \in I\} \cup \{v^{\circ },v^{\bullet },v^{*}_1,v^{*}_2\}$ and $A := \{(v_i,v^{\circ }), (v_i,v^{\bullet }) \mid i \in I\} \cup \{(v^{\circ }, v^{*}_1), (v^{\bullet }, v^{*}_2)\}$. Define $S := \{v_i \mid i \in I\}$ and $T := \{v^{*}_1,v^{*}_2\}$. Define $c(a) := 1$, $\tau _1(a) := 0$, and $\tau _2(a) := 0$ for each arc a in A. Define $b(v_i) := \pi (i)$ for each element i in I. Define $u(v^{*}_1) := -\pi (I)$ and $u(v^{*}_2) := -\pi (I)$. Define $q_1 :=1$ and $q_2 := 1$. Define $\mathrm{\Theta } := (\pi (I) / 2) - 1$. Lastly, we define vectors $w_1, w_2$ in $\mathbb {Z}_+^A$ as follows. For each arc $a = (x,y)$ in A, we define

$$\begin{aligned} w_1(a) := {\left\{ \begin{array}{ll} 1 &{} \text{ if } x = v^{\circ } \text{ or } y=v^{\circ }\\ 0 &{} \text{ otherwise } \end{array}\right. } \ \ \ \ \ \ w_2(a) := {\left\{ \begin{array}{ll} 1 &{} \text{ if } x = v^{\bullet } \text{ or } y = v^{\bullet }\\ 0 &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

Assume that there exists a subset J of I such that $\pi (J) = \pi (I\!\setminus \!J)$. Then, we define vectors $d_1,d_2$ in $\mathbb {Z}^{S \cup T}$ by

$$\begin{aligned} d_1(v) \ \text{(resp., } d_2(v)\text{) } := {\left\{ \begin{array}{ll} \pi (i) \ \text{(resp., } \text{0) }&{} \text{ if } v = v_i \text{ for } \text{ some } i \in J \\ 0 \ \text{(resp., } \pi (i)\text{) }&{} \text{ if } v = v_i \text{ for } \text{ some } i \in I\!\setminus \!J \\ -\pi (I) \ \text{(resp., } \text{0) }&{} \text{ if } v = v^{*}_1 \\ 0 \ \text{(resp., } -\pi (I)\text{) }&{} \text{ if } v = v^{*}_2. \end{array}\right. } \end{aligned}$$

Since $\pi (J) = \pi (I\!\setminus \!J) = \pi (I)/2$, $(d_1,d_2,w_1,w_2)$ is a feasible assignment.

Conversely, we assume that there exists a feasible assignment $(d_1,d_2,w_1,w_2)$ such that $d_1(v),d_2(v) \in \{0,b(v)\}$ for every vertex v in S and $d_1(v),d_2(v) \in \{0,u(v)\}$ for every vertex v in T. Since $\mathrm{\Theta } = (\pi (I)/2) - 1$, we have $d_1(S) = \pi (I) /2$ and $d_2(S) = \pi (I) /2$. Thus, if we define J as the set of elements i in I such that $d_1(v_i) = b(v_i)$, then $\pi (J) = \pi (I\!\setminus \!J)$. This completes the proof.    $\square$

5 Case Study

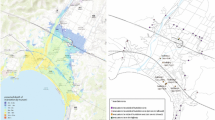
Here we apply our model to the case study of Minabe town in Wakayama prefecture, which was designated as those in which safe evacuation from tsunami is difficult when Nankai Trough Earthquake occurs. The population of Minabe town is about 12000. According to the census data of 2013, the number of people living in the tsunami inundation area of this town is 4745. The left figure of Fig. 1 shows the map of this area and the expected height of the tsunami caused by Nankai Trough Earthquake. The town is surrounded by mountains of height ranging from 100 to 200 m.

Fig. 1.

(Left) The target area and its inundation depth. (Right) The road network in the target areas and evacuation sites.

It is predicted that in twelve minutes after that earthquake occurs, the first tsunami of height 1 m arrives, and then that of height 5m (and of 10 m, respectively) will arrive after 15 min (and 24 min, respectively). Since people usually start evacuation five minutes after the earthquake occurs, the actual time remaining for evacuation is from five to fifteen minutes depending on where they live. Since there are not enough evacuation buildings in the center of the town, most of the people will have to go to the outside of the tsunami inundation area, and thus some of them may not succeed to evacuate to a safety place.

Under this circumstance, we consider the following experiments. Our computational experiment aims at the inundation area of Minabe town whose population is 4745. We prepare two scenarios. The first one is that people should have to evacuate to the outside of the inundation area. The second is that people should have to evacuate to the outside of the inundation area or to tsunami evacuation buildings located inside of the inundation area. There exist six evacuation buildings inside the inundation area (numbered from 1 through 6 in the right figure of Fig. 1) whose sizes (i.e., the maximum number of evacuees that can be accommodated) are 1472, 2000, 1128, 3014, 654 and 454, respectively. We constructed a model of a dynamic network by using the GIS databases: the fundamental map information (1/2500, the Geospatial Information Authority of Japan), the population census (2010, the Ministry of Internal Affairs and Communications of Japan), and the Japan digital road map (Japan Digital Road Map Association). The road network has 860 nodes and 1,106 arcs.

We assign to a sink vertex the capacity of the evacuation site located at the vertex, i.e., the maximum number of evacuees that the site accommodates. In our experiment, the capacity of a building was computed based on the available floor space, assuming that two persons per m$^2$ can be accommodated. The capacity of an evacuation site which is outside the tsunami inundation area is assumed to be infinity. However, since a hill top may have an upper limit on the number of evacuees that can be accommodated, its capacity is estimated based on an aerial photograph. Evacuation by cars is only possible to the outside of the tsunami inundation area, and thus is assumed to be not allowed to tsunami evacuation buildings or hill tops. Since there are not enough tsunami evacuation buildings, the delay of evacuation is predicted. (In our experiment, we solve me by using a linear programming solver. Thus, we can add additional constraints to our model. Furthermore, the minimum evacuation completion time can be computed by the binary search.)

5.1 Computational Results

We use Gurobi Optimizer (see http://www.gurobi.com/) as the solver to solve linear programs corresponding to our experimental data.

As seen from Table 1, in each scenario, the result for the case where cars are allowed to use is much better in the minimum evacuation completion time than the one where they are not allowed. Comparing the scenario 2 with the scenario 1, the number of evacuees who walked to the evacuation site increased since evacuation buildings located in the town center can be used in the scenario 2.

Table 1. Computational results of each scenario.

Fig. 2.

(Left) The transition of the accumulated number of evacuees that completed evacuation in the scenario 1. (Right) The transition of the accumulated number of evacuees that completed evacuation in the scenario 2.

Fig. 3.

(Left) Distribution of evacuees that used cars in the scenario 1. (Right) Distribution of evacuees that used cars in the scenario 2. (Color figure online)

Fig. 4.

(Left) The number of evacuees that arrived at each evacuation site, and the ratio of evacuees who arrived at the site by walking and those who arrived there by a car in the scenario 1 (Right) The number of evacuees that arrived at each evacuation site, and the ratio of evacuees who arrived at the site by walking and those who arrived there by a car in the scenario 2.

Now let us look at Fig. 2 that shows how the number of evacuees that have completed evacuation increases as time proceeds since the evacuation starts. It is observed that in the latter half for the whole time period, the number of evacuees that completed evacuation rapidly increases in both scenarios. Ideally, it is desired that the number of evacuees that completed evacuation is large in the early stage. This point should be taken into account in order to improve the current model.

Let us look at the way of evacuation (by walking or a car) at each vertex. In Fig. 3, if the color at each vertex is close to blue, it means that a majority of people used cars for evacuation while on the other hand, if it is close to red, a majority of people walked for evacuation. Comparing the scenarios 1 and 2, the car usage significantly decreased in the scenario 2 near the coast since there are evacuation buildings nearby.

Figure 4 shows the number of evacuees that arrived at each evacuation site, and the ratio of evacuees who arrived at the site by walking and those who arrived there by a car. In the scenario 1, for most of evacuation sites, the number of evacuees who arrived by cars exceeds that of evacuees who arrived by walking. On the other hand in the scenario 1, many evacuees living near the town center evacuated to evacuation buildings inside the inundation area.

6 Conclusion

In this paper, we introduce the mixed evacuation problem that is motivated by making an evacuation plan in an emergent situation in which people can evacuation on foot or by car. We study this problem from the theoretical and practical viewpoints. An apparent future work from the theoretical viewpoint is to reveal the computational complexity of the mixed evacuation problem in the general case. From the practical viewpoint, it is a future work to apply our model to areas other than Minabe town. There exist many small towns on the coastal area facing the Pacific Ocean whose local governments are faced with a serious problem that they have to spend a significant percentage of their budget for building a tsunami evacuation buildings in order to reduce the loss of human lives from tsunami triggered by Nankai Trough Earthquake that are expected to occur with 70 % within the coming 30 years [1]. In this respect, we hope that the methods developed for facility location problems will help to reduce the budget to be used for such disaster prevention.