Safe Sets in Graphs: Graph Classes and Structural Parameters

Abstract

A safe set of a graph $G=(V,E)$ is a non-empty subset S of V such that for every component A of G[S] and every component B of $G[V \setminus S]$, we have $|A| \ge |B|$ whenever there exists an edge of G between A and B. In this paper, we show that a minimum safe set can be found in polynomial time for trees. We then further extend the result and present polynomial-time algorithms for graphs of bounded treewidth, and also for interval graphs. We also study the parameterized complexity of the problem. We show that the problem is fixed-parameter tractable when parameterized by the solution size. Furthermore, we show that this parameter lies between tree-depth and vertex cover number.

1 Introduction

In this paper, we only consider finite and simple graphs. The subgraph of a graph G induced by $S \subseteq V (G)$ is denoted by G[S]. A component of G is a connected induced subgraph of G with an inclusionwise maximal vertex set. For vertex-disjoint subgraphs A and B of G, if there is an edge between A and B, then A and B are adjacent.

In a graph $G = (V,E)$, a non-empty set $S \subseteq V$ of vertices is a safe set if, for every component A of G[S] and every component B of $G[V \setminus S]$ adjacent to A, it holds that $|A| \ge |B|$. If a safe set induces a connected subgraph, then it is a connected safe set. The safe number $\mathsf {s}(G)$ of G is the size of a minimum safe set of G, and the connected safe number $\mathsf {cs}(G)$ of G is the size of a minimum connected safe set of G. It is known that $\mathsf {s}(G) \le \mathsf {cs}(G) \le 2 \cdot \mathsf {s}(G) - 1$ [10].

The concept of (connected) safe number was introduced by Fujita et al. [10]. Their motivation came from a variant of facility location problems, where the goal is to find a “safe” subset of nodes in a network to place facilities. They showed that the problems of finding a minimum safe set and a minimum connected safe set are NP-hard in general. They also showed that a minimum connected safe set in a tree can be found in linear time.

The main contribution of this paper is to give polynomial-time algorithms for finding a minimum safe set on trees, graphs of bounded treewidth, and interval graphs. We also show that the problems are fixed-parameter tractable when parameterized by the solution size.

The rest of the paper is organized as follows. In Sect. 2, we present an $O(n^{5})$-time algorithm for finding a minimum safe set on trees. In Sect. 3, we generalize the algorithm to make it work on graphs of bounded treewidth. In Sect. 4, we show that the problem can be solved in $O(n^{8})$ time for interval graphs. In Sect. 5, we show the fixed-parameter tractability of the problem when the parameter is the solution size. We also discuss the relationship of safe number to other important and well-studied graph parameters. In the final section, we conclude the paper with a few open problems.

2 Safe Sets in Trees

Recall that a tree is a connected graph with no cycles. In this section, we prove the following theorem.

Theorem 2.1

For an n-vertex tree, a safe set of the minimum size can be found in time $O(n^{5})$.

We only show that the size of a minimum safe set can be computed in $O(n^{5})$ time. It is straightforward to modify the dynamic program below for computing an actual safe set in the same running time.

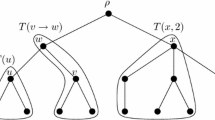
In the following, we assume that a tree $T = (V,E)$ has a root and that the children of each vertex are ordered. For a vertex $u \in V$, we denote the set of children of u by $C_{T}(u)$. By $V_{u}$ we denote the vertex set that consists of u and its descendants. We define some subtrees induced by special sets of vertices as follows (see Fig. 1):

• For a vertex $u \in V$, let $T(u) = T[V_{u}]$.

• For an edge $\{u, v\} \in E$ where v is the parent of u, let $T(u \rightarrow v) = T[\{v\} \cup V_{u}]$.

• For $u \in V$ with children $w_{1}, \dots , w_{d}$, let $T(u,i) = T \left[ \{u\} \cup \bigcup _{1 \le j \le i} V_{w_{j}} \right]$.

Note that $T(u,1) = T(w_{1} \rightarrow u)$ if $w_{1}$ is the first child of u, $T(u) = T(u, |C_{T}(u)|)$ if u is not a leaf, and $T = T(\rho )$ if $\rho$ is the root of T.

Fig. 1.

Subtrees T(u), $T(v \rightarrow w)$, and T(x, 2).

Fragments: For a subtree $T'$ of T and $S \subseteq V(T')$, a fragment in $T'$ with respect to S is the vertex set of a component in $T'[S]$ or $T'[V(T') \setminus S]$. We denote the set of fragments in $T'$ with respect to S by $\mathcal {F}(T',S)$. The fragment that contains the root of $T'$ is active, and the other fragments are inactive. Two fragments in $\mathcal {F}(T', S)$ are adjacent if there is an edge of $T'$ between them. A fragment $F \in \mathcal {F}(T', S)$ is bad if it is inactive, $F \subseteq S$, and there is another inactive fragment $F' \in \mathcal {F}(T', S)$ adjacent to F with $|F| < |F'|$.

$(T', \mathsf {b}, s, a)-feasible sets$ : For $\mathsf {b}\in \{\mathsf {t}, \mathsf {f}\}$, $s \in \{0,\dots ,n\}$, and $a \in \{1,\dots ,n\}$, we say $S \subseteq V(T')$ is $(T', \mathsf {b}, s, a)$ -feasible if $|S| = s$, the size of the active fragment in $\mathcal {F}(T', S)$ is a, there is no bad fragment in $\mathcal {F}(T', S)$, and $\mathsf {b}= \mathsf {t}$ if and only if the root of $T'$ is in S.

Intuitively, a $(T', \mathsf {b}, s, a)$-feasible set S is “almost safe.” If A is the active fragment in $\mathcal {F}(T', S)$, then $S \setminus A$ is a safe set of $T'[V(T') \setminus A]$.

For $S \subseteq V(T')$, we set $\partial _{T'}^{\max }(S)$ and $\partial _{T'}^{\min }(S)$ to be the sizes of maximum and minimum fragments, respectively, adjacent to the active fragment in $\mathcal {F}(T',S)$. If there is no adjacent fragment, then we set $\partial _{T'}^{\max }(S) = -\infty$ and $\partial _{T'}^{\min }(S) = +\infty$.

DP Table: We construct a table with values $\mathsf {ps}(T', \mathsf {b}, s, a) \in \{0,\dots ,n\} \cup \{+\infty ,-\infty \}$ for storing information of partial solutions, where $\mathsf {b}\in \{\mathsf {t}, \mathsf {f}\}$, $s \in \{0,\dots ,n\}$, and $a \in \{1,\dots ,n\}$, and $T'$ is a subtree of T such that either $T' = T(u)$ for some $u \in V$, $T' = T(u \rightarrow v)$ for some $\{u,v\} \in E$, or $T' = T(u, i)$ for some $u \in V$ and $1 \le i \le |C_{T}(u)|$. The table entries will have the following values:

$$\begin{aligned} \mathsf {ps}(T', \mathsf {t}, s, a)&= {\left\{ \begin{array}{ll} +\infty &{} \text {if no } (T', \mathsf {t}, s, a)\text {-feasible set exists}, \\ \displaystyle \min _{(T', \mathsf {t}, s, a)\text {-feasible } S} \partial _{T'}^{\max }(S) &{} \text {otherwise}, \end{array}\right. }\\ \mathsf {ps}(T', \mathsf {f}, s, a)&= {\left\{ \begin{array}{ll} -\infty &{} \text {if no } (T', \mathsf {f}, s, a)\text {-feasible set exists}, \\ \displaystyle \max _{(T', \mathsf {f}, s, a)\text {-feasible } S} \partial _{T'}^{\min }(S) &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

The definition of the table $\mathsf {ps}$ implies the following fact.

Lemma 2.2

$\mathsf {s}(T)$ is the smallest s such that there is $a \in \{1,\dots ,n\}$ with $\mathsf {ps}(T, \mathsf {t}, s, a) \le a$ or $\mathsf {ps}(T, \mathsf {f}, s, a) \ge a$.

Proof

Assume that S is a safe set of T such that $|S| = s$ and the root is contained in S. Let A be the active fragment in $\mathcal {F}(T,S)$. Then, S is $(T, \mathsf {t}, s, |A|)$-feasible. Since A cannot be smaller than any adjacent fragment, we have $\partial _{T}^{\max }(S) \le |A|$. Hence $\mathsf {ps}(T, \mathsf {t}, s, |A|) \le |A|$ holds. By a similar argument, we can show that if the root is not in S, then $\mathsf {ps}(T, \mathsf {f}, s, |A|) \ge |A|$.

Conversely, assume that $\mathsf {ps}(T, \mathsf {t}, s, a) \le a$ for some $a \in \{1,\dots ,n\}$. (The proof for the other case, where $\mathsf {ps}(T, \mathsf {f}, s, a) \ge a$, is similar.) Let S be a $(T, \mathsf {t}, s, a)$-feasible set with $\partial _{T}^{\max }(S) = \mathsf {ps}(T, \mathsf {t}, s, a)$. Since there is no bad fragment in $\mathcal {F}(T,S)$ and the active fragment (of size a) is not smaller than the adjacent fragments (of size at most $\partial _{T}^{\max }(S) = \mathsf {ps}(T, \mathsf {t}, s, a) \le a$), all fragments included in S are not smaller than their adjacent fragments. This implies that S is a safe set of size s.    $\square$

By Lemma 2.2, after computing all entries $\mathsf {ps}(T', \mathsf {b}, s, a)$, we can compute $\mathsf {s}(T)$ in time $O(n^{2})$. There are $O(n^{3})$ tuples $(T', \mathsf {b}, s, a)$, and thus to prove the theorem, it suffices to show that each entry $\mathsf {ps}(T', \mathsf {b}, s, a)$ can be computed in time $O(n^{2})$ assuming that the entries for all subtrees of $T'$ are already computed.

We compute all entries $\mathsf {ps}(T', \mathsf {b}, s, a)$ in a bottom-up manner: We first compute the entries for T(u) for each leaf u. We then repeat the following steps until none of them can be applied. (1) For each u such that the entries for T(u) are already computed, we compute the entries for $T(u \rightarrow v)$, where v is the parent of u. (2) For each u such that the entries for $T(u, i-1)$ and $T(w_{i} \rightarrow u)$ are already computed, where $w_{i}$ is the ith child of u, we compute the entries for T(u, i).

Lemma 2.3

For a leaf u of T, each table entry $\mathsf {ps}(T(u), \mathsf {b}, s, a)$ can be computed in constant time.

Proof

The set $\{u\}$ is the unique $(T(u), \mathsf {t}, 1, 1)$-feasible set. Since $\mathcal {F}(T(u), \{u\})$ contains no inactive fragment, we set $\mathsf {ps}(T(u), \mathsf {t}, 1, 1) = - \infty$. Similarly the empty set is the unique $(T(u), \mathsf {f}, 0, 1)$-feasible set. We set $\mathsf {ps}(T(u), \mathsf {f}, 0, 1) = + \infty$. For the other tuples, there are no feasible sets. We set the values accordingly for them. Clearly, each entry can be computed in constant time.    $\square$

Lemma 2.4

For a vertex u and its parent v in T, each table entry $\mathsf {ps}(T(u \rightarrow v), \mathsf {b}, s, a)$ can be computed in O(n) time, using the table entries for the subtree T(u).

Proof

We separate the proof into two cases: $a \ge 2$ and $a = 1$. If $a \ge 2$, then we can compute the table entry in constant time. If $a = 1$, we need O(n) time.

Case 1: $a \ge 2$. In this case, for every $(T(u \rightarrow v), \mathsf {b}, s, a)$-feasible set S, u and v are in the active fragment of $\mathcal {F}(T(u \rightarrow v), S)$ since the root v of $T(u \rightarrow v)$ has the unique neighbor u.

Case 1-1: $\mathsf {b}= \mathsf {t}$. Let S be a $(T(u \rightarrow v), \mathsf {t}, s, a)$-feasible set that minimizes $\partial _{T(u \rightarrow v)}^{\max }(S)$. Observe that $S \setminus \{v\}$ is $(T(u), \mathsf {t}, s-1, a-1)$-feasible and that $\partial _{T(u \rightarrow v)}^{\max }(S) = \partial _{T(u)}^{\max }(S \setminus \{v\})$. We claim that $\partial _{T(u)}^{\max }(S \setminus \{v\}) = \mathsf {ps}(T(u), \mathsf {t}, s-1, a-1)$, and thus

$$\begin{aligned} \mathsf {ps}(T(u \rightarrow v), \mathsf {t}, s, a) = \mathsf {ps}(T(u), \mathsf {t}, s-1, a-1). \end{aligned}$$

Suppose that some $(T(u), \mathsf {t}, s-1, a-1)$-feasible set Q satisfies $\partial _{T(u)}^{\max }(Q) < \partial _{T(u)}^{\max }(S \setminus \{v\})$. Now $Q \cup \{v\}$ is $(T(u \rightarrow v), \mathsf {t}, s, a)$-feasible. However, it holds that

$$\begin{aligned} \partial _{T(u \rightarrow v)}^{\max }(Q \cup \{v\}) = \partial _{T(u)}^{\max }(Q) < \partial _{T(u)}^{\max }(S \setminus \{v\}) = \partial _{T(u \rightarrow v)}^{\max }(S). \end{aligned}$$

This contradicts the optimality of S.

Case 1-2: $\mathsf {b}= \mathsf {f}$. Let S be a $(T(u \rightarrow v), \mathsf {f}, s, a)$-feasible set that maximizes $\partial _{T(u \rightarrow v)}^{\min }(S)$. The set S is also $(T(u), \mathsf {f}, s, a-1)$-feasible and satisfies $\partial _{T(u \rightarrow v)}^{\min }(S) = \partial _{T(u)}^{\min }(S)$. We claim that $\partial _{T(u)}^{\min }(S) = \mathsf {ps}(T(u), \mathsf {t}, s, a-1)$, and thus

$$\begin{aligned} \mathsf {ps}(T(u \rightarrow v), \mathsf {f}, s, a) = \mathsf {ps}(T(u), \mathsf {f}, s, a-1). \end{aligned}$$

Suppose that there is a $(T(u), \mathsf {t}, s, a-1)$-feasible set Q with $\partial _{T(u)}^{\min }(Q) > \partial _{T(u)}^{\min }(S)$. Since Q is also $(T(u \rightarrow v), \mathsf {f}, s, a)$-feasible, it holds that

$$\begin{aligned} \partial _{T(u \rightarrow v)}^{\min }(Q) = \partial _{T(u)}^{\min }(Q) > \partial _{T(u)}^{\min }(S) = \partial _{T(u \rightarrow v)}^{\min }(S). \end{aligned}$$

This contradicts the optimality of S.

Case 2: $a = 1.$ For every $(T(u \rightarrow v), \mathsf {b}, s, 1)$-feasible set S, the set $\{v\}$ is the active fragment, and the vertex u is in the unique fragment adjacent to the active fragment.

Case 2-1: $\mathsf {b}= \mathsf {t}$. Let S be a $(T(u \rightarrow v), \mathsf {t}, s, 1)$-feasible set. Then $S \setminus \{v\}$ is a $(T(u), \mathsf {f}, s-1, a')$-feasible set for some $a'$. Moreover, since $\mathcal {F}(T(u \rightarrow v), S)$ does not contain any bad fragment, $\partial _{T(u)}^{\min }(S \setminus \{v\}) \ge a'$. Thus we can set $\mathsf {ps}(T(u \rightarrow v), \mathsf {t}, s, 1)$ as follows:

$$\begin{aligned} \mathsf {ps}(T(u \rightarrow v), \mathsf {t}, s, 1)&= {\left\{ \begin{array}{ll} \min \{a' \mid \mathsf {ps}(T(u), \mathsf {f}, s-1, a') \ge a'\} &{} \text {if such } a' \text { exists},\\ +\infty &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Case 2-2: $\mathsf {b}= \mathsf {f}$. Let S be a $(T(u \rightarrow v), \mathsf {f}, s, 1)$-feasible set. The set S is a $(T(u), \mathsf {t}, s, a')$-feasible set for some $a'$. Since $\mathcal {F}(T(u \rightarrow v), S)$ does not contain any bad fragment, $\partial _{T(u)}^{\max }(S) \le a'$. Thus we can set $\mathsf {ps}(T(u \rightarrow v), \mathsf {f}, s, 1)$ as follows:

$$\begin{aligned} \mathsf {ps}(T(u \rightarrow v), \mathsf {f}, s, 1)&= {\left\{ \begin{array}{ll} \max \{a' \mid \mathsf {ps}(T(u), \mathsf {t}, s, a') \le a' \}&{} \text {if there is such an } a', \\ -\infty &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

In both Cases 2-1 and 2-2, we can compute the entry $\mathsf {ps}(T(u \rightarrow v), \mathsf {b}, s, 1)$ in O(n) time by looking up at most n table entries for the subtree T(u).    $\square$

Lemma 2.5

For a non-leaf vertex u with the children $w_{1}, \dots , w_{d}$ and an integer i with $2 \le i \le d$, each table entry $\mathsf {ps}(T(u,i), \mathsf {b}, s, a)$ can be computed in $O(n^{2})$ time, using the table entries for the subtrees $T(u,i-1)$ and $T(w_{i} \rightarrow u)$.

Proof

For the sake of simplicity, let $T_{1} = T(u,i-1)$ and $T_{2} = T(w_{i} \rightarrow u)$. Let S be a $(T(u,i), \mathsf {b}, s, a)$-feasible set and A be the active fragment in $\mathcal {F}(T(u,i), S)$. For $j \in \{1,2\}$, let $S_{j} = S \cap V(T_{j})$ and $A_{j} = A \cap V(T_{j})$. Observe that $S_{j}$ is a $(T_{j}, \mathsf {b}, |S_{j}|, |A_{j}|)$-feasible set. If $\mathsf {b}= \mathsf {t}$, then $S_{1} \cap S_{2} = \{u\}$; otherwise $S_{1} \cap S_{2} = \emptyset$. Thus $|S_{1}| + |S_{2}| = |S| + 1$ if $\mathsf {b}= \mathsf {t}$, and $|S_{1}| + |S_{2}| = |S|$ otherwise. Similarly, since $A_{1} \cap A_{2} = \{u\}$, it holds that $|A_{1}| + |A_{2}| = |A| + 1$. Therefore, we can set the table entries as follows:

$$\begin{aligned} \mathsf {ps}(T(u,i), \mathsf {t}, s, a)&= \min _{\begin{array}{c} s_{1} + s_{2} = s + 1 \\ a_{1} + a_{2} = a + 1 \end{array}} \max \{\mathsf {ps}(T_{1}, \mathsf {t}, s_{1}, a_{1}), \mathsf {ps}(T_{2}, \mathsf {t}, s_{2}, a_{2})\},\\ \mathsf {ps}(T(u,i), \mathsf {f}, s, a)&= \max _{\begin{array}{c} s_{1} + s_{2} = s \\ a_{1} + a_{2} = a + 1 \end{array}} \min \{\mathsf {ps}(T_{1}, \mathsf {f}, s_{1}, a_{1}), \mathsf {ps}(T_{2}, \mathsf {f}, s_{2}, a_{2})\}. \end{aligned}$$

In both cases, we can compute the entry $\mathsf {ps}(T(u,i), \mathsf {b}, s, a)$ in $O(n^{2})$ time since there are O(n) possibilities for each $(s_{1}, s_{2})$ and $(a_{1}, a_{2})$.    $\square$

A graph is unicyclic if it can be obtained by adding an edge to a tree. Using the algorithm for weighted paths presented in [2] as a subroutine, we can extend the algorithm in this section to find a minimum safe set and a minimum connected safe set of a unicyclic graph in the same running time.

3 Safe Sets in Graphs of Bounded Treewidth

In this section, we show that for any fixed constant k, a minimum safe set and a minimum connected safe set of a graph of treewidth at most k can be found in $O(n^{5k+8})$ time.

Basically, the algorithm in this section is a generalization of the one in the previous section. The most crucial difference is that here we may have many active fragments, and each active fragment may have many vertices adjacent to the “outside.” This makes the algorithm much more complicated and slow.

A tree decomposition of a graph $G = (V,E)$ is a pair $(\{X_{p} \mid p \in I\}, T)$ such that each $X_{p}$, called a bag, is a subset of V, and T is a tree with $V(T) = I$ such that

• for each $v \in V$, there is $p \in I$ with $v \in X_{p}$;

• for each $\{u,v\} \in E$, there is $p \in I$ with $u, v \in X_{p}$;

• for $p,q,r \in I$, if q is on the p–r path in T, then $X_{p} \cap X_{r} \subseteq X_{q}$.

The width of a tree decomposition is the size of a largest bag minus 1. The treewidth of a graph, denoted by $\mathsf {tw}(G)$, is the minimum width over all tree decompositions of G.

A tree decomposition $(\{X_{p} \mid p \in I\}, T)$ is nice if

• T is a rooted tree in which every node has at most two children;

• if a node p has two children q, r, then $X_{p} = X_{q} = X_{r}$ (such a node p is a join node);

• if a node p has only one child q, then either

  • $X_{p} = X_{q} \cup \{v\}$ for some $v \notin X_{q}$ (p is a introduce node), or

  • $X_{p} = X_{q} \setminus \{v\}$ for some $v \in X_{q}$ (q is a forget node);

• if a node p is a leaf, then $X_{p} = \{v\}$ for some $v \in V$.

Theorem 3.1

Let k be a fixed constant. For an n-vertex graph of treewidth at most k, a (connected) safe set of minimum size can be found in time $O(n^{5k+8})$.

Proof

We only show that $\mathsf {s}(G)$ and $\mathsf {cs}(G)$ can be computed in the claimed running time. It is straightforward to modify the dynamic program below for computing an actual set in the same running time.

Let $G = (V,E)$ be a graph of treewidth at most k. We compute a nice tree decomposition $(\{X_{p} \mid p \in I\}, T)$ with at most 4n nodes. It can be done in O(n) time [4, 12]. For each $p \in I$, let $V_{p} = X_{p} \cup \bigcup _{q} X_{q}$, where q runs through all descendants of p in T.

Fragments: For a node p and a vertex set $S \subseteq V_{p}$, a fragment is a component in G[S] or $G[V_{p} \setminus S]$. We denote the set of fragments with respect to p and S by $\mathcal {F}(p,S)$. A fragment $F \in \mathcal {F}(p,S)$ is active if $F \cap X_{p} \ne \emptyset$, and it is inactive otherwise. Two fragments in $\mathcal {F}(p,S)$ are adjacent if there is an edge of $G[V_{p}]$ between them. A fragment F is bad if it is inactive, $F \subseteq S$, and there is another inactive fragment $F'$ adjacent to F with $|F| < |F'|$.

DP Table: For storing information of partial solutions, we construct a table with values $\mathsf {ps}(p, s, \mathcal {A}, \beta , \gamma , \phi , \psi ) \in \{\mathsf {t}, \mathsf {f}\}$ with indices $p \in I$, $s \in \{0, \dots , n\}$, a partition $\mathcal {A}$ of $X_{p}$, $\beta :\mathcal {A} \rightarrow \{1,\dots ,n\}$, $\gamma :\mathcal {A} \rightarrow \{1,\dots ,n\} \cup \{\pm \infty \}$, $\phi :\mathcal {A} \rightarrow \{\mathsf {t}, \mathsf {f}\}$, and $\psi :\left( {\begin{array}{c}\mathcal {A}\\ 2\end{array}}\right) \rightarrow \{\mathsf {t},\mathsf {f}\}$. We set

$$\begin{aligned} \mathsf {ps}(p, s, \mathcal {A}, \beta , \gamma , \phi , \psi ) = \mathsf {t}\end{aligned}$$

if and only if there exists a set $S \subseteq V_{p}$ of size s with the following conditions:

• there is no bad fragment in $\mathcal {F}(p,S)$,

• for each active fragment F in $\mathcal {F}(p,S)$,

  • there is a unique element $A_{F} \in \mathcal {A}$ such that $A_{F} = F \cap X_{p}$,

  • $\beta (A_{F}) = |F|$,

  • $\phi (A_{F}) = \mathsf {t}$ if and only if $F \subseteq S$,

  • if $F \subseteq S$, then $\gamma (A_{F})$ is the size of a maximum inactive fragment adjacent to F (if no such fragment exists, we set $\gamma (A_{i}) = -\infty$),

  • if $F \not \subseteq S$, then $\gamma (A_{F})$ is the size of a minimum inactive fragment adjacent to F if no such fragment exists, we set $\gamma (A_{i}) = +\infty$),

• for two active fragments $F, F'$ in $\mathcal {F}(p,S)$, $\psi (\{A_{F}, A_{F'}\}) = \mathsf {t}$ if and only if F and $F'$ are adjacent, where $A_{F} = F \cap X_{p}$ and $A_{F'} = F' \cap X_{p}$.¹

Let $\rho$ be the root of T. The definition of the table $\mathsf {ps}$ implies the following fact.

Observation 3.2

$\mathsf {s}(G)$ is the smallest s with $\mathsf {ps}(\rho , s, \mathcal {A}, \beta , \gamma , \phi , \psi ) = \mathsf {t}$ for some $\mathcal {A}$, $\beta$, $\gamma$, $\phi$, and $\psi$ such that $\beta (A) \ge \gamma (A)$ for each $A \in \mathcal {A}$ with $\phi (A) = \mathsf {t}$, $\beta (A) \le \gamma (A)$ for each $A \in \mathcal {A}$ with $\phi (A) = \mathsf {f}$, and $\beta (A) \ge \beta (A')$ for any $A, A' \in \mathcal {A}$ with $\phi (A) = \mathsf {t}$ and $\psi (A, A') = \mathsf {t}$.

For computing $\mathsf {cs}(G)$, we need to compute additional information for each tuple $(p, s, \mathcal {A}, \beta , \gamma , \phi , \psi )$. For $A \in \mathcal {A}$, let $\beta '(A)$ be the size of the fragment in $\mathcal {F}(\rho , S)$ that is a superset of the fragment $F_{A} \supseteq A$ in $\mathcal {F}(p, S)$. If $A \subseteq S$, then $\beta '(A) = \beta (A)$; otherwise $\beta '(A) = |C_{A} \setminus X_{p}| + \sum _{A' \in \mathcal {A}, \; A' \subseteq C_{A}} \beta (A')$, where $C_{A}$ is the component in $G[(V \setminus V_{p}) \cup (X_{p} \setminus S)]$ that includes A. We can compute $\beta '(A)$ for all $A \in \mathcal {A}$ in time O(n) by running a breadth-first search from $X_{p} \setminus S$.

Observation 3.3

$\mathsf {cs}(G)$ is the smallest s with $\mathsf {ps}(p, s, \mathcal {A}, \beta , \gamma , \phi , \psi ) = \mathsf {t}$ for some p, $\mathcal {A}$, $\beta$, $\gamma$, $\phi$, and $\psi$ such that $\beta (A) \ge \gamma (A)$ for each $A \in \mathcal {A}$ with $\phi (A) = \mathsf {t}$, $\beta (A) \le \gamma (A)$ for each $A \in \mathcal {A}$ with $\phi (A) = \mathsf {f}$, and $\beta (A) \ge \beta '(A')$ for any $A, A' \in \mathcal {A}$ with $\phi (A) = \mathsf {t}$ and $\psi (A, A') = \mathsf {t}$.

By Observations 3.2 and 3.3, provided that all entries $\mathsf {ps}(p, s, \mathcal {A}, \beta , \gamma , \phi , \psi )$ are computed in advance, we can compute $\mathsf {s}(G)$ and $\mathsf {cs}(G)$ by spending time O(1) and O(n), respectively, for each tuple. We compute all entries $\mathsf {ps}(p, s, \mathcal {A}, \beta , \gamma , \phi , \psi )$ by a bottom-up dynamic program. Due to the space limitation, we omit this part in the conference version.    $\square$

For a vertex-weighted graph $G = (V,E)$ with a weight function $w :V \rightarrow \mathbb {Z}^{+}$, a set $S \subseteq V$ is a weighted safe set of weight $\sum _{s \in S} w(s)$ if for each component C of G[S] and each component D of $G[V \setminus S]$ with an edge between C and D, it holds that $w(C) \ge w(D)$. Bapat et al. [2] show that finding a minimum (connected) weighted safe set is weakly NP-hard even for stars. Let $W = \sum _{v \in V} w(v)$. Our dynamic program above works for the weighted version if we extend the ranges of parameters s, $\beta$, and $\gamma$ by including $\{1,\dots ,W\}$. The running time becomes polynomial in W.

Theorem 3.4

For a vertex weighted graph of bounded treewidth, a weighted (connected) safe set of the minimum weight can be found in pseudo-polynomial time.

4 Safe Sets in Interval Graphs

In this section, we present a polynomial-time algorithm for finding a minimum safe set and a minimum connected safe set in an interval graph.

A graph is an interval graph if it can be represented as the intersection graph of intervals on a line. Given a graph, one can determine in linear time whether the graph is an interval graph, and if so, find a corresponding interval representation in the same running time [6].

Theorem 4.1

For an n-vertex interval graph, a minimum safe set and a minimum connected safe set can be found in time $O(n^{8})$.

Proof

Let G be a given interval graph. As we can deal with each component of G separately, we assume that G is connected. The algorithm is a dynamic programming on an interval representation of G. We assume that its vertices (i.e. intervals) $v_1,\dots ,v_n$ are ordered increasingly according to their left ends, and write $X_i=\{v_1,\dots ,v_i\}$.

At each step i of the algorithm, we want to store all subsets $S \subseteq X_i$ which can potentially be completed (with vertices from $G \setminus X_i$) into a safe set. The number of such sets can be exponential: we thus define a notion of signature, and store the signatures of the sets instead of storing the sets themselves. The cost of this storage is bounded by the number of possible signatures, which is polynomial in n.

We will then prove that all possible signatures of sets at step i can be deduced from the set of signatures at step $i-1$. The cardinality of a minimum safe set (and a minimum connected safe set) can finally be deduced from the set of signatures stored during the last step. We can easily modify the algorithm so that it also outputs a minimum set.

We define the signature of S at step i as the 8-tuple that consists of the following items (see Fig. 2):

• 1. The size of S.

• 2. The vertex $v^S_r$ of S with the most neighbors in $G\setminus X_i$.

• 3. The vertex $v^{\bar{S}}_r$ of $\bar{S} := X_i\setminus S$ with the most neighbors in $G\setminus X_i$.

• 4. The size of $S_r$ (the rightmost component of S).

• 5. The size of $\bar{S}_r$ (the rightmost component of $\bar{S}$).

• 6. The largest size of a component of $\bar{S}\setminus \bar{S}_r$ adjacent with $S_r$.

• 7. The smallest size of a component of $S\setminus S_r$ adjacent with $\bar{S}_r$.

• 8. A boolean value indicating whether S is connected.

Fig. 2.

The dynamic programming on an interval graph.

Assuming that we know the signature of a set S at step i, we show how to obtain the signature at step $i+1$ of (a) $S' = S$ and (b) $S' = S\cup \{v_{i+1}\}$. With this procedure, all signatures of step $i+1$ can be obtained from all signatures at step i.

• 1. The size of $S'$ (at step i: |S|).

  • (a) |S|.

  • (b) $|S|+1$.

• 2. The vertex of $S'$ with the most neighbors in $G\setminus X_{i+1}$ (at step i: $v^S_r$).

  • (a) $v^S_r$.

  • (b) The one of $v^S_r$ and $v_{i+1}$ which has the most neighbors in $G\setminus X_{i+1}$.

• 3. The vertex of $\bar{S}' := X_{i+1} \setminus S'$ with the most neighbors in $G\setminus X_{i+1}$ (at step i: $v^{\bar{S}}_r$).

  • (a) The one of $v^{\bar{S}}_r$ and $v_{i+1}$ which has the most neighbors in $G\setminus X_{i+1}$.

  • (b) $v^{\bar{S}}_r$.

• 4. The size of the rightmost component $S'_{r}$ of $S'$ (at step i: $|S_r|$).

  • (a) $|S_r|$.

  • (b) $|S_r|+1$ if $v_{i+1}$ and $v^S_r$ are adjacent, and 1 otherwise (new component).

    In the latter case, we discard the signature if $|S_r|$ is strictly smaller than the largest size of a component of $\bar{S}\setminus \bar{S}_r$ adjacent with $S_r$ at step i.

• 5. The size of the rightmost component $\bar{S}'_{r}$ of $\bar{S}'$ (at step i: $|\bar{S}_r|$).

  • (a) 1 if $v_{i+1}$ and $v^{\bar{S}}_r$ are not adjacent (new component), and $|\bar{S}_r|+1$ otherwise.

    In the latter case, we discard the signature if $|\bar{S}_r|$ is strictly larger than the smallest size of a component of $S\setminus S_r$ adjacent with $\bar{S}_r$ at step i.

  • (b) $|\bar{S}_r|$.

• 6. The largest size of a component of $\bar{S}' \setminus \bar{S}'_r$ adjacent with $S'_r$ (at step i: c).

  • (a) c if no new component of $\bar{S}'$ was created (see 5.), and $\max \{c, |\bar{S}'_r|\}$ otherwise.

  • (b) c if no new component of $S'$ was created (see 4.), and $-\infty$ otherwise.

• 7. The smallest size of a component of $S' \setminus S'_r$ adjacent with $\bar{S}'_r$ (at step i: c).

  • (a) c if no new component of $\bar{S}'$ was created (see 5.), and $+\infty$ otherwise.

  • (b) c if no new component of $S'$ was created (see 4.), and $\min \{c, |S'_r|\}$ otherwise.

• 8. A boolean variable indicating whether $S'$ is connected (at step i: $\mathsf {b}$).

  • (a) $\mathsf {b}$

  • (b) $\mathsf {t}$ if $|S|=0$, $\mathsf {b}$ if $v_{i+1}$ and $v^S_r$ are adjacent, and $\mathsf {f}$ otherwise.

When all signatures at step n have been computed, we use the additional information that S and $\bar{S}$ cannot be further extended to discard the remaining signatures corresponding to non-safe sets. That is, we discard a signature if $|S_r| < |\bar{S}_r|$, or $|S_r|$ is strictly smaller than the largest size of a component of $\bar{S}\setminus \bar{S}_r$ adjacent to it, or $|\bar{S}_r|+1$ is strictly larger than the smallest size of a component of $S\setminus S_r$ adjacent to it.

The minimum sizes of a safe set and a connected safe set can be obtained from the remaining signatures. For each step i, there are $O(n^{7})$ signatures. From a signature for step i, we can compute the corresponding signature for step $i+1$ in O(1) time. Therefore, the total running time is $O(n^{8})$.    $\square$

5 Fixed-Parameter Tractability

In this section, we show that the problems of finding a safe set and a connected safe set of size at most s is fixed-parameter tractable when the solution size s is the parameter. For the standard concepts in parameterized complexity, see the recent textbook [8].

We first show that graphs with small safe sets have small treewidth. We then show that for any fixed constants s the property of having a (connected) safe set of size at most s can be expressed in the monadic second-order logic on graphs. Then we use the well-known theorems by Bodlaender [4] and Courcelle [7] to obtain an FPT algorithm that depends only linearly on the input size.

Lemma 5.1

Let $G = (V,E)$ be a connected graph. If $\mathsf {tw}(G) \ge s^{2}-1$, then $\mathsf {s}(G) \ge s$.

Proof

It is known that every graph G has a path of $\mathsf {tw}(G)+1$ vertices as a subgraph [3]. Thus $\mathsf {tw}(G) \ge s^{2}-1$ implies that G has a path of $s^{2}$ vertices as a subgraph.

Let P be a path of $s^{2}$ vertices in G, and let $S \subseteq V$ be an arbitrary set of size less than s. By the pigeon-hole principle, there is a subpath Q of P such that $|Q| \ge s$ and $S \cap V(Q) = \emptyset$. Hence there is a component B of $G[V \setminus S]$ with $V(Q) \subseteq B$. Since G is connected there is a component A of G[S] adjacent to B. Now we have $|A| \le |S| < s \le |Q| \le |B|$, which implies that S is not a safe set.    $\square$

The syntax of the monadic second-order logic of graphs (MS$_{2}$) includes (i) the logical connectives $\vee$, $\wedge$, $\lnot$, $\Leftrightarrow$, $\Rightarrow$, (ii) variables for vertices, edges, vertex sets, and edge sets, (iii) the quantifiers $\forall$ and $\exists$ applicable to these variables, and (iv) the following binary relations:

• $v \in U$ for a vertex variable v and a vertex set variable U;

• $e \in F$ for an edge variable e and an edge set variable F;

• $\mathsf {inc}(e,v)$ for an edge variable e and a vertex variable v, where the interpretation is that e is incident with v;

• equality of variables.

Now we can show the following.

Lemma 5.2

For a fixed constant s, the property of having a safe set of size at most s can be expressed in MS$_{2}$.

Corollary 5.3

For a fixed constant s, the property of having a connected safe set of size at most s can be expressed in MS$_{2}$.    $\square$

Theorem 5.4

The problems of finding a safe set and a connected safe set of size at most s is fixed-parameter tractable when the solution size s is the parameter. Furthermore, the running time depends only linearly on the input size.

Proof

Let G be a given graph. Since we can handle the components separately, we assume that G is connected. We first check whether $\mathsf {tw}(G) < (s+1)^{2} - 1$ in O(n) time by Bodlaender’s algorithm [4]. If not, Lemma 5.1 implies that $\mathsf {s}(G) \ge s+1$. Otherwise, Bodlaender’s algorithm gives us a tree decomposition of G with width less than $(s+1)^{2} - 1$. Courcelle’s theorem [7] says that it can be checked in linear time whether a graph satisfies a fixed MS$_{2}$ formula if the graph is given with a tree decomposition of constant width (see also [1]). Therefore, Lemma 5.2 and Corollary 5.3 imply the theorem.    $\square$

5.1 Relationship to Other Structural Graph Parameters

As we showed in Lemma 5.1, the treewidth of a graph is bounded by a constant if it has constant safe number. Here we further discuss the relationship to other well-studied graph parameters: tree-depth and vertex cover number. As bounding these parameters is more restricted than bounding treewidth, more problems can be solved efficiently when the problems are parameterized by tree-depth or vertex cover number (see [9, 11]). In the following, we show that safe number lies between these two parameters. This implies that parameterizing a problem by safe number may give a finer understanding of the parameterized complexity of the problem.

Tree-Depth. The tree-depth [13] (also known as elimination tree height [14] and vertex ranking number [5]) of a connected graph G is the minimum depth of a rooted tree T such that $T^{*}$ contains G as a subgraph, where $T^{*}$ is the supergraph of T with the additional edges connecting all comparable pairs in T. We can easily see that the tree-depth of a graph is at least its treewidth. It is known that a graph has constant tree-depth if and only if it has a constant upper bound on the length of paths in it [13]. Hence the proof of Lemma 5.1 implies the following relation.

Lemma 5.5

The tree-depth of a connected graph is bounded by a constant if it has constant safe number.

The converse of the statement above is not true in general. The complete k-ary tree of depth 2 has tree-depth 2 and safe number k.

Vertex Cover Number. A set $C \subseteq V(G)$ is a vertex cover of a graph G if each edge in G has at least one end in C. The vertex cover number of a graph is the size of a minimum vertex cover in the graph. We can see that C is a vertex cover if and only if each component of $G \setminus C$ has size 1. Thus a vertex cover is a safe set, and the following relation follows.

Lemma 5.6

The safe number of a graph is at most its vertex cover number.

Again the converse is not true. Consider the graph obtained from the star graph $K_{1,k}$ by subdividing each edge. It has a (connected) safe set of size 2, while its vertex cover number is k.

Note that Lemma 5.6 and Theorem 5.4 together imply that the problem of finding a (connected) safe set is fixed-parameter tractable when parameterized by vertex cover number.

6 Concluding Remarks

A graph is chordal if it has no induced cycle of length 4 or more. Trees and interval graphs form the most well-known subclasses of the class of chordal graphs. A natural question would be the complexity of the problems on chordal graphs. Another question is about planar graphs. As the original motivation of the problem was from a facility location problem, it would be natural and important to study the problem on planar graphs.²

Our algorithm for graphs of treewidth at most k runs in $n^{O(k)}$ time. Such an algorithm is called an XP algorithm, and an FPT algorithm with running time $f(k) \cdot n^{c}$ is more preferable, where f is an arbitrary computable function and c is a fixed constant. It would be interesting if one can show that such an algorithm exists (or does not exist under some complexity assumption).