Fast Searching on Complete k-partite Graphs

Abstract

Research on graph searching has recently gained interest in computer science, mathematics, and physics. This paper studies fast searching of a fugitive in a graph, a model that was introduced by Dyer, Yang and Yaşar in 2008. We provide lower bounds and upper bounds on the fast search number (i.e., the minimum number of searchers required for capturing the fugitive) of complete k-partite graphs. We also investigate some special classes of complete k-partite graphs, such as complete bipartite graphs and complete split graphs. We solve the open problem of determining the fast search number of complete bipartite graphs, and present upper and lower bounds on the fast search number of complete split graphs.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Graph searching, also called Cops and Robbers games or pursuit-evasion problems, has many models, such as edge searching, node searching, mixed searching, fast searching, etc. [1, 3, 4, 7–10]. Let G denote an undirected graph. In the fast search model, a fugitive hides either on vertices or on edges of G. The fugitive can move at a great speed at any time from one vertex to another along a path that contains no searchers. We call an edge contaminated if it may contain the fugitive, and we call an edge cleared if we are certain that it does not contain the fugitive. In order to capture the fugitive, one launches a set of searchers on some vertices of the graph; these searchers then clear the graph edge by edge while at the same time guarding the already cleared parts of the graph. This idea is modelled by rules that describe the searchers’ allowed moves, as explained in Sect. 2. A fast search strategy of a graph is a sequence of actions of searchers that clear all contaminated edges of the graph. The fast search number of G, denoted by $\mathrm {fs}(G)$, is the smallest number of searchers needed to capture the fugitive in G.

Stanley and Yang [11] presented a linear time algorithm for computing the fast search number of Harlin graphs and their extensions, as well as a quadratic time algorithm for computing the fast search number of cubic graphs. Yang [13] proved that the problem of finding the fast search number of a graph is NP-complete; and it remains NP-complete for Eulerian graphs. He also proved that the problem of determining whether the fast search number of G equals to a half of the number of odd vertices in G is NP-complete for planar graphs with maximum degree 4. Dereniowski et al. [5] gave characterizations of graphs for which 2 or 3 searchers are sufficient in the fast search model. Xue and Yang [12] investigated Cartesian products of graphs, and proved an explicit formula for computing the fast search number of the Cartesian product of an Eulerian graph and a path. They also presented upper and lower bounds on the fast search number of hypercubes.

The fast search problem has a close relationship with the edge search problem [6]. Alspach et al. [2] presented a formula for the edge search number of complete k-partite graphs. Dyer et al. [6] proved the fast search number of complete bipartite graphs $K_{m,n}$ when m is even. They also presented lower and upper bounds respectively on the fast search number of $K_{m,n}$ when m is odd. However, the gap between the lower and upper bounds can be arbitrarily large, and this open problem remains unsolved for eight years.

In this paper, we provide lower and upper bounds on the fast search number of complete k-partite graphs. Further, we investigate some special classes of k-partite graphs, such as complete bipartite graphs and complete split graphs. We solve the open problem of determining the fast search number of complete bipartite graphs. We also present lower and upper bounds on the fast search number of complete split graphs.

2 Preliminaries

Throughout this paper, we only consider finite undirected graphs that have no loops or multiple edges. Let $G=(V,E)$ denote a graph with vertex set V and edge set E. We also use V(G) and E(G) to denote the vertex set and edge set of G respectively. Let uv be an edge with two endpoints u and v. For a vertex $v \in V$, the degree of v is the number of edges incident on v, denoted by $\mathrm{{deg}}_G(v)$. We say a vertex is odd if its degree is odd, and we say a vertex is even if its degree is even. An odd graph is a graph in which all vertices are odd. An even graph is a graph in which all vertices are even. Define $V_\mathrm{{odd}}(G)= \{ v \in V : v~\mathrm{is~odd}\}$.

For a subset $V' \subseteq V$, we use $G[V']$ to denote the subgraph induced by $V'$, which consists of all vertices of $V'$ and all the edges of G between vertices in $V'$. We use $G - V'$ to denote the induced subgraph $G[V \setminus V']$. For a subset $E' \subseteq E$, we use $G - E'$ to denote the subgraph $(V, E \setminus E')$. Let $G_1 = (V_1, E_1)$ and $G_2 = (V_2, E_2)$ be two subgraphs of G. The union of two graphs $G_1$ and $G_2$ is the graph $G_1 \cup G_2 = (V_1 \cup V_2, E_1 \cup E_2)$. We use $G_1 + V_2$ to denote the induced subgraph $G[V_1 \cup V_2]$.

A walk is a list $v_0, e_1, v_1, \dots , e_k, v_k$ of vertices and edges such that each edge $e_i$, $1 \le i \le k$, has endpoints $v_{i-1}$ and $v_i$. A path is a walk that does not contain the same vertex twice, except that its first vertex might be the same as its last vertex. We use $v_0v_1...v_k$ to denote a path with ends $v_0$ and $v_k$. A trail is a walk in which no edge occurs multiple times. For a connected subgraph $G'$ with at least one edge, an Eulerian trail of $G'$ is a trail that traverses every edge of $G'$ exactly once. A circuit is a trail whose first vertex is the same as its last. An Eulerian circuit is an Eulerian trail that begins and ends on the same vertex. A graph is called Eulerian if it contains an Eulerian circuit that traverses all its edges. Note that we only consider finite graphs with no loops or multiple edges in this paper. So, throughout this paper, we assume that an Eulerian circuit or Eulerian subgraph contains at least three edges.

In the fast search model, initially every vertex in V and every edge in E is considered contaminated. We call a vertex $v \in V$ cleared if all edges incident on v are cleared, and we call v partially cleared if v has both contaminated and cleared incident edges. A fast search strategy proceeds as follows. First, it places some number of searchers on some vertices in V. Then, it performs sliding actions along contaminated edges until either every edge in E is cleared or no more sliding actions are possible. A searcher on vertex u can slide along the edge $e=uv$ if e is contaminated and (1) u contains one additional searcher or (2) e is the only contaminated edge incident on u. After sliding along e, the searcher then resides on v and e is cleared. Intuitively, the sliding rules ensure that the searchers guard the already cleared parts of the graph, so that the fugitive cannot hide there. The following lemmas give two known lower bounds on the fast search number.

Lemma 1

[6]. For any connected graph G, $\mathrm {fs}(G) \ge \frac{1}{2}|V_\mathrm{odd}(G)|$.

Lemma 2

[11]. For any connected graph G with no leaves, $\mathrm {fs}(G) \ge \frac{1}{2} |V_\mathrm{odd}(G)|+2$.

Let $K_{n_1,\dots ,n_k} = (V_1, \dots , V_k, E)$ denote a complete k-partite graph, where $V_1, \dots$, $V_k$ are disjoint independent sets, $|V_i| = n_i$ and $n_i \le n_{i+1}$ for all $1 \le i \le k-1$. Each vertex in $V_i$ is adjacent to all the vertices in $V(K_{n_1,\dots ,n_k}) \setminus V_i$. We use $K_{m,n}=(V_1, V_2, E)$ to denote a complete bipartite graph, where $|V_1|=m$, $|V_2|=n$ and $1 \le m \le n$. We use $S_{m,n}=(V_1, V_2, E)$ to denote a complete split graph, where $V_1$ and $V_2$ are disjoint sets, $V_1$ induces a clique with m vertices and $V_2$ is an independent set with n vertices. In $S_{m,n}$, each vertex in $V_1$ is adjacent to all the other vertices in $V_1 \cup V_2$.

Note that for any connected graph G, the fast search number of G is always at least the edge search number of G. From Theorem 2 in [2], we have the next lemma.

Lemma 3

For any connected graph G that contains a clique $K_m$ of order m, where $m \ge 4$, we have $\mathrm {fs}(G) \ge m$.

3 Complete k-partite Graphs

In the following, we give lower bounds and upper bounds on the fast search number of complete k-partite graphs. Throughout this section, in order to better describe our proof ideas, we assume that placing actions of searchers can be inserted after sliding actions of searchers in a fast search strategy. If we want all placing actions to happen before all sliding actions in a fast search strategy, then we can simply move all placing actions before all sliding actions in that fast search strategy.

Lemma 4

For a complete k-partite graph $K_{n_1, \dots , n_k}$, where $k \ge 2$ and $n_1 \le \dots \le n_k$, we have $\mathrm {fs}(K_{n_1,\dots ,n_k}) \ge \sum _{i=1}^{k-1} n_i$.

Lemma 5

For a complete k-partite graph $K_{n_1, \dots , n_k}$, where $k \ge 3$ and $n_1 \le \dots \le n_k$, if $\sum _{i=1}^{k-1} n_i \ge 3$ and $n_k \ge 3$, then $\mathrm {fs}(K_{n_1, \dots , n_k}) \ge 2 + \sum _{i=1}^{k-1} n_i$.

Proof

For any graph G, $\mathrm {fs}(G)$ is greater than or equal to the edge search number of G. Thus, it follows from Theorem 6 in [2] that $\mathrm {fs}(K_{n_1, \dots , n_k}) \ge 2 + \sum _{i=1}^{k-1} n_i$.

Theorem 1

For a complete k-partite graph $K_{n_1, \dots , n_k}$, where $k \ge 3$, $n_1 \le \dots \le n_k$ and $\sum _{i=1}^{k} n_i = n$, if $\sum _{i=1}^{k-1} n_i \ge n_k = 3$, then $\mathrm {fs}(K_{n_1, \dots , n_k}) = n - 1$.

Proof

From Lemma 5, we have $\mathrm {fs}(K_{n_1, \dots , n_k}) \ge n - n_k +2 = n-1$. We will show that $n-1$ searchers can clear the graph. Let $V_k = \{v_1, v_2, v_3\}$ and $X=K_{n_1, \dots , n_k} - V_k$. Place $n-3$ searchers on $v_1$ and slide them to each vertex of X. Since $k \ge 3$, X is connected. We have three cases for the graph X.

Case 1. X is Eulerian. The following fast search strategy can clear all edges of the graph $K_{n_1, \dots , n_k} - \{v_1\}$ using $n-1$ searchers.

• 1. Place a searcher on a vertex u of X.

• 2. Slide one of the two searchers on u along the Eulerian circuit of X to clear all its edges.

• 3. Slide the two searchers on u to $v_2$ and $v_3$ respectively.

• 4. Place a searcher on $v_2$. Let Y be the graph formed by all the remaining contaminated edges of $K_{n_1, \dots , n_k}$.

  • (a) If $\mathrm {deg}_Y(v_2)$ is even (Y is Eulerian in this case), then slide one of the two searchers on $v_2$ along the Eulerian circuit of Y to clear all its edges.

  • (b) If $\mathrm {deg}_Y(v_2)$ is odd (Y has an Eulerian trail in this case), then slide one of the two searchers on $v_2$ to $v_3$ along the Eulerian trail of Y to clear all its edges.

Case 2. X is odd. So $X+\{v_2\}$ is Eulerian. We first place two searchers on $v_2$. Then slide one of the two searchers on $v_2$ along the Eulerian circuit of $X+\{v_2\}$ to clear all its edges. Finally, slide all searchers on X to $v_3$ to clear all the remaining contaminated edges of $K_{n_1, \dots , n_k}$.

Case 3. X has both even and odd vertices. Suppose that X has 2h odd vertices. Let $a_1$ and $b_1$ be two odd vertices of X such that there is a path $P_1$ between them which does not contain any vertex in $V_\mathrm{odd}(X)$ as an internal vertex. Let $H_1=X-E(P_1)$. For $i = 2, \dots , h$, let $a_i$ and $b_i$ be two odd vertices of $H_{i-1}$ such that there is a path $P_i$ between them which does not contain any vertex in $V_\mathrm{odd}(H_{i-1})$ as an internal vertex. Let $H_i=H_{i-1}-E(P_i)$. It is easy to see that $H_h$ contains no odd vertices. In particular, we select $P_i$ in the following manner:

(1) If X contains at least two even vertices, say u and $u'$, then for $i = 1, \dots , h$, let $P_i=a_iu'b_i$.

(2) If X contains only one even vertex, say u, then we first show that $V_1 = \{u\}$. Note that all vertices in $V_j$, $1 \le j \le k-1$, have the same degree in X. Therefore, we know $|V_1|=1$ and u is the only vertex in $V_1$. Further, if there is a vertex set $V_j$, $2 \le j \le k - 1$, which contains three vertices, then each of the three vertices is even in X. This is a contradiction. Hence, $|V_{j}|=2$ for all $2 \le j \le k-1$. We have two subcases for k.

(2.1) If $k>3$, then we can find a matching for all odd vertices of X. Note that there are $2k-4$ odd vertices on X. Let $V_2=\{a_1, b_{k-2}\}$ and $V_j=\{a_{j-1}, b_{j-2}\}$, $3 \le j \le k-1$. For $1 \le i \le k-2$, it is easy to see that $a_i$ is adjacent to $b_i$. Hence, we can let $P_i=a_ib_i$. Clearly, u is not included in $P_i$.

(2.2) If $k=3$, then we have $|V_1|=1$, $|V_2|=2$ and $|V_3|=3$. Further, $a_1$ and $b_1$ are the only two odd vertices of X. Let $V(X)=\{u,a_1,b_1\}$ and $P_1=a_1ub_1$.

If X contains at least two even vertices or X contains only one even vertex and $k > 3$, then similar to Case 1, we clear all edges of the graph $K_{n_1, \dots , n_k} - \{v_1\}$ using the following fast search strategy. Let U be a connected component in $H_h$ that contains u.

• 1. Place a searcher on the vertex u.

• 2. Slide one of the two searchers on u along the Eulerian circuit of U to clear all its edges. Note that all edges of X incident on u are cleared after this step.

• 3. Slide the two searchers on u to $v_2$ and $v_3$ respectively.

• 4. Place a searcher on $v_2$. Let H be the graph formed by all the remaining contaminated edges of $K_{n_1, \dots , n_k}$ except edges in $\cup _{i=1}^{h}E(P_i)$.

  • (a) If $\mathrm {deg}_H(v_2)$ is even (so H is Eulerian), then slide one of the two searchers on $v_2$ along the Eulerian circuit of H to clear all its edges.

  • (b) If $\mathrm {deg}_H(v_2)$ is odd (so H has an Eulerian trail), then slide one of the two searchers on $v_2$ from $v_2$ to $v_3$ along the Eulerian trail of H to clear all its edges.

• 5. Let $G_P$ be the graph formed by the paths $P_1, \dots , P_h$ ($E(G_P)$ is the set of all the remaining contaminated edges of $K_{n_1, \dots , n_k}$). Note that $a_h$ and $b_h$ are two vertices of degree one on $G_P$. Slide the searcher on $a_h$ along $P_h$ to $b_h$. Then $a_{h-1}$ and $b_{h-1}$ are two vertices of degree one on $G_P-E(P_h)$. Slide the searcher on $a_{h-1}$ along $P_{h-1}$ to $b_{h-1}$. Continuing like this we see that all edges of $G_P$ can be cleared.

If X contains only one even vertex and $k = 3$, then similar to Case 1, we clear all edges of the graph $K_{1,2,3} - \{v_1\}$ using the following fast search strategy. Place a searcher on $a_1$ and $v_2$ respectively. Slide one of the two searchers on $a_1$ along $P_1$ to $b_1$. Slide the two searchers on $b_1$ to $v_2$ and $v_3$ respectively. Note that the graph formed by all the remaining contaminated edges of $K_{1,2,3}$ is Eulerian. Slide one of the searchers on $v_2$ along the path $v_2uv_3a_1v_2$ to clear all its edges. Then, $K_{1,2,3}$ is cleared.

Theorem 2

For a complete k-partite graph $K_{n_1, \dots , n_k}$, if there is an $n_j$, $1 \le j \le k$, such that $\sum _{i=1}^{k} n_i -n_j \ge 4$ and $\sum _{i=1}^{k} n_i -n_j$ is even, then $\mathrm {fs}(K_{n_1, \dots , n_k}) \le \sum _{i=1}^{k} n_i - n_j +3.$

Proof

If $n_j \le 3$, from Theorem 5.1 in [13], we see that the claim holds. If $k=2$ and $\sum _{i=1}^{k} n_i -n_j \ge 6$, from Lemma 5 in [6], we know that the claim holds. If $k=2$ and $\sum _{i=1}^{k} n_i -n_j = 4$, similar to Lemma 5 in [6], we can show that the claim also holds. So we assume that $n_j \ge 4$ and $k \ge 3$ in the rest of the proof. Let $V_j = \{v_1, v_2, \dots , v_{n_j}\}$ and $X=K_{n_1, \dots , n_k} - V_j$. Let $\sum _{i=1}^{k} n_i -n_j = m$ and $V(X) = \{u_1, u_2, \dots , u_m\}$. If $n_j$ is odd, then place m searchers on $v_{n_j}$ and slide them to each vertex of X. If $n_j$ is even, then place m searchers on each vertex of X. Without loss of generality, we assume that $n_j$ is even. Place three additional searchers on $u_1$, $u_2$ and $u_3$ respectively.

Since $k \ge 3$, we know that X is a complete $(k-1)$-partite graph. So X is connected. If X is Eulerian, then slide a searcher from $u_1$ along the Eulerian circuit of X to clear all its edges. Without loss of generality, we assume that X is not Eulerian. Suppose that X has 2h odd vertices. Let $H_0=X$. Similar to Case 3 in the proof of Theorem 1, let $a_i$ and $b_i$ be two odd vertices of $H_{i-1}$ such that there is a path $P_i$ between them which does not contain any vertex in $V_\mathrm{odd}(H_{i-1})$ as an internal vertex. Let $H_i=H_{i-1}-E(P_i)$, $1 \le i \le h$. We now describe a fast search strategy that can clear all edges of $K_{n_1, \dots , n_k}$ using $m+3$ searchers.

• 1. In the following procedure, at any moment when a vertex $u_i$ ($1 \le i \le m$) contains two searchers, if $H_h$ has a connected component that contains $u_i$ and no edges of the component are cleared, then slide a searcher from $u_i$ along the Eulerian circuit of the component to clear all its edges.

• 2. Slide a searcher from $u_1$ to $v_1$ along $u_1v_1$, slide a searcher from $u_2$ to $v_1$ along $u_2v_1$ and slide a searcher from $u_3$ to $v_2$ along $u_3v_2$.

• 3. Note that the subgraph induced by all the edges across $\{u_4, \dots , u_m\}$ and $\{v_1,v_2\}$ has an Eulerian trail (since m is even). Slide a searcher from $v_1$ to $v_2$ along the Eulerian trail to clear all its edges.

• 4. Slide a searcher from $v_1$ to $u_3$ along $v_1u_3$, slide a searcher from $v_2$ to $u_1$ along $v_2u_1$ and slide a searcher from $v_2$ to $u_2$ along $v_2u_2$. After this step, $v_1$ and $v_2$ are cleared.

• 5. Similar to Steps 2, 3 and 4, we can clear $v_3$ and $v_4$, and then clear $v_5$ and $v_6$ (if they exist), and so on, until $v_{n-1}$ and $v_n$ are cleared.

• 6. Let $G_P$ be the graph formed by the paths $P_1, \dots , P_h$ ($E(G_P)$ is the set of all the remaining contaminated edges of $K_{n_1, \dots , n_k}$). Similar to Step 5 in Case 3 of the proof of Theorem 1, we can clear all edges of $G_P$.

Theorem 3

For a complete k-partite graph $K_{n_1, \dots , n_k}$, if there is an $n_j$, $1 \le j \le k$, such that $\sum _{i=1}^{k} n_i -n_j \ge 3$ and $\sum _{i=1}^{k} n_i -n_j$ is odd, then $\mathrm {fs}(K_{n_1, \dots , n_k}) \le \sum _{i=1}^{k} n_i - \left\lfloor \frac{n_j}{2} \right\rfloor .$

Proof

If $n_j \le 3$, similar to Theorem 5.1 in [13], we can prove the claim. If $k=2$, from Lemma 7 in [6], we see that the claim holds. So we assume that $n_j \ge 4$ and $k \ge 3$ in the remainder of the proof. Let $V_j = \{v_1, v_2, \dots , v_{n_j}\}$ and $X=K_{n_1, \dots , n_k} - V_j$. Let $\sum _{i=1}^{k} n_i -n_j = m$ and $V(X) = \{u_1, u_2, \dots , u_m\}$. Note that X is connected since $k \ge 3$. Suppose that X has 2h odd vertices. Similar to Case 3 in the proof of Theorem 1, we can define $a_i$, $b_i$, $P_i$ and $H_i$ for $1 \le i \le h$.

Case 1. $n_j=4\ell +1$. Place m searchers on $v_1$, place one searcher on each of $u_1$, $v_2$ and $v_3$. Place one searcher on each of $v_{4i+2}$ and $v_{4i+3}$ for $i=1, \dots , \ell -1$ (i.e., we place two searchers for every four vertices in $V_j \setminus \{v_1\}$). In total we use $m+1+\frac{n_j-1}{2}$ searchers.

• 1. In the following process, at any moment when a vertex $u_i$ ($1 \le i \le m$) contains two searchers, if $H_h$ has a connected component that contains $u_i$ and no edges of the component are cleared, then slide a searcher from $u_i$ along the Eulerian circuit of the component to clear all its edges.

• 2. Slide m searchers from $v_1$ to each vertex of X. Slide one of the two searchers on $u_1$ along the Eulerian circuit induced by all the edges across $\{u_1, u_2, \dots , u_{m-1}\}$ and $\{v_2, v_3\}$ to clear all its edges.

• 3. Slide a searcher from $v_2$ to $v_4$ along $v_2u_mv_4$ and slide a searcher from $v_3$ to $u_5$ along $v_3u_mv_5$ to clear $v_2$ and $v_3$. Slide a searcher on $u_1$ along the Eulerian circuit induced by all the edges across $\{u_1, u_2, \dots , u_{m-1}\}$ and $\{v_4, v_5\}$ to clear all its edges.

• 4. Repeat the above step for all of $v_{4i+2}$ and $v_{4i+3}$ where $i=1, \dots , \ell -1.$ First clear the Eulerian circuit induced by all the edges across $\{u_1, u_2, \ldots , u_{m-1}\}$ and $\{v_{4i+2}, v_{4i+3}\}$ with a searcher on $u_1$. Slide the searcher on $v_{4i+2}$ along $v_{4i+2}u_mv_{4i+4}$ and the searcher on $v_{4i+3}$ along $v_{4i+3}u_mv_{4i+5}$. Then clear the Eulerian circuit induced by all the edges across $\{u_1, u_2, \dots ,$ $u_{m-1}\}$ and $\{v_{4i+4}, v_{4i+5}\}$ with a searcher on $u_1$.

• 5. Let $G_P$ be the graph formed by the paths $P_1, \dots , P_h$. Similar to Step 5 in Case 3 of the proof of Theorem 1, we can clear all edges of $G_P$.

Case 2. $n_j=4\ell +2$. Place the searchers as in Case 1. So $m+1+\frac{n_j-2}{2}=m+\frac{n_j}{2}$ searchers are placed on the graph. Clear all vertices in $V_j \setminus \{v_{n_j}\}$ with the same strategy used in Steps 1–4 in Case 1. Note that the only contaminated edges are the ones incident on $v_{n_j}$ and the edges of $G_P$. We can arrange the vertices of X before placing actions such that $u_1=a_h$, which is a vertex of degree one on $G_P$. Since m is odd, there is at least one vertex u such that $\mathrm {deg}_X(u)$ is even. For each vertex $u \in V(X)$ whose $\mathrm {deg}_X(u)$ is even, if $u \notin V(G_P)$, then slide a searcher on u to $v_{n_j}$ along $u v_{n_j}$. Slide a searcher from $u_1$ to $v_{n_j}$ along $u_1 v_{n_j}$; slide the other searcher on $u_1$ (i.e., $a_h$) along $P_h$ to $b_h$, during which, when a vertex $u_i$ of $P_h$ has only one contaminated edge (i.e., $u_iv_{n_j}$), incident on it, slide a searcher on $u_i$ along $u_iv_{n_j}$ to $v_{n_j}$. Then $a_{h-1}$ and $b_{h-1}$ are two vertices of degree one on $G_P-E(P_h)$. Slide a searcher from $v_{n_j}$ to $a_{h-1}$ along $v_{n_j}a_{h-1}$, and slide this searcher along $P_{h-1}$ to $b_{h-1}$, during which, when a vertex $u_i$ of $P_{h-1}$ has only one contaminated edge incident on it, slide a searcher on $u_i$ along $u_iv_{n_j}$ to $v_{n_j}$. Continuing like this we can clear all edges of $G_P$ and all edges incident on $v_{n_j}$.

Case 3. $n_j=4\ell +3$. Place the searchers as in Case 1. Place another searcher on $u_m$. Hence we use $m+1+\frac{n_j-3}{2}+1=m+\frac{n_j+1}{2}$ searchers. Use the same strategy as in Steps 1–4 in Case 1 to clear every vertex in $V_j \setminus \{v_{n_j-1}, v_{n_j}\}$. Now there is one searcher on every vertex of X except $u_1$ and $u_m$ on which there are two searchers. We can arrange the vertices of X before placing actions such that $u_m=a_h$. Slide one of the two searchers on $u_m$ along $P_h$ to $b_h$ to clear all its edges. Then, $b_h$ contains two searchers. Slide a searcher on $b_h$ along $b_h v_{n_j-1}$ and $b_h v_{n_j}$ respectively. Slide a searcher on $u_1$ to clear the Eulerian circuit induced by all the edges across $V(X) \setminus \{b_1\}$ and $\{v_{n_j-1}, v_{n_j}\}$. Finally, similar to Step 5 in Case 1, we can clear all edges of $G_P - E(P_h)$.

Case 4. $n_j=4\ell$. Place a searcher on every vertex in $\{u_1, u_2,\dots , u_{m-1}, v_1, v_2,\dots , v_{2\ell }\}$ and place a second searcher on $u_1$. Hence we use $m+\frac{n_j}{2}$ searchers. We can arrange the vertices of X before placing actions such that $\mathrm {deg}_X(u_m)$ is even and $u_1=a_h$. Let $P_i=a_iu_mb_i$, $1 \le i \le h$.

• 1. Slide the searcher from $u_1$ along the Eulerian circuit induced by all the edges across $\{u_1, u_2, \dots , u_{m-1}\}$ and $\{v_1, v_2, \dots , v_{2\ell }\}$. Then slide each searcher on $v_i \in \{v_1, v_2, \dots , v_{2\ell }\}$ along $v_i u_m$ to clear $\{v_1, v_2, \dots , v_{2\ell }\}$.

• 2. Slide a searcher on $u_m$ to each vertex in $\{v_{2\ell +1}, v_{2\ell +2}, \dots , v_{4\ell -2}\}$. Slide a searcher on $u_1$ to clear the Eulerian circuit induced by all the edges across $\{u_1, u_2, \dots , u_{m-1}\}$ and $\{v_{2\ell +1}, v_{2\ell +2},\dots , v_{4\ell -2}\}$. Slide a searcher on $u_1$ to $b_h$ along $P_h$.

• 3. In the following process, at any moment when a vertex $u_i$ ($1 \le i \le m$) contains two searchers, if $H_h$ has a connected component that contains $u_i$ and no edges of the component are cleared, then slide a searcher from $u_i$ along the Eulerian circuit of the component to clear all its edges.

• 4. Slide a searcher on $b_h$ along $b_hv_{4\ell -1}$ and $b_hv_{4\ell }$ respectively and $b_h$ is cleared. Then, slide a searcher on $u_m$ to clear the Eulerian circuit induced by all the edges across $V(X) \setminus \{b_h\}$ and $\{v_{4\ell -1}, v_{4\ell }\}$.

• 5. Finally, similar to Step 5 in Case 1, we can clear all edges of $G_P - E(P_h)$.

Corollary 1

For a complete k-partite graph $K_{n_1, \dots , n_k}$, define $\alpha _j$, $1 \le j \le k$, as

$$\begin{aligned} \alpha _j= \left\{ \begin{aligned}&\sum _{i=1}^{k} n_i - n_j +3,&{if \sum \nolimits _{i=1}^{k}\ n_i -n_j\ is\ even\ and \sum \nolimits _{i=1}^{k} n_i -n_j \ge 4,} \\&\sum _{i=1}^{k} n_i - \left\lfloor \frac{n_j}{2} \right\rfloor ,&{if} \sum \nolimits _{i=1}^{k}\ n_i -n_j\ is\ odd\ and\ \sum \nolimits _{i=1}^{k} n_i -n_j \ge 3, \\&\sum _{i=1}^{k} n_i,&\text {else.}\end{aligned} \right. \end{aligned}$$

Then $\mathrm {fs}(K_{n_1, \dots , n_k}) \le \min _{1 \le j \le k}\alpha _j.$

4 Complete Bipartite Graphs

In Sects. 4 and 5, we focus on some special classes of complete k-partite graphs. When $k=2$, $K_{n_1,\dots ,n_k}$ is a complete bipartite graph. Dyer et al. [6] proved several results on the fast search number of $K_{m,n}$. The fast search problem on $K_{m,n}$ has been solved when m is even. However, the fast search problem remains open when m is odd, and they only gave lower and upper bounds on $\mathrm {fs}(K_{m,n})$ in [6]:

• When m is odd, n is even and $3 \le m \le n$, we have $\max \{m+2, \frac{n}{2}\} \le \mathrm {fs}(K_{m,n}) \le \min \{n+3, m + \frac{n}{2}\}$.

• When m and n are odd and $3 \le m \le n$, we have $\max \{m+2, \frac{m+n}{2}\} \le \mathrm {fs}(K_{m,n}) \le m + \frac{n+1}{2}$.

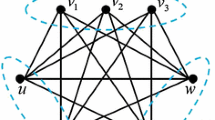
In the following, we will prove that for a complete bipartite graph $K_{m,n}$ with $3 \le m \le n$, if m is odd, then $\mathrm {fs}(K_{m,n})$ equals to the upper bounds given above. Let ${\mathcal {S}}_{K_{m,n}}$ denote an optimal fast search strategy for $K_{m,n}$, which uses the minimum number of sliding actions to clear the first cleared vertex of $K_{m,n}$ among all optimal fast search strategies for $K_{m,n}$. We use $w_1$ to denote the first cleared vertex of $K_{m,n}$. Let $t_1$ denote the moment at which $w_1$ is cleared (see Fig. 1(1)). Note that vertices of $K_{m,n}$ are partitioned into two vertex sets $V_1$ and $V_2$. We use $w_2$ to denote the first cleared vertex in another vertex set of $K_{m,n}$ which does not contain $w_1$. That is, if $w_1 \in V_1$, then $w_2 \in V_2$; if $w_1 \in V_2$, then $w_2 \in V_1$. Let $t_2$ denote the moment after which the next sliding action clears $w_2$ (see Fig. 1(2)). Without loss of generality, we first assume that $w_1 \in V_2$. In a similar way, we can prove the lower bound on $\mathrm {fs}(K_{m,n})$ when $w_1 \in V_1$.

Fig. 1.

(1) After searcher $\lambda$ slides from $v_1$ to $u_1$, $v_1$ becomes the first cleared vertex of $K_{3,3}$. Let this moment be denoted by $t_1$, and we have $w_1 = v_1$. (2) Searcher $\lambda$ will slide from $u_3$ to $v_3$ in the next step. After that, $u_3$ becomes the first cleared vertex in $V_1$. Let $t_2$ denote this moment, and we have $w_2 = u_3$.

Throughout this section, we assume m is odd. We use $A_1$ to denote the set of all vertices in $V_2\setminus \{w_1\}$ which contain a searcher at $t_1$ and have cleared incident edges at $t_2$. We use $A_2$ to denote the set of all vertices in $V_2\setminus \{w_1\}$ which contain a searcher and have cleared incident edges at $t_2$. Let $a_1=|A_1|$ and $a_2=|A_2|$, it is easy to see that $a_1 + a_2 \ge |A_1 \cup A_2|$. Figures 2 and 3 illustrate $A_1$ and $A_2$.

Fig. 2.

At the moment $t_1$, each vertex in $A_1$ contains a searcher. Further, each vertex in $A_1$ has cleared incident edges at $t_2$ (see Fig. 3). In this case, $A_1 = \{v_2, v_3\}$.

Fig. 3.

At the moment $t_2$, each vertex in $A_2$ contains a searcher, and all vertices in $A_1$ and $A_2$ have cleared incident edges. In this case, $A_2 = \{v_4\}$.

Note that at the moment $t_1$, all vertices in $A_2 \setminus \{A_1 \cap A_2\}$ are contaminated and contain no searchers, and hence contain no searchers at the beginning of ${\mathcal {S}}_{K_{m,n}}$ either. Since m is odd, we know all vertices in $A_2$ are odd. Therefore, each vertex in $A_2 \setminus \{A_1 \cap A_2\}$ must contain a searcher at the end of ${\mathcal {S}}_{K_{m,n}}$.

Lemma 6

For a complete bipartite graph $K_{m,n}$ with $m,n \ge 3$, let $\mathcal {S}_{K_{m,n}}$ be an optimal fast search strategy for clearing $K_{m,n}$. Suppose that $w_1 \in V_2$ in ${\mathcal {S}}_{K_{m,n}}$, then we have $a_1 + a_2 \ge |A_1 \cup A_2| \ge n - 2$.

Lemma 7

For a complete bipartite graph $K_{m,n}$ with $m,n \ge 3$, let $\mathcal {S}_{K_{m,n}}$ be an optimal fast search strategy for clearing $K_{m,n}$. Suppose that $w_1 \in V_2$ in ${\mathcal {S}}_{K_{m,n}}$. If (1) each vertex in $V_1 \cup A_1$ contains exactly one searcher at $t_1$, and (2) $w_1$ contains no searchers at $t_1$, then each vertex in $A_1$ has at least two contaminated incident edges at $t_1$.

4.1 Both m and n Are Odd

Lemma 8

For a complete bipartite graph $K_{m,n}$ with $3 \le m \le n$, suppose that both m and n are odd. If $w_1 \in V_2$, then $\mathrm {fs}(K_{m,n}) \ge m + \frac{n+1}{2}$.

Proof

If $3 = m \le n$, then it follows from Lemma 2 that $\mathrm {fs}(K_{m,n}) \ge \frac{m+n}{2} +2= \frac{n+1}{2} + 3=m+\frac{n+1}{2}$. So we only need to consider $5 \le m \le n$ in the following. Since $w_1 \in V_2$ and $w_1$ is cleared at $t_1$, we know each vertex in $V_1$ must be guarded by a searcher at the moment $t_1$. If $\max \{a_1,a_2\} \ge \frac{n+1}{2}$, then $\mathrm {fs}(K_{m,n}) \ge m + \frac{n+1}{2}$. Suppose that $\max \{a_1,a_2\} \le \frac{n-1}{2}$. Note that $a_1 + a_2 \ge n-2$ and both m and n are odd. We know $\min \{a_1,a_2\} \ge \frac{n-3}{2}$. Further, $a_1$ and $a_2$ cannot both equal to $\frac{n-3}{2}$; otherwise, $a_1 + a_2 = n - 3 < n - 2$. Hence, there are two cases.

Case 1. $a_1 = \frac{n-1}{2}$. If $w_1$ contains a searcher at $t_1$, then $\mathrm {fs}(K_{m,n}) \ge |V_1| + |A_1| + 1 = m + a_1 + 1 = m + \frac{n+1}{2}$. If $w_1$ contains no searchers at $t_1$, then for the sake of contradiction, we assume that $m + \frac{n-1}{2}$ searchers can clear $K_{m,n}$. Since $|V_1 \cup A_1| = m + \frac{n-1}{2}$, we know each vertex in $V_1 \cup A_1$ contains exactly one searcher at $t_1$, and no searchers are located on other vertices. Consider the moment $t_1$. From Lemma 7, we know each vertex in $A_1$ has at least two contaminated incident edges at $t_1$. Further, since $|V_2 \setminus \{A_1 \cup \{w_1\}\}| = n - \frac{n-1}{2} - 1 \ge 2$, there are at least two vertices in $V_2$ which have no cleared incident edges. Therefore, each vertex in $V_1$ has at least two contaminated incident edges. Observe that every vertex in $V_1 \cup A_1$ contains exactly one searcher and has at least two contaminated incident edges. Therefore, all searchers get stuck at $t_1$, which contradicts that $m + \frac{n-1}{2}$ searchers can clear $K_{m,n}$. Hence, $\mathrm {fs}(K_{m,n}) \ge m + \frac{n+1}{2}$.

Case 2. $a_1 = \frac{n-3}{2}$. Since $\max \{a_1,a_2\} \le \frac{n-1}{2}$ and $a_1 + a_2 \ge n-2$, we know $a_2 = \frac{n-1}{2}$. Further, since $a_1 + a_2 = n - 2$, we know $A_1 \cap A_2 = \emptyset$, and hence each vertex in $A_2$ should always contain a searcher after $t_2$. For the sake of contradiction, assume that $m + \frac{n-1}{2}$ searchers can clear $K_{m,n}$. Recall that at the moment $t_2$, each vertex in $A_2 \cup V_1$ is occupied by a searcher and $|A_2 \cup V_1| = m + \frac{n-1}{2}$, we know each vertex in $A_2 \cup V_1$ is occupied by exactly one searcher at $t_2$. Let $x_1x_2$ denote the last cleared edge before $t_2$, which is cleared by sliding a searcher from $x_1$ to $x_2$. Note that each vertex in $V_1$ is occupied by a searcher between $t_1$ and $t_2$. We know $x_2$ must be in $A_2$, and $x_2$ contains no searchers before $x_1x_2$ is cleared. Thus, $x_1x_2$ is the only cleared edge incident on $x_2$ at $t_2$. Recall that $a_1 + a_2 = n - 2$, it is easy to see that there is still a vertex in $V_2$, say $x_3$, which has no cleared incident edges at $t_2$. Hence, $w_2x_3$ must be cleared by the next sliding action after $t_2$. When $w_2$ is cleared, we know both of $x_2$ and $x_3$ have exactly one cleared incident edge, and the two edges must be $w_2x_2$ and $w_2x_3$. Therefore, when $w_2$ is cleared, each vertex in $V_1$ except $w_2$ has at least two contaminated incident edges. Note that each vertex in $A_2$ should be guarded by a searcher after $t_2$. Hence, every searcher gets stuck after $w_2$ is cleared. This contradicts that $m + \frac{n-1}{2}$ searchers can clear $K_{m,n}$. Therefore, $\mathrm {fs}(K_{m,n}) \ge m + \frac{n+1}{2}$.

Corollary 2

For a complete bipartite graph $K_{m,n}$ with $3 \le m \le n$, suppose that both m and n are odd. If $w_1 \in V_1$, then $\mathrm {fs}(K_{m,n}) \ge m + \frac{n+1}{2}$ when $m = 3$, and $\mathrm {fs}(K_{m,n}) \ge n + \frac{m+1}{2}$ when $m \ge 5$.

From Lemma 8 and Corollary 2, we are ready to present the lower bound on $\mathrm {fs}(K_{m,n})$ when both m and n are odd. Note that since $m \le n$, $\min \{m + \frac{n+1}{2}, n + \frac{m+1}{2}\} = m + \frac{n+1}{2}$.

Theorem 4

Given a complete bipartite graph $K_{m,n}$ with $3\le m \le n$, if both m and n are odd, then $\mathrm {fs}(K_{m,n}) \ge m + \frac{n+1}{2}$.

4.2 m is Odd and n is Even

Lemma 9

For a complete bipartite graph $K_{m,n}$ with $3 \le m < n$, suppose that m is odd and n is even. If $w_1 \in V_2$, then $\mathrm {fs}(K_{m,n}) \ge m + \frac{n}{2}$.

Proof

If $\max \{a_1,a_2\} \ge \frac{n}{2}$, then it is easy to see that $\mathrm {fs}(K_{m,n}) \ge m + \frac{n}{2}$. Suppose that $\max \{a_1,a_2\} < \frac{n}{2}$. Since $a_1 + a_2 \ge n - 2$ and n is even, we know $a_1 = a_2 = \frac{n - 2}{2}$ and $A_1 \cap A_2 = \emptyset$. Consider the moment $t_1$. We know each vertex in $V_1 \cup A_1$ contains a searcher. For the sake of contradiction, we assume that $m + \frac{n-2}{2}$ searchers can clear $K_{m,n}$. Then each vertex in $V_1 \cup A_1$ contains exactly one searcher at $t_1$. From Lemma 7, we know each vertex in $A_1$ has at least two contaminated incident edges. Further, since $A_1 \cap A_2 = \emptyset$ and $|V_2 \setminus \{A_1 \cup \{w_1\}\}| = n - \frac{n-2}{2} - 1 \ge 2$, we know there are at least two vertices in $V_2$ which have no cleared incident edges at $t_1$. Thus, each vertex in $V_1$ has at least two contaminated incident edges at $t_1$, and hence, all searchers get stuck at $t_1$. This contradicts that $m + \frac{n-2}{2}$ searchers can clear $K_{m,n}$. Therefore, $\mathrm {fs}(K_{m,n}) \ge m+\frac{n}{2}$.

In the following, we consider the case when $w_1 \in V_1$.

Lemma 10

For a complete bipartite graph $K_{m,n}$ with $3 \le m < n$, suppose that m is odd and n is even. If $w_1 \in V_1$, then $\mathrm {fs}(K_{m,n}) \ge n + 1$ when $m = 3$, and $\mathrm {fs}(K_{m,n}) \ge n + 3$ when $m \ge 5$.

Proof

If $w_1 \in V_1$, then $w_2 \in V_2$. At the moment $t_1$, since $w_1$ is the first cleared vertex, each vertex in $V_2$ is occupied by a searcher. Let $w_3$ denote the second cleared vertex of $K_{m,n}$. If $w_3 \in V_2$, then we know each vertex of $K_{m,n}$ except $w_1$ and $w_3$ must be occupied by a searcher before $w_3$ is cleared. Hence, $\mathrm {fs}(K_{m,n}) \ge m + n - 2$. If $w_3 \in V_1$, then we have two cases:

Case 1. $m=3$. Assume that n searchers can clear $K_{m,n}$. Consider the moment $t_1$. Note that $|V_2| = n$ and each vertex in $V_2$ is occupied by a searcher at $t_1$. Hence, each vertex in $V_2$ contains exactly one searcher at $t_1$ and no searchers are located on other vertices. Since there are still two vertices in $V_1$ which have no cleared incident edges, then each vertex in $V_2$ has two contaminated incident edges. Thus, it is impossible to move any of the searchers located on $V_2$ after $t_1$. This contradicts our assumption that n searchers can clear $K_{m,n}$. Therefore, $\mathrm {fs}(K_{m,n}) \ge n+1$ when $m=3$.

Case 2. $m \ge 5$. For the sake of contradiction, we assume that $n+2$ searchers are sufficient to clear $K_{m,n}$. We have three subcases:

Case 2.1. $w_3$ contains no searchers after it is cleared. Then the last two cleared edges incident on $w_3$ are both cleared by sliding a searcher from $w_3$ to $V_2$. After $w_3$ is cleared, all searchers will get stuck within five steps. This contradicts the assumption that $n + 2$ searchers are sufficient to clear $K_{m,n}$. Therefore, $\mathrm {fs}({K_{m,n}}) \ge n + 3$.

Case 2.2. $w_3$ contains exactly one searcher after it is cleared. Note that $w_3$ has degree at least 6, we know the last cleared edge incident on $w_3$ has to be cleared by sliding a searcher from $w_3$ to $V_2$. Consider the moment when $w_3$ is cleared. Note that each vertex in $V_2$ is occupied by a searcher between $t_1$ and $t_2$, and there are at least $m - 2 \ge 3$ vertices in $V_1$ which contain no searchers and have no cleared incident edges. Since we assume that $n + 2$ searchers are sufficient to clear $K_{m,n}$, hence, there is only one vertex in $V_2$ which contains two searchers. It is easy to see that all searchers get stuck within one step after $w_3$ is cleared, which is a contradiction. Therefore, $\mathrm {fs}(K_{m,n}) \ge n + 3$.

Case 2.3. $w_3$ contains exactly two searchers after it is cleared. Consider the moment at which $w_3$ is cleared. Note that there are still at least $m - 2 \ge 3$ vertices in $V_1$ which contain no searchers and have no cleared incident edges. Further, each vertex in $V_2$ is occupied by exactly one searcher. Hence, it is easy to see that all searchers get stuck after $w_3$ is cleared. Therefore, $\mathrm {fs}(K_{m,n}) \ge n + 3$.

From the above cases, if $w_1 \in V_1$, then $\mathrm {fs}(K_{m,n}) \ge \min \{m + n - 2, n + 1\} = n + 1$ when $m = 3$, and $\mathrm {fs}(K_{m,n}) \ge \min \{m + n - 2, n + 3\} = n + 3$ when $m \ge 5$.

From Lemmas 9 and 10, we know: (1) when $m = 3$, $\mathrm {fs}(K_{m,n}) \ge \min \{m + \frac{n}{2}, n + 1\} = m + \frac{n}{2}$ ; (2) when $m \ge 5$, $\mathrm {fs}(K_{m,n}) \ge \min \{m + \frac{n}{2}, n + 3\}$. Hence, we are now ready to give the lower bound on $\mathrm {fs}(K_{m,n})$ when m is odd, n is even and $3 \le m \le n$.

Theorem 5

For a complete bipartite graph $K_{m,n}$ with $3\le m < n$, if m is odd and n is even, then $\mathrm {fs}(K_{m,n}) \ge \min \{n+3, m+ \frac{n}{2}\}$.

From Theorems 4 and 5 above, in combination with Lemma 4 and Theorem 4 in [6], we have a complete solution to $\mathrm {fs}(K_{m,n})$.

Theorem 6

For a complete bipartite graph $K_{m,n}$ with $3 \le m \le n$,

5 Complete Split Graphs

In this section, we consider complete split graphs $S_{m,n}$ with $m,n \ge 1$, which also form a special class of k-partite graphs $K_{n_1,\dots ,n_k}$ when $1 = n_1 = \dots = n_{k-1} \le n_k$. We start with some initial cases.

Lemma 11

For a complete split graph $S_{m,n}$, if $n = 1$, then

$$\begin{aligned} \mathrm {fs}(S_{m,1})= \left\{ \begin{aligned}&1,&m=1,&\\&2,&m=2,&\\&m+1,&m \ge 3.&\\ \end{aligned} \right. \end{aligned}$$

In the following, we consider the fast search number of $S_{m,n}$ when $n \ge 2$. Let $\mathcal {S}_{S_{m,n}}$ denote an optimal fast search strategy for clearing $S_{m,n}$. Let $w_1'$ denote the first cleared vertex in $\mathcal {S}_{S_{m,n}}$, and let $t_1'$ denote the moment at which $w_1'$ is cleared.

5.1 m is Odd and $n \ge 2$

When $m=1$ and $n \ge 2$, $S_{m,n}$ is a star with n leaves. It is easy to see that $S_{1,n}$ can be cleared with $\lceil \frac{n}{2}\rceil$ searchers. Further, it follows from Lemma 1 that $\mathrm {fs}(S_{1,n}) \ge \frac{1}{2}|V_\mathrm{odd}(S_{1,n})| = \lceil \frac{n}{2}\rceil$. Hence, we have the next lemma.

Lemma 12

For a complete split graph with $m = 1$, if $n \ge 2$, then $\mathrm {fs}(S_{1,n}) = \lceil \frac{n}{2}\rceil$.

Lemma 13

For a complete split graph $S_{m,n}$ with $m \ge 3$ and $n \ge 2$, if m is odd, then $\mathrm {fs}(S_{m,n}) = m+ \lceil \frac{n}{2}\rceil$.

Proof

If $w_1' \in V_1$, then each vertex of $S_{m,n}$ except $w_1'$ should be guarded by a searcher at the moment $t_1'$. Hence, $\mathrm {fs}(S_{m.n}) \ge m-1+n$. If $w_1' \in V_2$, then we have two cases:

Case 1. n is even. If $n = 2$, then it follows from Lemma 3 that $\mathrm {fs}(S_{m,n}) \ge m+1 = m + \frac{n}{2}$. If $n \ge 4$, then similar to the proof of Lemma 9, we can show that $\mathrm {fs}(S_{m,n}) \ge m + \frac{n}{2}$.

Case 2. n is odd. If $n = 3$, then it follows from Lemma 5 that $\mathrm {fs}(S_{m,n}) \ge 2 + m = m + \frac{n+1}{2}$. If $n = 5$, then similar to the proof of Lemma 8 when $n \ge 5$, we can show that $\mathrm {fs}(S_{m,n}) \ge m + \frac{n+1}{2}$.

From the above cases, when $m \ge 3$ and $n \ge 2$, $\mathrm {fs}(S_{m,n}) \ge \min \{m - 1 + n, m + \lceil \frac{n}{2} \rceil \} = m + \lceil \frac{n}{2} \rceil$. In combination with Theorem 3, we have $\mathrm {fs}(S_{m,n}) = m + \lceil \frac{n}{2} \rceil$, when $m \ge 3$ and $n \ge 2$.

From Lemmas 12 and 13, we are ready to give the fast search number of $S_{m,n}$ when m is odd and $n \ge 2$.

Theorem 7

For a complete split graph $S_{m,n}$, if m is odd, then

$$\begin{aligned} \mathrm {fs}(S_{m,n})= \left\{ \begin{aligned}&\left\lceil \frac{n}{2}\right\rceil ,&m=1,&~n \ge 2, \\&m+\left\lceil \frac{n}{2}\right\rceil ,&m \ge 3,&~n \ge 2. \\ \end{aligned} \right. \end{aligned}$$

5.2 m is Even and $n \ge 2$

Now we consider the complete split graph $S_{m,n}$ where m is even and $n \ge 2$. We first give the following upper bound on $\mathrm {fs}(S_{m,n})$.

Lemma 14

For a complete split graph $S_{m,n}$ with $m = 2$ and $n \ge 2$, we have $\mathrm {fs}(S_{2,n}) \le 3$.

Proof

Let $V_1 = \{u_1,u_2\}$ and $V_2 = \{v_1,v_2,\dots ,v_n\}$. Place a searcher on $u_1$ and $u_2$ respectively. Place a second searcher, say $\lambda$, on $u_1$. Hence we use 3 searchers. Let $\lambda$ clear $v_1$ by sliding along the path $u_1v_1u_2$. Next let $\lambda$ clear $v_2$ by sliding along the path $u_2v_2u_1$. Repeat this process to clear all the other vertices of $S_{m,n}$.

Lemma 15

For a complete split graph $S_{m,n}$ with $m = 4$ and $n \ge 3$, we have $\mathrm {fs}(S_{4,n}) \le 6$.

Lemma 16

For a complete split graph $S_{m,n}$ with $m \ge 4$ and $n = 2$, we have $\mathrm {fs}(S_{m,2}) \le m+1$.

Theorem 8

For a complete graph $S_{m,n}$,

$$\begin{aligned} \mathrm {fs}(S_{m,n})= \left\{ \begin{aligned}&3,&m=2,&~n \ge 2, \\&6,&m = 4,&~n \ge 3, \\&m+1,&m \ge 4,&~n=2, \\&m+2,&m \ge 6,&~n = 3. \\ \end{aligned} \right. \end{aligned}$$

Proof

• (1) $m=2$ and $n\ge 2$. If $w_1' \in V_1$, then $\mathrm {fs}(S_{2,n}) \ge |V_1 \cup V_2| - 1 = 2+n-1 \ge 3$. If $w_1' \in V_2$, then let $w_1'x_1$ denote the last sliding action at $t_1'$. Suppose that two searchers are sufficient to clear $S_{m,n}$. When $w_1'$ is cleared, each vertex in $V_1$ should be occupied by a searcher. Therefore, at the moment $t_1'$, each vertex in $V_1$ is occupied by exactly one searcher and no searchers are located on other vertices. Hence, $x_1$ has no cleared incident edges before $w_1'x_1$ is cleared. Further, the only edge between two vertices in $V_1$ is contaminated when $w_1'x_1$ is cleared. Since there is at least one vertex in $V_2$ which has no cleared incident edges, we know each vertex in $V_1$ has at least two contaminated incident edges. Therefore, no searchers can move after $w_1'$ is cleared. This is a contradiction. Thus, when $m=2$ and $n \ge 2$, $\mathrm {fs}(S_{2,n}) \ge 3$.

• (2) $m = 4$ and $n \ge 3$. It follows from Lemmas 5 and 15 that $\mathrm {fs}(S_{4,n}) = m + 2 = 6$.

• (3) $m \ge 4$ and $n = 2$. Clearly, $S_{m,2}$ contains a clique $K_{m+1}$. From Lemmas 3 and 16, we have $\mathrm {fs}(S_{m,2}) = m+1$.

• (4) $m \ge 6$ and $n = 3$. It follows from Theorem 1 that $\mathrm {fs}(S_{m,3}) = m + n - 1 = m + 2$.

From Lemma 5 and Theorem 2, we give a lower bound and an upper bound on $\mathrm {fs}(S_{m,n})$ when $m \ge 6$ and $n \ge 4$.

Theorem 9

For a complete split graph $S_{m,n}$ with $m \ge 6$ and $n \ge 4$, if m is even, then $m + 2 \le \mathrm {fs}(S_{m,n}) \le m +3$.

6 Conclusion and Open Problems

We established both lower bounds and upper bounds on the fast search number of complete k-partite graphs. For $k=2$, in combination with existing upper bounds, we completely resolved the open question of determining the fast search number of complete bipartite graphs. In addition, we presented some new and nontrivial bounds on the fast search number of complete split graphs.

State-of-the-art knowledge and intuition about the fast search model is not developed as well as for most other search models. Our lower bounds required new proof approaches compared to the existing results in the literature; thus our results shed light on the general problem of finding optimal fast search strategies.

The following problems are left open which we consider worth to investigate:

• (1) For complete split graphs $S_{m,n}$ with $m \ge 6$ and $n \ge 4$, resolve the gap of 1 between the upper bound and lower bound on the fast search number when m is even.

• (2) Determine the fast search number of $K_{n_1,\dots ,n_k}$ for general values of $n_1$, $\dots$, $n_k$. We conjecture that in Corollary 1, if $\sum _{i=1}^{k} n_i -n_j$ is odd and $\sum _{i=1}^{k} n_i -n_j \ge 3$, then $\mathrm {fs}(K_{n_1, \dots , n_k}) = \min _{1 \le j \le k}\alpha _j$, where $\alpha _j = \sum _{i=1}^{k} n_i - \left\lfloor \frac{n_j}{2} \right\rfloor$.