Keywords

1 Introduction

A massive amount of traffic in communication networks that flows from providers of large data (such as video streaming services) to many clients at once leads to various optimization problems for broadcasting of multiple messages. Similar types of problems arise in master/workers parallel computations on specific networks when multiple tasks are simultaneously distributed from one node (master) to all other nodes (workers). This has been subject of research for many years. For surveys on broadcasting and other communication protocols in various kinds of networks see e.g. [8, 9, 12–14].

We restrict ourselves to synchronous networks, where at each time unit messages can be sent from nodes to all their neighbors in one unit of time. A network is modeled by a graph. As an example we consider namely tori, meshes, and hypercubes, perhaps the most popular and extensively studied networks [15], but our approach is more general.

Since networks have limited capacity of links, any larger data to be broadcast needs to be split into multiple messages and sent individually. This leads to a more general variant of broadcasting in which several different messages need to be simultaneously transmitted from one source node, called the originator. The problem of multiple broadcasting was first defined in [5] and previously studied under several different models in [1, 2, 10]. The minimal overall time needed for simultaneous broadcasting and the maximal number of messages that can be simultaneously broadcast were considered in [1, 6, 10, 16–18], respectively.

Here we consider a scenario when each message (or task) needs to be handled (or processed) at each node in a time unit before it is sent out further to other selected neighbors. It is reasonable to demand that each node has to handle at each time unit only a single message (task). Equivalently, each node receives at most one message in each time unit. We call this restriction a 1-in-port model. Furthermore, every received message is send out only in the next time unit and no message is sent to already informed vertex. In other words, nodes have no buffers to store messages for delayed transmission. This simplification is motivated by memory or security restrictions, or a need for uninterrupted data flow. As usual, we also assume full-duplex mode.

For this scenario, the concept of level-disjoint partitions was developed in [6] to study how many messages and in what time they can be simultaneously broadcast from a given originator vertex in a given graph, see the definitions in the next section. The same concept was further developed in [7] where results on existence of optimal number of level-disjoint partitions in general graphs were obtained. It was also shown in [7] that the problem of simultaneous broadcasting in a graph G can be solved locally on a suitable subgraph H of G and then extended to a solution for the whole graph G (c.f. Proposition 2), but without guarantee of optimality.

In this paper, the latter result is improved in the terms of optimality by showing that if H satisfies additional properties, namely if H contains all neighbours of the originator vertex v and preserves distances to v, then simultaneous broadcasting from v on H with optimal time for each destination vertex can be extended to simultaneous broadcasting from v on G again with optimal time for each destination vertex (Theorem 1).

Furthermore, we identify particular subgraphs, namely wheels and biwheels, that play a key role for simultaneous broadcasting. We show (Theorems 2–4) that they can be used for simultaneous broadcasting (of optimal number) of messages in optimal time for a wide class of graphs.

In particular, since biwheels naturally occur in Cartesian products (Propositions 3 and 4), we obtain tight results for bipartite tori, meshes, and hypercubes. For these graphs we also provide an explicit description how optimal simultaneous broadcasting can be realized (Sect. 4). We also answer affirmatively a conjecture from [6] asserting that the n-dimensional hypercube admits simultaneous broadcasting of n messages in optimal time \(3n-2\). We conclude with summary of open problems and conjectures (Sect. 5).

2 Concept of Level-Disjoint Partitions

In this paper we use the concept of level-disjoint partitions, introduced in [6], to capture broadcasting under the considered communication model. We use standard graph terminology and notation. An open neighborhood of a vertex u in a graph G is denoted by \(N_G(u)\), the degree of u by \({\mathrm {deg}}_G(u)\), the distance between vertices u and v by \(d_G(u,v)\). The eccentricity of a vertex u, i.e. the maximal distance from u to other vertices, is denoted by \({\mathrm {ecc}}_{G}(u)\). The subscript G is omitted whenever the graph is clear from context.

A level partition of a graph G is a partition \(\mathcal {S}=(S_0,\dots ,S_h)\) of V(G) into a tuple of sets, called levels, such that \(S_{i}\subseteq N(S_{i-1})\) for every \(1\le i \le h\); that is, every vertex has a neighbor from previous level. The number \(h=h(\mathcal {S})=|\mathcal {S}|-1\) is called the height of \(\mathcal {S}\). The broadcasting starts at all vertices from the level \(S_0\), at each time unit the same message is sent from all vertices of the current level to all vertices in the next level through edges of the graph, till the hth time unit, when the message is spread to all vertices of G. Note that we do not care which particular edges are used. In the case when the starting level \(S_0\) is a singleton, say \(S_0=\{v\}\), we say that the level partition is rooted at v (or v-rooted) and the vertex v is called the root of \(\mathcal {S}\).

A level partition \((S_0,\dots ,S_h)\) of G with \(S_i=\{u\in V(G) \mid d_G(u,S_0)=i\}\) for every \(0\le i \le h\) is called a distance level partition. Clearly, a distance level partition is determined by the choice of the starting level \(S_0\) and it has minimal height among all level partitions with the same starting level. If, moreover, it is rooted at a vertex v, it corresponds to the breadth-first-search tree from v (up to the choice of edges).

Two level partitions \(\mathcal {S}=(S_0,\dots ,S_{h(\mathcal {S})})\) and \(\mathcal {T}=(T_0,\dots ,T_{h(\mathcal {T})})\) are said to be level-disjoint if \(S_i \cap T_i=\emptyset \) for every \(1\le i \le \min (h(\mathcal {S}),h(\mathcal {T}))\). Note that we allow \(S_0 \cap T_0 \ne \emptyset \) since we consider the case when different messages have the same originator. Level partitions \(\mathcal {S}^1, \dots , \mathcal {S}^k\) are said to be (mutually) level-disjoint if each two partitions are level-disjoint. Then we say that \(\mathcal {S}^1, \dots , \mathcal {S}^k\) are level-disjoint partitions, shortly LDPs. If every partition is rooted in the same vertex v and they are level-disjoint (up to the starting level \(\{v\}\)), we say that \(\mathcal {S}^1, \dots , \mathcal {S}^k\) are level-disjoint partitions with the same root v, shortly v-rooted LDPs. For an example of four v-rooted LDPs of a circulant graph, see Fig. 2. Note that the 4-tuple at a vertex denotes its levels in each partition.

Let \(\mathcal {S}^1, \dots , \mathcal {S}^k\) be level partitions of G, not necessarily level-disjoint. The set of levels \(\{l \mid u\in S_l^i \text{ for } \text{ some } 1\le i \le k\}\) in which a given vertex u occurs is called the range of u with respect to \(\mathcal {S}^1, \dots , \mathcal {S}^k\), denoted by \(R_{}(u)\).

The number of level-disjoint partitions determines how many messages can be broadcast simultaneously while their maximal height determines the overall time of the broadcasting. Hence a general aim is to construct for a given graph

  • as many as possible (mutually) level-disjoint partitions; and

  • with as small maximal height as possible.

In [7] some necessary conditions on the number of v-rooted LDPs as well as on their maximal height were given. Assume that \(\mathcal {S}^1, \dots , \mathcal {S}^k\) are v-rooted LDPs of G. Clearly, for every vertex u except v, \(\max (R(u)) \ge d(u,v)+k-1\) since u cannot appear in a level smaller than the distance to the root v and \(|R(u)|=k\). If equality holds, we say that u has perfect range; that is,

$$R(u)=\{d(u,v),d(u,v)+1,\dots ,d(u,v)+k-1\}.$$

This means that all k messages will be delivered to the vertex u in the best time possible for this vertex. If all vertices (up to the root v) have perfect range, we say that level-disjoint partitions \(\mathcal {S}^1, \dots , \mathcal {S}^k\) are perfect.

Furthermore, the above definition is adjusted for bipartite graphs. If G is bipartite, then for any same-rooted LDPs of G, the range of each vertex contains elements of the same parity. It follows that no vertex can have perfect range as defined above (except the trivial case of a single partition). So the concept of perfect range is relaxed for bipartite graphs as follows. In a bipartite graph G, for every vertex u except v, \(\max (R(u))\ge d(u,v)+2k-2\). If equality holds, we say that u has biperfect range; that is,

$$R(u)=\{d(u,v),d(u,v)+2,\dots ,d(u,v)+2k-2\}.$$

If all vertices (up to the root v) have biperfect range, we say that level-disjoint partitions \(\mathcal {S}^1, \dots , \mathcal {S}^k\) are biperfect. Further, the following necessary conditions on same-rooted LDPs were proven in [7].

Proposition 1

([7]). Let \(\mathcal {S}^1,\dots ,\mathcal {S}^{k}\) be level-disjoint partitions of a graph G with the same root v. Then,

$$\begin{aligned} k&\le \deg (v) \end{aligned}$$
(1)
$$\begin{aligned} \max _{1 \le i \le k}h(\mathcal {S}^i) \ge {\left\{ \begin{array}{ll} \ {\mathrm {ecc}}(v)+k-1 &{} {if \,G\, is\, not\, bipartite},\\ \ {\mathrm {ecc}}(v)+2k-2 &{} {if \,G \,is\, bipartite}.\end{array}\right. } \end{aligned}$$
(2)

2.1 Subgraph Extension Technique

In [7] it was shown that it suffices to find v-rooted LDPs on some suitable subgraph H of G and then extend them to v-rooted LDPs of the whole graph G as stated by the following proposition. Let \(G-v\) denote the graph obtained by removing a vertex v and all incident edges from a G.

Proposition 2

([7]). Let v be a vertex of a graph G and H be a subgraph of G containing v and some vertex from each component of \(G-v\). Then any k v-rooted level-disjoint partitions of H can be extended to k v-rooted level-disjoint partitions of G.

Our first result in this paper extends Proposition 2 in terms of preserving (bi)perfectness. It shows that it suffices to find (bi)perfect LDPs locally on a subgraph H of G that covers all neighbors of the root v and preserves distances to v. Then they can be extended to (bi)perfect, respectively, LDPs with the same root to the whole graph G. We say that a subgraph H of a graph G preserves distances to a vertex \(v\in V(H)\) if \(d_H(u,v)=d_G(u,v)\) for every \(u \in V(H)\). If a subgraph \(H \subseteq G\) does not contain a vertex v of G, we denote by \(H+v\) the subgraph of G obtained by adding v and all incident edges from G to H.

Theorem 1

Let v be a vertex of a graph G and H be a subgraph of G containing \(N(v) \cup \{v\}\) and preserving distances to v. Then any k (bi)perfect v-rooted level-disjoint partitions of H can be extended to k (bi)perfect, respectively, v-rooted level-disjoint partitions of G.

Proof

Let \(\mathcal {S}^1,\ldots ,\mathcal {S}^k\) be (bi)perfect level-disjoint partitions of H rooted in v and assume \(V(H)\subsetneq V(G)\); for otherwise we are done. We show that they can be extended to (bi)perfect, respectively, v-rooted level-disjoint partitions of \(H'=H+u\) for some vertex u of G uncovered by H such that \(H'\) preserves distances to v. Then, by incremental extension until no uncovered vertex remains, we obtain (bi)perfect v-rooted level-disjoint partitions of G.

Let u be a vertex of G that is not in H but has a neighbor w in H distinct from v such that w belongs to some shortest path in G between u and v. Note that such u exist since \(N(v) \subseteq V(H)\). Since H preserves distances to v, for \(H'=H+u\) we have

$$d_{H'}(u,v)=d_H(w,v)+1=d_G(w,v)+1=d_G(u,v),$$

and thus \(H'\) preserves distances to v as well.

Let us denote by \(l_i\) the level of w in \(\mathcal {S}^i\); that is, \(w\in S^i_{l_i}\) for every \(1\le i \le k\). Then, we extend \(\mathcal {S}^1,\ldots ,\mathcal {S}^k\) to \(H'\) by adding u to the \((l_i+1)\)-th level of \(\mathcal {S}^i\) for every \(1\le i \le k\). Clearly, such extended partitions are level partitions of \(H'\). Moreover, they are level-disjoint since u was added into distinct levels of level-disjoint partitions \(\mathcal {S}^1,\ldots ,\mathcal {S}^k\). Finally, if \(\mathcal {S}^1,\ldots ,\mathcal {S}^k\) are perfect, then

$$R(w)=\{l_i \mid 1\le i \le k\} = \{d_H(w,v),d_H(w,v)+1,\dots ,d_H(w,v)+k-1\},$$

and therefore the vertex u has perfect range as well:

$$R(u)=\{l_i+1 \mid 1\le i \le k\} = \{d_{H'}(u,v),d_{H'}(u,v)+1,\dots ,d_{H'}(u,v)+k-1\}.$$

Similarly, if \(\mathcal {S}^1,\ldots ,\mathcal {S}^k\) are biperfect, then

$$R(w)=\{l_i \mid 1\le i \le k\} = \{d_H(w,v),d_H(w,v)+2,\dots ,d_H(w,v)+2k-2\},$$

and therefore the vertex u has biperfect range as well:

$$R(u)=\{l_i+1 \mid 1\le i \le k\} = \{d_{H'}(u,v),d_{H'}(u,v)+2,\dots ,d_{H'}(u,v)+2k-2\}.$$

   \(\square \)

The above theorem is applied in the next section to obtain (bi)perfect level-disjoint partitions of a wide class of graphs, including particular Cartesian products.

3 Simultaneous Broadcasting in Cartesian Products

A Cartesian product of graphs G and H is the graph \(G \mathbin {\square } H\) with the vertex set \(V(G \mathbin {\square } H)=V(G)\times V(H)\) and the edge set \(E(G \mathbin {\square } H)=\{(u,v)(u',v)\mid uu'\in E(G), v\in V(H)\} \cup \{(u,v)(u,v') \mid u\in V(G), vv'\in E(H)\}.\) As an example, consider the hypercube. The n-dimensional hypercube \(Q_n\) is the graph on vertices \(V(Q_n)=\{0,1\}^n\) and edges between vertices that differ in precisely one coordinate. Observe that \(Q_n\) can be viewed as the n-fold Cartesian product of \(K_2\).

In [6] we developed a concept of composing level-disjoint partitions with certain properties of graphs G and H into level-disjoint partitions of \(G \mathbin {\square } H\). Here we present a different approach of so called biwheels. We define biwheels in the next Subsect. 3.1 and show that they naturally occur in Cartesian products. Then in the Subsect. 3.2 we show how they can be used for construction of optimal number of same-rooted level-disjoint partitions of optimal height in Cartesian products. Finally, in the Subsect. 4 we consider particular Cartesian products: meshes, tori, hypercubes and we present optimal constructions for them also explicitly.

3.1 Biwheels in Cartesian Products

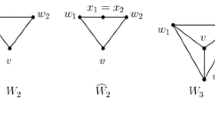
First we formally define wheels and biwheels. A k-wheel \(W_k\) for \(k\ge 0\) centered at a vertex v is the graph on vertices \(v,w_1,\dots ,w_k\) with edges joining v to all \(w_i\)’s and edges joining \(w_i\) and \(w_{i+1}\) for every \(1\le i \le k\) where \(w_{k+1}\) is identified as \(w_1\). Note that for technical reasons we allow \(k\le 2\). A k-wheel for \(k\ge 3\) is a join of a k-cycle and a vertex.

A k-biwheel \(\widehat{W}_k\) for \(k\ge 0\) centered at a vertex v is the subdivision of \(W_k\) centered at v obtained by inserting a new vertex \(x_i\) to the edge between \(w_i\) and \(w_{i+1}\) for every \(1\le i \le k\). Clearly, k-biwheel is bipartite for every k whereas k-wheel is bipartite only for \(k=0,1\). See Fig. 1 for an illustration of small wheels and biwheels.

Fig. 1.
figure 1

k-wheels and k-biwheels centered at v for \(k=0,1,2,3\).

Full size image

Biwheels naturally occur in Cartesian products of graphs as stated by the following proposition.

Proposition 3

Let u, v be vertices in graphs G, H respectively. Then \(G \mathbin {\square } H\) has a 2k-biwheel centered at (u, v) for any \(0\le k \le \min ({\mathrm {deg}}_G(u),{\mathrm {deg}}_H(v))\).

Proof

It suffices to prove the statement for \(k={\mathrm {deg}}_G(u)={\mathrm {deg}}_H(v)\) for otherwise we may use subgraphs \(G'\) of G and \(H'\) of H such that \(k={\mathrm {deg}}_{G'}(u)={\mathrm {deg}}_{H'}(v)\) as \(G' \mathbin {\square } H'\) is a subgraph of \(G \mathbin {\square } H\). For \(1\le i \le k\) let us denote the i-th neighbor of u, v by \(u_i\), \(v_i\), respectively. We define the vertices of a 2k-biwheel in \(G\mathbin {\square }H\) as follows:

$$\begin{aligned} w_{2i-1}&=(u_i,v),&x_{2i-1}&=(u_i,v_i),\\ w_{2i}&=(u,v_i),&x_{2i}&=(u_{i+1},v_i) \end{aligned}$$

for every \(1\le i \le k\) where \(u_{k+1}\) is identified as \(u_1\).

Note that all vertices \(w_{2i-1}\), \(x_{2i-1}\), \(w_{2i}\), \(x_{2i}\) are distinct, vertices \(w_{2i-1}\), \(w_{2i}\) are adjacent to (u, v), and \(w_{2i-1}x_{2i-1}\), \(x_{2i-1}w_{2i}\), \(w_{2i}x_{2i}\), \(x_{2i}w_{2i+1}\) are edges in \(G\mathbin {\square }H\) for every \(1\le i \le k\). Hence these vertices form a 2k-biwheel in \(G \mathbin {\square }H\) centered at (u, v).    \(\square \)

In particular, if \({\mathrm {deg}}_G(u)={\mathrm {deg}}_H(v)\) then \(G\mathbin {\square }H\) has a \({\mathrm {deg}}_{G\mathbin {\square }H}((u,v))\)-biwheel centered at (u, v); that is, the largest possible biwheel at (u, v). For example, \(P_2 \mathbin {\square } P_2\) contains a 2-biwheel (with center in any vertex) or \(P_3 \mathbin {\square } P_3\) contains a 4-biwheel centered in the degree-4 vertex. In fact, \(P_2 \mathbin {\square } P_2 \simeq \widehat{W}_2\) and \(P_3 \mathbin {\square } P_3 \simeq \widehat{W}_4\).

For another example, by recursive applications we obtain an n-biwheel in the hypercube \(Q_n\) for every \(n=2^m\) where m is an integer since \(Q_{2^m}\simeq Q_{2^{m-1}} \mathbin {\square } Q_{2^{m-1}}\). However, we would like to have n-biwheel in \(Q_n\) for any n. For this purpose we need a more general result as follows.

Proposition 4

Let u, v be vertices in graphs G, H respectively, with \({\mathrm {deg}}_G(u)\ge {\mathrm {deg}}_H(v)\ge 1\) and \(l=\max (2,{\mathrm {deg}}_G(u)-{\mathrm {deg}}_H(v)+1)\). If G has at least l-biwheel centered at u, then \(G \mathbin {\square } H\) has a k-biwheel centered at (u, v) for any \(0\le k \le {\mathrm {deg}}_G(u)+{\mathrm {deg}}_H(v)={\mathrm {deg}}_{G\mathbin {\square }H}((u,v))\).

Proof

Let \(k=2k'+l'\) where \(k'\) is the maximal integer such that \(k'\le {\mathrm {deg}}_H(v)\) and \(l'\ge 0\). It follows that \(l'\le l-1\). Indeed, if \(k' < {\mathrm {deg}}_H(v)\) then \(l'=0\) or \(l'=1\), and if \(k'={\mathrm {deg}}_H(v)\) then

$$l'\le {\mathrm {deg}}_G(u)+{\mathrm {deg}}_H(v)-2k'={\mathrm {deg}}_G(u)-{\mathrm {deg}}_H(v)\le l-1.$$

(The first inequality holds since \(k=2k'+l'\le {\mathrm {deg}}_G(u)+{\mathrm {deg}}_H(v)\) and the last inequality holds since \({\mathrm {deg}}_G(u)-{\mathrm {deg}}_H(v)+1\le l\).)

Let us denote by \(u_i\) for \(1\le i \le {\mathrm {deg}}_G(u)\) the i-th neighbor of u, and by \(v_j\) for \(1\le j \le {\mathrm {deg}}_H(v)\) the j-th neighbor of v. Furthermore, let \((u_1,y_1,\dots , u_{l'},y_{l'},u_{l'+1})\) be a subpath of the at least l-biwheel of G centered at u where \(d_G(u,y_i)=2\) for all \(1\le i \le l'\). We define the vertices of a k-biwheel in \(G\mathbin {\square }H\) as follows:

$$\begin{aligned} w_i&=(u_i,v),&x_i&=(y_i,v)&\text{ for } \text{ all } i=1,\dots ,l',\\ w_{l'+2j-1}&=(u_{l'+j},v),&x_{l'+2j-1}&=(u_{l'+j},v_j)&\text{ for } \text{ all } j=1,\dots ,k',\\ w_{l'+2j}&=(u,v_j),&x_{l'+2j}&=(u_{l'+j+1},v_j)&\text{ for } \text{ all } j=1,\dots ,k'-1,\\ w_{l'+2j}&=(u,v_j),&x_{l'+2j}&=(u_1,v_j)&\text{ for } j=k'. \end{aligned}$$

Note that all vertices \(w_{i}\), \(x_{i}\) are distinct, vertices \(w_{i}\) are adjacent to (u, v), and \(w_{i}x_{i}\), \(x_{i}w_{i+1}\) are edges in \(G\mathbin {\square }H\) for every \(1\le i \le k=2k'+l'\). Hence these vertices form a k-biwheel in \(G \mathbin {\square }H\) centered at (u, v).    \(\square \)

3.2 (Perfect) Level-Disjoint Partitions from Wheels and Biwheels

Both k-wheels and k-biwheels (except for \(k=2\)) have obvious k perfect, respectively biperfect, level-disjoint partitions rooted in their centers. Indeed, let the i-th level partition \(\mathcal {S}^i\) for \(1\le i \le k\) of \(W_k\) where \(k\ge 1\) be

$$\mathcal {S}^i=(\{v\},\{w_i\},\{w_{i+1}\},\dots ,\{w_{i+k-1}\})$$

with the indices taken cyclically; that is, modulo \((k+1)\) plus 1. Clearly, \(\mathcal {S}^{i}\) and \(\mathcal {S}^{j}\) are level-disjoint up to the root v for any distinct i, j. Similarly for a k-biwheel where \(k\ge 3\), let the i-th level partition \(\mathcal {T}^i\) for \(1\le i \le k\) of \(\widehat{W}_k\) be

$$\mathcal {T}^i=(\{v\},\{w_i\},\{x_i\},\{w_{i+1}\},\{x_{i+1}\},\dots ,\{w_{i+k-1}\},\{x_{i+k-1}\})$$

with the indices taken cyclically; that is, modulo \((k+1)\) plus 1. Clearly, \(\mathcal {T}^{i}\) and \(\mathcal {T}^{j}\) are level-disjoint up to the root v for any distinct i, j.

Note that the above level-disjoint partitions of \(W_k\) and \(\widehat{W}_k\) are perfect, respectively biperfect. Hence their maximal height is optimal in the sense of Proposition 1. Also their number is optimal. Indeed, \(k={\mathrm {deg}}_{W_k}(v)={\mathrm {deg}}_{\widehat{W}_k}(v)\), \(W_k\) is non-bipartite, \(\widehat{W}_k\) is bipartite, and the maximal heights are

$$\max _{1\le i \le k}h(\mathcal {S}^i)=k={\mathrm {ecc}}_{W_k}(v)+k-1, \qquad \max _{1\le i \le k}h(\mathcal {T}^i)=2k={\mathrm {ecc}}_{\widehat{W}_k}(v)+2k-2.$$

The above partitions together with Proposition 2 lead to following sufficient conditions on existence of k level-disjoint partitions with the same root. A vertex v is a cut-vertex in a graph G if \(G-v\) is disconnected.

Theorem 2

If a graph G has a k-wheel for \(k\ge 1\) or k-biwheel for \(k\ge 3\) centered at a vertex v and v is not a cut-vertex, then G has k level-disjoint partitions rooted at v.

Note that the above theorem can be easily generalized for a vertex v that is not a cut-vertex and is adjacent to k vertices on an arbitrarily large cycle in G. Theorem 2 together with Propositions 3 and 4 applies in particular for Cartesian products of (nontrivial) connected graphs as they are 2-connected.

Furthermore, applying Theorem 1 we obtain a sufficient condition on existence of optimal number of (bi)perfect level-disjoint partitions with the same root.

Theorem 3

Let v be a vertex of degree \(k\ge 1\) in a graph G. If G has a k-wheel centered at v, then G has k perfect level-disjoint partitions rooted at v. If G is bipartite, \(k\ge 3\), and G has a k-biwheel centered at v, then G has k biperfect level-disjoint partitions rooted at v.

Proof

Let H denote the k-wheel resp. k-biwheel centered at v. All neighbors of v in G are also in H. In addition, distances to v from G are preserved in H. (Note that in the case of k-biwheel we have \(d_G(v,x_i)=d_H(v,x_i)=2\) for every \(1\le i \le k\) since G is bipartite.) Hence we may apply Theorem 1 to extend the above (bi)perfect level-disjoint partitions of H to G.    \(\square \)

Theorem 3 can be applied to obtain perfect or biperfect level-disjoint partitions for various graphs. For an example, see the four biperfect level-disjoint partitions of the circulant graph in Fig. 2. Further examples are provided in the next subsection.

Fig. 2.
figure 2

Four perfect level-disjoint partitions of a circulant graph rooted at v obtained from a 4-biwheel.

Full size image

Next we generalize Theorem 3. If l divides k, then the above k (bi)perfect level-disjoint partitions of \(W_k\) or \(\widehat{W}_k\) can be compressed into l (bi)perfect level-disjoint partitions. Let \(k=pl\) for some integers l, p and let the i-th level partition of \(W_k\) for \(1\le i \le l\) be \(\mathcal {U}^i=(U_0^i=\{v\},U_1^i,\dots ,U_l^i)\) where

$$U_j^i=\{w_{i+j-1+l}, w_{i+j-1+2l},\dots ,w_{i+j-1+pl}\}$$

for \(1\le j \le l\) and the indices are taken cyclically; that is, modulo \((k+1)\) plus 1. Clearly, \(\mathcal {U}^{i}\) and \(\mathcal {U}^{j}\) are level-disjoint for any distinct \(1\le i,j \le l\). Similarly for a k-biwheel with \(k=pl\), let the i-th level partition of \(\widehat{W}_k\) for \(1\le i \le l\) be \(\mathcal {V}^i=(\{v\},U_1^i,X_1^i,\dots ,U_l^i,X_l^i)\) where \(U_j^i\) is as above and

$$X_j^i=\{x_{i+j-1+l}, x_{i+j-1+2l},\dots ,x_{i+j-1+pl}\}$$

for \(1\le j \le l\) and the indices are taken cyclically; that is, modulo \((k+1)\) plus 1. Clearly, \(\mathcal {V}^{i}\) and \(\mathcal {V}^{j}\) are level-disjoint for any distinct \(1\le i,j \le l\).

These partitions lead to generalization of Theorem 3 as follows. Additional properties of these partitions, called partitions modulo p, have been studied in [6].

Theorem 4

Let v be a vertex in a graph G of degree \(k\ge 1\) divisible by an integer \(l\ge 1\). If G has a k-wheel centered at v, then G has l perfect level-disjoint partitions rooted at v. If G is bipartite, \(k\ge 3\), and G has a k-biwheel centered at v, then G has l biperfect level-disjoint partitions rooted at v.

4 Particular Networks

In this section we consider particular examples of Cartesian products and provide explicit constructions for them. We also propose several problems and conjectures.

4.1 Torus \(C_{2n} \mathbin {\square } C_{2m}\)

First we consider a bipartite 2-dimensional torus; that is, the graph \(C_{2n} \mathbin {\square } C_{2m}\) where \(n,m\ge 2\). By Proposition 3, it has a 4-biwheel centered at any vertex r. Hence by Theorem 3, it has four level-disjoint partitions rooted at r of (optimal) height

$$ecc_{C_{2n} \mathbin {\square } C_{2m}}(r)+6=n+m+6.$$

Explicitly, let us denote the vertices of cycles \(C_{2n}, C_{2m}\) by \(C_{2n}=(u_1,\dots ,u_{2n})\), \(C_{2m}=(v_1,\dots ,v_{2m})\) and assume \(r=(u_1,v_1)\). We define a function f(i, j, k) for \(1\le i \le 2n\), \(1\le j \le 2m\), \(1\le k \le 4\) determining the level of each vertex \((u_i,v_j)\) in the k-th level partition by

$$f(i,j,k)=d(i,j)+{\left\{ \begin{array}{ll} \ 2((k-1) \bmod 4) &{} \text{ if } 1< i \le n \text{ and } 1\le j \le m,\\ \ 2(k \bmod 4) &{} \text{ if } i=1 \text{ or } n< i \le 2n, \text{ and } 2\le j \le m,\\ \ 2((k+1) \bmod 4) &{} \text{ if } n< i \le 2n, \text{ and } j=1 \text{ or } m< j \le 2m,\\ \ 2((k+2) \bmod 4) &{} \text{ if } 1\le i \le n \text{ and } m< j \le 2m\\ \end{array}\right. } $$

and \(f(1,1,k)=0\), where \(d(i,j)=d_{C_{2n}\mathbin {\square }C_{2m}}((u_i,v_j),(u_1,v_1))\) is

$$d(i,j)={\left\{ \begin{array}{ll} \ i+j-2 &{} \text{ if } 1\le i \le n \text{ and } 1\le j \le m,\\ \ 2n-i+j &{} \text{ if } n< i \le 2n \text{ and } 1\le j \le m,\\ \ 2n-i+2m-j+2 &{} \text{ if } n< i \le 2n \text{ and } m< j \le 2m,\\ \ i+2m-j &{} \text{ if } 1\le i \le n \text{ and } m< j \le 2m. \end{array}\right. }$$

Then it is easy to verify that \(\mathcal {S}^k=(S^k_0,\dots ,S^k_h)\) for \(k=1,\dots ,4\) where \(h=n+m+6\) and

$$S^k_l=\{(u_i,v_j)\mid f(i,j,k)=l, 1\le i \le 2n, 1\le j \le 2m\}$$

for every \(0\le l \le h\) are biperfect level-disjoint partitions of \(C_{2n}\mathbin {\square } C_{2m}\). For example see Fig. 3.

Fig. 3.
figure 3

Four biperfect level-disjoint partitions of \(C_6 \mathbin {\square } C_4\) rooted at \(r=(u_1,v_1)\) of maximal height 11. The eccentric vertex to r, denoted by \(\overline{r}\), is in the (last) 11th level of the second partition. The arrows denote how these LDPs are constructed from LDPs of the 4-biwheel centered at r.

Full size image

Furthermore, by applying Theorem 4 we obtain two same-rooted level-disjoint partitions of \(C_{2n}\mathbin {\square }C_{2m}\) of (optimal) height \(n+m+2\). Trivially, a single distance partition from the root has (optimal) height \(n+m\) as well. Hence it remains a question whether \(C_{2n}\mathbin {\square } C_{2m}\) has three same-rooted level-disjoint partitions of (optimal) height \(n+m+4\), which is perhaps easy to resolve. More interestingly, this can be generalized for higher dimensions as follows.

Conjecture 1

The (bipartite) generalized torus \(C_{2n_1} \mathbin {\square } C_{2n_2} \mathbin {\square } \cdots \mathbin {\square } C_{2n_d}\) where \(d\ge 2\) and \(n_1,\dots ,n_d \ge 2\) has l same-rooted level-disjoint partitions of optimal height for every \(1\le l \le 2d\).

We only know from Theorem 4 that Conjecture 1 holds if l divides 2d. Note that by (2), an optimal height of four r-routed level-disjoint partitions of a non-bipartite torus is \({\mathrm {ecc}}(r)+3\) instead of \({\mathrm {ecc}}(r)+6\) for bipartite case. This leads us to pose the following problem. Clearly, if Conjecture 1 holds, this problem reduces only to non-bipartite cases.

Problem 1

Which of generalized tori \(C_{m_1} \mathbin {\square } C_{m_2} \mathbin {\square } \cdots \mathbin {\square } C_{m_d}\) admit 2d same-rooted level-disjoint partitions of optimal height?

4.2 Mesh \(P_{n} \mathbin {\square } P_{m}\)

For 2-dimensional meshes \(P_{n} \mathbin {\square } P_{m}\) where \(n,m\ge 3\) we obtain similar results as for tori, up to choice of the root. Let us denote the vertices of paths \(P_n\), \(P_m\) by \(P_n=(u_1,\dots ,u_n)\), \(P_m=(v_1,\dots ,v_m)\). A vertex \((u_i,v_j)\) of \(P_{n} \mathbin {\square } P_{m}\) is an inner vertex if \(1<i<n\) and \(1<j<m\); and a border vertex otherwise.

By Proposition 3, the mesh \(P_{n} \mathbin {\square } P_{m}\) has a 4-biwheel centered at any inner vertex. Hence by Theorem 3 it has four level-disjoint partitions rooted at the same inner vertex \(r=(u_i,v_j)\) of (optimal) height \(ecc_{P_n\mathbin {\square } P_m}(r)+6\) where

$$ecc_{P_n\mathbin {\square } P_m}((u_i,u_j))=\max (i+j-2,i+m-j-1,n-i+m-j,n-i+j-1).$$

For example, see Fig. 4.

Fig. 4.
figure 4

Four biperfect level-disjoint partitions of \(P_6 \mathbin {\square } P_4\) rooted at \(r=(u_2,v_2)\) of maximal height 12. The eccentric vertex to r, denoted by \(\overline{r}\), is in the (last) 12th level of the fourth partition. The arrows denote how these LDPs are constructed from LDPs of the 4-biwheel centered at r.

Full size image

Furthermore, by applying Theorem 4 we obtain two level-disjoint partitions rooted at the same inner vertex r of (optimal) height \(ecc(r)+2\). Explicit constructions of such level-disjoint partitions can easily be derived in a similar way as for torus. We leave them out as they are merely technical. Similarly as for bipartite tori, we propose the following conjecture.

Conjecture 2

The generalized mesh \(P_{m_1} \mathbin {\square } P_{m_2} \mathbin {\square } \cdots \mathbin {\square } P_{m_d}\) where \(d\ge 2\) and \(m_1,\dots ,m_d \ge 3\) has l r-rooted level-disjoint partitions of optimal height for every \(1\le l \le 2d\) and every inner vertex r.

Note that Conjecture 2 implies Conjecture 1 since a bipartite torus contains a mesh with the same parameters \(2n_1,\dots ,2n_d\) as a spanning subgraph, and the mesh has an inner vertex with eccentricity equal to the eccentricity of any vertex of the torus. We only know from Theorem 4 that Conjecture 2 holds if l divides 2d. Note that we considered only inner vertices as roots since for border vertices in 2-dimensional meshes there are no k-biwheels with \(k\ge 3\).

Problem 2

Determine the maximal number of r-rooted level-disjoint partitions of optimal height in the generalized mesh \(P_{m_1} \mathbin {\square } P_{m_2} \mathbin {\square } \cdots \mathbin {\square } P_{m_d}\) for all vertices r and all parameters \(d\ge 2\), \(m_1,\dots ,m_d \ge 2\).

4.3 Hypercube \(Q_n\)

We view the n-dimensional hypercube \(Q_n\) for \(n\ge 3\) as the Cartesian product of \(C_4\simeq \widehat{W}_2\) and the \((n-2)\)-fold Cartesian product of \(K_2\); that is, \(Q_n\simeq C_4 \mathbin {\square } (K_2)^{n-2}\). By recursive application of Proposition 4, we obtain that \(Q_n\) for any \(n\ge 3\) has an n-biwheel centered at any vertex v. Explicitly, let us assume that \(v=0^n=(0,\dots ,0)\). Then an n-biwheel centered at v is formed (for example) by vertices \(w_i=e_i\) for \(i=1,\dots ,n\), \(x_i=e_{i}\oplus e_{i+1}\) for \(i=1,\dots , n-1\), and \(x_n=e_1 \oplus e_n\), where \(e_i\) denotes the vector with 1 exactly in the ith coordinate.

Hence by Theorem 3 we obtain the following result, answering affirmatively a conjecture from [6] where only the case when \(n=3 \cdot 2^i\) or \(n=4 \cdot 2^i\) for some integer \(i\ge 0\) was shown. See examples for \(n=3\) and \(n=4\) on Fig. 5.

Corollary 1

For every \(n\ge 3\) there exist n level-disjoint partitions of \(Q_n\) with the same root and with the maximal height \(3n-2\).

Fig. 5.
figure 5

(a) Three biperfect level-disjoint partitions of \(Q_3\) rooted at v of maximal height 7. (b) Four biperfect level-disjoint partitions of \(Q_4\) rooted at v of maximal height 10.

Full size image

Explicitly, we define a function f(u, k) for \(u\in V(Q_n)\), \(1\le k \le n\) determining the level of each vertex u in the k-th level partition as

$$f(u,k)={\left\{ \begin{array}{ll}\ 0 &{}\text{ if } u=v\ (=0^n),\\ \ 2((n+k) \bmod n)+2&{}\text{ if } u=x_n\ (=e_1 \oplus e_n),\\ \ 2((i+k) \bmod n)+j&{}\text{ otherwise } \end{array}\right. }$$

where i is the position of the leftmost 1 in u and j is the number of 1’s in u. Then it is easy to verify that \(\mathcal {S}^k=(S^k_0,\dots ,S^k_h)\) for \(k=1,\dots ,n\) where \(h=3n-2\) and \(S^k_l=\{u\in V(Q_n)\mid f(u,k)=l\}\) for every \(0\le l \le h\) are biperfect level-disjoint partitions of \(Q_n\).

Note that the above definition of f(u, k) is based on the fact that each vertex u except v or \(x_n\) has a shortest path to the root v that goes through \(w_i=e_i\) and avoids \(x_n\), where i is the position of the leftmost 1 in u. Indeed, from u by consecutively changing the rightmost 1 to 0 we obtain all vertices of such a path. Furthermore, from \(x_i\) we go to \(w_i=e_i\) along these paths for each \(i=1,\dots ,n-1\) which agrees with the partition of the n-biwheel \(\widehat{W}_n\). Therefore, we may extend the canonical biperfect level-disjoint partitions of \(\widehat{W}_n\) along these paths to biperfect level-disjoint partitions of \(Q_n\) by applying Theorem 1, which corresponds to the above prescription for f(u, k).

Furthermore, from Theorem 4 we obtain that \(Q_n\) for any \(n\ge 3\) has k biperfect level-disjoint partitions rooted at the same vertex (of maximal height \(n+2k-2\)) if k divides n. We propose that it holds for any \(k\ge 1\).

Conjecture 3

For any \(1\le k \le n\), \(n \ge 3\), the hypercube \(Q_n\) has k same-rooted level-disjoint partitions of optimal height.

5 Conclusions

In this work the concept of level-disjoint partitions which was originally introduced in [6] is employed to describe simultaneous broadcasting of multiple messages from the same originator in the considered communication model.

It is shown that a local solution on a suitable subgraph can be extended to the whole graph without loss of optimality. In this paper we use specifically wheels and biwheels as local subgraphs. This could be further generalized for other subgraphs such as subdivisions of wheels.

This approach leads to simultaneous broadcasting in optimal time on particular Cartesian products of graphs. However, it can be applied for a much larger class of graphs. For example, for some circulant graphs or Knödel graphs that have been previously studied in the context of broadcasting [3, 4, 11].

For bipartite tori, meshes, and hypercubes we provided tight results based on construction of optimal number of biperfect level-disjoint partitions from biwheels. We believe that simultaneous broadcasting can be achieved in optimal time for any number of messages on generalized bipartite tori, generalized meshes, and hypercubes (Conjectures 1–3). The problem of simultaneous broadcasting in optimal time remains open for general tori (Problem 1) and meshes with border originator vertices (Problem 2).