Dynamics on Linear Influence Network Games Under Stochastic Environments

Abstract

A linear influence network is a broadly applicable conceptual framework in risk management. It has important applications in computer and network security. Prior work on linear influence networks targeting those risk management applications have been focused on equilibrium analysis in a static, one-shot setting. Furthermore, the underlying network environment is also assumed to be deterministic.

In this paper, we lift those two assumptions and consider a formulation where the network environment is stochastic and time-varying. In particular, we study the stochastic behavior of the well-known best response dynamics. Specifically, we give interpretable and easily verifiable sufficient conditions under which we establish the existence and uniqueness of as well as convergence (with exponential convergence rate) to a stationary distribution of the corresponding Markov chains.

1 Introduction

The application of game theory to networks has received much attention in the literature [1, 2] in the past decade. The underlying model typically consists of agents, connected by physical or virtual links, who must strategically decide on some action given the actions of the other users and the network structure. The well-founded motivations for this study and the specific applications examined have spanned many fields such social or economic networks [3], financial networks [4, 5], and a diverse range (packets, robots, virtual machines, sensors, etc.) of engineering networks [6–10]. These different contexts all have in common the presence of inter-agent influences: the actions of individual agents can affect others in either a positive or negative way, which are typically called externalities. As a simple example, consider two web-enabled firms [11] that have customers in common that use the same passwords on both sites. In this case, an investment in computer system security from one firm naturally strengthens the security of the other, resulting in larger effective investment of the other firm compared to its own, independent investment. On the other hand, this investment may shrink the effective investment of a third firm (a competitor) in the same business, as this enhanced security on the two firms makes the attack on the third firm more attractive.

As another example, technology innovation is another instance where a network of agents’ actions can produce inter-dependent effects on one another. Here the concept of innovation risk glues together the investments made by each agent: if a social media company (e.g. Facebook) is seeking to expand its enterprise by innovating on new products, then a partnering video games (e.g. Zynga) company whose games are played on that social media platform will be benefited and will in turn benefit the social media company with its own investment. On the other hand, a similar effort made by another competing social media company (e.g. Myspace) will cause negative impact on both of the prior firms and will be negatively impacted by them as well.

In all these examples, this feature of inter-agent influences is captured by a linear influence network, which was first employed in [11, 12] to study and manage the risk in computer security settings. In a nutshell and in the words of [11], “[i]n this model, a matrix represents how one organization’s investments are augmented by some linear function of its neighbors investments. Each element of the matrix, representing the strength of influence of one organization on another, can be positive or negative and need not be symmetric with respect to two organizations.” [13] very recently generalized this interdependence model to an influence network, where every agent’s action is augmented by some (arbitrary) function of its neighbors’ joint action to yield a final, effective action, thus allowing for a general influence effect in terms of both directions and values.

We mention that in addition to the examples mentioned above, linear influence network model is a broadly applicable conceptual framework in risk management. The seminal work [14] provides more applications (one in security assets which generalizes [11] and another in vulnerabilities) and numerical examples to illustrate the versatility and power of this framework, to which the readers are referred to for an articulate exposition. On this note, we emphasize that the application of game theory to security has many different dimensions, to which the linear influence network model is but one. See [15] for an excellent and comprehensive survey on this topic.

On the other hand, all the prior work on linear influence networks and the applications [11–14, 16] have been focused on equilibrium analysis in a static, one-shot setting. Further, the influence matrix, which represents the underlying network environment, is assumed to be deterministic. Although prior analyses provide an important first step in gaining the insights, both of these assumptions are somewhat stringent in real applications: agents tend to interact over a course of periods and the influences are random and can fluctuate from period to period. Consequently, we aim to incorporate these two novel elements into our study.

In this paper, we consider a stochastic formulation of the best response dynamics by allowing the underlying network environment to be stochastic (and time-varying) and study its stochastic behavior. In the deterministic network environment case [11, 12, 16], it is known that the best response dynamics has the desired property of converging to the unique Nash equilibrium when the influence matrix is strictly diagonally dominant. The linear influence network represented by a strict diagonally dominant influence matrix has direct and intuitive interpretations [11, 12, 16] in the applications and constitutes an important class for study. Building on this observation, we aim to characterize the stochastic behavior of the best response dynamics when the influence matrix is sometimes strictly diagonally dominant and sometimes not. Our stochastic formulation is a rather broad framework in that we do not impose any exogenous bounds on each agent’s action, nor on the randomness of the network environment. Of course, the same stochastic stability results hold should one wish to impose such constraints for a particular application.

We then give two sufficient conditions on the stochastic network environment that ensure the stochastic stability of the best response dynamics. These conditions have the merits of being both easily interpretable and easily verifiable. These two sufficient conditions (Theorem 3) serve as the main criteria under which we establish the existence and uniqueness of as well as convergence to a stationary distribution of the corresponding Markov chains. Furthermore, convergence to the unique stationary distribution is exponentially fast. These results are the most desired convergence guarantees that one can obtain for a random dynamical system. These sufficient conditions include as a special case the interesting and simultaneously practical scenario, in which we demonstrate that the best response dynamics may converge in a strong stochastic sense, even if the network itself is not strictly diagonally dominant on average.

2 Model Formulation

We start with a quick overview of the linear influence network model and the games induced therein. Our presentation mainly follows [14, 16]. After disusing some of the pertinent results, we conclude this section with a motivating discussion in Sect. 2.4 on the main question and the modeling assumptions we study in this paper.

2.1 Linear Influence Network: Interdependencies and Utility

A linear influence network consists of a set of players each taking an action $x_i \in [0, \infty )$, which can be interpreted as the amount of investment made by player i. The key feature of an influence network is the natural existence of interdependencies which couple different players’ investments. Specifically, player i’s effective investment depends not only on how much he invests, but on how much each of his neighbors (those whose investments produce direct external effects on player i) invests. A linear influence network is an influence network where such interdependencies are linear.

We model the interdependencies among the different players via a directed graph, $\mathcal {G} = \{\mathcal {N},\mathcal {E}\}$ of nodes $\mathcal {N}$ and edges $\mathcal {E}$. The nodes set $\mathcal {N}$ has N elements, one for each player i, $i = 1 \ldots N$. The edges set $\mathcal {E}$ contains all edges (i, j) for which a decision by i directly affects j. For each edge, there is an associated weight, $\psi _{ij} \in \mathbb {R}$, either positive or negative, representing the strength of player i’s influence on player j (i.e. how much player j’s effective investment is influenced per player i’s unit investment). Consequently, the effective investment $x_i^{eff}$ of player i is then $x_i^{eff} = x_i + \sum _{j \ne i} \psi _{ji} x_j$.

We can then represent the above linear influence network in a compact way via a single network matrix, $\mathbf {W} \in \mathbb {R}^{N \times N}$, as follows:

$$\begin{aligned} \mathbf {W}_{ij} = \left\{ \begin{array}{ll} 1 &{} \text {if }i = j \\ \psi _{ji} &{} \text {if } (j,i) \in \mathcal {E}\\ 0 &{} \text {otherwise}. \end{array}\right. \end{aligned}$$

(1)

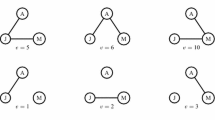
In particular, we call into attention that $\mathbf {W}_{ij}$ represents the influence of player j on player i. An example network and the associated $\mathbf {W}$ matrix are shown in Fig. 1.

We can therefore rewrite the effective investment of player i as $x_i^{eff} = x_i + \sum _{j \ne i} \psi _{ji} x_j = \sum _{j=1}^N \mathbf {W}_{ij}x_j$. Written compactly in matrix forms, if $\mathbf {x}$ denotes the vector of individual investments made by all the players, then the effective investment is given by $\mathbf {x}^{eff} = \mathbf {W} \mathbf {x}$.

Fig. 1.

An instance of a linear influence network.

Each player i has an utility function that characterizes his welfare:

$$\begin{aligned} U_i(\mathbf {x}) = V_i(x_i^{eff}) - c_i x_i. \end{aligned}$$

(2)

The utility function has two components that admit a simple interpretation. $V_i$ gives the value that player i places on the total effective investment made (resulting from player i’s investment and the externalities coming from its neighbors.) The second component is the cost on player i’s side for investing $x_i$ amount, where $c_i$ is the relative trade-off parameter that converts the value and the cost on the same scale.

Drawing from the literature on utility theory, we impose the following standard assumptions on the value function. Remark 1 gives an intuitive explanation on those assumptions.

Definition 1

The continuously differentiable function $V_i(\cdot ): [0, \infty ) \rightarrow \mathbf {R}$ ¹ is called admissible if the following conditions hold:

• 1. strictly increasing,

• 2. strictly concave,

• 3. $V_i'(0) > c_i$ and

• 4. $\lim _{x \rightarrow \infty }V_i'(x) < c_i$.

Remark 1

Here we use the network security example to provide intuition on why the assumptions constituting an admissible value function are natural. Here the value function for each player (firm) can be viewed to represent the level of its network security or the profitability derived from that level of security, as a result of the total effective investment. The first condition says that if the total effective investment made by a firm increases, then this level of security increases as well. The second conditions says that the marginal benefit of more effective investment is decreasing. The third condition says that it is always in the interest of a firm to have a positive effective investment. The fourth condition says that the marginal benefit of more effective investment will eventually drop below the unit cost of investment.

For the remainder of the paper, we will assume each $V_i$ is admissible.

2.2 Nash Equilibrium of the Induced Game: Existence, Uniqueness and Convergence

With the above utility (payoff) function $U_i$, a multi-player single-stage complete-information game is naturally induced. We proceed with the standard solution concept Nash equilibrium (NE), defined here below:

Definition 2

Given an instance of the game $(\mathcal {N}, \mathcal {E}, \mathbf {W}, \{V_i\}_{i \in \mathcal {N}}, \{c_i\}_{i \in \mathcal {N}})$, the investment vector $\mathbf {x}^*$ is a (pure-strategy) Nash equilibrium if, for every player i, $U_i(x_i^*, \mathbf {x}_{-i}^*) \ge U_i(x_i, \mathbf {x}_{-i}^*), \forall x_i \in [0, \infty ),$ where $\mathbf {x}_{-i}^*$ is the vector of all investments but the one made by player i.

The existence and uniqueness of a NE in the induced game on a linear influence network has been studied and characterized in depth by [11, 12, 14, 16], where the connection is made between a NE and a solution to an appropriate Linear Complementarity Problem (LCP), the latter being an extensively studied problem [17]. As such, different classes of matrices (i.e. assumptions made on the network matrix $\mathbf {W}$) have been shown to lead to either existence or uniqueness (or both) of a NE.

As has been emphasized by the previous work [11, 12, 14], a particular class of network matrices $\mathbf {W}$ that deserve special and well-motivated attention is the class of strictly diagonally dominant matrices, defined next.

Definition 3

Let $\mathbf {W} \in \mathbf {R}^{N \times N}$ be a square matrix.

• 1. $\mathbf {W}$ is a strictly diagonally row dominant matrix if for every row i: $\sum _{j \ne i}|\mathbf {W}_{ij}| < |\mathbf {W}_{ii}|$.

• 2. $\mathbf {W}$ is a strictly diagonally column dominant matrix if its transpose is strictly diagonally row dominant.

A strictly diagonally dominant matrix is either a strictly diagonally row dominant matrix or a strictly diagonally column dominant matrix.

The class of strictly diagonally dominant matrices play a central role in linear influence networks because they are both easily interpretable and present. For instance, a strictly diagonally row dominant matrix represents a network where each player’s influence on his own is larger than all his neighbors combined influence on him. A strictly diagonally column dominant matrix represents a network where each player’s influence on his own is larger than his own influence on all of his neighbors combined. It turns out, as stated in the following theorem, a strictly diagonally dominant influence matrix ensures the existence of a unique Nash equilibrium. We mention in passing that although there are other classes of matrices that ensure the existence of a unique Nash equilibrium (such as the class of positive definite matrices), they do not have direct interpretations and do not easily correspond to practical scenarios of an linear influence network.

Theorem 1

Let $(\mathcal {N}, \mathcal {E}, \mathbf {W}, \{V_i\}_{i \in \mathcal {N}}, \{c_i\}_{i \in \mathcal {N}})$ be a given instance of the game. If the network matrix $\mathbf {W}$ is strictly diagonally dominant, then the game admits a unique Nash equilibrium.

Proof

See [12, 16].

2.3 Convergence to NE: Best Response Dynamics

The existence and uniqueness results of NE play an important first step in identifying the equilibrium outcomes of the single-stage game on linear influence networks. The next step is to study dynamics for reaching that equilibrium (should a unique NE exist), a more important one from the engineering perspective. An important class of dynamics is that of best response dynamics, which in addition to being simple and natural, enjoys the attractive feature of being model-agnostic, to be described below. We first define the best response function.

Definition 4

The best response function $g_i(\mathbf {x})$ for player i is defined as: $g_i(\mathbf {x}) = {\text {arg max}}_{x_i \ge 0}\; U_i(x_i, \mathbf {x}_{-i})$. The best response function for the network is denoted by $g(\mathbf {x}) = (g_1(\mathbf {x}), g_2(\mathbf {x}), \ldots , g_N(\mathbf {x}))$

In the current setting, we can obtain an explicit form for the best response function. Let $b_i$ represent the (single) positive value at which $V_i'(\cdot ) = c_i$, which is always guaranteed to uniquely exist due to the assumption that $V_i$ is admissible. Then, it can be easily verified that:

$$\begin{aligned} g(\mathbf {x}) = \mathop {\text {max}}(\mathbf {0},(\mathbf {I}-\mathbf {W})\mathbf {x} + \mathbf {b}). \end{aligned}$$

(3)

With the above notation, we are now ready to state best response dynamics (formally given in Algorithm 1): it is simply a distributed update scheme where in each iteration, every player chooses its investment in response to the investments his neighbors have chosen in the previous iteration. Note that each player i, in order to compute its best response investment for the current iteration, need not know what his neighboring players’ investments were in the previous iteration. Instead, it only needs to know the combined net investments ($\sum _{j \ne i} \psi _{ji}x_j$) his neighbors has induced to him. This combined net investments can be inferred since player i knows how much he invested himself in the previous iteration and observes the current payoff he receives. This constitutes perhaps the single most attractive feature of best response dynamics in the context of linear influence network games: the model-agnostic property.

Writing the distributed update in Algorithm 1 more compactly, we have: $\mathbf {x}(t+1) = g(\mathbf {x}(t)) = \mathop {\text {max}}(\mathbf {0},(\mathbf {I}-\mathbf {W})\mathbf {x}(t) + \mathbf {b})$. It turns out that convergence for $\mathbf {x}(t)$ is guaranteed when $\mathbf {W}$ is strictly diagonally dominant.

Theorem 2

If the network matrix $\mathbf {W}$ is strictly diagonally dominant, then the best response dynamics in Algorithm 1 converges to the unique NE.

Proof

See [12, 16].

2.4 Motivation and Main Question of the Paper

The best response dynamics, for reasons mentioned before, have enjoyed popularity in prior work. However, the convergence property of the best response dynamics rests on the crucial yet somewhat unrealistic assumption that the underlying network environment is fixed over time, i.e. $\mathbf {W}$ stays constant in every time period. In practice, $\mathbf {W}^t$ encode the influence of players over its neighbors and should be inherently dynamic and time-varying.

Here we lift this assumption by allowing $\mathbf {W}^t$ to be random and time-varying. Consequently, using X(t) to denote the (random) investment vector at time t, the best response dynamics should be re-written as:

$$\begin{aligned} X(t+1) = \mathop {\text {max}}(\mathbf {0},(\mathbf {I}-\mathbf {W}^t)X(t) + \mathbf {b}). \end{aligned}$$

(4)

Our principal goal in this paper is then to study the stochastic behavior of the resulting power iterate $\{X(t)\}_{t=0}^{\infty }$ (which is now a stochastic process) and to identify sufficient conditions under which stochastic stability is guaranteed. For simplicity, we assume that random network matrix $\mathbf {W}^t$ is iid. The iid case, although simple, provides illuminating structural insights and can be easily extended to the stationary and ergodic network environment environments case.

Observe that under iid assumption, the iterates $\{X(t)\}_{t=0}^{\infty }$ in the best response dynamics form a Markov chain. Our principal focus in the next section is to characterize conditions under which the Markov chain admits a unique stationary distribution with guaranteed convergence properties and/or convergence rates. These results are of importance because they establish the stochastic stability (in a strong sense to be formalized later) of the best response dynamics in the presence of random and time-varying network environments.

In addition, this stochastic process $\{X(t)\}_{t=0}^{\infty }$ can be generated in a variety of ways, each corresponding to a different practical scenario. Section 3.2 makes such investigations and presents two generative models and draw some interesting conclusions.

3 Main Criteria for Stochastic Stability Under Random Network Environment

In this section, we characterize the behavior of the best response dynamics under stochastic (and time-varying) network environment and give the main criteria for ensuring stochastic stability. Our focus here is to identify sufficient conditions that are broad enough while at the same time interpretable and efficiently verifiable.

Our assumption on the random network is rather mild: $\{\mathbf {W}^t\}_{t=1}^{\infty }$ is drawn iid according to some fixed distribution with bounded first moments from some support set $\mathcal {W} \subset \mathbf {R}^{N \times N}$, where $\mathcal {W}$ can be either discrete or continuous. Alternatively, this means that each individual influence term $\mathbf {W}_{ij}$ is absolutely integrable: $\mathbf {E}[{|\mathbf {W}_{ij}}|] < \infty$. It is understood that $\mathbf {W}_{ii} = 1$ for each $\mathbf {W} \in \mathcal {W}$ since one’s own influence on oneself should not fluctuate.

3.1 Two Main Sufficient Conditions for Stochastic Stability

The state space for the Markov chain $\{X(t)\}_{t=1}^{\infty }$ will be denoted² by $\mathcal {X} = \mathbf {R}^N_+$. $(\mathcal {X}, \mathcal {B}(\mathcal {X}))$ is then the measurable space, where $\mathcal {B}(\mathcal {X})$ is the Borel sigma algebra on $\mathcal {X}$, induced by some vector norm. Since all finite-dimensional norms are equivalent (up to a constant factor), the specific choice of the norm shall not concern as here since they all yield the same Borel sigma algebra³. The transition kernel K(x, A) denotes the probability of transitioning in one iteration from $x \in \mathcal {X}$ into the measurable set $A \in \mathcal {B}(\mathcal {X})$. $K^t(x, A)$ then denotes the t-step transition probability. We use $K^t(x, \cdot )$ to denote the probability measure (distribution) of the random variable X(t) with the initial point at x.

Definition 5

Let $\Vert \cdot \Vert$ be any vector norm on $\mathbf {R}^n$, A be a square matrix on $\mathbf {R}^{n \times n}$, w be a strictly positive weight vector in $\mathbf {R}^n$ and v be a generic vector in $\mathbf {R}^n$.

• 1. The induced matrix norm $\Vert \cdot \Vert$ is defined by $\Vert A\Vert = \max _{\Vert x\Vert = 1}\Vert Ax\Vert$.

• 2. The weighted $l_{\infty }$ norm with weight w is defined by $\Vert v\Vert _{\infty }^w = \max _{i} |\frac{v_i}{w_i}|$.

• 3. The weighted $l_1$ norm with weight w is defined by $\Vert v\Vert _1^w = \sum _{i=1}^n |\frac{v_i}{w_i}|$.

Since we are using the same notation to denote both the vector norm and the corresponding induced matrix norm, the context shall make it clear which norm is under discussion. In the common special case where w is the all-one vector, the corresponding induced matrix norms will be denoted conventionally by $\Vert \cdot \Vert _1, \Vert \cdot \Vert _{\infty }$. The following proposition gives known results about the induced matrix norms $\Vert \cdot \Vert _1^w, \Vert \cdot \Vert _{\infty }^w$. See [18].

We are now ready to state, in the following theorem, our main sufficient conditions for the bounded random network environment case. The proof⁴ is omitted here due to space limitation.

Theorem 3

Let $\mathbf {W}$ be the random network matrix with bounded support from which $\mathbf {W}^t$ is drawn iid. Assume that either one of the following two conditions is satisfied:

• 1. There exists a strictly positive weight vector w such that $\mathbb {E}[\log \Vert \mathbf {I} -\mathbf {W}\Vert _{\infty }^w] < 0$;

• 2. There exists a strictly positive weight vector w such that $\mathbb {E}[\log \Vert \mathbf {I} -\mathbf {W}\Vert _{1}^w] < 0$.

Then:

• 1. The Markov chain $\{X(t)\}_{t=0}^{\infty }$ admits a unique stationary distribution $\pi (\cdot )$.

• 2. The Markov chain converges to the unique stationary distribution in Prokhorov metric irrespective of the starting point: $\forall X(0) \in \mathcal {X}, d_{\rho }(K^t(X(0), \cdot ), \pi (\cdot )) \rightarrow 0$ as $t \rightarrow \infty$, where $d_{\rho }(\cdot , \cdot )$ is the Prokhorov metric⁵ induced by the Euclidean metric $\rho$.

• 3. The convergence has a uniform exponential rate: There exists an r (independent of X(0)), with $0< r < 1$, such that $\forall x \in \mathcal {X}$, there exists a constant $C_{X(0)} > 0$ such that $d_{\rho }(K^t(X(0), \cdot ), \pi (\cdot )) \le C_{X(0)}r^t, \forall t$.

Remark 2

First, note that $\mathbb {E}[\log \Vert \mathbf {I} -\mathbf {W}\Vert _{\infty }^w] < 0$ is a weaker condition than $\mathbb {E}[\Vert \mathbf {I} -\mathbf {W}\Vert _{\infty }^w] < 1$, since by Jensen’s inequality, $\mathbb {E}[\Vert \mathbf {I} -\mathbf {W}\Vert _{\infty }^w] < 1$ implies $\mathbb {E}[\log \Vert \mathbf {I} -\mathbf {W}\Vert _{\infty }^w] < 0$. Similarly, $\mathbb {E}[\log \Vert \mathbf {I} -\mathbf {W}\Vert _{1}^w] < 0$ is a weaker condition than $\mathbb {E}[\Vert \mathbf {I} -\mathbf {W}\Vert _{1}^w] < 1$.

Second, it follows from basic matrix theory that any square matrix satisfies $\Vert A\Vert _{1}^w = \Vert A^{\text {T}}\Vert _{\infty }^{\frac{1}{w}}$. Consequently, the second sufficient condition can also be cast in the first by taking the transpose and inverting the weight vector: There exists a strictly positive weight vector w such that $\mathbb {E}[\log \Vert \mathbf {I} -\mathbf {W}\Vert _{1}^w] < 0$ if and only if there exists a strictly positive weight vector $\tilde{w}$ such that $\mathbb {E}[\log \Vert (\mathbf {I} -\mathbf {W})^{\text {T}}\Vert _{\infty }^{\tilde{w}}] < 0$.

Third, for a deterministic matrix A, one can efficiently compute its induced weighted $l_1$ and weighted $l_{\infty }$ norms. Further, for a fixed positive weight vector w and a fixed distribution on $\mathbf {W}$, one can also efficiently verify whether $\mathbb {E}[\log \Vert \mathbf {I} -\mathbf {W}\Vert _{\infty }^w] < 0$ holds or not (similar for $\mathbb {E}[\log \Vert \mathbf {I} -\mathbf {W}\Vert _{1}^w] < 0$). The most common and natural weight vector is the all-ones vector in the context of strictly diagonally dominant matrices. This point is made clear by the discussion in Sect. 3.1, which also sheds light on the motivation for the particular choices of the induced norms in the sufficient conditions.

3.2 A Generative Model: Discrete-Support Random Network Environment

Here we proceed one step further and give an interesting and practical generative model for the underlying random network for which there is a direct interpretation. In this generative model, we assume that each influence term $\mathbf {W}_{ij}$ ($i \ne j$) comes from a discrete set of possibilities. This is then equivalent to the network matrix $\mathbf {W}^t$ being drawn from a discrete support set $\mathcal {W} = \{W^1, W^2, \dots \}$. This generative model of randomness has the intuitive interpretation that one player’s influence on another can be one of the possibly many different values, where it can be positive at one time and negative at another time.

In the special case that each $W^i$ in $\mathcal {W}$ is either strictly diagonally row dominant or strictly diagonally column dominant, then stochastic stability is guaranteed, as given by the following statement.

Corollary 1

Let the support $\mathcal {W}$ be a set of strictly diagonally row dominant matrices. Then for any probability distribution on $\mathcal {W}$ from which $\mathbf {W}^t$ is sampled, the Markov chain $\{X(t)\}_{t=0}^{\infty }$ given by the best response dynamics satisfies the following:

• 1. The Markov chain $\{X(t)\}_{t=0}^{\infty }$ admits a unique stationary distribution $\pi (\cdot )$.

• 2. The Markov chain converges to the unique stationary distribution in Prokhorov metric irrespective of the starting point: $\forall X(0) \in \mathcal {X}, d_{\rho }(K^t(X(0), \cdot ), \pi (\cdot )) \rightarrow 0$ as $t \rightarrow \infty$, where $d_{\rho }(\cdot , \cdot )$ is the Prokhorov metric induced by the Euclidean metric $\rho$.

• 3. The convergence has a uniform exponential rate: There exists an r (independent of X(0)), with $0< r < 1$, such that $\forall x \in \mathcal {X}$, there exists a constant $C_{X(0)} > 0$ such that $d_{\rho }(K^t(X(0), \cdot ), \pi (\cdot )) \le C_{X(0)}r^t, \forall t$.

The same conclusions hold if $\mathcal {W}$ is a set of strictly diagonally column dominant matrices.

Proof

Take the weight vector $w = \mathbf {1}$. Then since each $W^l \in \mathcal {W}$ is strictly diagonally row dominant, it follows that for each i, $\sum _{j \ne i} |W^l_{ij}| < 1$. Let $i_l^*$ be the row that maximizes the row sum for $W^l$: $i_l^* = \arg \max _i \sum _{j \ne i} |W^l_{ij}|$, then for every l, $\sum _{j \ne i_l^*} |W^l_{ij}| < 1$.

Let P(l) be the probability that $\mathbf {W} = W^l$. Then, we have

$$ \mathbb {E}[\Vert \mathbf {I} -\mathbf {W}\Vert _{\infty }^w] = \sum _{l} P(l) \max _i \sum _{j \ne i} |W^l_{ij}| = \sum _{l} P(l) \sum _{j \ne i_l^*} |W^l_{ij}| < 1.$$

Consequently, by Jensen’s inequality, $\mathbb {E}[\log \Vert \mathbf {I} -\mathbf {W}\Vert _{\infty }^w] < 0$. Theorem 3 implies the results.

The strictly diagonally column dominant case can be similarly established using the weighted $l_1$ norm.

It is important to mention that even if $\mathcal {W}$ does not solely consist of strictly diagonally row dominant matrices, the stochastic stability results as given in Corollary 1 may still be satisfied. As a simple example, consider the case where $\mathcal {W}$ only contains two matrices $W^1, W^2$, where: $W^1 = \left[ \begin{array}{cc} 1 &{} 2 \\ 2 &{} 1 \end{array} \right]$, $W^2 = \left[ \begin{array}{cc} 1 &{} 0.45 \\ 0.45 &{} 1 \end{array} \right]$, with the former and latter probabilities 0.5, 0.5 respectively. Then one can easily verify that $\mathbb {E}[\log \Vert \mathbf {I} -\mathbf {W}\Vert _{\infty }] = -0.053 < 0$. Consequently, Theorem 3 ensures that all results still hold. Note that in this case, $\mathbb {E}[\Vert \mathbf {I}-\mathbf {W}\Vert _{\infty }] = 1.225 > 1$. Therefore, it is not a contraction on average.

So far, we have picked the particular all-ones weight vector $w = \mathbf {1}$ primarily because it yields the maximum intuition and matches with the strictly diagonally dominant matrices context. It should be evident that by allowing for an arbitrary positive weight vector w, we have expanded the applicability of the sufficient conditions given in the previous section, since in certain cases, a different weight vector may need to be selected.

4 Conclusions and Future Work

In addition to the conjecture we mentioned at the end of the previous section, we mention in closing that although there are different classes of network matrices that achieve existence and/or uniqueness of NE, it is not well-studied whether the best response dynamics will converge to a NE in other classes of network matrices (even if that class of network matrices guarantee the existence and uniqueness of a NE). For instance, best response dynamics may not converge when $\mathbf {W}$ is positive definite, although a unique NE is guaranteed to exist in that case. Expanding on such convergence results can be interesting and worthwhile and also shed additional light to the stochastic stability type of results.