A Tweak for a PRF Mode of a Compression Function and Its Applications

Abstract

We discuss a tweak for the domain extension called Merkle-Damgård with Permutation (MDP), which was presented at ASIACRYPT 2007. We first show that MDP may produce multiple independent pseudorandom functions (PRFs) using a single secret key and multiple permutations if the underlying compression function is a PRF against related key attacks with respect to the permutations. Using this result, we then construct a hash-function-based MAC function, which we call FMAC, using a compression function as its underlying primitive. We also present a scheme to extend FMAC so as to take as input a vector of strings.

1 Introduction

Background. HMAC [3] is the widely deployed function for message authentication (MAC function) constructed from a cryptographic hash function. HMAC is defined with a hash function H as follows:

$$\begin{aligned} \mathsf {HMAC}(K,M)=H((K\oplus \mathtt {opad})\Vert H((K\oplus \mathtt {ipad})\Vert M)) , \end{aligned}$$

where K is a secret key, M is an input message, $\Vert$ represents concatenation, $\oplus$ represents bitwise XOR, $\mathtt {ipad}=\mathtt {0x3636\cdots 36}$ and $\mathtt {opad}=\mathtt {0x5c5c\cdots 5c}$.

Due to the length extension property of standardized hash functions such as SHA-1, SHA-256 and SHA-512 [14], HMAC invokes the underlying hash function twice. The drawback of the adoption of this structure is inefficiency for short messages. Inefficiency of HMAC may also come from the padding of the underlying hash function based on the Merkle-Damgård strengthening. More efficient scheme is expected to be constructed if a compression function of a hash function is used as an underlying primitive instead of the hash function itself.

Recently, an approach attracts a lot of interest to construct symmetric-key schemes using a public permutation. It is emerged from the sponge construction [7], which is the basis of the SHA-3 hash function [15]. Following the approach, methods to construct authenticated encryption schemes and pseudorandom generators are proposed [8]. The Even-Mansour cipher [12, 13], which is constructed from a public permutation, also attracts renewed interest, and schemes for encryption, message authentication and authenticated encryption are proposed based on it [19–21, 27]. Chaskey is a recently proposed MAC function based on a permutation [23].

The approach to construct secret-key schemes using a compression function is not new. In the context of multi-property preservation [6], some schemes are proposed such as EMD [6] and MDP [16], which may produce PRFs with some appropriate keying strategies. Yasuda [28] also presents a novel PRF mode of a compression function, which almost maximizes the efficiency of the Merkle-Damgård iteration. The recent proposal OMD [11] for authenticated encryption is constructed with a compression function.

Our Contribution. This paper extends the MDP domain extension [16] to construct efficient pseudorandom functions (PRFs). It is first shown that the MDP domain extension with a single key and multiple permutations may produce multiple independent PRFs if the underlying compression function is PRF against related key attacks with respect to the permutations. Based on this result, a PRF with minimum padding is proposed, which is called FMAC (compression-Function-based MAC). We say that padding is minimum if the produced message blocks does not include message blocks only with the padding sequence for any non-empty input message. Finally, a vector-input PRF is constructed with FMAC, which is called vFMAC. A vector-input PRF (vPRF) takes as input a vector of strings. For vFMAC, the number of the components in an input vector is bounded from above and the upper bound is determined by the number of the permutations used in vFMAC.

Related Work. It is shown that HMAC is a PRF if the compression function of the underlying hash function is a PRF with respect to two keying strategies [1]. In particular, for one of the keying strategies, the compression function is required to be a PRF against related key attacks with respect to $\mathtt {ipad}$ and $\mathtt {opad}$.

Yasuda [30] presented a secure HMAC variant without the second key, which is called $H^{2}$-MAC. It is shown to be a PRF on the assumption that the underlying compression function is a PRF even if an adversary is allowed to obtain a piece of information on the secret key.

AMAC [2] is a MAC function using a hash function encapsulated with an unkeyed output function. Typical candidates for the output function are truncation and the mod function. AMAC is more efficient than HMAC especially for short messages. It is shown that AMAC is a PRF if the underlying compression function remains a PRF under leakage of the key by the output function.

The plain Merkle-Damgård cascade is shown to be a PRF against adversaries making prefix-free queries if the underlying compression function is a PRF [4].

Yasuda’s PRF mode of a compression function in [28] is shown to be a PRF if the underlying compression function is a PRF against a kind of related key attacks.

Sandwich construction for an iterated hash function is shown to produce a PRF if the underlying compression function is a PRF with respect to two keying strategies [29].

Minimum padding is already common among block-cipher-based MAC functions such as CMAC [25] and PMAC [10]. CMAC, which is based on OMAC (One-key CBC-MAC) [17], originated from XCBC [9]. The idea to finalize the iteration with multiple permutations is used in the secure CBC-MAC variants GCBC1 and GCBC2 [24].

Rogaway and Shrimpton [26] introduced the notion of vPRF. They also presented a generic scheme to construct a vPRF from a common PRF taking a single string as input. Minematsu [22] also proposed a vPRF using his universal hash function based on bit rotation.

Organization. Sect. 2 gives notations and definitions used in the remaining parts of the paper. It is shown in Sect. 3 that the MDP domain extension may produce multiple independent PRFs with a single secret key and multiple permutations. Based on the result in Sect. 3, FMAC and vFMAC is presented and their security is confirmed in the manner of provable security in Sect. 4. Section 5 concludes the paper.

2 Preliminaries

2.1 Notations and Definitions

Let ${\varSigma }=\{0,1\}$. For any non-negative integer l, ${\varSigma }^{l}$ is identified with the set of all ${\varSigma }$-sequences of length l. ${\varSigma }^{0}$ is the set of the empty sequence $\varepsilon$. ${\varSigma }^{1}$ is identified with ${\varSigma }$. For $l\ge 1$, let $({\varSigma }^{l})^{*}=\bigcup _{i\ge 0}({\varSigma }^{l})^{i}$ be the set of all ${\varSigma }$-sequences whose lengths are multiples of l. Let $({\varSigma }^{l})^{+} =({\varSigma }^{l})^{*}\setminus \{\varepsilon \} .$ For $k_{1}\le k_{2}$, let $({\varSigma }^{l})^{[k_{1},k_{2}]}=\bigcup _{i=k_{1}}^{k_{2}}({\varSigma }^{l})^{i}$.

For $x\in {\varSigma }^{*}$, the length of x is denoted by |x|. The concatenation of $x_1$ and $x_2$ in ${\varSigma }^{*}$ is denoted by $x_1\Vert x_2$.

The operation of selecting element s from set S uniformly at random is denoted by $s\twoheadleftarrow S$.

Let $f:\mathcal {K}\times \mathcal {D}\rightarrow \mathcal {R}$ be a family of functions from $\mathcal {D}$ to $\mathcal {R}$ indexed by keys in $\mathcal {K}$. Then, $f(K,\cdot )$ is a function from $\mathcal {D}$ to $\mathcal {R}$ for each key $K\in \mathcal {K}$ and is often denoted by $f_K(\cdot )$.

Let F $(\mathcal {D},\mathcal {R})$ denote the set of all functions from $\mathcal {D}$ to $\mathcal {R}$. Let P $(\mathcal {D})$ denote the set of all permutations on $\mathcal {D}$. $id$ represents an identity permutation.

2.2 Pseudorandom Functions

For $f:\mathcal {K}\times \mathcal {D}\rightarrow \mathcal {R}$, let $\textit{A}$ be an adversary trying to distinguish $f_K$ from a function $\rho$, where K and $\rho$ are chosen uniformly at random from $\mathcal {K}$ and $\varvec{F}(\mathcal {D},\mathcal {R})$, respectively. $\textit{A}$ is given access to $f_K$ or $\rho$ as an oracle and makes adaptive queries in $\mathcal {D}$ and obtains the corresponding outputs. The prf-advantage of $\textit{A}$ against f is defined as

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}^{{{\mathrm{{\mathrm {prf}}}}}}_{f}(\textit{A})= \left| \mathrm{Pr}\left[ \textit{A}^{f_K}=1\right] -\mathrm{Pr}\left[ \textit{A}^{\rho }=1\right] \right| , \end{aligned}$$

where $K\twoheadleftarrow \mathcal {K}$ and $\rho \twoheadleftarrow \varvec{F}(\mathcal {D},\mathcal {R})$. In this notation, adversary $\textit{A}$ is regarded as a random variable.

f is called a pseudorandom function, or PRF in short, if no efficient adversary $\textit{A}$ can have any significant prf-advantage against f.

The definition of the prf-advantage can naturally be extended to adversaries with multiple oracles. The prf-advantage of adversary $\textit{A}$ with access to m oracles is defined as

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}^{m{{{\mathrm{{-\mathrm{prf}}}}}}}_{f}(\textit{A})= \left| \mathrm{Pr}[A^{F_{K_{1}},\ldots ,F_{K_{m}}}=1] -\mathrm{Pr}[A^{\rho _{1},\ldots ,\rho _{m}}=1]\right| , \end{aligned}$$

where $(K_1,\ldots ,K_m)\twoheadleftarrow \mathcal {K}^m$ and $(\rho _1,\ldots ,\rho _m)\twoheadleftarrow \varvec{F}(\mathcal {D},\mathcal {R})^m$.

The following lemma is a paraphrase of Lemma 3.3 in [4]:

Lemma 1

Let $\textit{A}$ be any adversary against f with access to m oracles. Then, there exists an adversary $\textit{B}$ against f such that

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}_{f}^{m{{{\mathrm{{-\mathrm{prf}}}}}}}(\textit{A})\le m\cdot {{\mathrm{{\mathrm {Adv}}}}}_{f}^{{{\mathrm{{\mathrm {prf}}}}}}(\textit{B}). \end{aligned}$$

The run time of $\textit{B}$ is approximately total of that of $\textit{A}$ and the time required to compute f to answer to the queries made by $\textit{A}$. The number of the queries made by $\textit{B}$ is at most $\max \{q_i\,|\,1\le i\le m\}$, where $q_i$ is the number of the queries made by $\textit{A}$ to its i-th oracle.

2.3 PRFs Under Related-Key Attacks

The notion of PRF under related-key attacks is formalized by Bellare and Kohno [5]. Let ${\varPhi }\subset \varvec{F}(\mathcal {K},\mathcal {K})$. Let $\mathsf {key}\in \varvec{F}({\varPhi }\times \mathcal {K},\mathcal {K})$ be a function such that $\mathsf {key}(\varphi ,K)=\varphi (K)$. Adversary $\textit{A}$ has oracle access to $g(\mathsf {key}(\cdot ,K),\cdot )$, where $g\in \varvec{F}(\mathcal {K}\times \mathcal {D},\mathcal {R})$. The oracle accepts $(\varphi ,x)\in {\varPhi }\times \mathcal {D}$ as a query and returns $g(\varphi (K),x)$. To simplify the notation, $g(\mathsf {key}(\cdot ,K),\cdot )$ is denoted by g[K]. The prf-rka-advantage of A against $f\in \varvec{F}(\mathcal {K}\times \mathcal {D},\mathcal {R})$ with a ${\varPhi }$-restricted related-key attack (${\varPhi }$-RKA) is given by

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}_{{\varPhi },f}^{{{\mathrm{\mathrm{prf}-\mathrm{rka}}}}}(\textit{A})=\left| \mathrm{Pr}[\textit{A}^{f[K]}=1]-\mathrm{Pr}[\textit{A}^{\rho [K]}=1]\right| , \end{aligned}$$

where $K\twoheadleftarrow \mathcal {K}$ and $\rho \twoheadleftarrow \varvec{F}(\mathcal {K}\times \mathcal {D},\mathcal {R})$.

The prf-rka-advantage can naturally be extended to adversaries with multiple oracles as well as the prf-advantage. The prf-rka-advantage of adversary $\textit{A}$ with access to m oracles launching a ${\varPhi }$-RKA is defined as

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}^{m{{{\mathrm{-\mathrm{prf}-\mathrm{rka}}}}}}_{{\varPhi },f}(\textit{A})= \left| \mathrm{Pr}[A^{f[K_{1}],\ldots ,f[K_{m}]}=1] -\mathrm{Pr}[A^{\rho _{1}[K_{1}],\ldots ,\rho _{m}[K_{m}]}=1]\right| , \end{aligned}$$

where $(K_1,\ldots ,K_m)\twoheadleftarrow \mathcal {K}^m$ and $(\rho _1,\ldots ,\rho _m)\twoheadleftarrow \varvec{F}(\mathcal {K}\times \mathcal {D},\mathcal {R})^m$.

2.4 MDP Domain Extension

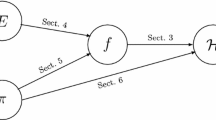
The MDP domain extension is a variant of the plain Merkle-Damgård iteration of a compression function [16]. It finalizes the iteration of the compression function by permuting the chaining variable fed into the final compression function with a permutation.

Let $F:{\varSigma }^{ n }\times {\varSigma }^{ w }\rightarrow {\varSigma }^{ n }$ be a compression function. Let $\pi$ be a permutation on ${\varSigma }^{ n }$. The MDP domain extension of F with $\pi$ is defined by the function $I ^{ F ,\pi }:{\varSigma }^{ n }\times ({\varSigma }^{ w })^{+}\rightarrow {\varSigma }^{ n }$ such that

$$\begin{aligned} I ^{ F ,\pi }(Y_{0},X_{1}\Vert X_{2}\Vert \cdots \Vert X_{x})=Y_{x} \end{aligned}$$

for any $Y_{0}\in {\varSigma }^{ n }$ and $X_{1},X_{2},\ldots ,X_{x}\in {\varSigma }^{ w }$, where

$$\begin{aligned} Y_{i}\leftarrow {\left\{ \begin{array}{ll} F (Y_{i-1},X_{i}) &{} \text { if }1\le i\le x-1 \\ F (\pi (Y_{x-1}),X_{x}) &{} \text { if }i=x. \end{array}\right. } \end{aligned}$$

$X_{1},X_{2},\ldots ,X_{x}$ are called blocks. $I ^{ F ,\pi }$ is also depicted in Fig. 1.

Fig. 1.

MDP domain extension $I ^{ F ,\pi }(Y_{0},X_{1}\Vert X_{2}\Vert \cdots \Vert X_{x})=Y_{x}$

3 Multiple PRFs Based on MDP

It is shown in this section that the MDP domain extension may produce multiple independent PRFs with a single compression function, a single secret key and multiple permutations.

For compression function $F:{\varSigma }^{ n }\times {\varSigma }^{ w }\rightarrow {\varSigma }^{ n }$ and set of permutations ${{\varPi }}=\{\pi _{1},\pi _{2},\ldots ,\pi _{d}\}\subset \varvec{P}({\varSigma }^{n})\setminus \{ id \}$, let $I ^{ F ,{\varPi }}= \{ I ^{ F ,\pi _{1}}, I ^{ F ,\pi _{2}},\ldots , I ^{ F ,\pi _{d}}\} .$

Let $\textit{A}$ be an adversary against $I ^{ F ,{\varPi }}$. The advantage of $\textit{A}$ is defined by

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}_{ I ^{ F ,{\varPi }}}^{{{\mathrm{{\mathrm {prfs}}}}}}(\textit{A})=\left| \mathrm{Pr}\left[ \textit{A}^{ I ^{ F ,\pi _{1}}_{K}, I ^{ F ,\pi _{2}}_{K},\ldots , I ^{ F ,\pi _{d}}_{K}}=1 \right] - \mathrm{Pr}\left[ \textit{A}^{\rho _{1},\rho _{2},\ldots ,\rho _{d}}=1 \right] \right| , \end{aligned}$$

where $K\twoheadleftarrow {\varSigma }^{n}$ and $(\rho _{1},\rho _{2},\ldots ,\rho _{d})\twoheadleftarrow \varvec{F}(({\varSigma }^{ w })^{+},{\varSigma }^{n})^d$. Notice that the setting is different from that of PRF for an adversary with multiple oracles in Sect. 2.2. $I ^{ F ,\pi _{1}}_{K}, I ^{ F ,\pi _{2}}_{K},\ldots , I ^{ F ,\pi _{d}}_{K}$ use a single key K.

For ${{\varPi }}$, let

$$\begin{aligned} \textit{p}_{{\varPi }}= \mathrm{Pr}\left[ \pi (X)=\pi '(X) \text { for some distinct } \pi ,\pi '\in {{\varPi }}\cup \{ id \} \right] , \end{aligned}$$

where X is a random variable with uniform distribution over ${\varSigma }^{ n }$.

The following theorem states that $I ^{ F ,{\varPi }}$ may produce multiple independent PRFs with a single key under the assumption that F is a PRF against related-key attacks restricted by ${{\varPi }}\cup \{ id \}$.

Theorem 1

Let $\textit{A}$ be any adversary against $I ^{ F ,{\varPi }}$ running in time at most t and making at most q queries in total. Suppose that each query consists of at most $\ell$ blocks. Then, there exists an adversary $\textit{B}$ against $F$ such that

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}_{ I ^{ F ,{\varPi }}}^{{{\mathrm{{\mathrm {prfs}}}}}}(\textit{A})\le \ell \>\!q\left( {{\mathrm{{\mathrm {Adv}}}}}_{{{\varPi }}\cup \{ id \}, F }^{{{\mathrm{\mathrm{prf}-\mathrm{rka}}}}}(\textit{B})+\textit{p}_{{\varPi }} \right) . \end{aligned}$$

B runs in time at most $t+O(\ell \>\!q\>\!T_{ F })$, and makes at most q queries. $T_{ F }$ is the time required to compute $F$.

Remark 1

Theorem 1 extends Theorem 2 in [16] in two ways. First, Theorem 1 deals with multiple instances of $I ^{ F ,\pi }$, while the latter shows the PRF security of a single instance. Second, Theorem 1 covers the case that $\textit{p}_{{\varPi }}\not =0$. Theorem 2 in [16] only covers the case that $\textit{p}_{\{\pi \}}=0$ for $\pi \in \varvec{P}({\varSigma }^{ n })$.

Remark 2

The probability $\textit{p}_{{\varPi }}$ should be negligibly small for ${{\varPi }}=\{\pi _{1},\pi _{2},\ldots ,\pi _{d}\}$. Let $c_{1},c_{2},\ldots ,c_{d}$ be distinct nonzero constants in ${\varSigma }^{ n }$.

• Suppose that $\pi _{i}(x)=x\oplus c_{i}$ for $1\le i\le d$. Then, $\textit{p}_{{\varPi }}=0$.

• Suppose that $\pi _{i}(x)=c_{i}\cdot x$ and $c_{i}\not =1$ for $1\le i\le d$. Then, $\textit{p}_{{\varPi }}=1/2^{ n }$.

Theorem 1 immediately follows from Lemmas 2 and 3.

Lemma 2

Let $\textit{A}$ be any adversary against $I ^{ F ,{\varPi }}$ running in time at most t and making at most q queries in total. Suppose that each query consists of at most $\ell$ blocks. Then, there exists an adversary $\textit{B}$ against $F$ with access to q oracles such that

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}_{ I ^{ F ,{\varPi }}}^{{{\mathrm{{\mathrm {prfs}}}}}}(\textit{A}) \le \ell \left( {{\mathrm{{\mathrm {Adv}}}}}_{{{\varPi }}\cup \{ id \}, F }^{q{{{\mathrm{-\mathrm{prf}-\mathrm{rka}}}}}}(\textit{B})+ q\>\!\textit{p}_{{\varPi }}\right) . \end{aligned}$$

$\textit{B}$ runs in time at most $t + O(\ell \>\!q\>\!T_{ F })$ and makes at most q queries.

Proof

Let $X=X_{1}\Vert X_{2}\Vert \cdots \Vert X_{l}$, where $|X_{i}|=w$ for $1\le i\le l$ and $l\le \ell$. For $1\le i_{1}\le i_{2}\le l$, let $X_{[i_{1},i_{2}]}=X_{i_{1}}\Vert X_{i_{1}+1}\Vert \cdots \Vert X_{i_{2}}$. For $i\in \{0,1,\ldots ,\ell \}$ and two functions $\mu :({\varSigma }^w)^{[1,\ell ]}\rightarrow {\varSigma }^n$ and $\xi :({\varSigma }^w)^{[0,\ell ]}\rightarrow {\varSigma }^n$, let $R [i]_{\mu ,\xi }^{ F ,\pi }:({\varSigma }^w)^{[1,\ell ]}\rightarrow {\varSigma }^n$ be a function such that

$$\begin{aligned} R [i]^{ F ,\pi }_{\mu ,\xi }(X)= {\left\{ \begin{array}{ll} \mu (X) &{} \text { if } l\le i,\\ I ^{ F ,\pi }(\xi (X_{[1,i]}),X_{[i+1,l]}) &{} \text { if } l\ge i+1, \end{array}\right. } \end{aligned}$$

where $X_{[1,i]}=\varepsilon$ if $i=0$. We define

$$\begin{aligned} P_{i}=\mathrm{Pr}\left[ \textit{A}^{ R [i]^{ F ,\pi _{1}}_{\mu _{1},\xi }, R [i]^{ F ,\pi _{2}}_{\mu _{2},\xi },\ldots , R [i]^{ F ,\pi _{d}}_{\mu _{d},\xi }}=1\right] , \end{aligned}$$

where $(\mu _{1},\ldots ,\mu _{d})\twoheadleftarrow \varvec{F}(({\varSigma }^{ w })^{[1,\ell ]},{\varSigma }^n)^{d}$ and $\xi \twoheadleftarrow \varvec{F}(({\varSigma }^{ w })^{[0,\ell ]},{\varSigma }^n)$. Then, the advantage of $\textit{A}$ is

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}^{{{\mathrm{{\mathrm {prfs}}}}}}_{ I ^{ F ,{\varPi }}}(\textit{A})=|P_{0}-P_{\ell }|. \end{aligned}$$

The algorithm of an adversary $\textit{B}$ against $F$ with q oracles is described below. Let the oracles $(g_1,\ldots ,g_q)$ of $\textit{B}$ be either $( F [K_{1}], F [K_{2}],\ldots , F [K_{q}])$ or $(\tilde{\rho }_{1},\tilde{\rho }_{2},\ldots ,\tilde{\rho }_{q})$ such that $(K_1,\ldots ,K_q)\twoheadleftarrow ({\varSigma }^{ n })^q$ and $(\tilde{\rho }_{1},\tilde{\rho }_{2},\ldots ,\tilde{\rho }_{q})\twoheadleftarrow \varvec{F}(({{\varPi }}\cup \{ id \})\times {\varSigma }^{ w },{\varSigma }^{ n })^{q}$. $\textit{B}$ uses $\textit{A}$ as a subroutine.

• 1. $\textit{B}$ selects r from $\{1,\ldots ,\ell \}$ uniformly at random.

• 2. If $r\ge 2$, then $\textit{B}$ selects functions $(\tilde{\mu }_{1},\ldots ,\tilde{\mu }_{d})$ from $\varvec{F}(({\varSigma }^{ w })^{[1,r-1]},{\varSigma }^{ n })^{d}$ uniformly at random.

• 3. $\textit{B}$ runs $\textit{A}$. Finally, $\textit{B}$ outputs the output of $\textit{A}$.

For $1\le k\le q$ and $1\le l\le \ell$, let $X=X_{1}\Vert X_{2}\Vert \cdots \Vert X_{l}$ be the k-th query made by A during the execution of $\textit{A}$. Suppose that X is given to the j-th oracle. If $l\ge r$, then $\textit{B}$ makes a query to the $idx (k)$-th oracle, where $idx :\{1,\ldots ,q\}\rightarrow \{1,\ldots ,q\}$ is a function such that

• $idx (k)= idx (k')$ if there exists a previous $k'$-th query $X'$ ($k'<k$) such that $X_{[1,r-1]}'=X_{[1,r-1]}$, and

• $idx (k)=k$ otherwise.

The query made by $\textit{B}$ is $(\pi _j,X_r)$ if $l=r$ and $( id ,X_r)$ if $l\ge r+1$. The answer of $\textit{B}$ to X is

$$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{\mu }_{j}(X) &{} \text { if } l\le r-1,\\ g_{ idx (k)}(\pi _{j},X_{r}) &{} \text { if } l=r,\\ I ^{ F ,\pi _{j}}(g_{ idx (k)}( id ,X_{r}),X_{[r+1,l]}) &{} \text { if } l\ge r+1. \end{array}\right. } \end{aligned}$$

Now, suppose that $\textit{B}$ is given oracles $( F [K_{1}],\ldots , F [K_{q}])$. Then, the answer of $\textit{B}$ to X is

$$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{\mu }_{j}(X) &{} \text { if }l\le r-1,\\ F _{\pi _{j}(K_{ idx (k)})}(X_{r}) &{} \text { if }l=r,\\ I ^{ F ,\pi _{j}}( F _{K_{ idx (k)}}(X_{r}),X_{[r+1,l]}) &{} \text {if } l\ge r+1. \end{array}\right. } \end{aligned}$$

$K_{ idx (k)}$ can be regarded as an output of a function chosen uniformly at random from $\varvec{F}(({\varSigma }^{ w })^{r-1},{\varSigma }^{ n })$ since $idx (k)$ depends on $X_{[1,r-1]}$ and $K_{ idx (k)}$ is chosen uniformly at random from ${\varSigma }^{ n }$. Thus, $\textit{B}$ provides $\textit{A}$ with the oracle $R [r-1]^{ F ,\pi _{j}}_{\mu _{j},\xi }$, and

$$\begin{aligned}&\mathrm{Pr}\left[ \textit{B}^{ F [K_{1}],\ldots , F [K_{q}]}=1\right] \\&\quad =\sum _{i=1}^{\ell }\mathrm{Pr}\left[ r=i\wedge \textit{B}^{ F [K_1],\ldots , F [K_q]}=1\right] =\frac{1}{\ell }\sum _{i=1}^{\ell }\mathrm{Pr}\left[ \textit{B}^{ F [K_1],\ldots , F [K_q]}=1\,\Big |\,r=i\right] \\&\quad =\frac{1}{\ell }\sum _{i=1}^{\ell }\mathrm{Pr}\left[ \textit{A}^{ R [i-1]^{ F ,\pi _{1}}_{\mu _{1},\xi }, R [i-1]^{ F ,\pi _{2}}_{\mu _{2},\xi },\ldots , R [i-1]^{ F ,\pi _{d}}_{\mu _{d},\xi }}=1\right] =\frac{1}{\ell }\sum _{i=1}^{\ell }P_{i-1}. \end{aligned}$$

Suppose that $\textit{B}$ is given oracles $(\tilde{\rho }_{1},\ldots ,\tilde{\rho }_{q})$. Then, the answer of $\textit{B}$ to X is

$$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{\mu }_{j}(X) &{} \text { if } l\le r-1,\\ \tilde{\rho }_{ idx (k)}(\pi _{j},X_{r}) &{} \text { if } l=r,\\ I ^{ F ,\pi _{j}}(\tilde{\rho }_{ idx (k)}( id ,X_{r}),X_{[r+1,l]}) &{} \text { if } l\ge r+1. \end{array}\right. } \end{aligned}$$

Notice that $\tilde{\rho }_{ idx (k)}(\pi _{1},\cdot ),\ldots ,\tilde{\rho }_{ idx (k)}(\pi _{d},\cdot )$ and $\tilde{\rho }_{ idx (k)}( id ,\cdot )$ are independent of each other. Thus, $\textit{B}$ provides $\textit{A}$ with the oracle $R [r]^{ F ,\pi _j}_{\mu _{j},\xi }$, and

$$\begin{aligned} \mathrm{Pr}[\textit{B}^{\tilde{\rho }_{1},\ldots ,\tilde{\rho }_{q}}=1]=\frac{1}{\ell }\sum _{i=1}^{\ell }P_i . \end{aligned}$$

Thus,

$$\begin{aligned} \left| \mathrm{Pr}\left[ \textit{B}^{ F [K_1],\ldots , F [K_q]}=1\right] - \mathrm{Pr}\left[ \textit{B}^{\tilde{\rho }_{1},\ldots ,\tilde{\rho }_{q}}=1\right] \right|&=\left| \frac{1}{\ell }\sum _{i=1}^{\ell }P_{i-1}-\frac{1}{\ell }\sum _{i=1}^{\ell }P_{i}\right| \\&=\frac{\left| P_0-P_{\ell }\right| }{\ell } =\frac{1}{\ell }{{\mathrm{{\mathrm {Adv}}}}}^{{{\mathrm{{\mathrm {prf}}}}}}_{ I ^{ F ,{\varPi }}}(\textit{A}). \end{aligned}$$

Now, let $(\rho _{1},\rho _{2},\ldots ,\rho _{q})\twoheadleftarrow \varvec{F}({\varSigma }^{ n }\times {\varSigma }^{ w },{\varSigma }^{ n })^{q}$. Then,

$$\begin{aligned}&\left| \mathrm{Pr}\left[ \textit{B}^{ F [K_1],\ldots , F [K_q]}=1\right] - \mathrm{Pr}\left[ \textit{B}^{\tilde{\rho }_{1},\ldots ,\tilde{\rho }_{q}}=1\right] \right| \\&\qquad {}\le \left| \mathrm{Pr}\left[ \textit{B}^{ F [K_1],\ldots , F [K_q]}=1\right] - \Pr \left[ \textit{B}^{\rho _{1}[K_1],\ldots ,\rho _{q}[K_q]}=1\right] \right| \\&\qquad \qquad \qquad {}+\left| \Pr \left[ \textit{B}^{\rho _{1}[K_1],\ldots ,\rho _{q}[K_q]}=1\right] - \Pr \left[ \textit{B}^{\tilde{\rho }_{1},\ldots ,\tilde{\rho }_{q}}=1\right] \right| \\&\qquad {}={{\mathrm{{\mathrm {Adv}}}}}_{{{\varPi }}\cup \{ id \}, F }^{q{{{\mathrm{-\mathrm{prf}-\mathrm{rka}}}}}}(\textit{B})+ \left| \Pr \left[ \textit{B}^{\rho _{1}[K_1],\ldots ,\rho _{q}[K_q]}=1\right] - \Pr \left[ \textit{B}^{\tilde{\rho }_{1},\ldots ,\tilde{\rho }_{q}}=1\right] \right| . \end{aligned}$$

$(\rho _{1}[K_1],\ldots ,\rho _{q}[K_q])$ and $(\tilde{\rho }_{1},\ldots ,\tilde{\rho }_{q})$ are identical as long as $\pi (K_{i})\not =\pi '(K_{i})$ for any distinct $\pi ,\pi '\in {{\varPi }}\cup \{ id \}$ for $1\le i\le q$. Thus,

$$\begin{aligned} \left| \Pr \left[ \textit{B}^{\rho _{1}[K_1],\ldots ,\rho _{q}[K_q]}=1\right] - \Pr \left[ \textit{B}^{\tilde{\rho }_{1},\ldots ,\tilde{\rho }_{q}}=1\right] \right| \le q\>\!\textit{p}_{{\varPi }} . \end{aligned}$$

To answer to the queries made by $\textit{A}$, $\textit{B}$ may compute $I ^{ F ,\pi _{1}},\ldots , I ^{ F ,\pi _{d}}$ and simulate $\tilde{\mu }$. It approximately costs at most $\ell \>\!q$ evaluations of $F$. $\square$

Lemma 3

Let $\textit{A}$ be any adversary with m oracles against $F$ running in time at most t, and making at most q queries. Then, there exists an adversary $\textit{B}$ against $F$ such that

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}_{{{\varPi }}\cup \{ id \}, F }^{m{{{\mathrm{-\mathrm{prf}-\mathrm{rka}}}}}}(\textit{A})\le m\cdot {{\mathrm{{\mathrm {Adv}}}}}_{{{\varPi }}\cup \{ id \}, F }^{{{\mathrm{\mathrm{prf}-\mathrm{rka}}}}}(\textit{B}). \end{aligned}$$

$\textit{B}$ runs in time at most $t+O(q\>\!T_{ F })$ and makes at most q queries, where $T_{ F }$ represents the time required to compute $F$.

Lemma 3 is a generalized version of Lemma 4 in [16], which only covers the case that $|{{\varPi }}|=1$. The proof of Lemma 3 is omitted since it is standard and similar to that of Lemma 4 in [16].

4 Applications

4.1 PRF with Minimum Padding

The proposed MAC function FMAC consists of a compression function $F :{\varSigma }^{ n }\times {\varSigma }^{ w }\rightarrow {\varSigma }^{ n }$ and distinct permutations $\pi _{1}$ and $\pi _{2}$ on ${\varSigma }^{ n }$.

The padding function used in FMAC is defined as follows: For any $M\in {\varSigma }^{*}$,

$$\begin{aligned} {{\mathrm{\mathsf {pad}}}}(M)= {\left\{ \begin{array}{ll} M &{} \text { if } |M|>0 \mathrm{and } |M|\equiv 0\pmod { w }\\ M\Vert 10^{l} &{} \text { if } |M|=0 \mathrm{or } |M|\not \equiv 0\pmod { w }, \end{array}\right. } \end{aligned}$$

where l is the minimum non-negative integer such that $|M|+1+l\equiv 0\pmod { w }$. In particular, ${{\mathrm{\mathsf {pad}}}}(\varepsilon )=10^{ w -1}$.

For any M, $|{{\mathrm{\mathsf {pad}}}}(M)|$ is the minimum positive multiple of $w$, which is greater than or equal to |M|. Let ${{\mathrm{\mathsf {pad}}}}(M)=\bar{M}_{1}\Vert \bar{M}_{2}\Vert \cdots \Vert \bar{M}_{m}$, where $|\bar{M}_{i}|= w$ for every i such that $1\le i\le m$. $m=1$ if $|M|=0$, and $m=\lceil |M|/w\rceil$ if $|M|>0$. $\bar{M}_{i}$ is called the i-th block of ${{\mathrm{\mathsf {pad}}}}(M)$.

FMAC is the MAC function $C ^{ F ,\{\pi _{1},\pi _{2}\}}:{\varSigma }^{ n }\times {\varSigma }^{*}\rightarrow {\varSigma }^{ n }$ defined by

$$\begin{aligned} C ^{ F ,\{\pi _{1},\pi _{2}\}}(K,M)= {\left\{ \begin{array}{ll} I ^{ F ,\pi _{1}}(K,{{\mathrm{\mathsf {pad}}}}(M)) &{} \text { if } |M|>0 \mathrm{and } |M|\equiv 0\pmod { w }\\ I ^{ F ,\pi _{2}}(K,{{\mathrm{\mathsf {pad}}}}(M)) &{} \text { if } |M|=0 \mathrm{or } |M|\not \equiv 0\pmod { w }. \end{array}\right. } \end{aligned}$$

$C ^{ F ,\{\pi _{1},\pi _{2}\}}$ is shown to be a PRF under the assumptions that F is a PRF against related-key attacks with respect to permutations $\pi _{1}$ and $\pi _{2}$ and that $\textit{p}_{\{\pi _{1},\pi _{2}\}}$ is negligibly small. The proof is omitted due to the page limit.

Corollary 1

Let $\pi _{1}$ and $\pi _{2}$ be permutations on ${\varSigma }^{n}$. Let $\textit{A}$ be any adversary against $C ^{ F ,\{\pi _{1},\pi _{2}\}}$ running in time at most t and making at most q queries. Suppose that the length of each query is at most $\ell w$. Then, there exists an adversary $\textit{B}$ against $F$ such that

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}_{ C ^{ F ,\{\pi _{1},\pi _{2}\}}}^{{{\mathrm{{\mathrm {prf}}}}}}(\textit{A})\le \ell \>\!q\left( {{\mathrm{{\mathrm {Adv}}}}}_{\{ id ,\pi _{1},\pi _{2}\}, F }^{{{\mathrm{\mathrm{prf}-\mathrm{rka}}}}}(\textit{B})+\textit{p}_{\{\pi _{1},\pi _{2}\}} \right) . \end{aligned}$$

B runs in time at most $t+O(\ell \>\!q\>\!T_{ F })$, and makes at most q queries. $T_{ F }$ is the time required to compute $F$.

4.2 Vector-Input PRF

A scheme is proposed to construct a vector-input PRF (vPRF) using instances of FMAC. In the original formalization [26], a vPRF accepts vectors with any number of components as inputs. In contrast, the proposed scheme has a parameter which specifies the maximum number of the components in an input vector.

Let d be a positive integer, which is the maximum number of the components in an input vector. Let $F :{\varSigma }^{ n }\times {\varSigma }^{ w }\rightarrow {\varSigma }^{ n }$ and ${{\varPi }}=\{\pi _{1},\pi _{2},\ldots ,\pi _{2d+2}\}\subset \varvec{P}({\varSigma }^{n})$. The proposed vector-input function vFMAC $V ^{ F ,{\varPi }}:{\varSigma }^{n}\times ({\varSigma }^{*})^{[0,d]}\rightarrow {\varSigma }^{n}$ is defined as follows: For an s-component vector $(S_{1},S_{2},\ldots ,S_{s})$ such that $0\le s\le d$,

$$\begin{aligned}&V ^{ F ,{\varPi }}(K,(S_{1},S_{2},\ldots ,S_{s}))\\&\qquad \qquad {}= {\left\{ \begin{array}{ll} C ^{ F ,\{\pi _{2d+1},\pi _{2d+2}\}}_{K}(\varepsilon ) &{} \text { if } s=0,\\ C ^{ F ,\{\pi _{2d+1},\pi _{2d+2}\}}_{K}\left( \bigoplus _{i=1}^{s} C ^{ F ,\{\pi _{2i-1},\pi _{2i}\}}_{K}(S_{i})\right) &{} \text { if } s\ge 1. \end{array}\right. } \end{aligned}$$

It is shown that $V ^{ F ,{\varPi }}$ is a vPRF if $F$ is a PRF against related-key attacks with respect to permutations in ${\varPi }$ and $\textit{p}_{{\varPi }}$ is negligibly small.

Corollary 2

Let ${{\varPi }}= \{\pi _{1},\pi _{2},\ldots ,\pi _{2d+2}\}\subset \varvec{P}({\varSigma }^{n})\setminus \{ id \}$. Let $\textit{A}$ be any adversary against $V ^{ F ,{\varPi }}$ running in time at most t and making at most q queries. Suppose that the length of each vector component in queries is at most $\ell w$ and that the total number of the vector components in all of the queries is at most $\sigma (\ge q-1)$. Then, there exists an adversary $\textit{B}$ against $F$ such that

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}_{ V ^{ F ,{\varPi }}}^{{{\mathrm{{\mathrm {prf}}}}}}(\textit{A})\le \ell (\sigma +q)\left( {{\mathrm{{\mathrm {Adv}}}}}_{{{\varPi }}\cup \{ id \}, F }^{{{\mathrm{\mathrm{prf}-\mathrm{rka}}}}}(\textit{B}) +\textit{p}_{{\varPi }}\right) +\frac{q(q-1)}{2^{ n +1}} . \end{aligned}$$

B runs in time at most $t+O(\ell \>\!\sigma \>\!T_{ F })$, and makes at most $(\sigma +q)$ queries. $T_{ F }$ is the time required to compute $F$.

Corollary 2 directly follows from Lemmas 4 and 5. The proofs are omitted.

Lemma 4

Let ${{\varPi }}= \{\pi _{1},\pi _{2},\ldots ,\pi _{2d+2}\}\subset \varvec{P}({\varSigma }^{n})\setminus \{ id \}$. Let $\textit{A}$ be any adversary against $\left\{ C ^{ F ,\{\pi _{2i-1},\pi _{2i}\}}\,\big |\,1\le i\le d+1\right\}$ running in time at most t and making at most q queries in total. Suppose that the length of each query is at most $\ell w$. Then, there exists an adversary $\textit{B}$ against $F$ such that

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}_{\left\{ C ^{ F ,\{\pi _{2i-1},\pi _{2i}\}}\,\big |\,1\le i\le d+1\right\} }^{{{\mathrm{{\mathrm {prfs}}}}}}(\textit{A}) \le \ell \>\!q\left( {{\mathrm{{\mathrm {Adv}}}}}_{{{\varPi }}\cup \{ id \}, F }^{{{\mathrm{\mathrm{prf}-\mathrm{rka}}}}}(\textit{B}) +\textit{p}_{{\varPi }}\right) . \end{aligned}$$

B runs in time at most $t+O(\ell \>\!q\>\!T_{ F })$, and makes at most q queries. $T_{ F }$ is the time required to compute $F$.

Lemma 5

Let ${{\varPi }}= \{\pi _{1},\pi _{2},\ldots ,\pi _{2d+2}\}\subset \varvec{P}({\varSigma }^{n})\setminus \{ id \}$. Let $\textit{A}$ be any adversary against $V ^{ F ,{\varPi }}$ running in time at most t and making at most q queries. Suppose that the length of each vector component in queries is at most $\ell w$ and that the total number of the vector components in all of the queries is at most $\sigma$. Then, there exists an adversary $\textit{B}$ against $\left\{ C ^{ F ,\{\pi _{2i-1},\pi _{2i}\}}\,\big |\,1\le i\le d+1\right\}$ such that

$$\begin{aligned} {{\mathrm{{\mathrm {Adv}}}}}_{ V ^{ F ,{\varPi }}}^{{{\mathrm{{\mathrm {prf}}}}}}(\textit{A})\le {{\mathrm{{\mathrm {Adv}}}}}_{\left\{ C ^{ F ,\{\pi _{2i-1},\pi _{2i}\}}\,\big |\,1\le i\le d+1\right\} }^{{{\mathrm{{\mathrm {prfs}}}}}}(\textit{B}) +\frac{q(q-1)}{2^{n+1}}. \end{aligned}$$

B runs in time at most t and makes at most $(\sigma +q)$ queries in total. The length of each query is at most $\ell \>\!w$.

5 Conclusion

We have presented a MAC function called FMAC, which is cascade of a compression function based on the MDP domain extension. We have also extended FMAC so as to take as input a vector of strings. We have confirmed their security as PRF on the assumption that the underlying compression function is PRF under related-key attacks. Future work is to evaluate their security as PRF in the multi-user setting.