Keywords

1 Introduction

Conventional Neural Networks (NN), e.g., Multi-Layer Perceptrons (MLP), are widely used in pattern recognition, computer vision, and machine learning. To succeed, NN usually requires to be trained with a sufficiently large number of samples [4]. When only few data are available, NN’s performance may however be significantly limited. Moreover, to facilitate the training of NN, input samples are usually assumed identically and independently distributed (i.i.d.). With the i.i.d. assumption, samples can be fed to NN sequentially; this hence enables a stochastic gradient descent algorithm for training a NN conveniently and efficiently. However, an i.i.d assumption may often be violated in practice; on the other hand, the learning procedure of human is not independent, but rather relies on previous knowledge. For example, if a child would like to learn running, his previous experience of walking can provide him some relevant knowledge which can help him learn running easier. Another example is that, if a British tries to learn French, previous memory about English study would benefit greatly the learning. Both examples above indicate that the memory and previous knowledge are very important and might be used to improve the present learning.

Motived from these examples, we propose a novel neural network framework called Memory Network (MN). Enjoying the similar structure with traditional neural networks (including input, hidden, and output layers), MN introduces additional memory structures that can appropriately take advantages of previous knowledge learned from previous samples for the present learning. When only limited data are available, previous learned knowledge (stored in the memory network) could significantly benefit the training for the present learning. More specifically, we keep a memory of the network structures for previous N training samples. Depending on if the present training sample share or not the same category (class label), we enforce different constraints on two activations in each layer of the present network and previous network. For example, if the previous sample shares the same label with present sample, we then force similar the two activations of the same layers between the present network and previous network; otherwise, we try to enlarge their activations of the same layers between the present and previous network. One appealing feature of our proposed MN is that, despite a seemingly complicated network, an efficient stochastic gradient descent algorithm can be readily applied to make the network easily optimized.

2 Notation and Background

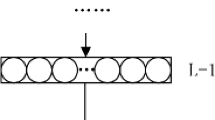
In this section, we present the notation used throughout the paper and also review the basic principles of conventional NN and Back Propagation (BP) algorithm. Essentially, NN is a stack of parametric non-linear and linear transformations [7]. Suppose an NN (with \(L-1\) hidden layers) is trained to perform predication in the scenario of classification. NN will map the M-dimension vector to the D-dimension label space. The matrix \(X_0\) denotes the input data matrix where each row of \(X_0\) represents a sample vector (\(X_{0,i}\) is the \(i^{th}\) sample vector with M dimensions). \(X_l\) indicates the activation of the \(l^{th}\) layer of NN (where \(l=1, 2,\ldots ,L-1) \) and \(X_L\) denotes the output of the NN. Y represents the labels each row of which is the label for corresponding sample with D dimensions. The problem of NN can be formulated as the following optimization problem:

$$\begin{aligned}&\min _{W_{1:L},b_{1:L}}\ \frac{1}{2}\Vert X_L-Y\Vert ^2\quad \text{ s. } \text{ t. }\nonumber \\&\ X_l\ =\ \sigma (X_{l-1}W_l+b_l), l=1,...,L-1 \\&X_L=X_{L-1}W_L+b_L\nonumber \end{aligned}$$
(1)

where \(\sigma (.)\) is the element-wise sigmoid function for a matrix. For each element x of matrix, the sigmoid function is defined as \(\sigma (x)=\frac{1}{1+\exp (-x)}\).

In NN, the sigmoid function is used to perform the non-linear transformation and it can be also replaced by other functions such as \(\max (0,x)\) and \(\tanh (x)\).

Fig. 1.
figure 1

The structure of conventional Neural Network

Full size image

We plot an illustrative example of a typical L-layer NN in Fig. 1, where \(X_l\) (\(l=1,2,\ldots ,L-1\)) represent the hidden layers. \(X_0\) denotes the input for the NN, and \(X_L\) indicates the output of the NN. The aim is to learn the optimum parameters \(W_{1:L}\) and \(b_{1:L}\). The common approach is BP and stochastic gradient decent (SGD).

Back Propagation is an abbreviation for “backward propagation of errors” which is a common approach for training NNs with an optimization method such as gradient descent. The method calculates the gradient of a loss function with respect to all the parameters of the network. The gradient is used in the optimization method which in turn uses it to update the parameters in order to minimize the loss function.

BP requires the inputs with corresponding labels in order to calculate the loss function gradient. Therefore, it is considered as a supervised learning method, although it is also used in some unsupervised models such as auto encoders. It is a generalization of the delta rule to multi-layered feed-forward networks, made possible by using the chain rule to iteratively calculate the gradients for each layer. Assuming that the activation function be differentiable, the whole procedure is shown as below:

$$\begin{aligned}&\frac{\mathrm {d}E}{\mathrm {d}X_L}=2(X_L-Y) \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\mathrm {d}E}{\mathrm {d}X_l}=(\frac{\mathrm {d}E}{\mathrm {d}X_{l+1}}\circ X_{l+1}\circ (1-X_{l+1}))W_{l+1} \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\mathrm {d}E}{\mathrm {d}W_l}=X_{l-1}^{T}(\frac{\mathrm {d}E}{\mathrm {d}X_l}\circ X_l\circ (1-X_l)) \end{aligned}$$
(4)
$$\begin{aligned}&\frac{\mathrm {d}E}{\mathrm {d}b_l}=mean(\frac{\mathrm {d}E}{\mathrm {d}X_l}\circ X_l\circ (1-X_l),1) \end{aligned}$$
(5)

where E is the value of the loss function and we can compute the gradients using the chain rule above. \(\circ \) represents the element-wise product and \(l=1,2,...L\). mean(., 1) denotes the average operation on matrices.

3 Memory Network

This section will introduce our proposed novel Memory Network (MN) in details. We will first present the structure of MN and then introduce the corresponding optimization algorithm.

3.1 Network Structure

The structure of MN is plotted in Fig. 2. As can be seen, the structure of MN consists of two parts, i.e., the present network and the memory part. We will detail these two parts one by one.

Fig. 2.
figure 2

Structure of Memory Network

Full size image

Present Network. The structure of present network is the same as the traditional NN (consisting of the input layer, hidden layers and the output layer).

Memory Part. The memory part contains N copies of present network. They have totally the same parameters with present network. The difference is that the past N samples are fed into the memory part. There are also additional connections between each layer of memory part and present network. These connections indicate the minus operations which are used to calculate the difference of activations between memory and present part.

The purpose of using the memory part is to exploit past knowledge (obtained from past samples) to help the present learning (present sample). There are two different cases: (1) if the present sample has the same class label as the past sample, we then try to make the activations of the same layers for present sample and past sample more similar; (2) if the present sample shares a different class from the past one, we should try to make the activations of top two layers for present sample and past sample more different. Motivated from these two cases, we then formulate the training of MN as follows.

3.2 Model Formulation

In order to exploit past knowledge (obtained from previous examples) for present learning, we design the model of our proposed MN as follows:

$$\begin{aligned} \min _{W_{1:L},b_{1:L}}&\frac{1}{2}\Vert X_L^t-Y^t\Vert ^2+\frac{1}{2}\sum _{j=1}^p\sum _{i=1}^Nk_j^{i}\Vert X_{L-j+1}^t-X_{L-j+1}^{t-i}\Vert ^2\quad \text{ s. } \text{ t. }\\&\ X_l^t\ =\ \sigma (X_{l-1}^tW_l+b_l), \quad l=1,...,L-1,\nonumber \\&X_L^t=X_{L-1}^tW_L+b_L \nonumber \end{aligned}$$
(6)

where \(X_l^t\) represents the activation of layer l for the present sample at time t, and \(Y^t\) is its corresponding class label; \(X_l^{t-i}\) represents activation of the previous \(i^{th}\) sample in layer l at time \(t-i\), while \(Y^{t-i}\) describes the corresponding label for this specific sample. The matrix \(\mathbf {k}\) (of the size \(p\,\times \,N\)) is a coefficient matrix. Its element \(k_j^{i}\) is defined as a positive value, if \(Y^t=Y^{t-i}\) (i.e., the previous \(i^{th}\) sample \(X_0^{t-i}\) shares the same class label as the present sample \(X_0^t\)); otherwise it is a negative value. In more details, a positive \(k_j^{i}\) encourages more similarity between activations (in the \(L-j+1\) layer) of the present learning (at t time) and the previous learning (at \(t-i\) time); this is reasonable, since the present sample, \(X_0^t\) shares the same label as the previous sample \(X_0^{t-i}\). Similarly, a negative \(k_j^{i}\) would enlarge the difference between the activations of the current learning and the previous learning, since the present sample and the previous sample have a different class label. We could also adapt the value of \(k_j^{i}\), depending on if how deep the layer \(L-j+1\) is. Usually, a deeper or topper layer (i.e., smaller j) is more important, leading that \(k_j^{i}\) should be set to a bigger value.

In a short summary, on one hand, the optimization problem (6) would try to minimize the loss at the current time t (when a sample \(X^t_0\) is fed), i.e., the first term in (6); on the other hand, the proposed MN would also try to reduce (or enlarge) the difference of the activations up to the last p layers between the present network and the previous networks, i.e., the memory loss in the second term of (6), depending if the present sample shares the same class label as the previous sample. By this process, knowledge trained from previous samples can be transferred to the present learning, making the network possible to achieve remarkable performance even if the training samples are limited.

3.3 Optimization

For solving the modified optimization problem above, we can still rely on the BP algorithm, since the gradients with respect to the parameters can be easily computed from Eq. (6). For example, when p is set to 2, we could calculate the gradients for the output layer L as:

$$\begin{aligned} \frac{\mathrm {d}E}{\mathrm {d}X_L}= & {} (X_L^t-Y^t)+\sum _{i=1}^Nk_1^i(X_L^t-X_L^{t-i})\\ \frac{\mathrm {d}E}{\mathrm {d}X_{L-1}}= & {} (\frac{\mathrm {d}E}{\mathrm {d}X_{L}}\circ X_{L}\circ (1-X_{L}))W_{L}+\sum _{i=1}^Nk_2^i(X_{L-1}^t-X_{L-1}^{t-i})\\ \frac{\mathrm {d}E}{\mathrm {d}X_l}= & {} (\frac{\mathrm {d}E}{\mathrm {d}X_{l+1}}\circ X_{l+1}\circ (1-X_{l+1}))W_{l+1} \\ \frac{\mathrm {d}E}{\mathrm {d}W_l}= & {} X_{l-1}^{T}(\frac{\mathrm {d}E}{\mathrm {d}X_l}\circ X_l\circ (1-X_l)) \\ \frac{\mathrm {d}E}{\mathrm {d}b_l}= & {} mean(\frac{\mathrm {d}E}{\mathrm {d}X_l}\circ X_l\circ (1-X_l),1) \end{aligned}$$

It is straightforward to extend the above cases to bigger p’s. With the above gradients, a BP can be easily conducted so that a local minimum can eventually obtained for the memory network.

4 Experiments

In this section, we conduct a series of experiments on two small-size data sets including face and handwriting data.

4.1 Experimental Setup

The face data set just contains 120 training samples [1] and the handwriting data set is a small portion of MNIST data set [3]. In the face data, a training and test set is respectively provided by following [8]. We hence train the different models on the training set and then report their performance on the test set. In the handwriting data, we randomly sampled 50, 100, and 500 digits from MNIST training set. We then report the performance on the test set. For fairness, we do the sampling five times and report the average classification accuracy. In order to compare the performance of the proposed Memory Network, we have implemented the conventional MLP, Linear and nonlinear Support Vector Machine with the rbf kernel function (in short, linear-SVM, and rbf-SVM) on these two data sets.

For these two data sets, the structure and parameters of the proposed network are set up differently. For different data sets, the network share the same depth with totally 5 layers, i.e., 1 input layer, 3 hidden layers, and 1 output layer. We exploit the deep structure, since deep networks are more flexible. For face data set, the input-hidden-output units are respectively set to \(100-300-100-40-15\), and for handwriting data set, the input-hidden-output units are \(100-200-300-100-10\). Both the structures are tuned in experiments. Again, p is set to 2, since the top layers are usually more stable. The memory weights \(k_j^i\) are tuned from the set \(\{0.0001, 0.001, 0.01, 0.1\}\). For SVM, the trade-off parameter C and the width \(\gamma \) is tuned via cross validation.

4.2 Face Recognition with Different Pose

The face data set contains totally 195 images for 15 persons [1]. Each person has 13 horizontal poses from \(-90\) to \(90^{\circ }\) with interval \(15^{\circ }\). We have done a series of preprocessing including resizing the images to \(48\,\times \,36\) and then reducing the dimension to 100 with Principal Component Analysis (PCA). We divide this data set into two parts, number 1–8 poses are used as the training set and number 9–13 poses are used as the test set.

Table 1 reports the performance (recognition rate) of different models. It can be noted that the test set shares very different pose from the training set which makes the problem very challenging. As observed, our novel Memory Network and rbf-SVM achieves the best performance with \(85.33\,\%\). More specifically, the proposed MN significantly improves the performance of MLP from 81.33 to 85.33! On the other hand, Fisher Discriminant Analysis (FDA) is the state-of-the-art algorithm for face recognition, which only achieved the error rate of \(69.33\,\%\) [8]. Moreover, other approaches such as the bilinear model, the style mixture model, the Field Bayesian Model and conventional Neural Network are obviously worse than our proposed Memory Network.

Table 1. Recognition rates of different models on face data. The proposed Memory Network and RBF-SVM significantly outperforms the other models. The other results (except Memory Network and conventional Neural Network) were copied from the associated papers due to the same setting.
Full size table

4.3 Handwriting Classification

We also test our proposed model on very famous handwriting digits data set, MNIST. MNIST is a large handwriting data set which has 60, 000 training samples and 10, 000 test samples. It is a portion of a larger data set NIST [2] and the samples have been size-normalized and centered in a fixed-size image (\(28\,\times \,28\)). In this experiment, we focus on the small sample set. Therefore, we sample the small portions from MNIST. In particular, 50, 100 and 500 samples are chosen from 60000 samples of MNIST database randomly. Before training, for increasing training speed, we reduce the dimension of samples from \(28\,\times \,28\) to \(10\,\times \,10\). For testing, we use all test samples of MNIST database, totally 10, 000 samples. We perform the experiments five times and then report the average accuracy.

Table 2. Recognition rates (%) of different models on hand-writing data.
Full size table

We compare the performance of our proposed MN model with the conventional MLP, linear-SVM, and rbf-SVM. Table 2 shows the performance (recognition rate). Our proposed MN demonstrates a distinct performance improvement when the training samples are fewer. In particular, it can be noted that our proposed model achieves much better performance over MLP on 50-sample set (from \(56.04\,\%\) to \(75.65\,\%\)) and 100-sample set (from \(67.76\,\%\) to \(81.60\,\%\)). There is just a slight improvement on 500-sample set (from \(88.79\,\%\) to \(91.35\,\%\)). Our proposed MN also outperform both linear-SVM and rbf-SVM significantly. This experiment further validates the advantages of our proposed MN, especially when the training samples are limited.

5 Conclusion

In this paper, we proposed a novel Memory Network which can appropriately take advantages of past knowledge. Specifically, we built a novel network with two parts: memory part and present part both of which share the same structures. We proposed to connect the top p layers of memory part and present part, which are exploited to deliver the past knowledge. We developed a modified stochastic optimization algorithm, which can efficiently optimize the proposed MN model. We conducted experiments on two small-size databases including face and handwriting data. Experimental results showed that our proposed model achieves the best performance on both the data sets compared with the other competitive models.