Optimal Drug Treatment in a Simple Pandemic Switched System Using Polynomial Approach

Abstract

The aim of this work is to investigate the optimal control of the treatment in a simple pandemic model as a switched nonlinear system. We used a newly developed approach based on the theory of moments. This approach allows to transform a nonlinear, non-convex optimal control problem to an equivalent linear and convex one. To illustrate our finding, we used the example of influenza pandemic to compare the full treatment approach to our optimal moment and time switching solution.

1 Introduction

In order to avoid high mortalities and as a result of the severity of these outbreaks over years, humans have focused their efforts on finding the best strategies to control the spread of infectious diseases.

Due to poor planning, these efforts frequently fall short. For example, the supplies of drug treatments are often inadequate and inefficient, causing health facilities to run out of resources before meeting the needs [28].

For these reasons, the optimization of the existing control resources is a continuous concern in the public health. The optimal control theory has been a powerful approach to solve optimality problems in many disciplines. The majority of the techniques used in optimal control disease outbreak models (see e.g. [25]) are based on the Pontryagin maximum principle [20] and forward-backward numerical algorithms to solve the state and adjoint system of equations (for the use of numerical methods in optimal control of epidemiological models see [2, 16] and for all other types of optimal control problems see [24]).

One of the issues in using the standard optimal control approach is the suggested control might not take into consideration some realistic constraints. For example, the control agent could be a drug treatment that is not necessarily available at all times [15] or simply might run-out [1]. In this case, it is clear that assuming that control agent to be a continuous function is too optimistic of an assumption. In this situation, a switched control system would be a better approach to deal with a control problem of this nature.

Switched control systems are a class of hybrid systems that are composed of a number of subsystems which are defined by the switches [17]. These systems have extensively been used in recent years due to their applications in engineering and other disciplines [5, 29]. Hence, different studies have adapted the maximum principle to find the optimal control switched systems [9, 23, 26, 27]. However, one the biggest problems of these versions of maximal principle of switched systems is that they are numerically expensive since they involve the use of mixed integer programming [3, 4].

The recent work of Mojica-Nava et al. [19] introduced a new approach to finding the optimal switched control system. This approach is based on the use of the theory of moments for global polynomial optimization via semidefinite programming, which eases the numerical burden of using the previous approaches.

In this work, we use this new approach [19] in a simple classical model that reflects the switched aspect of the control in a pandemic model. A similar version of this model without switched control can be found in a recent work of Brauer [6, 7]. Our goal is to minimize the outflow from infected classes.

The paper is organized as follows: We introduce the problem in Sect. 2 then we transform the problem to an optimal control of switched system in Sect. 3. In Sect. 4, we present relaxation using moments approach where we transform the nonlinear, non-convex optimal control problem to a linear and convex one. Issues related to the implementation of the proposed method are presented in Sect. 5. Finally, we illustrate our results with simulation in Sect. 6. We draw conclusions and present discussion of our findings in Sect. 6.

2 Problem Statement

The aim of this work is to investigate the effect of treatment run-out supplies during a pandemic. For this reason, we consider the following simple pandemic treatment model

$$\begin{aligned} \begin{array}{ccl} \dot{S} &{} = &{} -\beta {\displaystyle \frac{S}{N}} (I+\delta T) ,\\ &{} &{} \\ \dot{I} &{} = &{} \beta {\displaystyle \frac{S}{N}}(I+\delta T) -(\alpha +\gamma u)I ,\\ &{} &{} \\ \dot{T} &{} = &{} \gamma u I -\eta T, \\ \end{array} \end{aligned}$$

(1)

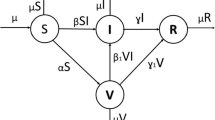
where the total population N is defined as $N=N(t_0)=S(t_0)+I(t_0)$. This SITR model is an extension of the standard model of Kermack and Mckendrick by adding a fraction of infectives to be treated [6, 7], where S, I and T represent the susceptible, the infected and treated individuals. The parameters in model (1) are defined as follows: $\beta$ is the transmission rate from susceptible to infected host and $\alpha$ is the per capita loss rate of infected individuals through both mortality and recovery. We assume that individuals in the T class have infectivity reduced by a factor $\delta$ and $\gamma$ is the rate of infectives that are treated. We also assume that the rate of removal from treated class is $\eta$.

The flow chart of our model is given in Fig. 1.

Fig. 1

Flow diagram of transitions between epidemiological classes of the STIR model

The basic reproduction number is calculated in [6] as

$$\begin{aligned} \mathscr { R}_0= {\displaystyle \frac{\beta }{\alpha +\gamma u}}+{\displaystyle \frac{\beta \delta \gamma u}{\eta (\alpha +\gamma u)}} \end{aligned}$$

(2)

and the final size is given by [7]

$$\begin{aligned} N-S_{\infty }=(\alpha +\gamma u) {\displaystyle \int ^{\infty }_{0}} I(t) dt. \end{aligned}$$

(3)

The parameter u in (1) is the treatment control which takes values 0 or 1, where $u=1$ means treatment is underway and $u=0$ means no treatment. Accordingly, system (1) can switch between two different subsystems (modes of operations), corresponding to $u=i, \ i =0,1$, as time progresses. Thus, we have a switched system.

3 The Switched System

By considering $x=(S,I,T)^\top$, we can rewrite our system (1) as

$$\begin{aligned} \dot{x}(t)= f_{\sigma (t)} (x(t)), \end{aligned}$$

(4)

where $f_{i} : { I\! R}^3 \rightarrow { I\! R}^3$ is the ith vector field, $\sigma : [t_0,t_f] \rightarrow \mathscr { Q}= \{ 0,1 \}$ is the switching signal, a piecewise constant function of time, and $[t_0, t_f]$ is the time interval under consideration. The initial conditions are given by $x(0)=(S(0),I(0),T(0))^\top$. Every mode of operation of the system corresponds to a specific subsystem $\dot{x}(t)= f_{i} (x(t))$, for each $i\in \mathscr { Q}$, where $i=0$ corresponds to $u=0$ and $i=1$ corresponds to $u=1$.

Our goal is to study the number of possible switches of treatment that allows us to reduce the burden of the infection by reducing the size of the pandemic. Each subsystem $\dot{x}(t)= f_{i} (x(t))$, for $i \in \mathscr { Q}$, corresponds to a mode of the switching signal $\sigma (t)$ which is our control input. The values of the switching input signal must be chosen in a way to satisfy the given initial conditions and the desirable final conditions that represent specific desirable pandemic outcome. The optimal switching signal $\sigma$ would represent a public health optimal strategy to control the pandemic within the limits of the available resources.

Before we continue our analysis, we assume the following [19]:

• There are no infinite switching accumulation points in time.

• The state does not have jump discontinuities.

Accordingly, we define the switched control of our system as a duplet of finite sequence of modes and a finite sequence of switching times $t_0<t_1<... <t_f$.

Our optimal control cost function is defined, in Bolza form, as the functional

$$\begin{aligned} J={\displaystyle \int _{t_0}^{t_{f}}}L_{\sigma (t)}(t,x(t))dt, \end{aligned}$$

(5)

with the running cost $L_{\sigma (t)}(t,x(t))$ is given by

$$\begin{aligned} L_{\sigma (t)}(t,x(t))=\alpha I(t) +\eta T (t), \end{aligned}$$

(6)

where the term $(\alpha I(t) +\eta T (t))$ represents the outflow from infected classes at time t  [12], and $\sigma (t)\in \{0,1\}$.

The switched optimal control problem becomes

$$\begin{aligned} \min _{\sigma (t)} J(t_0,t_f,x(t),\sigma (t)) \end{aligned}$$

(7)

subject to

$$\begin{aligned} \dot{x}(t)= f_{\sigma (t)} (x(t)), \end{aligned}$$

(8)

where J is defined by (5) and $\sigma (t)\in \{0,1\}$.

Following the approach in [19], we use Lagrange polynomials to transform the system (8) to a continuous non-switched control system. Therefore, we introduce a new continuous control variable $w \in \varOmega =\{w\in { I\! R}\,\big |\,g(w)=0\}$, where

$$\begin{aligned} g(w)=w(w-1). \end{aligned}$$

(9)

Let the kth Lagrange polynomial, $l_k(w),\ k=0,1$, be defined by

$$\begin{aligned} l_0(w)=(1-w),\;\;\;\; l_1(w)=w. \end{aligned}$$

(10)

Then, according to Proposition 4 in [19], we can write system (8) as the following equivalent continuous system with polynomial dependence, $\mathscr { F}(x,w)$, in the new control variable $w\in \varOmega$:

$$\begin{aligned} \dot{x}=\mathscr { F}(x,w)= f_{0}(x)l_0(w)+ f_{1}(x)l_1(w). \end{aligned}$$

(11)

Similarly, the running cost $L_{\sigma (t)}(t,x(t))$ is equivalently represented by the polynomial $\mathscr { L}(x,w)$ of degree 1 in w:

$$\begin{aligned} \mathscr { L}(x,w) = L_{0}(t,x(t))l_0(w)+L_{1}(t,x(t))l_1(w) \end{aligned}$$

(12)

and the cost function J in (5) becomes

$$\begin{aligned} J(t_0,t_f,x(t),w)=\int _{t_0}^{t_f}\mathscr { L}(x,w)dt. \end{aligned}$$

(13)

Finally, the polynomial equivalent optimal control problem (PEOCP) can be stated as

$$\begin{aligned} \min _{w\in \varOmega } J(t_0,t_f,x(t),w) \end{aligned}$$

(14)

subject to

$$\begin{aligned} \dot{x}=\sum \limits _{k=0}^1 f_k(x) l_k(w), \end{aligned}$$

(15)

with $x(0)=x_0$, a given initial state. The polynomial constraint $w\in \varOmega$ ($g(w)=0$) makes the problem nonconvex, as the feasible set $\varOmega$ is non convex. To overcome the nonconvexity of the problem, the moments approach, described in the next section, is used to redefine the PEOCP in terms of moment variables which will render the optimization problem convex.

4 Relaxation Using Moments Approach

In this section, the moments approach is described for the relaxation of the PEOCP which transforms the nonconvex PECOP into convex semidefinite programs (SDPs). This approach is based on the concepts of moment and localizing matrices of probability measures supported in $\varOmega$.

4.1 Moment and Localizing Matrices

The concept of moment and localizing matrices of a probability measure is described in details in [13, 14]. For the convenience of the reader, we report only the important aspects.

Let $\mathscr {P}_r$ be the space of univariate polynomials of degree at most r in the variable $x\in { I\! R}$. If $\mu$ is a probability measure supported in some set $A\subset { I\! R}$, the ith moment of $\mu$ is defined as

$$ m_{i}=\int _{A} x^{i}\mu (dx) $$

with $m_0=1$. If $p(x)\in \mathscr { P}_r$ of degree r, $\displaystyle p(x)=\sum _{i=0}^r p_{i} x^{i},$ then

$$ \int _{A} p_r(x)\mu (dx)=\sum _{i=0}^r p_{i} m_{i}. $$

Now, if $m=\{m_{j}\}_{j=0}^{2r}$ is a sequence a moments of some probability measure $\mu$, the moment matrix $M_r(m)$ is defined as the symmetric $(r+1)\times (r+1)$ matrix with (i, j) entries $M_r(m)(i,j)=m_{i+j},\ 0\le i,j\le r$, i.e.,

$$ M_r(m)=\left[ \begin{array}{cccc} m_0&{}m_1&{}\cdots &{} m_r\\ m_1&{}m_2&{}\cdots &{}m_{r+1}\\ \vdots &{}\vdots &{}\cdots &{}\vdots \\ m_{r}&{}m_{r+1}&{}\cdots &{}m_{2r} \end{array} \right] . $$

The localizing matrix relative to a polynomial q(x) is defined as follows. Given a polynomial q(x) of degree s, $\displaystyle q(x)=\sum _{i=0}^s q_{i} x^{i}$, the localizing matrix denoted by $M_r(q\,m)$ is defined as the symmetric matrix of size $(r+1)\times (r+1)$ with (i, j) entries, $0\le i,j\le r$, given by

$$ M_r(q\,m)(i,j)=\sum _{k=0}^s q_k m_{i+j+k}. $$

As an example, in the case of $r=3$, the moment matrix $M_3(m)$ is

$$ M_3(m)=\left[ \begin{array}{ccccc} m_0&{}m_1&{}m_2&{}m_3\\ m_1&{}m_2&{}m_3&{}m_4\\ m_2&{}m_3&{}m_4&{}m_5\\ m_3&{}m_4&{}m_5&{}m_6 \end{array} \right] . $$

If $q(x)=2-x^2$, $\{q_i\}=\{2,0,-1\}$, the (i, j) entries of the localizing matrix is given by $M_3(q\,m)(i,j)=2m_{i+j} -m_{i+j+2}$, i.e.,

$$ M_3(q\,m)=\left[ \begin{array}{ccccc} 2m_0-m_2&{}2m_1-m_3&{}2m_2-m_4&{}2m_3-m_5\\ 2m_1-m_3&{}2m_2-m_4&{}2m_3-m_5&{}2m_4-m_6\\ 2m_2-m_4&{}2m_3-m_5&{}2m_4-m_6&{}2m_5-m_7\\ 2m_3-m_5&{}2m_4-m_6&{}2m_5-m_7&{}2m_6-m_8\end{array} \right] . $$

A key property of $M_r(m)$ and $M_r(q\,m)$ used in this paper is their positive semidefiniteness stated in the following proposition.

Proposition 1

If $m=\{m_i\}$ is a sequence of moments of some probability measure $\mu$ supported in some set $A\subset { I\! R}$ and $q(x)=\sum \limits _k q_k x^k$ is a polynomial with $q(x)\ge 0$, $\forall \ x\in A$, then the matrices $M_r(m)$ and $M_r(q\,m)$ are positive semidefinite.

Proof

Let $c=(c_0,c_1,\ldots ,c_r)\in { I\! R}^{r+1}$. Let $\displaystyle p(x)=\sum _{i=0}^r c_i x^i$. Then

$$ c M_r(m) c^\top =\sum _{i=0}^r \sum _{j=0}^r c_ic_jm_{i+j}=\sum _{i=0}^r \sum _{j=0}^r c_ic_j \int _A x^{i+j}\mu (dx)= \int _A (p(x))^2\mu (dx)\ge 0. $$

$$\begin{aligned} c M_r(q\,m) c^\top= & {} \sum _{i=0}^r \sum _{j=0}^r \sum _{k}c_ic_j q_km_{i+j+k}\\= & {} \sum _{i=0}^r \sum _{j=0}^r \sum _{k} c_ic_jq_k \int _A x^{i+j+k}\mu (dx)= \int _A q(x)(p(x))^2\mu (dx)\ge 0. \end{aligned}$$

which prove the positive semidefiniteness of $M_r(m)$ and $M_r(q\,m)$, since c is an arbitrary vector in ${ I\! R}^{r+1}$.

4.2 Semidefinite Programs Using Moments Approach

It has been shown in [13], see also [14], that the minimisation problem (14) is equivalent to the minimisation problem

$$\begin{aligned} \min _{\mu \in P(\varOmega )}\int _{\varOmega }J\,\mu (dw), \end{aligned}$$

(16)

that is,

$$\begin{aligned} \min _{w\in \varOmega }J= & {} \min _{\mu \in P(\varOmega )}\int _{\varOmega } J\mu (dw) \end{aligned}$$

where $P(\varOmega )$ is the space of probability measures supported in $\varOmega$. Since J is a polynomial of degree 1 in w (see (12) and (13)), we can rewrite the minimisation problem in terms of the moments of $\mu$ as

$$\begin{aligned} \min _{\mu \in P(\varOmega )}\int _{\varOmega } J \mu (dw) = \min _{m\in \mathscr { M}}\int _{t_0}^{t_f}\sum _{k=0}^1\sum _{i=0}^1L_k(t,x(t)) \alpha _{ki} m_i, \end{aligned}$$

(17)

where $\alpha _{00}=1, \alpha _{01}=-1, \alpha _{10}=0, \alpha _{11}=1$, are the coefficients of the Lagrange polynomials $l_0(w)$ and $l_1(w)$ in (10), and $\mathscr { M}$ is the space of moments defined by

$$ \mathscr { M}=\{m=\{m_i\},\ m_i = \int _{\varOmega }w^i\mu (dw), \mu \in P(\varOmega )\}. $$

The system state, Eq. (15), is rewritten in terms of the moments $m_i$ as

$$\begin{aligned} \dot{x}=\sum _{k=0}^1 \sum _{i=0}^1 f_k(x)\alpha _{ki} m_i. \end{aligned}$$

(18)

The constraint $m\in \mathscr {M}$ in (17) states that m is a vector of moments of some probability measure. This implies that

$$ M_1(m)=\left[ \begin{array}{cc} m_0&{}m_1\\ m_1&{}m_2 \end{array} \right] \succeq 0. $$

The constraint on the control variable $w\in \varOmega$, $g(w)=w(w-1)=w^2-w=0$, is written as two inequality constraints:

$$\begin{aligned} g_1(w)= g(w)=w^2-w\ge 0,\end{aligned}$$

(19)

$$\begin{aligned} g_2(w)= -g(w)=w-w^2\ge 0. \end{aligned}$$

(20)

The degree of both constraint functions $g_1$ and $g_2$ is even $({=}2)$, so following the results in [13], we consider the family of relaxed convex SDPs, with relaxation order $r\ge \max (\text {degree}(g_1)/2,\text {degree}(g_2)/2)=1$:

$$\begin{aligned} \text{ SDP }_r: \left\{ \begin{array}{l} \displaystyle \min _{m} \int _{t_0}^{t_f}\sum _{k=0}^1\sum _{i=0}^1 L_k(t,x(t))\alpha _{ki}m_i\,dt, \\ \\ M_r(m)\succeq 0,\\ M_{r-1}(g_1\;m)\succeq 0,\\ M_{r-1}(g_2\;m)\succeq 0,\\ \displaystyle \dot{x}=\sum _{k=0}^1 \sum _{i=0}^1 f_k(x)\alpha _{ki} m_i. \end{array}\right. \end{aligned}$$

(21)

It was shown also in [13] that $\min \,$ SDP$_r$ is an increasing sequence of lower bounds for $\min \,J$, and as $r\longrightarrow \infty$, $\min \,$ SDP$_r\,\uparrow \min J$.

For the lowest order of relaxation $r=1$, we have the following SDP

$$\begin{aligned} \text{ SDP }_1: \left\{ \begin{array}{l} \displaystyle \min _{m} \int _{t_0}^{t_f}\sum _{k=0}^1\sum _{i=0}^1 L_k(t,x(t))\alpha _{ki}m_i\,dt, \\ \\ M_1(m)\succeq 0,\\ M_{0}(g_1\;m)=m_2-m_1\succeq 0,\\ M_{0}(g_2\;m)=m_1-m_2\succeq 0,\\ \displaystyle \dot{x}=\sum _{k=0}^1 \sum _{i=0}^1 f_k(x)\alpha _{ki} m_i. \end{array}\right. \end{aligned}$$

(22)

It is worth mentioning that one can use a higher relaxation order r but the number of moment variables will increase, which can make the problem numerically inefficient. However, it is found that in many situations the lowest order of relaxation can achieve the optimal value. In our simulation, we treat our problem with the lowest order of relaxation $r=1$.

5 Numerical Implementation

In this section, we explain the numerical implementation steps used to solve (22). The SDP in (22) is a constrained minimisation problem over the moments m(t) which are time dependent. We discretize the interval $[t_0,t_f]$ with nodal points $t_i$, $i=0,1,\ldots ,N$, with $t_N=t_f$, using a uniform step h. Denote by ${\mathbf m_i}$ the vector of the ith moments, i.e., ${\mathbf m_i}=\{m_i(t_j)\}_{j=0,1,\ldots ,N-1}$. Note that ${\mathbf m_0}=[1,\ 1, \ldots ,\ 1]$, since the zeroth moment $m_0=1$ for all t. Let the vector ${\mathbf m}=[{\mathbf m_1} \ {\mathbf m_2}]$ of length 2N.

The integral defining the objective function and the state constraint differential equation in (22) are descritized using appropriate quadratures. A trapezoidal rule quadrature for the integral and a one-step forward discretization of the state equation give the following discrete version of (22):

$$\begin{aligned} \text{ SDP }_1: \left\{ \begin{array}{l} \displaystyle \min _{{\mathbf m}} h\sum _{j=0}^{N-1} \sum _{k=0}^1\sum _{i=0}^1 L_k(t_j,x(t_j))\alpha _{ki}m_i(t_j) \\ \\ M_1({\mathbf m})\succeq 0,\\ M_{0}(g_1\;{\mathbf m})={\mathbf m_2}-{\mathbf m_1}\succeq 0,\\ M_{0}(g_2\;{\mathbf m})={\mathbf m_1}-{\mathbf m_2}\succeq 0,\\ \displaystyle x(t_{j+1})=x(t_j)+h \sum _{k=0}^1 \sum _{i=0}^1 f_k(x(t_j))\alpha _{ki} m_i(t_j). \end{array}\right. \end{aligned}$$

(23)

where the minimisation is now over the vector ${\mathbf m}=[{\mathbf m_1} \ {\mathbf m_2}]$.

Problem (23) is solved using the built in Matlab function fmincon, which is a function designed for solving numerically nonlinear constrained minimization problems.

Once an optimal solution $\mathbf {m}^*(t_j)=(m_1^*(t_j), m_2^*(t_j))$ of (23) is reached, the switching signal $\sigma (t_j)$ is determined using a rank condition [19] as follows. If $\mathrm {rank}(\textit{M}_1(\mathbf {m}^*(\textit{t}_\textit{j})))=\text{ rank }(\textit{M}_0(\mathbf {m}^*(\textit{t}_\textit{j})))=1$, then the optimal switching signal at $t_j$ is $\sigma (t_j)=m_1(t_j)$, otherwise we use a sum up rounding procedure [21] as follows

$$\begin{aligned} \sigma (t_j)=\left\{ \begin{array}{l} \lceil m_1(t_j)\rceil \qquad \text{ if } \ \displaystyle \int _{t_0}^{t_j}m_1(\tau )d\tau - h\sum _{k=0}^{j-1} \sigma (t)k) \ge 0.5 h,\\ \lfloor m_1(t_j)\rfloor \qquad \text{ otherwise },\end{array} \right. \end{aligned}$$

(24)

where $\lceil \cdot \rceil$ and $\lfloor \cdot \rfloor$ are the ceiling and floor functions, respectively.

6 Numerical Simulation

To illustrate our model, we need to simulate the results of our analysis. We choose the influenza pandemic as parameters of our model. The following parameters can be found in different papers that have studied the influenza pandemic. In our case, we used the parameters for models that studied the control strategy via vaccination and treatment [8, 10, 11]. The parameters are presented in Table 1.

Table 1 Parameter estimation

Fig. 2

The moment function $m_1(t)$ (top) and the optimal switched control of the treatment $\sigma (t)$ (bottom)

Fig. 3

The time series of the Susceptible, Infected and Treated. The plot displays these variable with no control $u=0$ (green), optimal switched control (blue), and full control $u=1$ (red)

The simulations illustrated in Fig. 2 describe the plot of the relaxed moment solution function $m_1^*(t_j)$ and the switching signal $\sigma (t_j)$. Figure 3 depicts the time series of the three compartments’ populations considered in the model.

The optimal moment function and optimal switching signal showed that range of the switches corresponding to optimal solution is between $t=0$ to $t=26$ time units (which is days in the case of influenza) to treat the infected population. After that time there is no need for treatment. This finding is reflected on the time series in Fig. 3 where the peak size and the peak time of the pandemic curve of $u=1$ (in red), which represent the full availability of the treatment at any given time, completely match the case of optimal switched control. This shows that we can achieve the same outcome of controlling the pandemic antiviral treatment by only treating (on and off) for a a limited period of time, hence, avoiding the consequences of the long term antiviral treatment which may exhaust drug stockpile and may develop drug resistance.

7 Conclusion

In this paper, we studied the optimal control problem of a SITR model. The control aimed to optimize the number of infected and treated population via only one control agent, i.e. the treatment. The method used for solving the optimal control problem of switched nonlinear systems was based on a polynomial approach developed by Mojica-Nava et al. [19]. The method based on transforming the problem into a polynomial system which was transformed into a relaxed convex problem using the method of moments [13].

Our results showed that, by using this approach, we can achieve the same outcome of continuous treatment by only limiting treatment for period of time. This indicates that if the treatment is not available or run-out after a specific time, the outcome of the pandemic would be the same as if treatment is available at all times. It is important to mention that the suggested control switches are all in the early time of the pandemic, which line-up with the results in [1, 10]. Although the antiviral drug in a pandemic, like influenza, has been considered as the first line of the defence [1], the long term use of this drug could lead to the development of drug-resistance. This finding also suggests a solution to the long and extensive use of the antiviral drug by limiting its use (on and off) in the beginning of the pandemic and for a limited period of time.

The model suggested in this work is very simple and does not include other control strategies such as vaccination and isolation, that are used to protect the public health in the case of pandemics such as influenza. Our next step is to include these defence measures as switched control in more extended models that include all different levels of heterogeneities.