An Interpolation-Based Approach to American Put Option Pricing

Abstract

In this paper, we discuss how to construct interpolation-based models for American put options. In particular, we derive a closed-form expression and suggest multi-parameter extensions. Our result makes no assumption about the dynamics of the underlying asset, and is constructed to satisfy the necessary no-arbitrage conditions. Finally, we discuss potential applications.

1 Introduction

Since the seminal work of Black and Scholes [4], a common approach in the derivative pricing literature has been to model the underlying asset’s price dynamics by a stochastic process. Since option prices based on the geometric Brownian motion model of Black and Scholes do not provide a reasonable fit to observed market prices, several extensions have been proposed. Well-known examples of such models include the jump-diffusion model of Merton [12], the stochastic volatility model of Heston [10], and the local volatility model of Dupire [7].

Although these extensions have a significantly better performance than the model of Black and Scholes, Epps [8], Alghalith [1] point out that there is no universal model that provides a consistently good fit to observed option prices. Moreover, Figlewski [9], Alghalith [2] point out that simple formulas, which make no assumption about the underlying process, can produce good results. This idea has been explored by Orosi [13] who finds that a nonparametric extension of Figlewski’s model provides a nearly perfect fit to European call options on the S&P 500 index. Additionally, interpolation-based models can be used to extract information from European call options (see for example (Orosi [14, 15]).

Motivated by these results, in this work, we introduce an interpolation-based model for American put options. Instead of making an assumption about the underlying, we construct a suitable pricing function based on no-arbitrage conditions. The rest of the paper is organized as follows. In Sect. 2, we state the necessary no-arbitrage constraints and review how to construct interpolation-based put option prices that satisfy well-known no arbitrage conditions. Moreover, we derive a closed-form American put option formula and introduce a three-parameter model. To illustrate the applicability of our method, we calibrate our models to market quotes in Sect. 3. Section 4 discusses the practical use of our findings and we propose further extensions. Finally, Sect. 5 presents our conclusions.

2 Constructing Suitable Pricing Functions

Merton [11] shows that an American put option function, P(K, T), with strike price K and time to expiry T, must satisfy the following no-arbitrage conditions: (i) P(K, T) is a convex and increasing function of K; (ii) $P(K,T)\le K;$ (iii) P(K, T) is an increasing and convex function of T; (iv) $\max (0,K-S)\le$ P(K, T) where S is the stock price; (v) $P(0,T)=0$; (vi) $\lim _{K\rightarrow \infty }\frac{P(K,T)}{K-S}=1$. Moreover, Carr and Wu [6] show that for put options written on non-defaultable assets $\left. \frac{\partial P(K,T)}{\partial K}\right| _{K=0}=0$. We will refer to these as the necessary no-arbitrage conditions.

To determine suitable put option functions, first, we apply the following transformations to the strikes and put option prices:

$$\begin{aligned} p= & {} \frac{P\left( K,T\right) }{S} \\ k= & {} \frac{K}{S}. \end{aligned}$$

The main idea behind our approach is that it easier to construct suitable pricing functions in the space that is rotated counterclockwise by $45^{\circ }$. Furthermore, we introduce the following function:

$$\begin{aligned} y=G\frac{x^{2}}{\left( \frac{1}{\sqrt{2}}-x\right) }+x, \end{aligned}$$

(1)

where y and x represent the rotated values of p and k, respectively. Then, the put option prices recovered from the above equation satisfy the necessary no-arbitrage properties (see the results in the Appendix).

To obtain the relation between p and k, one must apply the transformation to x and y that rotates these clockwise by $45^{\circ }$. This transformation gives the following relation between the above variables:

$$\begin{aligned} p= & {} \frac{y-x}{\sqrt{2}} \\ k= & {} \frac{y+x}{\sqrt{2}}. \end{aligned}$$

Moreover, substituting (1) for y gives

$$ p=\frac{1}{\sqrt{2}}\left( G\frac{x^{2}}{\left( \frac{1}{\sqrt{2}}-x\right) } +x\right) -\frac{1}{\sqrt{2}}x, $$

where

$$ x=\frac{k-p}{\sqrt{2}}. $$

Finally, an analytic solution for p can be obtained from

$$\begin{aligned} p=\frac{1}{\sqrt{2}}\left( G\frac{\left( \frac{k-p}{\sqrt{2}}\right) ^{2}}{ \left( \frac{1}{\sqrt{2}}-\frac{k-p}{\sqrt{2}}\right) }\right) \end{aligned}$$

(2)

that is given by

$$\begin{aligned} p=\frac{-\sqrt{2(G-1)k+k^{2}+1}+(G-1)k+1}{G-2}. \end{aligned}$$

(3)

Therefore, the arbitrage-free American put option function for a fixed maturity is given by

$$\begin{aligned}&P(K,T)=S\cdot p \nonumber \\= & {} \frac{-S\left( \sqrt{2(G-1)k+k^{2}+1}+(G-1)k+1\right) }{G-2}. \end{aligned}$$

(4)

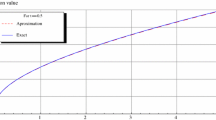
Moreover, to incorporate the property that put options are an increasing function of expiry, larger values of G can be fitted to longer expiries. This is illustrated in Fig. 1 that plots arbitrage-free American put prices with two different parameters.

Fig. 1

American put prices generated by the single-parameter model for two different values: $G=0.03$ and $G=0.1$. The value of the stock price is assumed to be 100

2.1 A Multi-Parameter Extension

Instead of (1), one could consider the following relation with three parameters:

$$\begin{aligned} y=G\frac{x^{\alpha }}{\left( \frac{1}{\sqrt{2}}-x\right) ^{\beta }}+x. \end{aligned}$$

(5)

It can be easily shown that the necessary arbitrage-free conditions are satisfied if the following the constraints are imposed on the parameters: $\alpha >1$ and $\beta >0$ (see the results in the Appendix). Although this three-parameter model provides a better fit to observed option prices, there is no analytic solution for the put prices. Therefore, these have to be determined numerically.

3 An Illustrative Example

In this section, to demonstrate the applicability of the models in (4) and (5), we calibrate these to market quotes. The models are fitted to near-the-money American put options written on Apple Inc. stock. We only consider options with the fixed expiry $T=1.093$ on December 18, 2015. Moreover, the models are calibrated by minimizing the Non-Linear Least Squares (NLS) objective:

$$ \mathop {\displaystyle \sum }\limits _{i=1}^{n}\left( P_{i}\left( \theta \right) -P_{i}\right) ^{2}, $$

where the $P_{i}$-s are the market prices for options, and the $P_{i}\left( \theta \right)$-s are the put option prices based on the model. The results are presented in Table 1 for the single-parameter model and in Table 2 for the three-parameter model. It can be observed that both models yields prices that are very close to the market prices. Moreover, all of the put option prices based on the three-parameter lie inside the bid-ask spread.

Although we leave rigorous empirical analysis of the performance of the models for further research, some advantages of the models to traditional approaches can be easily highlighted. For example, Brooks and Chance [5] point out that the most commonly used option pricing models rely on a constant interest rate as an input. However, according to them, it is difficult to determine what interest rate one should use for the purposes of option pricing. Moreover, they point out that even small errors in the interest rate used can lead to misestimated option prices and implied volatilities. In particular, the prices of American options are very sensitive because of the impact of the interest rate on early exercise. Since our models do not use interest rate as an input, option prices and hedge ratios can be efficiently and accurately calculated from observed market prices.

Table 1 The resulting call option prices of the one-parameter model with the best fit parameter G on Apple Inc. stock with $T=1.093$ on December 18, 2015

Table 2 The resulting call option prices of the three-parameter with the best fit parameter G, $\alpha$ and $\beta$ on Apple Inc. stock with $T=1.093$ on December 18, 2015

4 Applications and Extensions

4.1 Model-Free Hedge Ratios

Bates [3], Reiss and Wystup [16] point out that a model-free deltas and gammas can be calculated if one has a continuous set of options as a function of strikes. For example, for puts and calls, it is reasonable to assume that

$$ O\left( aK,aS,T\right) =aO\left( K,S,T\right) , $$

where $O\left( K,S,T\right)$ is the option price, K is the strike price, $S\$is the price of the asset, and a is a positive constant. Then, a model-free delta, $O_{S}$, can be calculated from the expression:

$$\begin{aligned} O_{S}S+O_{K}K=O\left( K,S,T\right) . \end{aligned}$$

(6)

Similarly, deltas and kappas satisfy the relations:

$$\begin{aligned} O_{S}\left( aK,aS,T\right)= & {} O_{S}\left( K,S,T\right) \\ O_{K}\left( aK,aS,T\right)= & {} O_{K}\left( K,S,T\right) . \end{aligned}$$

From the above, the following equations can be obtained:

$$\begin{aligned} O_{SS}S+O_{KS}K= & {} 0 \\ O_{KS}S+O_{KK}K= & {} 0. \end{aligned}$$

Then, eliminating $O_{KS}$ from the above yields

$$\begin{aligned} O_{SS}S^{2}=O_{KK}K^{2}. \end{aligned}$$

(7)

Finally, $O_{KK}$ and $O_{K}$ can be calculated numerically or analytically, and model-free deltas and gammas can be obtained.

4.2 A Further Extension

Instead of (1) or (5), one could consider the following relation:

$$ y=G\frac{s(x)}{\left( \frac{1}{\sqrt{2}}-x\right) ^{\beta }}+x, $$

where s(x) is a function with an arbitrary number of parameters or a nonparametric function. Note that if $\beta >0$, $s(0)=0$, $s^{\prime }(0)=0$, $s^{\prime }(x)\ge 0$, and $s^{\prime \prime }(x)\ge 0,$ then the put option prices satisfy the necessary no-arbitrage conditions (see the results in the Appendix).

5 Conclusion

In this paper, we demonstrate how to construct interpolation-based models for American put options. Our approach is constructed to satisfy the necessary no-arbitrage conditions, and makes no assumption about the dynamics of the underlying asset. We also briefly explain the advantage of the proposed models and discuss potential applications.

Appendix

In this section, we show that put prices obtained from (1) or (5) satisfy the necessary no-arbitrage conditions.

Claim 1

If a function $y=f(x)$ is convex on $x\in \left[ 0,\infty \right)$ and $f^{\prime }(x)\geqslant 1$, then the resulting function obtained by rotating f(x) clockwise by $45^{\circ }$ is convex and increasing on $\left[ 0,\infty \right)$.

Proof

First, note that the rotated function $p=g(k)$ is given by the equations

$$\begin{aligned} p= & {} \frac{1}{\sqrt{2}}y-\frac{1}{\sqrt{2}}x \\ k= & {} \frac{1}{\sqrt{2}}y+\frac{1}{\sqrt{2}}x. \end{aligned}$$

From the above, the following can be obtained:

$$ p=\frac{1}{\sqrt{2}}\left( f(x)-x\right) =\frac{1}{\sqrt{2}}\left( f\left( \frac{k-p}{\sqrt{2}}\right) -\frac{k-p}{\sqrt{2}}\right) . $$

Then,

$$ \frac{dp}{dk}=p^{\prime }=\frac{1}{\sqrt{2}}\left( f^{\prime }\left( \frac{ k-p}{\sqrt{2}}\right) \frac{1-p^{\prime }}{\sqrt{2}}-\frac{1-p^{\prime }}{ \sqrt{2}}\right) =\frac{1}{2}\left( f^{\prime }\left( \frac{p-k}{\sqrt{2}} \right) -1\right) \left( 1-p^{\prime }\right) $$

and

$$ p^{\prime }=\frac{\frac{1}{2}\left( f^{\prime }\left( \frac{k-p}{\sqrt{2}} \right) -1\right) }{1+\frac{1}{2}\left( f^{\prime }\left( \frac{k-p}{\sqrt{2} }\right) -1\right) }. $$

Therefore, $p^{\prime }\geqslant 0$ because $f^{\prime }(x)\geqslant 1.$ Moreover,

$$ \frac{d^{2}p}{dk^{2}}=p^{\prime \prime }=\frac{1}{2}\left( f^{\prime \prime }\left( \frac{k-p}{\sqrt{2}}\right) \left( \frac{1-p^{\prime }}{\sqrt{2}} \right) \right) \left( 1-p^{\prime }\right) +\frac{1}{2}\left( f^{\prime }\left( \frac{k-p}{\sqrt{2}}\right) -1\right) \left( -p^{\prime \prime }\right) $$

and

$$ \frac{d^{2}p}{dk^{2}}=p^{\prime \prime }=\frac{\frac{1}{2}\left( f^{\prime \prime }\left( \frac{k-p}{\sqrt{2}}\right) \left( \frac{1-p^{\prime }}{\sqrt{ 2}}\right) \right) \left( 1-p^{\prime }\right) }{1+\frac{1}{2}\left( f^{\prime }\left( \frac{k-p}{\sqrt{2}}\right) -1\right) }. $$

Therefore, $p^{\prime \prime }\geqslant 0$ because both the numerator and denominator are positive.$\blacksquare$

Moreover, if a continuous function $y=f(x)$ is convex on $x\in \left[ 0, \frac{1}{\sqrt{2}}\right)$, $\ f^{\prime }(x)\geqslant 1,$ and $\lim _{x\rightarrow \frac{1}{\sqrt{2}}}f(x)=\infty ,$ then it is bounded by the lines: $y=x$, $x=\frac{1}{\sqrt{2}}$, and the y-axis. Hence, the function obtained by rotating f(x) clockwise by $45^{\circ }$ is bounded by the following lines: the k-axis (the horizontal axis), $p=k$ (that line that passes through the original and has a slope of 1), and $p=k-1.$ Moreover,

$$\begin{aligned} \lim _{p\rightarrow \infty }\frac{g(k)}{k-1}= & {} 1,\text { } \\ g(0)= & {} 0\text { iff }f(0)=0, \\ \text {and }f^{\prime }(0)= & {} 1\text { iff }g^{\prime }(0)=0. \end{aligned}$$

Consequently, we require f(x) to satisfy the following requirements: $f(0)=0,$ $f^{\prime }(0)=1$, $\lim _{x\rightarrow \frac{1}{\sqrt{2}} }f(x)=\infty$, $\ f(x)$ is convex on $x\in \left[ 0,\frac{1}{\sqrt{2}} \right) ,$ and $f^{\prime }(x)\geqslant 1$. Then, the put prices obtained from

$$ P(K,T)=P(k\cdot S,T)=S\cdot p=S\cdot g(k) $$

satisfy the necessary no-arbitrage conditions with the exception of condition (iii). Finally, condition (iii) is satisfied if the parameter G in (4) or (5) is and increasing function of T.