Normalizing Chemical Reaction Networks by Confluent Structural Simplification

Abstract

Reaction networks can be simplified by eliminating linear intermediate species in partial steady states. In this paper, we study the question whether this rewrite procedure is confluent, so that for any given reaction network, a unique normal form will be obtained independently of the elimination order. We first contribute a counter example which shows that different normal forms of the same network may indeed have different structures. The problem is that different “dependent reactions” may be introduced in different elimination orders. We then propose a rewrite rule that eliminates such dependent reactions and prove that the extended rewrite system is confluent up to kinetic rates, i.e., all normal forms of the same network will have the same structure. However, their kinetic rates may still not be unique, even modulo the usual axioms of arithmetics. This might seem surprising given that the ODEs of these normal forms are equal modulo these axioms.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Chemical reaction networks are widely used in systems biology for modeling the dynamics of biochemical molecular systems [1, 4, 6, 11]. A chemical reaction network has a graph structure that can be identified with a Petri net [2]. Beside of this, it assigns to each of its reactions a kinetic rate that models the reaction’s speed. Chemical reaction networks can either be given a deterministic semantics in terms of ordinary differential equations (ODEs), which describes the evolution of the average concentrations of the species of the network over time, or a stochastic semantics in terms of continuous time Markov chains, which defines the evolution of molecule distributions of the different species over time. In this paper, we focus on the deterministic semantics.

Reaction networks may become very large when modeling molecular biological systems in sufficient detail, see e.g. the examples in the BioModels database [8]. Therefore much effort has been spent on their simplification (see [18] for an overview). The traditional approach is by reducing the ODEs of the network by symbolic rewriting techniques [9, 10]. While clearly beneficial, such approaches have the disadvantage that the simplified ODEs cannot always be translated back to a reaction network [3], so that these simplifications cannot be understood directly as simplifications of biological systems.

Another major problem with large biological reaction networks is that precise kinetic rates are rarely available [14, 16]. In the worst case, no kinetic information is available, so that no ODEs can be derived. The only simplifications that are possible in this case rely purely on the graph structure of the reaction network [12, 17]. In a less extreme setting, the kinetic rates are given by arithmetic expressions with unknown parameters. In this case, the purely structural methods must be lifted so that they can properly account for the kinetic rates.

The common objective of the structural simplification methods is to eliminate intermediate species that are irrelevant to the external behaviour of the system. This can be done in an exact manner – when assuming partial steady states – so that the solutions of the ODEs of reaction networks are preserved [13, 19, 21]. It should be noticed that any structural reduction algorithm preserving the ODE’s solutions necessarily induces an exact reduction method on the underlying ODE level. Indeed the above methods are based on the same idea, which is to resolve the partial steady state equation of some intermediate species along its concentration variable, so that this variable can be eliminated from the ODEs. The restriction that makes this possible is that the kinetic rates of the network’s reactions are linear in the concentration of the intermediate species.

The structural reduction method for intermediate elimination from [13] removes the intermediates stepwise one by one. The approach of [21] is similar with an extension to rapid equilibrium assumption. The alternative method of [19] removes several intermediates simultaneously. We verified that both methods perform the same reductions when restricted to a single intermediate, even though these are computed by quite differently algorithms. The yet independent method from [17, 18] also performs simultaneous elimination of intermediates, but not necessarily in a unique manner. The intermediates are eliminated from the reaction graph by computing elementary modes in a first step, and in a second, appropriate kinetic rates are assigned to reduced graph. Their method can also be applied in the nonlinear case, but then with some approximations.

In this paper, we study the question of whether the stepwise elimination of linear intermediates is confluent, so that for any given reaction network, a unique normal form will be obtained independently of the elimination order. If confluence would hold, one could compare reaction networks for equivalence, by computing and comparing their normal forms. Furthermore, the unique normal form would be the natural target for simultaneous reduction methods such as [18, 19]. Indeed, a confluence statement was claimed in Sect. 5 of [19] (for the case without conservation laws), but without proof.

We first contribute a counter example which shows that the elimination of linear intermediates on the same network may lead to normal forms with different graph structure. This example contradicts the confluence statement from [19]. The problem is that different “dependent reactions” may be introduced in different elimination orders. We then propose a rewrite rule that eliminates such dependent reactions and prove that the extended rewrite system is confluent up to kinetic rates, so that all normal forms of a same network will have the same structure. This yields a method to eliminate linear intermediates from a reaction graph in a unique manner, while no uniqueness result was stated in [17, 18]. However, the kinetic rates may still not be unique, even not modulo the usual axioms of arithmetics. This might seem surprising given that the ODEs of these normal forms are equal modulo these axioms. Finally, we present an example reaction network from systems biology for the failure of confluence with respect to kinetic rates, that we found in the BioModels SBML database [8] with an implementation of our rewrite rules.

Our positive confluence result shows that the graph structure of reaction networks after intermediate and dependency reduction is unique, and thus potentially meaningful biologically. The two negative confluence results show that the situation may be different without dependency reduction, and also for the kinetic rates that can be assigned to the reactions of the reduced network.

All proofs and missing parts are available in the Appendix of the long version.

2 Confluence Notions

We recall confluence notions and their relationships from the literature.

Let $(S,\sim )$ be a set with an equivalence relation and $\rightarrow {}\subseteq S\times S$ a binary relation. We define $\rightarrow ^0\ =\ \sim$ and $\rightarrow ^k\ =\ \rightarrow \circ \rightarrow ^{k-1}$ for all $k>0$. The relation $\rightarrow ^*\ =\ \cup _{k\ge 0}\rightarrow ^k$ is called the reflexive transitive closure of $\rightarrow$. We write $\rightarrow ^\epsilon \ =\ \rightarrow ^{1}\cup \rightarrow ^{0}$, and $\leftarrow \ =\ \{(s,s')\mid s'\rightarrow s\}$.

Definition 1

(Confluence modulo). We say that a binary relation $\rightarrow$ on $(S,\sim )$ is confluent if $\leftarrow ^*\circ \rightarrow ^*\ \subseteq \ \rightarrow ^* \circ \ ^{*}{\leftarrow }$, locally confluent if $\leftarrow \circ \rightarrow \ \subseteq \ \rightarrow ^* \circ \ ^{*}{\leftarrow }$, strongly confluent if $\leftarrow \circ \rightarrow \ \subseteq \ \rightarrow ^\epsilon \circ \sim \circ \ \ ^{\epsilon }{\leftarrow }$, and uniformly confluent if $\leftarrow \circ \rightarrow \ \subseteq \ {\sim } \mathrel {\cup } (\rightarrow \circ \sim \circ \leftarrow )$.

Clearly, uniform confluence implies strong confluence, and strong confluence implies local confluence. It is also folklore that there exist locally confluent relations that are not confluent, while strong confluence implies confluence [7]. Uniform confluence implies for any $s\in S$ that all complete reduction sequences starting with s have the same length [15], which may be $\infty$ though.

In this paper, we will always use binary relations that are terminating, i.e., for any $s\in S$ there exists a $k\ge 0$ such that $\{s'\mid s\rightarrow ^k s'\}=\emptyset$, i.e., the length reduction sequences starting with s is bounded. It is well known that locally confluent and terminating relations are confluent (Newman’s lemma).

We say that $\sim$ commutes with $\rightarrow$ if $\sim \circ \rightarrow \ \subseteq \ \rightarrow \circ \sim$.

Lemma 1

If $\rightarrow$ is confluent for $(S,\sim )$ and commutes with $\sim$, then the relation $\sim \circ \rightarrow \circ \sim$ is confluent for $(S,=_S)$.

3 Simplification of Systems of Equations

In this section, we recall the definition of arithmetic expressions and ordinary differential equations. It is well known that such systems can be inferred from reaction networks with deterministic semantics and partial steady state assumptions. We will then show how to simplify such systems in a confluent manner by eliminating intermediate variables.

Systems of Equations. Let $\mathbb {R}_+$ be the set of non-negative real numbers, and $\mathbb {N}_0\subseteq \mathbb {R}_+$ the set of natural numbers including 0. Denote by $\textit{Vars}$ a countable set of variables for functions of type $\mathbb {R}_+\rightarrow \mathbb {R}_+$, and by $\textit{Param}$ a set of parameters. We define the set of arithmetic expression as the terms $e,e'\in \textit{Expr}$ with the following abstract syntax:

$$ e,e'\in \textit{Expr} ~{:}{:}=x{} \mid k \mid n \mid e+e' \mid e*e' \mid 1/e \mid -e $$

where $x{} \in \textit{Vars}$, $k \in \textit{Param}$, $n \in \mathbb {R}$. In the following, the expression 1 / e is permitted only if e can never become zero, as explained below. For convenience, we will write $ee'$ for $e*e'$; $e/e'$ for $e*(1/e')$, $e-e'$ for $e+(-e')$ and $e^n$ for $e*\ldots *e$ with n repetitions of e.

We map variables to functions on non-negative real numbers, and parameters to positive numbers (different from 0), which are identified with positive constant functions on non-negative real numbers. Given an assignment $\alpha : (\textit{Vars}\rightarrow (\mathbb {R}_+\rightarrow \mathbb {R}_+)) \cup (\textit{Param}\rightarrow \mathbb {R}_+^*)$, any expression $e \in \textit{Expr} _{}$ can be interpreted as a function $\llbracket e\rrbracket _{\alpha }: \mathbb {R}_+\rightarrow \mathbb {R}_+$ in the usual way.

A system of equations S is a combination of equations and constraints, with some existential variables, defined as follows:

$$ S {:}{:}= {dx} / {dt} = e \mid x = e \mid nzero (e) \mid \textit{cst}(e) \mid S \wedge S' \mid \exists x.\ S. $$

${dx} / {dt} = e$ is an ordinary differential equation (ODE), and $x=e$ an arithmetic equation, for the variable x and with an expression $e \in \textit{Expr} _{}$. The non-zero constraint $nzero (e)$ is satisfied by an assignment $\alpha$ if e is never equal to zero, that is $\forall t.\ \llbracket e\rrbracket _{\alpha }(t) \ne 0$. The positive constant constraint $\textit{cst}(e)$ is satisfied by a variable assignment $\alpha$ if $\llbracket e\rrbracket _{\alpha }$ is a positive constant function. And $\exists x.S$ allows us to existentially quantify some variables, that we actually want to remove to simplify S. We denote by $\textit{Vars}(e)$ the set of variables of an expression e and by $\textit{Vars}(S)$ the set of free variables of a system S. The set of solutions of a system of equations S is the set of assignments on the free variables of S that make S true, that is $sol(S) = \{\alpha \mid \; \llbracket S\rrbracket _{\alpha }= true \}$.

Example 1

The system of equations in Fig. 1 contains 4 ODEs for the variables , and two arithmetic equations and positive constant constraints for the existentially quantified variables .

Fig. 1.

The system of equations $\textit{S}(N_{X})$.

Similar Systems. We now define a syntactic notion of similarity between systems of equations, so that similar systems will have the same solutions. The similarity relation $\sim$ on arithmetic expressions is the least congruence that includes the usual arithmetic axioms of a field: commutativity and associativity of $+$ and $*$, removal of neutral elements 0 in sums and 1 in products, uniqueness and laws of inverses for −, distributivity, and simplification of real numbers. Similarity is decidable, by rewriting expressions to a fraction of polynomials, with the same denominator, and comparing the numerators.

We always identify arithmetic expressions up to similarity (rather than syntactic equality), i.e., we rewrite modulo $\sim$. Given an assignment $\alpha$, two similar expressions $e \sim e'$ have trivially the same interpretation $\llbracket e\rrbracket _{\alpha }=\llbracket e'\rrbracket _{\alpha }$. The similarity relation is lifted to systems of equations in the obvious manner.

Safe Linear Systems. We will consider only valid systems of equations in which there is exactly one arithmetic equation per quantified variable and at most one ODE for all others. We also assume that the systems are linear in the existentially quantified variables as defined below, but not necessarily in the others:

Definition 2

Given a sequence of variables $\tilde{x} = x_1, \dots , x_n$, an expression $e'$ is called $\tilde{x}$-linear if $e'$ is similar to some expression $e + \sum _{1 \le i \le n} x_ie_i$, where e and $e_i$ do not contain any variables from $\tilde{x}$. We call a system $\exists \tilde{x}. S$ linear (in the quantified variables) if for any quantified variable $x \in \textit{Vars}(\tilde{x})$, the system S is similar to some system $x=e\wedge S'$ where e is an $\tilde{x}$-linear expression.

In order to always avoid division by zero during the repeated elimination of quantified variables to come (see Lemmas 2 and 3), we introduce the following safety restriction of linear systems, which will be satisfied most of the time in the applications. Without this restriction, the simplification procedure could be shown to be only partially correct, similarly to [19].

Definition 3

Let S be a system $\exists x_1,\ldots ,x_n.\ S'$ that is linear in the quantified variables, such that $S'$ has the form $\bigwedge _{1 \le i \le n} x_i = e^i {+} \sum _{1 \le j \le n} x_je^i_j \; \wedge S''$. We define a set expression $L_{S'}$ in which x and y are fresh variables:

$$L_{S'} =_{df}\{\ (x,y) \mid \bigvee _{1 \le i,j \le n} x=x_i \wedge y=x_j \wedge nzero (e_i^j) \ \}.$$

For any assignment of the free variables in the subexpressions $e^i_j$, the set expression $L_{S'}$ denotes a binary relation, that we call the linking relation of $S'$. We call the system S safe if $S'$ entails the following formula:

$$ S' \models \bigwedge _{i=1}^n\ \bigvee _{k=1}^n L^*_{S'}(x_i,x_k) \wedge nzero (e^k) \; \wedge \; (\ e^i \ge 0 \; \wedge \; \bigwedge _{j=1}^n \ e^i_j \ge 0\ ). $$

We denote by $\textit{SafeLin}$ the set of safe linear systems of equations.

Simplifying Safe Linear Systems. We want to simplify safe linear systems of equations by removing existentially quantified variables, while preserving the solutions. To do that, given an expression $x=e$ for a quantified variable x, we will substitute x by e, as described in the simplification rule in Fig. 2.

Fig. 2.

Elimination of an existentially quantified variable x in a system of equations.

A substitution is the replacement of any occurrences of $x_1$ by the expression e. Additionally, we also want to preserve the linearity and safety. Therefore, we define a linear substitution, that rewrites arithmetic expressions into linear ones after the substitution. Formally, given a $\tilde{x}$-linear expression $e \sim e^1+ x_2e^1_2 + \sum _{3 \le i \le n}x_ie^1_i$ and an equation $E_2 = (x_2 = e^2+ x_1e^2_1 + \sum _{3 \le i \le n}x_ie^2_i)$, with $\tilde{x} = \{x_1,\ldots , x_n\}$, the linear substitution of $x_1$ by e in $E_2$ is:

The idea is to a) substitute $x_1$ by e in the equation of $x_2$, b) bring the factor $e_1^2 e_2^1 x_2$ from the right to the left, c) factorize the $x_2$, and d) divide by the factor $1-e^2_1e^1_2$ of $x_2$ we obtained.

Lemma 2

If S is safe and with the above equations then $S \models nzero (1-e^2_1e^1_2)$.

We define by replacing $x_1$ by e in the ODEs and the constraints of S and by performing the linear substitution as above to all nondifferential equations of S. The relation $S\Rightarrow S'$ defined in Fig. 2 simplifies a safe linear system S to $S'$: a quantified variable is eliminated by applying a linear substitution.

Lemma 3

The simplification of a safe linear system is a safe linear system.

Lemma 4

The simplification preserves the solutions of safe linear systems: if $S \Rightarrow _{} S'$, then $sol(S)=sol(S')$.

Example 2

For instance, in the system from Example 1, we can substitute the intermediate variable by . Since we still have the constraint , the constraint $\textit{cst}(e)$ can be simplified into . The never-zero constraint $nzero (1 - \dfrac{k_5k_6}{(k_3+k_5)k_6})$ is similar to $nzero ((k_3+k_5)k_6 - k_5k_6)$ and then $nzero (k_3k_6)$, and therefore is always true , and can be removed. We obtain the system depicted in Fig. 3 (left). By doing the same with the variable , we obtain the system in Fig. 3 (right). Note that we used the fact that $k_6 / k_6 \sim 1$, that is always true, since parameters are assigned to positive numbers.

Fig. 3.

Simplifications of $\textit{S}(N_{X})$.

For safe linear systems, this simplification modulo similarity is confluent, implying that whatever the order adopted for the elimination of quantified variables, it is always possible to find the same fully simplified system, modulo similarity. We actually establish uniform confluence, implying that any simplification leading to the fully simplified system will have the same number of steps.

Theorem 1

The binary relation $\Rightarrow _{}$ on $(\textit{SafeLin},\sim )$ is uniformly confluent.

4 Reaction Networks

In this section, we introduce reaction networks, intermediate species, and the interpretation of a network as a system of equations.

Let $\textit{Spec}$ be a countable set of molecular species ranged over by A. We associate to each species A a concentration variable $x_A$, and denote the set of these variables by $\textit{Vars}= \{ x_A \mid A \in \textit{Spec}\}$. A kinetic expression is a non-negative arithmetic expression on variables $\textit{Vars}$, i.e. for any non-negative assignment $\alpha$ for the concentrations, $\llbracket e\rrbracket _{\alpha }(t) \ge 0$ for all t.

We define a (chemical) solution $s \in \textit{Sol}: \textit{Spec}\rightarrow \mathbb {N}_0$ as a multiset of molecular species, i.e. a function from species to natural numbers, with finite support. Given numbers $n_1, \ldots , n_k$, we denote by $n_1A_1 + \cdots + n_kA_k$ the solution that contains $n_i$ molecules of species $A_i$ for $1 \le i \le k$, and 0 molecules of others species. Given $s_1, s_2 \in Solutions$, their intersection is defined for any A by $(s_1 \cap s_2)(A) = min(s_1(A),s_2(A))$. A kinetic reaction is a pair composed of a reaction and a kinetic expression $e \in \textit{Expr} _{}$. The reaction transforms the solution $s_1$, called reactants, into the solution $s_2$, called products. The reaction vector $\textit{vr}_{r}$ of the reaction r is defined for any $A \in \textit{Spec}$ by . We denote by $kin (r)=e$ the kinetic expression of r.

Given a reaction and the solution $s = s_1 \cap s_2$, the normalization of r is the reaction . In the following, we always assume that every reaction is normalized, and normalization is implicitly applied after every simplification. A reaction network $N_{}$ is composed of normalized kinetic reactions, constraints, and bound species (that we want to remove):

$$ N_{} {:}{:}= r \mid \textit{cst}(e) \mid N_{} \wedge N_{} ' \mid \exists X.\ N_{} $$

We assume the usual structural congruence rules for conjunction and existential quantification. We denote by $C(N_{})$ the set of constraints of $N_{}$.

Once again, we need to add some conditions on the bound species, called intermediate species, in order to be able to fully remove them in a confluent way. We usually denote by $\mathcal {U}$ the intermediate species, and by $\bar{\mathcal {U}}$ the other species.

Given a set $\mathcal {U}$ of molecules, and a reaction , we define the consumption (resp. production ) of r with respect to $\mathcal {U}$ as the molecules of $\mathcal {U}$ that are consumed (resp. produced) by r.

A molecule $X \in \mathcal {U}$ is output-connected (resp. input-connected) in $N_{}$ with respect to $\mathcal {U}$ if $\exists r \in N_{}$ with $Cons_\mathcal {U}(r) = \{X\}$ (resp. $Prod_\mathcal {U}(r) = \{X\}$) and either $Prod_\mathcal {U}(r) = \emptyset$ (resp. $Cons_\mathcal {U}(r) = \emptyset$), or $Prod_\mathcal {U}(r) = \{Y\}$ (resp. $Cons_\mathcal {U}(r) = \{Y\}$) with Y output-connected (resp. input-connected). This property will correspond to the safety property of quantified variables in linear systems of equations.

A reaction network $\exists \mathcal {U}.\ N$ is linear if the following properties hold:

• connectivity: for any $X \in \mathcal {U}$, X is output and input-connected in $N_{}$,

• $\mathcal {U}$-stoichiometry: $\forall r \in N_{}$, $| Cons_\mathcal {U}(r) | \le 1$ and $| Prod_\mathcal {U}(r) | \le 1$,

• $\mathcal {U}$-linearity: $\forall r \in N.\ Cons_\mathcal {U}(r) = \{X\} \Rightarrow kin (r) = x_Xe$, with $\forall Y \in \mathcal {U}. x_Y \notin e$,

• kinetic non-interaction: $\forall r \in N_{}$, $Cons_\mathcal {U}(r) = \emptyset$ and $Prod_\mathcal {U}(r) \ne \emptyset$ implies $x_X \notin kin (r)$ for any $X \in \mathcal {U}$,

• partial steady-state: $\forall X \in \mathcal {U}$, $\textit{cst}(x_X) \in C(N_{})$.

In the following, we will only consider linear networks, and denote by $\textit{Nets}_{}$ the set of linear reaction networks.

Given a linear network $N_{} \in \textit{Nets}_{}$, we can define the interpretation of $N_{}$ in terms of a system of equations $\textit{S}(N_{})$, as described in Fig. 4.

Fig. 4.

Definition of the system of equations S(N), for the network N, with intermediate species $\mathcal {U}$ and with $\tilde{x} = \{x_X \mid X \in \mathcal {U}\}$.

Fig. 5.

The reaction network $N_{X}$.

Lemma 5

For any $N \in \textit{Nets}_{}$, the interpretation S(N) is a (valid) safe linear system.

Example 3

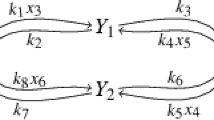
We consider the reaction network $N_{X}$ in Fig. 5, with the reactions on the left and the reaction graph on the right. The set of species is , where and are considered intermediates, and the set of reactions is . The parameters in the rates are some positive reals $k_1,\ldots ,k_6$. All reactions have mass action kinetics, except for reaction which is activated by . Its associated system is $\textit{S}(N_{X})$, described in Example 1.

Given a network $N_{}$, we can compute its system of equations $\textit{S}(N_{})$, and then simplify it in a confluent way, as explained in Sect. 3. But we might sometimes be more interested in the network itself, rather than its system of equations and unfortunately, rebuilding a reaction network from the equations can be difficult, and the network obtained is not unique [3]. It seems then more appropriate to proceed with the simplification directly on the reaction network.

5 Elimination of Intermediate Species

In this section, we introduce the Intermediate simplification rule for reaction networks, and apply it to an example.

The (intermediate) rule presented in Fig. 6 aims at removing an intermediate species $X \in \mathcal {U}$: any reaction $r_{prod}$ that produces X is combined with any reaction $r_{cons}$ that consumes X, and $x_X$ is replaced by its value at steady state in the other reactions. This merging operation is achieved by the operator $\diamond _e$:

Since we only consider normalized reactions, in merged reactions the intermediate molecule is implicitly discarded.

Fig. 6.

Intermediate simplification rule, with C(N) the constraints of N.

The interpretation S(N) is a simulation from $(\textit{Nets}_{},\Rrightarrow _{}^{\tiny {\text {Inter}}})$ to $(\textit{SafeLin},\Rightarrow _{})$:

Lemma 6

Given a network $N \in \textit{Nets}_{}$, if $N \Rrightarrow _{}^{\tiny {\text {Inter}}} N'$, then $S(N) \Rightarrow _{} S(N')$.

This implies as expected that both a network and its simplification have the same deterministic dynamics.

The next example shows that the rewriting system given by the elimination of intermediate species alone is not confluent, given that different dependent reactions may be produced for different elimination orders.

Fig. 7.

Two elimination strategies to simplify $N_{X}$ of Fig. 5: either first eliminate Z to obtain the network $N_{XZ}$ and then Y to obtain $N_{XZY}$, or swap the elimination order to obtain first $N_{XY}$ and then $N_{XYZ}$. Simplified networks $N_{XZY}$ and $N_{XYZ}$ are structurally different since the latter has the additional reaction $r_{1356}$. The new parameters are $K_1 = k_3+k_5$ and $K_2 = k_1k_5+k_2K_1$.

Example 4

Starting from network $N_{X}$ from Fig. 5, we can either remove or and obtain the networks depicted in Fig. 7. If we first remove , then we obtain the reaction network $N_{XZ}$. From $N_{XZ}$ we can eliminate the intermediate and obtain $N_{XZY}$. This network cannot be simplified any further. Alternatively, we can eliminate from $N_{X}$ in a first step, obtain $N_{XY}$, and then remove and obtain the network $N_{XYZ}$.

Unfortunately, $N_{XYZ}$ and $N_{XZY}$ do not have the same structure, since $N_{XYZ}$ has an additional reaction , which is a combination of and . Such dependent reactions can be removed, as we will show in the next section.

6 Elimination of Dependent Reactions

In this section we clarify the notion of dependency between reactions, and introduce an additional simplification rule based on this notion. The addition of this rule is sufficient to establish confluence for the structure of simplified networks. However, we will show that this modification is not enough, in general, to guarantee full confluence.

We formalize the notion of dependency with respect to an initial set of reactions with the notion of flux. Flux vectors at steady state are a standard tool for computing elementary modes [5], that correspond to the unique set of reactions in the network normal form that we obtain with the techniques of this paper. Our simplification method, unlike the elementary modes approach, deals with the impact of the simplification on kinetic rates as well as the network structure.

Given an ordered set of m reactions $\mathcal{R}= \{r_1, \dots , r_m\}$ called reaction basis, a flux is a pair $w=(v;e)$ of a flux vector $v\in \mathbb {R}^m$ and an expression $e\in \textit{Expr}$. The function $\textit{react}_{\mathcal{R}}$ maps fluxes to reactions w.r.t. a reaction basis $\mathcal{R}$ as follows:

Consequently, the i-th vector $\mathsf {u}_{i}$ of the standard basis is mapped to the i-th reaction $r_i$ of the reaction basis $\mathcal{R}$. Now, instead of simplifying reaction networks, we directly simplify flux networks W defined as reaction networks but with fluxes in place of reactions:

$$ W {:}{:}=w \mid \textit{cst}(e) \mid W \wedge W' \mid \exists X.\ W. $$

We lift $\textit{react}_{\mathcal{R}}$ to map flux networks to reaction networks as follows:

$$ \begin{array}{c} \textit{react}_{\mathcal{R}}(\textit{cst}(e)) = \textit{cst}(e), \quad \textit{react}_{\mathcal{R}}(W \wedge W')=\textit{react}_{\mathcal{R}}(W) \wedge \textit{react}_{\mathcal{R}}(W'), \\ \textit{react}_{\mathcal{R}}(\exists X.\ W) = \exists X.\ \textit{react}_{\mathcal{R}}(W). \end{array} $$

We denote $\textit{FNets}_{\mathcal{R}}$ the set of flux networks W such that $\textit{react}_{\mathcal{R}}(W)$ is a linear reaction network for $\mathcal {U}$. The interpretation of $W\in \textit{FNets}_{\mathcal{R}}$ in terms of system of equations is defined as $S_\mathcal{R}(W)=S(\textit{react}_{\mathcal{R}}(W))$. Finally, we translate some previous definitions to the context of flux networks:

$$ \begin{array}{c} Prod_\mathcal{R}(w) = Prod(\textit{react}_{\mathcal{R}}(w)),\qquad Cons_\mathcal{R}(w) = Cons(\textit{react}_{\mathcal{R}}(w)),\\ kin (v;e) = e,\qquad (v;e)\diamond _{e''}(v';e') = (v+v';\frac{ee'}{e''}). \end{array} $$

Fig. 8.

Simplification rules of flux networks.

We then define two simplification rules for flux networks in Fig. 8. First, (Intermediate) is simply a reformulation of the one in Fig. 6 but in the terminology of flux networks. The new rule (Dependent) removes a dependent flux, that is one whose flux vector can be written as a positive linear combination of the flux vectors of some other fluxes. The rate of the removed flux is added to the rate of the fluxes that it depends on. This guarantees that the system of ordinary differential equations associated to the reaction network is unchanged:

Lemma 7

Given $W \in \textit{FNets}_{\mathcal{R}}$, if $W \Rrightarrow _{\mathcal{R}}^{\tiny {\text {Dep}}} W'$, then $S_\mathcal{R}(W) \sim S_\mathcal{R}(W')$.

Two fluxes are structurally similar, denoted $({v},{e}) \sim ^{struc} ({v'},{e'})$, if they have the same flux vector, that is $v=v'$. Two vector networks are structurally similar, denoted $W \sim ^{struc} W'$ if they have structurally similar fluxes.

We can now state the Theorem on the structural confluence for this simplification system. We denote by $\Rrightarrow _{\mathcal{R}}^{\tiny {\text {}}} = (\Rrightarrow _{\mathcal{R}}^{\tiny {\text {Inter}}} \cup \Rrightarrow _{\mathcal{R}}^{\tiny {\text {Dep}}})$ the simplification of vector networks with the rules of Fig. 8.

Theorem 2

The relation $\Rrightarrow _{\mathcal{R}}^{\tiny {\text {}}}$ on $(\textit{FNets}_{\mathcal{R}},\sim ^{struc})$ is confluent.

Proof

(Scetch). The outline of the proof is as follows:

• 1. the simplification relation $\Rrightarrow _{\mathcal{R}}^{\tiny {\text {}}}$ preserves the set of intermediate species,

• 2. the local confluence holds for $\Rrightarrow _{\mathcal{R}}^{\tiny {\text {}}}$,

• 3. the binary relation is terminating, so by Newman’s lemma, it is confluent.

Note that adding a rule that eliminates reactions whose reaction vectors can be written as sums of the reaction vectors of other reactions in the same network (instead of using a reaction basis) does not guarantee the confluence for the network structure.

Example 5

In Example 4, the elimination of the intermediates Y and Z in two different orders was shown to generate two different networks $N_{XZY}$ and $N_{XYZ}$ the latter having the additional reaction $r_{1356}$. Let us take $\{r_1,\ldots ,r_6\}$ as a reaction basis. If we translate the simplifications to flux networks, the flux vector associated to reaction $r_{ij}$ is $\mathsf {u}_{i} + \mathsf {u}_{j}$. Also, the flux vector associated to $r_{1356}$ is $\mathsf {u}_{1} + \mathsf {u}_{3} + \mathsf {u}_{5} + \mathsf {u}_{6}$, that is the sum of the flux vectors of $r_{13}$ and $r_{56}$. Thus, the application of the (Dependent) rule to the flux associated to $r_{1356}$ results in a flux network W such that $\textit{react}_{\mathcal{R}}(W)=N_{XYZ} '$. Since $r_{1356}$ is eliminated, the networks $N_{XZY}$ and $N_{XYZ} '$ have the same structure. The rate of reaction $r_{13}$ in $N_{XYZ} '$ is given by the rate of $r_{13}$ in $N_{XYZ}$, plus the rate of $r_{1356}$ in $N_{XYZ}$, and is therefore equal to , that is the rate of $r_{13}$ in $N_{XZY}$. Similarly, one can show that the rates of $r_{56}$ in the two networks also coincide, and both networks have the same kinetics.

The following variation on the same example shows that confluence of the kinetics is not in general guaranteed.

Fig. 9.

Initial network $(N_{\epsilon })$ and network $(N_{XYZ} ')$ obtained after elimination of X, Y, dependent rule $r_{15}$ and then Z. We have $K_1 = k_3+k_5$.

Example 6

Now we shall examine again the simplifications performed in Example 4, but this time we look at the reaction networks as simplifications of the larger network $N_{\epsilon }$ in Fig. 9 from which $N_{X}$ results after elimination of X. The reaction basis is now $\mathcal{R}'=\{r_{1'}, r_{2'}, r_{3}, r_{4'}, r_{5'}, r_{6}\}$ and the reaction $r_1$ in $N_{X}$ is obtained from $N_{\epsilon }$ by merging $r_{1'}$ and $r_{2'}$ (that, following our convention, we denote $r_{1'2'}$) and is thus associated to the flux w.r.t. $\mathcal{R}'$. Similarly, $r_2 = r_{1'4'}$ is associated to , , and $r_5 =r_{4'5'}$ to .

The eliminations of Z first and Y after, represented in Fig. 7, generate the reactions $r_{26}$, $r_{56}$, $r_{13}$ and $r_{236}$ (with flux vectors respectively $\mathsf {u}_{1} + \mathsf {u}_{4} + \mathsf {u}_{6}$, $\mathsf {u}_{4} + \mathsf {u}_{5} + \mathsf {u}_{6}$, $\mathsf {u}_{1} + \mathsf {u}_{2} + \mathsf {u}_{3}$ and $\mathsf {u}_{1} + \mathsf {u}_{3} + \mathsf {u}_{4} + \mathsf {u}_{6}$), with no dependent reactions. Consider now the elimination of Y from $N_{X}$. Reaction $r_{15}$ has flux in network $N_{XY}$ and is dependent on reactions $r_2$ and $r_4$. If we choose to eliminate reaction $r_{15}$ using the (dependent) rule and apply the (intermediate) rule on Z we obtain the network $N_{XYZ} '$ in Fig. 9. No further simplification rule can be applied. Notice that this network is structurally the same as network $N_{XZY}$ in Fig. 7, but all reactions have different kinetic rates.

7 Normalization Modulo Kinetic Rates

We now present the principal result of this paper, about confluence of the simplification system modulo the kinetic rates. In other words, whatever the order of simplification, we can always obtain a fully simplified network with the same structure and with similar system of equations, but the kinetic rates associated to the fluxes can be different, as illustrated before in the Example 6.

Given a fixed set of intermediate species $\mathcal {U}$ and an initial reaction basis $\mathcal{R}$, two networks are similar, denoted $W \sim _{\mathcal{R}} W'$, if they are structurally similar ($W \sim ^{struc} W'$), and their systems of equations are similar ($S_\mathcal{R}(W) \sim S_\mathcal{R}(W')$).

Theorem 3

The relation $\Rrightarrow _{\mathcal{R}}^{\tiny {\text {}}}$ on $(\textit{FNets}_{\mathcal{R}},\sim _{\mathcal{R}})$ is confluent.

8 An Example from the BioModels Database

We have shown that the simplification system that we presented can exhibit non-confluence of the rates, even in a simple scenario with a small number of intermediates. To find if such a situation occurs in practice, we investigated the SBML models in the curated BioModels database [8]. For each mass-action model, we created the graph of complexes and searched it for cycles of intermediates, to identify possible candidates for non-confluence. Then, with an implementation of the simplification rules, we considered the elimination of triples or quadruples of intermediates in different orders, and compared the resulting networks.

We were thus able to identify two different reduced networks for model BIOMD0000000173. This is a model of the Smad-based signal transduction mechanisms from the cell membrane to the nucleus, presented in [20]. A subnetwork of this model is represented in Fig. 10. It includes all reactions involving cytoplasmic and nuclear Smad4 and Smad2/Smad4 complexes (abbreviated $S4_c$, $S4_n$, $S24_c$ and $S24_n$): shuttling of Smad4, formation of Smad2/Smad4 complex, import of Smad2/Smad4 into the nucleus, and formation of EGFP-Smad2/Smad4 complex. This network is linear for the four intermediate species $S4_c$, $S4_n$, $S24_c$, $S24_n$. The different orders of elimination yield simplified networks with the same structure but different kinetics. This confirms that the or of simplifying a biological network may indeed affect the result.

Fig. 10.

Subnetwork of the Smad signal transduction network in [20].

Conclusion

We have shown that the elimination of linear intermediate species is not confluent in general. We provided a new simplification rule to remove dependent reactions, and proved that the extended rewrite system is confluent up to kinetic rates, that is, all normal forms of the same network will have the same structure and similar systems of equations, but can have different kinetic rates. Future research efforts is needed to characterize networks that possess a unique normal form.