Keywords

1 Introduction

The fight against bacterial virulence represents one of the big challenges of modern medicine. Indeed, due to the large-scale proliferation and inappropriate use of antibiotics, new strains antibiotic-resistant bacteria begin to emerge. These new, stronger bacteria pose a significant threat to humans health and welfare. To fight antibiotic-resistant bacteria, we propose to engineer synthetic cells, insert them in a population of bacteria, and then control the dynamics and virulence of the entire population [9]. We note that while previous work [6, 26] proposed to engineer cells to kill the antibiotic-resistant bacteria, this kind of approaches may actually select strains that can survive under such therapies. In contrast, in this paper, we design an autonomous controller that can not only regulate the cell-cell communication, but also manipulate the environment signals in order to reduce bacterial virulence and prevent selective pressure among antibiotic-resistant strains.

Getting now into details, bacteria can form biofilms, express virulence, and become resistant to antibiotics after reaching a quorum through cell-cell communication. Quorum sensing (QS) is a fundamental cell-cell communication that is used by bacteria to obtain cell density information and hence, alter their genes expression [4]. In particular, the QS system used by Gram-negative bacteria is mediated by diffusible signaling molecules, termed “autoinducers”Footnote 1 [4]. For instance, the opportunistic human pathogen Pseudomonas aeruginosa (PA) possess a complex QS system that regulates genes and operons which constitute over 6 % of the genome. Those genes coordinate the biofilm formation and produce large amounts of virulence factors, such as elastase, rhamnolipids, and pyocyanin [10].

Fig. 1.
figure 1

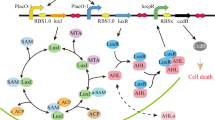
(a) Interconnection of the las and pqs QS system of PA. The small orange circles represent autoinducer molecules (AIs) that move freely through the cell membrane; the purple circles and triangles represent the QS signals of pqs QS system; the green particles represent the pyoverdine molecules. The red, orange, blue, and purple ovals represent LasR, LasI, PqsR, PqsA, and PqsE, respectively. (b) The simulation environment, where bacteria (green cells) flow in space and release the QS signals (orange circles). By placing the synthetic (red) cells in the environment, they first react to the QS signals and then express the inhibitors (purple diamonds) that can quench the communication among bacteria. (c) The diagram of the proposed control system. The environment signal (d) (e.g., nutrient availability) can be viewed as the input to the intracellular bacterial regulations system. The control variables (u) are the QSI inhibitors which can control the dynamics of bacteria. The process variable (y) can be detected by the synthetic controller. (Color figure online)

Full size image

QS regulation can be strongly affected by various environmental factors [11]; for example, in PA, the nutrient availability have been shown to affect the expression of QS genes [24]. Several other studies have demonstrated that high iron concentrations favor the formation of biofilms and higher growth rates, but restrict the expression of QS signals [12, 22]. On the other hand, QS also regulates bacteria access to nutrients and environmental niches that favor their growth and defense.

The intertwined regulation between QS and environmental signals enable bacteria to thrive in a stringent environment [2, 15]; indeed, under such conditions, bacteria must coordinate the expression of related genes in order to successfully form and maintain biofilms [16]. For example, a shortage of iron availability in the environment leads to the increased expression of iron acquisition system [3, 5] and decreased activity of pathways that rely on relatively large amounts of iron [10]. However, a rigorous mathematical model that can precisely capture the complex relationship between the QS system and bacteria growth has not yet been explored. Additionally, most studies published so far focus on observing the qualitative behaviors of bacteria and lack the ability to predict long term evolution dynamics under different environmental conditions [18].

We argue that having a quantitative model of QS behavior available can not only capture the important dynamics of bacteria growth, but also give credible predictions for the long term behaviors of bacteria virulence; this analytical QS model is the first major contribution of this work. We also raise another important question: Given such an analytical (i.e., quantitative) model, what are the strategies to control bacteria virulence and growth rate, while lowering the chances of developing drug resistance or inducing selective pressure among bacteria wild type and mutants? To address this second question, we propose an autonomous biological controller that can dynamically generate different types of inhibitors; this controller is based on genetic parts used to design genetic circuits [1].

To shed light on the complex relationship between QS and environment signals, we use the opportunistic pathogen PA as a canonical example (Fig. 1(a)). PA requires an abundance of iron to produce and sustain infections. Hence, iron depletion prevents bacterial growth and affects their metabolism [19]. By expressing siderophores, PA can sequester iron from environment and regain the ability to form biofilm [25]. Two major genetic components of QS, namely, the las and pqs QS systems have been identified in PA [5]. As shown in Fig. 1(a), the las QS system sits at the upstream of pqs QS system and positively regulates the operons of the pqs QS system [2]. The pqs QS system produces molecules that mediate the expression of the siderophores [5, 7]. To enhance the expression of the siderophores, the upstream las QS system needs to highly express proteins in order to induce the downstream pqs QS system. Hence, as the iron concentration is relatively low, the las QS system is highly expressed and vice versa. However, bacteria can become more virulent when the las QS system strongly expresses proteins as this can regulate the virulence genes.

In summary, in an iron depletion environment, the growth of bacteria can be delayed but the virulence can actually increase [12]. To control both the virulence and the growth rate of bacteria simultaneously, we use two different kinds of inhibitors that target the las QS system and the iron availability in the environment. Different types of inhibitors can have different effects on virulence and growth rate, hence, multi-inhibitor schemes can be more effective. To synthesize inhibitors and control the iron concentration, a few simple genetic circuits can serve as the basic control units which automatically detect and react to environment changes. For example, we can construct the genetic circuits by cloning the genes in the plasmid, such as the aiiA gene which expresses the enzyme that hydrolyzes the AI [17] (Fig. 1(b)). However, synthesizing excessive amounts of inhibitors in the environment can have toxic effects on the host.

Therefore, in this paper, we propose a dynamic optimization problem that incorporates bacteria QS, growth, and control dynamics. Solving this optimization problem allows us to choose the biological parameters that can be further used to design controllers that can generate the optimal amount of inhibitors adaptively. By placing the biological controller into the bacterial environment, it becomes possible to detect the concentration of the signaling molecules in the environment and then generate the right amount of inhibitors in real-time. Consequently, the proposed system aims at a paradigm shift from manual to autonomous control of bacteria population dynamics (Fig. 1(c)). Taken together, our contribution is threefold:

  • First, we develop a new (cellular-level) ordinary differential equations (ODEs) based model of pqs QS system and propose new synthetic circuitry to control bacteria virulence and growth. To the best of our knowledge, this is the first design that formally considers the autonomous control of the QS and environmental signals in populations of bacteria.

  • Second, we formulate a constrained optimization problem based on the QS and control dynamics. We illustrate the design procedures for the biological controller by solving this optimization problem; this provides the theoretical basis for synthesizing the controller.

  • Third, we verify our proposed controller via detailed simulations at population-level. As such, the design procedure we provide can serve as a general guideline towards in vitro construction of synthetic cellular controllers.

The remainder of this paper is organized as follows. Section 2 focuses on the mathematical modeling of the QS regulation system (i.e., las and pqs) of PA, bacteria growth, and QSI model. Section 3 analyzes the QS system response and bacteria growth model via simulation. Section 4 formulates the constrained optimization problem for designing the biological controller and provides a design example based on the proposed design guidelines. Section 5 utilizes the bacteria simulator proposed in [21] to validate the model under various scenarios that mimic realistic settings. Finally, conclusions are drawn in Sect. 6.

2 Cellular-Level Mathematical Modeling

In this section, we model the dynamics of bacteria QS, growth, and inhibition systems based on ODEs. To uncover the complex interaction between the QS and environment signals (i.e., iron), we first model the las and the pqs QS systems and the growth of PA explicitly. Next, we calibrate our models with the reported experimental data [12]; that is, at different iron concentration levels, we calibrate the relative concentration change of the LasR protein (main receptor in las QS system); this provides the basis for examining the QS system response and subsequently designing the biological controller.

2.1 QS Model of PA

The QS regulatory network of PA consists of two main systems: las and pqs. The las and the pqs QS systems are linked by (1) LasR-AI complex which directly up regulates the expression of the PqsR and the PqsH proteins and (2) iron-chelated complex which down regulates the expression of the LasR protein and then reduces the expression of the siderophore (a negative feedback loop). The entire QS system is modeled as follows:

las QS Model. The regulatory network of the las QS system has two feedback loops. As shown in Fig. 1(a), the LasR-AI complex up regulates the expression of both lasR and the lasI genes. Based on the ODE models proposed in [13, 23], we have the following equations for the las QS system:

$$\begin{aligned} \frac{d[A]}{dt}&= c_{A}+\frac{V_{A}[C]}{K_{A}+[C]} - \alpha _{RA}[R][A]+ \delta _{RA}[RA] -b_{A}[A] -\frac{d_{A}}{\rho } ([A_{EX}] - [A])\end{aligned}$$
(1)
$$\begin{aligned} \frac{d[A_{EX}]}{dt}&= -b_{A_{EX}}[A_{EX}] -\frac{d_{A}}{1-\rho } ([A_{EX}] - [A]) \end{aligned}$$
(2)
$$\begin{aligned} \frac{d[R]}{dt}&= c_{R}+\frac{V_{R}[C]}{K_{R}+[C]} - \alpha _{RA}[R][A]+ \delta _{RA}[RA] - b_{R}[R] \end{aligned}$$
(3)
$$\begin{aligned} \frac{d[RA]}{dt}&= \alpha _{RA}[R][A] -2\alpha _{RA^2}[RA]^{2} - \delta _{RA}[RA] + 2\delta _{RA^2}[C] \end{aligned}$$
(4)
$$\begin{aligned} \frac{d[C]}{dt}&= \alpha _{RA^2}[RA]^{2} - \delta _{RA^2}[C] \end{aligned}$$
(5)

where [X] denotes the concentration of a particular molecular species X. In our formulation, A stands for AI, \(A_{EX}\) is the extracellular AI, R is LasR, RA is the LasR-AI complex and C is the dimerized complex. The meaning of biological constants are listed in Table 1 while their numerical values are listed in Tables 2 and 3 in the Appendix.

Table 1. Table with model parameters
Full size table

pqs QS Model. The pqs QS system consists of two kinds of signaling molecules, PQS (2-heptyl-3,4-dihydroxyquinoline) and HHQ (4-hydroxy-2-heptylquinoline); in addition we have one receptor regulator PqsR. The PqsR protein can bind to the HHQ and the PQS molecules and up regulate the pqsABCDE operon; this forms a positive feedback since the PqsA protein directly up regulates the synthesis of the HHQ molecules. Another signaling molecule, PQS, is converted from HHQ via PqsH protein. Therefore, pqs QS system forms a second positive feedback loop. By explicitly capturing regulations among proteins and molecules based on molecular transcription and translation, we propose the following new ODEs to describe the pqs QS system:

$$\begin{aligned} \frac{d[pR]}{dt}&= c_{pR} + \frac{V_{pR} [C]}{K_{pR} + [C]} \!-\! \alpha _{pR} ( [pR][A_1] + [pR][A_2] ) \!+\! \delta _{pR} ( [C_1] + [C_2] )\! -\!b_{pR} [pR] \end{aligned}$$
(6)
$$\begin{aligned} \frac{d[pH]}{dt}&= c_{pH} + \frac{V_{pH} [C]}{K_{pH} + [C]} -b_{pH} [pH] \end{aligned}$$
(7)
$$\begin{aligned} \frac{d[pA]}{dt}&= c_{pA} + \frac{V_{pA,1} [C_1]}{K_{pA,1} + [C_1]} \frac{V_{pA,2} [C_2]}{K_{pA,2} + [C_2]} -b_{pA} [pA] \end{aligned}$$
(8)
$$\begin{aligned} \frac{d[pE]}{dt}&= c_{pE} + \frac{V_{pE, 1} [C_1]}{K_{pE, 1} + [C_1]} \frac{V_{pE, 1} [C_2]}{K_{pE, 1} + [C_2]} -b_{pE} [pE] \end{aligned}$$
(9)
$$\begin{aligned} \frac{d[C_1]}{dt}&= \alpha _{pR} [pR] [A_1] - \delta _{pR} [C_1] \end{aligned}$$
(10)
$$\begin{aligned} \frac{d[C_2]}{dt}&= \alpha _{pR} [R_2][A_2] - \delta _{pR} [C_2] \end{aligned}$$
(11)
$$\begin{aligned} \frac{d[A_1]}{dt}&= \beta _{pA} [pA]\frac{K_{A_1}}{K_{A_1} \!+ \! [pE]} \! - \! \alpha _{pR} [pR][A_1] \!+\! \delta _{pR} [C_1] \!-\! b_{A_1} [A_1] \! + \!\frac{d_{A_1}}{\rho } ([A_{1EX}] \!-\! [A_1]) \end{aligned}$$
(12)
$$\begin{aligned} \frac{d[A_{1EX}]}{dt}&= - b_{A_1} [A_{1EX}] -\frac{d_{A_1}}{1-\rho } ( [A_{1EX} - [A_1]) \end{aligned}$$
(13)
$$\begin{aligned} \frac{d[A_2]}{dt}&= \beta _{pH} [pH] [A_1] \! -\! \alpha _{pR} [pR][A_2] + \delta _{pR} [C_2] - b_{A_2} [A_2] +\frac{d_{A_2}}{\rho } ([A_{2EX}] - [A_2]) \end{aligned}$$
(14)
$$\begin{aligned} \frac{d[A_{2EX}]}{dt}&= - b_{A_2} [A_{2EX}] -\frac{d_{A_2}}{1 - \rho } ([A_{2EX}] - [A_2]) \end{aligned}$$
(15)
$$\begin{aligned} \frac{d[Pyo]}{dt}&= c_{Pyo} + \frac{V_{Pyo} [pE]}{K_{Pyo} + [pE]} - b_{Pyo} [Pyo] + \frac{d_{Pyo}}{\rho } ([Pyo_{EX}] -[Pyo]) \end{aligned}$$
(16)
$$\begin{aligned} \frac{d[Pyo_{EX}]}{dt}&= - \alpha _{I} [Pyo_{EX}][I] - b_{Pyo_{EX}} [Pyo_{EX}] + \frac{d_{Pyo}}{1 - \rho } ([Pyo_{EX}] - [Pyo]) \end{aligned}$$
(17)
$$\begin{aligned} \frac{d[Q]}{dt}&= - b_{Q} [Q] + \frac{d_Q}{\rho } ([Q_{EX}] - [Q]) \end{aligned}$$
(18)
$$\begin{aligned} \frac{d[Q_{EX}]}{dt}&= \alpha _{I} [Pyo_{EX}][I] + \frac{d_{Q}}{1 - \rho } ([Q_{EX}] - [Q]) \end{aligned}$$
(19)

where [X] denotes the concentration of a particular molecular species X. In our formulation, pA, pE, pH, and pR stand for PqsA, PqsE, PqsH and PqsR, respectively. \(A_1\), \(A_2\), \(C_1\) and \(C_2\) represent HHQ, PQS, PqsR-HHQ and PqsR-PQS, respectively. Pyo and I represent pyoverdine and iron, respectively. Q is the iron-chelated complex.

Given the pqs QS system, we modify the expression of the LasR protein in (3) as follows:

$$\begin{aligned} \frac{d[R]}{dt} = c_{R}+\frac{V_{R}[C]}{K_{R}+[C]}\frac{V_{Q}K_{Q}}{K_{Q} + [Q] } - \alpha _{RA}[R][A]+ \delta _{RA}[RA] -b_{R}[R] \end{aligned}$$
(20)

where we add a new term to account for the effect of iron-chelated complex Q. In this equation, the parameters \(V_Q\) and \(K_Q\) represent the maximum production rate and Michaelis-Menten constant, respectively.

2.2 Bacteria Growth Model and Virulence Measure

To describe bacteria growth, Monod introduced the concept of single nutrient controlled kinetics [14], which relates the specific growth rate (\(\mu _{X}\)) of a bacterium cell mass (X) to the substrate concentration (S). The kinetic parameters, i.e., maximum specific growth rate (\(k_{X}\)) and substrate affinity (\(K_{S}\)), are assumed to be constant and dependent on strain, medium, and growth conditions (e.g. temperature, pH). In our model, however, we need to consider a second nutrient source and add a new term Q to describe it. However, when cells are metabolically active, but not growing or dividing, they may still take up substrate.

To address bacteria size reduction, a maintenance rate (m) is generally used; consequently, we improve Monod’s model as follows:

$$\begin{aligned}&\mu _{X} = k_{X} \cdot \frac{S+Q}{S+Q+K_{g}}&\end{aligned}$$
(21)
$$\begin{aligned}&\frac{dX}{dt} = (\mu _{X}-m)\cdot X&\end{aligned}$$
(22)

We also define the virulence (V) as the concentration of LasR-AI complex as it controls the downstream virulence expressions; therefore, the total virulence (TV) of the bacteria population is defined as the product of the virulence and the number of bacteria (N)Footnote 2:

$$\begin{aligned} TV = V \times N \end{aligned}$$
(23)

We note that, as discussed later in Sect. 4, both V and N are variables that depend on time (t) and the set of biological parameters (\(\mathbf {p}\)).

2.3 Inhibition Model

We target the bacterial iron acquisition as a strategy to control the virulence of bacteria. From our previous discussion, the QS signaling pathways are the primary target. More precisely, to control the iron uptake rate of PA, we propose two strategies that can either modulate the iron uptake or inhibit the upstream las QS system:

AI Inhibitors. The AI inhibitor hydrolyzes the extracellular AI molecules which can be viewed as a degradation source and assumed to follow the Michaelis-Menten kinetics. Accordingly, (2) should be modified as:

$$\begin{aligned} \frac{d[A_{EX}]}{dt}&= - b_{A_{EX}} [A_{EX}] - \frac{d_{A}}{1-\rho } ([A_{EX}] - [A]) - \frac{V_{E} [A_{I_{EX}}] [A_{EX}] }{K_{A_{EX}} + [A_{EX}] } \end{aligned}$$
(24)

where \(A_{I_{EX}}\) denotes the extracellular AI inhibitor.

Iron Inhibitors. Different species of bacteria can produce different kinds of siderophores that trap the iron from environment, e.g. Enterobactin produced by \(\textit{E. coli}\) cannot be up-taken by PA. If the amount of iron is limited, bacteria compete with each other in order to retain the essential resources. Therefore, we consider the siderophores produced by other bacteria as iron inhibitors that can limit the availability of iron in the environment. The dynamics of the available iron in the environment can be simply modeled as:

$$\begin{aligned}{}[I_{ava}] = [I](\frac{[Pyo_{EX}]}{[I_I] + [Pyo_{EX}]}) \end{aligned}$$
(25)

where \(I_{ava}\) denotes the available iron in the environment and \(I_I\) stands for the iron inhibitor. By replacing I with \(I_{ava}\) in (17) and (19), we can incorporate the iron inhibitor dynamics to the QS model.

2.4 Biological Controller

To dynamically and autonomously generate either AI or iron inhibitors, we propose to use synthetic methods to construct the genetic circuitry. To obtain variable combinations of the inhibitors with optimal expression levels, we build two circuits separately. More precisely, to generate AI inhibitor, we can assemble the aiiA genes with the lux promoter to sense the concentration of LasR-AI (C). Similarly, the iron inhibitor circuit is built with genes that can express the competing siderophores and sense the concentration of iron-chelated complexes (Q). Based on the general modeling of genetic circuitry [20], we model the dynamics of the new biological controller with the following ODEs:

$$\begin{aligned} \frac{d[A_I]}{dt}&= P_{{A_I}} (\frac{1}{r_{A_I}} + \frac{[C]^2}{K_{A_I}^2 + [C]^2 }) - b_{A_I} [A_{I}] + \frac{d_{A_I}}{\rho _{s}} ( [A_{I_{EX}}] - [A_{I}] ) \end{aligned}$$
(26)
$$\begin{aligned} \frac{d[A_{I_{EX}}]}{dt}&= - \frac{d_{A_{I}}}{1-\rho _{s}} ( [A_{I_{EX}}] - [A_{I}] ) - b_{A_{I_{EX}}} [A_{I_{EX}}] \end{aligned}$$
(27)
$$\begin{aligned} \frac{d[I_I]}{dt}&= P_{{I_I}} (\frac{1}{r_{I_I}} + \frac{[Q]^2}{K_{I_I}^2 + [Q]^2 }) - b_{I_I} [I_{I}] + \frac{d_{I_I}}{\rho _{s}} ( [I_{I_{EX}}] - [I_{I}] ) \end{aligned}$$
(28)
$$\begin{aligned} \frac{d[I_{I_{EX}}]}{dt}&= - \frac{d_{I_I}}{1-\rho _s} ( [I_{I_{EX}}] - [I_{I}] ) - b_{I_{I_{EX}}} [I_{I_{EX}}] \end{aligned}$$
(29)

where \(A_I\) (\(I_I\)) and \(A_{I_{EX}}\) \((I_{I_{EX}})\) denote the intracellular and extracellular concentration of the AI (iron) inhibitors, respectively. The inhibitors production rate (second term) in (26) and (28) can be characterized by the binding of the LasR-AI and iron-chelated complex, respectively. The product of the promoter strength (\(P_{A_I}\) and \(P_{I_I}\)) and the basal production rate (\(r_{A_1}\) and \(r_{I_{I}}\)) characterize the minimal expression rate when there is no LasR-AI and iron-chelated complex present, respectivelyFootnote 3.

3 QS System Analysis

In this section, we first examine the QS system responses to different chemical substances. Next, we examine the effects of substrate utilization constant on bacteria growth. Finally, we examine the effectiveness of AI and iron inhibitors.

Fig. 2.
figure 2

Simulation results of the PA QS system responses to different iron concentrations. At first, the iron concentration is 0.01 (a.u.); later at time t = 5000 (a.u.), it is changed to 1 (a.u.). (a) As iron concentration increases, the expression of LasR proteins is repressed due to the negative feedback of iron-chelated complexes (see Fig. 1(a)). (b) The concentration of the LasR-AI complex decreases accordingly. The downstream proteins (i.e., (c) PqsR, (d) PqsA, and (e) PqsE) are all positively regulated by LasR. Hence, they change in accordance with LasR protein. The (f) PqsR-HHQ and (g) PqsR-PQS concentrations also decrease due to the decrease of PqsR. (h) Pyoverdine (Pyo) concentration shows similar profile since it is positively regulated by PqsE. (i) The concentration of iron-chelated (Pyo-Iron) complex increases due to the high affinity of pyoverdine and iron.

Full size image

3.1 QS System Responses

We first examine the responses of the las and pqs QS systems by varying the concentration of available iron in the environment. Figure 2 shows the QS system responses to several chemical substances. At first, the concentration of iron is 0.01 (arbitrary unit (a.u.)); at \(t = 5000\) (a.u.), the concentration of iron is changed to 1.00 (a.u.) (i.e., one hundred fold increase). We observe that the LasR protein concentration decreases due to the increase of the iron concentration; this is discussed in [12] and illustrated with the negative feedback (see also Fig. 1(a)). The other chemical substances show similar patterns except the iron-chelated complex which directly increases the growth rate. This way, the system responses confirm that our model can precisely describe the changes of chemical substance concentrations when the concentration of iron changes; this confirms the experiments in [12].

3.2 Growth Model: Utilization Constant

In Monod’s bacterial growth model, bacteria consume the substrate for their growth. We assume the utilization of substrate (\(U_S\)) is constant under different iron concentrations. However, the exact values of the utilization constant are hard to measure and estimate experimentally. To determine the \(U_S\) value, we examine the changes of total virulence and biomass under different iron concentrations.

Fig. 3.
figure 3

Substrate utilization constant (\(U_s\)) selection. (a) The effect of substrate utilization constant on total virulence under different iron concentrations. (b) The effect of substrate utilization constant on biomass under different iron concentrations.

Full size image
Fig. 4.
figure 4

The concentration changes of LasR-AI, biomass, and the TV due to the effect of different inhibitors. (a), (b), and (c) show the effect of iron concentration alone. (d), (e), and (f) show the effect of AI inhibitors alone. (g), (h), and (i) show the combined effect of iron and AI inhibitors. The set points in (c), (f), and (i) are denoted as \(S_A\), \(S_B\), and \(S_C\), respectively; they are used to derive results in Fig. 5

Full size image

As shown in Fig. 3(a), once a certain concentration of iron is reached, the larger the \(U_S\), the greater the total virulence; this is because a consumption rate of substrate that is low results in a nutrient abundant environment that favors bacteria growth. We can observe that the biomass and the total virulence are almost identical if \(U_S\) is greater than 10. Hence, in the following analysis, we set \(U_S\) to 10.

3.3 Inhibitors Effectiveness

From Fig. 2(a), we note that when the iron concentration is high, the expression of the LasR is repressed (Fig. 4(a)). On the other hand, the biomass increases due to the higher growth rate (Fig. 4(b)). By using (23), the TV increases as the concentration of iron increases as shown in Fig. 4(c).

Figures 4(d)–(f) show the effect of adding the AI inhibitor into the environment, both LasR-AI complex and biomass decrease (Fig. 4(d), (e)). Hence, the TV decreases as the amount of inhibitors increases.

Our most important observation shows that if we vary both the iron concentration and AI inhibitors, we may decrease the TV. Indeed, Fig. 4(i) shows that TV decreases as we increase the concentration of AI inhibitors and decrease the iron concentration. The AI inhibitor and iron concentration have opposite effects on the LasR-AI complex and the biomass. More precisely, lower concentrations of iron result in higher concentrations of the LasR-AI complex (Fig. 4(g)), but a decrease in the biomass production (Fig. 4(h)).

4 Autonomous Biological Control System

The autonomous biological controller we propose can automatically detect signals, react to environment, and adaptively release chemical substances for intended objectives. To control the TV, the objective is to find a set of biological parameters \(\mathbf {p}\) that minimize (23). However, this objective function is subject to various biological constraints including the bacteria QS, growth and QSI, as well as control dynamics. Given the mathematical model in Sect. 2, we formulate a constrained dynamic optimization problem and solve it through numerical methods.

Fig. 5.
figure 5

Operation points for different types of inhibitors. Different color indicates the TV of a certain combination of biological parameters (promoter strength (P) and basal production rate (r) described in (26)–(29)). (a) and (b) show the operation points \(O_A\) and \(O_B\) for iron and AI inhibitor alone; they can achieve TV around 0.1 and 0.001 where we choose the setting points \(S_A\) and \(S_B\) in Fig. 4(c) and (f), respectively. Based on the operation points we choose, we can solve the optimization problem and obtain the corresponding biological parameters where \(P = 100, r= 250\) and \(P = 2, r= 250\), respectively. (c) The operation point \(O_C\) for multi-inhibitors. In this case, \(P = 100\) and \(r= 250\).

Full size image

4.1 Problem Formulation

Based on the general constrained dynamic optimization formulation and control dynamics (see Appendix), we can formulate our problem as follows:

$$\begin{aligned} \begin{aligned}&\underset{\mathbf {p}}{\text {min}} \qquad \qquad TV_{t} = V(x_t, \mathbf {p})\times N(x_t, \mathbf {p}) \\&\text {subject to} \quad \quad \dot{x}_{t} = f(x_t, u_t, d_t, \mathbf {p}) \ \dot{u}_t = h(u_t, e_t, \mathbf {p}) \\&\qquad \qquad \quad ~ y_t = g(x_t, \mathbf {p}) e_t = y_t - r_t \forall t \in [t_0, t_{FL}] \\&\qquad \qquad \quad ~ x_{t_0}(\mathbf {p}) = x_0(\mathbf {p}) \\&\qquad \qquad \quad ~ \mathbf {p}^L \le \mathbf {p} \le \mathbf {p}^U \\ \end{aligned} \end{aligned}$$
(30)

where \(t \in \mathbb {R}\) represents time, \(t_0, t_{FL}\) are the initial and final time, respectively, \(t_i \in [t_0, t_{FL}],\) \(\mathbf {x}\) and \(\mathbf {\dot{x}} \in \mathbb {R}^n\) are the state variables and their time derivatives, respectively, and \(\mathbf {p} \in \mathbb {R}^r\) capture the time-invariant biological parameters that can vary within \([\mathbf {p}^L, \mathbf {p}^U]\). The functions f and h are QS and QSI models, respectively. The function g selects the process variables (y) (i.e., LasR-AI and iron-chelated complexes in our case). The state variable \(\mathbf {x}\) represents the set of concentrations of chemical substances described by (1)–(19); the environment input (d) describes the environment conditions such as the nutrient availability. The control variables (u) are the inhibitors which target the AI and iron availability.

The genetic circuit can be thought of as an integral controller which reacts to the concentration of LasR-AI and iron-chelated complexes, respectively. The error signal (e) is computed as the difference between the process variable and the reference signal (r); this then feeds back to the controller, which forms a closed loop (see Fig. 1(c)).

4.2 Biological Parameters Design

To design the biological parameters for our controller, we can numerically solve the above optimization problem by sampling biological parameters within the given constraints. From our analyses in Sect. 3, we notice that TV is a monotonically decreasing function (Fig. 4(i)). Consequently, by setting (23) to a desired value, we can solve (30) for biological parameters to fulfill the design specifications.

We now provide a design example for the control circuitry that can effectively achieve the setting objective value. As shown in Fig. 4(c), (f), (i), we first choose the setting points \(S_A\), \(S_B\), and \(S_C\) for three different strategies that can achieve desired TVs (0.1, 0.001 and 0.001 in this design examples). The biological parameters we choose to engineer are the promoter strength (P) and the basal production rate (r) in (26)–(29) since we can tune their values through the evolution method [1]. Next, by solving (30) through varying the value of a set of biological parameters within the given constraints ([\(\mathbf {p^L}, \mathbf {p^U}\)]), we can obtain the most suitable combination of biological parameters that express the minimal amount of inhibitors. Figure 5 shows the operation points \(O_A\), \(O_B\) and \(O_C\) for three strategies that can achieve the setting values (\(S_A\), \(S_B\), and \(S_C\)), respectively. Based on the operation points, we obtain the set of desired biological parameters.

5 Population-Level Simulation Results

In this section, we validate the proposed control system by using a 3D microfluidic environment agent-based simulator [21]. First, we explicitly apply the cellular-level model to each agent (bacterium). Next, we consider several physical and stochastic effects (physical interactions between bacteria, variation in the QS systems, growth model, etc.) and examine the growth and virulence of populations of bacteria.

The environmental configurations used in these simulations are presented in the Appendix. As shown in Fig. 6(a), for the case without inhibitors, the values of TV surpass the other strategies after 70 h of cultivation (i.e., the time we grow bacteria in wet-lab); this is because the bacteria growth rate (\(\mu _X\) in (21)) without inhibitors is larger compared to inhibitor schemes (Fig. 6(c)). If we use AI inhibitors alone, the concentration of LasR-AI complex is reduced, but this can not repress the growth of bacteria. On the contrary, the iron inhibitor alone can inhibit the bacteria growth but the LasR-AI concentration increases (Fig. 6(b)). The multi-inhibitor strategy shows the best results; indeed it can lower the concentration of LasR-AI and bacteria growth simultaneously.

Fig. 6.
figure 6

The simulation results for (a) TV (b) concentration of LasR-AI complex (c) number of bacteria for four different scenarios. Note that TV is the product of the concentration of LasR-AI complex and the number of bacteria as shown in (23). We observe that the multi-inhibition strategy is the most effective in reducing TV.

Full size image

6 Conclusion

In this work, we have proposed an autonomous optimal controller that incorporates the bacteria QS regulation and growth models and operates within a synthetic cell. By analyzing the system characteristics through numerical methods and simulations, we have shown that such synthetic cells can control the expression level of QS signals and cells growth.

We have also formulated a dynamic optimization problem to design the biological parameters of the proposed controller; this provides general guidelines to synthesize such optimal controllers in vitro. The proposed autonomous controlled system represents a first step towards a paradigm change in controlling the dynamics of communicating bacteria.