Fast and Improved SLEX Analysis of High-Dimensional Time Series

Abstract

We address the problem of segmenting a multi-dimensional time series into stationary blocks by improving AutoSLEX [1], which has been successfully used for this purpose. AutoSLEX finds the best basis in a library of smoothed localized exponentials (SLEX) basis functions that are orthogonal and localized in both time and frequency. We introduce DynamicSLEX, a variant of AutoSLEX that relaxes the dyadic intervals constraint of AutoSLEX, allowing for more flexible segmentation while maintaining tractability. Then, we introduce RandSLEX, which uses random projections to scale-up SLEX-based segmentation to high dimensional inputs and to establish a notion of strength of splitting points in the segmentation. We demonstrate the utility of the proposed improvements on synthetic and real data.

1 Introduction

When analyzing neural data such as Electroencephalography (EEG), magnetoencephalography (MEG), local field potential (LFP) or spike trains, it is typical to encounter non-stationary multidimensional time series whose spectra change over time depending on external stimuli and behavioral states of the organism [2]. In such cases, one can assume the signal to be locally stationary and hence, it is desirable to decompose the time series into orthogonal basis functions that are localized in both time and frequency. To achieve these qualities, Ombao et al. [1] proposed the use of smooth localized exponentials (SLEX). The SLEX transform constructs orthogonal basis functions that are localized in time and frequency by applying two special window functions to the Fourier bases. The AutoSLEX model creates a library of SLEX basis functions that correspond to dyadic time intervals of decreasing length. A segmentation of a time series into stationary segments can be obtained by selecting the best basis from the library using the best basis algorithm (BBA) [3]. The choice of dyadic intervals makes the segmentation problem tractable. However, it limits the obtainable segmentations. More recent methods relaxed that limitation, at the expense of having an intractable problem for which MCMC based methods are employed [4]. After reviewing SLEX in Sect. 2. We introduce two improvements to SLEX-based segmentation: in Sect. 3 we propose DynamicSLEX, a variant of SLEX that overcomes the dyadic intervals limitation of AutoSLEX while maintaining tractability; and in Sect. 4 we propose RandSLEX, a method to scale-up SLEX analysis to high-dimensional inputs using random projections.

2 Background

2.1 SLEX Transform

SLEX basis functions are obtained by applying special pairs of window functions to the Fourier basis. A SLEX basis function has the form

$$\begin{aligned} \phi _\omega (t) = \varPsi _+ (t) \exp (i2\pi \omega t) + \varPsi _- (t) \exp (-i 2\pi \omega t), \end{aligned}$$

(1)

where $\omega \in [-1/2,1/2]$. The window functions $\varPsi _+$ and $\varPsi _-$ are parametrized by an interval $[\alpha _0, \alpha _1]$ and overlap $\epsilon$ and have compact support on $[\alpha _0 - \epsilon , \alpha _1 + \epsilon ]$ .¹ In more detail, $\varPsi _+$ and $\varPsi _-$ are given by

$$\begin{aligned} \varPsi _+(t)&= r^2 \left( \frac{t - \alpha _0}{\epsilon } \right) r^2 \left( \frac{t - \alpha _1}{\epsilon } \right) \\ \varPsi _-(t)&= r \left( \frac{t - \alpha _0}{\epsilon } \right) r \left( \frac{\alpha _0 - t}{\epsilon } \right) - r \left( \frac{t - \alpha _1}{\epsilon } \right) r \left( \frac{\alpha _1 - t}{\epsilon } \right) , \end{aligned}$$

where r(.) is the iterated sine function given by

$$\begin{aligned} r_0(t)&= \sin \left[ \frac{\pi }{4}(1 + t)\right] \\ r_{d+1}(t)&= r_d \left( \sin \frac{\pi }{2} t \right) . \end{aligned}$$

The choice of d controls the steepness in the rising and falling phases of $\varPsi$ and hence time-frequency localization properties. Note that if $\varPsi _- \equiv 0$ we revert to STFT. The existence of the proper $\varPsi _-$ is what makes the SLEX basis orthogonal and localized. Figure 1 depicts sample realizations of $\varPsi _+$ and $\varPsi _-$.

Fig. 1.

$\varPsi _+$ and $\varPsi _-$ constructed with $\alpha _0 = 128$, $\alpha _1 = 256$ and $\epsilon = 8$

A SLEX library is a collection of bases, each of which consists of localized SLEX waveforms that span dyadic time intervals. Figure 2(b), demonstrates this idea; each block consists of all waveforms that span the corresponding interval. Similar to [1], we use S(j, b) to refer to the $b^{th}$ block in the $j^{th}$ level where S(0, 0) is the root block that spans the entire time series. Each choice of non-overlapping blocks that span the time series corresponds to a basis and a segmentation (see Fig. 2(c)). The SLEX coefficients of block S(j, b) for an input series X can be computed as follows:

$$\begin{aligned} d_{j,b}(\omega _k) = \frac{1}{\sqrt{M_j}} \sum _t X(t) \overline{\phi _{j,b,\omega _k}(t)}, \end{aligned}$$

(2)

where $M_j = |S(j,b)| = \frac{T}{2^j}$ and $\phi _{j,b,\omega _k}$ is defined as in (1) for window functions $\varPsi _+$ and $\varPsi _-$ that correspond to the block S(j, b). Note that the sum over t corresponds to applying a window function followed by inner product with a Fourier basis function. Therefore $d_{j,b}(\omega _k)$ can be computed for all $\omega _k = k / M_j$ for $k = -M_j/2+1, \dots , M_j/2$ in $O(T \log T)$ time using fast Fourier transform (FFT).

2.2 Basis Selection

To select a SLEX basis, we define a cost function C(j, b) for each block

$$\begin{aligned} C(j,b) = \sum _{k = -M_j/2+1}^{M_j/2} \log I_{j,b}(\omega _k) + \beta _j \sqrt{M_j} \end{aligned}$$

(3)

where $\beta _j$ is a penalty parameter that prevents oversegmentation and $I_{j,b}(\omega _k)$ is obtained by smoothing the SLEX periodogram $|d_{j,b}(\omega _k)|^2$ using a kernel smoother. The smoothing bandwidth is chosen by generalized cross validation (GCV), as detailed in [1]. After computing the costs, basis selection is performed using best basis algorithm [3] which simply proceeds bottom up, merging two sibling blocks if the cost of their parent is less than the sum of their costs.

2.3 The Multivariate SLEX

The straightforward extension of SLEX transform to multiple time series is to assume they are independent and consequently assume that the net cost of a block is the sum of costs of all series [1, 3]. To ensure that spectral information is non-redundant in the presence of correlation, Ombao et al. [5] propose computing the cost based on the eigen spectrum of the smoothed cross-periodogram matrix given by

$$\begin{aligned} I_{j,b}^{(i,j)}(\omega _k) = d_{j,b}^{(X_i)} (\omega _k) \overline{d_{j,b}^{(X_j)} (\omega _k)}, \end{aligned}$$

(4)

The proposed multivariate cost function is given by

$$\begin{aligned} C(j,b) = \sum _{k = -M_j/2+1}^{M_j/2} \sum _{d=1}^P \frac{\lambda _{j,b}^d (\omega _k) \log \lambda _{j,b}^d(\omega _k)}{\sum _{d'=1}^P \lambda _{j,b}^{d'} (\omega _k)} + \beta _j \sqrt{M_j}, \end{aligned}$$

(5)

where P is the number of time series and $\lambda ^d(\omega _k)$ is the $d^{th}$ eigenvalue of the smoothed cross-periodogram matrix at frequency $\omega _k$. This can be thought of as applying the additive cost method on non-stationary principal components that have zero coherence. With the new formulation, basis selection can proceed as described in 2.2. The multivariate SLEX transform can be summarized as follows:

• 1. For each block S(j, b), compute the SLEX coefficients based on (2) using FFT. Use the coefficients to compute the cross-periodogram matrix for each block based on (4).

• 2. For each block S(j, b), smooth the cross-periodograms $I_{j,b}^{(i,j)}(\omega _k)$ along frequency using a window smoother whose bandwidth is optimized based on GCV.

• 3. For each block S(j, b), compute the eigenvalues of the smoothed cross-periodogram matrix at each frequency and use them to compute the cost based on (5).

• 4. Use BBA to obtain best segmentation and extract the smoothed cross-periodogram matrices corresponding to selected blocks.

3 Flexible Segmentation Using DynamicSLEX

Although AutoSLEX analysis provides an appealing segmentation method, it suffers from a fundamental limitation; if the best basis contains the interval $[2m \frac{T}{2^k}, 2(m+1) \frac{T}{2^k}]$ then it must contain its sibling in the dyadic structure as well as the sibling of the parent, the sibling of the grand parent and so on up to $[0,\frac{T}{2}]$ and $[\frac{T}{2},T]$. Therefore, AutoSLEX can result in spurious splits of the time series, as demonstrated in Fig. 2, or otherwise miss splitting points. To mitigate this problem, we introduce DynamicSLEX, a variant of SLEX analysis that is also tractable but, at the same time, is capable of producing any segmentation whose splitting points are located at integer multiples of $\frac{T}{2^K}$ regardless of the length and starting position of each segment. DynamicSLEX uses the same dyadic bottom-up strategy to select basis functions using BBA. Recall that, in AutoSLEX, a single BBA step determines the best segmentation of a block S(j, b) given the best segmentations of it children $S(j+1,2b)$ and $S(j+1,2b)$ (denoted in Fig. 3 as “input”). BBA for AutoSLEX can decide to merge the blocks, removing all splitting points or to split the blocks, keeping their splitting points and introducing a middle one that separates them. DynamicSLEX introduces a third option, to concatenate the blocks by keeping the splitting points intact. This is demonstrated in Fig. 3. Effectively, DynamicSLEX is able to merge between adjacent blocks that have different parents and possibly are at different levels, preventing unnecessary splits. With proper bookkeeping, it is easy to compute the cost of blocks resulting concatenation without affecting the tractability of BBA. The algorithm is outlined in Algorithm 1. The algorithm makes use of ComputeIntervalCost function, which computes the cost of a given interval according to (3) or its multivariate version (5)².

Fig. 2.

Limitation of SLEX-based segmentation: to recover the left (bright) segment in (a), bba needs to choose the shaded basis intervals in (b) which produce the segmentation shown in (c).

Fig. 3.

The effect of merging, split and concatenation on two adjacent intervals. The vertical dashed lines indicate splitting points whereas the window functions indicate the spans of the selected basis functions.

4 Fast SLEX Analysis Using RandSLEX

One problem with AutoSLEX is that it does not scale well to high-dimensional time series. For a P–dimensional series, the cost of computation and smoothing of the cross periodograms is $O(P^2 T)$ and the cost of eigenvalue decomposition of the cross periodograms is $O(P^3 T)$. This cost can be substantial or even prohibitive for the analysis of massive datasets of high dimensional time series. We propose the use of random projections to speed up SLEX analysis. Specifically, we choose $p \ll P$ and generate a p-dimensional time series by taking random Gaussian-distributed linear combinations of the input series X. The use of random projection for dimensionality reduction was successful in numerous applications [7, 8]. In our case, the use of random projection is motivated by the observation that a random Gaussian combination of a piecewise-stationary multivariate timeseries preserves stationarity break points almost surely.

Since $p \ll P$, SLEX segmentation will be much faster and can be repeated k times with different randomly generated combinations, potentially resulting in different splitting points. The results of multiple segmentations can be aggregated in a split-count graph as shown in Fig. 4. The split-count graph is a visual summary that gives, for each position in the time series, the number of times that RandSLEX detected a splitting point at that position out of the k different runs. This number can be interpreted as a measure of strength for each splitting point and can be used to obtain segmentations at increasing resolutions by filtering out splitting points whose strength is below a given threshold. Once a segmentation is chosen, the coefficients of the full input series X w.r.t the chosen basis can be computed in $O(P T \log T)$ time.

Fig. 4.

Top: A sample split-count graph for k = 10 runs of RandSLEX. Bottom: segmentation obtained by setting strength threshold to 7.

5 Experiments

5.1 Synthetic Experiments

In the first experiment, we demonstrate the utility of DynamicSLEX. We generated time series data from three auto regressive (AR) processes $P_1 := AR(1)[0.9]$, $P_2 = AR(2)[1.69,-0.81]$ and $P_3 = AR(3)[1.35,-0.65]$. We generated a piecewise-stationary series of length $T = 1024$ by switching the source process at T / 4, T / 2, 3T / 4. We experimented with four categories of series shown in Table 1. Categories (b) and (d) are essentially “harder” versions of categories (a) and (c), with $P_3$ less distinguishable from $P_2$ than $P_1$. For each category, we generate 100 time series which are then segmented using AutoSLEX and DynamicSLEX with minimum block length of T / 4 and penalty parameter $\beta = 1$. Table 1 shows the number of times a splitting point was generated at T / 4, T / 2 and 3T / 4. While AutoSLEX and DynamicSLEX are comparable in categories (a) and (b), AutoSLEX consistently produces a spurious split at T / 2 in category (c). In category (d) AutoSLEX fails to detect the splits at T / 4 and 3T / 4 more often than DynamicSLEX.

Table 1. Categories of time series used to test DynamicSLEX and the number of times each splitting point is generated by AutoSLEX and DynamicSLEX for each category across 100 trials.

In the second experiment, we asses the ability of RandSLEX to efficiently recover segmentations of a multivariate time series. For this purpose we generate four different time series, which switch from process $P_1$ to process $P_2$ at times T / 16, T / 8, 5T / 16 and 11T / 16 respectively $(T = 8192)$. From these four series, a 10 dimensional series is obtained by taking random linear combinations of the base signals where the combinations weights are sampled from a standard normal distribution. We run RandSLEX on top of DynamicSLEX with $p = 1$ and $k = 10$ and for each confidence threshold $1 \le \theta \le k$ we count true positive, false positive and false negative splitting points, where a positive splitting point is one that is reported at least $\theta$ times. We aggregate the counts over 100 different instantiations of that experiment and based on that compute precision (the percentage of reported splitting points that are true) and recall (the percentage of true splitting points that were reported) for each confidence threshold $\theta$. The results are summarized in the PR curve depicted in Fig. 5(left). The curve shows that, for example, RandSLEX can achieve 94.5 % recall with 81.3 % precision. Surprisingly, RandSLEX outperformed DynamicSLEX (marked as a green circle in the figure), which gives 81 % at 41 % recall.

Fig. 5.

left: PR curve for RandSLEX on synthetic time series right: Mean and standard errors of split strength on LFP data (Color figure online)

5.2 Analysis of Local Field Potential Data

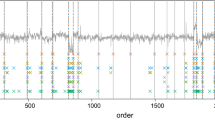
In this experiment, we demonstrate RandSLEX on Local field potentials (LFP) recorded in the Frontal Eye Fields (FEF). Data were acquired through a 16-channel linear probe at 1 kHz from an alert rhesus macaque monkey during performance of a memory-guided saccade task. The animal was required to fixate a central dot during presentation of a visual cue. The visual cue was a brief flash (at time 0.0) at a fixed eccentricity in one of eight directions relative to fixation (spaced by 45$^\circ$). From time 0.0, the animal had to maintain fixation for a delay period of 500 ms after which the central fixation dot was removed. The animal was rewarded for a successful saccadic eye movement to the remembered direction of the visual cue. The time series, consisting of 1500 samples, was zero-padded to the next power of two. We applied RandSLEX on 100 trials of each direction, for a total of 800 trials. The minimum block size was set to 128 and the parameters p and k set to 1 and 16 respectively. The hypothesis is that changes in the stimulus are expected to change the spectral properties of the time series and cause splitting points. Figure 5(right) summarizes the strength of splitting points across trials (zero padding interval not included). Note that two significant splits were found at 0.0 and 0.5 s, where there is a change in the stimulus. Switching on the fixation dot at around −0.3 s is captured by another less significant splitting point. It is remakable that the model employs no prior knowledge of the stimulus. We speculate that the rightmost splitting point could be attributed to zero padding or other edge effects.

6 Discussion

We introduced an efficient method for segmenting a multivariate into stationary segments. The method provides two enhancements over AutoSLEX: An expanded library of bases that allows for more flexible segmentation (DynamicSLEX) and the use of random projections to scale up to high-dimensional time series and provide a notion of segmentation strength. Our experiments revealed that the introduced method gives promising results on synthetic and real data.