Keywords

1 Introduction

At present, Germany’s logistics industry shows a rapid development and faces a number of challenges. There is a certain potential to increase the efficiency and productivity in this branch as well there is a number of problems to be solved (Hagenlocher et al. 2013). For example currently there is a serious problem in recruiting junior staff to have enough drivers in Germany (Dashkovskiy and Nieberding 2014). Moreover, there is a number of regulations and restriction that affect the performance of the haulers (Meyer 2006).

Every management decision on logistics network operation should be equipped with an appropriate measurement instrument for supply chain performance (Lai et al. 2002). Moreover, the effects of these decisions should be carefully analyzed and estimated in advance. The motivation for such approach is twofold. First, it helps to avoid undesirable effects which may appear as a result of management decisions. Second, it provides information about the capacity of potential changes in supply chain performance. This information can be taken into account while estimating the cost of implementing of new technologies and management solutions.

The aim of this paper is to analyze how the changes in some parameters of logistics network (like average speed, loading/unloading time, etc.) can influence overall productivity and additional revenue. Moreover as it will be shown, some adjustments of the parameters of logistics network may not lead to an additional revenue of the freight companies, but have a large influence on the work conditions of the truck drivers. It is especially important since for the past several years a profession of a truck driver becomes more and more unattractive (Bretzke and Barkawi 2010). So the hypothetical changes proposed in this paper may potentially improve the attractiveness of truck driver profession. For sure it will involve more responsible and professional people to the industry and become an additional driver of industry’s growth.

The results of this paper are based on the data provided by our industrial partners. From this data we have elaborated the most common weekly route of a truck with full load. Throughout the paper we will refer to this route as a “case scenario”. We believe that it reflects the actual situation of the most freight companies and allows to quantitatively estimate positive/negative effects properly.

2 Notation

Throughout the paper, we will use the following notations to describe a case scenario for one truck during the whole week. Let \( t_{D} \) be the driving time, \( t_{P} \) be the time that a truck driver spends on the preparation of his vehicle for a run, \( t_{L} \) be the time for loading/unloading procedures including a change of pallets, \( t_{Q} \) be the time of a truck spending in a queue waiting for a ramp to unload, \( t_{W} \) be the time that driver spends on paperwork and signing documents with the customers. Let an average number of orders be \( N_{L} \) customers per week and the whole covered distance over a week be d. The actual values of the parameters are presented in Table 8.1.

Table 8.1 Actual values of the main parameters of a case scenario
Full size table

3 Effects of Speed Increasing

Let \( z \in {\mathbb{N}} \) be a number of additional orders for customers that a truck serves in a week due to an average speed increment. We provide a formula to calculate the average speed of a truck depending on additional number of customers. An average speed is a distance divided by the whole driving time. To get to the new average speed, one has to subtract the product of the number of additional orders and average time for an order

$$ v(z) = \frac{d}{{t_{D} - z \cdot \frac{{t_{L} + t_{Q} + t_{A} + t_{W} }}{{N_{L} }}}}. $$

The inverse \( v^{ - 1} (z) \) of this function gives a function for additional orders depending on the average speed

$$ N_{D} (y): = v^{ - 1} (y) = \frac{{(t_{D} \cdot y - d) \cdot N_{L} }}{{y \cdot (t_{L} + t_{Q} + t_{A} + t_{W} )}},\quad N_{D}^{*} (y) = \left[ {\frac{{(t_{D} \cdot y - d) \cdot N_{L} }}{{y \cdot (t_{L} + t_{Q} + t_{A} + t_{W} )}}} \right], $$

where \( \left[ y \right] \) is a function that returns the largest integer value less or equal to y. A plot of this dependence is presented on Fig. 8.1.

Fig. 8.1
figure 1

A plot of the function \( N_{D}^{*} (y) \) starting at the current average speed of 61.875 km/h and ending with the maximum speed allowed for trucks in Germany. Realistically, the maximum possible improvement could be to generate around 4–5 more orders per week

Full size image

So every increment of the average speed by approximately ≈2.14 km/h gives an opportunity to serve one additional customer in a week-long run. The ways to increase average speed can be the following: increasing the maximum speed allowed for trucks (which is not too realistic because of safety reasons), route optimization, better connections between industrial parks and highways. Additionally, local sensor data and electronic toll collection data can be used for prediction and improvement of motorways traffic performance and average speed increment (Heilmann et al. 2011). On the other hand, saved driving time can extend the resting time of a truck driver with no additional revenue to the company. Our calculations show that the increasing of an average speed by 5 km/h leads to the increasing of resting time of the driver by 5 %. It will make the profession of truck driver more attractive and enlist more qualified and responsible workers to the industry.

4 Pallet System Adjustments

An improvement of loading/unloading efficiency is one of the main ways to improve an overall performance of a logistic process. The Paletten-Tagging-Roboter (PaTRo 2015) for instance, is one of the techniques to make it. To calculate the benefits from the adjustments of the time spending on pallets, we need to modify the un/loading time with our parameter x which is the fraction of loading/unloading time that can be saved in percent. Then \( t_{L} \cdot x \) is the time that can be saved, \( t_{L} \cdot (1 - x) \) is the remaining time within the process. So the new average time for an order is

$$ t_{AL} (x): = \frac{{t_{L} (1 - x) + t_{Q} + t_{A} + t_{W} }}{{N_{L} }}. $$

A division of the saved time through the new average time for an order leads to

$$ N_{P} (x) = \frac{{x \cdot t_{L} \cdot N_{L} }}{{t_{L} (1 - x) + t_{Q} + t_{A} + t_{W} }}. $$

Like the previous, it also has to be a natural number, so

$$ N_{P}^{*} (x) = \left[ {\frac{{x \cdot t_{L} \cdot N_{L} }}{{t_{L} (1 - x) + t_{Q} + t_{A} + t_{W} }}} \right]. $$

This dependence is presented on Fig. 8.2.

Fig. 8.2
figure 2

A plot of \( N_{P}^{*} (x) \) beginning at the current point with 0 % saving and ending with a maximum of 50 %. As the figure shows, it is possible to generate up to 6 more orders per week

Full size image

Every 7.5 % of saved time enables the truck driver to serve an additional customer in a week-long run. Reducing this parameter by 50 % will benefit into 5.16 % additional leisure time for the driver. How such massive change in loading/unloading time can be reached? For example, by introducing one-way recyclable pallets. In this situation a truck driver will not care about loading empty pallets after unloading his trailer and will follow his next loading/unloading point. A detailed examination of reverse logistics practices can be found in (Rogers and Tibben-Lembke 2001).

5 Synergistic Effect

Now we try to apply these two approaches simultaneously. This chapter is divided into two parts. In the first one, one has to take a look to the summation of the speed increasing and pallet system formulas. Afterwards we can improve this process even more, as we can include the modification of the average time for an order to the speed increasing part.

We assume that the average speed has been increased as well as the time spending for pallets has been decreased. The combination of both formulas leads to the following:

$$ N_{D + P} (x,y) = N_{D} (y) + N_{P} (x) = \frac{{(t_{D} \cdot y - d) \cdot N_{L} }}{{y \cdot (t_{L} + t_{Q} + t_{A} + t_{W} )}} + \frac{{x \cdot t_{L} \cdot N_{L} }}{{t_{L} (1 - x) + t_{Q} + t_{A} + t_{W} }} $$

Like in the previous sections the number of additional orders that could be served, has to be a real number (Fig. 8.3).

$$ N_{D + P}^{*} (x,y) = \left[ {\frac{{(t_{D} \cdot y - d) \cdot N_{L} }}{{y \cdot (t_{L} + t_{Q} + t_{A} + t_{W} )}} + \frac{{x \cdot t_{L} \cdot N_{L} }}{{t_{L} (1 - x) + t_{Q} + t_{A} + t_{W} }}} \right] $$
Fig. 8.3
figure 3

A plot for the function \( N_{D + P}^{*} (x,y) \). A synergy effect can be seen as the maximum amount of this combined function, the 15 orders cannot be reached with the results of the two other functions themselves

Full size image

The synergy effect comes into play, when the results of both single functions with a specific improvement are slightly lower than it has to be for a further increase but it is enough for the combination of these functions.

Let us have a look at some examples to illustrate this:

Let the improvement for the speed \( y = 62.72 \) km/h and for the pallet system either (i) 6 %, (ii) 11 % and (iii) 15 %.

(i)

(ii)

(iii)

\( \begin{aligned} & N_{D}^{*} (62.72) = 0 \\ & N_{P}^{*} (6) = 0 \\ & N_{D + P}^{*} (6;62.72) = 1 \\ \end{aligned} \)

\( \begin{aligned} & N_{D}^{*} (62.72) = 0 \\ & N_{P}^{*} (11) = 1 \\ & N_{D + P}^{*} (11;62.72) = 1 \\ \end{aligned} \)

\( \begin{aligned} & N_{D}^{*} (62.72) = 0 \\ & N_{P}^{*} (15) = 1 \\ & N_{D + P}^{*} (15;62.72) = 2 \\ \end{aligned} \)

One can see, that the synergy effect is effective for (i) and (iii) but has no impact for case (ii).

This calculations ensures that a slight increase of an average speed cannot benefit into an additional customer since \( N_{D}^{*} (62.72) = 0 \). The same situation can be seen with pallets—a 6 % of saved time does not lead to any new customers. So these two improvements do not benefit into an additional revenue of a freight company. However, these improvements make the working time of a truck driver less intensive. He can spend saved working time on the rest. On the other hand, a combination of these two improvements lead to an opportunity to serve a new customer since \( N_{D + P}^{*} (6;62.72) = 1 \).

Furthermore \( N_{D} (y) \) can be updated with the implementation of the time saving x as from pallet system section to the average time for the orders to the following:

$$ N_{D}^{\dag } (x,y) = \frac{{(t_{D} \cdot y - d) \cdot N_{L} }}{{y \cdot (t_{L} (1 - x) + t_{Q} + t_{A} + t_{W} )}}. $$

A combination of this with the previous leads to the formula:

$$ \begin{aligned} N_{D + P}^{\dag } (x,y) & = N_{D}^{\dag } (x,y) + N_{P} (x) \\ & = \frac{{(t_{D} \cdot y - d) \cdot N_{L} }}{{y \cdot (t_{L} (1 - x) + t_{Q} + t_{A} + t_{W} )}} + \frac{{x \cdot t_{L} \cdot N_{L} }}{{t_{L} (1 - x) + t_{Q} + t_{A} + t_{W} }} \\ & = \frac{{(t_{D} \cdot y - d) \cdot N_{L} + y \cdot x \cdot t_{L} \cdot N_{L} }}{{y \cdot (t_{L} (1 - x) + t_{Q} + t_{A} + t_{W} )}} = \frac{{((x \cdot t_{L} + t_{D} ) \cdot y - d) \cdot N_{L} }}{{y \cdot (t_{L} (1 - x) + t_{Q} + t_{A} + t_{W} )}} \\ \end{aligned} $$

As this result must also be a natural number, we get (Fig. 8.4)

$$ N_{D + P}^{\dag *} (x,y) = \left[ {\frac{{((x \cdot t_{L} + t_{D} ) \cdot y - d) \cdot N_{L} }}{{y \cdot (t_{L} (1 - x) + t_{Q} + t_{A} + t_{W} )}}} \right] $$
Fig. 8.4
figure 4

A plot for the function \( N_{D + P}^{\dag *} (x,y) \). An additional effect is visible as the 18 possible orders are a further improvement in relation to the function \( N_{D + P}^{*} (x,y) \)

Full size image

Let us have a look at two examples.

(i)

(ii)

(iii)

\( \begin{aligned} & N_{D}^{*} (65.96) = 2 \\ & N_{P}^{*} (18) = 1 \\ & N_{D + P}^{*} (18;65.96) = 4 \\ & N_{D + P}^{\dag *} (18;65.96) = 4 \\ \end{aligned} \)

\( \begin{aligned} & N_{D}^{*} (65.96) = 2 \\ & N_{P}^{*} (23) = 2 \\ & N_{D + P}^{*} (23;65.96) = 4 \\ & N_{D + P}^{\dag *} (23;65.96) = 5 \\ \end{aligned} \)

\( \begin{aligned} & N_{D}^{*} (65.96) = 2 \\ & N_{P}^{*} (25) = 2 \\ & N_{D + P}^{*} (25;65.96) = 5 \\ & N_{D + P}^{\dag *} (25;65.96) = 5 \\ \end{aligned} \)

Here one can see, that the function \( N_{D + P}^{\dag *} (x,y) \) increases the advantage even more, as there is an overall synergy effect in (ii).

For a look at the upper limit, we calculate improvements with \( x = 50\,\% \) and \( y = 80 \) km/h. The results are the following:

$$ \begin{array}{*{20}l} {N_{P}^{*} (50) = 6} \hfill & {N_{D + P}^{*} (50;80) = 15} \hfill \\ {N_{D}^{*} (80) = 8} \hfill & {N_{D + P}^{\dag *} (50;80) = 18} \hfill \\ \end{array} $$

As one can see, the combination of two improvements lead to much better results than its separate applications. So \( N_{D + P}^{\dag *} (x,y) \ge N_{D + P}^{*} (x,y) \ge N_{D}^{*} (y) + N_{P}^{*} (x) \)—this is a synergistic effect in logistics network. A synergy effect can be seen even at minor improvements of the parameters but it will stack even more for huge ones.

6 Influence of Saved Time on the Probability of Getting New Customers

In the previous sections, we considered the ways to save driving and working time of a truck driver and its influence on an overall performance of logistics network. As it was shown it benefits a lot into additional revenue of a freight company. The reason is that a truck can serve an additional number of customers. However challenging questions appear in this context. Is it easy to find new customers on the route? And how to estimate the change of probability of getting new customers depending on the saved driving time? With no additional driving time a driver should strictly follow the original route. However, an additional driving time enables to construct a route more flexible. The alternative routes between segments (even if these routes are not the shortest) may result in finding a new customer. The problem is how to distribute an additional driving time over the entire route. What segments should keep its original route and what segments should be replaced with an alternative way? The aim of this section is to propose a quantitative estimation of the influence of additional driving time onto a probability of finding new customers.

To answer aforementioned questions we create a mathematical model of this logistics process. Here we assume that customers are distributed uniformly over a route with the rate of \( \delta \) potential customers per one kilometer of a route. Let \( n\, \in \,{\mathbb{N}} \) be a number of segments, \( x_{i} = (x_{i}^{\alpha } ,x_{i}^{\beta } , \ldots )\, \in \,R^{{k_{i} }} ,\;i = 1, \ldots ,n \) be a vector of alternative distances between two points of i-th segment via different routes, \( x_{{i_{0} }} \) be a distance between two points of i-th segment via the initial route. Let T be a previously saved time, \( v_{i} \, \in \,R_{ + } ,\;i = 1, \ldots ,n \) be an average speed on i-th segment. For every value of saved time T our goal is to find vectors \( \lambda_{i} \, \in \,R^{{k_{i} }} ,\;i = 1, \ldots ,n \) with elements from \( \{ 0,1\} \) such that

$$ \delta \cdot \sum\limits_{i = 1}^{n} {\frac{{\left\langle {\lambda_{i} ,x_{i} } \right\rangle }}{{x_{{i_{0} }} }} \to \hbox{max} } ,\quad \sum\limits_{i = 1}^{n} {\frac{{\left\langle {\lambda_{i} ,x_{i} } \right\rangle }}{{v_{i} }}\, \le \,T} ,\quad \sum\limits_{j = 1}^{{_{{k_{i} }} }} {\lambda_{i}^{j} = 1,\quad i = 1, \ldots ,n,} $$

where \( \left\langle {\lambda_{i} ,x_{i} } \right\rangle = \sum\nolimits_{j = 1}^{{k_{i} }} {\lambda_{i}^{j} \cdot x_{i}^{{k_{i} }} } \) is a scalar product of two vectors, \( k_{i} \) is a dimension of vectors \( x_{i} \) and \( \lambda_{i} ,\;i = 1, \ldots ,n \), e.g. \( k_{i} \) is a number of alternative routes between two points of i-th segment.

We have solved the following problem of optimization for a case scenario route of a truck with full load.

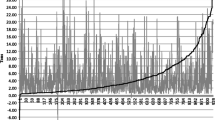
The results are presented on Fig. 8.5. The horizontal axis indicates an additional time T that a truck driver can use on driving in hours per day. The vertical one indicates the ratio of probabilities to find a potential customer between original and optimized route R. The probability of getting a new customer increases almost linearly. However at around \( T = 35 \) min of saved time it has a slight jump. A saving of 35 min of driving time increases the probability of finding new customers by 50 %.

Fig. 8.5
figure 5

A ratio of probabilities of finding new customers between the initial and optimized route depending on additional driving time

Full size image

As one may intuitively guess, the ratio of probability of getting new customers between original and optimized routes R behaves almost like a linear function of an additional driving time T. Indeed, a regression analysis of this dependence shows that it can be well approximated by a linear function \( R(T) = 0.76 \cdot T + 0.99. \)

A residual sum of squares for this approximation is not more than 0.014. A correlation coefficient is \( r \,\approx\, 0.997 \).

This analysis ensures that there is a direct dependence between the ratio of probabilities R and an additional time T as a linear function with a slope of ≈0.76. So one may conclude: more additional time we have saved, more possibilities of finding new customers we get.

7 Conclusion

We have analyzed the influence of the average speed increasing and loading/unloading time decreasing on the overall performance of logistics network. A saved working time can be spent either on serving additional customers or on the resting time of a truck driver. Each of these options has its advantages and should be considered as a trade-off between freight company owner and a truck driver. It was shown that a simultaneous application of these improvements leads to a synergistic effect and benefits more than a separate usage of the proposed improvements. A change of probability of finding new customers depending on a saved driving time has also been estimated.

The results of the paper can be useful for justification of management decisions in logistics network functioning. The paper provides the implications of the proposed solutions and estimates them quantitative.