Simulations of Transport Characteristics of Core-Shell Nanowire Transistors with Electrostatic All-Around Gate

Abstract

A mathematical model of the investigated semiconductor core-shell nanowire transistor with all-around gate, computation methods and calculated transport characteristics of the device are presented. The influence of applied gate voltage and drain-source voltage on the potential energy profile of the system is determined, electric current flowing through it is calculated and dependence of operation regime of the device on these voltages is discussed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Vertical semiconductor core-shell nanowires can be manufactured with surrounding gate electrodes (all-around gates) by various top-down, bottom-up or mixed methods [1,2,3,4]. Such devices can be used as efficient transistor components because transmission through it can be controlled by applied gate voltage.

In top-down methods, the nanodevice is carved out of a larger piece of bulk material which is partially covered by some protective layers to distinguish between a produced device and the rest of material. Methods of this kind include electrophoresis, optical lithography, or electron-beam lithography [5, 6].

On the other hand, bottom-up methods consist of growing the nanodevice on the surface of the substrate by adding atoms of subsequent elements, which allows fabrication of a nanowires build of many layers of different materials. In this category methods like electrochemical deposition, vapor–liquid–solid growth or epitaxy can be found [2, 5].

These technologies allow production of efficient three-dimensional transistors (surrounding gate transistors or SGT) which can be placed with very high density on a single chip and can be very useful in advanced nanoelectronic devices. Experimental realization of such transistors is presented in [4, 7], and gated nanowires that are shown in them have typical static current–voltage characteristics of three terminal devices.

We present computational study of the nanostructure of this kind—a core-shell nanowire transistor with surrounding gate placed asymmetrically in the vicinity of the drain electrode, and discuss influences of applied gate and drain-source voltages its on transport properties. Potential energy profiles of the device in different states, transmission coefficients and static current–voltage characteristics are calculated and assessed. Algorithm and implementation is also briefly described.

Table 1 Parameters of calculations

The paper is organized as follows: in Sect. 2, a three-dimensional model of the semiconductor core-shell nanowire with the asymmetrically placed all-around gate is presented; equations, theoretical methods used for their solving and investigation of the transport properties of the considered nanowire are described in Sect. 3; Sect. 4 contains presentation and discussion of the obtained results; a brief summary and conclusions are given in Sect. 5.

2 Model of Nanowire Transistor

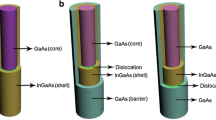
A semiconductor core-shell nanowire transistor with all-around gate electrode and circular cross-section is modeled as a rod with large aspect ratio of length and diameter. It consists of few cylindrical layers of semiconductors, metals and oxides with different material constants (starting from the axis): a core, a shell, an insulation, and a gate electrode. The shape of the nanowire is fully characterized by radius and thicknesses of every layer ($r_c$, $t_s$, $t_o$, $t_g$), length of the whole nanowire and the gate ($l_w$, $l_g$) and distance of the gate from drain electrode ($l_d$)—see Table 1. To obtain a proper calculation box for numerical methods, certain lengths of electrodes are also specified.

It is assumed that both ends of the wire are attached to reflectionless reservoirs of electrons through the perfect contacts but the gate is isolated from the wire—there is no electric transport to or from it. These reservoirs are termed source (s) and drain (d). A schematic of the single nanodevice is presented in Fig. 1. A typical nanowire transistor consists of an array of tens or hundreds of such nanodevices connected to common source and drain electrodes. In this work we consider them separately.

Fig. 1

Schematic (not in scale) of the modeled core-shell nanowire transistor with all-around gate in the vicinity of the drain electrode. Source and drain electrodes are not included in the picture. Dimensions, materials, and material constants are described in Table 1

3 Calculations

To determine the potential profile $V\left( \mathbf {r}\right)$ of the nanowire, Poisson’s equation with varying electric permittivity is solved in 3D

$$\begin{aligned} -\nabla \cdot \left[ \epsilon (\mathbf{{r}})\nabla V(\mathbf{{r}})\right] = \rho \left( \mathbf {r}\right) , \end{aligned}$$

(1)

where $\epsilon \left( \mathbf {r}\right)$ is the position-dependent electric permittivity set as piecewise constant function for each layer and $\rho \left( \mathbf {r}\right)$ is the density of electric charge which currently is uniformly set to 0. This equation is numerically solved with Dirichlet boundary conditions where $V\left( \mathbf {r}\right) =0$ is set at limits of computation box and $V\left( \mathbf {r}\right) =V_g$ is set at gate electrode. Since electric potentials are additive, at this point drain-source voltage ($V_{ds}$) is set to 0 and external linear potential caused by it will be added in later steps of calculations. Parallel explicit multigrid relaxation is used to solve the equation.

Although the implicit method has better convergence and requires less memory as it is performed in-place, it destroys the symmetry of the obtained solution which can create slight differences between degenerated eigenstates of Schrödinger’s equation calculated in the next step, and indispose optimizations of following steps calculations—each of these states would have to be considered separately. Usage of an explicit method ensures that initial symmetry of the system is preserved.

Density of the grid is increased 4 times for every dimension simultaneously in order to obtain final resolution. Each time all sizes are doubled and intermediate points are calculated as arithmetic means of surrounding values: first in every dimension, then on diagonals. Perpendicular cross-sections of the final grid are used in the following calculations. A one-dimensional longitudinal profile calculated for the axis of the wire is also used in later steps.

Parallelization of this step is performed at intermediate level—inside the Poisson’s equation solving method, inside each of its iterations, but at most external loop—for every plane of the grid. Every line of every plane and every cell of every line is calculated sequentially, but multiple planes are calculated simultaneously. Parallelization is most efficient when the count of calculations to be performed simultaneously is the same or a small multiple of the count of available computation cores (processors) (but the count of parallel threads should not exceed the count of cores, surplus calculations need to be performed later in sequence to avoid switching of threads); so there is no reason to parallelize multiple levels of calculations (for example for multiple dimensions) when a single level has a greater size than count of available cores. If only hundreds of cores are available, parallelization of one dimension is enough, for two dimensions it would need tens of thousands and for three dimensions millions of cores to work at full efficiency (there are hundreds of points in each dimension).

In the next step one-particle spinless Schrödinger’s equation for conduction band electrons is solved within adiabatic [8,9,10,11] and effective-mass approximation:

$$\begin{aligned} \bigg [ -\frac{\hbar ^2}{2m^{*}} \bigg ( \frac{\partial ^2}{\partial x^2} + \frac{\partial ^2}{\partial y^2} \bigg ) + U_{\perp }\big (x,y|z;V_g\big ) \bigg ]\chi _n\left( x,y|z\right) \nonumber \\ = E_n^{\perp }\left( z;V_g\right) \chi _n\left( x,y|z\right) , \end{aligned}$$

(2)

where $U_{\perp }\left( x,y|z;V_g\right)$ is a perpendicular energy profile of cross-section at distance of z from source electrode under $V_g$, $\chi _n\left( x,y|z\right)$ is a perpendicular wave function and $E_n^{\perp }\left( z;V_g\right)$ is the energy of n-th eigenstate at that cross-section;

$$\begin{aligned} \bigg [ -\frac{\hbar ^2}{2m^{*}}\frac{d^2}{dz^2} + E_n^{\perp }\left( z;V_g\right) + U_{\parallel } \left( V_{ds}, z \right) \bigg ] \phi _n\left( z\right) = E \phi _n\left( z\right) . \end{aligned}$$

(3)

where $\phi _n\left( z\right)$ is a parallel wave function and $U_{\parallel } \left( V_{ds}, z \right) = e \left( V_{ds}/l_w\right) z$ is a parallel energy profile of electric field caused by applied drain-source voltage. The effect of modes mixing is neglected in this approach.

Equation (2) is solved by the finite differences method with Dirichlet boundary conditions $\lim _{(x,y)\rightarrow \infty }\chi _n(x,y;z)=0$ while (3) is solved by quantum transmitting boundary method [12] with open boundary conditions and plain waves of equal amplitude entering the system from both end electrodes (wave functions which leave the system can be calculated from the solution). From Eq. 2 we obtain only eigenenergies and eigenstates of transport channels while Eq. 3 is solved for every channel and every discrete energy value in considered range. Wave function of n-th channel is given by the formula

$$\begin{aligned} \psi _n\left( \mathbf {r}\right) = \chi _n\left( x,y|z\right) \phi _n\left( z\right) . \end{aligned}$$

(4)

and electric current at the drain ($I_d$) is calculated by the formula [13, 14]:

$$\begin{aligned} I(V_{ds}, V_g, T) = \frac{e}{\pi \hbar } \sum _{n} \int _{0}^{\infty }dE \nonumber \\ T_n^{\parallel }(E;V_{ds}, V_g) \times [f_{FD}(E;\mu _S, T)-f_{FD}(E;\mu _D, T)], \end{aligned}$$

(5)

where $f_{FD}$ is Fermi–Dirac distribution function of the electrons in the source (drain) contact with electrochemical potential $\mu _{S(D)}$ where $\mu _D = \mu _S - eV_{ds}$, T is temperature and $T_n^{\parallel }(E;V_{ds}, V_g)$ is transmission coefficient of n-th channel given by the formula

$$\begin{aligned} T_n^{\parallel }(E;V_{ds}, V_g) = \frac{J_n\left( l_w, E\right) }{J_n\left( 0, E\right) }, \end{aligned}$$

(6)

where $J_n\left( z, E\right)$ is probability current in the ingoing and outgoing wave given by the formula

$$\begin{aligned} J_n\left( z, E\right) = \frac{\hbar }{m^{*}} \mathfrak {Im} \left\{ \phi _n^{*}\left( z\right) \frac{d}{dz} \phi _n\left( z\right) \right\} . \end{aligned}$$

(7)

Parallelization of the second step is performed at high level—every cross-section is calculated sequentially, but multiple cross-sections are calculated at the same time. The count of cross-sections is similar to the count of planes in previous step, but in this particular problem, a bit smaller: cross-sections in vicinity of the source electrode are far from the gate, so it has no significant influence on them and they have very similar, almost the same, plain potential profile as it can be seen at Fig. 2. As some of them can be omitted from calculations of this step to save time and result from adjacent one will be used instead. In this case, the count of parallel calculations is also in the order of hundreds, which justifies limitation of previous parallelization to just one dimension—it is the same for both cases.

Fig. 2

Map of potential dependency on cylindrical coordinates in the nanowire for $V_g=0.1$ V applied to the gate. Lines on the graph indicate borders of layers of the nanodevice

Fig. 3

Cross-section of the wire perpendicular to its axis in the middle of the gate electrode ($z=1150$ nm) at different applied gate voltages $V_g$ and $V_{ds}=0$ V

In third step results for various drain-source voltages are calculated simultaneously. Count of these values depends on range and resolution of $V_{ds}$ calculations and is fully independent from sizes of previous parallel sections of algorithm; but this step of the problem is relatively small and is calculated in short time; so in case of such necessity, a greater number of iterations in a sequence is acceptable.

Our software can dynamically lock and free resources such as computation cores or operating memory, but their availability can also be limited by operating system and other processes, usually it is somehow managed, so we have to assume that it is assigned as requested and constant for the whole duration of calculations and therefore the algorithm is optimized for about one hundred cores.

Fig. 4

Example potential energy profiles for selected applied gate voltages $V_g$ and positive and negative drain-source voltage $V_{ds}$ along the axis of the wire. Dashed lines represent Fermi levels in the source and drain electrodes

4 Results

In this section results of calculations for a single cylindrical core-shell nanowire transistor with all-around gate with parameters having values given in Table 1 are presented (Figs. 3 and 4).

With such parameters a coherent transport regime with eight well separated open channels in the transport window was obtained. The total transmission coefficient is visible at Fig. 5.

Fig. 5

Total transmission coefficient dependence on drain-source voltage $V_{ds}$ and gate voltage $V_g$. Threshold voltage dependence on both input voltages is observed in second quarter of the graph and strong transmission dependence on gate voltage is observed in fourth quarter

Current-voltage (I-V) characteristics of the investigated device are shown at Fig. 6. As can be seen the applied gate voltage ($V_g$) has strong influence on transmission of conduction electrons and it can be used to control the flow of the current in the analyzed nanodevice. The saturation current depends significantly on the gate voltage when $V_{ds} < 0$ and $V_g > 0$, so this can be regarded as transistor operation regime of the nanowire with all-around gate designed and placed as in our experiment. For $V_{ds} > 0$ saturation current remains almost the same and only threshold voltage changes significantly. Because of large length of the gate electrode, $V_g < 0$ causes a very wide potential barrier to appear in the system and it can completely prevent electronic transmission through the nanodevice. In this case the threshold value of this voltage depends on $V_{ds}$, which bows the barrier efficiently reducing its length. For $V_{ds}>0$ and $V_g>0$ total transmission coefficient is close to the number of open channels, which means that its value is close to 1 for every open channel and electrons can pass through the device coherently—these voltage values have almost no influence on the transport through the considered device.

Fig. 6

The current–voltage characteristics of core-shell nanowire transistor with asymmetrically placed all-around gate for selected gate voltages $V_g$

5 Conclusion

Properties of a cylindrical three-dimensional semiconductor core-shell nanowire transistor with all-around gate were considered in the coherent regime of electronic transport. In the studied case conduction electrons are confined to the core of nanowire. Because of asymmetric location of the gate near the drain contact, the sign of drain-source voltage unequivocally determines the regime of transistor operation, where the gate voltage can be used to control electronic current, which works this way only for negative value of $V_{ds}$ and positive values of $V_g$. For positive values of $V_{ds}$ the saturation current remains almost constant for every value of $V_g$, while negative values of $V_g$ totally block the transport in the wire if $V_{ds}$ is not positive and large enough.