Keywords

1 Introduction

Centrifugation method is widely used in many fields of technology and industry. Separation method is particularly widely used in the fields of medicine, biology, chemical and agricultural industries. For example, to study the material composition of ores and soil samples are often used for the separation. Centrifugation is commonly called emulsions separation emulsions [1–3]. This process is carried out in a continuous wall with rotors and can be compared with the process of sedimentation in the gravity field of emulsions. Examples of this process are the separation of the cream from the milk, the water from lubricating oils, separation of massecuite, etc. [4, 5]. Many mathematical models in describing the motion of solids emulsions were limited to the study of planar motion [6–8], which does not give a complete picture of the process. Also, experimental studies [9, 10] show the importance of taking into account fluctuations and their effect on the mechanical system as a whole. In this regard, it was built a number of different analytical and numerical models [11, 12] to describe these processes.

2 Statement of the Problem and the Equations of Motion

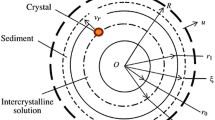
The rotor is mounted symmetrically about the supports on the flexible shaft, rotating with the angular velocity \( \omega \). The rotor is a circular disc on which at certain distances from the axis of rotation symmetrically suspended containers with suspension.

Containers are can rotate around its horizontal axis (Fig. 1). The angle of rotation is determined by the container from a vertical angle \( \alpha \); \( {\Omega} = \dot{\alpha } \)—the angular speed of rotation of the containers, \( L_{cm} \)—distance from the rotor axis to the axis of rotation of containers, \( L_{M} \)—distance to the particles of the suspension M with a mass \( {\Delta} m \), \( r \)—containers radius, \( g \)—acceleration of gravity, \( L \)—containers length.

Fig. 1
figure 1

Scheme the rotor system and disc with containers

Full size image

The rotor position is determined relative to a fixed coordinate system \( O_{1} x_{1} y_{1} z_{1} \) (Fig. 1). The position of the studied particles M is determined by the relative moving coordinate system \( Oxyz \). \( Oy \) axis is directed along the axis of symmetry of the container bottom, an \( Oz \) axis directed along the rotational axis of the container.

In the calculation the following assumptions were used:

  1. (1)

    the angular speed of the rotor is large enough so that we can ignore the force of gravity suspension (\( g \ll \omega^{2} \));

  2. (2)

    spherical shape of particles assumed;

  3. (3)

    particle mean free path is much larger its size;

  4. (4)

    no turbulence suspension (laminar flow);

  5. (5)

    the interaction forces between the particles and the walls of the container (test tube) absent;

  6. (6)

    container (test tube) is rather narrow radius is much smaller than its length (\( r_{0} \ll L \));

  7. (7)

    after deposition of the particles on the wall of the container stop moving;

  8. (8)

    the friction force between the containers and their axes of rotation, as well as a change in gravity from the suspensions disregarded containers;

  9. (9)

    the force of friction between the solid particles and the container wall disregarded.

Unlike other studies [1, 8, 13], where the movement of the particles only axis of the container, in this paper we investigate the three-dimensional motion of a particle M.

After determining the acceleration vector of the portable moving coordinate system

$$ \left. \begin{aligned} W_{ex} & = \omega \sin \alpha \cdot [\omega (x\sin \alpha - y\cos \alpha ) - {\Omega} z] - (L_{cm} \cos \alpha + x)(\omega^{2} + {\Omega}^{2} ) \\ & \quad + \dot{{\Omega} }(L_{cm} \cos \alpha + x) - z\dot{\omega }\sin \alpha , \\ W_{ey} & = - \omega \cos \alpha \cdot [\omega (x\sin \alpha - y\cos \alpha ) - {\Omega} z] - (L_{cm} \sin \alpha + y)(\omega^{2} + {\Omega}^{2} ) \\ & \quad + \dot{{\Omega} }(L_{cm} \cos \alpha + x) - z\dot{\omega }\sin \alpha , \\ W_{ez} & = - {\Omega} \cdot [\omega (x\sin \alpha - y\cos \alpha ) - {\Omega} z] - z(\omega^{2} + {\Omega}^{2} ) + \dot{\omega } \cdot (L_{cm} + y\sin \alpha + x\cos \alpha ). \\ \end{aligned} \right\} $$
(1)

represent the equation of motion of the particle M in the suspension, taking into account transportation and Coriolis forces of inertia and the assumptions made in the form of:

$$ \left. \begin{aligned} {\Delta} m{\ddot x} & = - {\Delta} mg\sin \alpha - 6\pi \eta r_{0} \dot{x} + {\Delta} m\{ (L_{cm} \cos \alpha + x)(\omega^{2} + {\Omega}^{2} ) - \omega \sin \alpha [\omega (x\sin \alpha \\ & \quad - y\cos \alpha ) - {\Omega} z] - \dot{{\Omega} }(L_{cm} \sin \alpha + y) + 2{\Delta} m(\omega \cdot \dot{z}\cos \alpha - \dot{y}{\Omega} ), \\ {\Delta} m{\ddot y} & = {\Delta} mg\sin \alpha - 6\pi \eta r_{0} \dot{y} + {\Delta} m\{ (L_{cm} \sin \alpha + y)(\omega^{2} + {\Omega}^{2} ) + \omega \cos \alpha [\omega (x\sin \alpha \\ & \quad - y\cos \alpha ) - {\Omega} z] - \dot{{\Omega} }(L_{cm} \cos \alpha + x) + 2{\Delta} m(\omega \cdot \dot{z}\sin \alpha + \dot{x}{\Omega} ), \\ {\Delta} m{\ddot z} & = - 6\pi \eta r_{0} \dot{z} + {\Delta} m\{ z(\omega^{2} + {\Omega}^{2} ) + {\Omega} [\omega (x\sin \alpha \\ & \quad - y\cos \alpha ) - {\Omega} z] - \dot{\omega }(L_{cm} + y\sin \alpha + x\cos \alpha ) - 2{\Delta} m\omega (\dot{y}\sin \alpha + \dot{x}\cos \alpha ). \\ \end{aligned} \right\} $$
(2)

where \( r_{0} \)—suspensions particle radius with a mass \( {\Delta} m \); \( \eta \)—dynamic viscosity of the fluid (suspension); \( 6\pi \eta r_{0} \)—friction coefficient of the particle M (coefficient of force environmental resistance) during its movement.

The system (2) is especially nonlinear, since \( \omega = \omega (t),\alpha = \alpha (t), \Omega = {\Omega} (t) \). Moreover the angle of rotation of the container \( \alpha (t) \) included in the arguments of trigonometric functions. In view of the above system (2) of the exact solution does not.

Let us consider the special cases.

1. The rotor is rotated at a constant angular speed,\( \omega = const \), that is \( \alpha \ne 0 = const \), \( \dot{\alpha } = {\Omega} = 0 \). At first we define the dependence of the angle \( \alpha \) of the angular speed of the rotor \( \omega \). For this purpose, we draw up the balance of forces acting on the container (pиc.3). Projecting force in the direction of \( \tau \tau \) we get (Fig. 2)

$$ g\,\sin \alpha = \omega^{2} (L_{cm} + l\,\sin \alpha )\cos \alpha . $$
(3)

where l—distance from the axis of rotation to center of gravity of the container with a suspension of. From here it follows that

$$ \omega = \sqrt {\frac{g \cdot tg\alpha }{{L_{cm} + l\sin \alpha }}} . $$
(4)
Fig. 2
figure 2

Determination of forces

Full size image

If \( \omega \to \infty ,\;\alpha \to \frac{\pi }{2} \) or \( \alpha \to \frac{\pi }{2},\;\omega \to \infty \). i.e. if \( \alpha \to \frac{\pi }{2} \) \( \omega \to \infty \), which follows from the physical meaning of the problem. From (3) we find the dependence of the angular speed \( {\Omega} \) of the container in \( \omega ,\alpha \), and other system parameters.

$$ {\Omega} = \frac{{2\omega \varepsilon (L_{cm} + l\sin \alpha )}}{{g\cos \alpha - \omega^{2} (l\cos 2\alpha - L_{cm} \sin \alpha )}}. $$
(5)

where \( \varepsilon = \dot{\omega } \). Case of indefinite increase of angular velocity \( \omega \to \infty \) the angular speed of the container goes to zero \( {\Omega} \to 0 \). As is shown above, if \( \omega \to \infty ,\; \alpha \to \frac{\pi }{2} \); these conclusions are valid, when the angular speed of the rotor increases homogeneous.

The maximum value of the angular velocity of the container we find the angular speed of the rotor. We then obtain

$$ \omega^{2} = \frac{g\cos \alpha }{{l\cos 2\alpha - L_{cm} \sin \alpha }}. $$

It follows, that when \( \alpha \to \frac{1}{4l}(\sqrt {L_{cm}^{2} + 8l^{2} } - L_{cm} ) \), the angular velocity increase without limit.

Hence, each value of \( \omega \) corresponds to the specific value of \( \alpha \). Then from (2) as \( \omega = const,\quad\alpha = const,\quad{\Omega} = 0,\quad\varepsilon = 0 \) we will have

$$ \left. {\begin{array}{*{20}l} {{\ddot x} + 2n\dot{x} = \omega^{2} \cos^{2} \alpha \cdot x - g\sin \alpha + (L_{cm} + y\sin \alpha )\omega^{2} \cos^{2} \alpha + 2\omega \cos \alpha \dot{z},} \hfill \\ {{\ddot y} + 2n\dot{y} = \omega^{2} \sin^{2} \alpha \cdot y + g\cos \alpha + (L_{cm} + x\cos \alpha )\omega^{2} \sin^{2} \alpha + 2\omega \sin \alpha \dot{z},} \hfill \\ {{\ddot z} + 2n\dot{z} = \omega^{2} z - 2\omega (\dot{y}\sin \alpha + \dot{x}\cos \alpha ).} \hfill \\ \end{array} } \right\} $$
(6)

where \( n = 3\pi \eta r_{0} \)—friction coefficient. From (6), equating coefficients of the same functions of time \( \exp( - \alpha_{0} t) \) and the constant terms, is possible get the system of algebraic equations for the unknown \( B_{1} ,B_{2} ,B_{0} ,P_{1} ,P_{2} ,P_{3} \), which solution has the form

$$ \left. {B_{0} = \sin \alpha \cdot C_{1} - L_{cm} \cos \alpha,\quad B_{1} = - \frac{\sin \alpha }{{\alpha_{0} }}C_{0},\quad B_{2} = - \sin \alpha \cdot k_{0},\quad P_{1} = P_{2} = P_{3} = 0.} \right\} $$
(7)

Considering (7) can be written law of motion of the particle suspensions

$$ \left. \begin{aligned} x & = A_{1} \text{e}^{{\alpha_{1} t}} + A_{2} \text{e}^{{ - \beta_{1} t}} - \frac{\sin \alpha }{{\alpha_{0} }}C_{0} \text{e}^{{ - \alpha_{0} t}} - \sin \alpha \cdot k_{0} t + \sin \alpha \cdot C_{1} - L_{cm} \cos \alpha , \\ y & = A_{1} tg\alpha \cdot \text{e}^{{\alpha_{1} t}} + A_{2} tg\alpha \cdot \text{e}^{{ - \beta_{1} t}} + \frac{\cos \alpha }{{\alpha_{0} }}C_{0} \text{e}^{{ - \alpha_{0} t}} + \cos \alpha \cdot k_{0} t - \cos \alpha \cdot C_{1} - L_{cm} \sin \alpha , \\ \end{aligned} \right\} $$
(8)
$$ z = E_{1} \text{e}^{{\alpha_{1} t}} + E_{2} \text{e}^{{ - \beta_{1} t}} . $$
(9)

Using the initial conditions of the problem, we find the integration constants \( A_{1} ,A_{2} ,C_{0} ,C_{1} ,E_{1} ,E_{2} \). For determining \( A_{1} ,A_{2} ,C_{0} ,C_{1} \) we have four algebraic equations:

$$ \left. {\begin{array}{*{20}l} {A_{1} + A_{2} - \frac{\sin \alpha }{{\alpha_{0} }}C_{0} + \sin \alpha \cdot C_{1} = x_{0} + L_{cm} \cos \alpha ,} \hfill \\ {\alpha_{1} A_{1} - \beta_{1} A_{2} + \sin \alpha \cdot C_{0} = \dot{x} - \sin \alpha \cdot k_{0} ,} \hfill \\ {(A_{1} + A_{2} )tg\alpha + \frac{\cos \alpha }{{\alpha_{0} }}C_{0} - \cos \alpha \cdot C_{1} = y_{0} + L_{cm} \sin \alpha ,} \hfill \\ {(\alpha_{1} A_{1} - \beta_{1} A_{2} )tg\alpha - \cos \alpha \cdot C_{0} = \dot{y} - \cos \alpha \cdot k_{0} .} \hfill \\ \end{array} } \right\} $$
(10)
$$ \left. {E_{1} + E_{2} = z_{0} ,\;\alpha_{1} E_{1} - \beta_{1} E_{2} = \dot{z}_{0} .} \right\} $$
(11)

The system of algebraic equations (10) and (11) are solved without difficulty.

Let us write the final value:

$$ \left. \begin{aligned} A_{1} & = \frac{{b_{1} \beta_{1} + b_{2} }}{{2\sqrt {n^{2} + \omega^{2} } }},\;A_{2} = \frac{{b_{1} \alpha_{1} - b_{2} }}{{2\sqrt {n^{2} + \omega^{2} } }},\;C_{0} = k_{0} + \dot{x}_{0} \sin \alpha - \dot{y}_{0} \cos \alpha , \\ C_{1} & = \frac{{k_{0} + \dot{x}_{0} \sin \alpha - \dot{y}_{0} \cos \alpha }}{{\alpha_{0} }} + x_{0} \sin \alpha - y_{0} \cos \alpha , \\ \end{aligned} \right\} $$
(12)

where

$$ b_{1} = x_{0} \cos^{2} \alpha + y_{0} \cos \alpha \sin \alpha + L_{cm} \cos \alpha,\quad b_{2} = \dot{x}_{0} \cos^{2} \alpha + \dot{y}_{0} \cos \alpha \sin \alpha , $$
(13)
$$ E_{1} = \frac{{z_{0} \beta_{1} + \dot{z}_{0} }}{{2\sqrt {n^{2} + \omega^{2} } }},\;E_{2} = \frac{{z_{0} \alpha_{1} - \dot{z}_{0} }}{{2\sqrt {n^{2} + \omega^{2} } }}. $$
(14)

From (22) we find the velocity of the particle suspensions in the direction of the Oy axis:

$$ y|_{t = T} = \alpha_{1} A_{1} tg\alpha \cdot \text{e}^{{\alpha_{1} T}} - \beta_{1} A_{2} tg\alpha \cdot \text{e}^{{ - \beta_{1} T}} - \alpha_{0} \cos \alpha \cdot C_{0} \text{e}^{{ - \alpha_{0} T}} + \cos \alpha \cdot k_{0} = 0. $$

If we consider that \( \beta_{1} - \alpha_{0} = n + \sqrt {n^{2} + \omega^{2} } - 2n = - n + \sqrt {n^{2} + \omega^{2} } = \alpha_{1} \), \( \alpha_{1} + \beta_{1} = 2\sqrt {n^{2} + \omega^{2} } \), and \( \omega \gg n \), then ignoring n in exponential functions in comparison with the (\( \sqrt {n^{2} + \omega^{2} } \)), we get

$$ \alpha_{1} A_{1} tg\alpha \cdot \text{e}^{{2\sqrt {n^{2} + \omega^{2} } T}} + (\cos \alpha \cdot k_{0} - \alpha_{0} \cos \alpha \cdot C_{0} )\text{e}^{{\sqrt {n^{2} + \omega^{2} } T}} - \beta_{1} A_{2} tg\alpha = 0. $$
(15)

If we denote \( \text{e}^{{\sqrt {n^{2} + \omega^{2} } T}} = \xi \), we obtain from (15) is a quadratic equation in the form

$$ a\xi^{2} + b\xi + c = 0, $$
(16)

where \( a = \alpha_{1} A_{1} tg\alpha ,\quad b = \cos \alpha \cdot k_{0} - \alpha_{0} \cos \alpha \cdot C_{0} ,\quad c = - \beta_{1} A_{2} tg\alpha \).

Here \( A_{1} ,A_{2} \) and \( C_{0} \) given by (12):

$$ \xi_{1} = \frac{{ - b + \sqrt {b^{2} - 4ac} }}{2a},\,\xi_{2} = \frac{{ - b - \sqrt {b^{2} - 4ac} }}{2a},\,T_{1} = \frac{{\ln \xi_{1} }}{{\sqrt {n^{2} + \omega^{2} } }},\,T_{2} = \frac{{\ln \xi_{2} }}{{\sqrt {n^{2} + \omega^{2} } }}. $$
(17)

Thus, the determined time separation of suspensions, taking into account the spatial movement of the solid particles of the suspension.

1. There should be considered a special case, which is more suitable for practical applications and determine the approximate time of separation.

Movements of suspensions of the particle in the direction of the axis Oy. Movement of particles of the suspension in the directions Ox and Oz disregarded. The angular speed of the rotor is large enough so that \( \alpha \to \frac{\pi }{2},\,\,\,{\Omega} \to 0 \). Then the differential equation of motion of a particle is given by

$$ {\ddot y} + \chi \dot{y} - (\omega^{2} \sin^{2} \alpha + {\Omega}^{2} )y = g\cos \alpha + (\omega^{2} + {\Omega}^{2} )L_{cm} \sin \alpha - \dot{{\Omega} }L_{cm} \cos \alpha . $$
(18)

As In the general case \( \omega = \omega (t),\; \alpha = \alpha (t),\;{\Omega} = {\Omega} (t) \), Eq. (18) is a differential equation with variable coefficients and finding its exact solution is very difficult. Therefore, to find an approximate solution of Eq. (18) we consider the established mode of the system when \( \omega = const \) and \( \alpha = const \), \( {\Omega} = 0 \). Under these conditions, Eq. (18) takes the form

$$ {\ddot y} + x\dot{y} - \omega^{2} \sin^{2} \alpha \cdot y = g\cos \alpha + L_{cm} \omega^{2} \sin \alpha . $$
(19)

Linear non-homogeneous differential equation (19) has a solution

$$ y = C_{1} \text{e}^{{b_{0} t}} + C_{2} \text{e}^{{ - b_{1} t}} - A_{0} , $$
(20)

where \( C_{1} ,C_{2} \)—integration constants, which are determined from the initial conditions of the problem and will be equal to:

$$ \left. \begin{aligned} b_{0} & = - \frac{x}{2} + \sqrt {\frac{{x^{2} }}{4} + \omega^{2} \sin^{2} \alpha }, \quad b_{1} = \frac{x}{2} + \sqrt {\frac{{x^{2} }}{4} + \omega^{2} \sin^{2} \alpha },\quad A_{0} = \frac{{g\cos \alpha + L_{cm} \omega^{2} \sin \alpha }}{{\omega^{2} \sin^{2} \alpha }}, \\ C_{1} & = \frac{{b_{1} (y_{0} + A_{0} ) + \dot{y}_{0} }}{{b_{0} + b_{1} }},\quad C_{2} = \frac{{b_{0} (y_{0} + A_{0} ) - \dot{y}_{0} }}{{b_{0} + b_{1} }},\quad \omega \ne 0,\alpha \ne 0. \\ \end{aligned} \right\} $$
(21)

Then final expression the law of motion of the particle takes the form

$$ y = \frac{1}{{b_{0} + b_{1} }}\{ [b_{1} (y_{0} + A_{0} ) + \dot{y}_{0} ]\text{e}^{{b_{0} t}} + [b_{0} (y_{0} + A_{0} ) - \dot{y}_{0} ]\text{e}^{{ - b_{1} t}} \} - A_{0} . $$
(22)

From formula (22) define the precipitation suspension. Thus, from formula (22) we have

$$ \frac{{(L + A_{0} )(b_{0} + b_{1} )}}{{b_{1} (y_{0} + A_{0} ) + \dot{y}_{0} }} = \text{e}^{{b_{0} T}} + \frac{{b_{0} (y_{0} + A_{0} ) - \dot{y}_{0} }}{{b_{1} (y_{0} + A_{0} ) + \dot{y}_{0} }}\text{e}^{{ - b_{1} T}} . $$
(23)

Given that the second term on the right-hand side of Eq. (23) by several orders of magnitude smaller than the first term (\( b_{1} > b_{0} ,\frac{1}{{\text{e}^{{b_{1} T}} }} \to 0 \) in \( \omega \to \infty \)), that taking into account this consideration, (23) we obtain an approximate value of deposition time of suspension:

$$ T = \frac{1}{{b_{0} }}\ln \left[ {\frac{{(L + A_{0} )(b_{0} + b_{1} )}}{{b_{1} (y_{0} + A_{0} ) + \dot{y}_{0} }}} \right]. $$
(24)

Thus, the dependence of the angle of rotation of the cup on the angular speed of the rotor, defined law of motion a of the particle suspensions and the deposition of it on the bottom of the cup (while the rotor stops), i.e. the time of separation suspension.

More precise separation of suspensions time can be achieved if coefficients neglected compared with the expression \( \sqrt {\frac{{x^{2} }}{4} + \omega^{2} \sin^{2} \alpha } \). Then the coefficients \( b_{0} \) and \( b_{1} \) are equal to those \( b_{0} = b_{1} = \sqrt {\frac{{x^{2} }}{4} + \omega^{2} \sin^{2} \alpha } = b \). In this case, formula (23) takes the form \( \xi^{2} + p\xi + q = 0 \), where

$$ p = - \frac{{2(L + A_{0} )b}}{{b(y_{0} + A_{0} ) + \dot{y}_{0} }},\quad q = \frac{{b(y_{0} + A_{0} ) - \dot{y}_{0} }}{{b(y_{0} + A_{0} ) + \dot{y}_{0} }},\quad \xi_{1,2} = - \frac{p}{2} \pm \sqrt {\frac{{p^{2} }}{4} + q},\quad T = \frac{\ln \xi }{b}. $$

Consider the case when the rotor shaft is adopted a rigid, but support—elastic, with a corresponding coefficient of elasticity.

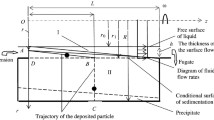
Rotor vibrations occur due to an imbalance of suspended containers (cups, test tubes, etc.). While containers are positioned symmetrically with respect to each other, however, the mass of suspensions in them may be different. The number of particles in finely ground them can not be equal, and the time also differs particle precipitation, etc. All of these factors may be the cause of imbalance in the rotor system, which causes oscillation of the rotor.

Figure 3 shows the model is equivalent to the rotor system with containers, taking into account rainfall the particle suspension. The mass, which creates an imbalance denote \( m_{0} \), rotor mass in m. The position of the rotor center of gravity (the shaft) is determined relative to Oxy. It is assumed that the rotor makes a plane-parallel movement. The position of the shaft in the Oxy coordinate system defined by the x and y.

Fig. 3
figure 3

The equivalent model

Full size image

Let us introduce the dissipative function in the form

$$ {\Phi} = \frac{\chi }{2}(\dot{x}^{2} + \dot{y}^{2} ) + \frac{{\chi_{0} }}{2}\dot{\alpha }^{2} + \frac{{\chi_{1} }}{2}\dot{l}^{2} . $$
(25)

Differential equations of motion systems are nonlinear, finding the exact solution that is very problematic.

In particular, the equations of motion are complicated when the rotation angle of the cup is a function of time \( \alpha = \alpha (t) \), as in the case of \( \alpha \) include trigonometric functions.

Consider the special case when the angle of rotation of the container fixed \( \alpha = const \).

(1) Case \( x = x(t),\,\,y = y(t),\,\,l = l(t),\,\,\alpha = const,\,\,{\Omega} = 0,\,\,\,0 < \alpha < \frac{\pi }{2} \). In this case, taking into account (25) we obtain the equations of motion of the system

$$ \begin{aligned} & \left. {\begin{array}{*{20}l} {(m + m_{0} ){\ddot x} + \chi \dot{x} + cx + m_{0} \sin \alpha \cos \omega t{\ddot l} - 2m_{0} \omega \sin \omega t\sin \alpha \dot{l}} \hfill \\ { - m_{0} \omega^{2} \cos \omega t\sin \alpha l = m_{0} \omega^{2} a\cos \omega t,} \hfill \\ {(m + m_{0} ){\ddot y} + \chi \dot{y} + cy + m_{0} \sin \alpha \sin \omega t{\ddot l} + 2m_{0} \omega \cos \omega t\sin \alpha \dot{l}} \hfill \\ { - m_{0} \omega^{2} \sin \omega t\sin \alpha l = m_{0} \omega^{2} a\sin \omega t.} \hfill \\ \end{array} } \right\} \\ & \sin^{2} \alpha {\ddot l} + 2n_{1} \dot{l} - \omega^{2} \sin^{2} \alpha l + ({\ddot x}\cos \omega t + {\ddot y}\sin \omega t)\sin \alpha = \omega^{2} a\sin \alpha + g(1 - \cos \alpha ). \\ \end{aligned} $$
(26)

The system (26) is the equation of motion of a system with periodically varying coefficients. When there is a periodically varying parameters growing vibrations of the system, i.e., A so-called parametric oscillation. Eccentricity in this case the system periodically varies, i.e. changing the force of inertia.

The system of Eq. (26) in the literature has been well studied, although the actual results were obtained only for some special cases. Of particular interest is the study of the conditions of stability of the system. For the equation with periodically varying coefficients of rigidity has a diagram Ainis-Strett, which can be found using the conditions of stability of the system.

You can lead one of the solution methods based on the method of complex amplitudes. The problem is solved in the complex plane, in this case, Eq. (26) will have the form:

$$ \left. {\begin{array}{*{20}l} {{\ddot z} + 2n\dot{z} + k^{2} z = - \frac{\sin \alpha }{1 + \mu }\left( {{\ddot l} + 2i\omega \dot{l} - \omega^{2} l} \right)\text{e}^{i\omega t} + \frac{{\omega^{2} a}}{1 + \mu }\text{e}^{i\omega t} ,} \hfill \\ {{\ddot l} + 2n_{0} \dot{l} - \omega^{2} l = - \frac{1}{\sin \alpha }{\ddot z}\text{e}^{ - i\omega t} + \frac{{\omega^{2} a}}{\sin \alpha } + \frac{g}{1 + \cos \alpha }.} \hfill \\ \end{array} } \right\} $$
(27)
$$ 2n = \frac{\chi }{{m + m_{0} }},\;k^{2} = \frac{c}{{m + m_{0} }},\,\,\mu = \frac{m}{{m_{0} }},\,\,\,2n_{0} = \frac{{\chi_{1} }}{{m_{0} \sin^{2} \alpha }},\; 2n_{1} = \frac{{\chi_{1} }}{{m_{0} }},\; z = x + iy. $$
(28)

From the system (27) excluding the \( ({\ddot l} - \omega^{2} l) \), obtain the

$$ \dot{l} = \frac{{(n_{0} + i\omega )}}{{2(n_{0}^{2} + \omega^{2} )}}\left[ {\frac{{\mu {\ddot z} + 2(1 + \mu )n\dot{z} + k^{2} (1 + \mu )z}}{\sin \alpha }} \right]\text{e}^{ - i\omega t} + a_{2} . $$
(29)

The vibrations of the rotor in the complex plane can be represented as

$$ z = A\text{e}^{i\omega t} . $$
(30)

Substituting (30) into (29) we find

$$ l = a_{1} At + a_{2} t + C, $$
(31)
$$ \left. {a_{1} = \frac{{n_{0} + i\omega }}{{2(n^{2} + \omega^{2} )\sin \alpha }}[ - \mu \omega^{2} + 2(1 + \mu )ni\omega + k^{2} (1 + \mu )],\quad a_{2} = \frac{{g(n_{0} + i\omega )}}{{2(n_{0}^{2} + \omega^{2} )(1 + \cos \alpha )}},} \right\} $$
(32)

C—constant of integration.

Substituting (30) and (31) we obtain

$$ A = - \frac{{a_{2} }}{{a{}_{1}}} = - \frac{g\sin \alpha }{{(1 + \cos \alpha )[ - \mu \omega^{2} + 2(1 + \mu )ni\omega + k^{2} (1 + \mu )]}}, $$
(33)
$$ C = \frac{{g(1 + \mu )(\omega^{2} - 2n\omega i - k^{2} )}}{{\omega^{2} [ - \mu \omega^{2} + 2(1 + \mu )ni\omega + k^{2} (1 + \mu )](1 + \cos \alpha )}} - \frac{a}{\sin \alpha }. $$
(34)

Substituting (32), (33) and (34) into (30) and (31) we obtain the motion law of the rotor and the point M of mass т, which moves along the container axis.

The law of motion of the rotor in the direction of the axes Ox and Oy:

$$ \left. {x = A_{0} \cos \omega t - A_{1} \sin \omega t,\quad y = A_{1} \cos \omega t + A_{0} \sin \omega t.} \right\} $$
(35)
$$ \left. {\begin{array}{*{20}l} {A_{0} = \frac{{g\sin \alpha (\mu \omega^{2} - k^{2} (1 + \mu ))}}{{(1 + \cos \alpha )\{ [\mu \omega^{2} - k^{2} (1 + \mu )]^{2} + 4(1 + \mu )^{2} n^{2} \omega^{2} \} }},} \hfill \\ {A_{1} = \frac{2g\sin \alpha (1 + \mu )n\omega }{{(1 + \cos \alpha )\{ [\mu \omega^{2} - k^{2} (1 + \mu )]^{2} + 4(1 + \mu )^{2} n^{2} \omega^{2} \} }},} \hfill \\ {A = A_{0} + iA_{1} .} \hfill \\ \end{array} } \right\} $$
(36)
$$ l = C = \frac{{g(1 + \mu )\{ (\omega^{2} - k^{2} )[(1 + \mu )k^{2} - \mu \omega^{2} ] - 2n^{2} \omega^{2} (1 + \mu )^{2} ]}}{{\omega^{2} (1 + \cos \alpha )\{ [k^{2} (1 + \mu ) - \mu \omega^{2} ]^{2} + 4(1 + \mu)^{2} n^{2} \omega^{2} \}}} - \frac{a}{\sin \alpha}. $$
(37)

From (35) it is obvious that the rotor performs harmonic oscillations. The point M a mass \( m_{0} \) has a certain position in accordance with (37), that is this point is at a distance \( l = C \) axis of containers rotation.

3 Conclusions

The important results were obtained within the framework of this study. The problem in this formulation is solved analytically. The analytical dependence of the angular speed of the container, the angle of rotation as a whole. Certain laws of spatial motion of a particle suspension and the deposition of it on the bottom of the container (the stop of the rotor)—the time separation of the suspension. When account is taken of the rotor vibration at fixed angles of rotation of the container was conducted stability analysis method of complex amplitudes, which suggests a harmonic vibration of the rotor.