Recent Developments in Quantum Zero-Error Information Theory

Abstract

In this chapter we review some papers in the literature which give new contributions to quantum zero-error information theory. Bell’s inequalities reveal some interesting contrasts between classical and quantum information theory. Quantum chromatic number and Kochen-Specker sets are based on graphs and deal with the same problem of contextuality and non-locality. Both Bell’s inequalities and Kochen-Specker theorem are essentially the same than quantum zero-error information theory. Wiedlant’s inequality is translated to the quantum domain and the concept of index of primitivity is used to prove a theorem of dichotomy of quantum zero-error capacity. A variant of the zero-error capacity for quantum channels which uses pre-shared entanglement is discussed. An approach to the zero-error capacity of quantum channels with commutative graphs is introduced, as well as a translation of the Lovász theta function to the quantum domain. An application of quantum channels with positive zero-error capacity helps in determining the complexity class of the quantum clique problem.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

In the previous Chaps. 6–7 some recent developments and applications of the quantum zero-error information theory were introduced. In this chapter we introduce some contributions from other authors to the field.

This chapter is organized as follows. We revisit some nonlocal phenomena by Bell’s inequalities and their consequences in Sect. 8.1. After that, we introduce some definitions that did not appear so far. We revisit relevant contrasts of classical and quantum correlations and discuss a proof of the Bell’s inequality. Also, due to their importance, we revisit Gleason’s and Kochen-Specker’s theorems. We observe that this section has a historical flavor, so the reader, based on his own background, can skip this first section and go straight to the next section.

The classical zero-error capacity of a quantum channel, introduced in Chap. 5, was defined in terms of the clique number of the characteristic graph of a quantum channel. Now, in Sect. 8.2, we comment on the results introduced more recently: the literature by Scarpa, Severini, and Mancinska [26, 32]. Their contribution, mainly the second one, clearly binds Kochen-Specker (also known as Bell-Kochen-Specker) theorems to the quantum zero-error information theory.

A quantum version of the Wielandt’s inequality [31] is described in Sect. 8.3. This inequality states an upper bound to the number of uses of a quantum channel in order to map an arbitrary density operator to a full rank operator. In this interesting paper, the authors state a remarkable relation with the quantum zero-error information theory intermediated by dichotomy theorems.

A variant of the zero-error capacity which considers entanglement assistance is presented in Sect. 8.4. Results of Winter et al. [14, 15, 17] in which non-commutative graphs are used for the quantum zero-error information theory are presented in Sect. 8.5. A quantum version of the Lovász theta function and some alternate definitions for the zero-error capacity of a quantum channel are presented as well.

A non-trivial application of zero-error quantum channels to help in determining the complexity class of a well-known problem was proposed by Beigi and Shor [5] which is now depicted in Sect. 8.5.

8.1 Bell’s Inequalities

Entanglement motivated the famous article “Can Quantum Mechanical Description of Physical Reality Be Considered Complete?” written by Einstein, Poldosky, and Rosen, EPR for short [19]. After an important and long discussion, concepts like principle of locality, elements of reality, and hidden variables were defeated. The principle of locality, for example, claims that the events occurring in place are independent of parameters, eventually controlled at another “distant place” in the same time, but it was not confirmed.

The main assumption in EPR argument is the a priori concept of element of reality that could be obeyed by the Nature. The EPR paper aimed to show that quantum mechanics was an incomplete theory based on a sufficient condition for a physical property to be an element of reality:

“If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unit) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity” [19].

Example 8.1 (Quantum Correlations are Stronger than the Classical Ones [29]).

This example sets forth that quantum correlations are in general stronger than the classical ones. Consider a block of explosive material, in rest at t = 0, so at this time with angular moment $\overrightarrow{J} = 0$ exploding in two asymmetric parts, as shown in Fig. 8.1. Due to conservation laws [39, p. 323], the two parts carry angular moments, $\overrightarrow{J_{1}} = -\overrightarrow{J_{2}}$, respectively.

Fig. 8.1

Classical setup with zero angular moment

Suppose observers detecting the fragments and measuring the classical dynamical variables $a =\mathop{ \mathrm{sign}}\nolimits (\overrightarrow{\alpha } \cdot \overrightarrow{ J_{1}})$ and $b =\mathop{ \mathrm{sign}}\nolimits (\overrightarrow{\beta } \cdot \overrightarrow{ J_{2}})$, respectively, where $\left \vert \boldsymbol{\alpha }\right \rangle$ and $\left \vert \boldsymbol{\beta }\right \rangle$ are arbitrary unit vectors chosen by the observers. Obviously, a, b = ±1.

For N repetitions of the experiment, with directions of $\overrightarrow{J_{1}}$ and $\overrightarrow{J_{2}}$ randomly distributed, the averages are near to zero, that is,

$$\displaystyle\begin{array}{rcl} \langle a\rangle = \frac{1} {N}\sum _{j=1}^{N}a_{ j} \approx 0,& \mbox{ }& \langle b\rangle = \frac{1} {N}\sum _{j=1}^{N}b_{ j} \approx 0.{}\end{array}$$

(8.1)

In order to compare their results, the observers calculate the correlation , defined by

$$\displaystyle{ \langle ab\rangle = \frac{1} {N}\sum _{j=1}^{N}a_{ j}b_{j}. }$$

(8.2)

The correlation is not zero in general. For concreteness, taking $\overrightarrow{\alpha } =\overrightarrow{ \beta }$, the observers get a _j  = −b _j , and in this case correlation yields 〈ab〉 = −1. 

For arbitrary $\overrightarrow{\alpha }$ and $\overrightarrow{\beta }$ the solution is [29]:

$$\displaystyle{ \langle ab\rangle = -1 + \frac{2\theta } {\pi },\ \ \ \ \ \ \ \ 0 \leq \theta \leq \pi, }$$

(8.3)

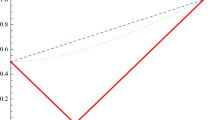
where θ stands for the angle between directions $\overrightarrow{\alpha }$ and $\overrightarrow{\beta }$. Notice that the correlation increases linearly from − 1 to + 1 as θ varies from 0 to π. Such correlation is shown in the plot of Fig. 8.2

Fig. 8.2

Classical and quantum correlations

Now let’s consider the quantum turn. Consider the quantum analogy taking into consideration the singlet (entangled state)

$$\displaystyle{ \left \vert \psi \right \rangle = \frac{\left \vert 01\right \rangle -\left \vert 10\right \rangle } {\sqrt{2}}. }$$

(8.4)

Assume that observers measure the observables $\overrightarrow{\alpha } \cdot \sigma _{a}$ along the axis $\overrightarrow{\alpha }$ and $\overrightarrow{\beta } \cdot \sigma _{b}$, along the axis $\overrightarrow{\beta }$, respectively. As before, in the classical analog, unit vectors are arbitrarily chosen by the observers and the possible values of a and b measurements are ± 1. The average values are both zero, that is

$$\displaystyle{ \langle a\rangle =\langle b\rangle = 0. }$$

(8.5)

Furthermore, correlation can be calculated, according to quantum mechanics rules, as

$$\displaystyle{ \langle ab\rangle = \left \langle \psi \right \vert (\overrightarrow{\alpha } \cdot \sigma _{a})(\overrightarrow{\beta } \cdot \sigma _{b})\left \vert \psi \right \rangle, }$$

(8.6)

where σ _a and σ _b are the Pauli matrices of the systems a and b, respectively.

For the singlet one has

$$\displaystyle{ \sigma _{a}\left \vert \psi \right \rangle = -\sigma _{b}\left \vert \psi \right \rangle. }$$

(8.7)

Therefore, using the identity $(\overrightarrow{\alpha }\cdot \sigma )(\overrightarrow{\beta }\cdot \sigma ) =\overrightarrow{ \alpha } \cdot \overrightarrow{\beta } + \imath (\overrightarrow{\alpha } \times \overrightarrow{\beta })\cdot \sigma$, the correlation is then obtained

$$\displaystyle{ \langle ab\rangle = -\cos \theta. }$$

(8.8)

The main remark here is that quantum correlation , which is also shown in Fig. 8.2, is stronger than the classical correlation for all values of θ, except θ = 0, $\frac{\pi }{2}$ and π.

The EPR paradox was solved by the Bell’s inequality. It is interesting to remark that the inequality is not about quantum mechanics, rather its proof is general and independent of Physics. The central statement is that if one assumes validity of principle of locality , then there is an upper bound to the correlation between distant events. What Bell’s inequality states is that local realism is incompatible with quantum mechanics.

In order to see an explanation why this happens, one must consider the thought experiment outlined in Fig. 8.3. Assuming the EPR principle , that is assuming the truth of local realism or the existence of hidden variables, we shall perform calculations to obtain the Bell’s CHSH inequalities¹ [11]. After, real measurements demonstrate the violation of those inequalities.

Fig. 8.3

Bell’s inequality

In the thought experiment, a physicist, say, Charlie, repeats a large number, N, of preparations of two particles (say “left” and “right,” respectively) and send, one by one, to his colleagues, Alice and Bob. The left particle is sent to Alice and the right one is sent to Bob. Later, Alice and Bob perform simultaneously measurements on their respective particles. Alice’s lab is too far from Bob’s lab in such a way their respective actions are concurrent [30], that is, their actions are relativistically disconnected.

Additionally, Alice is free to choose directions $\overrightarrow{\alpha }$ or $\overrightarrow{\beta }$ to perform her measurements, which results in a random variable denoted by A = ±1, if she chooses direction $\overrightarrow{\alpha }$, or a random variable denoted by B = ±1 if she chooses direction $\overrightarrow{\beta }$. Similarly, Bob is free to choose directions $\overrightarrow{\gamma }$ or $\overrightarrow{\delta }$, and from his measurement obtains random variables C = ±1 and D = ±1, respectively.

Now consider the random variable V defined by the following sum

$$\displaystyle\begin{array}{rcl} V & =& AC + BC + BD - AD{}\end{array}$$

(8.9)

$$\displaystyle\begin{array}{rcl} & =& (A + B)C + (B - A)D,{}\end{array}$$

(8.10)

where (8.10) follows from a simple rearrangement. From (8.10), it is clear that, as A = ±1 and B = ±1, either (A + B)C = 0 or (B − A)B = 0. From this, according to Table 8.1, it is easy to check that

$$\displaystyle{ V = AC + BC + BD - AD = \pm 2. }$$

(8.11)

Table 8.1 Values assumed by the random variables A and B

Now consider the expected value $\mathbb{E}[V ]$:

$$\displaystyle\begin{array}{rcl} \mathbb{E}[V ]& =& \mathbb{E}[AC + BC + BD - AD]{}\end{array}$$

(8.12)

$$\displaystyle\begin{array}{rcl} & =& \sum _{a,b,c,d}\Pr [a,b,c,d](ac + bc + bd - ad){}\end{array}$$

(8.13)

$$\displaystyle\begin{array}{rcl} & \leq & 2\sum _{a,b,c,d}\Pr [a,b,c,d]{}\end{array}$$

(8.14)

$$\displaystyle\begin{array}{rcl} & \leq & 2,{}\end{array}$$

(8.15)

where (8.12) and (8.13) are definitions, (8.14) is justified by (8.11), and (8.15) is because probabilities sum to one. On the other hand, from linearity of the expectation

$$\displaystyle{ \mathbb{E}[V ] = \mathbb{E}[AC] + \mathbb{E}[BC] + \mathbb{E}[BD] - \mathbb{E}[AD] }$$

(8.16)

Comparing (8.15) with (8.16), we get the Bell’s CHSH inequality:

$$\displaystyle{ \mathbb{E}[AC] + \mathbb{E}[BC] + \mathbb{E}[BD] - \mathbb{E}[AD] \leq 2. }$$

(8.17)

Recall that the last inequality , shown in (8.17), was obtained based on the principle of local realism, and there is nothing wrong with this formula under that assumption. However, here, the authors objective was to check its validity for quantum mechanics. A question that arises is: how to perform this task?

Fortunately, the expectations on the left side of (8.17) can be estimated, with accuracy $\frac{1} {\sqrt{N}}$, through repeating the experiments N times. For example, let $\widehat{\mathbb{E}[AC]}$ denote the estimate of $\mathbb{E}[AC]$, then

$$\displaystyle{ \widehat{\mathbb{E}[AC]} = \frac{\sum _{j=1}^{N}a_{j}c_{j}} {N} \longrightarrow \mathbb{E}[AC], }$$

(8.18)

with high probability, as the number of repetitions, N, increases [28].

Now, consider quantum mechanics into account. As it is suggested in Fig. 8.3, Charlie sends the left qubit to Alice and the right qubit to Bob. The random variables A, B, C, and D are defined by the results of measurements of the following observables:

$$\displaystyle\begin{array}{rcl} A = Z_{1}& \ \ \ \ \ & C = \frac{-Z_{2} - X_{2}} {\sqrt{2}}{}\end{array}$$

(8.19)

$$\displaystyle\begin{array}{rcl} B = X_{1}& \ \ \ \ \ & D = \frac{Z_{2} - X_{2}} {\sqrt{2}}{}\end{array}$$

(8.20)

where subscripts 1, 2 stand for the left and right qubits sent by Charlie, respectively. The calculation of the expected values is straightforward, for example,

$$\displaystyle{ \mathbb{E}[AC] = \left \langle \psi \right \vert \Big(Z_{1} \otimes \frac{-Z_{2} - X_{2}} {\sqrt{2}} \Big)\left \vert \psi \right \rangle, }$$

(8.21)

and similar to BC, BD, and AD. But these calculations turn out to:

$$\displaystyle{ \mathbb{E}[AC] = \mathbb{E}[BC] = \mathbb{E}[BD] = -\mathbb{E}[AD] = \frac{1} {\sqrt{2}}. }$$

(8.22)

But, with these values, the sum adds up to:

$$\displaystyle{ \mathbb{E}[AC] + \mathbb{E}[BC] + \mathbb{E}[BD] - \mathbb{E}[AD] = 2\sqrt{2}. }$$

(8.23)

The result obtained in (8.23) shows a clear violation to the upper bound obtained in (8.17).

The conflicting results of Bell’s CSHS inequality and the last result obtained from quantum mechanics vide (8.23) only can be solved via experimental procedures. Several such procedures were performed starting in the decades of 1960 and 1970. One of the most important was the work of Aspect et al. [3] that used two-photon atomic transitions in the setup. The results corroborated the predictions of quantum mechanics.

What the prior description shows is that for entangled states it is viable to find a pair of observables correlated in such a way their correlations violate the Bell’s inequality. The meaning is that quantum mechanics produces statistical predictions that cannot be explained if one assumes the Einstein locality , that is, assuming that the results of experiments performed in a location are independent of another, discretionary one performed in another distant location, simultaneously.

8.1.1 Functional Consistency

Due to the complexity in demonstrating mentioned violations of Bell’s CHSH inequality, new ways for demonstrated nonlocality were proposed [27]. Given a set of commuting observables A, B, C, … and a set of quantum states $\left \vert \psi \right \rangle,\left \vert \phi \right \rangle,\ldots$, then it is viable measuring the observables simultaneously and to obtain the joint distribution of the values of the observables chosen from that set. Consider an ensemble of identically prepared systems, in the state, say, $\left \vert \phi \right \rangle$, and suppose these states are described by observables A, B, C, …. Each measure shall assign numerical values for each observable, v(A),  v(B),  v(C), …. Quantum rules require that v(A) is dependent only on the operator A, not on the state $\left \vert \phi \right \rangle$, and require also that in a commuting set of observables the only allowed results of simultaneous measurement are in the set of simultaneous eigenvalues.

From requirements considered [27], it is possible to notice that for any particular functional identity

$$\displaystyle{ f(A,B,C,\ldots ) = 0, }$$

(8.24)

fulfilled by the commuting observables, should be fulfilled by the set of eigenvalues, that is

$$\displaystyle{ f(v(A),v(B),v(C),\ldots ) = 0. }$$

(8.25)

For example, if A and B commute, then

$$\displaystyle\begin{array}{rcl} C = A + B& \mathop{\Longrightarrow}\limits^{([A,B] = 0)}& v(C) = v(A) + v(B),{}\end{array}$$

(8.26)

or, equivalently,

$$\displaystyle\begin{array}{rcl} C - A - B = 0& \mathop{\Longrightarrow}\limits^{([A,B] = 0)}& v(C) - v(A) - v(B) = 0.{}\end{array}$$

(8.27)

But, implications (8.26) or (8.27) are valid only if A and B commute! Because if it is not this way, A’s and B’s eigenvalues are different and they cannot be simultaneously measured. There is no evidence supporting those identities. However, in the sense of mean, (8.27) holds ever, that is, for any quantum state $\left \vert \phi \right \rangle$, it is true that

$$\displaystyle{ \left \langle \phi \right \vert A + B\left \vert \phi \right \rangle = \left \langle \phi \right \vert A\left \vert \phi \right \rangle + \left \langle \phi \right \vert B\left \vert \phi \right \rangle, }$$

(8.28)

even despite the fact that A and B do not commute. Historically, famous mistakes happened probably motivated by this caveat [36].

We have seen that one important meaning of the Bell’s CHSH inequalities is that for an entangled quantum state it is viable to find pairs of observables such that quantum mechanics statistics predictions are incompatible with the requirement of locality (also referred to as Einstein locality) . Equivalently, this means that the results of measurements made at a given place are not all independent of those obtained at a remote lab.

An n × n matrix M is said to be diagonalizable if and only if the sum of the dimensions of the its eigenspaces equals n or, equivalently, if and only if M is similar to a diagonal matrix, that is, there exist an invertible matrix P such that

$$\displaystyle{ P^{-1}MP = \left (\begin{array}{*{10}c} \lambda _{1} & 0&\ldots & 0 \\ 0& \lambda _{2} & \ldots & 0\\ \vdots & \vdots &\vdots & \vdots \\ 0&0&\ldots &\lambda _{n} \end{array} \right ), }$$

(8.29)

where the scalars λ _i  (i = 1, 2, … n) are the eigenvalues of M. From

$$\displaystyle{ MP = P\left (\begin{array}{*{10}c} \lambda _{1} & 0&\ldots & 0 \\ 0& \lambda _{2} & \ldots & 0\\ \vdots & \vdots &\vdots & \vdots \\ 0&0&\ldots &\lambda _{n} \end{array} \right ) = \left (\begin{array}{*{10}c} \lambda _{1}\left \vert \alpha _{1}\right \rangle & \lambda _{2}\left \vert \alpha _{2}\right \rangle & \ldots & \lambda _{n}\left \vert \alpha _{n}\right \rangle \end{array} \right ), }$$

(8.30)

where P can be written as

$$\displaystyle{ P = \left (\left \vert v_{1}\right \rangle,\left \vert v_{2}\right \rangle,\ldots,\left \vert v_{n}\right \rangle \right ). }$$

(8.31)

In this representation $\left \vert \alpha _{i}\right \rangle (i = 1,2,\ldots,n)$ and α _i (i = 1, 2, …, n) are the eigenvectors and eigenvalues of M, respectively.

If for a matrix M there is only one basis in which it is diagonal, that basis corresponds to a maximal quantum test which is equivalent to a measurement of the observable represented by M. If $\left [M,N\right ] = 0$ (M and N commute), it is possible to find a basis in which both matrices are diagonal. This basis corresponds to a maximal test, which provides a measurement of both M and N. Therefore two commuting operators can be simultaneously measured, otherwise they are said to be incompatible.

Generalization is straightforward. A set of matrices are said to be simultaneously diagonalizable if there exists a single invertible matrix P such that P ⁻¹ MP is a diagonal matrix for every M in the set. A set of diagonalizable matrices commutes if and only if the set is simultaneously diagonalizable. A set of commuting operators is said to be complete if there exists a single basis in which all these operators are diagonal.

8.1.2 Context

If, regardless of the previously mentioned ambiguity, we insist in assuming that the measurement of an operator M depends uniquely on the objective properties of the measured quantum system, then we are assuming validity of contextualization of the setup to determine the measurement results completely. For example, if $\left [M,N\right ] = 0$ and also, $\left [M,V \right ] = 0$, we can jointly measure M and N, or jointly M and V, then we wait that the result of the measurement of M does not depend on its context , specifically, whether we measure only M, or M and N, etc. Notice that the assumption made is clearly counterfactual, that is, it cannot be put under an experimental setup.

Considered jointly, contextuality and functional consistency are indeed incompatible with the predictions of quantum theory , in spite of their “reasonability.” The following example is particularly illustrative of this point.

Example 8.2 (Peres [29]).

Consider a pair of qubits, not necessarily entangled (singlets), and the operators displayed in the following matrix

$$\displaystyle{ \mathcal{A} = \left (\begin{array}{*{10}c}\mathbb{1} \otimes Z & & Z\otimes\mathbb{1} & & Z \otimes Z \\ X\otimes\mathbb{1} & &\mathbb{1} \otimes X & &X \otimes X \\ X \otimes Z & & Z \otimes X & & Y \otimes Y \end{array} \right ). }$$

(8.32)

It is possible to verify that:

• Each operator has eigenvalue ± 1;

• In each row the three operators commute;

• In each column the three operators commute;

• Each operator is product of the two others, with exception of the third column, that requires a minus sign.

On the other hand, consider the sequences

$$\displaystyle\begin{array}{rcl} (X \otimes Z)(Z \otimes X)& =& (XZ) \otimes (ZX){}\end{array}$$

(8.33)

$$\displaystyle\begin{array}{rcl} & =& (-\imath Y ) \otimes (\imath Y ){}\end{array}$$

(8.34)

$$\displaystyle\begin{array}{rcl} & =& Y \otimes Y,{}\end{array}$$

(8.35)

and

$$\displaystyle\begin{array}{rcl} (Z \otimes Z)(X \otimes X)& =& (ZX) \otimes (XZ){}\end{array}$$

(8.36)

$$\displaystyle\begin{array}{rcl} & =& (-\imath Y ) \otimes (-\imath Y ){}\end{array}$$

(8.37)

$$\displaystyle\begin{array}{rcl} & =& -Y \otimes Y.{}\end{array}$$

(8.38)

Due to the opposite signs in (8.35) and (8.38), we cannot assign ± 1 values to entries of matrix $\mathcal{A}$ in such a way that those came out of measuring the operators form $\mathcal{A}$.

8.1.3 Gleason’s Theorem

This important theorem states that for Hilbert spaces of dimension at least three, the only possible probability measures are that of the form

$$\displaystyle{ \langle A\rangle =\mathop{ \mathrm{Tr}}\nolimits \left (\rho A\right ), }$$

(8.39)

where ρ stands for a prepared quantum state and A is an observable. This means that there is not observable other than (8.39). The proof of that theorem is recognized as difficult.²

One of the issues raised by Gleason is that assuming only the primitives:

• Decision tests (only yes/no answers allowed) are represented by projectors in a Hilbert space;

• Compatible tests simultaneously correspond to commuting projectors ;

• If P and Q are orthogonal projectors, then their sum, S = P + Q, which is itself a projector, obeys

  $$\displaystyle{ \langle S\rangle =\langle P\rangle +\langle Q\rangle, }$$

  (8.40)

then, for Hilbert spaces with dimension larger than 2, (8.39) is the only that gives the corrected statistics for the measurements. The main remark is that the projector $S,\ \mathop{\mathrm{Tr}}\nolimits S = 2$, can be decomposed in unlimited number of manners. For instance, take

$$\displaystyle\begin{array}{rcl} P_{1}& =& \left \vert \alpha \right \rangle \left \langle \alpha \right \vert,{}\end{array}$$

(8.41)

$$\displaystyle\begin{array}{rcl} P_{2}& =& \left \vert \beta \right \rangle \left \langle \beta \right \vert,{}\end{array}$$

(8.42)

projectors onto orthonormal vectors $\left \vert \alpha \right \rangle$ and $\left \vert \beta \right \rangle$, respectively. Consider the next “rotations”:

$$\displaystyle\begin{array}{rcl} \left \vert a\right \rangle & =& \frac{\left \vert \alpha \right \rangle + \left \vert \beta \right \rangle } {\sqrt{ 2}},{}\end{array}$$

(8.43)

$$\displaystyle\begin{array}{rcl} \left \vert b\right \rangle & =& \frac{\left \vert \alpha \right \rangle -\left \vert \beta \right \rangle } {\sqrt{ 2}}.{}\end{array}$$

(8.44)

Clearly $\left \vert a\right \rangle$ and $\left \vert b\right \rangle$ are also orthonormal. The projectors onto these last vectors are

$$\displaystyle\begin{array}{rcl} Q_{1}& =& \left \vert a\right \rangle \left \langle a\right \vert,{}\end{array}$$

(8.45)

$$\displaystyle\begin{array}{rcl} Q_{2}& =& \left \vert b\right \rangle \left \langle b\right \vert.{}\end{array}$$

(8.46)

The last two decompositions satisfy

$$\displaystyle\begin{array}{rcl} Q_{1} + Q_{2}& =& \left \vert a\right \rangle \left \langle a\right \vert + \left \vert b\right \rangle \left \langle b\right \vert {}\end{array}$$

(8.47)

$$\displaystyle\begin{array}{rcl} & =& \frac{(\left \vert \alpha \right \rangle + \left \vert \beta \right \rangle )(\left \langle \alpha \right \vert + \left \langle \beta \right \vert )} {2} + \frac{(\left \vert \alpha \right \rangle -\left \vert \beta \right \rangle )(\left \langle \alpha \right \vert -\left \langle \beta \right \vert )} {2}{}\end{array}$$

(8.48)

$$\displaystyle\begin{array}{rcl} & =& P_{1} + P_{2}.{}\end{array}$$

(8.49)

The identity Q ₁ + Q ₂ = P ₁ + P ₂ is considered as trivial, but, in contrast, the similar statement about the averages is not. Such statement regarding the averages can be formally written as:

$$\displaystyle{ \langle P_{1}\rangle +\langle P_{1}\rangle =\langle Q_{1}\rangle +\langle Q_{2}\rangle. }$$

(8.50)

Considering such non-trivial nature, it deserves to be experimentally verified [29].

8.1.4 The Kochen-Specker Theorem

Mermin [27] introduced the following reasoning. Take observables with eigenvalues 1 or 0 with corresponding spin components 0, ±1. The sums of the squared spin components along any three orthogonal axis, x,  y,  z obey

$$\displaystyle{ S_{x}^{2} + S_{ y}^{2} + S_{ z}^{2} = s(s + 1) = 2. }$$

(8.51)

This is valid for particles with spin s = 1. Additionally, the squared components S _x ²,  S _y ², and S _z ² form a mutually commuting set. The results of measurement are 0 or 1 for each direction, x, y, or z, additionally, that results must fulfill condition (8.51).

Assume that a set of directions with many orthogonal trials is given, in conjunction with the set of observables (squared spins components) alongside that directions. As the observables along orthogonal axes, the squared components are mutually commuting and due to constraint (8.51), the measured values equals one of the three triads (1, 1, 0),  (1, 0, 1) or, (0, 1, 1).

The contextuality , that is, the impossibility of description supported on local hidden variables, can be proved revealing quantum states for which the statistics of their respective observables (S _x ², S _y ², S _y ²), connected with the orthogonal axes, cannot be obtained by any assignments of 1s and 0s to every direction in the set, such that condition (8.51) holds.

The Kochen-Specker theorem exhibits a set of vectors, called Kochen-Specker (KS) sets such that it is impossible to assign 1’s (associated with a color red) and 0’s (associated with a color blue) and condition (8.51) is kept.

Notice that no statistics relative of the states is necessary for justification. This exclusion of statistics from the problem is similar to the change from the classical information theory, where asymptotically small probability of error is admitted to the zero-error information theory where no error is admitted. In the first, the ordinary information theory, probability measures are essential. For the last, zero-error information theory, graph theory and combinatorics are the main tools for analysis.

From the last discussion, it is possible to give a concise statement of the KS theorem in terms of the following problem.

Problem 8.1 (Mermin [27]).

Determine a set of directions (vectors) in a 3-dimensional space such that it is impossible to assign a color (red or blue) to each direction under the condition that every subset of three mutually orthogonal vectors contains exactly one blue and two red vectors.

For the sake of completeness, the solution (proof) given by Mermin [27] is sketched here. Firstly, notice that only directions are essential, one is free to modify the size of the vectors. Without loss of generality assume the unit vector $\mathbf{z}$, blue, defining this axis. Take the red vector $\mathbf{a}$ living in the y-z plane:

$$\displaystyle{ \mathbf{a} =\mathbf{ z} +\alpha \mathbf{ y},\ 0 <\alpha < 0.5. }$$

(8.52)

Then consider the following remarks:

• As $\mathbf{z}$ is blue, $\mathbf{x}$ and $\mathbf{y}$ are both red. Indeed, any vector in the x-y must be red, due to the condition that one cannot have two orthogonal blue vectors, that is

  $$\displaystyle{ \mathbf{c} =\beta \mathbf{ x} +\mathbf{ y},\ \text{for any}\ \beta. }$$

  (8.53)

  must be red.

• Additionally, since $\mathbf{a}$ and $\mathbf{x}$ are red, any vector in their plane must be red. To the proof, we shall soon verify that an interesting red vector in this plane is

  $$\displaystyle{ \mathbf{d} = \frac{1} {\beta } \mathbf{x} -\frac{1} {\alpha } \mathbf{a}. }$$

  (8.54)

• Notice that because $\mathbf{a} =\mathbf{ z} +\alpha \mathbf{ y}$, then d is orthogonal to $\mathbf{c} =\beta \mathbf{ x} +\mathbf{ y}$. To see this, it is enough to perform the scalar product (denoted by “⋅ ” ):

  $$\displaystyle\begin{array}{rcl} \mathbf{d} \cdot \mathbf{ c}& =& \left (\frac{1} {\beta } \mathbf{x} -\frac{1} {\alpha } \mathbf{a}\right ) \cdot \left (\beta \mathbf{x} +\mathbf{ y}\right ) {}\end{array}$$

  (8.55)
  $$\displaystyle\begin{array}{rcl} & =& \|\mathbf{x}\|^{2} -\frac{\beta } {\alpha }\left (\mathbf{z} +\alpha \mathbf{ y}\right ) \cdot \mathbf{ x} -\frac{1} {\alpha } \left (\mathbf{z} +\alpha \mathbf{ y}\right ) \cdot \mathbf{ y} {}\end{array}$$

  (8.56)
  $$\displaystyle\begin{array}{rcl} & =& \|\mathbf{x}\|^{2} -\|\mathbf{ y}\|^{2} {}\end{array}$$

  (8.57)
  $$\displaystyle\begin{array}{rcl} & =& 0. {}\end{array}$$

  (8.58)

• Recall that $\mathbf{c}$ and $\mathbf{d}$ are both red, so the normal to their plane must be blue. Therefore, any vector in their plane must be red. So, the following sum is red:

  $$\displaystyle{ \mathbf{e} =\mathbf{ d} +\mathbf{ c}. }$$

  (8.59)

• Since α ∈ (0, 0. 5), then $\frac{1} {\alpha } > 2$, and, for $\beta \in \mathbb{R}$,

  $$\displaystyle{ \left \vert \beta +\frac{1} {\beta } \right \vert \in (2,\infty ), }$$

  (8.60)

  it is viable determined a value of β such that $\mathbf{e}$ is parallel to

  $$\displaystyle{ \mathbf{f} =\mathbf{ x} -\mathbf{ z}. }$$

  (8.61)

  Also, changing the signal of β results in another $\mathbf{e}$ parallel to

  $$\displaystyle{ \mathbf{g} = -\mathbf{x} -\mathbf{ z}. }$$

  (8.62)

• Since $\mathbf{e}$ is red independently of the β value, both $\mathbf{f}$ and $\mathbf{g}$ must be red.

• But, $\mathbf{f} \cdot \mathbf{ g} = 0$, they are orthogonal; so the normal to their plane is blue and any vector in their plane is surely red.

• Notice that

  $$\displaystyle{ \mathbf{z} = -\frac{1} {2}\mathbf{f} -\frac{1} {2}\mathbf{g} }$$

  (8.63)

  lives in the $\mathbf{f},\ \mathbf{g}$ plane, but $\mathbf{z}$ is blue. This is the contradiction sought.

A chain of simpler and simpler proofs of quantum contextuality has been introduced since the KS theorem has appeared in the literature . One of these recent simplifications was introduced by Cabello et al. [9]. Experimental apparatus has also been explored in this same kind of sequence of simplifications [16].

An interesting approach concerning the plethora of nonlocality proofs is given in van Dam et al. [35], where the authors, rooted on Kullback-Lieber distance, propose a measure for the amount of evidence provided by the experimental setup.

In the following sections, recent results related with quantum zero-error information theory are examined.

8.2 Quantum Chromatic Number and Kochen-Specker Sets

Throughout this section we shall use definitions from graph theory introduced earlier in Chap. 4 Eventually, for the sake of easiness, some of those may be redundant.

Scarpa and Severini [32] and Mancinska et al. [26] introduced conditions for equality and strict inequality between three quantities associated with a graph G:

• The minimum dimension of orthogonal representation, denoted by ξ(G);

• The quantum chromatic number, denoted by χ _q (G);

• The ordinary quantum chromatic number, denoted by χ(G).

One remarkable contribution introduced in the mentioned works is the outstanding role performed by the KS sets in the proofs. These sets are collections of vectors with applications to investigations about the calculation of quantum zero-error capacities of quantum channels.

The quantum chromatic number is a remarkable parameter for at least one reason: it is a tool for differentiating aspects of quantum and classical behavior, in particular, for entanglement-assisted communications . Also the quantum chromatic eases comprehension of combinatorial parameters as, e.g., the Lovász theta function and the minimum dimension of an orthogonal representation of a simple graph.

In this section only simple graphs (unweighted, unidirected graphs without self-loops) are considered and, as before, for a graph G, V (G) and E(G) denote its vertex and edge sets, respectively.

Before introducing the relationship between the concepts of quantum chromatic number, KS sets, and their consequences for the zero-error information theory, however, due to its importance, we shall review main concepts related to the Kochen-Specker theorem, following mainly the reading given in Peres [29].

A proper k-coloring of a graph is an assignment of k colors such that every two adjacent vertices have different colors. The chromatic number of a graph G, χ(G), is the minimum number of colors k needed to build a proper k−coloring map of G.

We now introduce a coloring game for a graph G = (V, E). We consider that Alice and Bob claim that they have a proper k-coloring for G and a referee tests this claim with a one-round game. The rules of the game do not allow communication between the players. The referee asks Alice the color, say a, for the vertex v and Bob for the color, say, b, for the vertex w. Alice and Bob win the game if, for $a,b \in \left \{1,\ldots,k\right \}$:

• IF v = w, THEN a = b;

• IF (v, w) ∈ E, THEN, a ≠ b.

A classical strategy is formed by two deterministic functions:

$$\displaystyle\begin{array}{rcl} g_{A}: V & \rightarrow & \{1,\ldots,k\},{}\end{array}$$

(8.64)

$$\displaystyle\begin{array}{rcl} g_{B}: V & \rightarrow & \{1,\ldots,k\}.{}\end{array}$$

(8.65)

It is clear that, independently of the strategy chosen by the players, including even probabilistic strategies, they cannot win the game with probability 1 if k < χ(G), that is, using less than the chromatic number of colors in their assumed proper k-coloring procedure.

A quantum strategy the players can take advantage of is a convenient entangled state $\left \vert \psi \right \rangle$ living in a Hilbert space of dimension d and two collections of POVMs in the following way:

• For all v ∈ V, Alice owns {E _va } _{a = 1, …, k} and similarly Bob owns {F _vb } _{b = 1, …, k} ;

• Alice applies her POVM {E _va } _{a = 1, …, k} to her part of the entangled state and get the value a;

• Bob applies his POVM {F _va } _{a = 1, …, k} to his part of the entangled state and get the value b.

In order to have consistent conditions, for a quantum strategy, the rules are adapted in such a way that Alice and Bob win the game, if only if

$$\displaystyle\begin{array}{rcl} \forall v \in V,\ \forall a\neq b,& & \left \langle \psi \right \vert \mathbf{E}_{va} \otimes \mathbf{F}_{vb}\left \vert \psi \right \rangle = 0,{}\end{array}$$

(8.66)

$$\displaystyle\begin{array}{rcl} \forall (v,w) \in \mathbf{E},\ \forall a,& & \left \langle \psi \right \vert \mathbf{E}_{va} \otimes \mathbf{F}_{wa}\left \vert \psi \right \rangle = 0.{}\end{array}$$

(8.67)

If these conditions are attained, the strategy is said to be a winning strategy. Notice that only the number of measurement operator is fixed, neither the dimension of the entangled stated nor the rank of the measurement operator is taken into consideration. This motivates the following definition.

Definition 8.1 (Quantum Chromatic Number [32]).

For all graphs G, the quantum chromatic number χ _q (G) is the minimum number k such that there exists a quantum k-coloring of G.

In the following $\overline{W}$ stands for the complex conjugate of the complex matrix W, that is, the (i, j) entry of $\overline{W}$ is obtained from the corresponding (i, j) entry of W taking its complex conjugate. The Hilbert-Schmidt product of two complex matrices W and V is given, as usual, by

$$\displaystyle{ \left \langle W\right \vert V \rangle =\mathop{ \mathrm{Tr}}\nolimits WV ^{\dag }. }$$

(8.68)

The normal form of a k-coloring emphasizes the simplicity of its structure.

Proposition 8.1 (Normality [32] ).

If G has a quantum k-coloring, then there exists a quantum k-coloring of G in normal form , with the following properties:

• 1. All POVMs are projective measurements with k projectors of rank r;

• 2. The state $\left \vert \psi \right \rangle$ is the maximally entangled of local dimension rk;

• 3. For all pairs v,a, the projectors of Alice and Bob are conjugate, that is, $\mathbf{E}_{v,a} = \overline{\mathbf{F}}_{v,a}$

• 4. The consistency conditions can be represented as

  $$\displaystyle{ \forall \ (v,w) \in E,\ \ \forall \ a \in \{ 1,\ldots k\},\ \ \ \langle \mathbf{E}_{va},\mathbf{E}_{wa}\rangle = 0. }$$

  (8.69)

The proof for this proposition was introduced by Scarpa and Severini [32]. The authors emphasize that the quantum chromatic number depends on the rank of the POVM elements adopted by Alice and Bob. This remark motivates the following definition.

Definition 8.2 (Rank-r Quantum Chromatic Number [32]).

The rank-r quantum chromatic number χ _q ^(r)(G) of G is the minimum number of colors k such that G has quantum k-coloring formed by projectors of rank r and a maximally entangled state of local dimension rk.

It can be observed that χ _q ^(r)(G) ≤ χ _q ^(s)(G) if r ≥ s [32]. For rank-1 quantum coloring, the dimension of the maximally entangled state equals k and, the rank-1 projectors for each vertice v, can be represented as the outer product

$$\displaystyle{ \left \vert e_{va}\right \rangle \left \langle e_{va}\right \vert,\ \ a \in \{ 1,\ldots,k\}, }$$

(8.70)

for an orthonormal basis $\{\left \vert e_{va}\right \rangle _{a\in \{1,\ldots,k\}}\}$. Therefore (8.69) can be rewritten as:

$$\displaystyle{ \forall (v,w) \in E(G),\ \forall a \in \{ 1,\ldots,k\},\ \ \left \langle e_{va}\right \vert e_{wa}\rangle = 0. }$$

(8.71)

If a quantum k-coloring of a graph G(V, E) is given, then a matrix representation of G can be constructed with the map:

$$\displaystyle\begin{array}{rcl} \varPhi: V & \rightarrow & \mathbb{C}^{k\times k},{}\end{array}$$

(8.72)

such that for all (v, w) ∈ E it is required

$$\displaystyle{ \mathop{\mathrm{diag}}\nolimits (\varPhi (v)^{\dag }\varPhi (w)) = 0. }$$

(8.73)

Here, $\mathop{\mathrm{diag}}\nolimits (A)$ stands for the vector formed with the A diagonal entries. The map Φ is built taking for all v ∈ V a unitary matrix U _v mapping the computational basis $\{\left \vert i\right \rangle _{i\in \{1,\ldots,k\}}\}$ to $\{\left \vert e_{va}\right \rangle,a \in \{ 1,\ldots,\}\}$. Notice that U _v is a k × k matrix and (8.71) condition assures that if (v, w) is an edge then the diagonal entries of U _v ^† U _w are zero.

8.2.1 Relationship Between ξ(G), χ _q ⁽¹⁾(G) and χ ₍ G)

A k-dimensional orthogonal representation of G = (V, E) is a map

$$\displaystyle{ \phi: V \rightarrow \mathbb{C}^{k}, }$$

(8.74)

such that for all (v, w) ∈ E, the inner product $\left \langle \phi (v)\right \vert \phi (w)\rangle = 0$. The orthogonal rank of a graph G, denoted by ξ(G), is defined as the minimum k such that an orthogonal representation of G in $\mathbb{C}^{k}$ exists.

For all graphs G the following inequalities hold [10]:

$$\displaystyle{ \xi (G) \leq \chi _{q}^{(1)}(G) \leq \chi (G). }$$

(8.75)

If we have two graphs G and H, we can now define the Cartesian product GH.

• The vertex set V (GH) = V (G) × V (H) is the Cartesian product of the vertex sets of G and H;

• An edge between vertices (a ₁, b ₁), (a ₂, b ₂) ∈ V (GH) is either

  • a ₁ = a ₂ and (b ₁, b ₂) ∈ E(H), or

  • (a ₁, a ₂) ∈ E(G) and b ₁ = b ₂.

Notice that a vertex in V (GH) corresponds to a pair (a, b) of vertices where a is from G and b is from H.

Let K _k be a complete graph with k vertices. The next proposition clarifies the relation between the minimum dimension of orthogonal representation and the quantum chromatic number.

Proposition 8.2 (Scarpa and Severini [32]).

For all graphs G:

$$\displaystyle{ \chi _{q}^{(1)} =\min \{ k:\xi (GK_{ c}) = k\}. }$$

(8.76)

From this proposition follows a condition for equality between the rank-1 quantum chromatic number and orthogonal rank of a graph G.

Theorem 8.1 (Scarpa and Severini [32]).

For all graphs G:

$$\displaystyle{ \chi _{q}^{(1)}(G) =\xi (G)\ \ \text{if only if}\ \ \xi (GK_{\xi (G)}) =\chi (G). }$$

(8.77)

8.3 Wielandt’s Inequality

We have defined a quantum channel, denoted $\mathcal{E}$, as a trace preserving completely positive linear map (TPCP), that is,

$$\displaystyle{ \mathcal{E}: \mathcal{M}_{D\times D} \rightarrow \mathcal{M}_{D\times D}, }$$

(8.78)

where $\mathcal{M}_{D\times D}$ is the space of the complex D × D matrices. The Kraus operators $W_{k} \in \{\mathcal{M}_{D\times D}\}_{k=1}^{d}$ are a versatile representation of quantum channel $\mathcal{E}_{W}$:

$$\displaystyle{ \mathcal{E}_{W}(\rho ) =\sum _{ k=1}^{d}W_{ k}\rho W_{k}^{\dag }. }$$

(8.79)

Unitary operations , some kind of measurements , addition of uncorrelated quantum systems, substituting of a input state by other state are some operations in a quantum channel that can be well represented by Kraus operators.

Another useful representation, that allows modeling any operation by a unitary operation on a larger Hilbert space , is the Stinespring theorem :

Theorem 8.2 (Stinespring Theorem).

Let $\mathcal{E}$ be a trace-preserving quantum operation on a Hilbert space $\mathcal{H}$ . Then there is an ancilla space $\mathcal{K}$ of dimension $\dim \mathcal{K}\leq \left (\dim \mathcal{H}\right )^{2}$ so that for any fixed $\left \vert \chi \right \rangle \in \mathcal{K}$ there is a unitary transformation $\hat{U }$ on $\mathcal{H}\otimes \mathcal{K}$ with

$$\displaystyle{ \mathcal{E}(\rho ) =\mathop{ \mathrm{Tr}}\nolimits _{\mathcal{K}}\{\hat{U } (\rho \otimes \left \vert \chi \right \rangle \left \langle \chi \right \vert )\hat{U } ^{\dag }\}. }$$

(8.80)

However, for quantum channels the representation by means of Kraus operators is actually more usual, at least for applications where discrete classical information are to be transmitted. In this section we discuss some relevant development of the notion of zero-error communications through quantum channels.

As usual we begin with a classical concept to later introduce extensions of that concept into the quantum framework. Recall the definition of a classical discrete memoryless channel (DMC) $(\mathcal{X}\times \mathcal{Y},W(Y \vert X))$ for which $\vert \mathcal{X}\vert =\vert \mathcal{Y}\vert = D$. The main elements of a DMC are shown in Fig. 8.4. The matrix W(Y | X) is defined as a stochastic matrix whose rows are indexed by the elements of $\mathcal{X}$ while the columns are indexed by those of the finite set $\mathcal{Y}$. The (x, y) entry of W(Y | X) is the probability that Y = y is received when X = x is transmitted.

Fig. 8.4

Classical communication systems

Source messages V are picked from a finite set (alphabet of the source) and are mapped by means of the encoder in codewords X ⁿ = (X ₁, X ₂, …, X _n ). Each X _i , i = 1, 2, …, n, is transmitted through the memoryless channel that produces an output Y _i in such a way that

$$\displaystyle{ \Pr \left (Y ^{n} = y^{n}\vert X^{n} = x^{n}\right ) =\prod _{ i=1}^{n}\Pr \left (Y _{ i} = y_{i}\vert X_{i} = x_{i}\right ). }$$

(8.81)

The right-hand product means the i-th output y _i of a DMC depends by a stochastic map only on the i-th input x _i . This is the motivation to the term memoryless in the definition.

If we take into account the input and output blocks, X ⁿ and Y ⁿ, respectively, it is natural to define a stochastic matrix for these blocks, say,

$$\displaystyle{ W^{(n)}(Y ^{n}\vert X^{n}) \triangleq \Pr \left (Y ^{n}\vert X^{n}\right ) =\mathop{\underbrace{ W \otimes W \otimes \ldots \otimes W}}\limits _{ n\ \text{times}}. }$$

(8.82)

Notice that the probability distributions W(⋅ | x) and W ⁽ⁿ⁾(⋅ | x ⁿ) correspond to the x-th and x ⁿ-th lines of the product matrix, respectively. If two input blocks X ⁿ and $\tilde{X}^{n}$ can lead to the same output block Y ⁿ, decoding cannot be performed without error. We say that X ⁿ and $\tilde{X}^{n}$ are confusable or indistinguishable.

Sanz et al. [31] proposed an extension of the classical Wielandt’s inequality to quantum channels. The concept concerns the number of applications of the channel to any source (probability distribution) for which any output will be reached.

Before introducing the formal definition for the quantum case, we will recall some important notions. A matrix is said to be positive if its entries are all strictly positive.³ This means that for a positive DMC matrix W, any output $y \in \mathcal{Y}$ can be reached from any input $x \in \mathcal{X}$ at the input.

Definition 8.3 (Primitive Matrix ).

A square stochastic matrix W is said to be primitive if there is an $m \in \mathbb{N}$ such that (W ^m) _ij  > 0 for all (i, j), that is if W ^m is positive. The minimum m for which this occurs, denoted p(W), is said to be the classical index of primitivity of W.

It means that if a DMC probability transition matrix W is primitive, then using p(W) times a DMC $\left (\mathcal{X}\times \mathcal{Y},W(Y \vert X)\right )$, any $y \in \mathcal{Y}$ can be reached from each input $x \in \mathcal{X}$ transmitted or, equivalently, for the product channel displayed in Fig. 8.4, all input blocks X ⁿ are confusable.

The Wielandt’s inequality [22, p. 520] states that, for every primitive matrix W, then:

$$\displaystyle{ p(W) \leq D^{2} - 2D + 2. }$$

(8.83)

Observe that the Wielandt’s inequality does not depend on the matrix elements; only its primitivity is required. There are applications of the Wielandt’s inequality for several fields, e.g., to graph theory, number theory, numerical analysis, etc. An extension of the concept of index of primitivity to the quantum framework was introduced by Sanz et al. [31] which is defined by the number of times a channel must be used, so that it maps any density operator to one with full rank.

Example 8.3.

The following D × D matrix

$$\displaystyle{ W = \left (\begin{array}{*{10}c} 0&1&0& \cdot &\ldots &0&0\\ 0 &0 &1 &0 &\ldots & \cdot &0\\ \vdots & \vdots & \vdots & \vdots &\vdots & \vdots & \vdots \\ 0&0&0&0&\ldots &0&1\\ \alpha & \beta &0 &0 &\ldots & \cdot &0 \end{array} \right ) }$$

(8.84)

is primitive, for α > 0 and β > 0, α +β = 1. The primitivity is due to the fact that W ^m is positive for m = D ² − 2D + 2. This is just the Wielandt bound  [28, p. 730]. For instance, fixing D = 5, we have p(W) = m = 17, which means that 17 uses of that DMC, every output block $Y ^{17} \in \mathcal{Y}^{17}$ can be reached from any $X^{17} \in \mathcal{X}^{17}$ input block of symbols.

The graph of transitions for the DMC induced by this matrix (D = 5) is displayed in Fig. 8.5.

Fig. 8.5

Graph of the DMC induced by the stochastic matrix of (8.84) for D = 5. Labels on the edge (x, y) stand for conditional probabilities, for instance, $\alpha =\Pr [Y = 0\vert X = 4]$

Consider the probability row vector p of the input X as:

$$\displaystyle{ \mathbf{p} = \left (p_{0},p_{1},p_{2},p_{3},p_{4}\right ). }$$

(8.85)

That is, $p_{x} =\Pr [X = x]$, $x \in \mathcal{X}$. Similarly denote

$$\displaystyle{ \mathbf{q} = \left (q_{0},q_{1},q_{2},q_{3},q_{4}\right ), }$$

(8.86)

the probability row vector of the output Y, that is, $p_{y} =\Pr [Y = y]$, $y \in \mathcal{Y}$. The transition channel matrix W defines the relationship between probability vectors p and q, as follows:

$$\displaystyle{ \mathbf{q} = \mathbf{p}W. }$$

(8.87)

8.3.1 Quantum Index of Primitivity

Let $\mathcal{E}_{W}$ be the quantum channel defined by Kraus operators $\{W_{k} \in \mathcal{M}_{D\times D}\}_{k=1}^{d}$, that is

$$\displaystyle{ \mathcal{E}_{W}\left (\rho \right ) =\sum _{ k=1}^{d}W_{ k}\rho W_{k}^{\dag }. }$$

(8.88)

The quantum index of primitivity, denoted by q, is defined to a quantum channel (TPCP map) by the least $m \in \mathbb{N}$ such that m uses of the channel assures that every positive semidefinite operator is mapped onto a positive definite operator, where D is the dimension of the Hilbert space, and d the number of linearly independent Kraus operators.

It is possible to show that

$$\displaystyle{ q \leq (D^{2} - d + 1)D^{2}, }$$

(8.89)

where D is the dimension of the Hilbert space, and d the number of linearly independent Kraus operators.

Our proposal now is to focus on the issues of the inequality (8.89) connected with the notion of quantum channels with positive zero-error capacity. In this way, we need to recall some preliminaries given in [31]. Firstly, the authors define $S_{n}(W) \in \mathcal{M}_{D\times D}$ as the linear space spanned by all possible products of exactly n Kraus operators , $W_{k_{1}}W_{k_{2}}\ldots W_{k_{n}}$ and denote W _k ⁽ⁿ⁾ the elements of S _n (W), with this, they define

$$\displaystyle{ H_{n}(W,\varphi ) \triangleq S_{n}(W)\left \vert \varphi \right \rangle \subseteq \mathbb{C}^{D}, }$$

(8.90)

as the space spanned by all vectors $W_{k_{1}}W_{k_{2}}\ldots W_{k_{n}}\left \vert \varphi \right \rangle$, where $\left \vert \varphi \right \rangle \in \mathbb{C}$. Secondly, Sanz et al. [31] recall the one-to-one correspondence between a quantum channel $\mathcal{E}$ and its Choi matrix

$$\displaystyle{ \omega (\mathcal{E}) \triangleq (\mathbb{1} \otimes \mathcal{E})(\varOmega ), }$$

(8.91)

where $\varOmega =\sum _{ i,j}^{D}\left \vert ii\right \rangle \left \langle jj\right \vert.$ Then, the observed $\mathop{\mathrm{rank}}\nolimits \left [\mathcal{E}_{W}^{n}(\left \vert \varphi \right \rangle \left \langle \varphi \right \vert )\right ] =\dim \left [H_{n}(W,\varphi )\right ]$.

Equipped with prior discussion, three properties are introduced.

• 1. Primitive Quantum Channel . A quantum channel $\mathcal{E}_{W}$ is said to be primitive if there exists some $n \in \mathbb{N}$ such that for all $\left \vert \phi \right \rangle \in \mathbb{C}^{D},\ H_{n}(W,\varphi ) = \mathbb{C}^{D}.$ The number $q(\mathcal{E}_{W})$ stands for the minimum n for which the condition is reached. This means that for every input density operator ρ the output $\mathcal{E}_{W}^{n}(\rho )$, obtained after n applications of the channel is full-rank. It is observed that if $\mathcal{E}_{W}$ is primitive, then for every $m \in \mathbb{N},\ \mathcal{E}_{W}^{m}$ is also primitive and we have

  $$\displaystyle{ H_{n}(W,\varphi ) = \mathbb{C}^{D}\ \ \text{for all }n \geq q(\mathcal{E}_{ W}). }$$

  (8.92)

• 2. Eventually Full Kraus Rank Quantum Channel . A quantum channel $\mathcal{E}_{W}$ is called eventually full Kraus rank if there exists some $n \in \mathbb{N}$ such that $S_{n}(W) = \mathcal{M}_{D\times D}$. This means that $\mathop{\mathrm{rank}}\nolimits \left [w(\mathcal{E}_{W}^{n})\right ] = D^{2}$. The number i(W) stands for the minimum n for which that condition is satisfied. Notice that if $\mathcal{E}_{W}$ fulfills this property, then $S_{n}(W) = \mathcal{M}_{D\times D}$ for all n ≥ i(W).

• 3. Strongly Irreducible Quantum Channel. A quantum channel $\mathcal{E}_{W}$ is said to be strongly irreducible if the following two conditions are fulfilled:

  • a. $\mathcal{E}_{W}$ has a unique eigenvalue, λ, with | λ |  = 1;

  • b. The corresponding eigenvector ρ is a positive definite operator (ρ > 0).

An important question now is how the classical Wielandt bound relates with the quantum one. The main tool is to make an embedding of the classical channel in the quantum framework, as it is shown in the next example.

Example 8.4.

Consider again the classical DMC illustrated in Fig. 8.5 (for D = 5) and respective stochastic matrix W given by (8.84). It is easy to see that embedding is obtained by intermediate the following map $\mathcal{E}_{W}$ defined by the Kraus operators

$$\displaystyle{ W_{x,y} = \sqrt{w_{x,y}}\left \vert y\right \rangle \left \langle x\right \vert,\ x \in \mathcal{X},y \in \mathcal{Y}. }$$

(8.93)

For an input (diagonal) operator

$$\displaystyle{ \rho =\delta _{x,y}p_{x} = \left (\begin{array}{*{10}c} p_{0} & 0 & 0 & 0 & 0 \\ 0 &p_{1} & 0 & 0 & 0 \\ 0 & 0 &p_{2} & 0 & 0 \\ 0 & 0 & 0 &p_{3} & 0 \\ 0 & 0 & 0 & 0 &p_{4} \end{array} \right ). }$$

(8.94)

Here, δ _x, y stands for the Kronecker function and p _x ,  x ∈ { 0, 1, 2, 3, 4}, are the entries of input probability vector p (recall Example 8.3). The output is given by

$$\displaystyle{ \sigma = \mathcal{E}_{W}(\rho )\delta _{x,y}q_{y} = \left (\begin{array}{*{10}c} q_{0} & 0 & 0 & 0 & 0 \\ 0 &q_{1} & 0 & 0 & 0 \\ 0 & 0 &q_{2} & 0 & 0 \\ 0 & 0 & 0 &q_{3} & 0 \\ 0 & 0 & 0 & 0 &q_{4} \end{array} \right ), }$$

(8.95)

where q _y ,  y ∈ { 0, 1, 2, 3, 4}, are the entries of the output vector q.

The set of Kraus operators are

$$\displaystyle{ \big\{\left \vert 1\right \rangle \left \langle 0\right \vert,\left \vert 2\right \rangle \left \langle 1\right \vert,\left \vert 3\right \rangle \left \langle 2\right \vert,\left \vert 4\right \rangle \left \langle 3\right \vert,\sqrt{\alpha }\left \vert 0\right \rangle \left \langle 4\right \vert,\sqrt{\beta }\left \vert 4\right \rangle \left \langle 4\right \vert \big\}. }$$

(8.96)

Assume W is a primitive DMC stochastic probability transition matrix with primitivity index p(W). The following is proved in [31].

Proposition 8.3.

Let W be a primitive stochastic map and let $\mathcal{E}_{W}$ be the corresponding TPCP. The channel $\mathcal{E}_{W}$ is also primitive and

$$\displaystyle{ q(W) = p(W) = i(W). }$$

(8.97)

Notice that equality of (8.97) holds for quantum channels resulting of the above DMC embedding. This fact is illustrated next.

Example 8.5.

Let us consider a “genuine” quantum channel, with D = 2 and d = 3 given by the Kraus operators

$$\displaystyle{ \Big\{W_{1} = \frac{1} {\sqrt{3}}X,\ W_{2} = \frac{1} {\sqrt{3}}Y,\ W_{3} = \frac{1} {\sqrt{3}}Z\Big\} }$$

(8.98)

where X, Y, and Z are the Pauli matrices. Explicitly, the map is given by

$$\displaystyle{ \mathcal{E}_{W}(\rho ) = \frac{1} {3}\Bigg(X\rho X^{\dag } + Y \rho Y ^{\dag } + Z\rho Z^{\dag }\Bigg), }$$

(8.99)

for an input state ρ.

It is straightforward to check that in this case $q(\mathcal{E}_{\mathcal{W}}) = 1$ and i(W) = 2. The quantum Wielandt’s bound is $8 = (D^{2} - d + 1)D^{2} \geq q(\mathcal{E}_{\mathcal{W}})$.

There is an open question if the quantum Wielandt’s bound is sharp, however the following theorem is very important because establishing a universal dichotomy behavior of the zero-error capacity of the important class of unital quantum channels. This dichotomy result is universal in the sense that it depends only on the dimension of the Hilbert space , D, and not on the channel itself.

Theorem 8.3 (Dichotomy Behavior  [31]).

Let $C^{(0)}(\mathcal{E})$ be the zero-error classical capacity of the quantum channel $\mathcal{E}$ . If $\mathcal{E}$ is a quantum channel with full-rank fixed point, then either $C^{(0)}(\mathcal{E}^{n}) \geq 1$ for all n or $C^{(0)}\left (\mathcal{E}^{q(\mathcal{E})}\right ) = 0$.

Notice that if $\mathcal{E}^{n}$ stands for the input–output relationship after n units of time or space then the theorem reveals the existence of a universal critical length $n = q(\mathcal{E})$ such that once a transmission is successfully viable then a successful transmission m ≥ n is possible.

8.4 Entanglement-Assisted Zero-Error Capacity

In Sect. 3.2.5 we saw different capacities of quantum channels. The entanglement-assisted capacity in particular considers that the parties share an unrestricted amount of previously shared entanglement which they can use in order to maximize the information changed through the quantum channel. In this section, we describe how entanglement can be used in a zero-error scenario for exchanging classical information.

Before introducing the entanglement-assisted zero-error communication, we need some background concepts. We start with the hypergraph of a quantum channel.

Definition 8.4 (Hypergraph of a Quantum Channel [13] ).

Let $\mathcal{E}$ be a quantum channel. The hypergraph of $\mathcal{E}$, denoted by $\mathbf{H}(\mathcal{E})$, is a set of vertices, denoted by S and a set of subsets of S. The set of vertices S is composed by the channel input. There is one hyperedge for each of the outputs, which contains all the inputs that have a nonzero probability of causing that output.

We also use the concept of clique in hypergraphs. A clique of $\mathbf{H}(\mathcal{E})$ is a set κ _i of possible inputs of a given output in a confusability graph. In other words, the clique κ _i contains all the inputs that can cause the same output.

In this current scenario, in particular, prior to information exchange through the quantum channel, Alice and Bob share a d-dimensional entangled state $\rho _{AB} = \left \vert \varPhi _{AB}\right \rangle \left \langle \varPhi _{AB}\right \vert$ given by

$$\displaystyle{ \left \vert \varPhi _{AB}\right \rangle = \frac{1} {\sqrt{d}}\sum _{i=0}^{d-1}\left \vert i_{ A}\right \rangle \left \vert i_{B}\right \rangle }$$

(8.100)

Considering that such pre-shared entanglement is available, Cubitt et al. [13] proposed a protocol for entanglement-assisted zero-error communication that is described as follows:

• 1. Alice chooses a message m ∈ { 1, …, K} from a set of messages, where K is the number of messages. Alice wants to send the message m to Bob;

• 2. Alice measures her half of the entangled system using a complete orthogonal basis , say $B_{m} = \left \{\left \vert \psi _{\acute{x}}\right \rangle \right \}$, where $\acute{x}$ is a vertice in a clique κ _m from the hypergraph $\mathbf{H}(\mathcal{E})$;

• 3. Alice sends the result of her measurement to Bob.

  Some clarifications are needed before proceeding. In the hypergraph $\mathbf{H}(\mathcal{E})$ the vertice x represents the unit vector $\left \vert \psi _{\acute{x}}\right \rangle$ such that if x and $\acute{x}$ are adjacent then $\left \langle \psi _{x}\right \vert \psi _{\acute{x}}\rangle = 0$. Recalling that K is the size of the messages set, the hypergraph has K cliques of size d , say {κ ₁, …, κ _K }. It is analogous to say that each message m has a d-size clique κ _m in the hypergraph $\mathbf{H}(\mathcal{E})$.

• 4. After Alice’s measurement, Bob’s state will collapse to $\left \vert \psi _{x}\right \rangle ^{{\ast}}$;

• 5. Bob will measure his state in $B_{m} =\{ \left \vert \psi _{x}\right \rangle \}$ in order to get the final state $\left \vert \psi _{\acute{x}}\right \rangle ^{{\ast}}$;

• 6. Bob output is denoted by y. His possible states are determined by those vertices x, for which $p(y\vert \acute{x}) > 0$ and these adjacent states are mutually orthogonal, i.e., for any $\acute{x}_{1}$ and $\acute{x}_{2}$, then $\left \langle \acute{x}_{1}\right \vert \acute{x}_{2}\rangle = 0$ [23].

For short, to send K messages using entanglement, Alice and Bob can use a maximally entangled state of rank d: to send m, Alice measures her side of the state in the bases B _m and obtains the outcome j (at random). She inputs (m; j) to the channel. Bob’s output tells him that Alice’s input was in some particular mutually confusable subset, but by construction, these inputs correspond to mutually orthogonal residual states of his subsystem, so he can perform a projective measurement to determine precisely which input Alice made to the classical channel, and hence which of the K messages she chose to send, with certainty [13].

Using the previously defined elements and protocol characterized, we can now characterize the entanglement-assisted zero-error classical capacity of quantum channels.

Theorem 8.4 (Entanglement-Assisted Zero-Error Capacity [13] ).

Let $\mathcal{E}$ be a quantum channel. The entanglement-assisted zero-error capacity of $\mathcal{E}$ , denoted by $C_{E}^{(0)}(\mathcal{E})$ , is given by

$$\displaystyle{ C_{E}^{(0)}(\mathcal{E}) =\lim _{ n\rightarrow \infty }\frac{1} {n}\log K^{E}(\mathcal{E}^{\otimes n}) \geq \log (K^{E}) }$$

(8.101)

where K ^E is the number of mutually non-adjacent input messages with entanglement assistance.

Theorem 8.5 (Cubitt-Leung-Matthews-Winter Theorem [13] via [23]).

For a quantum channel $\mathcal{E}$ with hypergraph $\mathbf{H}(\mathcal{E})$ , there exists an entanglement-assisted quantum communication protocol that can send one of K messages with zero error ; hence for entanglement-assisted asymptotic classical zero error capacity

$$\displaystyle\begin{array}{rcl} \log (K) \leq C^{(0)}(\mathcal{E})& =& \lim _{ n\rightarrow \infty }\frac{1} {n}\log (K(\mathcal{E}^{\otimes n})) < C_{ E}^{(0)}(\mathcal{E}) \\ & =& \lim _{n\rightarrow \infty }\frac{1} {n}\log K^{E}(\mathcal{E}^{\otimes n}) \geq \log (K^{E}).{}\end{array}$$

(8.102)

This theorem shows us that entanglement can sometimes be used to increase the number of classical messages which can be sent perfectly over quantum channels [13].

Some results in the literature have interesting connections with the entanglement-assisted zero-error capacity. Leung et al. [25], using certain input codewords (based on a Pauli graph ), show that entanglement can help to increase the classical zero-error capacity to the maximum achievable HSW capacity.

In general, it is possible to observe the following relation between the classical zero-error quantities:

$$\displaystyle{ C^{(0)}(\mathcal{E}) < C_{ E}^{(0)}(\mathcal{E}) \leq C_{ 1,\infty }(\mathcal{E}) }$$

(8.103)

Recalling that the zero-error capacity is a quantity hard to compute even for small characteristic graphs, upper bounds play an important role, in particular, the Lovász ϑ function is commonly considered . Beigi [4] verified that the Lovász ϑ function is an upper bound on the zero-error capacity even in the presence of entanglement between the sender and receiver.

8.5 Non-Commutative Graphs and Quantum Lovász ϑ Function

The works of Duan, Cubitt, Severini, Winter, and other collaborators [14, 15, 17] introduce the theory of non-commutative graphs in the study of quantum zero-error capacity problem. Starting with the Kraus form of representation of a quantum channel, the authors define a generalization of the classical adjacency graph called non-commutative (confusability) graph by the operator space:

$$\displaystyle{ S \triangleq \mathop{\mathrm{span}}\nolimits \{W_{j}^{\dag }W_{ k}: j,k\} < \mathcal{L}(\mathcal{H}) }$$

(8.104)

where $\mathcal{L}(\mathcal{H})$ stands for the set of observable on Hilbert space $\mathcal{H}$.

According to this graph definition, a zero-error code consists in the anti-clique of the corresponding graph. The biggest anti-clique, called independence number and denoted by α(G), corresponds to the maximum number of messages that can be transmitted through the channel with probability of error equal to zero. This way, the classical zero-error capacity of a channel with graph G is given by

$$\displaystyle{ C^{(0)}(G) =\lim _{ n\rightarrow \infty }\log \alpha (G^{n}) =\sup _{ n}\log \alpha (G^{n}). }$$

(8.105)

Translating this concept to the quantum scenario, we have a quantum channel $\mathcal{E}: \mathcal{B}(\mathcal{H}_{X}) \rightarrow \mathcal{B}(\mathcal{H}_{Y })$, where $\mathcal{B}(\cdot )$ is the space of linear operators from a given Hilbert space. This way, the event $E_{x,y}: \mathcal{H}_{X} \rightarrow \mathcal{H}_{Y }$, that corresponds to the input of a quantum state $x \in \mathcal{X}$ and the output of a quantum state $y \in \mathcal{Y}$ in this quantum channel, is given by

$$\displaystyle{ E_{x,y} = \sqrt{p(y\vert x)}\left \vert y\right \rangle \left \langle x\right \vert. }$$

(8.106)

This way, we can define the confusability graph of a quantum channel (or non-commutative graph) as being a subspace

$$\displaystyle{ S =\mathop{ \mathrm{span}}\nolimits \left \{E_{x',y'}^{\dag }\cdot E_{ x,y}\neq 0;x,x' \in \mathcal{X},y,y' \in \mathcal{Y}\right \}. }$$

(8.107)

It is interesting to notice that such definition emphasizes the channel’s input that can be confused, while in Chap. 5 the approach was to emphasize inputs that are not adjacent. Despite this difference, both definitions are equivalent.

Example 8.6 (Confusability Graph of a Quantum Channel).

Let $\mathcal{E}$ be a quantum channel shown in Fig. 8.6a. The input alphabet contains the symbols $\mathcal{X} = \left \{a,b\right \}$ and the output alphabet contains the symbols $\mathcal{Y} = \left \{c,d\right \}$.

Fig. 8.6

Example of a graph of a quantum channel (a ) transitions probabilities at the channel’s end (b ) confusability graph

According to (8.106), we have the following events:

$$\displaystyle\begin{array}{rcl} E_{a,c}& =& 1 \cdot \left \vert c\right \rangle \left \langle a\right \vert = \left \vert c\right \rangle \left \langle a\right \vert,{}\end{array}$$

(8.108)

$$\displaystyle\begin{array}{rcl} E_{a,d}& =& 0 \cdot \left \vert d\right \rangle \left \langle a\right \vert = 0,{}\end{array}$$

(8.109)

$$\displaystyle\begin{array}{rcl} E_{b,c}& =& \sqrt{\frac{1} {3}}\left \vert c\right \rangle \left \langle b\right \vert,{}\end{array}$$

(8.110)

$$\displaystyle\begin{array}{rcl} E_{b,d}& =& \sqrt{\frac{2} {3}}\left \vert d\right \rangle \left \langle b\right \vert.{}\end{array}$$

(8.111)

It is important to emphasize that these events have a straight correspondence with the quantum channel it is related. From these events, we can consider the following elements that will compose the confusability graph (see (8.107))

$$\displaystyle\begin{array}{rcl} E_{a,c}^{\dag }\cdot E_{ a,c}& =& \left \vert a\right \rangle \left \langle a\right \vert,{}\end{array}$$

(8.112)

$$\displaystyle\begin{array}{rcl} E_{a,c}^{\dag }\cdot E_{ b,c}& =& \sqrt{\frac{1} {3}}\left \vert a\right \rangle \left \langle b\right \vert,{}\end{array}$$

(8.113)

$$\displaystyle\begin{array}{rcl} E_{b,c}^{\dag }\cdot E_{ a,c}& =& \sqrt{\frac{1} {3}}\left \vert b\right \rangle \left \langle a\right \vert,{}\end{array}$$

(8.114)

$$\displaystyle\begin{array}{rcl} E_{b,c}^{\dag }\cdot E_{ b,c}& =& \frac{1} {3}\left \vert b\right \rangle \left \langle b\right \vert,{}\end{array}$$

(8.115)

$$\displaystyle\begin{array}{rcl} E_{b,d}^{\dag }\cdot E_{ b,d}& =& \frac{2} {3}\left \vert b\right \rangle \left \langle b\right \vert.{}\end{array}$$

(8.116)

Thus,

$$\displaystyle{ S =\mathop{ \mathrm{span}}\nolimits \left \{E_{a,c}^{\dag }\cdot E_{ a,c},E_{a,c}^{\dag }\cdot E_{ b,c},E_{b,c}^{\dag }\cdot E_{ a,c},E_{b,c}^{\dag }\cdot E_{ b,c},E_{b,d}^{\dag }\cdot E_{ b,d}\right \}. }$$

(8.117)

Considering the subspace S we can denote the zero-error capacity of a quantum channel. This capacity is given by the following expression, considering that the biggest set of self-orthogonal states is given by $\left \{\left \vert \phi _{m}\right \rangle: m = 1,\ldots,N\right \}$

$$\displaystyle{ \forall m\neq m': \left \vert \phi _{m}\right \rangle \left \langle \phi _{m'}\right \vert \in S^{\perp }, }$$

(8.118)

where S ^⊥ is an orthogonal subspace to S given in (8.107). The expression in (8.118) has some relations with the corresponding independence number of the graph. In Example 8.6, for instance, we have that $S^{\perp } = \varnothing$. It implies that the classical zero-error capacity of the quantum channel $\mathcal{E}$ is equal to zero.

For every confusability graph $S \leq \mathcal{B}(\mathcal{H}_{X})$ we have the following relation

$$\displaystyle{ \alpha _{q}(S) \leq \alpha (S) \leq \tilde{\alpha }_{U}(S) \leq \tilde{\alpha } (S) \leq \hat{\alpha } (S) }$$

(8.119)

where each of these αs, called independence numbers , has relation with a different kind of zero-error capacity , as shown in Table 8.2. Detailed information about how to obtain such numbers can be found in the work of Duan et al. [17, 18].

Table 8.2 Alternative definitions for zero-error capacities considering independence numbers

The classical zero-error capacity C ⁽⁰⁾ and the quantum zero-error capacity Q ⁽⁰⁾ of a quantum channel were deeply discussed in Chap. 5. The zero-error capacity assisted by entanglement was introduced in the previous section.

Among the independence numbers showed, the only which is not directly related to a zero-error capacity is $\tilde{\alpha }_{U}(S)$ because it considers unitary restrictions in its definitions. The numbers α _q (S), α(S), $\tilde{\alpha }(S)$ are $\hat{\alpha }(S)$ computable. However, finding a computable expression to the associated zero-error capacity cannot be a trivial task.

Regarding the Lovász theta function , presented in Sect. 4.3 for the classical scenario, it works as an upper bound for the zero-error capacity of a DMC . It is natural to pursue a quantum version of such definition. It was presented by the authors and is formally defined as follows.

Definition 8.5 (Quantum Lovász Theta Number [17]).

Let S be the non-commutative graph of a quantum channel $\mathcal{E}$. The quantum Lovász theta number is given by

$$\displaystyle\begin{array}{rcl} \tilde{\vartheta }(S)& =& \sup _{n}\vartheta (S \otimes \mathcal{L}(\mathbf{C}^{n})){}\end{array}$$

(8.120)

$$\displaystyle\begin{array}{rcl} & =& \sup _{n}\max \{\Vert\mathbb{1} + T\Vert: T \in S^{\perp }\otimes \mathcal{L}(\mathbf{C}^{n}),\mathbb{1} + T \geq 0\},{}\end{array}$$

(8.121)

where the supremum is over all integers n, and the maximum is taken over Hermitian operators T.

The authors show more results regarding characteristics of this quantum version of the Lovász theta number, such as its monotonicity and supermultiplicativity.

Considering the independence numbers and their corresponding zero-error capacities as well as the Lovász theta number, both characterized using the same approach of non-commutative graphs, the authors believe that these results suggest that there might be a much more systematic way in which operator systems generalize Graph Theory to the non-commutative domain. They are pursuing new results in such direction.

8.6 $\mathcal{Q}\mathcal{M}\mathcal{A}$-Completeness of Quantum Clique

In this section we are going to explore the results of Beigi and Shor regarding the computational complexity of the quantum clique problem which was found out to be $\mathcal{Q}\mathcal{M}\mathcal{A}$-complete [5]. According to the authors, the original problem of finding the quantum clique can be written in terms of finding the zero-error capacity of a quantum channel. Exploring the zero-error behavior in this scenario brought relevant contributions to the theory of complexity , enlightening the classification of an important problem according to quantum complexity classes.

Theory of Complexity is a subarea of computer science whose goal is to prove for important problems that their solutions require certain minimum resources [38]. When considering each solution, it takes into account a model of computation (classical Turing machines, probabilistic Turing machines, quantum Turing machines, for instance) and a certain resource (for example, memory or time) [34].

Problems are grouped into complexity classes , according to the model used and to a function of the amount of resources their best solutions demand over a certain size of input in a worst-case scenario. For classical models of computation and when time resources are considered, the complexity classes $\mathcal{P}$ and $\mathcal{N}\mathcal{P}$ are widely studied.

An algorithmic problem belongs to the complexity class $\mathcal{P}$ of polynomially solvable problems if it can be solved by an algorithm with polynomial worst-case runtime [38]. The class $\mathcal{P}$ is felt to capture the notion of problems with efficient time solutions considering classical (deterministic) Turing machines [2].

The complexity class $\mathcal{N}\mathcal{P}$ contains problems having efficiently verifiable solutions. In other words, if x is a solution to the problem (certificate), it is possible to verify that in deterministic polynomial time [2]. For example, the subset sum is in the $\mathcal{N}\mathcal{P}$ class. In this problem, given a list of n numbers A ₁, A ₂, …, A _n and a number T, one must decide if there is a subset of numbers that sums up to T. The certificate for this problem is the list of members in this subset. For a practical example in the problem considered, if the list of numbers is {4, −8, 0, 22, −17, 3, 2} and T = 1, then the certificate {4, −8, 3, 2} can be verified as a solution to the problem in polynomial time.

Any problem in $\mathcal{P}$ is also in the $\mathcal{N}\mathcal{P}$ class because we can solve it in polynomial time even without the need of a certificate [12]. However, the question if the classes $\mathcal{P}$ and $\mathcal{N}\mathcal{P}$ are equal or different remains as one of the most important challenges for computer science. Certain problems in the $\mathcal{N}\mathcal{P}$ class, in particular, have a special classification. A problem in $\mathcal{N}\mathcal{P}$ is called an $\mathcal{N}\mathcal{P}$ -complete problem if any efficient algorithm for it can be converted into an efficient algorithm for any other problem in $\mathcal{N}\mathcal{P}$ [20].

Considering this brief introduction of computational complexity, from now on we will examine more closely the contribution and the results of Beigi and Shor [5]. Some definitions and argumentation presented below in this section are from their original work and the reader is referred to it for more details.

The clique of a graph is a widely known $\mathcal{N}\mathcal{P}$-complete problem. Given a graph G a clique is a subset of vertices, every two of which are adjacent, and the size of a clique is the number of its vertices . The clique problem is that given a graph G and an integer number k, decide whether G contains a clique of size k or not.

Let G ^C be the complement of the graph G. In the complement of G a clique is changed to an independent set. A subset of a graph G where no two vertices are adjacent characterize an independent set. The maximum size of an independence set is the independence number of the graph G, denoted by α(G). So the clique problem in the complement graph reduces to decide whether α(G) ≥ k, and then it is $\mathcal{N}\mathcal{P}$-complete. This reduction is important because the problem of computing α(G) is related to the problem of computing the zero-error capacity of a classical discrete memoryless channel, as shown extensively on Chap. 4

The quantum version of the clique problem, known as quantum clique problem , is also to decide whether $\alpha (\mathcal{E}) \geq k$ for a given quantum channel $\mathcal{E}$. It is equivalent to decide whether there exists quantum states ρ ₁, …, ρ _k such that $\mathcal{E}(\rho _{1}),\ldots,\mathcal{E}(\rho _{k})$ have orthogonal supports or not. Note that, for any two states σ ₁, σ ₂, then $\mathop{\mathrm{Tr}}\nolimits (\sigma _{1}\sigma _{2}) \geq 0$ and equality holds iff σ ₁ and σ ₂ have orthogonal supports.

Let σ _1, 2 = σ ₁ ⊗σ ₂ then $\mathop{\mathrm{Tr}}\nolimits (\sigma _{1}\sigma _{2}) =\mathop{ \mathrm{Tr}}\nolimits (S\sigma _{1,2})$, where S is the swap gate ($S\left \vert \psi \right \rangle \left \vert \varphi \right \rangle = \left \vert \varphi \right \rangle \left \vert \psi \right \rangle$). We can estimate $\mathop{\mathrm{Tr}}\nolimits (\sigma _{1}\sigma _{2})$ by applying the swap gate. We must notice that if σ _1, 2 is not separable then the equality does not hold and the orthogonality is not implied by $\mathop{\mathrm{Tr}}\nolimits (S\sigma _{1,2}) = 0$. To avoid this problem we must restrict ourselves to entanglement breaking channels.

Definition 8.6 (Entanglement Breaking Quantum Channel [5] ).

A quantum channel $\mathcal{E}$ is called an entanglement breaking quantum channel if there are POVM {M _i } and states σ _i such that

$$\displaystyle{ \mathcal{E}(\rho ) =\sum _{i}\mathop{ \mathrm{Tr}}\nolimits (M_{i}\rho )\sigma _{i} }$$

(8.122)

for any ρ. In this case, $\mathcal{E}^{\otimes 2}(\rho _{1,2})$ is always separable, $\mathop{\mathrm{Tr}}\nolimits (S\mathcal{E}^{\otimes 2}(\rho _{1,2})) \geq 0$ and equality implies $\mathcal{E}(\rho _{1})$ and $\mathcal{E}(\rho _{2})$ are orthogonal.

Putting all the concepts together, we can now formally define the quantum clique problem.

Definition 8.7 (Quantum Clique Problem [5] ).

The quantum clique problem $(\mathcal{E},k,a,b)$ is defined as follows:

• Input. Integer numbers n and k; non-negative real numbers a and b with an inverse polynomial gap b − a > n ^−c; and $\mathcal{E}$ an entanglement breaking quantum channel that acts on n-qubit states;

• Promise. Either exists ρ ₁ ⊗ … ⊗ρ _k such that $\sum _{i,j}\mathop{ \mathrm{Tr}}\nolimits (S\mathcal{E}(\rho _{i}) \otimes \mathcal{E}(\rho _{j})) \leq a$ or for any states ρ _{1, 2, …, k} we have $\sum _{i,j}\mathop{ \mathrm{Tr}}\nolimits (S\mathcal{E}^{\otimes 2}(\rho _{i,j})) \geq b$;

• Output. Decide which one is the case.

Despite the deep understanding of the clique problem as an $\mathcal{N}\mathcal{P}$-complete problem in the classical case, the same does not happen to the quantum clique problem prior to the work discussed here. Even nowadays, our knowledge regarding quantum complexity theory is still not rich as its classical analogue.

Now we are going to characterize the $\mathcal{Q}\mathcal{M}\mathcal{A}$ quantum complexity class that, loosely speaking, is the quantum version of the $\mathcal{N}\mathcal{P}$ class [37] . The acronym of this complexity class stands for Quantum-Merlin-Arthur where Merlin is an oracle with infinite computational power and Arthur is a quantum polynomial time verifier. Merlin answers decision problems of the type “Is x in L?” and accompany the answer with a polynomial certificate y which Arthur can verify in polynomial time using a quantum machine [1]. We associate two probabilities with the $\mathcal{Q}\mathcal{M}\mathcal{A}$ class which are related to the completeness and soundness . The formal definition of such complexity class is presented as follows.

Definition 8.8 ($\mathcal{Q}\mathcal{M}\mathcal{A}$ Complexity Class [37] ).

A language L is said to be in $\mathcal{Q}\mathcal{M}\mathcal{A}(2/3,1/3)$ if there exists a quantum polynomial time verifier V such that

• Completeness. $\forall x \in L,\exists \left \vert \xi \right \rangle \in \mathcal{H}^{p(\vert x\vert )},\Pr (V (\left \vert x\right \rangle \left \vert \xi \right \rangle ) = 1) \geq 2/3$;

• Soundness. $\forall x\not\in L,\forall \left \vert \xi \right \rangle \in \mathcal{H}^{p(\vert x\vert )},\Pr (V (\left \vert x\right \rangle \left \vert \xi \right \rangle ) = 1) \leq 1/3$;

After the $\mathcal{Q}\mathcal{M}\mathcal{A}$ complexity class was characterized, Kitaev introduced a problem from Physics called the “local Hamiltonian problem” and showed that it is $\mathcal{Q}\mathcal{M}\mathcal{A}$-complete. This problem is the quantum analogue of the classical SAT problem and these results are the analogue of the Cook-Levin theorem [5]. The formal definition of this problem is described below.

Definition 8.9 (Local Hamiltonian Problem [24]).

The k-local Hamiltonian problem (H ₁, …, H _s , a, b) is defined as follows:

• Input. An integer n, real numbers a, b such that b − a > n ^−c, and polynomially many Hermitian non-negative semidefinite matrices H ₁, …, H _s with bounded norm $\Vert H_{i}\Vert \leq 1$, such that each of them acts just on k of n qubits;

• Promise. The smallest eigenvalue of H ₁ + … + H _s is either less than a or greater than b;

• Output. Decide which one is the case.

Intuitively, a k-local matrix assigns a real number to any quantum state on n qubits. This number depends only on the reduced state of the k qubits where a quantum operator M acts non-trivially, and can be thought of as a locally defined penalty on a given quantum state. Loosely speaking, the k-local Hamiltonian problem asks whether there exists a quantum state that can significantly avoid a collection of such penalties [37].

Considering the quantum clique problem, the following theorem states its complexity.

Theorem 8.6 (Quantum Clique is $\mathcal{Q}\mathcal{M}\mathcal{A}$-Complete [5] ).

The quantum clique problem $(\mathcal{E},k,a,b)$ where $\mathcal{E}$ is an entanglement breaking channel on n-qubit states and has the operator-sum representation

$$\displaystyle{ \mathcal{E}(\rho ) =\sum _{ i=1}^{r}E_{ i}\rho E_{i}^{\dag }, }$$

(8.123)

where $\sum _{i}E_{i}^{\dag }E_{i} =\mathbb{1}$ and r = poly(n), is $\mathcal{Q}\mathcal{M}\mathcal{A}$ -complete.

The proof of this theorem consists in showing that $(\mathcal{E},k,a,b)$ is $\mathcal{Q}\mathcal{M}\mathcal{A}$. To prove the hardness, the authors establish a polynomial time reduction from the local Hamiltonian problem to quantum clique . In this result, a is a positive number that means that some probability of error is allowed.

If we consider the case a = 0, we will try to find a protocol with no error. In this case, $(\mathcal{E},k,a = 0,b)$ exactly says that whether $\alpha (\mathcal{E}) \geq k$ or not. We can achieve this by using a zero-error quantum channel $\mathcal{E}$ where

$$\displaystyle{ \mathcal{E}(\rho ) =\sum _{ i-1}^{r}\mathop{ \mathrm{Tr}}\nolimits (M_{ i}\rho )\left \vert i\right \rangle \left \langle i\right \vert, }$$

(8.124)

where {M ₁, …, M _r } is a POVM and $\left \vert 1\right \rangle,\ldots,\left \vert r\right \rangle$ are orthogonal states . Checking orthogonality of two outcomes states is accomplished in the following way: given two states $\mathcal{E}(\rho )$ and $\mathcal{E}(\rho ')$ we measure them in the basis $\left \vert 1\right \rangle,\ldots,\left \vert r\right \rangle$. If the outcome of the measurements are the same, then their supports are not orthogonal.

So, the quantum clique problem $(\mathcal{E},k,a = 0,b)$ where $\mathcal{E}$ is a zero-error quantum channel that can be implemented exactly by a polynomial time verifier is $\mathcal{Q}\mathcal{M}\mathcal{A}_{1}$-complete. The article of Beigi and Shor contains the entire version of the proofs briefly discussed here [5].

Some promise problems in the literature are known to be $\mathcal{Q}\mathcal{M}\mathcal{A}$-complete, such as variants of the local Hamiltonian problem, the density matrix consistency problem, and also other problems about quantum circuits [37]. However, the quantum clique problem is the only so far in this complexity class whose complexity was described using zero-error quantum channels.

This section described the complexity classification of the quantum clique problem. We presented the results of Beigi and Shor that showed a non-trivial result where zero-error quantum channels helped in determining the quantum complexity of a problem. The contributions of these authors enrich the knowledge regarding quantum complexity classes and the classification of an important quantum problem, which may have implications in algorithms and protocols for practical applications.

8.7 Further Reading

In this section we could see some developments in the literature that provide new results and insights into the quantum zero-error information theory. We saw the background which relates quantum zero-error information theory with Kochen-Specker sets and Bell’s inequality. The quantum version of the Wielandt’s inequality which states an upper bound to the number of uses of a quantum channel in order to map an arbitrary density operator to a full rank operator was also discussed. An alternative version of the zero-error capacity of quantum channels considering entanglement assistance was introduced. The approach for zero-error capacity considering non-commutative graphs and the quantum counterpart of the Lovász theta function was also considered. Lastly, an application of quantum zero-error channels to find the complexity class of a problem showed a non-trivial application of the concepts discussed along the book.

Other recent results besides those discussed here can also be found in the literature. Blume-Kohout et al. [7] developed a framework to handle quantum information that can be perfectly preserved (i.e, with zero-error) by the system dynamics. According to the authors, the system dynamics affects the kind of information that can be carried or store (classical, quantum or neither, for instance). Taking that into account, the main purpose of their operational framework is to describe how to perfectly preserve information despite the system dynamics. This framework considers not only quantum channels with positive zero-error capacity, but also quantum error-correcting codes, decoherence-free subspaces and subsystems and even other methods proposed by the own authors, such as the unconditionally preserved codes. This work provides an exhaustive classification of ways that information can be preserved.

Regarding practical implementations, Gyongyosi and Imre [21] considered the use of multiple optical channels to send information. Each of these individual channels has no positive zero-error capacity, but when used jointly the zero-error capacity is superactivated. Their idea is to adopt such strategy as part of the implementation of quantum repeaters, devices that can extend the range of quantum communication between sender and receiver.

Besides the already described results on superactivation of zero-error capacity, Shirokov [33] showed a special kind of superactivation of quantum channels under block coding.

Brië t et al. considered the use of quantum entanglement in the zero-error source-channel coding problem [8]. In their scenario, Alice and Bob are each given an input from a random source and get access to a noisy channel through which Alice can send messages to Bob. Their goal is to minimize the average number of channel uses per source input such that Bob can learn Alice’s inputs with zero probability of error. Their results show lower bound and optimum rate of entanglement-assisted source codes and the advantage that entanglement can give in the source-channel coding problem.

We hope that much more results on quantum zero-error information theory are yet to come.