Abstract
This chapter develops the theory of rectangle measures: finitely-additive tiling measures defined on rectangles in the plane. Every real-parameter persistence module gives rise to such a measure, the ‘persistence measure’ of the module. An equivalence theorem asserts that a rectangle measure can be represented as a diagram of decorated points in the plane. In particular, the persistence measure of a persistence module gives rise to its persistence diagram. The diagram carries no structural information in regions of the plane where the measure is infinite. For this reason, we isolate various tameness conditions on persistence modules that guarantee finiteness in regions of the extended plane; the most important of these is q-tameness. Vanishing lemmas ease the computation of persistence diagrams by identifying regions of the plane where the diagram is empty. Finally, we show that our measure-theoretic diagrams agree with the traditionally defined diagrams in certain standard settings (such as the sublevelset persistent homology of a Morse function on a compact manifold).
Access provided by Autonomous University of Puebla. Download chapter PDF
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
For a decomposable \({\mathbf {R}}\)-persistence module
we have defined the decorated persistence diagram to be the multiset
and the undecorated persistence diagram to be the multiset
If we don’t know that \({\mathbb {V}}\) is decomposable then we have to proceed differently. We are guided by the following heuristic: if we know how many points of \({\mathsf {Dgm}}\) belong to each rectangle in the half-space, then we know \({\mathsf {Dgm}}\) itself. For persistence modules, counting points in rectangles turns out to be easy.
The language of measure theory is well suited to this argument. We will see that a persistence module defines an integer-valued measure on rectangles. If the module is tame then this measure is finite-valued, and therefore (Theorem 3.12) it is concentrated at a discrete set of points. These points, taken with their multiplicities, constitute the persistence diagram. In the case where the module is decomposable, the persistence diagram constructed this way agrees with the persistence diagram defined earlier. When the module is not known to be decomposable, we can proceed regardless.
The persistence measures that we construct are not true measures on subsets of \({\mathbf {R}}^2\): they are additive in the sense of tiling rather than in the usual sense of disjoint set union. The discrepancy arises when we split a rectangle into two: what happens to the points on the common edge? To which rectangle do they belong? Decorated points resolve this question, and moreover the formalism fits perfectly with our use of decorations to distinguish open and closed ends of intervals.
3.1 The Persistence Measure
Let \({\mathbb {V}}\) be a persistence module. The persistence measure of \({\mathbb {V}}\) is the function

defined on rectangles \(R = [a,b] \times [c,d]\) in the plane with \(a< b \le c < d\).
For a decomposable persistence module, there is a clear relationship between \(\mu _{\mathbb {V}}\) and the interval summands of \({\mathbb {V}}\). Let us first consider the case of an interval module.
Proposition 3.2
Let \({\mathbb {V}}= \mathbf {k}^J\) where \(J = ( p^*, q^* )\) is a real interval. Let \(R = [a,b] \times [c,d]\) where \(a< b \le c < d\). Then
Proof
It is clear that \(\mathbf {k}^J\) restricted to \(\{a,b,c,d\}\) is an interval or is zero. Thus, \(\mu _{\mathbb {V}}(R) \le 1\). Moreover \(\mu _{\mathbb {V}}(R) = 1\) precisely when

which happens if and only if \(b,c \in J\) and \(a,d \not \in J\). This is equivalent to the condition \([b,c] \subseteq J \subseteq (a,d)\). \(\square \)
Proposition 3.2 has a graphical interpretation. Represent the interval \(J \subseteq {\mathbf {R}}\) as a decorated point in the extended plane. The following picture indicates exactly which decorated points \(( p^*,q^* )\) are detected by \(\mu _{\mathbb {V}}(R)\):

If (p, q) is in the interior of R then \(( p^*,q^* )\) is always detected regardless of the decoration. If (p, q) is on the boundary, then \(( p^*,q^* )\) is detected if the tick is directed inwards.
We formalise this by defining a membership relation between decorated points and rectangles.
Definition 3.3
Let \(R = [a,b] \times [c,d]\) where \(a< b \le c < d\), and consider a decorated point \((p^*, q^*)\) with \(p^* < q^*\). We write \((p^*, q^*) \in R\) if any of the following equivalent statements is true:
-
We have \(p^* \in [a,b]\) and \(q^* \in [c,d]\) in the notation of Eq. (2.3).
-
We have \(a< p^* < b\) and \(c< q^* < d\) in the total order of Eq. (2.1).
-
We have \(a^+ \le p^* \le b^-\) and \(c^+ \le q^* \le d^-\) in the total order of Eq. (2.1).
-
The real interval \((p^*, q^*)\) is sandwiched \([b,c] \subseteq (p^*, q^*) \subseteq (a,d)\).
-
The point-with-tick \((p^*, q^*)\) lies in the closed rectangle R.
The set  is called the r-interior of R. We also
make use of its undecorated counterpart
,
is called the r-interior of R. We also
make use of its undecorated counterpart
,  , the interior in the standard sense of the finite rectangle \(R = [a,b] \times [c,d]\).
, the interior in the standard sense of the finite rectangle \(R = [a,b] \times [c,d]\).
Remark 3.4
The expressions \((p^*, q^*) \in R\) and  mean the same thing but we will tend to prefer the former. In the same spirit, we write \(|_R\) to indicate the restriction of a multiset of decorated points to (the r-interior of) the rectangle R.
mean the same thing but we will tend to prefer the former. In the same spirit, we write \(|_R\) to indicate the restriction of a multiset of decorated points to (the r-interior of) the rectangle R.
Corollary 3.5
Suppose \({\mathbb {V}}\) is a decomposable persistence module over \({\mathbf {R}}\):
Then
for every rectangle \(R = [a,b] \times [c,d]\) with \(a< b \le c < d\).
Proof
This follows from Propositions 3.2 and 2.16 (direct sums). \(\square \)
We now have a strategy for defining the persistence diagram without assuming a decomposition: having constructed \(\mu _{\mathbb {V}}\), we look for a multiset of decorated points \({\mathsf {Dgm}}({\mathbb {V}})\) which satisfies Eq. (3.1) for all rectangles. For this to work, we need to know that such a multiset exists and is unique. Theorem 3.12 will take care of this under the hypothesis that \(\mu _{\mathbb {V}}\) is finite and additive; it is a sort of ‘Riesz representation theorem’ for measures on rectangles. By Corollary 3.5, the new and old definitions agree in the case where \({\mathbb {V}}\) is decomposable.
3.2 The Persistence Measure (Continued)
We call \(\mu _{\mathbb {V}}\) a measure because it is additive with respect to splitting a rectangle into two rectangles. We prove this shortly. First we consider the ‘alternating sum’ formula for \(\mu _{\mathbb {V}}(R)\) that appears in [19]:
Proposition 3.6
Let \({\mathbb {V}}\) be a persistence module, and let \(a< b \le c < d\). If the vector spaces \(V_a\), \(V_b\), \(V_c\), \(V_d\) are finite-dimensional, or less stringently if \({{\mathrm {r}}}^b_c < \infty \), then

(Here as before \({{\mathrm {r}}}^s_t = {\mathrm {rank}}(v^s_t : V_s \rightarrow V_t)\).)
Proof
Decompose the 4-term module \({\mathbb {V}}_{\!\{a,b,c,d\}}\) into intervals. The left-hand side counts intervals of type [b, c]. By the restriction principle, the four terms on the right-hand side evaluate as follows:

These expressions are all finite: the hypothesis \({{\mathrm {r}}}^b_c < \infty \) implies that the other three ranks are finite too (Example 2.20). We can legitimately take the alternating sum, and all terms on the right-hand side cancel except for the  . \(\square \)
. \(\square \)
We give three proofs of additivity. The first is completely general, whereas the other two work under restricted settings but are illuminating in their own way.
Proposition 3.7
\(\mu _{\mathbb {V}}\) is additive under vertical and horizontal splitting, meaning that
whenever \(a< p< b \le c< q < d\).
This additivity property is illustrated by the following figure

where the claim is that \(\mu _{\mathbb {V}}(R) = \mu _{\mathbb {V}}(S) + \mu _{\mathbb {V}}(T) = \mu _{\mathbb {V}}(U) + \mu _{\mathbb {V}}(V)\).
Proof
(first version) Let \(a< p< b \le c< q < d\). Then we calculate

for additivity with respect to a horizontal split, and

for additivity with respect to a vertical split. \(\square \)
Proof
(second version, assuming \({{\mathrm {r}}}^b_c < \infty \)) The alternating sum formula (Proposition 3.6) gives
and
as required. Note that \({{\mathrm {r}}}^b_c < \infty \) implies \({{\mathrm {r}}}^p_c < \infty \) and \({{\mathrm {r}}}^b_q < \infty \), so the formula is valid for all the rectangles in question. \(\square \)
This second proof is particularly transparent when drawn geometrically in the plane: the \(+\) and − signs at the corners of the rectangles cancel in a pleasant way:

Proof
(third version, assuming \({\mathbb {V}}\) is decomposable) By Corollary 3.5, the measure of a rectangle counts the interval summands whose corresponding decorated points lie in the rectangle. Additivity follows from the observation that a decorated point in R belongs to exactly one of its subrectangles S and T, and to exactly one of its subrectangles U and V. \(\square \)
Here are two further descriptions of \(\mu _{\mathbb {V}}([a,b]\times [c,d])\).
Proposition 3.8
We have the following formulae:

Proof
This is covered, for instance, in the localisation discussion in Sect. 5.1 of [8]. The two formulae are obtained by localising at c and b, respectively. \(\square \)
Proposition 3.8 expresses the measure of a rectangle as the dimension of a vector space constructed functorially from \({\mathbb {V}}\). (Ostensibly there are two vector spaces, one for each formula, but the map \(v^b_c\) induces a natural isomorphism between them.) Functoriality has its advantages, but in other regards this characterisation is harder to use. For instance, additivity is not as obvious in this formulation.
3.3 Abstract r-Measures
We now consider rectangle measures more abstractly. Persistence measures are of course our primary example, but the general formulation allows for many other situations. For ease of exposition, we initially work in the plane \({\mathbf {R}}^2\) rather than the extended plane \(\overline{{\mathbf {R}}}{}^2\). The picture is completed in Sect. 3.6 when we discuss the points at infinity.
Definition 3.9
Let \(\mathcal {D}\) be a subset of \({\mathbf {R}}^2\). Define
(the set of closed rectangles contained in \(\mathcal {D}\)). A rectangle measure or r-measure on \(\mathcal {D}\) is a function
which is additive under vertical and horizontal splitting (as in Proposition 3.7).
Proposition 3.10
Let \(\mu \) be an r-measure on \(\mathcal {D}\subseteq {\mathbf {R}}^2\). Then:
-
If \(R \in {\mathrm {Rect}}(\mathcal {D})\) can be written as a union \(R = R_1 \cup \dots \cup R_k\) of rectangles with disjoint interiors, then \(\mu (R) = \mu (R_1) + \dots + \mu (R_k)\).
-
If \(R \subseteq S\) then \(\mu (R) \le \mu (S)\).
In other words, \(\mu \) is finitely additive and monotone.
Proof
(Finitely additive) Let \(R = [a,b] \times [c,d]\). By induction and the vertical splitting property, it follows that finite additivity holds for decompositions of the form
where \(R_i = [a_i,a_{i+1}] \times [c,d]\) with \(a = a_1< a_2< \dots < a_m = b\). By induction and the horizontal splitting property, it then follows that finite additivity holds for ‘product’ decompositions
where \(R_{ij} = [a_i, a_{i+1}] \times [c_j, c_{j+1}]\) with \(a = a_1< a_2< \dots < a_m = b\) and \(c = c_1< c_2< \dots < c_n = d\). For an arbitrary decomposition \(R = R_1 \cup \dots \cup R_k\), finally, the result follows by considering a product decomposition of R by which each \(R_i\) is itself product-decomposed.
(Monotone) Decompose S into a collection of rectangles R and \(R_1, \dots , R_{k-1}\) which are interior-disjoint. (This can be done with at most 9 rectangles using a product decomposition.) Then
by finite additivity and the fact that \(\mu \ge 0\). \(\square \)
Here is one more plausible-and-also-true statement about abstract r-measures.
Proposition 3.11
(Subadditivity) Let \(\mu \) be an r-measure on \(\mathcal {D}\subseteq {\mathbf {R}}^2\). If a rectangle \(R \in {\mathrm {Rect}}(\mathcal {D})\) is contained in a finite union
of rectangles \(R_i \in {\mathrm {Rect}}(\mathcal {D})\), then
Proof
Let
include all the x-coordinates of the corners of all the rectangles, and let
include all the y-coordinates. Each rectangle is then tiled as a union of pieces
with disjoint interiors, and the measure of the rectangle is the sum of the measures of its tiles, by additivity. Since each tile belonging to R must also belong to one or more of the \(R_i\), the inequality follows. \(\square \)
3.4 Equivalence of Measures and Diagrams
We wish to establish a correspondence between r-measures and decorated diagrams. The task of defining a continuous persistence diagram can then be replaced by the simpler task of defining an r-measure. This works best when the measure is finite; in Sect. 3.5 we consider measures that are not finite .
The r-interior of a region \(\mathcal {D}\subseteq {\mathbf {R}}^2\) is defined as follows:

This is the set of decorated points that can be ‘accessed’ by some rectangle in \(\mathcal {D}\). The decorated diagram will be a multiset in  . Clearly, an r-measure in \(\mathcal {D}\) cannot tell us what happens outside
. Clearly, an r-measure in \(\mathcal {D}\) cannot tell us what happens outside  . The interior of \(\mathcal {D}\) in the classical sense is written
. The interior of \(\mathcal {D}\) in the classical sense is written  . In terms of rectangles, we have
. In terms of rectangles, we have

where we recall that  denotes the interior of the closed rectangle \(R = [a,b]\times [c,d]\). The undecorated
diagram
will be a multiset in
denotes the interior of the closed rectangle \(R = [a,b]\times [c,d]\). The undecorated
diagram
will be a multiset in  .
.
Theorem 3.12
(The equivalence theorem) Let \(\mathcal {D}\subseteq {\mathbf {R}}^2\). There is a bijective correspondence between:
-
Finite r-measures \(\mu \) on \(\mathcal {D}\). ‘Finite’ means that \(\mu (R) < \infty \) for every \(R \in {\mathrm {Rect}}(\mathcal {D})\).
-
Locally finite multisets \(\mathsf {A}\) in
 . ‘Locally finite’ means that \({\text {card}}(\mathsf {A}|_R) < \infty \) for every \(R \in {\mathrm {Rect}}(\mathcal {D})\).
. ‘Locally finite’ means that \({\text {card}}(\mathsf {A}|_R) < \infty \) for every \(R \in {\mathrm {Rect}}(\mathcal {D})\).
The measure \(\mu \) corresponding to a multiset \(\mathsf {A}\) is related to it by the formula
for every \(R \in {\mathrm {Rect}}(\mathcal {D})\).
Remark 3.13
We can write Eq. (3.2) equivalently as
where

is the multiplicity function for \(\mathsf {A}\).
Assuming the theorem, we define the persistence diagrams of a measure.
Definition 3.14
Let \(\mu \) be a finite r-measure on a region \(\mathcal {D}\subseteq {\mathbf {R}}^2\).
-
The decorated diagram of \(\mu \) is the unique locally finite multiset \({\mathsf {Dgm}}(\mu )\) in
 such that $$ \mu (R) = {\text {card}}({\mathsf {Dgm}}(\mu )|_R) $$
such that $$ \mu (R) = {\text {card}}({\mathsf {Dgm}}(\mu )|_R) $$for every \(R \in {\mathrm {Rect}}(\mathcal {D})\).
-
The undecorated diagram of \(\mu \) is the locally finite multiset in


obtained by forgetting the decorations on the points and restricting to the interior.
Remark 3.15
Note that \(\mathsf {dgm}\) is locally finite in  , but not necessarily locally finite in \({\mathbf {R}}^2\)—it may have accumulation points on the boundary of \(\mathcal {D}\).
, but not necessarily locally finite in \({\mathbf {R}}^2\)—it may have accumulation points on the boundary of \(\mathcal {D}\).
Proof
(Theorem 3.12) One direction of the correspondence is easy. If \(\mathsf {A}\) is a multiset on  then the function \(\mu (R)\) on rectangles defined by Eq. (3.2) is indeed an r-measure. It is finite if \(\mathsf {A}\) is locally finite. To verify additivity, suppose that a rectangle R is split vertically or horizontally into two rectangles \(R_1, R_2\). Notice that every decorated point \((p^*,q^*) \in R\) belongs to exactly one of \(R_1, R_2\). It follows that
then the function \(\mu (R)\) on rectangles defined by Eq. (3.2) is indeed an r-measure. It is finite if \(\mathsf {A}\) is locally finite. To verify additivity, suppose that a rectangle R is split vertically or horizontally into two rectangles \(R_1, R_2\). Notice that every decorated point \((p^*,q^*) \in R\) belongs to exactly one of \(R_1, R_2\). It follows that
as required.
The reverse direction takes more work. Given an r-measure \(\mu \) we will (1) construct a multiset \(\mathsf {A}\) in  , (2) show that \(\mu \) and \(\mathsf {A}\) are related by Eq. (3.2), and (3) show that \(\mathsf {A}\) is unique. In practice, we construct the multiplicity function \({\mathrm {m}}\) and establish Eq. (3.3), rather than referring to \(\mathsf {A}\) directly
.
, (2) show that \(\mu \) and \(\mathsf {A}\) are related by Eq. (3.2), and (3) show that \(\mathsf {A}\) is unique. In practice, we construct the multiplicity function \({\mathrm {m}}\) and establish Eq. (3.3), rather than referring to \(\mathsf {A}\) directly
.
Step 1. (Multiplicity formula.) Let \(\mu \) be a finite r-measure on \(\mathcal {D}\). Define
for \((p^*,q^*)\) in  . Note that the minimum is attained because the set is nonempty and \(\mu \) takes values in the natural numbers.
. Note that the minimum is attained because the set is nonempty and \(\mu \) takes values in the natural numbers.
Here is an alternative characterisation. Instead of minimising over all rectangles, we take the limit through a decreasing sequence of rectangles:
Lemma 3.16
Let \((\xi _i)\) and \((\eta _i)\) be non-increasing sequences of positive real numbers which tend to zero as \(i \rightarrow \infty \). Then
and similarly
Proof
The key observation is that the sequence of rectangles \(R_i = [p,p+\xi _i] \times [q,q+\eta _i]\) is cofinal in the set of rectangles R containing \((p^+,q^+)\). In other words, for any such R we have \(R_i \subseteq R\) for all sufficiently large i.
By monotonicity, the sequence of nonnegative integers \(\mu (R_i)\) is non-increasing, and hence eventually stabilises to a limit. Then
for any R containing \((p^+, q^+)\). Taking the minimum over all R, the right-hand side becomes \({\mathrm {m}}(p^+,q^+)\) and hence by squeezing
The other three cases of the lemma are similar. \(\square \)
We return to the main proof.
Step 2. Having defined \({\mathrm {m}}(p^*,q^*)\), we now show that this is the ‘correct’ definition, meaning that Eq. (3.3) is satisfied. We have seen already that \({\mathrm {m}}\) corresponds to an r-measure
and it remains to show (for this step) that \(\nu = \mu \). We prove this by induction on \(k = \mu (R)\).
Base case. \(\mu (R) = 0\). Then for every \((p^*,q^*) \in R\) we have
so \(\nu (R) = 0\).
Inductive step. Suppose \(\mu (R) = \nu (R)\) for every rectangle R with \(\mu (R) < k\). Consider a rectangle \(R_0\) with \(\mu (R_0) = k\). We must show that \(\nu (R_0) = k\).
Split the rectangle into four equal quadrants \(S_1, S_2, S_3, S_4\). Certainly
by finite additivity (Proposition 3.10). If every quadrant satisfies \(\mu (S_i) < k\), then by induction we deduce that \(\mu (R_0) = \nu (R_0)\). Otherwise, one of the quadrants has \(\mu = k\) and the other three quadrants satisfy \(\mu = 0\) (and hence \(\nu = 0\)). Let \(R_1\) be the distinguished quadrant, so \(\mu (R_1) = k\). It is now enough to show that \(\nu (R_1) = k\).
We repeat the argument. Subdivide \(R_i\) into four equal quadrants. Either all four quadrants satisfy the inductive hypothesis \(\mu < k\), in which case we are done. Otherwise we find a quadrant \(R_{i+1}\) with \(\mu (R_{i+1}) = k\), and we are reduced to showing that \(\nu (R_{i+1}) = k\).
In the worst case—the remaining unresolved case—this iteration never terminates and we obtain a sequence of closed rectangles
each being a quadrant of the previous one, with \(\mu (R_i) = k\). Since the diameters of the rectangles tend to zero, their intersection \(\bigcap _i R_i\) contains a single point (r, s).
We are now in a position to show that \(\nu (R_0)=k\), by evaluating the sum explicitly over all decorated points in \(R_0\).
First of all, consider decorated points that eventually leave the sequence \((R_i)\). Specifically, suppose that \((p^*,q^*) \in R_0\) but \((p^*,q^*) \in R_{i-1} - R_i\) for some i. This means that \((p^*,q^*)\) belongs to one of the three quadrants of \(R_{i-1}\) for which \(\mu =0\). It follows immediately that \({\mathrm {m}}(p^*,q^*) = 0\).
Thus, the only contribution to \(\nu (R_0)\) comes from decorated points \((p^*,q^*)\) which belong to every rectangle in the sequence \((R_i)\). Clearly these must be decorated versions \((r^*,s^*)\) of the intersection point (r, s). There are 4, 2 or 1 of them depending on how the nested sequence of rectangles converges to its limit. Here we illustrate the three cases:

Suppose first that (r, s) lies in the interior of every rectangle \(R_i\), so that all four decorated points \((r^+,s^+)\), \((r^+,s^-)\), \((r^-,s^+)\), \((r^-,s^-)\) belong to every \(R_i\). Divide each \(R_i\) into 4 subrectangles \(R_i^{++}\), \(R_i^{+-}\), \(R_i^{-+}\), \(R_i^{--}\), which share a common corner at (r, s) so that each of the four decorated points \((r^*,s^*)\) belongs to one of the subrectangles in the obvious notation. By Lemma 3.16,
and moreover each of these decreasing integer sequences eventually stabilises at its limiting value. Thus, for sufficiently large i,
as required.
A similar argument (with fewer terms) can be made in the cases where only 2 or 1 of the decorated points \((r^*,s^*)\) belong to every \(R_i\). For instance, if (r, s) lies on the interior of the right-hand edge of the rectangles \((R_i)\) for all sufficiently large i, we split each rectangle into two parts \(R_i^{-+}\) and \(R_i^{--}\) and obtain
in the same way. In this case \((r^+,s^+)\) and \((r^+,s^-)\) eventually leave (or were never in) the sequence \((R_i)\) and therefore do not contribute to \(\nu (R_0)\). We omit the details of the remaining cases, which are equally straightforward.
This completes the inductive step. Thus \(\mu (R) = \nu (R)\) for every \(R \in {\mathrm {Rect}}(\mathcal {D})\).
Step 3. Suppose \({\mathrm {m}}'(p^*, q^*)\) is some other multiplicity function on  whose associated r-measure
whose associated r-measure
satisfies \(\mu = \nu '\). We must show that \({\mathrm {m}}= {\mathrm {m}}'\).
Consider an arbitrary decorated point  . Let R be a rectangle which contains \((p^*,q^*)\) at its corner. Since
. Let R be a rectangle which contains \((p^*,q^*)\) at its corner. Since
there are only finitely many other decorated points \((r^*,s^*) \in R\) with positive multiplicity in \({\mathrm {m}}\) or \({\mathrm {m}}'\). By making R smaller, we can therefore assume that \((p^*, q^*)\) is the only decorated point in R with positive multiplicity in either measure. Then
Since \((p^*,q^*)\) was arbitrary it follows that \({\mathrm {m}}= {\mathrm {m}}'\).
This completes the proof of Theorem 3.12. \(\square \)
3.5 Non-finite Measures
If an r-measure is not everywhere finite, we restrict our attention to the parts of the plane where it is finite. Define the finite r-interior of an r-measure \(\mu \) to be the set of decorated points

The finite interior is the set of undecorated points

This is an open subset of the plane, being a union of open rectangles. It is easy to see that  if and only if
if and only if  for all possible decorations
. A (decorated) point
that is not in the finite (r-)interior may be called singular.
for all possible decorations
. A (decorated) point
that is not in the finite (r-)interior may be called singular.
Although these interiors are defined in a pointwise sense, the next two propositions show that the finiteness extends to any rectangle contained in them.
Proposition 3.17
Let \(R \in {\mathrm {Rect}}(\mathcal {D})\). If  then \(\mu (R) < \infty \).
then \(\mu (R) < \infty \).
Proof
We show that each \((p,q) \in R\) is contained in the interior relative to R of a rectangle \(S \subseteq R\) of finite measure. If (p, q) lies in the interior of R, then each of the four decorated points \((p^*,q^*)\) belongs to  so we can find four finite-measure rectangles containing them. The union of these rectangles contains a neighbourhood of (p, q), and we can take \(S \subseteq R\) to be a rectangle contained in this union with (p, q) in its interior. It has finite measure, by subadditivity (Proposition 3.11). The other cases are similar: if (p, q) lies on the interior of an edge, we take two finite-measure rectangles containing a relative neighbourhood of (p, q); and if (p, q) is a corner point we take just one rectangle.
so we can find four finite-measure rectangles containing them. The union of these rectangles contains a neighbourhood of (p, q), and we can take \(S \subseteq R\) to be a rectangle contained in this union with (p, q) in its interior. It has finite measure, by subadditivity (Proposition 3.11). The other cases are similar: if (p, q) lies on the interior of an edge, we take two finite-measure rectangles containing a relative neighbourhood of (p, q); and if (p, q) is a corner point we take just one rectangle.
To finish, we note that R, being compact, is the union of finitely many of these rectangles; therefore by subadditivity it has finite measure. \(\square \)
The undecorated version is an immediate consequence.
Proposition 3.18
Let \(R \in {\mathrm {Rect}}(\mathcal {D})\). If  then \(\mu (R) < \infty \). \(\square \)
then \(\mu (R) < \infty \). \(\square \)
Theorem 3.19
Let \(\mu \) be an r-measure
on \(\mathcal {D}\subseteq {\mathbf {R}}^2\). Then there is a uniquely defined locally finite multiset \({\mathsf {Dgm}}(\mu )\) in  such that
such that
for every \(R \in {\mathrm {Rect}}(\mathcal {D})\) with  .
.
Proof
Within each rectangle S of finite measure, Theorem 3.12 provides a multiset in  such that Eq. (3.6) holds for all subrectangles \(R \subseteq S\). Uniqueness implies that the multisets for overlapping rectangles agree on the common intersection. Thus we obtain a multiset defined in the union of these
such that Eq. (3.6) holds for all subrectangles \(R \subseteq S\). Uniqueness implies that the multisets for overlapping rectangles agree on the common intersection. Thus we obtain a multiset defined in the union of these  , which by definition is equal to
, which by definition is equal to  , with the property that Eq. (3.6) holds for all rectangles R of finite measure. By Proposition 3.17, this means all rectangles with
, with the property that Eq. (3.6) holds for all rectangles R of finite measure. By Proposition 3.17, this means all rectangles with  . \(\square \)
. \(\square \)
Now we can define the persistence diagrams of a general r-measure.
Definition 3.20
Let \(\mu \) be an r-measure on a region \(\mathcal {D}\subseteq {\mathbf {R}}^2\).
-
The decorated diagram of an r-measure \(\mu \) is the pair
 , where \({\mathsf {Dgm}}(\mu )\) is the multiset in
, where \({\mathsf {Dgm}}(\mu )\) is the multiset in  described in Theorem 3.19.
described in Theorem 3.19. -
The undecorated diagram is the pair
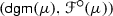 , where
, where 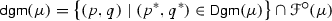
is the locally finiteFootnote 1 multiset in
 obtained by forgetting the decorations in \({\mathsf {Dgm}}(\mu )\) and restricting to the finite
interior.
obtained by forgetting the decorations in \({\mathsf {Dgm}}(\mu )\) and restricting to the finite
interior.
Remark 3.21
To make this backwards-compatible with the previously defined persistence diagrams of a finite r-measure on a region \(\mathcal {D}\), we can regard \({\mathsf {Dgm}}(\mu )\) and \(\mathsf {dgm}(\mu )\) as abbreviations for  and
and  .
.
Remark 3.22
It is sometimes useful to adopt the region extension convention : an r-measure defined on a subset \(\mathcal {D}\subset {\mathbf {R}}^2\) can be interpreted as an r-measure on the whole plane \({\mathbf {R}}^2\), by agreeing that \(\mu (R) = \infty \) for any rectangle that meets \({\mathbf {R}}^2 - \mathcal {D}\). The extension has the same diagram as the original r-measure.
3.6 Measures and Diagrams in the Extended Plane
We now consider r-measures in the extended plane \(\overline{{\mathbf {R}}}{}^2\). In Sect. 3.7, we will use this to define the decorated and undecorated diagrams of an arbitrary persistence module. The points at infinity take account of possible infinite interval summands of the module. The development proceeds almost exactly as with the standard plane. What is new is that we use infinite rectangles and we admit \(-\infty ^+\) and \(+\infty ^-\) as possible coordinates of decorated points.
A rectangle in the extended plane is a set of the form
where now \(-\infty \le a < b \le +\infty \) and \(-\infty \le c < d \le +\infty \). Thus there are various types of infinite rectangle . The r-interior of a rectangle \(R = [a,b] \times [c,d]\) is the set of decorated points

exactly as before, with the understanding that \(-\infty ^+\) and \(+\infty ^-\) are permissible values of \(p^*, q^*\). The interior of R requires a little care:

For instance, if \(R = [-\infty ,b]\times [c,d]\) where b, c, d are finite, then  . We adopt this convention because we do not wish to lose the points at infinity when we pass from a decorated diagram to its undecorated counterpart.
. We adopt this convention because we do not wish to lose the points at infinity when we pass from a decorated diagram to its undecorated counterpart.
For \(\mathcal {D}\subseteq \overline{{\mathbf {R}}}{}^2\), let \({\mathrm {Rect}}(\mathcal {D})\) denote the set of rectangles \(R \subseteq \mathcal {D}\). The r-interior and interior of \(\mathcal {D}\) are formally the same as before (with  as above):
as above):

An r-measure on \(\mathcal {D}\) is a function
which is additive with respect to the vertical or horizontal splitting of a rectangle into two rectangles. Propositions 3.10 and 3.11 (finite additivity, monotonicity, subadditivity) follow as before. The finite r-interior and finite interior are

if \(\mu \) is finite, then  and
and  .
.
Claim
Theorems 3.12 and 3.19 are valid, verbatim, for r-measures on \(\mathcal {D}\subseteq \overline{{\mathbf {R}}}{}^2\). The multiplicity of a point in \({\mathsf {Dgm}}(\mu )\) may be computed using Eq. (3.4).
Proof
The statements (and indeed the proofs) of Theorems 3.12, 3.19, and Eq. (3.4) are invariant under reparametrisations of the plane of the form
where f, g are homeomorphic embeddings. We can view \(\overline{{\mathbf {R}}}{}^2\) as a rectangle in \({\mathbf {R}}^2\) via a transformation of this type; for instance
identifies \(\overline{{\mathbf {R}}}{}^2\) with the rectangle \([-\pi /2,\pi /2] \times [-\pi /2, \pi /2]\) in \({\mathbf {R}}^2\). Through this hack, the original theorems are transferred to the extended plane. \(\square \)
Definition 3.23
The decorated and undecorated diagrams of an r-measure \(\mu \) are the ordered pairs  and
and  , where \({\mathsf {Dgm}}(\mu )\) is given by Theorem 3.19, and \(\mathsf {dgm}(\mu )\) is obtained from \({\mathsf {Dgm}}(\mu )\) by forgetting the
decorations and restricting to
, where \({\mathsf {Dgm}}(\mu )\) is given by Theorem 3.19, and \(\mathsf {dgm}(\mu )\) is obtained from \({\mathsf {Dgm}}(\mu )\) by forgetting the
decorations and restricting to  .
.
So far we have treated the extended plane almost exactly like the standard plane. When we come to prove the stability theorem for persistence diagrams (Sects. 5.6–5.8), where metric properties become relevant, we end up considering the points at infinity separately from the points in the standard plane. For this, we make use of certain ‘measures at infinity’ that we derive now.
Consider an r-measure \(\mu \) on \(\overline{{\mathbf {R}}}{}^2\). (If \(\mu \) is given on a proper sub-region \(\mathcal {D}\subset \overline{{\mathbf {R}}}{}^2\), extend it to \(\overline{{\mathbf {R}}}{}^2\) using the region extension convention of Remark 3.22.) The extended plane has 4 lines at infinity
and 4 points at infinity
There are measures defined on each of these. On the four lines at infinity, they are ‘interval measures’ (the 1-dimensional analogue of r-measures, defined on closed intervals and additive with respect to splitting an interval into two). At the four points at infinity, each measure is simply a number. We write out the three cases of direct relevance to persistence modules. The other five cases are analogous.
-
the line \((-\infty , {\mathbf {R}})\):
$$ \mu (-\infty , [c,d]) = \lim _{b \rightarrow -\infty } \mu ([-\infty ,b]\times [c,d]) = \min _b \, \mu ([-\infty ,b]\times [c,d]) $$for any interval \([c,d] \subseteq {\mathbf {R}}\).
-
the line \(({\mathbf {R}}, +\infty )\):
$$ \mu ([a,b], +\infty ) = \lim _{c \rightarrow +\infty } \mu ([a,b]\times [c,+\infty ]) = \min _c \, \mu ([a,b]\times [c,+\infty ]) $$for any interval \([a,b] \subseteq {\mathbf {R}}\).
-
the point \((-\infty , +\infty )\):
$$ \mu (-\infty , +\infty ) = \lim _{e \rightarrow +\infty } \mu ([-\infty , -e]\times [e,+\infty ]) = \min _e \, \mu ([-\infty , -e]\times [e,+\infty ]) $$
Monotonicity of \(\mu \) guarantees that each limit exists. Each measure has a straightforward interpretation in terms of \({\mathsf {Dgm}}(\mu )\). We give two sample propositions.
Proposition 3.24
(1) If \(\mu (-\infty , [c,d])\) is finite, then it counts the decorated points of \({\mathsf {Dgm}}(\mu )\) of the form \((-\infty ^+, q^*)\) where \(q^* \in [c,d]\).
(2) If \(\mu (-\infty , [c,d])\) is infinite, then  for some \(q^* \in [c,d]\).
for some \(q^* \in [c,d]\).
Proof
(1) If the limit is finite, then for some finite \(b_0\) the rectangle \([-\infty ,b_0] \times [c,d]\) has finite measure and therefore contains finitely many points of \({\mathsf {Dgm}}(\mu )\). For all sufficiently small b, then, the rectangle \([-\infty ,b] \times [c,d]\) contains exactly those points with first coordinate \(-\infty ^+\).
(2) Suppose the conclusion failed. Then, arguing as in Proposition 3.17, there would be a finite collection of rectangles \([-\infty , b_i] \times [c_i, d_i]\) of finite measure which together cover \(\{ -\infty \} \times [c,d]\). Then the rectangle \([-\infty ,\min (b_i)] \times [c,d]\) would have finite measure, contradicting the hypothesis. \(\square \)
Proposition 3.25
(1) If \(\mu (-\infty , +\infty )\) is finite, then it counts the multiplicity of \((-\infty ^+, +\infty ^-)\) in \({\mathsf {Dgm}}(\mu )\).
(2) If \(\mu (-\infty , +\infty )\) is infinite, then  .
.
Proof
Similar, but easier (especially (2)). \(\square \)
3.7 The Measure Persistence Diagram
We obtain the measure persistence diagrams of a persistence module \({\mathbb {V}}\) by defining its persistence measure \(\mu _{\mathbb {V}}\) on the extended half-plane \(\overline{\mathcal {H}}\).
Definition 3.26
(persistence measure in extended plane) Let \({\mathbb {V}}\) be a persistence module, and let \(-\infty \le a< b \le c < d \le +\infty \). We define

where for infinite rectangles we take \(V_{-\infty } = 0\) and \(V_{+\infty } = 0\) as needed.
It is easy to see (directly, or by using the arctan trick) that this extended version of \(\mu _{\mathbb {V}}\) satisfies the same properties as before: additivity, monotonicity, and so on . In particular, the alternating sum formula of Proposition 3.6 becomes:

The first of these corresponds to the ‘k-triangle lemma’ of [19].
In this way \(\mu _{\mathbb {V}}\) becomes an r-measure on the extended half-plane
with its diagram \({\mathsf {Dgm}}(\mu _{\mathbb {V}})\) defined on the subset of the r-interior

over which \(\mu _{\mathbb {V}}\) is finite. Proposition 3.2 and Corollary 3.5 extend straightforwardly to infinite rectangles:
Corollary 3.27
If \({\mathbb {V}}\) is decomposable into interval modules, then the measure \(\mu _{\mathbb {V}}(R)\) of any rectangle R in the extended half-plane precisely counts the interval summands corresponding to decorated points which lie in R. \(\square \)
Definition 3.28
Let \({\mathbb {V}}\) be a persistence module . Its measure persistence diagrams are the decorated diagram

and the undecorated diagram

We work in the extended half-plane, so that the finite r-interior and finite interior  ,
,  are subsets of
are subsets of  ,
,  , respectively. When
, respectively. When  ,
,  are clear from the context, we may allow ourselves to abuse notation and omit them.
are clear from the context, we may allow ourselves to abuse notation and omit them.
The relationship between the measure and decomposition diagrams is explained in the following proposition:
Proposition 3.29
If \({\mathbb {V}}\) is decomposable into intervals, then \(\mathsf {Int}({\mathbb {V}})\) agrees with \({\mathsf {Dgm}}(\mu _{\mathbb {V}})\) where the latter is defined, that is, on  .
.
Proof
By Corollary 3.27 we have
for all rectangles. On the other hand, we have
for all rectangles with \(\mu _{\mathbb {V}}(R) < \infty \). By uniqueness, it follows that \(\mathsf {Int}({\mathbb {V}})\) and \({\mathsf {Dgm}}(\mu _{\mathbb {V}})\) must be the same multiset when restricted to  . \(\square \)
. \(\square \)
Neither definition strictly outperforms the other, as the following examples show .
Example 3.30
(decomposition \(\ge \) measure) Let
where the undecorated pairs \((p_\ell , q_\ell )\) form a dense subset of the half-plane \(\overline{\mathcal {H}}\). Then \(\mathsf {Int}({\mathbb {V}})\) is defined; but \(\mu _{\mathbb {V}}(R) = \infty \) for every rectangle, so  is the empty set and \({\mathsf {Dgm}}(\mu _{\mathbb {V}})\) is nowhere defined.
is the empty set and \({\mathsf {Dgm}}(\mu _{\mathbb {V}})\) is nowhere defined.
Example 3.31
(measure \(\ge \) decomposition) We adapt the example of Webb [48], from our Theorem 2.8, to be indexed over \({\mathbf {R}}\). Let \({\mathbb {W}}\) be the persistence module with vector spaces
and maps \(w^s_t\) taken to be the canonical inclusion \(W_s \subseteq W_t\) when \(t \le 0\) and zero otherwise. This is not decomposable into intervals because its restriction to \(-{\mathbf {N}}\) is not decomposable into intervals (Theorem 2.8(3)). On the other hand, we have

except when \(a = -\infty \), and

except when \(c \le 0 < d\). Each of these terms dominates

which is therefore finite for all rectangles that do not contain \((-\infty ^+, 0^+)\). Thus, the measure persistence diagram \({\mathsf {Dgm}}(\mu _{\mathbb {W}})\) is defined everywhere except at that decorated point. We will complete the calculation of \({\mathsf {Dgm}}(\mu _{\mathbb {W}})\) in Sect. 3.10.
3.8 Tameness
We now describe several different levels of ‘tameness’ for a persistence module, beginning with the most docile.
-
A persistence module is of finite type if it is a direct sum of finitely many interval modules. This is the notion of tameness most commonly used in the persistence literature, either explicitly or by implication. Traditionally these modules have simply been called ‘tame’.
-
A persistence module is locally finite if it is a direct sum of interval modules, and satisfies the condition that any bounded subset of \({\mathbf {R}}\) meets only finitely many of the intervals. By a compactness argument, it is sufficient to require that every \(t \in {\mathbf {R}}\) has a neighbourhood which meets at most finitely many of the intervals.
-
A persistence module \({\mathbb {V}}\) is pointwise finite-dimensional (pfd) if each vector space \(V_t\) is finite dimensional. As indicated in Theorem 2.8, all such modules have been shown to admit an interval decomposition by Crawley-Boevey [25]. This class of modules is favoured in the work of Lesnick and Bauer [3, 42].
For a module \({\mathbb {V}}\) that is of finite type, locally finite, or pfd, it is easy to see that  . The measure and decomposition diagrams agree and are defined everywhere on \(\overline{\mathcal {H}}\), including on the diagonal and at infinity. Any diagonal points are decorated \((p^-,p^+)\), since only these belong to rectangles in \(\overline{\mathcal {H}}\).
. The measure and decomposition diagrams agree and are defined everywhere on \(\overline{\mathcal {H}}\), including on the diagonal and at infinity. Any diagonal points are decorated \((p^-,p^+)\), since only these belong to rectangles in \(\overline{\mathcal {H}}\).
We introduce four more kinds of tameness. The assumptions here concern the finiteness of \(\mu _{\mathbb {V}}\) over different types of rectangle: quadrants, horizontal strips, vertical strips, and bounded rectangles (Fig. 3.1). Each condition guarantees the existence of the persistence diagram over a certain subset of the extended half-plane. The finite part of the plane (except the diagonal) is always included; it is at infinity that the four conditions differ.
-
We say that \({\mathbb {V}}\) is q-tame, if \(\mu _{\mathbb {V}}(Q) < \infty \) for every quadrant Q not touching the diagonal. In other words

(that is, \({{\mathrm {r}}}^b_c < \infty \)) for all \(b < c\). The persistence diagram \({\mathsf {Dgm}}(\mu _{\mathbb {V}})\) is defined over the set:
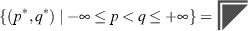
-
We say that \({\mathbb {V}}\) is h-tame, if \(\mu _{\mathbb {V}}(H) < \infty \) for every horizontally infinite strip H not touching the diagonal. In other words,

for all \(b< c < d\). The persistence diagram \({\mathsf {Dgm}}(\mu _{\mathbb {V}})\) is defined over the set:

-
We say that \({\mathbb {V}}\) is v-tame, if \(\mu _{\mathbb {V}}(V) < \infty \) for every vertically infinite strip V not touching the diagonal. In other words,

for all \(a< b < c\). The persistence diagram \({\mathsf {Dgm}}(\mu _{\mathbb {V}})\) is defined over the set:

-
We say that \({\mathbb {V}}\) is r-tame, if \(\mu _{\mathbb {V}}(R) < \infty \) for every finite rectangle R not touching the diagonal. In other words,

for all \(a< b< c < d\). The persistence diagram \({\mathsf {Dgm}}(\mu _{\mathbb {V}})\) is defined over the set:

Here is the diagram of implications between the different conditions:
One can show that all of the implications are ‘strict’, in the sense that they cannot be reversed; examples are easily found. The consequent implications
are also both strict; examples are suggested by the diagrams in Fig. 3.2. The second of these examples is no surprise, and a better question is this: does every r-tame module decompose as the direct sum of an h-tame module and a v-tame module? This is certainly true if the module is decomposable into intervals, but the general situation seems more subtle and we do not know the answer .
Remark 3.32
Later we show that the class of ‘q-tame’ modules may be interpreted as the closure of the class of ‘locally finite’ modules: a persistence module is q-tame if and only if it can be approximated arbitrarily well by locally finite modules. See Theorem 5.21.
3.9 Tameness (Continued)
Many naturally occurring persistence modules are q-tame, particularly those arising from persistent homology constructions on compact spaces. We consider some typical examples in this section, using algebraic topology arguments.
A general result of the following kind was published by Cagliari and Landi [6]:
Theorem 3.33
Let X be a compact polyhedron,Footnote 2 and let \(f: X \rightarrow {\mathbf {R}}\) be a continuous function. Then the persistent homology \( {\text {H}}({\mathbb {X}}_\mathrm {sub}) \) of the sublevelset filtration of (X, f) is q-tame.
Proof
For any \(b < c\) we must show that
has finite rank. Begin with any triangulation of X, and subdivide it repeatedly until no simplex meets both \(f^{-1}(b)\) and \(f^{-1}(c)\). If we define Y to be the union of the closed simplices which meet \(X^b\), then we have
and hence the factorisation
Since Y is a compact polyhedron, \({\text {H}}(Y)\) is finite dimensional and so \({\text {H}}(X^b) \rightarrow {\text {H}}(X^c)\) has finite rank. \(\square \)
Corollary 3.34
Let X be a locally compact polyhedron, and let \(f: X \rightarrow {\mathbf {R}}\) be a properFootnote 3 continuous function which is bounded below. Then \({\text {H}}({\mathbb {X}}_\mathrm {sub})\) is q-tame.
Proof
To show that \({\text {H}}(X^b) \rightarrow {\text {H}}(X^c)\) has finite rank, it is enough to find a compact subpolyhedron of X that contains \(X^c\), because we can then apply Theorem 3.33 in this subpolyhedron. Accordingly, choose a locally finite triangulation of X and consider the closed simplices that meet \(X^c\). There are only finitely many of them because \(X^c = f^{-1}[\min (f),c]\) is compact. The union of these simplices is the required subpolyhedron. \(\square \)
Corollary 3.35
(persistent homology of offsets) Let A be a nonempty compact subset of \(X = {\mathbf {R}}^n\) and let f be the ‘distance from A’ in some norm, so \(f(x) = \min _{a \in A} \Vert x - a \Vert \). It follows from Corollary 3.34 that \({\text {H}}({\mathbb {X}}_\mathrm {sub})\) is q-tame. \(\square \)
Sublevelsets of the ‘distance from A’ function are generally known as offsets of the compact set A in the given norm, and written \(A^\varepsilon = f^{-1}(-\infty , \varepsilon ]\). There is a rich body of results in the computational geometry literature which govern the topology of these offsets, usually for small \(\varepsilon \). These results generally assume that A is ‘sufficiently regular’, and indeed an important part of that work is to formulate effective regularity conditions that guarantee that offsets are well-behaved. In contrast, Corollary 3.35 tells us that no regularity conditions are needed to guarantee that the persistent homology be q-tame .
Remark 3.36
Under some circumstances, we can obtain stronger tameness results for offsets. If A is a polyconvex set—that is, a finite union of compact convex sets—then \({\text {H}}({\mathbb {X}}_\mathrm {sub})\) is of finite type. Indeed, the topology of the offsets can be modelled by a finite filtered simplicial complex, specifically the nerve of the family of offsets of the original convex sets. This works in any norm. On the other hand, the result does not extend to submanifolds. One can manufacture a smooth embedding of the circle in \({\mathbf {R}}^2\) such that the distance function has infinitely many critical points.
We can drop ‘bounded below’ in Corollary 3.34 without losing too much:
Theorem 3.37
Let X be a locally compact polyhedron, and let \(f: X \rightarrow {\mathbf {R}}\) be a proper continuous function. Then the persistent homology \( {\text {H}}({\mathbb {X}}_\mathrm {sub}) \) of the sublevelset filtration of (X, f) is h-tame and v-tame.
This means that \({\text {H}}({\mathbb {X}}_\mathrm {sub})\) can behave badly only at \((-\infty , +\infty )\). It is easy to construct examples which are definitely not q-tame. The simplest example is \(X = {\mathbf {Z}}\) (the integers), with \(f(n) = n\). The 0-homology of any sublevelset is infinite dimensional, and all inclusions have infinite rank.
Proof
(h-tameness) Let \(b< c < d\). We must show that

Begin with a triangulation of X. Only finitely many simplices meet the compact set \(f^{-1}(b)\), so again after a finite number of subdivisions no simplex meets both \(f^{-1}(b)\) and \(f^{-1}(c)\).
Now let Y be the union of the closed simplices which meet \(X^b\), and let Z be the union of the closed simplices which meet \(X^d\). This gives a diagram of inclusions
Note that the polyhedron Z differs from its subpolyhedron Y by the addition of only finitely many simplices, since each such simplex must meet the compact set \(f^{-1}[b,d]\). Thus the relative homology \({\text {H}}(Z,Y)\) is finite-dimensional.
We now work with the induced homology diagram
In the obvious notation,

By the homology long exact sequence for the pair (Z, Y), we have
which is finite-dimensional. This confirms (h-*).
v-tameness. Let \(a< b < c\). We must show that

Using a similar argument to the above, we construct a diagram of inclusions
where Y, Z are polyhedra with \({\text {H}}(Z,Y)\) finite-dimensional. Working with the homology diagram
we estimate

By the homology long exact sequence of the pair (Z, Y), we have
which is finite-dimensional. This confirms (v-*). \(\square \)
There are many other examples of naturally occurring q-tame modules. It is shown in [16] that the Vietoris–Rips and Čech complexes of a compact metric space have q-tame persistent homology. This is a situation where persistence is manifestly necessary, because such complexes can behave very badly at individual parameter values. For instance, J.-M. Droz [28] has constructed a compact metric space whose Vietoris–Rips complex has homology of uncountable dimension at uncountably many parameter values (indeed, over an entire interval). The construction is not at all pathological in appearance; see [16] for additional examples.
3.10 Vanishing Lemmas
Here are some easy lemmas that guarantee the vanishing of the persistence diagram in certain parts of the plane. These lemmas simplify the task of computing \({\mathsf {Dgm}}\), often reducing it to a few specific quiver calculations.
Lemma 3.38
Let \({\mathbb {V}}\) be a persistence module, and let \(s < t\).
-
(1)
The map \(v^s_t\) is surjective iff \({\mathsf {Dgm}}({\mathbb {V}})\) is empty in the rectangle \([s,t] \times [t,+\infty ]\).
-
(2)
The map \(v^s_t\) is injective iff \({\mathsf {Dgm}}({\mathbb {V}})\) is empty in the rectangle \([-\infty ,s] \times [s,t]\).
‘Empty’ means that the r-interior of the rectangle contains no points or singular points of \({\mathsf {Dgm}}({\mathbb {V}})\). See Fig. 3.3.
Metaphorically, the surjectivity of \(v^s_t\) tells us that every feature that survives to time t already existed at time s. Injectivity tells us that every feature that survives to time s remains alive time t. The small triangle between the two rectangles is the ‘wiggle-room’: new features may appear in the time interval (s, t) but must also disappear in the same time interval, and vice versa. The lemma makes these claims precise in terms of the persistence diagram.
Proof
Indeed,

the right-hand side of which is zero iff \(v^s_t\) is surjective; and

the right-hand side of which is zero iff \(v^s_t\) is injective. \(\square \)
In many situations the maps \(v^s_t\) are surjective or injective everywhere in some interval. The following lemma is stated carefully to give a sharp statement for all possible interval types (open, closed, half-open, infinite).
Lemma 3.39
Let \({\mathbb {V}}\) be a persistence module and let \(J = (p^*, q^*)\) be an interval.
-
(1)
The maps \((v^s_t \mid s,t \in J\, \text {with}\, s < t)\) are all surjective iff \({\mathsf {Dgm}}({\mathbb {V}})\) is empty in the vertical band
$$ \{ (x^*, y^*) \in \overline{\mathcal {H}}\mid x^* \in J \}. $$ -
(2)
The maps \((v^s_t \mid s,t \in J\, \text {with}\, s < t)\) are all injective iff \({\mathsf {Dgm}}({\mathbb {V}})\) is empty in the horizontal band
$$ \{ (x^*, y^*) \in \overline{\mathcal {H}}\mid y^* \in J \}. $$
(We recall from Eq. (2.3) that \(x^* \in J\) means \(p^*< x^* < q^*\).) See Fig. 3.4.
The shaded green band indicates the region where the persistence diagram is guaranteed to be empty when the maps \((v^s_t)\) over the interval J are: (left) surjective; (right) injective. Along each of the parallel boundary edges, vanishing of the diagram for points with inward ticks is guaranteed if J contains its corresponding endpoint
Proof
This follows from Lemma 3.38, since the vertical (resp. horizontal) band is the union, over \(s,t \in J\) with \(s < t\), of the r-interiors of the vertical (resp. horizontal) rectangles of the lemma. \(\square \)
We now calculate the persistence diagram for the example of Webb given earlier.
Example 3.40
(Continuation of Example 3.31) Recall that \({\mathbb {W}}\) was defined by setting
and taking \((w^s_t)\) to be the canonical inclusion maps or zero maps. We also take \(W_{-\infty } = W_{+\infty } = 0\) to allow uniform treatment of finite and infinite rectangles. Then the maps \((w^s_t)\) are surjective over the intervals
and injective over the intervals
so Lemma 3.39 allows only the possibilities
for \((x^*,y^*)\) that are points or singular points of \({\mathsf {Dgm}}({\mathbb {W}})\). We can determine the multiplicity of \((-n^+,0^+)\) by enclosing it in a rectangle that contains no other candidate points: say \([-n,-n+1] \times [0,+\infty ]\). Let \(\hat{{\mathbb {W}}}\) be the restriction
of \({\mathbb {W}}\) to the index set \(\{ -n, -n+1, 0\}\). Then

The fourth equality follows from the injectivity of \(W_{-n+1} \rightarrow W_0\), which implies that  vanishes.
vanishes.
The conclusion is that each \((-n^+,0^+)\) occurs exactly once in the persistence diagram. Finally, we have already seen that \((-\infty ^+,0^+)\) is a singular point of \(\mu _{\mathbb {W}}\).Footnote 4 All decorated points in \(\overline{\mathcal {H}}\) have been accounted for. See Fig. 3.5.
3.11 Vanishing Lemmas (Continued)
In this optional section, we provide a set of four infinitesimal vanishing lemmas to accompany the results of the previous section. These lemmas are expressed in terms of direct limits and inverse limits. The reader unfamiliar with these concepts from category theory may wish to consult a standard textbook, such as [43], for additional details and context.
We begin with the observation that any persistence module over the real line has a canonical extension to the totally ordered set
defined using direct limits and inverse limits in the category of vector spaces. Here are the constructions.
Definition 3.41
(extension to \(t^-\)) Let \({\mathbb {V}}\) be a persistence module and let \(t \in {\mathbf {R}}\). We define
This direct limit can be defined explicitly as the quotient of the direct sum vector space
by the subspace generated by all vectors of the form \(x_a \oplus - v^a_b (x_a) \in V_a \oplus V_b\) where \(a< b < t\).
Definition 3.42
(extension to \(t^+\)) Let \({\mathbb {V}}\) be a persistence module and let \(t \in {\mathbf {R}}\). We define
This inverse limit can be defined explicitly as the subspace of the product vector space
that comprises those product vectors \((x_a \mid a > t)\) satisfying the constraint \(x_b = v^a_b (x_a)\) whenever \(t< a < b\).
Note that for \(a< t < b\) there are canonical maps

induced, respectively, from the inclusion of \(V_a\) into the direct sum of (3.7) and from the projection of the product of (3.8) onto \(V_b\). We observe that
where the union is a nested union and the intersection is a nested intersection. In the other direction, there are canonical maps

resulting from the universal properties of direct and inverse limits stated below. It is not difficult to check that these maps, and their various composites with each other and with the maps \(v^s_t\), define an extension of the persistence module \({\mathbb {V}}\) to the index set \({\mathbf {R}}\cup {\mathbf {R}}^*\). The details are left to the reader.
Here are the universal properties that characterise these direct and inverse limits:
Proposition 3.43
(universal property of \(V_{t^-}\)) Given a vector space W and a family of linear maps \((f^a: V_a \rightarrow W \mid a < t)\) such that \(f^a = f^b v^a_b\) whenever \(a< b < t\), there is a unique linear map \(f: V_{t^-} \rightarrow W\) such that \(f_a = f v^a_{t^-}\) whenever \(a < t\).\(\square \)
Proposition 3.44
(universal property of \(V_{t^+}\)) Given a vector space U and a family of linear maps \((f_a: U \rightarrow V_a \mid a > t)\) such that \(f_b = v^a_b f_a\) whenever \(t< a < b\), there is a unique linear map \(f: U \rightarrow V_{t^+}\) such that \(f_a = v^{t^+}_a f\) whenever \(a > t\). \(\square \)
These universal properties are easily verified from the explicit definitions above. The following diagrams represent these properties schematically:

Double arrows indicate a system of maps that commute with the \((v^a_b)\).
Here is the main result of this section, stated in terms of the maps in (3.10).
Theorem 3.45
(infinitesimal vanishing lemmas) Let \({\mathbb {V}}\) be a q-tame persistence module, and let \(t \in {\mathbf {R}}\). In the following, restrict to \(p< t < q\).
-
(1)
If \(v^{t^-}_t\) is surjective then \({\mathsf {Dgm}}({\mathbb {V}})\) contains no points of the form \((t^-, q^*)\).
-
(2)
If \(v^{t^-}_t\) is injective then \({\mathsf {Dgm}}({\mathbb {V}})\) contains no points of the form \((p^*, t^-)\).
-
(3)
If \(v^t_{t^+}\) is surjective then \({\mathsf {Dgm}}({\mathbb {V}})\) contains no points of the form \((t^+, q^*)\).
-
(4)
If \(v^t_{t^+}\) is injective then \({\mathsf {Dgm}}({\mathbb {V}})\) contains no points of the form \((p^*, t^+)\).
The q-tameness assumption is needed for elementary numerical reasons in all four cases, and also for deeper structural reasons in the case of (3).
Proof
(1) Suppose \(t< c < q\). We will find \(a < t\) such that the rectangle \([a,t] \times [c, +\infty ]\) has measure zero. This will imply that \({\mathsf {Dgm}}({\mathbb {V}})\) does not contain \((t^-, q^*)\).
Using the sequence

and the surjectivity hypothesis,  , we calculate
, we calculate

It follows from the first assertion of (3.9) that
where the right-hand side is a nested union. Since the left-hand side is finite-dimensional, \({\mathbb {V}}\) being q-tame, it follows that there exists \(a < t\) such that
and for this a we have \(\mu _{\mathbb {V}}([a,t] \times [c, +\infty ]) = 0\) as required.
(2) Suppose \(p< b < t\). We will find c with \(b< c < t\) such that the rectangle \([-\infty ,b] \times [c,t]\) has measure zero. This will imply that \({\mathsf {Dgm}}({\mathbb {V}})\) does not contain \((p^*, t-)\). We use the sequence

and the injectivity hypothesis, \(\langle \text{[ }1.5em]{_{ {}}\bullet _{t^-}}\,\text{[ }1.3em]{---}\text{[ }1.3em]{_{ {}}\circ _{t}} \rangle = 0\), to calculate

analogously to the computation in (1). Note that this quantity is finite, since it is bounded by  . This time we use
. This time we use
which follows from the fact that any element of \(V_c\) that maps to zero in \(V_{t^-}\) must map to zero in some \(V_{c'}\) with \(c< c' < t\). Now the right-hand side is a nested increasing union of subspaces of finite codimension in the left-hand side. It follows that there exists \(c < t\) such that
therefore for this c we have \(\mu _{\mathbb {V}}([-\infty ,b] \times [c,t])\) as required.
(3) Suppose \(t< c < q\). We will find b with \(t< b < c\) such that the rectangle \([t,b] \times [c,+\infty ]\) has measure zero. This will imply that \({\mathsf {Dgm}}({\mathbb {V}})\) does not contain \((t^+, q^*)\). We use the sequence

and the surjectivity hypothesis \(\langle \text{[ }1.3em]{_{ {}}\circ _{t}} \text{[ }1.3em]{---}\, \text{[ }1.5em]{_{ {}}\bullet _{t^+}} \rangle \) to calculate

in the usual way. We now proceed to deduce
from the q-tameness of \({\mathbb {V}}\). Certainly the left-hand side is contained in the right-hand side. Conversely, suppose that \(x_c \in V_c\) lies in the image of every \(V_b\). We have to find a consistent family \((x_b \mid t < b \le c)\) of vectors \(x_b \in V_b\) which map to \(x_c\). It suffices to consider an arbitrary decreasing sequence \((b_i)\) that converges to t, and define a consistent family \((x_{b_i})\). We begin with \(b_0 = c\), and then recursively select \(x_{b_i} \in V_{b_i}\) so that \(x_{b_{i}}\) maps to \(x_{b_{i-1}}\) and is contained in the intersection of the subspaces \({\mathrm {im}}(v^b_{b_{i}})\) where \(t< b < b_i\). The crucial property is that each such nested decreasing family of images is eventually constant; this is the Mittag-Leffler condition, which is satisfied by q-tame modules because each image has finite dimension. Using this property, we set \(x_{b_i} = v^b_{b_i}(x_b)\) for some \(x_b\) mapping to \(x_{b_{i-1}}\) where b is sufficiently small that the nested images in \(V_{b_i}\) have stabilised.
With (3.13) established, the eventual constancy of the images on the right-hand side implies that there exists \(b > t\) such that
and for this b we have \(\mu _{\mathbb {V}}([t,b] \times [c,+\infty ]) = 0\) as required.
(4) Suppose \(p< b < t\). We will find \(d > t\) such that the rectangle \([-\infty ,b]\times [t,d]\) has measure zero. This will imply that \({\mathsf {Dgm}}({\mathbb {V}})\) does not contain the point \((p^*, t^+)\). We use the sequence

and the injectivity hypothesis,  , to calculate
, to calculate

as usual. This quantity is finite, being bounded by  . Now we use
. Now we use
which follows from the second assertion of (3.9). Since the codimension of the left-hand side is finite in any of the kernels on the right-hand side, this nested decreased family of kernels must eventually be constant. Thus there exists \(d > t\) such that
and for this d we have \(\mu _{\mathbb {V}}([-\infty ,b] \times [t,d]) = 0\) as required. \(\square \)
Remark 3.46
In the language of abelian categories, identities (3.11)–(3.14) result from the exactness properties of direct and inverse limits of vector spaces. Indeed, (3.11) and (3.12) follow from the right- and left-exactness of the direct-limit functor, and (3.14) follows from the left-exactness of the inverse-limit functor. The difficulty with (3.13) is that the inverse-limit functor is not right-exact. When \({\mathbb {V}}\) satisfies the Mittag-Leffler condition, however, the derived functor \({\varprojlim }{}^1\) evaluates to zero on \({\mathbb {V}}|_{(t,+\infty )}\) and restores right-exactness precisely where we need it.
We finish this section with two corollaries. The first of these originally appeared in Cerri et al. [12] as the assertion that certain ‘size functions’ are right-continuous.
Corollary 3.47
([12] Proposition 2.9) Let \({\mathbb {X}}_\mathrm {sub}\) be the sublevelset filtration of a pair (X, f) where X is a compact polyhedron, and let \(\check{\text {H}}= \check{\text {H}}_k(-;\mathbf {k})\) be a Čech homology functor.Footnote 5 Then the only points of \({\mathsf {Dgm}}(\check{\text {H}}({\mathbb {X}}_\mathrm {sub}))\) away from the diagonal are of the form \((p^-, q^-)\).
Proof
The q-tameness of \(\check{\text {H}}({\mathbb {X}}_\mathrm {sub})\) follows the proof of Theorem 3.33, since Čech homology agrees with simplicial homology on the intermediate polyhedron Y.
Chapter X, Theorem 3.1 of [32] implies that the natural map
is an isomorphism for every t. Parts (3) and (4) of Theorem 3.45 now constrain the off-diagonal points in the persistence diagram to negative decorations only. \(\square \)
Remark 3.48
In the compact ‘Morselike’ situations of Example 3.51, a stronger conclusion holds for simpler reasons and in any homology theory.
Corollary 3.49
Let \({\mathbb {X}}_\mathrm {sub}^\circ \) be the open sublevelset filtrationFootnote 6 of a pair (X, f) where X is a compact polyhedron, and let \({\text {H}}= {\text {H}}_k(-,\mathbf {k})\) be a singular homology functor. Then the only points of \({\mathsf {Dgm}}(\check{\text {H}}({\mathbb {X}}_\mathrm {sub}))\) away from the diagonal are of the form \((p^+, q^+)\).
Proof
The q-tameness of \({\text {H}}({\mathbb {X}}_\mathrm {sub}^\circ )\) follows the proof of Theorem 3.33, with the compact polyhedron Y equally well serving as an intermediate space between open sublevelsets.
Since singular simplices are compactly supported, the natural map
is an isomorphism for every t. Parts (1) and (2) of Theorem 3.45 now constrain the off-diagonal points in the persistence diagram to positive decorations only. \(\square \)
3.12 Finite Approximations
We finish this chapter by relating our measure-theoretic persistence diagrams to the diagrams constructed more traditionally, perhaps by computer, in situations of finite information.
We begin by noting that, away from its finite r-interior, a persistence measure gives only a limited view of the structure of its persistence module. For example:
-
It is not possible to distinguish between the many non-isomorphic persistence modules \({\mathbb {V}}\) for which \(\mu _{\mathbb {V}}\) is infinite on every rectangle.
-
If the persistence diagram of \({\mathbb {V}}\) contains a sequence of points \(( p^*_n, q^*_n )\) with \(p_n\) converging to r from below and \(q_n\) converging to r from above, then there is no way to determine the multiplicity of \(( r^-, r^+ )\) from the measure alone.
On the other hand, from \(\mu _{\mathbb {V}}\) we do recover all information obtainable by restricting \({\mathbb {V}}\) to finite subsets \({\mathbf {T}}\subset {\mathbf {R}}\). We may call this the ‘finitely observable’ part of \({\mathbb {V}}\). Specifically, for any finite index set
we can determine the interval decomposition of \({\mathbb {V}}_{\mathbf {T}}\) (the restriction of \({\mathbb {V}}\) to the index set \({\mathbf {T}}\)) in terms of the measure \(\mu _{\mathbb {V}}\). There are four plausible naming conventions for intervals in \({\mathbf {T}}\):
Here \(a_0, a_{n+1}\) are to be interpreted as \(-\infty , +\infty \) respectively. It is conventional in this setting, for reasons that we will come to shortly, to agree to adopt the second convention. Then we have

If we now draw the interval decomposition of \({\mathbb {V}}_{\mathbf {T}}\) as a persistence diagram, identifying the half-open intervals \([a_i,a_{j+1})\) with decorated points \((a_i^-, a_{j+1}^-)\) in the usual way, we find that \({\mathsf {Dgm}}({\mathbb {V}}_{\mathbf {T}})\) is obtained by ‘snapping’ each decorated point of \({\mathsf {Dgm}}({\mathbb {V}})\) upwards and rightwards to the grid determined by \({\mathbf {T}}\). Figure 3.6 illustrates this for the case \(n = 3\). This is the ‘snapping principle’ of [14, 15].
A persistence module \({\mathbb {V}}\) discretised at \({\mathbf {T}}= \{ a, b, c \}\). The persistence diagram \({\mathsf {Dgm}}({\mathbb {V}}_{{\mathbf {T}}})\) is localised at six grid vertices, corresponding to the six possible interval summands of a 3-index persistence module. The multiplicity of each vertex of \({\mathsf {Dgm}}({\mathbb {V}}_{{\mathbf {T}}})\) is equal to the number of decorated points of \({\mathsf {Dgm}}({\mathbb {V}})\) in the rectangle immediately below and to the left of it, and may be computed by evaluating \(\mu _{\mathbb {V}}\) on that rectangle. The tick directions indicate lower-closed half-open intervals. Decorated points of \({\mathsf {Dgm}}({\mathbb {V}})\) in the remaining triangular regions do not show up in \({\mathsf {Dgm}}({\mathbb {V}}_{{\mathbf {T}}})\)
There are some well known situations where the entire structure of \({\mathbb {V}}\) determined by its behaviour on a particular finite index set.
Definition 3.50
We say that \({\mathbb {V}}\) is Morselike if there exists a finite set of indices \({\mathbf {T}}= \{a_1, \dots , a_n\}\) such that \(v^s_t\) is an isomorphism whenever \(s < t\) belong to an interval \([a_i, a_{i+1})\) for some \(1 \le i \le n\), and also \(V_t = 0\) for \(t < a_1\).
When \({\mathbb {V}}\) is Morselike, it follows from Lemma 3.39 that if \((x^*,y^*)\) is a point or singular point of \({\mathsf {Dgm}}({\mathbb {V}})\) then
The possibility that \(x^* = -\infty ^+\) is ruled out by the vanishing of \({\mathbb {V}}\) below \(a_1\). The remaining candidates are the points \((a_i^-, a_{j+1}^-)\) with \(1 \le i \le j \le n\). Similarly to Example 3.40, we compute the multiplicity of each candidate by finding a rectangle that contains that candidate alone:
Thus \({\mathsf {Dgm}}({\mathbb {V}}) = {\mathsf {Dgm}}({\mathbb {V}}_{{\mathbf {T}}})\) exactly, provided we use the half-open convention for intervals in \({\mathbf {T}}\) that we agreed on earlier.
Example 3.51
The sublevelset persistent homology \({\text {H}}({\mathbb {X}}_\mathrm {sub})\) of a pair (X, f) is Morselike if
-
X is a compact manifold and f is a Morse function; or
-
X is a compact polyhedron and f is piecewise linear.
Indeed, let \({\mathbf {T}}\) be the set of critical points of the Morse function, or the set of vertex-values of the piecewise-linear function. Then the inclusion \(X^{a_i} \subseteq X^{t}\) is a homotopy equivalence whenever \(t \in [a_i, a_{i+1})\), so \({\text {H}}(X^s) \rightarrow {\text {H}}(X^t)\) is an isomorphism whenever \(s < t\) belong to the same half-open interval \([a_i, a_{i+1})\).
Remark 3.52
Compare Example 3.51 with Corollary 3.47.
Example 3.53
Let S be a finite simplicial complex, and let \(f: S \rightarrow {\mathbf {R}}\) be a function on its simplices such that \(f(\sigma ) \le f(\tau )\) whenever \(\sigma \le \tau \). This defines a nested family \(\mathbb {S}\) of simplicial complexes
and their inclusions. Then \({\text {H}}(\mathbb {S})\) is Morselike with respect to the index set \({\mathbf {T}}= f(S)\), since \(S^t\) is constant over each half-open interval \([a_i, a_{i+1})\). This class of examples occurs frequently in topological data analysis; the Vietoris–Rips filtration of a finite metric space is perhaps the most commonly used. The classical algorithms [30, 50] take (S, f) as their input and return the summands of \({\text {H}}(\mathbb {S})\) as a list of half-open intervals .
Notes
- 1.
As before, this does not rule out accumulation points on the boundary of
 .
. - 2.
By ‘polyhedron’ we mean the realisation of a simplicial complex as a topological space. A compact (resp. locally compact) polyhedron is the realisation of a finite (resp. locally finite) complex.
- 3.
By ‘proper’ we mean that the preimage \(f^{-1}(K)\) of every compact set \(K \subset {\mathbf {R}}\) is compact.
- 4.
In retrospect it’s even clearer: any rectangle containing \((-\infty ^+,0^+)\) must also contain infinitely many of the points \((-n^+,0^+)\) that we have calculated to have multiplicity 1, and therefore must have infinite measure.
- 5.
The theory of Čech homology is described in detail by Eilenberg and Steenrod [32].
- 6.
The spaces are the open sublevelsets \(X^t_\circ = f^{-1}(-\infty ,t)\) and the maps are their inclusions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2016 The Author(s)
About this chapter
Cite this chapter
Chazal, F., de Silva, V., Glisse, M., Oudot, S. (2016). Rectangle Measures. In: The Structure and Stability of Persistence Modules. SpringerBriefs in Mathematics. Springer, Cham. https://doi.org/10.1007/978-3-319-42545-0_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-42545-0_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-42543-6
Online ISBN: 978-3-319-42545-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 . ‘Locally finite’ means that
. ‘Locally finite’ means that  such that
such that 

 , where
, where  described in Theorem
described in Theorem 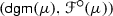 , where
, where 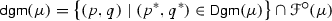
 obtained by forgetting the decorations in
obtained by forgetting the decorations in 

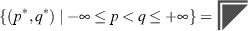











 .
.