Abstract
This chapter introduces the basic properties of persistence modules. These can be defined over any partially ordered set; we are primarily interested in persistence modules over the real line or over a finite subset of the real line. In the best cases, a persistence module can be expressed as a direct sum of ‘interval modules’, the atomic building blocks of the theory. We introduce decorated real numbers to distinguish open and closed endpoints of real intervals. Not every persistence module is decomposable into interval modules, so we spend much of the monograph developing techniques that bypass this assumption. These techniques depend on a thorough understanding of certain finitely-indexed persistence modules known as \(A_n\) quiver representations. We develop the necessary algebraic tools, including a special ‘quiver calculus’ notation to facilitate the computation of numerical invariants of quiver representations.
Access provided by Autonomous University of Puebla. Download chapter PDF
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
All vector spaces are taken to be over an arbitrary field \(\mathbf {k}\), fixed throughout.
2.1 Persistence Modules Over a Real Parameter
A persistence module \({\mathbb {V}}\) over the real numbers \({\mathbf {R}}\) is defined to be an indexed family of vector spaces
and a doubly-indexed family of linear maps
which satisfy the composition law
whenever \(r \le s \le t\), and where \(v_t^t\) is the identity map on \(V_t\).
Remark 2.1
Equivalently, a persistence module is a functor [43] from the real line (viewed as a category with a unique morphism \(s \rightarrow t\) whenever \(s \le t\)) to the category of vector spaces. The uniqueness of the morphism \(s \rightarrow t\) corresponds to the fact that all possible compositions
from \(V_s\) to \(V_t\) are equal to each other, and in particular to \(v^s_t\).
Here is the standard class of examples from topological data analysis. Let X be a topological space and let \(f : X \rightarrow {\mathbf {R}}\) be a function (not necessarily continuous). Consider the sublevelsets:
The inclusion maps \( (i^s_t: X^s \rightarrow X^t \mid s \le t) \) trivially satisfy the composition law and the identity map condition. Collectively this information is called the sublevelset filtration of (X, f ) and we call it \({\mathbb {X}}_\mathrm {sub}\) or \({\mathbb {X}}^f_\mathrm {sub}\).
Remark 2.2
Here we are using closed sublevelsets \(\{ x \in X \mid f(x) \le t \}\), but one might instead choose to work with open sublevelsets \(\{ x \in X \mid f(x) < t \}\).
We can obtain a persistence module by applying to this filtration any functor from topological spaces to vector spaces. For example, let \({\text {H}}= {\text {H}}_k(-; \mathbf {k})\) be the functor ‘k-dimensional singular homology with coefficients in \(\mathbf {k}\)’. We define a persistence module \({\mathbb {V}}\) by setting
using the fact that functors operate on maps as well as objects. We can express this definition concisely by writing \({\mathbb {V}}= {\text {H}}({\mathbb {X}}_\mathrm {sub})\).
In the applied topology literature, there are many examples (X, f) whose persistent homology is of interest. Very often X is a finite simplicial complex and each \(X^t\) is a subcomplex. It follows that the vector spaces \({\text {H}}(X^t)\) are finite-dimensional; and as t increases there are finitely many ‘critical values’ at which the complex changes, growing by one or more new cells. Suppose these critical values are
Then all the information in the persistence module is contained in the finite diagram
of finite-dimensional vector spaces and linear maps. In this situation,
-
the isomorphism type of \({\text {H}}({\mathbb {X}}_\mathrm {sub})\) admits a compact description [30, 50];
-
there is a fast algorithm for computing this description [30, 50];
-
the description is continuous (indeed 1-Lipschitz) with respect to f [19].
This description is the famous persistence diagram, or barcode. It encodes the structure of the diagram as a list of intervals of the form \([b,d) = [a_i,a_j)\) or \([a_i, +\infty )\). Each such interval represents a ‘feature’ that is ‘born’ at b and ‘dies’ at d.
There are good grounds for extending the results of [30, 50, 19] beyond the case of finite diagrams. For example, theoretical guarantees are commonly formulated in terms of an idealised model; for instance the sampled data may be an approximation to an underlying continuous space. Finiteness becomes unnatural and difficult to enforce in these ideal models, but one still wants the main results to be true.
Here is (what we believe to be) a good notion of tameness: a persistence module \({\mathbb {V}}\) is q-tame if
The definition is taken from [15], where such modules are simply called ‘tame’. Since that word is overloaded with too many different meanings in the persistence literature, we say ‘q-tame’ instead (see Sect. 3.8 for the etymology).
It is shown in [15] that persistence diagrams can be constructed for q-tame persistence modules, and that these diagrams are stable with respect to certain natural metrics. We reproduce these results here, using different methods for many of the arguments. We complete the picture by showing that the map from q-tame persistence modules to persistence diagrams is an isometry. This isometry theorem is due to Lesnick [42].
We believe that q-tame persistence modules are a good class of objects for two complementary reasons: (i) we can prove almost everything we want to prove about q-tame modules and their persistence diagrams; and (ii) they occur in practice. For example, a continuous function on a finite simplicial complex has q-tame sublevelset persistent homology (Theorem 3.33). See [16] for many other examples.
2.2 Index Posets
We can define a persistence module over any partially ordered set, or poset, \({\mathbf {T}}\), in the same way as for \({\mathbf {R}}\), by specifying indexed families
of vector spaces and linear maps, for which \(v^s_t \circ v^r_s = v^r_t\) whenever \(r \le s \le t\), and where \(v_t^t\) is the identity on \(V_t\) . The resulting collection of data is called a \({\mathbf {T}}\) -persistence module or a persistence module over \({\mathbf {T}}\).
If \({\mathbb {V}}\) is a \({\mathbf {T}}\)-persistence module and \({\mathbf {S}}\subset {\mathbf {T}}\), then we get an \({\mathbf {S}}\)-persistence module by considering only those spaces and maps with indices in \({\mathbf {S}}\). This is the restriction of \({\mathbb {V}}\) to \({\mathbf {S}}\), and may be written \({\mathbb {V}}_{\mathbf {S}}\) or \({\mathbb {V}}|_{\mathbf {S}}\). Most commonly, we work with finite subsets \({\mathbf {T}}\subset {\mathbf {R}}\). We collect information about an \({\mathbf {R}}\)-persistence module by considering its restriction to different finite subsets. This works well because persistence modules over \(\{1,2,\dots ,n\}\) are well understood.
In Chap. 4, we make use of certain posets that are subsets of \({\mathbf {R}}^2\).
2.3 Module Categories
A homomorphism \(\varPhi \) between two \({\mathbf {T}}\)-persistence modules \({\mathbb {U}}, {\mathbb {V}}\) is a collection of linear maps \( ( \phi _t : U_t \rightarrow V_t \mid t \in {\mathbf {T}}) \) such that the diagram

commutes for all \(s \le t\). Composition is defined in the obvious way, as are identity homomorphisms. This makes the collection of persistence modules into a category. The category contains kernel, image, and cokernel objects for every map \(\varPhi \), and there is a zero object. Write
Note that \({\text {End}}({\mathbb {V}})\) is a \(\mathbf {k}\)-algebra. Later we consider homomorphisms that shift the index, in order to define the interleaving relation between persistence modules.
2.4 Interval Modules
The building blocks of persistence are the interval modules . One seeks to understand a persistence module by decomposing it into intervals. This is not always possible, but it is sufficiently possible for our purposes.
An interval in a totally ordered set \({\mathbf {T}}\) is a subset \(J \subseteq {\mathbf {T}}\) such that if \(r \in J\) and \(t \in J\) and \(r< s < t\) then \(s \in J\). For any nonempty interval \(J \subseteq {\mathbf {T}}\), the interval module \({\mathbb {I}}= \mathbf {k}^J\) is defined to be the \({\mathbf {T}}\)-persistence module with vector spaces
and linear maps
In informal language, the module \(\mathbf {k}^J\) represents a ‘feature’ which ‘persists’ over exactly the interval J and nowhere else. We write \(\mathbf {k}^J_{\mathbf {T}}\) when we wish to name the index set explicitly.
Intervals in a finite set \({\mathbf {T}}= \{a_0< a_1< \dots < a_n\}\) are usually written as closed intervals \([a_i, a_j]\), and sometimes as half-open intervals \([a_i, a_{j+1})\) with the convention that \(a_{n+1} = +\infty \). We often lower the superscript when naming the corresponding modules, writing \(\mathbf {k}[a_i,a_j]\) rather than \(\mathbf {k}^{[a_i,a_j]}\) for ease of reading.
Intervals in the real line \({\mathbf {R}}\) merit a special notation of their own. Each non-empty real interval has endpoints (possibly \(\pm \infty \)) defined by its infimum and supremum, and it may or may not attain its finite endpoints. To distinguish the various cases, we introduce decorated reals , written as ordinary real numbers with a superscript \(^+\) (plus) or \(^-\) (minus). For finite intervals we adopt the following dictionary :
We require \(p < q\) except for the special case \(( r^-, r^+ )\) which represents the 1-point interval [r, r]. For infinite intervals we use the symbols \(-\infty ^+\) and \(+\infty ^-\):
When we wish to refer to a decorated number but don’t know what the decoration is, we use an asterisk. Thus \(p^*\) means \(p^+\) or \(p^-\).
The collection of decorated and undecorated numbers is totally ordered by setting
for all \(p < q\) . One advantage of doing this is that nonempty real intervals now correspond exactly to pairs \((p^*, q^*)\) such that \(-\infty< p^*< q^* < +\infty \), with the single statement
uniformly replacing the nine dictionary definitions given above. Sometimes it is helpful to extend membership of a real interval to decorated real numbers. We adopt the convention that
for any \(t^*\) and \((p^*,q^*)\). The interval itself continues to be a set of undecorated real numbers; we are simply overloading the symbol ‘\(\in \)’ with an additional meaning.
We finish with some visual conventions for interval modules over \({\mathbf {R}}\). Let

be the half-plane of points in \({\mathbf {R}}^2\) which lie on or above the diagonal. A finite interval module \(\mathbf {k}{( p^*, q^* )}\) may be represented in several different ways (see Fig. 2.1):
-
as an interval in the real line;
-
as a function
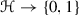 , defined by \((s,t) \mapsto {\mathrm {rank}}(i^s_t)\);
, defined by \((s,t) \mapsto {\mathrm {rank}}(i^s_t)\); -
as a point (p, q) in
 , with a tick to specify the decoration.
, with a tick to specify the decoration.
Here are the four tick directions explicitly :

The convention is that the tick points into the quadrant suggested by the decorations. We can represent infinite intervals by working in the extended half-plane

This can be drawn schematically as a triangle; see Fig. 2.2.
Remark 2.3
Persistence diagrams have traditionally been drawn without ticks. This is adequate for most purposes, and indeed in most traditional examples the intervals that occur are half-open intervals \([p,q) = (p^-, q^-)\) and there is no need to consider other possibilities. In the present work, the extra precision provided by decorations is essential to the correspondence between diagrams and measures.
2.5 Interval Decomposition
The direct sum \({\mathbb {W}}= {\mathbb {U}}\oplus {\mathbb {V}}\) of two persistence modules \({\mathbb {U}}, {\mathbb {V}}\) is defined as follows :
This generalises immediately to arbitrary (finite or infinite) direct sums.
A persistence module \({\mathbb {W}}\) is indecomposable if the only decompositions \({\mathbb {W}}= {\mathbb {U}}\oplus {\mathbb {V}}\) are the trivial decompositions \({\mathbb {W}}\oplus 0\) and \(0 \oplus {\mathbb {W}}\).
Direct sums play both a synthetic role and an analytic role in our theory. On the one hand, given an indexed family of intervals \(\left( J_\ell \mid \ell \in L \right) \) we can synthesise a persistence module
whose isomorphism type depends only on the multiset \(\{ J_\ell \mid \ell \in L \}\). In light of the direct-sum decomposition, we can think of \({\mathbb {V}}\) as having an independent feature for each \(\ell \in L\), supported over the interval \(J_\ell \). On the other hand, we can attempt to analyse a given persistence module \({\mathbb {V}}\) by decomposing it into submodules isomorphic to interval modules.
Remark 2.4
The decomposition of a persistence module is frequently described in metaphorical terms. The index \(t \in {\mathbf {R}}\) is interpreted as ‘time’. Each interval summand \(\mathbf {k}^J\) represents a ‘feature’ of the module which is ‘born’ at time \(\inf (J)\) and ‘dies’ at time \(\sup (J)\).
We now present the necessary theory. A ‘building block’ in a module category can be characterised by having a comparatively simple endomorphism ring. Interval modules have the simplest possible:
Proposition 2.5
Let \({\mathbb {I}}= \mathbf {k}^J_{\mathbf {T}}\) be an interval module over \({\mathbf {T}}\subseteq {\mathbf {R}}\); then \({\text {End}}({\mathbb {I}}) = \mathbf {k}\).
Proof
Any endomorphism of \({\mathbb {I}}\) acts on each nonzero \(I_t = \mathbf {k}\) by scalar multiplication. By the commutative square for morphisms, it is the same scalar for each t. \(\square \)
Proposition 2.6
Interval modules are indecomposable.
Proof
Given a decomposition \({\mathbb {I}}= {\mathbb {U}}\oplus {\mathbb {V}}\), the projection maps onto \({\mathbb {U}}\) and \({\mathbb {V}}\) are idempotent endomorphisms.Footnote 1 The only idempotents in \({\text {End}}({\mathbb {I}}) = \mathbf {k}\) are 0 and 1. \(\square \)
Theorem 2.7
(Krull–Remak–Schmidt–Azumaya) Suppose a persistence module over \({\mathbf {T}}\subseteq {\mathbf {R}}\) can be expressed as a direct sum of interval modules in two different ways:
Then there is a bijection \(\sigma : L \rightarrow M\) such that \(J_\ell = K_{\sigma (\ell )}\) for all \(\ell \).
Proof
This is from Azumaya [2] (Theorem 1), along with the trivial observation that \(\mathbf {k}^J \cong \mathbf {k}^K\) implies \(J = K\). The theorem requires a ‘locality’ condition on the endomorphism ring of each possible interval module: if \(\alpha , \beta \in {\text {End}}({\mathbb {I}})\) are non-isomorphisms then \(\alpha +\beta \) is a non-isomorphism. Since each \({\text {End}}({\mathbb {I}}) = \mathbf {k}\), the only non-isomorphism is the zero map and the condition is satisfied. \(\square \)
In other words, provided we can decompose a given persistence module \({\mathbb {V}}\) as a direct sum of interval modules, then the multiset of intervals is an isomorphism invariant of \({\mathbb {V}}\). But when does such a decomposition exist?
Theorem 2.8
(Gabriel, Auslander, Ringel–Tachikawa, Webb, Crawley-Boevey) Let \({\mathbb {V}}\) be a persistence module over \({\mathbf {T}}\subseteq {\mathbf {R}}\). Then \({\mathbb {V}}\) can be decomposed as a direct sum of interval modules in either of the following situations:
-
(1)
\({\mathbf {T}}\) is a finite set; or
-
(2)
each \(V_t\) is finite-dimensional.
On the other hand, (3) there exists a persistence module over \({\mathbf {Z}}\) (indeed, over the nonpositive integers) which does not admit an interval decomposition.
Proof
(1) The decomposition of a diagram
into interval summands, when each \(\dim (V_i)\) is finite, is one of the simpler instances of Gabriel’s theorem [35]; see [50] or [8] for a concrete explanation. The extension to infinite-dimensional modules follows abstractly from a theorem of Auslander [1] and, independently, Ringel and Tachikawa [47]. Alternatively, observe that the argument given in [8] does not require finite-dimensionality (although it is presented as such).
(2) The result for \({\mathbf {T}}= {\mathbf {Z}}\), and therefore for any locally finite \({\mathbf {T}}\subset {\mathbf {R}}\), follows from Propositions 2 and 3 and Theorem 3 of Webb [48]. This was generalised to \({\mathbf {T}}= {\mathbf {R}}\), and therefore to any \({\mathbf {T}}\subseteq {\mathbf {R}}\), more recently by Crawley-Boevey [25].
(3) Webb [48] gives this example, indexed over the nonpositive integers \(-{\mathbf {N}}\):
The \(w^{-m}_{-n}\) are taken to be the canonical inclusion maps. We can succinctly describe this module as an infinite product \({\mathbb {W}}= \prod _{n \ge 0} \mathbf {k}[-n,0]\).
Suppose \({\mathbb {W}}\) has an interval decomposition. Since each map \(w^{-n-1}_{-n}\) is injective, all of the intervals must be of the form \([-n,0]\) or \((-\infty ,0]\). The multiplicity of \([-n,0]\) may then be calculated as \(\dim (W_{-n}/W_{-n-1}) = 1\). The multiplicity of \((-\infty ,0]\) is zero, because any summand of that type requires a nonzero element of \(W_0\) that is in the image of \(w^{-n}_0\) for all \(n \ge 0\), but \(\bigcap _{n \ge 0} W_{-n} = \{0\}\) so such an element doesn’t exist. All of this implies that \({\mathbb {W}}\cong \bigoplus _{n \ge 0} \mathbf {k}{[-n,0]}\). This contradicts the fact that \(\dim (W_0)\) is uncountableFootnote 2 so \({\mathbb {W}}\) does not admit an interval decomposition after all. \(\square \)
In Examples 3.31 and 3.40, we show what we can do with the Webb module.
Remark 2.9
Here are other examples of persistence modules that lack an interval decomposition . Crawley-Boevey [24] proposed the infinite product \(\prod _{n \ge 1} \mathbf {k}[0,1/n]\). A dimension count implies that any interval decomposition must include uncountably many copies of \(\mathbf {k}[0,0]\), but this contradicts the fact that \(\bigcap _{t>0} {\mathrm {ker}}(v^0_t)\) is trivial . Nor is uncountable dimensionality a necessary feature. Lesnick [41] proposed the following example that has countable dimension at every index in \(-{\mathbf {N}}\):
The \(\ell ^{-m}_{-n}\) are taken to be the canonical inclusion maps when \(n \ge 1\), while \(\ell ^{-m}_0\) is the ‘augmentation map’ which takes the sum of the entries of the sequence. Given an interval decomposition, consider the unique summand that meets \(L_0\) nontrivially. We can rule out \(\mathbf {k}(-\infty ,0]\) since \(\bigcap _{n \ge 1} L_{-n} = \{0\}\), so it is isomorphic to some \(\mathbf {k}[-m,0]\). No other summands reach \(L_0\), so \(\ell ^{-m-1}_0\) must be the zero map; but it isn’t.
For a persistence module which decomposes into intervals, the way is now clear to define its persistence diagram: it is simply the list of intervals, with multiplicity, that occur in the decomposition. Theorem 2.7 tells us that this multiset is an isomorphism invariant.
Given that an arbitrary persistence module over \({\mathbf {R}}\) is not guaranteed an interval decomposition, here are three possible ways to proceed:
-
Work in restricted settings to ensure that the structure of \({\mathbb {V}}\) depends only on finitely many index values \(t \in {\mathbf {R}}\). For example, if X is a compact manifold and f is a Morse function, then \({\text {H}}({\mathbb {X}}_\mathrm {sub})\) is determined by the finite sequence
$$ {\text {H}}(X^{a_1}) \longrightarrow {\text {H}}(X^{a_2}) \longrightarrow \dots \longrightarrow {\text {H}}(X^{a_n}) $$where \(a_1, a_2, \dots , a_n\) are the critical values of f. This is the traditional approach. In this setting, the word ‘tame’ typically refers to pairs (X, f) for which \({\text {H}}({\mathbb {X}}_\mathrm {sub})\) is determined by a finite diagram of finite-dimensional vector spaces.
-
Sample the persistence module \({\mathbb {V}}\) over a finite grid. Consider limits as the grid converges to the whole real line. This is the strategy adopted in [15], where it is shown that the q-tame hypothesis is sufficient to guarantee good limiting behaviour.
-
Show that the persistence intervals (in the decomposable case) can be inferred from the behaviour of \({\mathbb {V}}\) on finite index sets.Footnote 3 Apply this indirect definition to define the persistence diagram in the non-decomposable case. This is the method of ‘rectangle measures’ developed in this monograph.
The first method is adequate for computational applications, at least on a first pass. The second and third methods both entail a certain amount of analytic work. The advantage of the third method is that this work is black-boxed as a technical result (Theorem 3.12) that allows one to move freely between rectangle measures and their corresponding persistence diagrams. The end-user is protected from the analytic details.
2.6 The Decomposition Persistence Diagram
If a persistence module \({\mathbb {V}}\) indexed over \({\mathbf {R}}\) can be decomposed
then we define the decorated persistence diagram to be the multiset
and the undecorated persistence diagram to be the multiset
where \(\varDelta = \{ (r,r) \mid r \in {\mathbf {R}}\}\) is the diagonal in the plane.
These are the decomposition persistence diagrams. In Sect. 3.7 we give a different definition of persistence diagrams based on the persistence measure. Often they coincide, but occasionally we need to distinguish them. In that case we use the alternate names \(\mathsf {Int}, \mathsf {int}\) for the diagrams defined here.
Theorem 2.7 implies that \(\mathsf {Dgm}({\mathbb {V}})\) and \(\mathsf {dgm}({\mathbb {V}})\) are independent of the choice of decomposition of \({\mathbb {V}}\). Notice that \(\mathsf {Dgm}\) is a multiset of decorated points in  , whereas \(\mathsf {dgm}\) is a multiset of undecorated points in the interior of
, whereas \(\mathsf {dgm}\) is a multiset of undecorated points in the interior of  . Here ‘interior’ means that we exclude the diagonal but keep the points at infinity. The information retained by \(\mathsf {dgm}\) is the information we care about later when we discuss bottleneck distances. See Chap. 5.
. Here ‘interior’ means that we exclude the diagonal but keep the points at infinity. The information retained by \(\mathsf {dgm}\) is the information we care about later when we discuss bottleneck distances. See Chap. 5.
A traditional example. Left: X is a smoothly embedded curve in the plane, and f is its y-coordinate or ‘height’ function. Right: The decorated persistence diagram of \({\text {H}}({\mathbb {X}}_\mathrm {sub})\): there are three intervals in \({\text {H}}_0\) (blue dots, marked 0) and one interval in \({\text {H}}_1\) (red dot, marked 1)
Example 2.10
Consider the curve in \({\mathbf {R}}^2\) shown in Fig. 2.3, filtered by the height function. The topology (that is, the homotopy type) of the sublevelsets of f is empty over \((-\infty , a)\) and constant over the intervals [a, b), [b, c), [c, d), [d, e), [e, f) and \([f,+\infty )\), so it is enough to consider the 6-term persistence modules obtained by restricting \({\text {H}}_*({\mathbb {X}}_\mathrm {sub})\) to the six critical values.

To decompose the \({\text {H}}_0\) diagram we need knowledge of the maps. Let [a], [b], [d] denote the 0-homology classes associated to the connected components born at times a, b, d respectively. When two components merge at index c we get the relation \([a]=[b]\). This becomes \([a]=[b]=[d]\) at index e. It follows that \({\text {H}}_0({\mathbb {X}}_\mathrm {sub})\) decomposes as follows.

The generator of each summand is shown on the left. Each generator has precisely the lifetime indicated by its interval module, and at each index the existing surviving generators form a basis for the homology at that index.
The 1-homology is already an interval module with no further decomposition necessary. It is generated by the 1-cycle [f] which appears at index f:

It follows that the full persistent homology of \({\mathbb {X}}_\mathrm {sub}\) looks like this:
The decorated persistence diagram is drawn in Fig. 2.3.
Remark 2.11
For a Morse function on a compact manifold with critical values \((a_i)\), the intervals are always half-open, of type \([a_i,a_j) = ( a_i^-,a_j^- )\), since the homotopy type of the sublevelsets is constant over the intervals \([a_i,a_{i+1})\). Compare Sect. 3.12. The persistence algorithm of Edelsbrunner, Letscher and Zomorodian [30], later presented in general form by Zomorodian and Carlsson [50], computes the interval decomposition and therefore persistence diagram for any example of this type.
Remark 2.12
Because of torsion phenomena in homology, different choices of field \(\mathbf {k}\) can lead to different persistence diagrams for a given geometric object.
2.7 Quiver Calculations
We now set up the notation and algebraic tools for handling persistence modules over a finite index set.
A persistence module \({\mathbb {V}}\) indexed over a finite subset
of the real line can be thought of as a diagram of n vector spaces and \(n-1\) linear maps:
Such a diagram is a representation of the following quiver:
We have seen (Theorem 2.8) that \({\mathbb {V}}\) decomposes as a finite sum of interval modules \(\mathbf {k}{[a_i, a_j]}\). When n is small, we can represent these interval modules pictorially. The following example illustrates how.
Example 2.13
Let \(a< b < c\). There are six interval modules over \(\{a,b,c\}\), namely:

A filled circle \(\bullet \) indicates a copy of the 1-dimensional vector space \(\mathbf {k}\); an empty circle \(\circ \) indicates the zero vector space. A map between two filled circles is always the identity; all other maps are by necessity zero.
Now let \({\mathbb {V}}\) be a persistence module indexed over \({\mathbf {R}}\). For any finite set of indices
and any interval \([a_i,a_j] \subseteq {\mathbf {T}}\), we define the multiplicity of \([a_i,a_j]\) in \({\mathbb {V}}_{\mathbf {T}}\) to be the number of copies of \(\mathbf {k}{[a_i,a_j]}\) to occur in the interval decomposition of \({\mathbb {V}}_{\mathbf {T}}\). This takes values in the set \(\{0, 1, 2, \dots , \infty \}\). (We do not distinguish different infinite cardinals.)
It is useful to have notation for these multiplicities. Again, we define by example.
Example 2.14
We write

for the multiplicity of  in the following 3-term module:
in the following 3-term module:
When \({\mathbb {V}}\) is clear from the context, we may simply write

The abbreviation \(\langle [b,c] \rangle \) is not permitted since it is ambiguous. For example, \(\langle [b,c] \mid {\mathbb {V}}_{b,c} \rangle \) and \(\langle [b,c] \mid {\mathbb {V}}_{a,b,c} \rangle \) are not generally the same. See Proposition 2.17 and Example 2.18.
Example 2.15
The invariants of a single linear map \(V_a \mathop {\longrightarrow }\limits ^{v} V_b\) are:

To see this when \(V_a, V_b\) are finite dimensional, observe that by elementary linear algebra we can find bases
for \(V_a\) and \(V_b\) respectively, such that \(v(e_i) = e'_i\) and \(v(f_j) = 0\) for all i, j. The basis elements define a decomposition of the module \((V_a \mathop {\longrightarrow }\limits ^{v} V_b )\) into interval summands of the three types
which are respectively isomorphic to  and
and  and
and  .
.
Proposition 2.16
(direct sums) Suppose a persistence module \({\mathbb {V}}\) can be written as a direct sum
Then
for any index set \({\mathbf {T}}= \{a_1, a_2, \dots , a_n\}\) and interval \([a_i,a_j] \subseteq {\mathbf {T}}\).
Proof
Each summand \({\mathbb {V}}^\ell _{\mathbf {T}}\) can be decomposed separately into interval modules. Putting these together we get an interval decomposition of \({\mathbb {V}}_{\mathbf {T}}\). The number of summands of a given type in \({\mathbb {V}}_{\mathbf {T}}\) is then equal to the total number of summands of that type in all of the \({\mathbb {V}}^\ell _{\mathbf {T}}\). \(\square \)
Often we wish to compare multiplicities of intervals in different finite restrictions of \({\mathbb {V}}\). The principle is very simple :
Proposition 2.17
(restriction principle) Let \({\mathbf {S}}, {\mathbf {T}}\) be finite index sets with \({\mathbf {S}}\subset {\mathbf {T}}\). Then
where the sum is over those intervals \({\mathbb {J}}\subseteq {\mathbf {T}}\) which restrict over \({\mathbf {S}}\) to \({\mathbb {I}}\).
Proof
Take an arbitrary interval decomposition of \({\mathbb {V}}_{\mathbf {T}}\). This induces an interval decomposition of \({\mathbb {V}}_{\mathbf {S}}\). Summands of \({\mathbb {V}}_{\mathbf {S}}\) of type \({\mathbb {I}}\) arise precisely from those summands of \({\mathbb {V}}_{\mathbf {T}}\) of types \({\mathbb {J}}\) as above. \(\square \)
Example 2.18
Suppose \(a< p< b< q < c\). Then we have

and

for instance. The extra term occurs when the inserted new index occurs between a clear node and a filled node, because then there are two possible intervals which restrict to the original interval.
Example 2.19
For any finite list of indices in which a, b and later c, d occur as adjacent pairs, the restriction principle gives

When \({\mathrm {rank}}(V_b \rightarrow V_c) < \infty \), this observation combines with Proposition 3.6 to give an easy expression for any interval multiplicity.
We will make frequent use of the restriction principle. Here is a simple illustration, to serve as a template for similar arguments that we will encounter later on.
Example 2.20
Consider the elementary fact that \({\mathrm {rank}}(V_b \rightarrow V_c) \ge {\mathrm {rank}}(V_a \rightarrow V_d)\) when \(a \le b \le c \le d\). The proof using quiver notation runs as follows:

The ‘three other terms’ are

as indicated by the restriction principle.
Notes
- 1.
An endomorphism e is idempotent if it satisfies \(ee=e\).
- 2.
No countable sequence of vectors \(w_1, w_2, w_3, \dots \) can span \(W_0\). Consider a vector \(x =(x_1, x_2, x_3, \dots )\) where for all \(k \ge 1\) the \(k+1\) terms \(x_{k^2}, x_{k^2+1}, \dots , x_{k^2+k}\) have been chosen to guarantee that x is not a linear combination of \(w_1, \dots , w_k\). Then \(x \not \in {\text {span}}(w_1, w_2, w_3, \dots )\).
- 3.
We consider index sets of length 4 to define the persistence measure, length 5 to show that it is additive, and length 8 to prove the stability theorem.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2016 The Author(s)
About this chapter
Cite this chapter
Chazal, F., de Silva, V., Glisse, M., Oudot, S. (2016). Persistence Modules. In: The Structure and Stability of Persistence Modules. SpringerBriefs in Mathematics. Springer, Cham. https://doi.org/10.1007/978-3-319-42545-0_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-42545-0_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-42543-6
Online ISBN: 978-3-319-42545-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


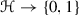 , defined by
, defined by  , with a tick to specify the decoration.
, with a tick to specify the decoration.

 with examples of each interval type drawn as points with ticks. Points on the left and top edges correspond to intervals that are unbounded below and above, respectively. Points on the diagonal correspond to singleton intervals
with examples of each interval type drawn as points with ticks. Points on the left and top edges correspond to intervals that are unbounded below and above, respectively. Points on the diagonal correspond to singleton intervals 