Abstract
We present an interactive and automated theorem prover for free higher-order logic. Our implementation on top of the Isabelle/HOL framework utilizes a semantic embedding of free logic in classical higher-order logic. The capabilities of our tool are demonstrated with first experiments in category theory.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Partiality and undefinedness are core concepts in various areas of mathematics. Modern mathematical proof assistants and theorem proving systems are often based on traditional classical or intuitionistic logics and provide rather inadequate support for these challenge concepts. Free logic [5, 6], in contrast, offers a theoretically and practically appealing solution. Unfortunately, however, we are not aware of any implemented and available theorem proving system for free logic.
In this extended abstract we show how free logic can be “implemented” in any theorem proving system for classical higher-order logic (HOL) [1]. The proposed solution employs a semantic embedding of free (or inclusive logic) in HOL. We present an exemplary implementation of this idea in the mathematical proof assistant Isabelle/HOL [4]. Various state-of-the-art first-order and higher-order automated theorem provers and model finders are integrated (modulo suitable logic translations) with Isabelle via the Sledgehammer tool [2], so that our solution can be utilized, via Isabelle as foreground system, with a whole range of other background reasoners. As a result we obtain an elegant and powerful implementation of an interactive and automated theorem proving (and model finding) system for free logic.
To demonstrate the practical relevance of our new system, we report on first experiments in category theory. In these experiments, theorem provers were able to detect a (presumably unknown) redundancy in the foundational axiom system of the category theory textbook by Freyd and Scedrov [3].
2 Free Logic
Terms in classical logic denote, without exceptions, entities in a non-empty domain of (existing) objects D, and it are these objects of D the universal and existential quantifiers do range over. Unfortunately, however, these conditions may render classical logic unsuited for handling mathematically relevant issues such as undefinedness and partiality. For example in category theory composition of maps is not always defined.
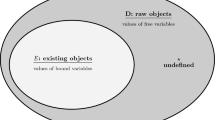
Free logic (and inclusive logic) has been proposed as an alternative to remedy these shortcomings. It distinguishes between a raw domain of possibly non-existing objects D and a particular subdomain E of D, containing only the “existing” entities. Free variables range over D and quantified variables only over E. Each term denotes in D but not necessarily in E. The particular notion of free logic as exploited below has been introduced by Scott [6]. A graphical illustration of this notion of free logic is presented in Fig. 1.
3 Implementing Free Logic in Isabell/HOL
We start out with introducing a type i of individuals. The domain of objects associated with this this type will serve as the domain of raw objects D, cf. Fig. 1. Moreover, we introduce an existence predicate E on type i. As mentioned, E characterises the subset of existing objects in D. Next, we declare a special constant symbol star  , which is intended to denote a distinguished “non-existing” element of D.
, which is intended to denote a distinguished “non-existing” element of D.

We postulate that  is a “non-existing” object in D.
is a “non-existing” object in D.

The two primitive logical connective we introduce for free logic are negation  and implication
and implication  . They are identified with negation
. They are identified with negation  and implication
and implication  in the underlying Isabelle/HOL logic. The internal names in Isabelle/HOL of the new logical connectives are \(f\!Not\) and \({f\!Implies}\) (the prefix f stands for “free”);
in the underlying Isabelle/HOL logic. The internal names in Isabelle/HOL of the new logical connectives are \(f\!Not\) and \({f\!Implies}\) (the prefix f stands for “free”);  and the infix operator
and the infix operator  are introduced as syntactical sugar.Footnote 1
are introduced as syntactical sugar.Footnote 1

The main challenge is to appropriately define free logic universal quantification  and free logic definite description (I). Again, we are interested to relate these logical operators to the respective operators
and free logic definite description (I). Again, we are interested to relate these logical operators to the respective operators  and THE in the Isabelle/HOL logic. Different to the trivial maps for
and THE in the Isabelle/HOL logic. Different to the trivial maps for  and
and  from above, their mappings are relativized in the sense that the existence predicate E is utilized as guard in their definitions.
from above, their mappings are relativized in the sense that the existence predicate E is utilized as guard in their definitions.
The definition of the free logic universal quantifier  thus becomes:
thus becomes:

Apparently, this definitions restricts the set of objects the  -operator is ranging over to the set of existing objects E. Note that this set can be empty (if desired, we may of course simply postulate that the domain E is non-empty:
-operator is ranging over to the set of existing objects E. Note that this set can be empty (if desired, we may of course simply postulate that the domain E is non-empty:  ).
).
The Isabelle framework supports the introduction of syntactic sugar for binding notations. Here we make use of this option to introduce binding notation for  . With the definition below we can now use the more familiar notation
. With the definition below we can now use the more familiar notation  instead of writing
instead of writing  or
or  .
.

Definite description I in free logic works as follows: Given an unary set \(\varPhi =\{a\}\), with a being an “existing” element in E, I returns the single element a of \(\varPhi \). In all other cases, that is, if \(\varPhi \) is not unary or a is not an element of E,  returns the distinguished “non-existing” object denoted by
returns the distinguished “non-existing” object denoted by  . With the help of Isabelle/HOL’s definite description operator THE, I can thus be defined as follows:
. With the help of Isabelle/HOL’s definite description operator THE, I can thus be defined as follows:

Analogous to above we introduce binder notation for I, so that we can write  instead of
instead of  or
or  .
.

Further logical connectives of free can now be defined in the usual way (and for  we again introduce binder notation).
we again introduce binder notation).

4 Functionality Tests
We exemplarily investigate some example proof problems from Scott’s paper [6], pp. 183–184, where a free logic with a single relation symbol r is discussed.

The implication  , where x is a free variable, is valid independently whether x is defined (i.e. “exists”) or not. In Isabelle/HOL this quickly confirmed by the simplification procedure simp.
, where x is a free variable, is valid independently whether x is defined (i.e. “exists”) or not. In Isabelle/HOL this quickly confirmed by the simplification procedure simp.

However, as intended, the formula  is not valid, since set of existing objects E could be empty. Nitpick quickly presents a respective countermodel.
is not valid, since set of existing objects E could be empty. Nitpick quickly presents a respective countermodel.

Consequently, also the implication  has a countermodel, where E is empty.
has a countermodel, where E is empty.

If we rule out that E is empty, e.g. with additional condition  in the antecedent of the above formula, then we obtain a valid implication. Isabelle trivially proves this with procedure simp.
in the antecedent of the above formula, then we obtain a valid implication. Isabelle trivially proves this with procedure simp.

We analyse some further statements (respectively statement instances) from Scott’s paper [6], p. 185. Because of space restrictions we do not further comment these statements here. Altogether they provide further evidence that our implementation of free logic in fact obeys the intended properties.

5 Application in Category Theory
We exemplarily employ our free logic reasoning framework from above for an application in category theory. More precisely, we study some properties of the foundational axiom system of Freyd and Scedrov; see their textbook “Categories, Allegories” [3], p. 3. As expected, the composition \(x \cdot y\), for morphisms x and y, is introduced by Freyd and Scedrov as a partial operation, cf. axiom A1 below: the composition \(x \cdot y\) exists if and only if the target of x coincides with the source of y. This is why free logic, as opposed to e.g. classical logic, is better suited as a starting point in this mathematical application area.Footnote 2
In the remainder we identify the base type i of free logic with the raw type of morphisms. Moreover, we introduce constant symbols for the following operations: source of a morphism x, target of a morphism x and composition of morphisms x and y. These operations are denoted by Freyd and Scedrov as  ,
,  and
and  , respectively. We adopt their notation as syntactic sugar below, even though we are not particularly fond of the use of
, respectively. We adopt their notation as syntactic sugar below, even though we are not particularly fond of the use of  in this context.
in this context.

Ordinary equality on morphisms is defined as follows:

We are now in the position to model the category theory axiom system of Freyd and Scedrov.

Experiments with our new reasoning framework for free logic quickly showed that axiom A2a is redundant. For example, as Isabelle’s internal prover metisFootnote 3 confirms, A2a is implied by A2b, A3a, A3b and A4a.

A human readable and comprehensible reconstruction of this redundancy is presented below. Our handmade proof employs axioms A2b, A3a, A3b, A4a and A5, that is, this proof could be further optimized by eleminating the dependency on A5.

Thus, axiom A2a can be removed from the theory. Alternatively, we could also eliminate A2b which is implied by A1, A2a and A3a:

In fact, by a systematic experimentation within our free logic theorem proving framework, we can show that Freyd’s and Scedroc’s axiomatic theory can be reduced to just the following five axioms:

The dropped axioms can then be introduced as lemmas.

6 Summary of Technical Contribution and Further Work
We have presented a new reasoning framework for free logic, and we have exemplary applied it for some first experiments in category theory. We have shown that, in our free logic setting, the category theory axiom system of Freyd and Scedrov is redundant and that three axioms can be dropped.
Our free logic reasoning framework is publicly available for reuse: Simply download Isabelle from https://isabelle.in.tum.de and initialize it (respectively import) the file FreeFOL.thy from our sources available at www.christoph-benzmueller.de/papers/2016-ICMS.zip. Our category theory experiments are contained in the file FreydScedrov.thy.
Comparisons with other theorem provers for free logic are not possible at this stage, since we are not aware of any other existing systems.
We also want to emphasize that this paper has been written entirely within the Isabelle framework by utilizing the Isabelle “build” tool; cf. [8], Sect. 2. It is thus an example of a formally verified mathematical document, where the pdf document as presented here has been generated directly from the verified source files mentioned above.Footnote 4
Further work includes the continuation of our formalization studies in category theory. It seems plausible that substantial parts of the textbook of Freyd and Scedrov can now be formalised in our framework. An interesting question clearly is how far automation scales and whether some further (previously unknown) insights can eventually be contributed by the theorem provers. Moreover, we have already started to compare the axiom system by Freyd and Scedrov with a more elegant set of self-dual axioms developed by Scott. Furthermore, we plan to extend our studies to projective geometry, which is another area where free logic may serve as a suitable starting point for formalisation.
In addition to our implementation of free logic as a theory in Isabelle/HOL, we plan to support an analogous logic embedding in the new Leo-III theorem prover [9]. The idea is that Leo-III can then be envoked with a specific flag telling it to automatically switch its underlying logic setting from higher-order classical logic to first-order and higher-order free logic, while retaining TPTP TH0 [7] as the common input syntax.
Notes
- 1.
The numbers in
 and
and 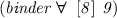 (see below) specify structural priorities and thus help to avoid brackets in formula representations.
(see below) specify structural priorities and thus help to avoid brackets in formula representations. - 2.
The precise logic setting is unfortunately not discussed in the very beginning of Freyd’s and Scedrov’s textbook. Appendix B, however, contains a concise formal definition of the assumed logic. Note the special notion of equality used below (which is different from Kleene equality) and also remember that we postulated a ‘non-existing’ entity.
- 3.
Metis is a trusted prover of Isabelle, since it returns proofs in Isabelle’s trusted proof kernel. Initially, however, we have worked with Isabelle’s Sledgehammer tool in our experiments, which in turn performs calls to several integrated first-order theorem provers. These calls then return valuable information on the particular proof dependencies, which in turn suggest the successful calls with metis as presented here.
- 4.
By suitably adapting the Isabelle call as contained in file runIsabelle.sh in our zip-package, the verification and generation process can be easily reproduced by the reader.
References
Benzmüller, C., Miller, D.: Automation of higher-order logic. In: Siekmann, J., Gabbay, D., Woods, J. (eds.) Handbook of the History of Logic, vol. 9. Logic and Computation, Elsevier (2014)
Blanchette, J., Böhme, S., Paulson, L.: Extending sledgehammer with SMT solvers. J. Autom. Reason. 51(1), 109–128 (2013)
Freyd, P.J., Scedrov, A.: Categories, Allegories. North Holland, Amsterdam (1990)
Nipkow, T., Paulson, L., Wenzel, M.: Isabelle/HOL: A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Heidelberg (2002)
Nolt, J.: Free logic. In: Zalta, E.N. (ed.) The Stanford Encyclopedia of Philosophy. Winter 2014 edn. (2014)
Scott, D.: Existence and description in formal logic. In: Schoenman, R., Russell, B. (eds.) Philosopher of the Century, pp. 181–200. George Allen & Unwin, London (1967). Reprinted with additions. In: Lambert, K. (ed.) Philosophical Application of Free Logic, pp. 28–48. Oxford Universitry Press, 1991
Sutcliffe, G., Benzmüller, C.: Automated reasoning in higher-order logic using the TPTP THF infrastructure. J. Formaliz. Reason. 3(1), 1–27 (2010)
Wenzel, M.: The isabelle system manual, February 2016. https://www.cl.cam.ac.uk/research/hvg/Isabelle/dist/Isabelle2016/doc/system.pdf
Wisniewski, M., Steen, A., Benzmüller, C.: LeoPARD — a generic platform for the implementation of higher-order reasoners. In: Kerber, M., Carette, J., Kaliszyk, C., Rabe, F., Sorge, V. (eds.) CICM 2015. LNCS, vol. 9150, pp. 325–330. Springer, Heidelberg (2015)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Benzmüller, C., Scott, D. (2016). Automating Free Logic in Isabelle/HOL. In: Greuel, GM., Koch, T., Paule, P., Sommese, A. (eds) Mathematical Software – ICMS 2016. ICMS 2016. Lecture Notes in Computer Science(), vol 9725. Springer, Cham. https://doi.org/10.1007/978-3-319-42432-3_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-42432-3_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-42431-6
Online ISBN: 978-3-319-42432-3
eBook Packages: Computer ScienceComputer Science (R0)





 and
and 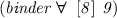 (see below) specify structural priorities and thus help to avoid brackets in formula representations.
(see below) specify structural priorities and thus help to avoid brackets in formula representations.