Abstract
In order to evaluate spherical array processing algorithms comprehensively under many different acoustic conditions, it is indispensable to use simulated acoustic impulse responses (AIRs) to characterize the source–microphone acoustic channel, most typically in a room or other enclosed acoustic environment. The image method proposed by Allen and Berkley is a well-established way of doing this for point-to-point AIRs with sensors in free space. However, it does not account for the acoustic scattering introduced by a rigid sphere. In this chapter, we present a method for simulating the AIRs between a sound source and microphones positioned on a rigid spherical array. In addition, three examples are presented based on this method: an analysis of a diffuse reverberant sound field, a study of binaural cues in the presence of reverberation, and an illustration of the algorithm’s use as a mouth simulator.
Portions of this chapter were first published in the Journal of the Acoustical Society of America [17], and are reproduced in accordance with the Acoustical Society of America’s Transfer of Copyright Agreement. The content of [17] has been edited here for brevity and to standardize the notation.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
In general , the evaluation of acoustic signal processing algorithms, such as direction of arrival (DOA) estimation (see Chap. 5) and speech enhancement (see Chap. 9) algorithms, makes use of simulated acoustic transfer functions (ATFs). By using simulated ATF it is possible to evaluate comprehensively an algorithm under many acoustic conditions, such as a range of reverberation times, room dimensions and source-array distances. Allen and Berkley’s image method [2] is a widely used approach to simulate ATFs between an omnidirectional sound source and one or more microphones in a reverberant environment. In the last few decades, several extensions have been proposed [21, 29].
In recent years the use of spherical microphone arrays has become prevalent. These arrays are commonly of one of two types (discussed in Sect. 3.4.2): the open array, where microphones are suspended in free space on an ‘open’ sphere, and the rigid array, where microphones are mounted on a rigid baffle. As discussed in the previous chapter, the rigid sphere is often preferred as it improves the numerical stability of many processing algorithms [32] and its acoustic scattering effects are can be calculated precisely [25].
Currently, many works relating to spherical array processing consider only free-field responses; however, when a rigid array is used, the rigid baffle causes scattering of the sound waves incident upon the array that the image method does not consider. This scattering has an effect on the ATFs, especially at high frequencies and/or for microphones situated on the occluded side of the array. Furthermore the reverberation due to room boundaries such as walls, ceiling and floor must also be considered, particularly in small rooms or rooms with strongly reflective surfaces .
While measured transfer functions include both these effects, they are both time-consuming and expensive to acquire over a wide range of geometries and rooms. A method for simulating ATFs in a reverberant room while accounting for scattering is therefore essential, allowing for fast, comprehensive and repeatable testing. In this chapter, we present the SMIR (Spherical Microphone array Impulse Response) method that combines a model of the scattering in the spherical harmonic domain (SHD) with a version of the image method that accounts for reverberation in a computationally efficient way [16, 17].
The simulated ATFs include the direct path, reflections due to room reverberation, scattering of the direct path and scattering of the reverberant reflections. Reflections of the scattered sound and multiple interactions between the room boundaries and the sphere are excluded as they do not contribute significantly to the sound field, provided the distances between the room boundaries and the sphere are several times the sphere’s radius [11], which is easily achieved in the case of a small scatterer [4]. Furthermore, we assume an empty rectangular shoebox room (with the exception of the rigid sphere) and specular reflections, as was assumed in the conventional image method [2]. Finally, the scattering model used assumes a perfectly rigid baffle, without absorption.
In this chapter, we first briefly summarize Allen and Berkley’s image method and then present the SMIR method in the SHD. Next, we discuss some implementation aspects, namely the truncation of an infinite sum in the ATF expression and the reduction of the method’s computational complexity, and then provide a pseudocode description of the method. An open-source software implementation is available online [14]. Finally, we show some example uses of the method and, where possible, compare the simulated results obtained with theoretical models.
4.1 Allen and Berkley’s Image Method
The source-image or image method [2] is one of the most commonly used room acoustics simulation methods in the acoustic signal processing community. The principle of the method is to model an ATF as the sum of a direct path component and a number of discrete reflections, each of these components being represented in the ATF by a free-space Green’s function. In this section, we review the free-space Green’s function and the image method .
4.1.1 Green’s Function
As detailed in Sect. 2.1, for a source at a position  and a receiver at a position
and a receiver at a position  ,Footnote 1 the free-space Green’s function, a solution to the inhomogeneous Helmholtz equation applying the Sommerfeld radiation condition, is given byFootnote 2
,Footnote 1 the free-space Green’s function, a solution to the inhomogeneous Helmholtz equation applying the Sommerfeld radiation condition, is given byFootnote 2

where \(\left| \left| \cdot \right| \right| \) denotes the 2-norm and the wavenumber k is related to frequency  (in Hz), angular frequency \(\omega \) (in \(\text {rad} \cdot \text {s}^{-1}\)) and the speed of sound c (in \(\text {m} \cdot \text {s}^{-1}\)) via the dispersion relation
(in Hz), angular frequency \(\omega \) (in \(\text {rad} \cdot \text {s}^{-1}\)) and the speed of sound c (in \(\text {m} \cdot \text {s}^{-1}\)) via the dispersion relation  .
.
In the time-domain, the Green’s function is given by

where \(\delta \) is the Dirac delta function and t is time. This corresponds to a pure impulse at time  , the propagation time from
, the propagation time from  .
.
4.1.2 Image Method
Consider a rectangular room with length \(L_x\), width \(L_y\) and height \(L_z\). The reflection coefficients of the four walls, floor and ceiling are \(\beta _{x_1}\), \(\beta _{x_2}\), \(\beta _{y_1}\), \(\beta _{y_2}\), \(\beta _{z_1}\) and \(\beta _{z_2}\), where the \(a_1\) coefficients (\(a \in \{x,y,z\}\)) correspond to the boundaries at \(a = 0\) and the \(a_2\) coefficients correspond to the boundaries at \(a = L_a\).
If the sound source is located at  and the receiver is located at
and the receiver is located at  , the images obtained using the walls at \(x = 0\), \(y = 0\) and \(z = 0\) can be expressed as a vector
, the images obtained using the walls at \(x = 0\), \(y = 0\) and \(z = 0\) can be expressed as a vector  :
:

where each of the elements in \(\mathbf {p} = (p_x,p_y,p_z)\) can take values 0 or 1, thus resulting in eight combinations that form a set \(\mathcal {P}\). To consider all reflections we also define a vector  which we add to
which we add to  :
:

where each of the elements in \(\mathbf {m} = (m_x,m_y,m_z)\) can take values between \(-N_m\) and \(N_m\), and \(N_m\) is used to limit computational complexity and circular convolution errors, thus resulting in a set \(\mathcal {M}\) of \((2N_m+1)^3\) combinations. The image positions in the x and y dimensions are illustrated in Fig. 4.1.
The distance between an image and the receiver is given by  . Using (4.1), the ATF H is then given by
. Using (4.1), the ATF H is then given by

Using (4.2), we obtain the acoustic impulse response (AIR)

4.2 SMIR Method in the Spherical Harmonic Domain
There exists a compact analytical expression for the scattering due to the rigid sphere in the SHD, therefore we first express the free-space Green’s function in this domain, and then use this to form an expression for the ATF including scattering.
4.2.1 Green’s Function
We define position vectors in spherical coordinates relative to the centre of our array. Letting r be the array radius and \(\varOmega \) an inclination-azimuth pair, the microphone position vector is defined as \({\mathbf {r}}~\triangleq ~(r,\varOmega )\) where \(\varOmega = (\theta ,\phi )\). Similarly, the source position vector is given by \(\mathbf {r}_{\text {s}}~\triangleq ~(r_{\text {s}},\varOmega _{\text {s}})\) where \(\varOmega _{\text {s}} = (\theta _{\text {s}},\phi _{\text {s}})\). Consistent with our approach in previous chapters, it is hereafter assumed that where the addition, 2-norm or scalar product operations are applied to spherical polar vectors, they have previously been converted to Cartesian coordinates using (2.12). In addition , we assume that the source is outside the array, i.e., \(r_{\text {s}} > r\).
The free-space Green’s function (4.1) can be expressed in the SHD using the spherical harmonic expansion (SHE) in (2.22) [40]:
where \(Y_{lm}\) is the spherical harmonic function of order l and degree m, \(j_l\) is the spherical Bessel function of order l and \(h_l^{(2)}\) is the spherical Hankel function of the second kind and of order l. This decomposition is also known as a spherical Fourier series expansion or spherical harmonic decomposition of the Green’s function.
Using the spherical harmonic addition theorem (2.23), which in many cases reduces the complexity of the implementation, we can simplify the Green’s function in (4.7) to

where  is the Legendre polynomial of order l and \(\varTheta _{\mathbf {r},\mathbf {r}_{\text {s}}}\) is the angle between \(\mathbf {r}\) and \(\mathbf {r}_{\text {s}}\). The cosine of the angle \(\varTheta _{\mathbf {r},\mathbf {r}_{\text {s}}}\) is obtained as the dot product of the two normalized vectors \(\hat{\mathbf {r}}_{\text {s}} = \mathbf {r}_{\text {s}}/r_{\text {s}}\) and \(\hat{\mathbf {r}} = \mathbf {r}/r\):
is the Legendre polynomial of order l and \(\varTheta _{\mathbf {r},\mathbf {r}_{\text {s}}}\) is the angle between \(\mathbf {r}\) and \(\mathbf {r}_{\text {s}}\). The cosine of the angle \(\varTheta _{\mathbf {r},\mathbf {r}_{\text {s}}}\) is obtained as the dot product of the two normalized vectors \(\hat{\mathbf {r}}_{\text {s}} = \mathbf {r}_{\text {s}}/r_{\text {s}}\) and \(\hat{\mathbf {r}} = \mathbf {r}/r\):
4.2.2 Neumann Green’s Function
The free-space Green’s function describes the propagation of sound in free space only. However, when a rigid sphere is present, a boundary condition must hold: the radial velocity must vanish on the surface of the sphere. The function \(G_{\text {N}}(\mathbf {r}|\mathbf {r}_{\text {s}},k)\) satisfying this boundary condition is called the Neumann Green’s function, and describes the sound propagation between a point \(\mathbf {r}_{\text {s}}\) and a point \(\mathbf {r}\) on the rigid sphere [40]:

where \((\cdot )'\) denotes the first derivative and the term
is often called the (farfield) mode strength. The Wronskian relation [40, Eq. 6.67]
allows us to simplify (4.11) to
For the open sphere, substituting \(b_l(k) = i^l j_l(kr)\) into (4.10) yields the free-space Green’s function \(G(\mathbf {r}|\mathbf {r}_{\text {s}},k)\).
4.2.3 Scattering Model
The rigid sphere scattering modelFootnote 3 used by the SMIR method has a long history in the literature; it was first developed by Clebsch and Rayleigh in 1871–72 [23]. It is presented in a number of acoustics texts [28, 36, 40], and is used in many theoretical analyses for spherical microphone arrays [26, 33].
4.2.3.1 Theoretical Behaviour
The behaviour of the scattering model is illustrated in Fig. 4.2, which plots the magnitude of the response between a source and a receiver on a rigid sphere of radius 5 cm for a source-array distance of 1 m, as a function of frequency and DOA. The response was normalized using the free-field/open sphere response, therefore the plot shows only the effect due to scattering. Due to rotational symmetry, we only looked at the one-dimensional DOA, instead of looking at both azimuth and inclination, and limited the DOA to the 0–\(180^{\circ }\) range.
When the source is located on the same side of the sphere as the receiver and the direction of arrival is \(0^{\circ }\), the rigid sphere response is greater than the open sphere response due to constructive scattering, tending towards a 6 dB magnitude gain compared to the open sphere at infinite frequency. The response on the back side of the rigid sphere is generally lower than in the open sphere case and lower than on the front side, as one would intuitively expect due to it being occluded. However, at the very back of the sphere, when the DOA is \(180^{\circ }\), we observe a narrow bright spot: the waves propagating around the sphere all arrive in phase at the \(180^{\circ }\) point and as a result sum constructively.
The polar plot of the magnitude response is shown in Fig. 4.3 and illustrates both the amplification on the front side of the sphere, and attenuation on the back side of the sphere, which both increase with increasing frequency. It should be noted that although the above results are for a fixed sphere radius, as the scattering model is a function of kr, the effects of a change in radius are the same as a change in frequency; indeed the relevant factor is the radius of the sphere relative to the wavelength.
These substantial differences between the open and rigid sphere responses confirm the need for a simulation method which accounts for scattering, even for sphere radii as small as 5 cm.
4.2.3.2 Experimental Validation
In addition to being widely used in theory, this model has also been experimentally validated by Duda and Martens [9] using a single microphone inserted in a hole drilled through a 10.9 cm radius bowling ball placed in an anechoic chamber. This is a reasonable approximation to a spherical microphone array; indeed a bowling ball was used by Li and Duraiswami to construct a hemispherical microphone array [22].
Duda and Martens’s experimental results broadly agree with the theoretical model. In our case we are most interested in the results in their Fig. 12a where the source-array distance is largest (20 times the array radius), as in typical spherical array usage scenarios the source is unlikely to be much closer to the array than this. The only notable difference between the theoretical and experimental results in this case is for a direction of arrival of \(180^{\circ }\), where the high frequency response is found to be lower than expected. The authors suggest this is due to small alignment errors, which would indeed have an effect given the narrowness of the bright spot in the model (see Fig. 4.3 for  kHz). Given these results, we conclude that the use of this scattering model is sufficiently accurate for simulating a small rigid array, such as the Eigenmike [27].
kHz). Given these results, we conclude that the use of this scattering model is sufficiently accurate for simulating a small rigid array, such as the Eigenmike [27].
4.2.4 SMIR Method
We now present the SMIR method proposed in [16, 17], incorporating the SHE presented in Sect. 4.2.1 and the scattering model introduced in Sect. 4.2.2.
Due to the differences between the SHD Neumann Green’s function in (4.10) and the spatial domain Green’s function in (4.1), as well as the directionality of the array’s response, two changes must be made to the image position vectors  and
and  in the SMIR method. Firstly, to compute the SHE in the Neumann Green’s function, we require the distance between each image and the centre of the array [\(r_{\text {s}}\) in (4.10)]; this is accomplished by computing the image position vectors using the position of the centre of the array rather than the position of the receiver. Secondly, to compute the SHE we require the angle between each image and the receiver with respect to the centre of the array [\(\varTheta _{\mathbf {r},\mathbf {r}_{\text {s}}}\) in (4.10)]. In Allen and Berkley’s image method, the direction of the vector
in the SMIR method. Firstly, to compute the SHE in the Neumann Green’s function, we require the distance between each image and the centre of the array [\(r_{\text {s}}\) in (4.10)]; this is accomplished by computing the image position vectors using the position of the centre of the array rather than the position of the receiver. Secondly, to compute the SHE we require the angle between each image and the receiver with respect to the centre of the array [\(\varTheta _{\mathbf {r},\mathbf {r}_{\text {s}}}\) in (4.10)]. In Allen and Berkley’s image method, the direction of the vector  is not always the same: in some cases it points from the receiver to the image and in others it points from the image to the receiver. This is not an issue for the image method as only the norm of this vector is used. Because we also require the angle of the images in the SMIR method, we modify the definition of
is not always the same: in some cases it points from the receiver to the image and in others it points from the image to the receiver. This is not an issue for the image method as only the norm of this vector is used. Because we also require the angle of the images in the SMIR method, we modify the definition of  such that the vector
such that the vector  always points from the centre of the array to the image.
always points from the centre of the array to the image.
We now incorporate these two changes into the definition of the image vectors  and
and  . If the sound source is located at
. If the sound source is located at  and the centre of the sphere is located at
and the centre of the sphere is located at  , the images obtained using the walls at \(x = 0\), \(y = 0\) and \(z = 0\) are expressed as a vector
, the images obtained using the walls at \(x = 0\), \(y = 0\) and \(z = 0\) are expressed as a vector  :
:

For brevity we define  , allowing us to express the distance between an image and the centre of the sphere as
, allowing us to express the distance between an image and the centre of the sphere as  and the angle between the image and the receiver as \(\varTheta _{\mathbf {r},\mathbf {R}_{\mathbf {p},\mathbf {m}}}\), computed in the same way as (4.9), where \(\mathbf {R_{p,m}}\) denotes the image positions in spherical coordinates. The image positions in the x dimension are illustrated in Fig. 4.4. Finally, the ATF \(H(\mathbf {r}|\mathbf {r}_{\text {s}},k)\) is the weighted sum of the individual responses \(G_{\text {N}}(\mathbf {r}|\mathbf {R}_{\mathbf {p,m}},k)\) for each of the imagesFootnote 4
and the angle between the image and the receiver as \(\varTheta _{\mathbf {r},\mathbf {R}_{\mathbf {p},\mathbf {m}}}\), computed in the same way as (4.9), where \(\mathbf {R_{p,m}}\) denotes the image positions in spherical coordinates. The image positions in the x dimension are illustrated in Fig. 4.4. Finally, the ATF \(H(\mathbf {r}|\mathbf {r}_{\text {s}},k)\) is the weighted sum of the individual responses \(G_{\text {N}}(\mathbf {r}|\mathbf {R}_{\mathbf {p,m}},k)\) for each of the imagesFootnote 4
Since we are working in the wavenumber domain, we can allow for frequency dependent boundary reflection coefficients in (4.15), if desired. The reflection coefficients would then be written as \(\beta _{x_1}(k)\), \(\beta _{x_2}(k)\) and so on. Chen and Maher [7] provide some measured reflection coefficients for a wall, window, floor and ceiling.
4.3 Implementation
4.3.1 Truncation Error
To compute the expression for the ATF in (4.15), the sum over an infinite number of orders l in the Neumann Green’s function \(G_{\text {N}}\) must be approximated by a sum \(\hat{G}_{\text {N}}\) over a finite order L. Choosing L too small will result in a large approximation error, while choosing L too large will result in too high a computational complexity. We now investigate the approximation error in order to provide some guidelines for the choice of the order L. The results for an open sphere are provided for reference, and were computed by using a truncated SHE of the Green’s function \(\hat{G}\) instead of a Neumann Green’s function.
For an open sphere, the error can be determined exactly because the Green’s function is a decomposition of the closed-form expression in (4.1). For a rigid sphere, however, no closed-form expression exists since the scattering term can be expressed only in the SHD. We therefore estimated the error by comparing the truncated Neumann Green’s function \(\hat{G}_{\text {N}}\) to a high-order Neumann Green’s function. We can assume the error involved in using a high-order Neumann Green’s function as a reference as opposed to the untruncated Neumann Green’s function is small, due to the uniform convergence of the SHE [12]. In practice, we cannot choose very large values of L because of numerical difficulties involved in multiplying high order spherical Bessel and Hankel functions. For typical sphere radii and source-array distances, this allows us to reach L values of up to about 100 using SMIRgen, a MATLAB implementation of the SMIR method [14].
We evaluated the truncated (Neumann) Green’s function at \(K = 1024\) discrete values of k (denoted by \(\dot{k}\)), forming a set \(\mathcal {K}\) corresponding to frequencies in the range 100 Hz–8 kHz,Footnote 5 and then calculated the normalized root-mean-square magnitude error \(\epsilon _{\text {m}}\) and the root-mean-square phase error \(\epsilon _{\text {p}}\):
We averaged the magnitude and phase errors over 32 microphone positions uniformly distributed on the array and 50 random source positions at a fixed distance from the centre of the array.
The resulting average errors are given in Fig. 4.5, for both the open and rigid sphere cases. Three different sphere radii were used: \(r = 4.2\) cm (the radius of the Eigenmike [24]), \(r~=~10\) cm and \(r = 15\) cm. A source-array distance of 1 m was used; results for 1–5 m are omitted as they are essentially identical. It can be seen that beyond a certain threshold, increases in L give only a very small reduction in error; this is due to the fast convergence of the spherical harmonic decomposition [12]. From Fig. 4.5, we can see that a sensible rule of thumb for choosing L is \(L > \lceil 1.1 \, k_\text {max} r \rceil \) where \(k_\text {max}\) is the largest wavenumber of interest.
4.3.2 Computational Complexity
As the ATFs are made up of a sum over all orders l which includes spherical Hankel functions \(h_l\) and Legendre polynomials  , we can make use of recursion relations over l to reduce the computational complexity of these functions. For the spherical Hankel function, we make use of the following relation [40, Eq. 6.69]
, we can make use of recursion relations over l to reduce the computational complexity of these functions. For the spherical Hankel function, we make use of the following relation [40, Eq. 6.69]
where
For the Legendre polynomial we use a similar recursion relation [1], known as Bonnet’s recursion formula

where  and
and  .
.
While replacing the exponential in (4.1) with a SHE does lead to an increase in computational complexity when computing the ATF for a single receiver (which is unavoidable in the rigid sphere case), this can have an advantage when simulating many receiver positions. For the conventional image method, we must compute the image positions and resulting response separately for each individual receiver. However, in the SMIR method the image positions are all computed with respect to the centre of our array, and therefore only once for all of the microphones in the array.
An alternative to (4.15) is obtained by changing the order of the summations in the ATF and computing the sum over all images only once, instead of once per receiver:
The expression in (4.21) requires \(O\left( (N_{\text {i}}+Q)(L+1)^2\right) \) operations per discrete frequency, where L is the maximum spherical harmonic order, \(N_{\text {i}}\) is the number of images and Q is the number of microphones, while the approach in (4.15) requires \(O\left( N_{\text {i}} Q (L+1)\right) \) operations per discrete frequency. Since the number of images \(N_{\text {i}}\) is typically very large, \((N_{\text {i}}+Q)(L+1)^2 \approx N_{\text {i}} (L+1)^2\). Assuming the operations in the two approaches are of similar complexity, it is therefore more efficient to use the expression in (4.15) for \(Q < L+1\) and the expression in (4.21) for \(Q > L+1\). Consequently the least computationally complex approach depends on the number of microphones Q and array radius r. In the remainder of this chapter we use the expression in (4.15); this is particularly appropriate in the applications in Sect. 4.4.2 where \(Q = 2\) and in Sect. 4.4.3 where \(Q = 1\).
4.3.3 Algorithm Summary
A summary of the SMIR method is presented in the form of pseudocode in Fig. 4.6. The variable nsample denotes the number of samples in the AIR, \(N_o\), the maximum reflection order, and fs, the sampling frequency.
The number of computations has been reduced by processing only half of the frequency spectrum because we know the AIR is real and the corresponding ATF is conjugate symmetric. The pseudocode necessary to compute the Hankel functions and Legendre polynomials is omitted here, since their computation is straightforward using recursion relations (4.18) and (4.20).
SMIRgen, a MATLAB/C++ implementation of the method in the form of a MEX-function, is available online [14].
4.4 Examples and Applications
In this section we give a number of examples that make use of the SMIR method. Wherever possible we compare the simulated results to theoretical results obtained using approximate models. These examples are given to illustrate and partially validate the SMIR method.
4.4.1 Diffuse Sound Field Energy
In statistical room acoustics (SRA), reverberant sound fields are modelled as diffuse sound fields, allowing for a statistical analysis of reverberation instead of computing each of the individual reflections. In this subsection, we compare a theoretical prediction of sound energy on the surface of a rigid sphere, based on a diffuse model of reverberation, to simulated results obtained using the SMIR method.
A diffuse sound field is composed of plane waves incident from all directions with equal probability and amplitude [20]. Using the scattering model previously introduced, we can determine the cross-correlation between the sound pressure at arbitrary positions \(\mathbf {r}\) and \(\mathbf {r}'\) on the surface of a sphere, due to a unit amplitude plane wave with a random uniformly distributed direction of arrival (see the Appendix for derivation) [15]:

where \(\varTheta _{\mathbf {r},\mathbf {r}'}\) is the angle between \(\mathbf {r}\) and \(\mathbf {r}'\). In the open sphere case, it is shown in the Appendix that this simplifies to the well-known spatial domain expression [20, 31, 39] \(\text {sinc}(k\left| \left| \mathbf {r} - \mathbf {r}'\right| \right| )\), where \(\text {sinc}\) denotes the unnormalized sinc function.
For the sound energy at a position \(\mathbf {r}\) we substitute \(\varTheta _{\mathbf {r},\mathbf {r}'} = 0\) and find \(C(\mathbf {r},\mathbf {r},k) = \sum _{l=0}^{\infty } |b_l(k)|^2 (2l+1)\). According to SRA theory [20, 39], for frequencies above the Schroeder frequency [20] the energy of the reverberant sound field \(H_{\text {r}}\) is then given by [39]
where \(\text {E}_{\text {s}}\left\{ \cdot \right\} \) denotes spatial expectation, \(\bar{\alpha }\) is the average wall absorption coefficient and A is the total wall surface area.
The above theoretical expression for the average reverberant energy can be compared to simulated results obtained using the SMIR method. We computed the spatial expectation using an average over 200 source-array positions, using the approach in Radlović et al. [31]: the array and source were kept in a fixed configuration (at a distance of 2 m from each other), which was then randomly rotated and translated. Both sources and microphones were kept at least half a wavelength from the boundaries of the room, helping to ensure the diffuseness of the reverberant sound field [20]. The reverberant component \(H_{\text {r}}\) of the ATFs was computed by subtracting the direct path \(H_{\text {d}}\) from the simulated ATFs.
The room dimensions were chosen as \(6.4\,\times \,5\,\times \,4\) m, as in [31, 38], such that the ratio of the dimensions was (1.6 : 1.25 : 1), as recommended in [18, 31] to approximate a diffuse sound field. The reverberation time \(\text {T}_{60}\) was set to 500 ms, giving an average wall absorption coefficient of \(\bar{\alpha } = 0.2656\). We simulated AIRs with a length of 4096 samples at a sampling frequency of 8 kHz. We considered frequencies from 300 Hz to 4 kHz, well above the Schroeder frequency of \(2000 \sqrt{\frac{0.5}{6.4 \times 5 \times 4}} = 125\) Hz, and the half-wavelength minimum distance is therefore 57 cm for a speed of sound of 343 m/s. We averaged the results over the 200 source-array positions and 32 microphone positions uniformly distributed on the array.
In Fig. 4.7, we plot the theoretical and simulated energy of \(H_{\text {r}}\) as a function of frequency, for two array radii (4.2 and 15 cm). We note that, except at low frequencies, there is a good match between the theoretical diffuse field energy expression we derived and the results obtained using the SMIR method. At lower frequencies, the theoretical equation overestimates the energy; we hypothesize that this is due to the reverberant sound field not being fully diffuse.
4.4.2 Binaural Interaural Time and Level Differences
The topic of binaural sound and in particular head-related transfer functions (HRTFs) or head-related impulse responses (HRIRs) is of interest to researchers and engineers working on surround sound reproduction, who for example aim to reproduce spatial audio through a pair of stereo headphones. In addition, the psychoacoustic community is interested in the ability of the human brain to localize sound sources using only two ears.
Two binaural cues that contribute to sound source localization in humans are the interaural time difference (ITD) and the interaural level difference (ILD) [34]. The ITD measures the difference in arrival time of a sound at the two ears, and the ILD measures the difference in level of the sound at the two ears. In this example, we study the long-term cues assuming the source signal is spectrally white. Therefore, we can compute the cues directly using the simulated ATFs.
We used the SMIR method to simulate a simple HRTF by considering microphones placed at locations on a rigid sphere corresponding to ear positions on the human head. Although real HRTFs vary from individual to individual, depending on many factors including the head, torso and pinnae, many of the main characteristics of the HRTF are also exhibited by a simple rigid sphere ATF [9]. The representation of HRTFs using spherical harmonics was studied in [3, 10].
Whereas HRTFs do not normally include the effects of reverberation, and as a result typically sound artificial and provide poor cues for the perception of sound source distance [37], the SMIR method also allows for the inclusion of reverberation in HRIRs. In this case, they are then referred to as binaural room impulse responses (BRIRs). BRIRs are important for the analysis of the effects of reverberation on auditory perception, for example its impact on localization accuracy. Since rotational symmetry no longer necessarily holds once the room reflections are taken into account, the measurement of BRIRs must be done for every source-head position and orientation and is therefore very time-consuming. Simulating BRIRs allows us to more easily study the effects of early and late reflections on the binaural cues.
We begin by looking at ITDs in an anechoic environment, in order to illustrate the effect of the head in isolation. We compare simulated results to approximate theoretical results provided by a ray-tracing formula attributed to Woodworth and Schlosberg that looks at the distance travelled from the source to an observation point on the sphere, either in free-space if the observation point is on the near side of the sphere, or via a point of tangency if the observation point is on the far side [9].
The simulated results were obtained by using the SMIR method to generate HRIRs at a sampling frequency of 32 kHz, with a sphere radius of 8.75 cm and microphones placed at \((\theta ,\phi ) = (90^{\circ }, 100^{\circ })\) (corresponding to the left ear) and \((\theta ,\phi ) = (90^{\circ }, 260^{\circ })\) (corresponding to the right ear). The HRIRs were then band-pass filtered between 2.8 and 3.2 kHz.Footnote 6 The DOA was varied by rotating the source around the sphere at a fixed distance of 1 m and inclination of \(90^{\circ }\). The simulated ITD was computed by determining the time delay that maximized the interaural cross-correlation between the two simulated and band-pass filtered HRIRs. The cross-correlation was interpolated using a second-order polynomial in order to obtain sub-sample delays.
In Fig. 4.8 we plot the ITDs as a function of direction of arrival, where \(0^{\circ }\) corresponds to the median plane on the front side of the sphere and \(180^{\circ }\) corresponds to the median plane on the back side of the sphere. As expected, as the DOA increases from \(0^{\circ }\) to \(80^{\circ }\) and the source gets closer to the ipsilateral ear, the ITD increases monotonically until it reaches its maximum at \(80^{\circ }\), at which point the source is furthest from the contralateral ear. The ITD then decreases from \(80^{\circ }\) to \(180^{\circ }\) as the source nears the median plane and gets closer to the contralateral ear. The response from \(180^{\circ }\) to \(360^{\circ }\) is not shown due to the symmetry about \(180^{\circ }\). As we expect, the simulated results are reasonably close to the theoretical ray-tracing results [9], with a difference of less than 70 \(\upmu \)s.
Using the SMIR method, we analyzed the ILDs in a reverberant environment under three scenarios: the sphere was either placed in the centre of the room with a DOA of \(0^{\circ }\) (where the source is equidistant from the two ears), or at a distance of approximately 0.5 m from one of the walls with DOAs of \(0^{\circ }\) and \(100^{\circ }\) (where the source is aligned with the left ear). In all three cases the source was placed at a distance of 1 m from the centre of the sphere. We chose a room size of \(9 \times 5 \times 3\) m with a reverberation time \(\text {T}_{60}\) of 500 ms, and simulated BRIRs with a length of 4096 samples at a sampling frequency of 8 kHz.
In Figs. 4.9, 4.10 and 4.11 we plot the ILDs for the three above cases, as well as the ILDs we would obtain in an anechoic environment, which are entirely due to scattering. The ILDs were computed by taking the difference in magnitude between the left ear response and the right ear response. A negative ILD therefore indicates that the magnitude of the ipsilateral ear response is lower than that of the contralateral ear response. The smoothed echoic ILDs were obtained using a Savitzky-Golay smoothing filter [35].
The main effect of reverberation we can observe is the introduction of random frequency-to-frequency variations; these are particularly obvious when most of the reverberant energy is diffuse, for example, when the sphere is placed in the centre of the room (Fig. 4.9). Room reflections also increase the overall reverberant energy, particularly in the contralateral ear which receives less direct path energy, thus reducing the ILDs. This is especially noticeable when the contralateral ear is placed near a wall: the contralateral ear receives more energy than in the anechoic case and the ILD is therefore closer to zero (Fig. 4.11).
Placement of the sphere near a wall additionally introduces systematic distortions in the ILDs associated with the prominent early reflection from this wall. This is visible in Fig. 4.11 and most noticeably in Fig. 4.10.
All these effects have also been observed experimentally with a manikin by Shinn-Cunningham et al. [37]. The SMIR method is therefore an inexpensive way of predicting the effects of head movement and environmental changes (such as reverberation time) on HRTFs or BRIRs, without as much need for physical and acoustic measurements to be performed.
4.4.3 Mouth Simulator
The principle of reciprocity can often be advantageously used in room acoustics measurements. The principle states that ATFs are symmetric in the coordinates of the sound source and the observation point: “If we put the sound source at \(\mathbf {r}\), we observe at point \(\mathbf {r}_0\) the same sound pressure as we did before at \(\mathbf {r}\), when the sound source was at \(\mathbf {r}_0\)” [20]. We can apply this principle to ATF simulations, and use the SMIR method to generate the ATF between one or more sources on a sphere and a single omnidirectional microphone placed away from the sphere.
A specific application of this is a mouth simulator: we model the head as a rigid sphere (as in Sect. 4.4.2) of radius \(r_{\text {h}}\), and the mouth as an omnidirectional point source placed on this rigid sphere. This is straightforwardly implemented in the SMIR method by replacing the source position with the microphone position \(\mathbf {r}_{\text {mic}}\), the microphone position with the mouth position \(\mathbf {r}_{\text {mouth}} = (r_{\text {h}}, \varOmega _{\text {mouth}})\), and the array position with the head position:
As a result we can simulate the ATF between a mouth on a head, and a single microphone in free space. Repeated use of the algorithm allows for multiple receivers.
Although more accurate modelling of the head and mouth is possible using finite element or boundary element methods [5, 30] for example, the SMIR method is valuable for application to this problem due its comparative simplicity and the fact that, if desired, it can also take into account room reverberation. The SMIR method can, for example, be used as a mouth simulator in the evaluation of a speech enhancement algorithm [13], instead of the omnidirectional source model that is commonly used. While the diameter of the mouth plays an important role in determining the filter characteristic of the vocal tract [8], we assume for the purposes of the scattering model that the mouth is a point source.
As an illustration of this application, Fig. 4.12 shows the energy of the ATF between the mouth and a microphone as a function of microphone position at frequencies of 100 Hz and 3 kHz in an anechoic environment. The mouth was positioned on a sphere of radius 8.75 cm. Only two dimensions, x and y, are shown for brevity since the z dimension is identical to x and y. We observe that at 100 Hz there is no scattering and the radiation pattern is omnidirectional so that the sphere has little effect. At 3 kHz the effect of scattering starts to become more significant, and the energy at the back of the sphere is reduced while the energy at the front is increased. Finally the bright spot discussed in Sect. 4.2.3 is particularly apparent at the very back of the sphere in the bottom plot.
4.5 Chapter Summary and Conclusions
Spherical microphone arrays on a rigid baffle are of great interest, due to their numerical robustness and precisely calculable scattering effects. In order to analyze, work with and develop acoustic signal processing algorithms that make use of a spherical microphone array, a simulator is needed that can take into account the effects of the acoustic environment of the array as well as the scattering effects of the rigid spherical baffle. Accordingly, in this chapter the SMIR method was presented for the simulation of AIRs or ATFs for a rigid spherical microphone array in a reverberant environment.
We presented a scattering model used to model the rigid sphere, justifying its use with references to the literature, and provided an overview of the model’s behaviour. We showed that the error with respect to the theoretical model can be controlled at the expense of increased computational complexity. Finally we provided a number of examples showing additional applications of this method.
Notes
- 1.
Vectors in Cartesian coordinates are denoted with a corner mark \(\llcorner \) to distinguish them from vectors in spherical coordinates, which are used throughout this book and will be introduced later in the chapter.
- 2.
This expression assumes the sign convention commonly used in electrical engineering, whereby the temporal Fourier transform is defined as \(\mathcal {F}(\omega ) = \int _{-\infty }^{\infty } f(t) e^{-i \omega t} \text {d}t\). For more information on this sign convention, the reader is referred to Sect. 2.3.
- 3.
Some texts [9] refer to the scattering effect as diffraction, although Morse and Ingard note that “When the scattering object is large compared with the wavelength of the scattered sound, we usually say the sound is reflected and diffracted, rather than scattered” [28], therefore in the case of spherical microphone arrays (particularly rigid ones which tend to be relatively small for practical reasons), scattering is possibly the more appropriate term.
- 4.
The sign in the powers of \(\beta \) is different from that in Allen and Berkley’s conventional image method, due to the change in the definition of
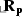 that is required for the SMIR method.
that is required for the SMIR method. - 5.
Very low frequencies are omitted due to the fact that the spherical Hankel function \(h_l(x)\) has a singularity around \(x = 0\).
- 6.
While the ray-tracing formula is frequency-independent, it has been shown [6] that ITDs actually exhibit some frequency dependence, and that because the ray-tracing concept applies to short wavelengths, this model yields only the high frequency time delay. Kuhn provides a more comprehensive discussion of this model and the frequency-dependence of ITDs [19]. It should be noted the simulation results in Fig. 4.8 are in broad agreement with Kuhn’s measured results at 3.0 kHz.
References
Abramowitz, M., Stegun, I.A. (eds.): Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover Publications, New York (1972)
Allen, J.B., Berkley, D.A.: Image method for efficiently simulating small-room acoustics. J. Acoust. Soc. Am. 65(4), 943–950 (1979)
Avni, A., Rafaely, B.: Sound localization in a sound field represented by spherical harmonics. In: Proceedings 2nd International Symposium on Ambisonics and Spherical Acoustics, pp. 1–5. Paris, France (2010)
Betlehem, T., Poletti, M.A.: Sound field reproduction around a scatterer in reverberation. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 89–92 (2009). doi:10.1109/ICASSP.2009.4959527
Botteldoore, D.: Finite-difference time-domain simulation of low-frequency room acoustic problems. J. Acoust. Soc. Am. 98(6), 3302–3308 (1995)
Brown, C., Duda, R.: A structural model for binaural sound synthesis. IEEE Trans. Speech Audio Process. 6(5), 476–488 (1998). doi:10.1109/89.709673
Chen, Z., Maher, R.C.: Addressing the discrepancy between measured and modeled impulse responses for small rooms. In: Proceedings of Audio Engineering Society Convention (2007)
Deller, J.R., Proakis, J.G., Hansen, J.H.L.: Discrete-Time Processing of Speech Signals. MacMillan, New York (1993)
Duda, R.O., Martens, W.L.: Range dependence of the response of a spherical head model. J. Acoust. Soc. Am. 104(5), 3048–3058 (1998). doi:10.1121/1.423886
Evans, M.J., Angus, J.A.S., Tew, A.I.: Analyzing head-related transfer function measurements using surface spherical harmonics. J. Acoust. Soc. Am. 104(4), 2400–2411 (1998)
Gumerov, N., Duraiswami, R.: Modeling the effect of a nearby boundary on the HRTF. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), vol. 5, pp. 3337–3340 (2001). doi:10.1109/ICASSP.2001.940373
Gumerov, N.A., Duraiswami, R.: Fast Multipole Methods for the Helmholtz Equation in Three Dimensions. Elsevier, Oxford (2005)
Habets, E.A.P., Benesty, J.: A two-stage beamforming approach for noise reduction and dereverberation. IEEE Trans. Audio, Speech, Lang. Process. 21(5), 945–958 (2013)
Jarrett, D.P.: Spherical microphone array impulse response (SMIR) generator. http://www.ee.ic.ac.uk/sap/smirgen/
Jarrett, D.P., Habets, E.A.P., Thomas, M.R.P., Gaubitch, N.D., Naylor, P.A.: Dereverberation performance of rigid and open spherical microphone arrays: theory and simulation. In: Proceedings Joint Workshop on Hands-Free Speech Communication and Microphone Arrays (HSCMA), pp. 145–150. Edinburgh (2011)
Jarrett, D.P., Habets, E.A.P., Thomas, M.R.P., Naylor, P.A.: Simulating room impulse responses for spherical microphone arrays. In: Proc. IEEE Intl. Conf. on Acoustics, Speech and Signal Processing (ICASSP), pp. 129–132. Prague, Czech Republic (2011)
Jarrett, D.P., Habets, E.A.P., Thomas, M.R.P., Naylor, P.A.: Rigid sphere room impulse response simulation: algorithm and applications. J. Acoust. Soc. Am. 132(3), 1462–1472 (2012)
Knudsen, V., Harris, C.: Acoustical Designing in Architecture. Wiley, New York (1950)
Kuhn, G.F.: Model for the interaural time differences in the azimuthal plane. J. Acoust. Soc. Am. 62(1), 157–167 (1977). doi:10.1121/1.381498
Kuttruff, H.: Room Acoustics, 4th edn. Taylor and Francis, London (2000)
Lehmann, E., Johansson, A.: Diffuse reverberation model for efficient image-source simulation of room impulse responses. IEEE Trans. Audio Speech Lang. Process. 18(6), 1429–1439 (2010). doi:10.1109/TASL.2009.2035038
Li, Z., Duraiswami, R.: Hemispherical microphone arrays for sound capture and beamforming. In: Proceedings of IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, pp. 106–109 (2005)
Logan, N.A.: Survey of some early studies of the scattering of plane waves by a sphere. Proc. IEEE 53(8), 773–785 (1965). doi:10.1109/PROC.1965.4055
Meyer, J., Agnello, T.: Spherical microphone array for spatial sound recording. In: Proc. Audio Engineering Society Convention, pp. 1–9. New York (2003)
Meyer, J., Elko, G.: A highly scalable spherical microphone array based on an orthonormal decomposition of the soundfield. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), vol. 2, pp. 1781–1784 (2002)
Meyer, J., Elko, G.W.: Position independent close-talking microphone. Signal Process. 86(6), 1254–1259 (2006). doi:10.1016/j.sigpro.2005.05.036
mh acoustics LLC: The Eigenmike microphone array. http://www.mhacoustics.com/mh_acoustics/Eigenmike_microphone_array.html
Morse, P.M., Ingard, K.U.: Theoretical Acoustics. International Series in Pure and Applied Physics. McGraw Hill, New York (1968)
Peterson, P.M.: Simulating the response of multiple microphones to a single acoustic source in a reverberant room. J. Acoust. Soc. Am. 80(5), 1527–1529 (1986)
Pietrzyk, A.: Computer modeling of the sound field in small rooms. In: Proceedings of AES International Conference on Audio, Acoustics and Small Spaces, vol. 2, pp. 24–31. Copenhagen (1998)
Radlović, B.D., Williamson, R., Kennedy, R.: Equalization in an acoustic reverberant environment: robustness results. IEEE Trans. Speech Audio Process. 8(3), 311–319 (2000)
Rafaely, B.: Plane-wave decomposition of the pressure on a sphere by spherical convolution. J. Acoust. Soc. Am. 116(4), 2149–2157 (2004)
Rafaely, B.: Analysis and design of spherical microphone arrays. IEEE Trans. Speech Audio Process. 13(1), 135–143 (2005). doi:10.1109/TSA.2004.839244
Sandel, T.T., Teas, D.C., Feddersen, W.E., Jeffress, L.A.: Localization of sound from single and paired sources. J. Acoust. Soc. Am. 27(5), 842–852 (1955). doi:10.1121/1.1908052
Savitzky, A., Golay, M.J.E.: Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 36(8), 1627–1639 (1964). doi:10.1021/ac60214a047
Sengupta, D.L.: The sphere. In: J.J. Bowman, T.B.A. Senior, P.L.E. Uslenghi (eds.) Electromagnetic and Acoustic Scattering by Simple Shapes, pp. 353–415. North-Holland (1969) (chap. 10)
Shinn-Cunningham, B.G., Kopco, N., Martin, T.J.: Localizing nearby sound sources in a classroom: binaural room impulse responses. J. Acoust. Soc. Am. 117(5), 3100–3115 (2005). doi:10.1121/1.1872572
Talantzis, F., Ward, D.B.: Robustness of multichannel equalization in an acoustic reverberant environment. J. Acoust. Soc. Am. 114(2), 833–841 (2003)
Ward, D.B.: On the performance of acoustic crosstalk cancellation in a reverberant environment. J. Acoust. Soc. Am. 110, 1195–1198 (2001)
Williams, E.G.: Fourier Acoustics: Sound Radiation and Nearfield Acoustical Holography, 1st edn. Academic Press, London (1999)
Author information
Authors and Affiliations
Corresponding author
Appendix: Spatial Correlation in a Diffuse Sound Field
Appendix: Spatial Correlation in a Diffuse Sound Field
The sound pressure at a position \(\mathbf {r} = (r,\varOmega )\) due to a unit amplitude plane wave incident from direction \(\varOmega _{\text {s}}\) is given by [40]
where \(\varphi (\varOmega _{\text {s}})\) is a random phase term and \(|\varphi (\varOmega _{\text {s}})|~=~1\). Assuming a diffuse sound field, the spatial cross-correlation between the sound pressure at two positions \(\mathbf {r} = (r,\varOmega )\) and \(\mathbf {r}' = (r,\varOmega ')\) is given by:
Using the orthonormality property of the spherical harmonics in (2.18) and the addition theorem in (2.23), we eliminate the cross terms followed by the sum over m and obtain

where \(\varTheta _{\mathbf {r},\mathbf {r}'}\) is the angle between \(\mathbf {r}\) and \(\mathbf {r}'\).
In the open sphere case, we can derive a simplified expression for \(C(\mathbf {r},\mathbf {r}',k)\). Firstly, we note that the expression in (4.25) is real, and therefore, for a reason which will soon become clear, \(C(\mathbf {r},\mathbf {r}',k)\) can advantageously be expressed as

where \(\mathfrak {I}\) denotes the imaginary part of a complex number. By substituting the open sphere mode strength \(b_l(k) = i^l j_l(kr)\) into (4.26), we obtain

Using \(\mathfrak {R}\{h_l^{(2)}(kr)\} = j_l(kr)\), where \(\mathfrak {R}\) denotes the real part of a complex number, we can now write (4.27) as

As the expression marked with a \(\star \) is real, its imaginary part is zero and (4.28) can be simplified to

Finally, using (4.7) and (4.8), we obtain the well-known spatial domain result for two omnidirectional receivers in a diffuse sound field [20, 31, 39]:
Rights and permissions
Copyright information
© 2017 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Jarrett, D.P., Habets, E.A.P., Naylor, P.A. (2017). Spherical Array Acoustic Impulse Response Simulation. In: Theory and Applications of Spherical Microphone Array Processing. Springer Topics in Signal Processing, vol 9. Springer, Cham. https://doi.org/10.1007/978-3-319-42211-4_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-42211-4_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-42209-1
Online ISBN: 978-3-319-42211-4
eBook Packages: EngineeringEngineering (R0)
















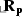 that is required for the SMIR method.
that is required for the SMIR method.