Keywords

15.1 Introduction

Magneto-hydrodynamics (MHD) is the branch of continuum mechanics which deals with the flow of electrically conducting fluids in electric and magnetic fields. Many natural phenomena and engineering problems are worth being subjected to an MHD analysis. Magneto-hydrodynamic equations are ordinary electromagnetic and hydrodynamic equations modified to take into account the interaction between the motion of the fluid and the electromagnetic field. The formulation of the electromagnetic theory in a mathematical form is known as Maxwell’s equations.

The flow and heat transfer of electrically conducting fluids in channels and circular pipes under the effect of a transverse magnetic field occurs in magneto-hydrodynamic (MHD) generators, pumps, accelerators and flow meters and have applications in nuclear reactors, filtration, geothermal systems and others. The interest in the outer magnetic field effect on heat-physical processes appeared seventy years ago. Research in magneto-hydrodynamics grew rapidly during the late 1950s as a result of extensive studies of ionized gases for a number of applications. Blum et al. [1] carried out one of the first works in the field of heat and mass transfer in the presence of a magnetic field. Many exciting innovations were put forth in the areas of MHD propulsion [5], remote energy deposition for drag reduction [32], plasma actuators, radiation driven hypersonic wind tunnel, MHD control of flow and heat transfer in the boundary layer [2, 23, 24, 39], enhanced plasma ignition [11] and combustion stability. Extensive research however has revealed that additional and refined fidelity of physics in modeling and analyzing the interdisciplinary endeavor are required to reach a conclusive assessment. In order to ensure a successful and effective use of electromagnetic phenomena in industrial processes and technical systems, a very good understanding of the effects of the application of a magnetic field on the flow of electrically conducting fluids in channels and various geometric elements is required.

The present trend in the field of chemical reaction analysis is to give a mathematical model for the system to predict the reactor performance. Much research was being carried out across the globe. The study of heat and mass transfer with chemical reaction is given primary importance in chemical and hydro-metallurgical industries. A study on chemical reaction on the flow past an impulsively started vertical plate with uniform heat and mass flux was made by Muthucumaraswamy and Ganesan [21]. The same type of problem with inclusion of constant wall suction was studied by Makinde and Sibanda [17]. Fan et al. [6] studied the same problem over a horizontal moving plate. Kandasamy and Anjalidevi [10] investigated the effect of chemical reaction of the flow over a wedge. Sattar [29] investigated the effect of free and forced convection boundary layer flow through a Porous medium with large suction. Atul Kumar Singh [30] analyzed the MHD free convection and mass transfer flow with heat source and thermal diffusion. Recently Prathap Kumar et al. [12,13,14,15,16] have studied Taylor dispersion of solute for immiscible fluids for viscous and for composite Porous media.

Umavathi [33] studied the combined effect of viscous and applied electrical field in a vertical channel. Later Umavathi and her group analyzed magneto-hydrodynamic flow and heat transfer for various geometries [18,19,20, 34,35,36,37,38]. Yao [41] studied the natural convection heat transfer from isothermal vertical wavy surfaces, such as sinusoidal surfaces. Rees and Pop [27] examined the natural convection flow over a vertical wavy surface with constant wall temperature in Porous media saturated with Newtonian fluids. Hossain and Rees [8] studied the heat and mass transfer in natural convection flow along a vertical wavy surface with constant wall temperature and concentration for Newtonian fluid. Cheng [3] presented the solution of heat and mass transfer in natural convection flow along a vertical wavy surface in Porous medium saturated with Newtonian fluid.

When the channel is divided into several passages by means of plane baffles, as usually occurs in heat exchangers or electronic equipment, it is quite possible to enhance the heat transfer performance between the walls and fluid by the adjustment of each baffle position and strength of separate flow streams. In such configurations, perfectly conductive and thin baffles may be used to avoid significant increase of the transverse thermal resistance. Chin-Hsiang et al. [4] studied the thermal characteristics of hydro dynamically and thermally fully developed flow in an asymmetrical heated horizontal channel, which is divided into two passages (by means of a baffle) for two separate flow streams. Salah El-Din [28] studied analytically, the laminar fully developed combined convection in a vertical double passage channel with different wall temperature and concluded that heat transfer in the channel is affected significantly by the baffle position.

The differential transformation method (DTM) is a numerical method based on a Taylor expansion. This method constructs an analytical solution in the form of a polynomial. The concept of differential transform method was first proposed and applied to solve linear and nonlinear initial value problems in electric circuit analysis by Zhou [42]. Unlike the traditional high order Taylor series method which requires a lot of symbolic computations, the differential transform method is an iterative procedure for obtaining Taylor series solutions. This method will not consume too much computer time when applying to nonlinear or parameter varying systems. But, it is different from Taylor series method that requires computation of the high order derivatives. The differential transform method is an iterative procedure that is described by the transformed equations of original functions for solution of differential equations. This method is well addressed in [9, 22, 25, 26, 40].

Keeping in view the practical applications where there is a requirement of enhancement of heat transfer by inserting a baffle and the effects of chemical reaction, it is the aim of this paper to understand the flow nature by inserting a baffle in a vertical channel filled with chemically reacting conducting fluid.

15.2 Mathematical Formulation

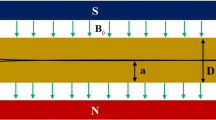
Consider a steady, two-dimensional laminar fully developed free convection flow in an open ended vertical channel filled with purely viscous electrically conducting fluid. The x-axis is taken vertically upward, and parallel to the direction of buoyancy, and the y-axis is normal to it. A uniform magnetic field is applied normal to the plates and uniform electric field is applied perpendicular to the plate. The thermal conductivity, dynamic viscosity, thermal and concentration expansion coefficients are considered as constant. The Oberbeck-Boussinesq approximation is assumed to hold and for the evaluation of the gravitational body force, the density \(\rho \) is assumed to depend on temperature according to the equation of state \((\rho =\rho _{0}(1-\beta (T-T_{0})))\). It is also assumed that the magnetic Reynolds number is sufficiently small so that the induced magnetic field can be neglected and the induced electric field is assumed to be negligible. Ohmic and viscous dissipations are included in the energy equation. The flow is assumed to be steady, laminar and fully developed. The walls are maintained at constant but different temperatures. The channel is divided into two passages by means of thin, perfectly conducting plane baffle and each stream will have its own pressure gradient and hence the velocity will be individual in each stream. After inserting the baffle, the fluid in Stream-I is concentrated.

The governing equations for velocity, temperature and concentration are

Stream-I

$$\begin{aligned} \rho g \beta _{T}(T_{1}-Tw_{2})+\rho g \beta _{c} (C_{1}-C_{0})-\frac{dP}{dX}+\mu \frac{d^{2 }U_{1}}{d Y^{2}}-\sigma _{e}(E_{0}+B_{0}U_{1})B_{0}=0, \end{aligned}$$
(15.1)
$$\begin{aligned} \frac{d^2 T_1}{d Y^2}+\frac{\nu }{\alpha C_{p}} \left( \frac{dU_{1}}{dY} \right) ^{2}+\frac{\sigma _{e}}{\alpha \rho C_p} (E_0 +B_0 U_{1})^{2}=0, \end{aligned}$$
(15.2)
$$\begin{aligned} D\frac{d^2 C_1}{d Y^2}-K_1C_1=0, \end{aligned}$$
(15.3)

Stream-II

$$\begin{aligned} \rho g \beta _{T}(T_{1}-Tw_{2})-\frac{\partial P}{\partial X}+\mu \frac{d^2 U_2}{dY^2}-\sigma _e(E_{0}+B_0U_2)B_0=0, \end{aligned}$$
(15.4)
$$\begin{aligned} \frac{d^2 T_2}{d Y^2}+\frac{\nu }{\alpha C_p}\left( \frac{d U_2}{d Y}\right) ^2+\dfrac{\sigma _e}{\alpha \rho C_p}(E_0+B_0 U-2)^{2}=0, \end{aligned}$$
(15.5)

which are subject to the boundary conditions on velocity, temperature and concentration as

$$\begin{aligned} U_{1}=0,~T_{1}=T_{W_{1}}=0,~C=C_1~~~\mathrm {at}~~~Y=-h, \nonumber \\ U_{2}=0,~T_{1}=T_{W_{2}}=0,~~~\mathrm {at}~~~Y=h, \nonumber \\ U_{1}=0,~U_{2}=0,~T_1=T_2,~\frac{dT_1}{dY}=\frac{dT_2}{dY},~C=C_2~~\mathrm {at}~~Y=h^*. \end{aligned}$$
(15.6)

Introducing the following non-dimensional variables in the governing equations for velocity temperature and concentration as

$$\begin{aligned} u_i=\frac{U_i}{U_1},~\theta =\frac{T_i-T_{w_{2}}}{T_{w_{1}}-T_{w_{2}}},~Gr=\frac{g\beta _{T}\triangle T h^3}{\upsilon ^2},\\ Gc=\frac{g\beta _{c}\triangle C h^3}{\upsilon ^2},~\phi _{1}=\frac{C-C_0}{C_1-C_0},~Re=\frac{\overline{U_1}h}{\upsilon },~Br=\frac{\overline{U}^{2}_{1} \mu }{k \bigtriangleup T}, \nonumber \\ Y^*=\frac{Y^*}{h},~p=\frac{h^2}{\mu \overline{U}_{1}}\frac{d p}{d X},~\bigtriangleup T=T_{w_{2}}-T_{w_{1}}, \nonumber \\ \bigtriangleup C=C_1-C_0,~Y=\frac{y}{h},~M^2=\frac{\sigma _{e}B^{2}_{0}h^2}{\mu },\nonumber \\ E=\frac{E_0}{B_0 \overline{u}_{1}},~\alpha =\frac{k_1 h^2}{D},~n=\frac{C_2-C_0}{C_1-C_0}.\nonumber \end{aligned}$$
(15.7)

one obtains the momentum, energy and concentration equations corresponding to Stream-I and Stream-II as

Stream-I

$$\begin{aligned} \frac{d^{2} u_{1}}{d y^{2}}+G R_{T}\theta _{1}+G R_{C} \phi _{1}-p-M^{2}(E+u_{1})=0, \end{aligned}$$
(15.8)
$$\begin{aligned} \frac{d^2 \theta _1}{d y^2}+Br\left( \left( \frac{d u_1}{d y} \right) ^{2}+M^2(E+u_1)^2 \right) =0, \end{aligned}$$
(15.9)
$$\begin{aligned} \frac{d^2 \phi _1}{d y^2}-\alpha ^{2} \phi _{1}=0, \end{aligned}$$
(15.10)

Stream-II

$$\begin{aligned} \frac{d^2 u_2}{d y^2}+GR_{T} \theta _{2}-p-M^2(E+u_2)=0, \end{aligned}$$
(15.11)
$$\begin{aligned} \frac{d^2 \theta _2}{d y^2}+Br\left( \left( \frac{d u_2}{d y} \right) ^{2}+M^2(E+u_2)^2 \right) =0, \end{aligned}$$
(15.12)

which are subject to the boundary conditions

$$\begin{aligned} u_1=0,~ \theta _1=1, ~\phi _1=1,~~~\mathrm {at}~~~y=-1, \\ u_2=0,~\theta _2=0~~~\mathrm {at}~~~y=1, \nonumber \\ u_1=0,~ u_2=0, ~\theta _1=\theta _2, ~\frac{d \theta _1}{d y}=\frac{d \theta _2}{d y},~\phi _1=n~~~\mathrm {at}~~~y=y^*,\nonumber \end{aligned}$$
(15.13)

where \(GR_T=\frac{Gr}{Re}\) and \(GR_C=\frac{Gc}{Re}\).

15.3 Solutions

Solution of (15.10) using boundary condition (15.13) becomes

$$\begin{aligned} \phi _1=B_1 \cosh (\alpha y)+B_2 \sinh (\alpha y). \end{aligned}$$
(15.14)

15.3.1 Perturbation Method

Equations (15.8), (15.9), (15.11) and (15.12) are coupled non-linear ordinary differential equations. Approximate solutions can be found by using the regular perturbation method. The perturbation parameter Br is usually small and hence regular perturbation method can be strongly justified. Adopting this technique, solutions for velocity and temperature are assumed in the form

$$\begin{aligned} u_i(y)=u_{i0}(y)+Br u_{i1}(y)+Br^2 u_{i2}(y)+\cdots , \end{aligned}$$
(15.15)
$$\begin{aligned} \theta _i(y)=\theta _{i0}(y)+Br \theta _{i1}(y)+Br^2 \theta _{i2}(y)+\cdots . \end{aligned}$$
(15.16)

Substituting (15.15) and (15.16) in (15.8), (15.9), (15.11) and (15.12), and equating the coefficients of like power of Br to zero and one, we obtain the zero and first order equations as

Stream-I

Zeroth order equations

$$\begin{aligned} \frac{d^2 u_{10}}{d y^2}+GR_T \theta _{10}+GR_C \phi _1-p-M^2(E+u_{10})=0, \end{aligned}$$
(15.17)
$$\begin{aligned} \frac{d^2 \theta _{10}}{d y^2}=0. \end{aligned}$$
(15.18)

First order equations

$$\begin{aligned} \frac{d^2 u_{11}}{d y^2}+GR_T \theta _{11}-M^2u_{11}=0, \end{aligned}$$
(15.19)
$$\begin{aligned} T_{b}=T_{1}(z)+\varepsilon _{t}T_{2}(z,t), \end{aligned}$$
$$\begin{aligned} \frac{d^2 \theta _{11}}{d y^2}+\left( \left( \frac{d u_{10}}{dy}\right) ^{2}+M^2(E+u_{10})^{2} \right) =0. \end{aligned}$$
(15.20)

Stream-II

Zeroth order equations

$$\begin{aligned} \frac{d^2 u_{20}}{d y^2}+GR_T \theta _{20}-p-M^2(E+u_{20})=0, \end{aligned}$$
(15.21)
$$\begin{aligned} \frac{d^2 \theta _{20}}{d y^2}=0. \end{aligned}$$
(15.22)

First order equations

$$\begin{aligned} \frac{d^2 u_{21}}{d y^2}+GR_T \theta _{21}-p-M^2(E+u_{20})=0, \end{aligned}$$
(15.23)
$$\begin{aligned} \frac{d^2 \theta _{21}}{d y^2}+\left( \left( \frac{d u_{20}}{dy}\right) ^{2}+M^2(E+u_{20})^{2} \right) =0. \end{aligned}$$
(15.24)

The corresponding boundary conditions reduces to

Zeroth order

$$\begin{aligned} u_{10}=0,~\theta _{10}=1,~\phi _{1}=1~~~\mathrm {at}~~~y=-1, \\ u_{20}=0,~\theta _{20}=0~~~\mathrm {at}~~~y=1, \nonumber \\ u_{10}=0,~u_{20}=0,~\theta _{10}=\theta _{20},~\frac{d \theta _{10}}{dy}=\frac{d \theta _{20}}{dy},~\phi _1=n~~~\mathrm {at}~~~y=y^*.\nonumber \end{aligned}$$
(15.25)

First order

$$\begin{aligned} u_{11}=0,~\theta _{11}=0~~~\mathrm {at}~~~y=-1, \\ u_{21}=0,~\theta _{21}=0~~~\mathrm {at}~~~y=1, \nonumber \\ u_{11}=0,~u_{21}=0,~\theta _{11}=\theta _{21},~\frac{d \theta _{11}}{dy}=\frac{d \theta _{21}}{dy},~\phi _1=n~~~\mathrm {at}~~~y=y^*.\nonumber \end{aligned}$$
(15.26)

The solutions of the zeroth and first order Eqs. (15.17)-(15.24) using the boundary conditions as in (15.25) and (15.26) become

Zeroth-order solutions

Stream-I

$$\begin{aligned} \theta _{10}=z_1y+z_2, \end{aligned}$$
(15.27)
$$\begin{aligned} u_{10}=A_1 \cosh (My)+A_2 \sinh (My)+r_1+r_2y+r_3 \cosh (\alpha y)+r_4 \sinh (\alpha y).\nonumber \\ \end{aligned}$$
(15.28)

Stream-II

$$\begin{aligned} \theta _{20}=z_3y+z_4, \end{aligned}$$
(15.29)
$$\begin{aligned} u_{20}=A_3 \cosh (My)+A_4 \sinh (My)+r_5+r_6y. \end{aligned}$$
(15.30)
Fig. 15.1
figure 1

Velocity profiles for different values of thermal Grashof number \(GR_T\) at a \(y^*=0.8\),  b \(y^*=0\), c \(y^*=0.8 \)

Full size image
Fig. 15.2
figure 2

Temperature profiles for different values of thermal Grashof number \(GR_T\) at a \(y^*=0.8\), b \(y^*=0\), c \(y^*=0.8 \)

Full size image
Fig. 15.3
figure 3

Velocity profiles for different values of concentration Grashof number \(GR_C\) at a \(y^*=-0.8\), b \(y^*=0\), c \(y^*=0.8 \)

Full size image
Fig. 15.4
figure 4

Temperature profiles for different values of concentration Grashof number \(GR_C\) at a \(y^*=-0.8\), b \(y^*=0\), c \(y^*=0.8 \)

Full size image
Fig. 15.5
figure 5

Velocity profiles for different values of Brikman number Br at a \(y^*=-0.8\), b \(y^*=0\), c \(y^*=0.8 \)

Full size image
Fig. 15.6
figure 6

Temperature profiles for different values of Brikman number Br at a \(y^*=-0.8\), b \(y^*=0\), c \(y^*=0.8 \)

Full size image
Fig. 15.7
figure 7

Velocity profiles for different values of chemical reaction parameter \(\alpha \) at a \(y^*=-0.8,\) b \(y^*=0\), c \(y^*=0.8 \)

Full size image
Fig. 15.8
figure 8

Temperature profiles for different values of chemical reaction parameter \(\alpha \) at a \(y^*=-0.8\), b \(y^*=0\), c \(y^*=0.8 \)

Full size image
Fig. 15.9
figure 9

Concentration profiles for different values of chemical reaction parameter \(\alpha \) at a \(y^*=-0.8\), b \(y^*=0\), c \(y^*=0.8 \)

Full size image
Fig. 15.10
figure 10

Velocity profiles for different values of Hartmann number M at a \(y^*=-0.8\), b \(y^*=0\), c \(y^*=0.8 \)

Full size image
Fig. 15.11
figure 11

Temperature profiles for different values of Hartmann number M at a \(~y^*=-0.8\), b \(y^*=0\), c \(y^*=0.8\)

Full size image
Fig. 15.12
figure 12

Velocity profiles for different values of electric field load parameter E at a \(y^*=-0.8\), b \(y^*=0\), c \(y^*=0.8 \)

Full size image
Fig. 15.13
figure 13

Temperature profiles for different values of electric field load parameter E at a \(y^*=-0.8\), b \(y^*=0\), c \(y^*=0.8\)

Full size image

First order solution

Stream-I

$$\begin{aligned} \theta _{11}=E_1+E_2y+q_1y^2+q_2y^3+q_3y^4+q_4 \cosh (\alpha y)+ \\ +q_5 \sinh (\alpha y)+q_6 \cosh (2 \alpha y)+q_7 \sinh (2 \alpha y)+q_8 \cosh (2 M y)+ \nonumber \\ +q_9 \sinh (2 M y)+q_{10} \cosh (M y)+q_{11} \sinh (M y)+q_{12} y \cosh (M y)+ \nonumber \\ +q_{13} y \sinh (M y)+q_{14} y \cosh (\alpha y)+q_{15} y \sinh (\alpha y)+q_{16} \cosh (\alpha +M) y+ \nonumber \\ +q_{17} \cosh (\alpha -M) y+q_{18} \sinh (\alpha +M)y+q_{19} \sinh (\alpha -M)y, \nonumber \end{aligned}$$
(15.31)
$$\begin{aligned} u_{11}=E_3 \cosh (My)+E_4 \sinh (My)+H_1+H_2y+H_3y^2+ \\ +H_4y^3+H_5y^4+H_6 \cosh (\alpha y)+H_7 \sinh (\alpha y)+\nonumber \\ +H_8 \cosh (2 \alpha y)+H_9 \sinh (2 \alpha y)+H_{10} \cosh (2 M y)+\nonumber \\ + H_{11} \sinh (2 M y)+H_{12}y \cosh (M y)+H_{13}y \sinh (M y)+\nonumber \\ +H_{14}y \cosh (\alpha y)+H_{15}y \sinh (\alpha y)+H_{16} \cosh (\alpha +M)y+\nonumber \\ +H_{17} \cosh (\alpha -M)y+ H_{18} \sinh (\alpha +M)y+H_{19} \sinh (\alpha - M) y+ \nonumber \\ +H_{20}y^2 \cosh ( M y)+H_{21}y^2 \sinh (M y). \nonumber \end{aligned}$$
(15.32)

Stream-II

$$\begin{aligned} \theta _{21}=E_5+E_6 y+F_1y^2+F_2 y^3+F_3 y^4+ \\ +F_4 \cosh (2My)+F_5 \sinh (2My)+ F_6 \cosh (My)+\nonumber \\ +F_7 \sinh (My)+F_8 y \cosh (My)+F_9 y \sinh (My),\nonumber \end{aligned}$$
(15.33)
$$\begin{aligned} u_{21}=E_7 \cosh (My)+E_8 \sinh (My)+\\ +H_{22}+H_{23}y+H_{24}y^2+H_{25}y^3+H_{26} y^4+ \nonumber \\ +H_{27} \cosh (2My)+H_{28} \sinh (2My)+H_{29}y \cosh (My)+ \nonumber \\ +H_{30}y \sinh (My)+H_{31} y^2 \cosh (My)+H_{32} y^2 \sinh (My). \nonumber \end{aligned}$$
(15.34)

The dimensionless total volume flow rate is given by

$$\begin{aligned} Q\nu =Q\nu _{1}+Q\nu _{2}, \end{aligned}$$
(15.35)

where

$$\begin{aligned} Q\nu _{1}=\int _{-1}^{y^*}u_1 dy,~~ Q\nu _{2}=\int _{y^*}^{1}u_2 dy. \end{aligned}$$
(15.36)

The dimensionless total heat rate added to the fluid is given by

$$\begin{aligned} E=H_{E_1}+H_{E_2}, \end{aligned}$$
(15.37)
$$\begin{aligned} H_{E_1}=\int _{-1}^{y^*}u_1 \theta _1dy,~~H_{E_2}=\int _{y^*}^{1}u_2 \theta _2dy. \end{aligned}$$
(15.38)

The dimensionless total species rate added to the fluid is given by

$$\begin{aligned} Cs=Cs_1+Cs_2, \end{aligned}$$
(15.39)

where

$$\begin{aligned} Cs_{1}=\int _{-1}^{y^*}u_1 \phi _1dy, ~~Cs_{2}=\int _{y^*}^{1}u_2 \phi _2dy. \end{aligned}$$
(15.40)
Table 15.1 Comparison of velocity and temperature with \(Br=0\) and \(y^{*}=0.0\)
Full size table
Table 15.2 Comparison of velocity and temperature with \(Br=0.05\) and \(y^{*}=0.0\)
Full size table
Table 15.3 Comparison of velocity and temperature with \(Br=0.15\) and \(y^{*}=0.0\)
Full size table
Table 15.4 Comparison of velocity and temperature with \(Br=0\) and \(y^{*}=-0.8\)
Full size table
Table 15.5 Comparison of velocity and temperature with \(Br=0.05\) and \(y^{*}=-0.8\)
Full size table
Table 15.6 Comparison of velocity and temperature with \(Br=0.1\) and \(y^*=-0.8\)
Full size table
Table 15.7 Comparison of velocity and temperature with \(Br=0\) and \(y^{*}=0.8\)
Full size table
Table 15.8 Comparison of velocity and temperature with \(Br=0.01\) and \(y^{*}=0.8\)
Full size table
Table 15.9 Comparison of velocity and temperature with \(Br=0.08\) and \(y^{*}=0.8\)
Full size table
Table 15.10 Volumetric flow rate
Full size table
Table 15.11 Species concentration
Full size table
Table 15.12 Total energy flow
Full size table
Table 15.13 Skin friction
Full size table
Table 15.14 Skin friction
Full size table
Table 15.15 Nomenclature
Full size table

15.3.2 Basic Concept of Differential Transform Method

The analytical solutions obtained in Sect. 15.3.1 are valid only for small values of Brinkman number Br. In many practical problems mentioned earlier, the values of Br are usually large. In that case analytical solutions are difficult, and hence we resort to semi-numerical-analytical method known as Differential Transform Method (DTM).

The general concept of DTM is explained here: The kth differential transformation of an analytical function F(k) is defined as (Zhou [42])

$$\begin{aligned} F(k)=\frac{1}{k!} \left[ \frac{d^k f(\eta )}{d \eta ^k}\right] _{\eta =\eta _{0}}, \end{aligned}$$
(15.41)

and the inverse differential transformation is given by

$$\begin{aligned} f(\eta )=\sum _{k=0}^{\infty }F(k)(\eta -\eta _{0})^{k}. \end{aligned}$$
(15.42)

Combining (15.41) and (15.42)

$$\begin{aligned} f(\eta )=\sum _{k=0}^{\infty }F(k)\frac{(\eta -\eta _{0})^{k}}{k!} \frac{d^k f(\eta )}{d \eta ^{k}}\vert _{\eta =\eta _{0}} . \end{aligned}$$
(15.43)

From (15.42), it can be seen that the differential transformation method is derived from Taylor’s series expansion. In real applications the sum \( \sum _{k=0}^{\infty }F(k)(\eta -\eta _{0})^{k} \) is very small and can be neglected when k is sufficiently large. So \( f(\eta ) \) can be expressed by a finite series, and (15.42) may be written as

$$\begin{aligned} f(\eta )=\sum _{k=0}^{n}F(k)(\eta -\eta _{0})^{k}, \end{aligned}$$
(15.44)

where the value of k depends on the convergence requirement in real applications and F(k) is the differential transform of \(f(\eta )\).

15.4 Results and Discussion

The velocity, temperature and concentration fields for an electrically conducting fluid in a vertical double passage are presented in Figs. 15.1, 15.2, 15.3, 15.4, 15.5, 15.6, 15.7, 15.8, 15.9, 15.10, 15.11, 15.12 and 15.13. The channel is divided into two passages by inserting a thin perfectly conducting baffle. The fluid is concentrated in passage one only after inserting the baffle. The basic equations are solved by using regular perturbation method valid for small values of Br. The Brinkman number is exploited as a perturbation parameter. To understand the fluid nature for large values of Brinkman number , the coupled nonlinear ordinary differential equations are solved by DTM which is a semi-numerical-analytical method. The case \(E=0\) corresponds to short circuit and \(E\ne 0\) corresponds to the open circuit case. The values of thermal Grashof number , mass Grashof number, Brinkman number , pressure gradient, first order chemical reaction parameter, wall concentration ratio, and Hartman number are fixed as 5, 5, –5, 0.5, 1, 4 for open circuit \((E=-1)\) for all the graphs and tables except the varying parameter.

The effect of thermal Grashof number \(GR_T\) (ratio of thermal Grashof number to Reynolds number ) on the velocity and temperature fields is shown in Figs. 15.1 and 15.2 at three different baffle positions \((y^*=-0.8,~0,~0.8)\) keeping the left wall at higher temperature. It is observed from Figs. 15.1 and 15.2 that the velocity and temperature increases at all the baffle positions as the thermal Grashof number increases. However when the baffle is placed near left wall the maximum point of velocity is in Stream-II, when the baffle is placed near the centre of the channel and near the right wall, the maximum point of velocity is in Stream-I. It is also seen from Fig. 15.1 that the velocity profiles in both the passages are not equal though there is a no-slip condition at the walls and near the baffle. One can infer this result as, the thermal Grashof number increases as the buoyancy force increases and the wall conditions on temperature are not equal (left wall is at higher temperature when compared to right wall). It is seen from Fig. 15.2 that the temperature profiles look similar at all the baffle positions. This is due to the reason that the temperature and heat flux are considered as continuous at the baffle positions. The optimum value of temperature is seen in Stream-II for the baffle position near the left wall and in Stream-I when the baffle position is near the right wall.

The effect of mass Grashof number \(GR_C \) (ratio of mass Grashof number to Reynolds number ) on the flow is shown in Figs. 15.3 and 15.4 at all baffle positions. The increase in mass Grashof number increases the velocity and temperature fields in both the streams at all the baffle positions. The enhancement of velocity is significant in Stream-I when compared to Stream-II. The reason for this nature is that fluid is concentrated only in Stream-I. It is viewed from Fig. 15.4b that though the fluid is not concentrated in Stream-II there is a slight increase in the velocity field when the baffle is positioned near the centre of the channel. This is because of the conditions imposed on temperature and heat flux. That is to say that, there is heat transfer from Stream-I to Stream-II and there is no mass transfer from Stream-I to Stream-II. However due to transfer of heat from Stream-I to Stream-II results in increase in thermal and concentration buoyancy forces and hence enhancement of velocity in small magnitude is observed in Stream-II as \(GR_C\) increases. There is no effect of \(GR_C\) in Stream-II when the baffle is positioned near the left and right walls. Similar results were also observed by Fasogbon [7] for regular channel in the absence of baffle. From Fig. 15.4a it is seen that the temperature does not vary significantly in both the streams as \( GR_C\) increases when the baffle is positioned near the left wall. However its influence is dominated in Stream-I when the baffle is placed in the centre of the channel and near the right wall.

As the Brinkman number increases, the velocity and temperature increases in both streams at all baffle positions as seen in Figs. 15.5 and 15.6, respectively. One can infer this nature is due to the fact that increase in Brinkman number increases the viscous dissipation and hence increases the temperature, which in turn influences the velocity field. Here also temperature profiles looks similar at all baffle positions.

The effect of the first order chemical reaction parameter \( \alpha \), on the velocity, temperature and concentration fields is observed in Figs. 15.7, 15.8 and 15.9, respectively. As \(\alpha \) increases the velocity and temperature decreases in Stream-I and does not influence in Stream-II. This is due to the fact that the fluid in Stream-I is concentrated. At any position of the baffle the effect of \(\alpha \) is to minimize the concentration field. Figure 15.9 shows the concentration profiles when the baffle is positioned at \(y^*=-0.8,~0,~0.8\) and respectively. Similar results were also observed by Srinivas and Muturaj [31] for mixed convective flow in a vertical channel in the absence of baffle.

The effect of Hartman number M on velocity and temperature field is shown in Figs. 15.10 and 15.11, respectively at three positions of the baffle. As the Hartman number M increases velocity decreases in both streams at different positions of the baffle for open circuits. The Hartman number M represents the ratio of the Lorentz force to the viscous force, implying that the larger the Hartman number, the stronger the retarding effect on the velocity field. Hence as Hartman number M increases the velocity decreases at all baffle positions. Further, as the width of the passage increases, the velocity profiles are flattened. Hence the velocity profiles are wider in Stream-II when the baffle is placed near the left wall, in Stream-I when the baffle is placed near the right wall and narrow when the baffle is placed in the centre of the channel. The temperature profiles are also reduced as the Hartman number increases in both the streams when the baffle is positioned at the centre and at the right wall. The temperature decreases as M increases at \( M=-0.5\) (approximately) and onwards, where as it increases in Stream-I. This nature can be inferred as when the baffle is near the right wall, which is at higher temperature, is not much influenced by the retarding effect of the Lorenz force. Further one can also observe that the temperature profile is wider in Stream-I when the baffle is placed near the right wall when compared to the baffle positioned in the centre of the channel.

The effect of the applied electric field E on the velocity and temperature is displaced in Figs. 15.12 and 15.13, respectively for both open and short circuits. The effect of negative E is to add the flow while the effect of positive E is to oppose the flow as compared to the case for the short circuit. Since the direction of flow is reversed by changing the values of E, the results can be applied to the practical problem where there is a requirement of reversal flow. The temperature increases as the electric field load parameter increases in both passages at all baffle positions. However, the magnitude of temperature is large for positive E when compared to negative E. Here also the temperature profiles are flat in wider passage. The effect of Hartman number and electric field load parameter on the flow show similar results as observed by Umavathi [33] in the absence of baffle and the first order chemical reaction.

Since the regular perturbation method (PM) is valid only for small values of Brinkman number , this restriction in relaxed by finding the solution of the governing equation using the DTM. Tables 15.1, 15.2, 15.3, 15.4, 15.5, 15.6, 15.7, 15.8 and 15.9 are the values of velocity and temperature when the baffle is positioned near the centre of the channel, near the left wall and near the right wall respectively. The validity of the DTM is justified by comparing the DTM solutions with the PM method in the absence of the Brinkman number . It is seen from Tables 15.1, 15.4, and 15.7 that the DTM and PM values are exact in the absence of the Brinkman number at all baffle positions in both streams. When the Brinkman number is 0.05, the percentage of error of the DTM and the PM is less when compared with the value of Br = 0.15 as seen in Tables 15.2, 15.3, 15.5, 15.6, 15.8, and 15.9, respectively at all baffle positions in both streams. Hence, one can conclude that regular perturbation method cannot be applied for large values of the Brinkman number as the error is greater. Further, one can infer from these tables that the percentage of error between the DTM and the PM is greater in the narrow passage \(y^*=0\) when compared with wider passage \(y^*=-0.8,~0.8\), for different values of the Brinkman number .

The effect of thermal Grashof number \(GR_T \), mass Grashof number \(GR_C\), Brinkman number Br, chemical reaction parameter \(\alpha \) and Hartmann number M on the volumetric flow rate in Stream-I and Stream-II at different positions of the baffle is tabulated in Table 15.10. It is seen that increase in the thermal Grashof number , mass Grashof number and the Brinkman number increases the volumetric flow rate of the fluid flowing through the vertical channel. This is due to the reasons that increase in the thermal Grashof number and mass Grashof number increases the buoyancy which tends to accelerate the fluid flow, thus raising the volumetric flow rate. Increase in the Brinkman number increases the viscous dissipation and hence accelerates the fluid flow. The chemical reaction parameter and the Hartmann number reduces the volumetric flow rates in both streams at all baffle positions, which is an expected result. The effect of governing parameters on species concentration is shown in Table 15.11. Increase in thermal Grashof number , mass Grashof number and Brinkman number accelerates the fluid flow, thus enhancing the mass transfer rate between the wall and the fluid flowing through the vertical channel. As the chemical reaction parameter \(\alpha \) and Hartmann number M increase, the dimensionless total species rate added to the fluid decreases.

The dimensionless total heat rate added to the fluid is tabulated in Table 15.12 as functions of thermal Grashof number \(GR_{T}\), mass Grashof number \(GR_{C}\), Brinkman number Br, chemical reaction parameter \(\alpha \) and Hartmann number M. As \(GR_T,~GR_{C}\) and Br increases, buoyancy tends to accelerate the fluid flow raising the heat transfer rate between wall and fluid and thus increases the total heat rate added to the fluid in the vertical channel. The first order chemical reaction parameter and Porous parameter reduces the total heat rate added to the fluid in both streams at all baffle positions.

The magnitude of skin friction at the left and right wall increase as \(GR_{T}\) and \(GR_{C}\) increase, and decreases with \(\alpha \) and M at all baffle positions in both streams as shown in Table 15.13. Similar nature is also observed on the Nusselt number at the left and right walls as it can be viewed in Table 15.14. That is to say that magnitude of Nusselt number increases at both plates as \(GR_{T},~GR_{C}\) and Br increases and decreases as alpha and M increase at all baffle positions in both streams.

15.5 Conclusion

The characteristics of heat and mass transfer of electrically conducting fluid in a vertical double passage channel with a perfectly conducting baffle was studied. The solutions of governing equations and the associated boundary conditions have been obtained by using regular the PM method valid for small values of the Brinkman number and by the DTM valid for all values of Br. The following conclusions are made

  1. 1.

    Increase in thermal Grashof number , mass Grashof number and Brinkman number enhances the flow in both passages at different baffle positions.

  2. 2.

    The maximum velocity profiles are obtained in Stream-II when the baffle is near the left wall and in Stream-I when the baffle position is in the middle of the channel and at the right wall.

  3. 3.

    Increase in chemical reaction parameter decreases the velocity, temperature and concentration in Stream-I and remains unaltered in Stream-II.

  4. 4.

    The effect of the Hartman number is to reduce the flow at all baffle positions. The flow profiles are flat in the wider passage when compared to the narrow one. The negative electric field load parameter is to increase the velocity field and opposite effect is observed for the positive one. The temperature field is enhanced for both positive and negative values of the electric field load parameter at all baffle positions.

  5. 5.

    An exact agreement was obtained with the results of the DTM and the PM in the absence of the Brinkman number error increases between DTM and PM as the Brinkman number increases.

  6. 6.

    The results of the present model agree with the results obtained by Fasogbon [7], Srinivas Mutturajan [31] and Umavathi [33] in the absence of the baffle and the first order chemical reaction.