Design Considerations for Filtering Delta Sigma Converters

Abstract

Many signal chains need to digitize signals in the presence of interferers. The usual way of accomplishing this is to use an analog anti-alias filter followed by a Nyquist ADC. Continuous-time $\varDelta \varSigma$ modulators (CT$\varDelta \varSigma$ M) are compelling alternatives to Nyquist rate ADCs. While oversampling relaxes the requirements of the anti-alias filter, it is natural to wonder if the built-in filtering of a CT$\varDelta \varSigma$ M, characterized by its Signal Transfer Function (STF), can be used to attenuate interferers so that an explicit filter up front can be dispensed with altogether. It turns out that the Signal Transfer Function (STF) of a conventional CTΔ ΣM is a by-product of NTF synthesis, with the designer having little control over it. The STF can be independently controlled by using a filter up front—however, this increases power dissipation and degrades linearity of the signal chain. Embedding the filter in the modulator achieves the same objective in a power efficient manner, while improving out-of-band linearity and reducing active area. This work reviews filtering $\varDelta \varSigma$ conversion and circuit techniques for such converters.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The direct conversion architecture is perhaps the most prevalent in contemporary radio receivers. Figure 4.1 shows a simplified block diagram of such a receiver. It consists of a low noise amplifier (LNA), mixers, variable gain amplifiers (VGA), low pass filters (LPF) and analog to digital converters (ADC). The role of the LPF is two-fold. Since the received signal can be potentially dominated by large interferers, the LPF attenuates them and thereby reduces the dynamic range (DR) required of the ADC. It also acts as an anti-alias filter and prevents noise from aliasing into the signal band. There is a trade off between the performance requirements of the filter and ADC. For instance, when a Nyquist rate ADC is used, its sampling rate is typically chosen to be about 4 times the bandwidth of the baseband signal. A lower sampling rate would necessitate a higher order filter, making its design particularly challenging.

Fig. 4.1

Simplified block diagram of the front end of a typical wireless receiver

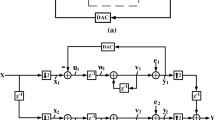
Continuous-time $\varDelta \varSigma$ modulators ( CTΔ ΣMs ) are a compelling choice for implementing the ADCs in wireless receivers. The block diagram of a CTΔ ΣM is shown in Fig. 4.2a. L _o (s) and L ₁(s) denote the transfer functions from the input u(t) and the DAC waveform v(t) to the loop filter’s output respectively. Assuming that quantization noise is additive, the functional block diagram of the CTΔ ΣM is shown in Fig. 4.2b. The input u(t) can be thought of as being filtered up front by a linear time invariant filter whose transfer function, denoted by ST​F(f), is called the signal transfer function (STF). The signal component of the modulator’s output v[n] is the sampled version of the output of the STF “filter”. Needless to say, the STF depends on L _o (s), L ₁(s) and the DAC pulse shape. It turns out that if the modulator’s loop filter is time invariant, the STF has nulls at multiples of the sampling frequency f _s . Thus, CTΔ ΣMs possess the inherent anti-aliasing property, which renders noise folding a non-issue. Quantization noise, denoted by the sequence e[n] appears in v[n] after being shaped, or high pass filtered by the noise transfer function (NTF). The aim of the design process is to choose the NTF so that the in-band quantization noise is sufficiently small. The decimation filter that follows the CTΔ ΣM eliminates out of band quantization noise.

Fig. 4.2

(a ) Block diagram of a continuous-time $\varDelta \varSigma$ modulator and (b ) its functional equivalent

When a CTΔ ΣM is used as the ADC in the radio receiver of Fig. 4.1, the role of the LPF is to eliminate interferers rather than address the aliasing of noise into the signal band. A CTΔ ΣM has several other advantages—it has a resistive input impedance, it is easy to drive and results in a simplified signal chain with reduced power dissipation. When compared to $\varDelta \varSigma$ ADCs employing switched capacitor techniques, the opamps used in CTΔ ΣMs have reduced slew rate requirements, thereby resulting in better linearity for a given speed and power dissipation. CTΔ ΣMs are also immune to substrate noise, since sampling occurs after the signal has been processed by the loop filter. Several high performance $\varDelta \varSigma$ modulators with signal bandwidths of several 10’s of MHz (keeping communication applications in mind) and about 11-12 bit resolution have been reported recently [1–3]. However, a filter is still needed to attenuate interferers, without which the dynamic range of the ADC would need to increase.

Since a CTΔ ΣM has a built-in filter (its STF), it is natural to wonder if the explicit filter of Fig. 4.1 can now be dispensed with. This, however, is problematic as explained below. Conventional CTΔ ΣM architectures do not allow independent control over the shape and bandwidth of the STF, as the STF is simply a by-product of NTF synthesis. The shape of the signal transfer function depends on the architecture of the loop filter used as illustrated below. Figure 4.3 shows commonly used (fourth order) modulator topologies—the cascade of integrators in feedback (CIFB), cascade of integrators in feedforward (CIFF) and cascade of integrators in feedforward-feedback (CIFF-B) and their corresponding STFs. B denotes the signal bandwidth. Keeping in mind a single-bit quantizer, the NTF is assumed to have an out-of-band gain of 1.5. In a CIFB structure (Fig. 4.3a), the STF has fourth order roll-off at high frequencies. However, such a structure is not power efficient, as the gain of the first integrator (a ₄∕s) is small in the signal band. Thus noise and distortion from succeeding integrators can be significant when referred to the input. Using a CIFF loop filter (Fig. 4.3b) avoids this problem, since the gain of the first integrator is large in the signal band. However, the STF now peaks outside the desired signal band and has only first order roll-off at high frequencies. The advantages of the CIFF and CIFB structures are combined in the CIFF-B topology (Fig. 4.3c) [3, 4]. This architecture results in a large in-band gain for the first integrator, and an STF that has third order roll-off at high frequencies. The STF still peaks at out-of-band frequencies. From the STFs shown in Fig. 4.3, it is clear that irrespective of the loop filter topology used, a CTΔ ΣM cannot attenuate nearby interferers—there are simply not enough degrees of freedom to specify the shape and bandwidth of the STF, and achieve the desired NTF at the same time. Without an explicit filter to reject interferers, the dynamic range of the CTΔ ΣM should be increased, like with any other ADC.

Fig. 4.3

(a ) CIFB, (b ) CIFF, (c ) CIFF-B loop filter realizations for a fourth order modulator and their STFs

Peaking in the STF further increases the in-band dynamic range needed in the modulator due to the following. To understand this, we consider an example of a single bit CTDSM. With an NTF whose out of band gain is 1.5, the maximum stable amplitude (MSA) for low frequency inputs is typically about − 3 dBFS. The MSA at a frequency f _in is ≈ 0. 7V _FS ∕ST​F(f _in ), where V _FS is the full scale voltage. A 6 dB STF peak restricts the CTΔ ΣM input to (1∕2)0. 7V _FS , necessitating a 6 dB smaller in-band noise to get the same in-band SNR, which increases power dissipation. A straightforward way of attenuating nearby interferers and addressing STF peaking at the same time is to use a filter up front. The filter, however, occupies additional area, consumes power, adds noise and potentially degrades linearity of the signal chain.

Alternatively, the filter can be incorporated into the $\varDelta \varSigma$ loop by moving it beyond the first integrator—this way, the noise from the filter is reduced by the in-band gain of the first integrator. The system noise budget, usually split between the filter and CTΔ ΣM, can now be allocated to the first integrator of the modulator. Alternatively, the filter and CTΔ ΣM can be combined so that the overall performance improves, for a given power dissipation. The authors of [5] embed a second order CTΔ ΣM inside a Rauch biquad. The design of [6] embeds a third order CTΔ ΣM in an active-RC biquad. Another version [7] by the same authors embeds a second order modulator into a third order active-RC filter. Several recent CTΔ ΣMs [8] also embed modulators into a filter.

This work reviews techniques to combine a filter and CTΔ ΣM ​​, and gives experimental results of a design where a second order active filter is embedded in a CIFF-B CTΔ ΣM with the aim of more effectively attenuating close by interferers [9, 10]. We show that this has the same functionality as having the filter up front, but achieves better linearity and noise performance (for the same power dissipation) when compared to a filter-CTΔ ΣM cascade. The rest of this paper is organized as follows. Section 4.2 reviews techniques to modify the STF of a CTΔ ΣM with the aim of reducing or eliminating peaking. Section 4.3 explains the technique of embedding a filter inside a CT$\varDelta \varSigma$ M. Noise, linearity, power consumption and active area of a CTΔ ΣM with a filter up front (H ₁-$\varDelta \varSigma$) are compared with those in a filtering CTΔ ΣM (Δ-H ₁-$\varSigma$). Architectural design considerations and the use of chopping to eliminate offset and flicker noise are given in Sect. 4.4. Section 4.5 discusses circuit details and measurement results of these designs, both of which incorporate a second order Butterworth filter in their STFs. The filter has a cutoff frequency which is twice the desired signal bandwidth. Measurements show that embedding the filter improves linearity and reduces area for the same power dissipation. Section 4.6 concludes the paper.

2 Signal Transfer Function Tailoring

Before embarking on a effort to find the best way of making a filtering CT$\varDelta \varSigma$ M, it is useful to review methods that address the problem of STF peaking by introducing feed-in paths from the input to the various internal states of the modulator. Referring to the generic block diagram of Fig. 4.2a, the STF is given by

$$\displaystyle{ ST\!F(j\omega ) = L_{o}(j\omega )NT\!F(e^{j\omega }). }$$

(4.1)

The aim of STF tailoring is to find ways of choosing L _o (s) so that

• a. Peaking of the STF is eliminated.

• b. The order of the loop filter is not increased.

• c. The NTF is not affected.

We illustrate with the “standard” second order CIFF modulator with $NT\!F(z) = (1 - z^{-1})^{2}$ shown in Fig. 4.4a. When k ₁ and k ₂ are zero,

$$\displaystyle{ L_{o}(s) = \frac{1.5s + 1} {s^{2}}. }$$

(4.2)

The resulting STF is

$$\displaystyle{ ST\!F(j\omega ) = \frac{1 + j1.5\omega } {-\omega ^{2}} (1 - e^{-j\omega })^{2} }$$

(4.3)

Fig. 4.4

(a ) Normalized second order CIFF CTΔ ΣM with feed-in paths and (b ) STF magnitude for different choices of k _o and k ₁

As shown in Fig. 4.4b, the STF peaks to about 2.2 (7 dB), which is not desirable. By adding feed-in paths with gains k _o and k ₁, L _o (s) is modified to

$$\displaystyle{ \hat{L}_{o}(s) = \frac{k_{o}s^{2} + (1.5 + k_{1})s + 1} {s^{2}}. }$$

(4.4)

How should k _o and k ₁ be chosen? One method is to use k ₀ = 0 and $k_{1} = -1.5$. This will cause the STF to resemble that of a CIFB loop, which is desirable. However, the output swing of the first integrator increases, just like in the CIFB case, causing noise and distortion problems. To avoid this, one could compromise—rather than demand that the STF have a filtering characteristic, we would be satisfied if peaking is eliminated. The aim, therefore, would be to choose k _o and k ₁ so that

$$\displaystyle{ ST\!F(j\omega ) = \frac{-k_{o}\omega ^{2} + (1.5 + k_{1})j\omega + 1} {-\omega ^{2}} NT\!F(e^{j\omega }) }$$

(4.5)

has unity magnitude for 0 < ω < π. The difficulty is that | NT​F(e ^jω) | cannot be expressed as a ratio of polynomials in ω ². An approach to circumvent this [11] is to use the so called bilinear inverse of the NTF, where e ^{j ω} is approximated as

$$\displaystyle{ e^{j\omega } \approx \frac{1 + \frac{j\omega } {2}} {1 -\frac{j\omega } {2}}. }$$

(4.6)

Equivalently, the NTF can be approximated (for low frequencies) as a polynomial in s, by replacing z with s according to

$$\displaystyle{ z \rightarrow \frac{1 - (s/2)} {1 + (s/2)} }$$

(4.7)

Applying this to our second order modulator yields k _o  = 0. 25 and $k_{1} = -0.5$. The STF peaking is reduced, as Fig. 4.4b shows, but is still about 3 dB. A more careful optimization yields k _o  = 0. 2 and $k_{1} = -0.8$, which results in a largely flat STF. However, the designer has no control over its bandwidth. From the discussion above, it is seen that adjusting feed-in path gains, while useful, cannot help with attenuating close in interferers.

3 Embedding a Filter into a CTΔ ΣM

The conceptually straightforward approach to control the STF is to use a filter up front. As mentioned earlier, this approach adds noise and distortion to the signal chain. Alternatively, the filter can be moved into the modulator. The first attempt at this was made in [12]. In that work, a first order passive RC filter was embedded inside a single bit CIFF CTΔ ΣM to “tame” the STF peak characteristic of a CIFF loop.

Figure 4.5a illustrates the basic idea. A first order low pass filter formed by R ₁ and C ₁ is placed after the first integrator of a CIFF CTΔ ΣM ​​. Introducing the filter into the $\varDelta \varSigma \,\,$ loop, in all likelihood, will destabilize it. To avoid this, a compensation path, shown in red, is introduced. Thanks to this path, the transfer function from v(t) to the input of L ₁(s) remains unchanged, and the NTF is not affected. Thus, the bandwidth of the low pass filter, which depends on the the R ₁ C ₁ product, can be chosen independent of the NTF. The STF, on the other hand, is the product of transfer function of the low pass filter and the STF of the original CIFF CTΔ ΣM ​​. Figure 4.5b, c show the front-ends of CTΔ ΣMs with the filter outside and inside the loop respectively. The filter bandwidth is 1∕(2π R C). When the filter is embedded, its impedance can be scaled (a > 1 in Fig. 4.5c), thereby reducing area.

Fig. 4.5

(a ) Basic idea behind embedding a first order filter inside a CTΔ ΣM (with a CIFF loop). (b ) Input stage of a filter+CTΔ ΣM with filtering upfront and (c ) Filtering CTΔ ΣM with the filter moved after the first integrator

What are the difficulties with such a structure? The first order filter offers limited selectivity and the active compensation path consumes extra power. Though not fundamental to the technique, the design of [12] used a single-bit quantizer. Due to the single bit DAC, the design is sensitive to clock jitter and the first opamp has to dissipate a lot of power to achieve the desired linearity. Another issue is the change in the NTF due to mismatch between the embedded low pass filter and the compensation path. Figure 4.6 shows Monte-Carlo simulations of the NTF with 2 % random mismatch. For these simulations, the oversampling ratio (OSR) was set to 64, with the 3 dB bandwidth of the low pass filter being twice the signal bandwidth. As with all $\varDelta \varSigma \,\,$ loops employing 1-bit quantizers, the out-of-band gain (OBG) of the NTF was chosen to be 1.5.

Fig. 4.6

Effect of 2 % mismatch between the embedded filter and the compensation path

Simulations show that the variations of the NTF are more (a) when the bandwidth of the embedded filter is smaller and (b) when NTF’s OBG is higher. These results make intuitive sense due to the following. The low pass filter adds delay into the $\varDelta \varSigma \,\,$ loop, and the compensation network attempts to mitigate it. Mismatch between the two affects the efficacy of excess delay compensation. With a lower filter bandwidth, the excess delay mismatch is inherently larger. With a higher OBG, the NTF is more sensitive to a given excess delay.

To improve the rejection of close-in interferers, a higher order filter needs to be used. For a sharp transition band, this filter needs to be active. As in the first order case, this filter can be moved into the $\varDelta \varSigma \,\,$ loop, leading to the filtering CTΔ ΣM architecture. Its evolution is shown in Fig. 4.7. Part (a) of the figure shows a modulator preceded by a low pass filter with transfer function H ₁(s). ω ₄∕s denotes the transfer function of the first integrator in the loop filter of the modulator. H ₁(s) can be moved beyond ω ₄∕s in the $\varDelta \varSigma$ loop so that the noise from the filter gets divided by the gain of the first integrator when referred to the input (Fig. 4.7b). Doing this modifies the NTF, which can be restored by a compensation path with transfer function $(1 - H_{1}(s)) \cdot (\omega _{4}/s)$, as shown in the figure. It is straightforward to see that the modulators of Fig. 4.7a, b have the same STF and NTF, and therefore, the same functionality. Specifically, note that the voltage v _c at the input of L ₁(s) will be the same in both realizations.

Fig. 4.7

(a ) Block diagram of a modulator with a filter H ₁(s) up front, (b ) H ₁(s) is moved beyond the first integrator in the $\varDelta \varSigma$ loop. The compensation path is necessary to restore loop stability

Assume that H ₁(s) is of second order, with transfer function

$$\displaystyle{ H_{1}(s) = \frac{1} {1 + \frac{s} {\omega _{o}Q} + \frac{s^{2}} {\omega _{o}^{2}} }. }$$

(4.8)

Since the dc gain of H ₁(s) is 1, (1 − H ₁(s)) has a zero at dc, which cancels the integrator pole in the compensation path. The response of the compensation path, therefore, is given by

$$\displaystyle{ H_{c}(s) = \frac{ \frac{\omega _{4}} {\omega _{o}Q} + \frac{s\omega _{4}} {\omega _{o}^{2}} } {1 + \frac{s} {\omega _{o}Q} + \frac{s^{2}} {\omega _{o}^{2}} }. }$$

(4.9)

The filter and the compensation path have identical denominator polynomials—and can be realized using the same network, as shown in Fig. 4.8. In this figure, calculations show that the transfer function from B to C is of the form required for the compensation path. Incorporating this into Fig. 4.7b yields Fig. 4.9a, which shows a CTDSM with an embedded second order filter, with no extra hardware needed for compensation. The output of the filter v _c in Fig. 4.9a, consists of two components: one through the main feedback path and one through the filter compensation path. Assuming the dc gain of the filter is 1 (R _f3 = R _f1), the transfer function from the modulator output D to v _c can be shown to be the following.

Fig. 4.8

Active RC realization of a second order filter and the compensation path

Fig. 4.9

(a ) A second order filter embedded in a $\varDelta \varSigma$ loop. (b ) Magnitude of transfer functions from resistor noise sources in the embedded filter to the modulator output in our design

$$\displaystyle{ \frac{v_{c}(s)} {D(s)} = - \frac{1 + \frac{sR_{in}C_{4}R_{f3}R_{f2}} {R_{q}R_{comp}} + \frac{s^{2}R_{ in}C_{4}R_{f3}R_{f2}C_{f1}} {R_{comp}} } {sR_{in}C_{4}\left [1 + \frac{sR_{f3}R_{f2}C_{f2}} {R_{q}} + s^{2}R_{f3}R_{f2}C_{f2}C_{f1}\right ]} }$$

(4.10)

It is apparent that if R _comp is chosen to be R _in C ₄∕C _f2, the numerator and the second order polynomial in the denominator cancel, yielding $\frac{v_{c}(s)} {D(s)} = \frac{-1} {sR_{in}C_{4}}$. This result makes intuitive sense due to the following. In the stand-alone CTΔ ΣM, the transfer function from D to v _c is $(\omega _{4}/s) = 1/(sR_{in}C_{4})$. The same must hold for the CTΔ ΣM with embedded filtering. From Fig. 4.9a, we see that the path from D to v _c at high frequencies is through the second integrator of the filter, whose transfer function is 1∕(sR _comp C _f2). Since this must equal 1∕(sR _in C ₄), it follows that $R_{comp} = R_{in}C_{4}/C_{f2}$. As far as quantization noise is concerned, it is as if the filter does not exist—implying that the NTF is unchanged. A filter of arbitrary order can be embedded in a CTΔ ΣM and compensated in a similar manner.

The technique discussed above can be used to move a filter into any CT$\varDelta \varSigma$ M. However, the benefits of doing so—namely, reduction of filter noise when referred to the input, accrue only when the gain of the first integrator (ω ₄∕s in Fig. 4.7a) over the signal band is larger than unity. To better understand this, consider our specific case of a CIFF-B CTΔ ΣM with an embedded second order filter, shown in Fig. 4.9a. The low frequency gain from V _in to the output of $\hat{A}_{3}$ is R _f1 R _f2 C _f2∕(C ₄ R _in R _q ). This can be deduced as follows. The low frequency current flowing through C _f2 is ≈ 0. Since the STF is unity in the signal band, it must follow that the low frequency gain from V _in to the output of $\hat{A}_{1}$ is R _f2∕R _comp . The voltage v _c at the input of L ₁(s) will be identical to that which would exist at the output of the first integrator of a CIFF-B modulator preceded by a second order filter. Further, due to the CIFF-B design, the gain from V _in to v _c in the signal band will be ≈ 0. Thus, the in-band current flowing through R _f3 is ≈ 0, and the low frequency gain from V _in to the output of $\hat{A}_{3}$ is R _f1 R _f2∕R _comp R _q . Using $R_{comp} = R_{in}C_{4}/C_{f2}$ [from (4.10)], we see that the gain from V _in to the output of the first integrator is R _f1 R _f2 C _f2∕(C ₄ R _in R _q ). As the filter bandwidth reduces (C _f2 increases), C ₄ has to increase to prevent $\hat{A}_{3}$ from saturating, thereby decreasing the gain of the first integrator in the signal band. Thus, choosing too low a filter bandwidth is counterproductive.

This is not restrictive, however, as the cutoff frequency of the filter should anyway be chosen so that the variation of the gain and group delay over the signal bandwidth is negligible. This holds whether the filter is embedded, or placed upfront. Denoting the signal bandwidth by B, calculations show that a second order Butterworth filter with a 3 dB bandwidth of 2B has only 0.25 dB gain droop across the signal band, whereas reducing the cutoff frequency to 1. 5B increased this droop to 0.8 dB. Based on this, and the discussion in the previous paragraph, we chose a second order Butterworth filter with a bandwidth of 2B. As shown in the next subsection, this choice still allows the first integrator to have a gain greater than unity at the edge of the signal band. In the discussion to follow, we compare the various performance metrics (noise, linearity, power consumption, active area) of a modulator with an embedded filter and its counterpart where the filter is placed up front.

3.1 Offset, Flicker and Thermal Noise

It is well known that offset and flicker noise are problematic in direct conversion receivers. Embedding the active filter into the $\varDelta \varSigma \,\,$ loop eliminates its dc offset and greatly reduces the 1/f noise it contributes to the entire signal chain. Thus, the first opamp of the filtering CTΔ ΣM remains, for all practical purposes, the only source of offset and 1/f noise. This makes it easy to manage. One way to do this is to chop the first OTA. Chopping renders the first integrator a linear periodically time varying (LPTV) system. Since the integrator processes shaped quantization noise whose out of band spectral density is several orders of magnitude higher than that in-band, down conversion of noise from multiples of the chopping frequency is a serious concern. Fortunately, this can be handled by the use of FIR feedback, which is also beneficial in other aspects as will be discussed in Sect. 4.4.

Figure 4.9b shows the transfer functions from the various resistor noise sources in the filter (Fig. 4.9a) to the modulator output. These transfer functions are calculated for our specific CIFF-B design where the oversampling ration (OSR) is 64. The signal bandwidth is denoted by B and the 3 dB bandwidth of the (Butterworth) filter is 2B. It is seen that thermal noise from the filter is first order shaped out of the signal band. If the filter is placed up front, the transfer function from all its resistor noise sources to the modulator output will be ≈ 1 in the signal band. From Fig. 4.9b it is clear that the total output noise is reduced when the filter is embedded into the modulator. Δ-H ₁-$\varSigma$ can therefore be impedance scaled to have the same input referred noise as that in H ₁-$\varDelta \varSigma$. This reduces the power consumption and active area. In our design, the first integrator and filter in Δ-H ₁-$\varSigma$ were impedance scaled by 1. 8 and 3 respectively, so as to have the same input referred noise as in H ₁-$\varDelta \varSigma$.

3.2 Linearity

To understand the effect of OTA nonlinearity in H ₁-$\varDelta \varSigma$ and Δ-H ₁-$\varSigma$, we simulated normalized fourth order single bit designs (with CIFF-B loop filters). The sampling rate and OSR were assumed to be 1 Hz and 64 respectively. The filter’s 3 dB bandwidth was set to twice the signal bandwidth. Keeping in view our final implementation, a 4-tap FIR feedback DAC was used. With the filter up front (H ₁-$\varDelta \varSigma$), the input resistance of the filter and CTDSM were chosen to be $1\,\Omega$. The OTA is assumed to be a single stage design, with the current in each leg modeled as

$$\displaystyle{ i = g_{m}v_{x} - g_{2}v_{x}^{2} - g_{ 3}v_{x}^{3} }$$

(4.11)

where v _x denotes the differential voltage at the input of the OTA. g _m , g ₂, g ₃ were chosen to be 100 S, 200 A∕V² and 4000 A∕V³ respectively. Third order intermodulation distortion manifests due to odd nonlinearity. Second order distortion is deliberately introduced through g ₂ in the equation above. This way, IM ₂ can be simulated by introducing random mismatches in passive components. For the CTΔ ΣM with embedded filter (Δ-H ₁-$\varSigma$), R,C’s in the first integrator and those in the filter were impedance (up)scaled by factors of 1.8 and 3 respectively. This choice resulted in an input referred noise spectral density which was equal to that of H ₁-$\varDelta \varSigma$. Regarding the OTAs, two cases were simulated, as described below.

Case A.:

The OTAs in the first integrator and the filter were also impedance scaled by 1.8 and 3 respectively. By “impedance scaling an OTA by a factor α”, we mean the following—the output current of the OTA in (4.11) above is modified as $\hat{i} = i/\alpha = \frac{1} {\alpha } (g_{m}v_{x} - g_{2}v_{x}^{2} - g_{ 3}v_{x}^{3})$. In a real transistor level design, this would correspond to reducing all transistor widths (and their quiescent currents) by a factor α, thereby resulting in lower power dissipation. It is thus seen that by scaling OTAs, Δ-H ₁-$\varSigma$ has lower power dissipation compared to H ₁-$\varDelta \varSigma$.

Case B.:

The OTAs in the first integrator and the filter in Δ-H ₁-$\varSigma$ of Case A above were impedance scaled by 1/3,1/3 and 1 so that the power dissipation is the same as in H ₁-$\varDelta \varSigma$.

Since distortion depends on the product of the OTA’s G _m and the integrating resistor [13], one should expect improved linearity in Case B when compared to Case A. This is confirmed by simulation results showing the in-band and out-of-band linearity of H ₁-$\varDelta \varSigma$ and Δ-H ₁-$\varSigma$. First, both designs were excited by two closely spaced − 10. 5 dBFS in-band tones. Figure 4.10a compares the strength of the IM ₃ tone. The distortion of H ₁-$\varDelta \varSigma$ and Δ-H ₁-$\varSigma$-Case A are comparable, but when power saved due to impedance scaling is put back into the OTAs as in Case B, embedding the filter results in enhanced linearity. Figure 4.10b shows out-of-band IM ₃ for both cases—the improvement is linearity is apparent. Similar results were obtained for IM ₂, as shown in the histograms of Fig. 4.11. The input for these simulations consisted of two − 10. 5 dBFS tones around B, where B denotes the edge of the signal band. From the discussion above, it is apparent that other metrics (power and noise) remaining the same, embedding the filter into a CTΔ ΣM improves linearity and reduces active area. Simulations (not given here due to space constraints) show embedding the filter does not influence the robustness of the CTDSM with respect to RC variations in any way.

Fig. 4.10

Comparison of IM ₃. (a ) Tones are in-band. The x-axis is the average frequency of the two input tones. (b ) Tones are out-of-band at frequencies f and 2f +Δ f

Fig. 4.11

Histogram of the power in inband IM ₂ tone from 100 Monte Carlo runs. The input consists of two − 10. 5 dBFS tones around B

4 Architectural Considerations

Having convinced ourselves that embedding an active filter into a $\varDelta \varSigma$ modulator is beneficial on all counts when compared to having the filter up front, the next task at hand is to examine the various design choices regarding the modulator itself.

Number of quantizer levels: CTΔ ΣMs which achieve high levels of linearity have typically used multibit quantizers. Such a choice has several advantages. First, the increased number of levels enables a lower OSR to achieve a desired signal to quantization noise ratio (SQNR). The reduced step size in the feedback waveform reduces the sensitivity of the modulator to clock jitter, as well as the slew rates required of the opamps in the loop filter. However, the complexity of the ADC used in the quantizer increases exponentially with the number of bits. Even though the comparators in the quantizer lend themselves to low power operation, clock generation and distribution can consume significant current. This, unfortunately, is difficult to estimate during the architectural design phase. Moreover, mismatch in the unit elements of the feedback DAC degrade in the inband SNDR of the modulator, necessitating some form of mismatch correction, like calibration or dynamic element matching (DEM). This further increases the power dissipation and design time of the quantizer.

An alternative to using a flash design for the ADC is to use a successive approximation register (SAR) ADC. The latter’s complexity increases linearly with the number of bits resolved. Comparator offset, which can be potentially problematic in a flash design, is benign. This approach has found favor in many recent designs, particularly those realized in nanometer CMOS technologies. The complexity of the DAC (which now needs a binary to thermometer decoder in the $\varDelta \varSigma \,\,$ loop, apart from DEM) still remains.

In contrast, using a single bit quantizer, where the feedback DAC is inherently linear, dramatically simplifies the quantizer design. However, the full scale two level feedback waveform places increased demands on the linearity of the loop filter, as well as increases the sensitivity of the modulator to clock jitter. From the discussion above, it is seen that a multibit loop complicates the quantizer design at the expense of a simplified loop filter. The opposite is true in a single bit modulator. Recognizing this, several recent works have attempted to alleviate the linearity and clock jitter problems associated with a single bit design. Pavan and Sankar [14] and Nandi et al. [15] use integrators based on opamp assistance, which is a circuit technique that enhances the linearity of an opamp in a power efficient manner. Shettigar and Pavan [16] uses a feedback DAC which incorporates a finite impulse response filter (FIR-DAC).

The FIR DAC principle is not new [17, 18]—however, relatively few designs seem to have exploited this technique. The basic idea behind the FIR DAC is to feedback a filtered version of the single-bit quantizer output, as shown in Fig. 4.12a. Due to the high frequency attenuation of the FIR filter, the DAC output is a multi-level waveform, like in a multibit quantizer. Thanks to this, the FIR-DAC approach has low clock jitter sensitivity and relaxes the linearity requirements of the loop filter. In practice, the filter and DAC combination are implemented in a semi-digital fashion, as shown in Fig. 4.12b, which makes the FIR DAC inherently linear in spite of mismatch. Due to the single-bit quantizer, the ADC design is simple and consumes very little power. A modulator employing a single-bit quantizer and an FIR DAC, therefore, combines the best features of single-bit and multibit operation.

Fig. 4.12

(a ) A single-bit CTΔ ΣM with FIR feedback and (b ) a semi-digital implementation of the feedback DAC

FIR feedback presents several design challenges. Due to the delayed nature of the feedback waveform, the modulator needs to be carefully stabilized to restore the noise transfer function. It can be shown that the NTF can be restored exactly. The design procedure and intuition behind this is given in [19].

4.1 Offset and Flicker Noise Reduction by Chopping

DC offset and flicker noise are very problematic in direct conversion receivers. While there are many mechanisms that result in offset and 1/f noise, the baseband section is a significant contributor. Using a filter up front to modify the modulator’s STF results in increased offset and flicker noise. Embedding the filter, on the other hand, reduces its contribution to the low frequency noise of the signal chain since it is shaped by the response of the first integrator of the modulator. Since the source of offset is the first integrator, it can be more easily managed.

Chopping is a classical and effective technique to address 1/f noise problems in low frequency amplifiers. The block diagram of a fully differential CTΔ ΣM (with or without embedded filtering), employing chopping in the first integrator is shown in Fig. 4.13. A natural question that arises is how one should choose the chopping frequency f _chp . Chopping renders the first integrator a linear periodically time varying (LPTV) system with frequency f _chp , where frequency translation effects cause signals and noise from frequencies around multiples of f _chp to dc. It turns out that in a chopped integrator where f _chp has a 50 % duty cycle, shaped noise aliases only from even multiples of f _chp . The first integrator of the CTΔ ΣM processes shaped quantization noise, whose out of band spectral density can be 100 dB higher than the in-band density. Thus, even a small amount of aliasing can dramatically degrade in-band performance.

Fig. 4.13

Chopping the first integrator of a CTΔ ΣM to reduce flicker noise

An FIR DAC solves the problem of shaped noise aliasing due to the following.The FIR filter introduces nulls in the spectrum of feedback waveform at multiples of f _s ∕N, as shown in Fig. 4.14 for the special case of a 12-tap FIR filter. If the chopping frequency is chosen such that $f_{chp} = f_{s}/2N$, noise that can potentially alias into the signal band is attenuated. Thus, frequency translation has minimal impact on the in-band spectral density.

Fig. 4.14

PSD of the signal processed by the first integrator without and with FIR feedback. A 12 tap FIR DAC, with equal taps, is assumed

Thus, the use of FIR feedback in a filtering CTΔ ΣM not only results in improved linearity of the loop filter and reduces jitter sensitivity, but also enables “chopping for free” if f _chp is appropriately chosen. A detailed analysis and experimental results can be found in [20].

5 Implementation Details and Measurements

Two modulators—one with up front filtering and another with embedded filtering were designed for the same nominal specifications in a 0. 13 μm CMOS process. We attempted to achieve about 80 dB of instantaneous peak dynamic range in a signal bandwidth of 2 MHz and a 0–18 dB variable gain for both designs. In view of the trade off between filter bandwidth and performance (see Sect. 4.3), a Butterworth filter with 4 MHz bandwidth was chosen.

5.1 Modulator with Upfront Filter (H ₁-Δ Σ)

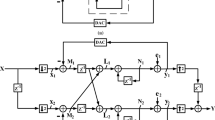
Figure 4.15 shows a simplified single-ended schematic of H ₁-$\varDelta \varSigma$. The filter was implemented as a Tow-Thomas biquad. Active-RC integrators were used for low noise and high linearity. Programmable gain was achieved by splitting it across the two stages of the filter (A _v1 and A _v2). A variable gain A _v1 was implemented by varying R _f1 by a factor 1, 2 or 4. The current in A₁ was made variable depending on A _v1. A _v2 can be programmed to be 1 or 2 by changing R _f2 and R _f3, as shown in the figure. Thus, up to 18 dB of gain can be incorporated into the filter. Two stage feedforward compensated opamps were used with an AC coupled feedforward stage to increase the output swing (similar to those in [16]).

Fig. 4.15

Fourth order modulator with a CIFF-B loop filter with a second order filter up front

The modulator employed a single bit quantizer, chosen for low power operation. Stability considerations, therefore, restricted the out-of-band gain of the NTF to 1.5. This necessitated a fourth order NTF with OSR = 64 (f _s  = 256 MHz) to achieve an in-band SQNR of about 96 dB—well below the desired signal to thermal noise ratio. A CIFF-B topology was used for the loop filter. R ₃₁ implements the feedforward path across the integrator I₃. R₁₂ realizes complex zeros in the NTF, and is implemented using a T-network. All capacitors were implemented as digitally tunable banks to trim RC variations. Switches are placed across all the integrating capacitors to reset their states to recover from overload.

The main feedback element, D​AC ₄, is a 4-tap FIR DAC with an NRZ pulse shape. This reduces jitter sensitivity and relaxes linearity requirements of the first integrator [16–18]. Rather than use equal tap weights, they are optimized to minimize noise due to jitter. The weights [0. 2, 0. 3, 0. 3, 0. 2] reduce jitter noise by 15 dB when compared to a single bit CTDSM without an FIR DAC. The delay introduced by DAC ₄ can destabilize the modulator. Another 4-tap FIR DAC, DAC ₂, with transfer function F _c (z) is used at the input of I ₂ to compensate the loop. The FIR DACs are realized in a semi-digital fashion as shown in Fig. 4.15. Any mismatch in the DAC resistors manifests as a variation in the FIR tap coefficients and not as nonlinearity.

5.2 Modulator with Embedded Filter (Δ-H ₁-Σ)

The simplified single-ended schematic of Δ-H ₁-$\varSigma$ is shown in Fig. 4.16. This is derived from the circuit of Fig. 4.15 by moving the filter beyond the first integrator of the modulator as discussed in Sect. 4.3. Since the main DAC (DAC ₄) is of the FIR kind, DAC ₃, which compensates for the delay of the embedded filter, is also an FIR DAC with the same coefficients. Variable gain is achieved by programming the input resistor. At high gains, the current in the first opamp is increased. Since the noise of the filter is shaped by the first integrator, it was impedance scaled. Power saved by doing this was used to improve linearity as described below.

Fig. 4.16

Fourth order modulator with an embedded second order filter

Figure 4.17 compares the impedance levels of H ₁-$\varDelta \varSigma$ and Δ-H ₁-$\varSigma$. In a well designed active-RC integrator, the input referred noise is dominated by the contribution from the resistors. Thus, the input referred noise spectral density of H ₁-$\varDelta \varSigma$ is ≈ 6R × 4kT. When the filter is embedded, the CTDSM input and DAC impedances are doubled and the filter impedance is scaled by ≈ 3×. In spite of this, the input noise density is smaller, at ≈ 5. 5R × 4kT. Thus, in principle, the currents in the OTAs $\mathrm{\hat{A}_{3}}$, $\mathrm{\hat{A}_{1}}$ and $\mathrm{\hat{A}_{2}}$ can be reduced by factors of ≈ 2, ≈ 3 and ≈ 3 respectively. Some of the power saved in this process can be used to enhance linearity of the OTAs. In our work $\mathrm{\hat{A}_{1}}$, $\mathrm{\hat{A}_{2}}$ and $\mathrm{\hat{A}_{3}}$ are scaled so that they consume 0. 65, 0. 33 and 0. 75 times the currents of A₁, A₂ and A₃ respectively. Denoting the transconductance of an OTA by G _OTA , the G_OTAR products for $\mathrm{\hat{A}_{1}}$, $\mathrm{\hat{A}_{2}}$ and $\mathrm{\hat{A}_{3}}$ are about 1. 95, 1, 1. 5 times the corresponding products for A₁, A₂ and A₃, indicating improved linearity of the integrators in Δ-H ₁-$\varSigma$. Thus, not only is overall power dissipation lower when the filter is embedded into the CTDSM, linearity is also enhanced with respect to a filter-CTDSM cascade, while achieving similar noise.

Fig. 4.17

Impedance levels in (a ) CIFF-B CTDSM with up front filter (b ) CTDSM with embedded filter

In our design, the LPF and the loop filter in H ₁-$\varDelta \varSigma$ consume 3. 4 mA to 4. 1 mA (depending on the gain). The corresponding current for Δ-H ₁-$\varSigma$ is 2. 3 mA to 2. 7 mA. The clock generation block consumes 0. 47 mA, while the quantizer and D-flip-flops draw about 0. 3 mA.

5.3 Measurement Results

Both designs described in the previous section were fabricated in a 0. 13 μm CMOS process through Europractice. H ₁-$\varDelta \varSigma$ and Δ-H ₁-$\varSigma$ have active areas of 0. 42 mm² and 0. 33 mm² respectively. For our choice of impedance scaling factors, embedding the filter results in approximately 25 % lesser active area. The modulator outputs were brought out using LVDS buffers. The single bit data streams were captured using a digital storage oscilloscope and then processed offline. 64K data points were used for spectral estimation and a Blackman-Harris window was used to minimize spectral leakage effects.

Figure 4.18a b show the measured STF and maximum stable amplitude (MSA) for the two modulators, where the latter is normalized to the value at DC. It is seen that the STF and MSA of the two filtering modulators are virtually identical, indicating the same functionality. The SNR/SNDR vs input amplitude plots are shown in Fig. 4.19a, b. H ₁-$\varDelta \varSigma$ and Δ-H ₁-$\varSigma$ have an overall DR of 90. 8 dB and 92 dB, and peak instantaneous DR/SNR/SNDR of $81/79.5/73.7\,\mathrm{dB}$ and $82/80.5/74.4\,\mathrm{dB}$ respectively. H ₁-$\varDelta \varSigma$ consumes 5. 9–6. 8 mW depending on the gain setting (including references) while Δ-H ₁-$\varSigma$ consumes 4. 34–5 mW. From these results, we see that embedding the filter achieves slightly better performance with lower area and power dissipation.

Fig. 4.18

Measured (a ) |STF| and (b ) MSA of the two modulators

Fig. 4.19

SNR/SNDR vs. input amplitude with (a ) up front filter and (b ) embedded filter. (a ) H ₁-$\varDelta \varSigma$. (b ) Δ-H ₁-$\varSigma$

Figure 4.20a compares the linearity of the two modulators in the presence of out-of-band interferers, which are placed such that one of their IM ₃ products falls at 1 MHz. The input consists of a small ( − 65 dBFS) desired signal and two large interferers at 4. 75 MHz and 10. 5 MHz (each of amplitude − 8 dBFS). A gain of 1 is used in the modulators. The filtering effect of the CTDSM is apparent. Further, the IM ₃ product at 1 MHz is around 23 dB smaller with the embedded filter, representing an IIP ₃ improvement of ≈ 11 dB. Again, it is seen that embedding the filter within the modulator enhances linearity for both in-band and out-of-band frequencies. To better appreciate this, we show time domain results, obtained by decimating the modulators’ output sequence. The input consists of a small desired signal and one − 8 dBFS blocker at 4. 75 MHz. Another blocker ( − 8 dBFS at 10. 5 MHz) is added to the input after 64 μs. Figure 4.20b shows the decimated outputs, with the insets zooming in around 64 μs. For the modulator with up front filter, the effect of distortion is clearly seen after the second interferer is applied, while the output of the modulator with embedded filter remains virtually unchanged, demonstrating improved linearity.

Fig. 4.20

Out-of-band linearity measurements in the presence of two − 8 dBFS tones at 4. 75 MHz and 10. 5 MHz, gain = 1. (a ) PSD at output of the modulators and (b ) time domain demonstration of the linearity improvement

6 Conclusions

When interferers are present, a low pass filter is needed to reduce the in-band dynamic range requirements of a conventional continuous-time $\varDelta \varSigma$ modulator. The filter can be embedded into the ADC. This achieves the same functionality as using a filter up front, but with better in band and out-of-band linearity, lower area and reduced power dissipation. Flicker noise and dc offset can be easily addressed by chopping if an FIR feedback is used. The latter also relaxes requirements on clock jitter and improves the linearity of the loop filter.