Data Mining in Medicine: Relationship of Scoliotic Spine Curvature to the Movement Sequence of Lateral Bending Positions

Abstract

We aim to determine relationships between scoliotic spine curvatures in movement sequence from left bending to erect to right bending positions in the frontal plane. A multi-body kinematic modelling approach is utilized to reconstruct the curvatures and study the relationships. The spine is considered as a chain of micro-scale motion-segments (MMSs). Linear regression method is adopted to identify relationships between angles of MMSs in erect and lateral bending positions. Excellent linear relationships (R² = 0.93 ± 0.09) were identified between angles of MMSs placed between each two successive vertebrae. We showed that these relationships give good estimates of the curvatures (Root-mean-square-error = 0.0172 ± 0.0114 mm) and the key parameters for scoliosis surgery planning; estimation errors for Cobb angle, spinal mobility, and flexibility were 0.0016 ± 0.0122°, 0.0010 ± 0.086°, and 0.0002 ± 0.0002 respectively. This paper provides an important insight: scoliotic spine curvatures in lateral bending positions and the key parameters for surgery planning can be predicted using spine curvature in erect position.

1 Introduction

Scoliosis is a complex 3-dimensional structural deformity of the human spine. Surgery is required for correction of severe scoliosis (i.e. Cobb angle¹ [1] >45º) [2]. To plan the surgery (e.g. selection of fusion levels), several X-ray images are taken from the scoliotic spine in different spine positions in the frontal plane of the human body. Considering the X-ray images of the scoliotic spine in the erect and lateral bending positions as the representative of a sequence of spine movement from left bending to erect to right bending positions, the motion data acquired from this sequence is used to measure the key parameters (e.g. Cobb angle, spinal mobility¹, spinal flexibility¹) for planning the surgery [3]. The scoliotic spine movement sequence is represented by the sequence of the first, intermediate, and end spine positions.

Radiological imaging exposes the scoliotic patients to harmful radiation. To mitigate radiation risks, reducing the number of the required X-ray images is potentially helpful. In this regard, motion capture [5], and inclinometer [6], methods have been adopted to obtain the required data from the sequence of the spine movement in order to measure the key parameters: spinal mobility and flexibility. However, Hresko et al. [7] found no significant statistical correlation between the measurements by using these methods and the X-ray images. It should be noted that the measurements on X-ray images are the gold standard for the values of the parameters [8, 9]. Another alternative to measurement of the parameters can be prediction of the scoliotic spine curvatures in the erect and lateral bending positions by using the information acquired from the movement sequence of the spine. However, to the best of our knowledge, study on such a prediction is considerably lacking in the existing literature.

In our attempt to study such a prediction, this paper aims to determine whether mathematical relationships exist between the scoliotic spine curvatures in the movement sequence from left bending to erect to right bending positions in the frontal plane. For this end, we utilize a multi-body kinematic modelling approach to reconstruct the spine curvatures in the positions. This study focuses on adolescent idiopathic scoliosis (AIS), which requires surgical correction. AIS is the most common form of the scoliosis (≈80 % [10]), and patients are predominantly female [11].

2 Scoliotic Spine

In this section, we briefly explain the scoliotic spine and its evaluation. Scoliosis is a side-to-side curvature of the spine with a twisting of the vertebral column about its axis (Fig. 1a) [12]. It has been diagnosed in 1.5 % to 3 % of the population [2]. The scoliotic deformity affects the thoracic and lumbar regions of the spine from the fifth vertebra (L5) of the lumbar region to the first vertebra (T1) of the thoracic region.

Fig. 1.

Scoliotic spine in erect position in frontal plane (a) spine regions, and (b) Cobb angles

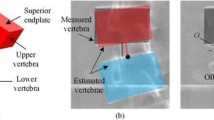
Scoliosis is normally evaluated by measuring Cobb angles on a 2-dimensional radiograph taken in the erect position in the frontal plane [1]. Cobb angles are measured between the inflection vertebra² and the end vertebrae³ (Fig. 1b) [13]. The severity of the scoliosis is determined by Cobb angle; Cobb angle greater than 45° corresponds to the severe scoliosis.

We define the terms below to describe the scoliotic spine curvatures in the frontal plane in order to study the relationships between the curvatures. The definitions are based on the concept of ‘vertebral body line’ proposed by Scoliosis Research Society (SRS) (term #2 in [14]).

• 1. Global coordinate system ( G ). G is represented by XYZ defined on the lowest vertebra in the spine (Fig. 2a). G has its origin at the mid-point of the vertebral body of the lowest vertebra. The mid-point of a vertebra is the intersection of the line drawn from the upper left corner to the lower right of the vertebral body and the line drawn from the upper right to the lower left of the vertebral body (the white circles in Fig. 2a) [15]. Y-axis of G is parallel to the line joining the left and right pedicles of the lowest vertebra. Z-axis is parallel to the line that passes through the center of the upper and lower endplates of the lowest vertebra. X-axis defines the anterior direction. The plane YZ is the frontal plane of the human body.

  Fig. 2.

  

  The global coordinate system of the spine, the spine curvature, and the geometrical parameters, i.e. location and orientation of vertebrae

• 2. Scoliotic spine curvature in the frontal plane. It is the curved line that passes through the mid-points of the vertebral bodies projected on the frontal plane (Fig. 2b).

• 3. Location of a vertebra in the frontal plane (LOC). It is the location of the mid-point (Fig. 2a) of the vertebral body in the frontal plane. LOC is given by the ordered pair of (Z,Y) according to the definition of G.

• 4. Orientation of a vertebra in the frontal plane ( Θ ). It is the angle between Z-axis and a line (Fig. 2a) passing through the center of the upper and lower endplates of the vertebra in the frontal plane.

• 5. Spinal mobility in the frontal plane. It is the angle between the lines connecting the mid-points of the lowest and uppermost vertebrae in the erect and left/right bending positions. It can be defined for a part of the spine, e.g. thoracic region.

• 6. Spinal flexibility in the frontal plane. It is the difference of spinal movement (excursion) from the erect to lateral bending positions [16]. A scoliosis flexibility index is calculated by (1) according to [7]. It can be defined for each spine region.

$$ {\text{Flexibility index}} = \left| {\frac{{{\text{Cobb}}_{\text{erect}} - {\text{Cobb}}_{{{\text{left}}/{\text{right }}}} }}{{{\text{Cobb}}_{\text{erect}} }}} \right| $$

(1)

Where, |·| is the absolute operation.

3 Methods

3.1 Subjects and Data Collection

After obtaining domain specific review board approval, pre-operative X-ray images of 18 patients with severe AIS were used for the study (Table 1). The images were taken in three posterior-anterior positions in the frontal plane: one erect position and two prone positions (left and right bending positions). These X-ray images represent the sequence of the scoliotic spine movement from the left bending to erect to right bending positions.

Table 1. Descriptive data of the patients

The patients had no neurologic deterioration, and they were admitted to hospital for surgical treatment. There were 12 female and six male patients between the ages of 12 and 19 years (mean age of 15 years). The thoracolumbar/lumbar and thoracic Cobb angles of the patients were 46.28 ± 13.94° (mean ± SD) and 49.78 ± 12.25° respectively.

To obtain the spine curvature in a position, the respective X-ray image was analyzed to measure LOC and Θ of the vertebrae from L4 to T2. LOC and Θ of a vertebra give the translation and rotation of the vertebra, respectively, with respect to its inferior vertebra when the spine moves from the erect to a bending position. It should be noted that L5 and T1 were excluded since they were not visible in the majority of the images. Section 3.2 explains how the curvatures are obtained by using LOC and Θ.

The accuracy limit of the measurement of LOC and Θ was 0.1 mm and 0.1º respectively. LOC and Θ were measured three times by two experts familiar with X-ray images of the scoliotic spine. The mean values of the measurements were considered for the parameters. The measurements were supervised by GL (one of the authors) who is an experienced scoliosis surgeon at National University Hospital, Singapore.

The repeatability and reliability of the measurements were evaluated by using Pearson correlation coefficient. The intra-observer coefficients were 0.95 ± 0.04 and 0.93 ± 0.05 for expert-1 and expert-2 respectively. The inter-observer coefficient was 0.91. These agreements are excellent and can show the repeatability and reliability of the measurements according to [17].

3.2 Reconstruction of the Spine Curvatures

The spine curvatures are obtained by fitting polynomials to LOC and Θ. The polynomials (2) have no first-degree and constant terms because the location and orientation of L4 are zero according to definition of G.

$$ {\text{P}}\left( {\text{Z}} \right) = \lambda_{t} {\text{Z}}^{t} + \lambda_{t - 1} {\text{Z}}^{t - 1} + \ldots + \lambda_{2} {\text{Z}}^{2} $$

(2)

The linear least squares method is adopted to fit the polynomial. The coefficients (λ) of P are given in terms of the measured parameters by

$$ {\varvec{\uplambda}} = \left( {{\mathbf{Z}}^{\text{T}} {\mathbf{Z}}} \right)^{ - 1} {\mathbf{Z}}^{\text{T}} {\mathbf{Y}} $$

(3)

Where, the ^T sign stands for the transpose operation. λ and Y are the vectors of the coefficients and measured parameters respectively. Z is the design matrix. λ, Y, and Z are given by (4).

The upper and lower halves of Y and Z correspond to the measured locations and orientations respectively. The order of each polynomial is adjusted in order to find the best fitting, i.e. the least RMSE for LOC and Θ.

$$ {\varvec{\uplambda}} = \left[ {\begin{array}{*{20}c} {\lambda_{t} } \\ {\lambda_{t - 1} } \\ \vdots \\ {\lambda_{2} } \\ \end{array} } \right],{\mathbf{Y}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{Y}}_{{{\text{L}}4}} } \\ {{\text{Y}}_{{{\text{L}}3}} } \\ \vdots \\ {{\text{Y}}_{{{\text{T}}2}} } \\ \end{array} } \\ {\_ \_ \_ \_ \_ \_} \\ {\begin{array}{*{20}c} {\tan \varTheta_{{{\text{L}}4}} } \\ {\tan \varTheta_{{{\text{L}}3}} } \\ \vdots \\ {\tan \varTheta_{{{\text{T}}2}} } \\ \end{array} } \\ \end{array} } \right],{\mathbf{Z}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{Z}}_{{{\text{L}}4}}^{t} } & {{\text{Z}}_{{{\text{L}}4}}^{t - 1} } & {} & \cdots & {{\text{Z}}_{{{\text{L}}4}}^{2} } \\ {{\text{Z}}_{{{\text{L}}3}}^{t} } & {{\text{Z}}_{{{\text{L}}3}}^{t - 1} } & {} & \cdots & {{\text{Z}}_{{{\text{L}}3}}^{2} } \\ \vdots & \vdots & {} & \ddots & \vdots \\ {{\text{Z}}_{{{\text{T}}2}}^{t} } & {{\text{Z}}_{{{\text{T}}2}}^{t - 1} } & {} & \cdots & {{\text{Z}}_{{{\text{T}}2}}^{2} } \\ \end{array} } \\ {\_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_ \_} \\ {\begin{array}{*{20}c} {t{\text{Z}}_{{{\text{L}}4}}^{t - 1} } & {\left( {t - 1} \right){\text{Z}}_{{{\text{L}}4}}^{t - 2} } & \cdots & {2{\text{Z}}_{{{\text{L}}4}}^{1} } \\ {t{\text{Z}}_{{{\text{L}}3}}^{t - 1} } & {\left( {t - 1} \right){\text{Z}}_{{{\text{L}}3}}^{t - 2} } & \cdots & {2{\text{Z}}_{{{\text{L}}3}}^{1} } \\ \vdots & \vdots & \ddots & \vdots \\ {t{\text{Z}}_{{{\text{T}}2}}^{t - 1} } & {\left( {t - 1} \right){\text{Z}}_{{{\text{T}}2}}^{t - 2} } & \cdots & {2{\text{Z}}_{{{\text{T}}2}}^{1} } \\ \end{array} } \\ \end{array} } \right] $$

(4)

Multi-body modelling approach considers the spine as a chain of motion segments comprising joints and links [18, 19]. By employing this approach, we consider the spine curvature as a chain of MMSs laying on the curvature (Fig. 3). An MMS consists of a rigid link and a 1-DOF rotary joint. The links of MMSs are equal in length. The chain is constrained at the first MMS attached to the mid-point of L4, and cannot translate with respect to this mid-point. The last MMS corresponds to the mid-point of the uppermost vertebrae considered in the spine curvature (T2 in this study).

Fig. 3.

The chain of MMSs that lays on the spine curvature and the coordinate systems

Denavit-Hartenberg convention [20] is adopted to represent the chain of MMSs. According to Denavit-Hartenberg convention, the angle (θ) of the rotary joints of MMSs must be identified to reconstruct the spine curvature in a certain position. θ of an MMS is defined with respect to X-axis attached to its inferior MMS in the counterclockwise direction (Fig. 3). For example, θ ₁ is the angle between X₁ and X₀, and it is measured with respect to X₀ in the counterclockwise direction.

The chain of MMSs is fully characterized to a given patient by specification of the number of MMSs and the length of their links. In this study, the total number of MMSs is considered 1000 according to our previous work [21], and the length of the links is 0.37 ± 0.03 mm. After the characterization, MMSs nearest (the shortest Euclidian distance) to the mid-point of the vertebrae in the erect position are considered as the representative of LOC and Θ of the vertebrae in all the positions.

4 Results

Fifty-four curvatures (3 positions × 1 movement sequence × 18 patients) were reconstructed by using the chain of MMSs. The RMSEs of curvatures estimated by the chain were 0.0000 mm. Besides, the RMSEs of Cobb angles, spinal mobility, and spinal flexibility were 0.0002º, 0.0004º, and 0.0000 respectively. These errors were calculated between the curvatures and parameters estimated by using the polynomial (the actual spine curvature) and chain. It should be noted that the estimates by using the polynomials are the reference in this study because we adopted Analytic Cobb method [22, 23] that measures the parameters on the spine curvature. The small RMSEs show that the curvatures estimated by the chain are good estimates of the actual spine curvatures, and the estimated curvatures give good estimates of the key parameters for planning scoliosis surgery.

For each patient, the chain gave θs for MMSs of the spine in the movement sequence from the left bending to erect to right bending positions. By utilizing linear regression method, it was found that a linear relationship (5) exists between θ _erect and θ _left/right of MMSs placed between the mid-points of each two successive vertebrae.

$$ \theta_{{{\text{left}}/{\text{right}}}} \approx \hat{\theta }_{{{\text{left}}/{\text{right}}}} = \alpha_{{{\text{left}}/{\text{right}}}} \left( i \right) \cdot \theta_{\text{erect}} + \beta_{{{\text{left}}/{\text{right}}}} \left( i \right) $$

(5)

Where, $\hat{\theta }$ represents the estimated θ. α and β are the slopes and intercepts of the linear relationships respectively. i corresponds to i ^th vertebra.

In total, 504 linear relationships (14 vertebrae × 2 positions × 18 patients) were identified. The coefficient of determination (R²) for the linear relationships was 0.93 ± 0.09 (Fig. 4a). The confidence interval of the mean was between 0.92 and 0.95, with the confidence level of 95 %. According to [17] and [24], these high R² show that there exists an excellent linear relationship between θ _erect and θ _left/right of MMSs between each two successive vertebrae. As an example, Fig. 4b shows the linear relationship identified between θ _erect and θ _left of MMSs placed between the mid-points of L3 and L4 for one of the patient.

Fig. 4.

(a) Mean ± SD of R² of the relationships between θ _erect and θ _left/right of MMSs placed between each two successive vertebrae, (b) an example of the linear relationship identified for L3-L4 of one of the patients in the movement from the erect to right bending position.

The curvatures of 36 spines (2 lateral bending positions × 18 patients) were reconstructed by $\hat{\theta }_{\text{left/right}}$, and compared with the actual curvatures (Fig. 5). The small RMSEs (0.0172 ± 0.0114 mm) demonstrate that the scoliotic spine curvatures estimated by using the linear relationships are good estimates of the actual curvatures.

Fig. 5.

RMSEs between the estimated and actual curvatures for each patient in the left and right bending positions

As mentioned in Sect. 1, the estimated curvatures are supposed to replicate the X-ray images taken in the lateral bending positions. Besides, Cobb angle and spinal mobility and flexibility are the key parameters measured on the X-ray images to plan the scoliosis surgery [3]. Therefore, the parameters measured on the estimated curvatures are to be a good estimate of the actual ones measured on the X-ray image. The parameters were obtained by using the estimated curvatures and compared with the actual parameters. The results are as follows.

Analytic Cobb method [22, 23] was adopted to measure Cobb angle in the frontal plane because the chain of MMSs provides the spine curvature in this plane. In Analytic Cobb method, Cobb angle is defined as the angle between the perpendiculars at inflectional points of the curvature in a specified plane (term #48 in [4]). Cobb angle was measured for the lumbar and thoracic regions of the scoliotic spine. The estimation errors are illustrated in Fig. 6. The small errors (0.0016 ± 0.0122º) show that Cobb angle measured on the estimated spine curvature can be an accurate estimate of the actual Cobb angle.

Fig. 6.

The error between the actual and estimated Cobb angles for the individual patients

The estimation errors of the spinal mobility and flexibility in the lateral bending positions are shown in Figs. 7 and 8. As can be seen the errors of these parameters are also quite small (0.0010 ± 0.0086º and 0.0002 ± 0.0002 for spinal mobility and flexibility respectively) showing that the parameters measured by using the estimated curvatures are good estimates of the parameters measured by using the actual curvatures.

Fig. 7.

The error between the actual and estimated spinal mobility

Fig. 8.

The error between the actual and estimated spinal flexibility

5 Discussion

This study utilized a multi-body kinematic modelling approach in order to perform a deep analysis in the relationships between scoliotic spine curvatures in the movement sequence from the left bending to erect to right bending positions. The spine is considered as a chain of MMSs. It was found that there is a linear relationship between θ _erect and θ _left/right of MMSs placed between the mid-points of each two successive vertebrae. We showed that by using the identified linear relationships, we reconstructed the spine curvatures that were good estimates of the actual curvatures. Besides, it was demonstrated that Cobb angle, the spinal mobility, and the spinal flexibility in the bending positions obtained from the estimated curvatures were also good estimates of the actual ones. Therefore, we can conclude that the spine curvatures in the bending positions can be related to the curvature in the erect position by the linear relationships. This paper has provided an important insight: the scoliotic spine curvatures in the bending positions can be predicted by using the spine curvature in the erect position. This study is an important step towards developing a method for prediction of the scoliotic spine curvatures in the bending positions in the frontal plane. By such method, we can obviate the need for the lateral bending radiographs when planning the surgery in order to mitigate the radiation risks.

It is worth mentioning that the movement sequence was from left bending to erect to right bending positions, but the movement was studied from the erect to the bending positions. We chose the erect position as the start position of the movement sequence, and the reference position for both characterization of the chain of MMSs and study of the prediction for the following reasons. The erect position is the reference for evaluating the scoliotic spine, its surgery planning, and assessment of the spinal mobility and flexibility [1]. In addition, radiological imaging of this position is part of scoliosis routine standard care [7]. Moreover, the evaluation of the scoliosis surgery outcome is mainly made by comparing the pre- and post-operative X-ray images taken in the erect position. Therefore, the X-ray image of the spine in the erect position is required and cannot be removed from the scoliosis routine standard care. As such, the erect position is an excellent choice to provide the information for predicting the spine curvature in the lateral bending positions.

Indeed, to predict the spine curvatures, α (slope) and β (intercept) of the identified linear relationships should be estimated. Estimation of α and β is out of the scope of this paper. Further studies should be done on the estimation of α and β. We are in the process of estimating α and β to fully characterize the identified relationships to develop a method for prediction of scoliotic spine curvatures in the bending positions.

The data was collected from Asian subjects. Thus, the results of this study may not be applicable to other races. In addition, the majority of the Lenke types in this study are types 1, 2, and 3. More information relating to patients with the Lenke types of more than three can help to better generalize the results to all Lenke types.

6 Conclusions

This paper studied the relationships between the scoliotic spine curvatures in the movement sequence from the left bending to erect to right bending positions in the frontal plane. We identified the relationships that give good estimates of the spine curvatures in the bending positions by using the curvature in the erect position. We also demonstrated that by using the estimated curvatures, good estimates of Cobb angle, spinal mobility, and spinal flexibility in the bending positions were obtained. The paper provides an important insight: scoliotic spine curvatures in lateral bending positions and the key parameters for surgery planning can be predicted using spine curvature in erect position. This study is an ideal starting point for developing a method for prediction of the scoliotic spine curvatures in the lateral bending positions in the frontal plane. By such method, we can reduce the number of the X-ray images required for planning the scoliosis surgery (i.e. X-ray of the bending positions) in the scoliosis standard care, and thus, reduce the radiation risks.