Modeling Parallel Optimization of the Early Stopping Method of Multilayer Perceptron

Abstract

Very often, overfitting of the multilayer perceptron can vary significantly in different regions of the model. Excess capacity allows better fit to regions of high, nonlinearity; and backprop often avoids overfitting the regions of low nonlinearity. The used generalized net will give us a possibility for parallel optimization of MLP based on early stopping algorithm.

1 Introduction

In a series of papers, the process of functioning and the results of the work of different types of neural networks are described by Generalized Nets (GNs). Here, we shall discuss the possibility for training of feed-forward Neural Networks (NN) by backpropagation algorithm. The GN optimized the NN-structure on the basis of connections limit parameter.

The different types of neural networks [1] can be implemented in different ways [2–4] and can be learned by different algorithms [5–7].

2 The Golden Sections Algorithm

Let the natural number N and the real number C be given. They correspond to the maximum number of the hidden neurons and the lower boundary of the desired minimal error.

Let real monotonous function f determine the error f(k) of the NN with k hidden neurons.

Let function c: R × R → R be defined for every x, y ∈ R by

$$ c(x,y) = \left\{ {\begin{array}{*{20}l} { 0 ; {\text{ if max(x; y) }} < {\text{ C}}} \hfill \\ {\frac{ 1}{ 2} ; {\text{ if x}} \le {\text{ C}} \le {\text{ y}}} \hfill \\ { 1 ; {\text{ if min(x, y) }} > {\text{ C}}} \hfill \\ \end{array} } \right. $$

Let $\varphi = \frac{\sqrt 5 + 1}{2} = 0.61$ be the Golden number.

Initially, let we put: L = 1; M = [φ ²:N] + 1, where [x] is the integer part of the real number x ≥ 0.

The algorithm is the following:

• 1. If L ≥ M go to 5.

• 2. Calculate c(f(L), f(M)). If

  $$ c(x,y) = \left\{ \begin{aligned} 1 {\text{ to go 3}} \hfill \\ \frac{ 1}{ 2}{\text{ to go 4}} \hfill \\ 0 {\text{ to go 5}} \hfill \\ \end{aligned} \right. $$

• 3. L = M + 1; M = M + [φ ² · (N−M)] + 1 go to 1.

• 4. M = L + [φ ² · (N−M)] + 1; L = L + 1 go to 1.

• 5. End: final value of the algorithm is L.

3 Neural Network

The proposed generalized-net model introduces parallel work in learning of two neural networks with different structures. The difference between them is in neurons’ number in the hidden layer, which directly reflects on the all network’s properties. Through increasing their number, the network is learned with fewer number of epoches achieving its purpose. On the other hand, the great number of neurons complicates the implementation of the neural network and makes it unusable in structures with elements’ limits [5].

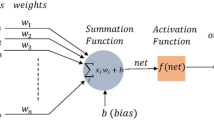
Figure 1 shows abbreviated notation of a classic tree-layered neural network.

Fig. 1

xxx

In the many-layered networks, the one layer’s exits become entries for the next one. The equations describing this operation are

$$ a^{ 3} = f^{ 3} \left( {w^{ 3} f^{ 2} \left( {w^{ 2} f^{ 1} \left( {w^{ 1} p + b^{ 1} } \right) + b^{ 2} } \right) + b^{ 3} } \right), $$

(1)

where

• a ^m is the exit of the m-layer of the neural network for m = 1, 2, 3;

• w is a matrix of the weight coefficients of the everyone of the entries;

• b is neuron’s entry bias;

• f ^m is the transfer function of the m-layer.

The neuron in the first layer receives outside the entries p. The neurons’ exit from the last layer determine the neural network’s exit a.

Because it belongs to the learning with teacher methods, the algorithm are submitted couple numbers (an entry value and an achieving aim—on the network’s exit)

$$ \left\{ {p_{ 1} ,t_{ 1} } \right\},\,\left\{ {p_{ 2} ,t_{ 2} } \right\},\, \ldots \,,\left\{ {p_{Q} ,t_{Q} } \right\}, $$

(2)

Q ∈ (1…n), n—numbers of learning couple, where p_Q is the entry value (on the network entry), and t _Q is the exit’s value replying to the aim. Every network’s entry is preliminary established and constant, and the exit have to reply to the aim. The difference between the entry values and the aim is the error—e = t − a.

The “back propagation” algorithm [6] uses least-quarter error

$$ \hat{F} = (t - a)^{2} = e^{ 2} . $$

(3)

In learning the neural network, the algorithm recalculates network’s parameters (W and b) to achieve least-square error.

The “back propagation” algorithm for i-neuron, for k + 1 iteration use equations

$$ w_{i}^{m} (k + 1) = w_{i}^{m} (k) - \alpha \frac{{\partial \hat{F}}}{{\partial w_{i}^{m} }}, $$

(4)

$$ b_{i}^{m} (k + 1) = b_{i}^{m} (k) - \alpha \frac{{\partial \hat{F}}}{{\partial b_{i}^{m} }}, $$

(5)

where

• α—learning rate for neural network;

• $\frac{{\partial \hat{F}}}{{\partial w_{i}^{m} }}$—relation between changes of square error and changes of the weights;

• $\frac{{\partial \hat{F}}}{{\partial b_{i}^{m} }}$—relation between changes of square error and changes of the biases.

The overfitting [8] appears in different situations, which effect over trained parameters and make worse output results, as show in Fig. 2.

Fig. 2

xxx

There are different methods that can reduce the overfitting—“Early Stopping” and “Regularization”. Here we will use Early Stopping [9].

When multilayer neural network will be trained, usually the available data must be divided into three subsets. The first subset named “Training set” is used for computing the gradient and updating the network weighs and biases. The second subset is named “Validation set”. The error on the validation set is monitored during the training process. The validation error normally decreases during the initial phase of training, as does the training set error. Sometimes, when the network begins to overfit the data, the error on the validation set typically begins to rise. When the validation error increases for a specified number of iterations, the training is stopped, and the weights and biases at the minimum of the validation error are returned [5]. The last subset is named “test set”. The sum of these three sets has to be 100 % of the learning couples.

When the validation error e_v increases (the changing $de_{v}$ have positive value) the neural network learning stops when

$$ de_{v} > 0 $$

(6)

The classic condition for the learned network is when

$$ e^{ 2} < E{ \hbox{max} }, $$

(7)

where Emax is maximum square error.

4 GN Model

All definitions related to the concept “GN” are taken from [10]. The network, describing the work of the neural network learned by “Backpropagation” algorithm [9], is shown in Fig. 3.

Fig. 3

xxx

The below constructed GN model is the reduced one. It does not have temporal components, the priorities of the transitions; places and tokens are equal, the place and arc capacities are equal to infinity.

Initially the following tokens enter in the generalized net:

• in place S _STR—α-token with characteristic

  $x_{0}^{\alpha } =$ “number of neurons in the first layer, number of neurons in the output layer”;

• in place S _e —β-token with characteristic

  $x_{0}^{\beta } =$ “maximum error in neural network learning Emax”;

• in place S _Pt —γ-token with characteristic

  $x_{0}^{\gamma } =$ “{p _1, t ₁}, {p _2, t ₂}, {p _3, t ₃}”;

• in place S _F —one δ-token with characteristic

  $x_{0}^{\delta } =$ “f ¹, f ^2, f ³”.

  The token splits into two tokens that enters respectively in places $S_{F}^{\prime }$ and $S_{F}^{\prime \prime }$;

• in place S _Wb —ε-token having characteristics

  $x_{0}^{\varepsilon } \, =$ “w, b”;

• in place S _con —ξ-token with a characteristics

  $x_{0}^{\xi } =$ “maximum number of the neurons in the hidden layer in the neural network—C _max ”.

• in place S _dev —ψ-token with a characteristics

  $x_{0}^{\psi } =$ “Training set, Validation set, Test set”.

Generalized net is presented by a set of transitions

$$ A = \{ Z_{ 1} ,Z_{ 2} ,Z_{3}^{\prime } ,Z_{3}^{\prime \prime } ,Z_{ 4} \} , $$

where transitions describe the following processes:

• Z ₁—Forming initial conditions and structure of the neural networks;

• Z ₂—Calculating a_i using (1);

• $Z_{3}^{\prime }$—Calculating the backward of the first neural network using (3) and (4);

• $Z_{3}^{\prime \prime }$—Calculating the backward of the second neural network using (3) and (4);

• Z ₄—Checking for the end of all process.

Transitions of GN model have the following form. Everywhere

• p—vector of the inputs of the neural network,

• a—vector of outputs of neural network,

• a _i —output values of the i neural network, i = 1, 2,

• e _i —square error of the i neural network, i = 1, 2,

• E _max—maximum error in the learning of the neural network,

• t—learn target;

• w _ik —weight coefficients of the i neural networks i = 1, 2 for the k iteration;

• b _ik —bias coefficients of the i neural networks i = 1, 2 for the k iteration.

$$ \begin{aligned} Z_{ 1} = & {\langle }\left\{ {S_{STR} ,S_{e} ,S_{Pt} ,S_{\text{con}} ,S_{\text{dev}} ,S_{ 4 3} ,\,S_{ 1 3} } \right\},\,\left\{ {S_{ 1 1} ,S_{ 1 2} ,S_{ 1 3} } \right\},R_{ 1} , \\ & \wedge ( \vee ( \wedge \left( {S_{e} ,\,S_{Pt} ,\,S_{\text{con}} ,S_{\text{dev}} } \right),S_{ 1 3} ), \vee \left( {S_{STR} ,S_{ 4 3} } \right)){\rangle }, \\ \end{aligned} $$

where:

and

• W _13,11 = “the learning couples are divided into the three subsets”;

• W _13,12 = “is it not possible to divide the learning couples into the three subsets”.

The token that enters in place S ₁₁ on the first activation of the transition Z ₁ obtain characteristic

$$ x_{0}^{{\theta^{\prime } }} =^{\prime \prime } pr_{1} x_{0}^{\alpha } ,\left[ {1;x_{0}^{\xi } } \right],pr_{2}^{{}} x_{0}^{\alpha } ,x_{0}^{\gamma } ,x_{0}^{\beta } \,^{\prime \prime } . $$

Next it obtains the characteristic

$$ x_{cu}^{{\theta^{\prime } }} \, = \,^{\prime \prime } pr_{1} x_{0}^{\alpha } ,\left[ {l_{\hbox{min} } ;l_{\hbox{max} } } \right],pr_{2}^{{}} x_{0}^{\alpha } ,x_{0}^{\gamma } ,x_{0}^{\beta } \,^{\prime \prime } , $$

where [l _min ;l _max ] is the current characteristics of the token that enters in place S ₁₃ from place S ₄₃.

The token that enters place S ₁₂ obtains the characteristic [l _min;l _max].

$$ \begin{aligned} & Z_{ 2} = {\langle }\{ S_{31}^{\prime } ,S_{31}^{\prime \prime } ,S_{11} ,S_{F} ,S_{Wb} ,S_{AWb} \} ,\,\{ S_{21} ,S_{F}^{\prime } ,S_{22} ,S_{F}^{\prime \prime } ,\} \,R_{2} \\ & \vee ( \wedge (S_{F} ,S_{11} ),\, \vee \,(S_{AWb} ,S_{Wb} ),\,(S_{31}^{\prime } ,S_{31}^{\prime \prime } )){\rangle }, \\ \end{aligned} $$

where

The tokens that enter places S ₂₁ and S ₂₂ obtain the characteristics respectively

$$ x_{cu}^{{\eta^{\prime } }} =^{\prime \prime } x_{cu}^{{\varepsilon^{\prime } }} ,x_{0}^{\gamma } ,x_{0}^{{\beta^{\prime \prime } }} ,a_{1} ,pr_{1}^{{}} x_{0}^{\alpha } ,\left[ {l_{\hbox{min} } } \right],pr_{2} x_{0}^{\alpha } \,^{\prime \prime } $$

and

$$ \begin{aligned} & \quad \quad \quad x_{cu}^{{\eta^{\prime \prime } }} =^{\prime \prime } x_{cu}^{{\varepsilon^{\prime } }} ,x_{0}^{\gamma } ,x_{0}^{{\beta^{\prime \prime } }} ,a_{2} ,pr_{1} x_{0}^{\alpha } ,[l_{\hbox{max} } ],pr_{2} x_{0}^{\alpha } \,^{\prime \prime } . \\ Z_{3}^{\prime } & = {\langle }\{ S_{21} ,S_{F}^{\prime } ,S_{3A}^{\prime } \} ,\{ S_{31}^{\prime } ,S_{32}^{\prime } ,S_{3A}^{\prime } \} ,\,R_{3}^{\prime } , \wedge (S_{21} ,S_{F}^{\prime } ,S_{3A}^{\prime } ){\rangle }, \\ \end{aligned} $$

where

and

• $W^{\prime }_{3A,31}$ = “e ₁ > E _max or $de_{1v} < 0$”;

• $W^{\prime }_{3A,32}$ = “e ₁ < E _max or $de_{1v} < 0$”;

• $W^{\prime }_{3A,33}$ = “(e ₁ > E _max and n ₁ > m) or $de_{1v} > 0$”;

where

• n ₁—current number of the first neural network learning iteration,

• m—maximum number of the neural network learning iteration,

• $de_{1v}$—validation error changing of the first neural network.

The token that enters place $S_{31}^{\prime }$ obtains the characteristic “first neural network: w(k + 1), b(k + 1)”, according (4) and (5). The $\lambda_{1}^{\prime }$ and $\lambda_{2}^{\prime }$ tokens that enter place $S_{32}^{\prime }$ and $S_{33}^{\prime }$ obtain the characteristic

$$ \begin{aligned} & \quad \quad \quad \quad \quad \quad \quad x_{0}^{{\lambda^{\prime }_{1} }} = x_{0}^{{\lambda^{\prime }_{2} }} =^{\prime \prime } l_{\hbox{min} }^{\prime \prime } \\ Z_{3}^{\prime \prime } = & {\langle }\{ S_{ 2 2} ,S_{F}^{\prime \prime } ,S_{A3}^{\prime \prime } \} ,\,\{ S_{31}^{\prime \prime } ,S_{32}^{\prime \prime } ,S_{33}^{\prime \prime } ,S_{A3}^{\prime \prime } \} ,\,R_{3}^{\prime \prime } \wedge (S_{ 2 2} ,S_{F}^{\prime \prime } ,S_{A3}^{\prime \prime } ){\rangle } \\ \end{aligned} $$

where

and

• $W_{3A,31}^{\prime \prime }$ = “e ₂ > E _max or $de_{2v} < 0$”,

• $W_{3A,32}^{\prime \prime }$ = “e ₂ < E _max or $de_{2v} < 0$”,

• $W_{3A,33}^{\prime \prime }$ = “(e ₂ > E _max and n₂ > m) or $de_{2v} > 0$”,

where

• n ₂—current number of the second neural network learning iteration;

• m—maximum number of the neural network learning iteration;

• $de_{2v}$—validation error changing of the second neural network.

The token that enters place $S_{31}^{\prime \prime }$ obtains the characteristic “second neural network: w(k + 1), b(k + 1)”, according (4) and (5). The $\lambda_{1}^{\prime \prime }$ and $\lambda^{\prime \prime }_{2}$ tokens that enter place $S_{32}^{\prime \prime }$ and $S_{33}^{\prime \prime }$ obtain, respectively

$$ \begin{aligned} & \quad \quad x_{0}^{{\lambda^{\prime \prime }_{1} }} = x_{0}^{{\lambda^{\prime \prime }_{2} }} =^{\prime \prime } l_{\hbox{max} }^{\prime \prime } \\ Z_{ 4} = {\langle } & \{ S_{32}^{\prime } ,S_{33}^{\prime } ,S_{32}^{\prime \prime } ,S_{33}^{\prime \prime } ,{\text{S}}_{ 4 4} \} ,\,\{ S_{ 4 1} ,S_{ 4 2} ,S_{ 4 3} ,S_{ 4 4} \} ,R_{ 4} , \\ & \quad \quad \wedge ({\text{S}}_{ 4 4} \vee (S_{32}^{\prime } ,S_{33}^{\prime } ,S_{32}^{\prime \prime } ,S_{33}^{\prime \prime } )){\rangle }, \\ \end{aligned} $$

where

and

• W _44,41 = “e ₁ < E _max” and “e ₂ < E _max”;

• W _44,42 = “e ₁ > E _max and n ₁ > m” and “e ₂ > E _max and n ₂ > m”;

• W _44,43 = “(e ₁ < E _max and (e ₂ > E _max and n ₂ > m)) or (e ₂ < E _max and (e ₁ > E _max and n ₁ > m))”.

The token that enters place S ₄₁ obtains the characteristic

Both NN satisfied conditions—for the solution is used the network who wave smaller numbers of the neurons.

The token that enters place S ₄₂ obtain the characteristic

There is no solution (both NN not satisfied conditions).

The token that enters place S ₄₄ obtains the characteristic

the solution is in interval [l _min; l _max]—the interval is changed using the golden sections algorithm.

5 Conclusion

The proposed generalized-net model introduces the parallel work in the learning of the two neural networks with different structures. The difference between them is in the number of neurons in the hidden layer, which reflects directly over the properties of the whole network.

On the other hand, the great number of neurons complicates the implementation of the neural network.

The constructed GN model allows simulation and optimization of the architecture of the neural networks using golden section rule.