Temporal Logic Modeling of Biological Systems

Abstract

Metabolic networks, formed by a series of metabolic pathways, are made of intracellular and extracellular reactions that determine the biochemical properties of a cell, and by a set of interactions that guide and regulate the activity of these reactions. Cancer, for example, can sometimes appear in a cell as a result of some pathology in a metabolic pathway. Most of these pathways are formed by an intricate and complex network of chain reactions, and can be represented in a human readable form using graphs which describe the cell signaling pathways. In this paper, we define a logic, called Molecular Interaction Logic (MIL), able to represent these graphs and we present a method to automatically translate graphs into MIL formulas. Then we show how MIL formulas can be translated into linear time temporal logic, and then grounded into propositional classical logic. This enables us to solve complex queries on graphs using only propositional classical reasoning tools such as SAT solvers.

Dedicated to Jair Minoro Abe for his 60th birthday

11.1 Introduction

Metabolic networks, formed by a series of metabolic pathways, are made of intracellular and extracellular reactions that determine the biochemical properties of a cell by consuming and producing proteins, and by a set of interactions that guide and regulate the activity of these reactions. These reactions are at the center of a cell’s existence, and are regulated by other proteins, which can either activate these reactions or inhibit them.

These pathways form an intricate and complex network of chain reactions, and can be represented in a human readable form using graphs which describe the cell signaling pathways.

These graphs can become extremely large, and although essential for knowledge capitalization and formalization, they are difficult to use:

• Reading is complex due to the very large number of elements, and reasoning is even more difficult.

• Using a graph to communicate goals is only partially suitable because the representation formalism requires expertise.

• Graphs often contain implicit knowledge, that is taken for granted by one expert, but is missed by another one.

Here, we show how classical propositional reasoning tools can be used to detect problems on these graphs, such as missing knowledge, and to answer complex queries.

The rest of this paper is organized as follows. Section 11.2 presents the important concepts and the problems to solve in layman’s words with a simple example, Sect. 11.3 describes the concepts of production and regulation which are the basic operations present in a graph, Sect. 11.4 presents the Molecular Interaction Logic (MIL) capable of describing and reasoning about general pathways, Sect. 11.5 studies the relation between MIL and Linear Time Temporal Logic, Sect. 11.6 presents temporal reasoning and a method for grounding temporal theories into classical propositional formulas, when assuming bounded time, Sect. 11.7 explains what kind of queries on graphs can be answered using classical propositional reasoning tools such as SAT solvers, Sect. 11.8 describes the current state of the operational implementation of this tool, and at last Sect. 11.9 gives a summary and discusses future works.

11.2 A Simple Classical Example

We are first going to describe a simple graph, which represents the regulation of the lac operon.¹ A detailed presentation is available at [21].

The lac operon (lactose operon) is an operon required for the transport and metabolism of lactose in many bacteria. Although glucose is the preferred carbon source for most bacteria, the lac operon allows for the effective digestion of lactose when glucose is not available. The lac operon is a sequence of three genes (lacZ, lacY and lacA) which encode 3 enzymes. Then, these enzyms carry the transformation of lactose into glucose. We will concentrate here on lacZ. LacZ encodes the $\beta$-galactosidase which cleaves lactose into glucose and galactose.

The lac operon uses a two-part control mechanism to ensure that the cell expends energy producing the enzymes encoded by the lac operon only when necessary. First, in the absence of lactose, the lac repressor halts production of the enzymes encoded by the lac operon. Second, in the presence of glucose, the catabolite activator protein (CAP), required for production of the enzymes, remains inactive.

Fig. 11.1

Lac operon

Figure 11.1 describes this regulatory mechanism. The expression of lacZ gene is only possible when RNA polymerase (pink) can bind to a promotor site (marked P, black) upstream the gene. This binding is aided by the cyclic adenosine monophosphate (cAMP in blue) which binds before the promotor on the CAP site (dark blue).

The lacl gene (yellow) encodes the repressor protein Lacl (yellow) which binds to the promotor site of the RNA polymerase when lactose is not available, preventing the RNA polymerase to bind to the promoter and thus blocking the expression of the following genes (lacZ, lacY and lacA): this is a negative regulation, or inhibition, as it blocks the production of the proteins. When lactose is present, the repressor protein Lacl binds with lactose and is converted to allolactose, which is not able to bind to the promotor site, thus enabling RNA polymerase to bind to the promotor site and to start expressing the lacZ gene if cAMP is bound to CAP.

cAMP is on the opposite a positive regulation, or an activation, as its presence is necessary to express the lacZ gene. However, cAMP is itself regulated negatively by glucose: when glucose is present, the concentration of cAMP becomes low, and thus cAMP does not bind to the CAP site, blocking the expression of lacZ.

In this graph, we have three kinds of entities which have different initial settings and temporal dynamics:

• lacl, lacZ and cAMP are initial external conditions of the model and they do not evolve in time.

• galactosidase and the repressor protein can only be produced inside the graph, and are always absent at the start (time 0) of the modeling. Their value will then evolve in time according to the processes described by the graph.

• glucose and lactose also evolve in time (like galactosidase and the repressor protein) according to the processes described by the graph, but they are also initial conditions of the system, and can either be present or absent at time 0, like lacl, lacZ and cAMP.

So, an entity must be classified according to two main characteristics:

C1::

It can evolve in time according to the cell reactions (appear and disappear), or it can be fixed, such as a condition which is independent of the cell reactions (temperature, protein always provided in large quantities by the external environment, etc...).

C2::

It can be an initial condition of the cell model (present or absent at the beginning of the modeling), or can only be produced by the cell.

There are thus three kind of entities, which have three kind of behaviour:

Exogenous entities::

an exogenous entity satisfies C1 and $\lnot C2$; their status never change through time: they are set once and for all by the environment or by the experimenter at the start of the simulation; the graph never modifies their value, and if they are used in a reaction, the environment will always provide “enough” of them.

Pure endogenous entities::

on the opposite, a pure endogenous entity satisfies $\lnot C1$ and C2; their status evolves in time and is set only by the dynamic of the graph. They are absent at the beginning of the reaction, and can only appear if they are produced inside the graph.

Weak endogenous entities::

weak endogenous entities satisfy C2 and C1; they can be present or absent at the beginning of the process (they are initial conditions of the model), however their value after the start of the process is entirely set by the dynamic of the graph. So they roughly behave like pure endogenous entities, but the initial condition can be set by the experimenter.

The status of a protein/condition is something which is set by the biologist, regarding his professional understanding of the biological process described by the graph.² However a rule of thumb is that exogenous entities are almost never produced inside the graph (they never appear at the right side of a production arrow), while endogenous entities always appear on the right side of a production arrow (but they can also appear on the left side of a production rule, especially weak endogenous entities).

These distinctions are fundamental, because the dynamics of these entities are different and they will have to be formalized differently.

11.3 Fundamental Operations

The mechanism described in the previous section is summarized in the simplified graph in Fig. 11.2. This example contains all the relationship operators that will be used in the rest of this document. We are going to present them one by one.

We separate these operations in two main sets: productions and regulations.

Productions can take two different forms, depending on whether the reactants are consumed by the reactions or not:

• In Fig. 11.2, lactose and galactosidase produce glucose, and are consumed while doing so, which is thus noted (galactosidase, lactose glucose).

• On the opposite, the expression of the lacZ gene to produce galactosidase (or of the lacl gene to produce the Lacl repressor protein) does not consume the gene, and we have thus (lacZ 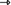galactosidase).

Generally speaking:

• If the reaction consumes completely the reactant(s) we write: $a_1,a_2,\ldots ,a_n$ b. Here the production of b completely consumes $a_1,\ldots ,a_n$

• If the reactants are not completely consumed by the reaction, we write $a_1,a_2,\ldots ,$ $a_n$ b. Here b is produced but $a_1$, $a_2,\ldots ,a_n$ are still present after the production of b.

Fig. 11.2

Functional representation of the lac operon

Regulations can also take two forms: every reaction can be either inhibited or activated by other proteins or conditions.

• In the example above, the production of galactosidase from the expression of the lacZ gene is activated by cAMP (we use cAMP to express activation)

• At the same time the same production of galactosidase is blocked (or inhibited) by the Lacl repressor protein (noted $Repressor \dashv$).

Fig. 11.3

Activations/Inhibitions

Fig. 11.4

Stacking

Generally speaking:

• we write $a_1,a_2,...a_n$ if the simultaneous presence of $a_1,a_2,...a_n$ activates a production or another regulation.

• we write $a_1,a_2,...a_n \dashv$ if the simultaneous presence of $a_1,a_2,...a_n$ inhibits a production or another regulation.

On Fig. 11.3, we have a summary of basic inhibitions/activations on a reaction: the production of b from $a_1,\ldots ,a_n$ is activated by the simultaneous presence of $c_1,\ldots ,c_n$ or by the simultaneous presence of $d_1,\ldots ,d_n$, and inhibited by the simultaneous presence of $e_1,\ldots ,e_n$ or by the simultaneous presence of $f_1,\ldots ,f_n$.

These regulations are often “stacked”, on many levels (see Fig. 11.4). For example in Fig. 11.2, the inhibition by the Lacl repressor protein of the production of galactosidase can itself be inhibited by the presence of lactose, while the activation of the same production by cAMP is inhibited by the presence of glucose.

A final word of warning is necessary. Graphs pragmatically describe sequences of operations that biologists find important. They are only a model of some of the biological, molecular and chemical reactions that take place inside the cell; they can also be written in many different ways, depending on the functional block or operations that biologists want to describe, and some relationships are sometimes simply left out because they are considered not important for the function which is described in a particular graph.

11.4 Molecular Interaction Logic

In this section we extend a previous approach to logical modelling of graphs made in terms of first-order logic with equality [8–10]. Our approach, Molecular Interaction Logic (MIL), is based on modal temporal logic, which will help us later to define connections with other logical approaches to temporal reasoning as well as studying graphs behaviour in the context of a modal approach. We start this section by introducing the concepts of pathway context and pathway formula. The former corresponds to the formalization of regulation while the latter is the formal representation of the production rules, both concepts were presented in Sect. 11.3.

Definition 11.1

(Pathway context) Given a set of entities, a pathway context is formed by expressions defined by the following grammar:

where P and Q are sets (possibly empty) of propositional variables representing the conditions of activation () and inhibition ($\dashv$) of the reaction. Every context can be associated with a (possibly empty) set of activation ($\alpha _i$, with $1 \le i \le n$) and inhibition ($\alpha _{j}$, with $n < j \le m$) contexts. One, or both sets can be empty. $\square$

Definition 11.2

(Pathway formula)

A Pathway formula is generated by the following grammar:

$$\begin{aligned} F\ {::}\!=\ [\alpha ] \left( P^\wedge \multimap q\right) \mid F \wedge F \end{aligned}$$

where $\alpha$ represents a context, $\multimap \in$ , $P^\wedge$ stands for a conjunction of all atoms in the set P and q corresponds to a propositional variable.$\square$

11.4.1 MIL Semantics

Before introducing the semantics we need to give a formal definition of the activation and inhibition expressions, since both concepts play an important role in the definition of the semantics.

Definition 11.3

(Activation and inhibition expressions)

Given a context of the form

we define the corresponding expressions $\mathcal{A}(\alpha )$ and $\mathcal{I}(\alpha )$ recursively as follows:

$$\begin{aligned} \mathcal{A}(\alpha )= & {} \bigwedge _{p \in P}p \wedge \bigwedge \limits _{i=1}^n \mathcal{A}(\alpha _i) \wedge (\bigvee _{q \in Q} \lnot q \vee \bigwedge \limits _{j=n+1}^m\ \mathcal{I}(\beta _j))\\ \mathcal{I}(\alpha )= & {} \bigvee _{p \in P}\lnot p \vee \bigvee \limits _{i=1}^n \mathcal{I}(\alpha _i) \vee (\bigwedge _{q \in Q} q \wedge \bigwedge \limits _{j=n+1}^m \mathcal{A}(\beta _j) ). \end{aligned}$$

$\square$

Informally speaking, $\mathcal{A}(\alpha )$ characterizes when the context $\alpha$ is active while $\mathcal{I}(\alpha )$ defines when it is inhibited. If one part of the context $\alpha$ is empty, then the corresponding part is of course absent in $\mathcal{A}(\alpha )$ and $\mathcal{I}(\alpha )$.

Definition 11.4

(Extended signature) Given a set of atoms $\varSigma$, its corresponding extended signature, $\widehat{\varSigma }$, is defined by the following expression:

$$\begin{aligned} \widehat{\varSigma } = \varSigma \cup \lbrace \mathbf {Pr}\left( p\right) \mid p \in \varSigma \rbrace \cup \lbrace \mathbf {Cn}\left( p\right) \mid p \in \varSigma \rbrace , \end{aligned}$$

where p is an endogenous variable. $\square$

Informally speaking, every atom of the form $\mathbf {Pr}\left( p\right)$ means that p is produced as a result of a chemical reaction. On the other hand, $\mathbf {Cn}\left( p\right)$ means that the reactive p has been consumed in a reaction. From now on, we will use the symbols $\varSigma$ and $\widehat{\varSigma }$ referring to, respectively, the signature and its corresponding extension.

Definition 11.5

(MIL interpretation)

Let $\varSigma$ be a set of propositional variables and $\widehat{\varSigma }$ its corresponding extended signature. We define a MIL interpretation, $\mathbf {V}= V_0,V_1,\ldots$, as an infinite sequence of sets of atoms on $\widehat{\varSigma }$ such that every endogenous variable $p \in \varSigma$ satisfies the following constraint:

$$\begin{aligned} \forall i \ge 0&\text { if } \quad \quad \mathbf {Pr}\left( p\right) \in V_i \hbox { or } \left( \mathbf {Cn}\left( p\right) \not \in V_i \hbox { and } p \in V_{i} \right) \nonumber \\&\text { then } \quad p \in V_{i+1}. \end{aligned}$$

(11.1)

$\square$

Definition 11.6

(Satisfaction relation) Given a MIL interpretation $\mathbf {V}= V_0,V_1,\ldots$, $i\ge 0$ and a pathway formula F on $\varSigma$, we will define recursively the satisfaction relation ($\mathbf {V}, i \models F$) as follows:

• $\mathbf {V}, i \models p$ iff $p \in V_i$, for any $p\in \varSigma$

• negation, disjunction and conjunction are satisfied as usual

• iff for all $j \ge i$, if $V, j \models \mathcal{A}(\alpha )$ and $P \subseteq V_j$, then $\mathbf {Pr}\left( q\right) \in V_j$ and for all $p \in P$, $\mathbf {Cn}\left( p\right) \in V_j$

• iff for all $j \ge i$ if $V, j \models \mathcal{A}(\alpha )$ and $P \subseteq V_j$ then $\mathbf {Pr}\left( q\right) \in V_j$. $\square$

11.5 Translating Molecular Interaction Logic into Linear Time Temporal Logic

In this section, we consider the connection between Molecular Interaction Logic and Linear Time Temporal Logic (LTL) [19] by showing a translation from our formalism into a restricted subset of LTL in which only operators $\bigcirc$ and $\Box$ are used. We start this section by providing some background on LTL.

Definition 11.7

(Temporal language) Temporal formulas are generated by the following grammar:

$$\begin{aligned}&\varphi \ {::}=\ \bot \mid p \mid \lnot \varphi _1 \mid \varphi _1 \wedge \varphi _2 \mid \varphi _1 \vee \varphi _2 \mid \varphi _1 \rightarrow \varphi _2 \mid \bigcirc \varphi _1 \mid \Box \varphi _1\mid \nonumber \\&\quad \quad \Diamond \varphi _1\mid \varphi _1 \mathcal{U}\varphi _2 \end{aligned}$$

(11.2)

where $\varphi _1$ and $\varphi _2$ are temporal formulas in their turn and p is any atom. Modal operators $\bigcirc$, $\Box$, $\Diamond$ and $\mathcal{U}$ are respectively read as “next”, “forever”, “possible” and “until”. $\square$

Definition 11.8

(LTL semantics) Let $\widehat{\varSigma }$ be a set of propositional variables. An LTL model is an infinite sequence, $\mathbf {V}= V_1,V_2, \ldots$, of sets of atoms on $\widehat{\varSigma }$. Given an LTL interpretation and $i \ge 0$, the LTL satisfaction relation is defined as follows:

• 1. $\mathbf {V}, i \models p$ iff $p \in V_i$, for $p \in \varSigma$.

• 2. Negation, conjunction and disjunction are satisfied in the usual way.

• 3. $\mathbf {V}, i \models \varphi \rightarrow \psi$ iff $\mathbf {V}, i \not \models \varphi$ or $\mathbf {V}, i \models \psi$.

• 4. $\mathbf {V}, i \models \bigcirc \varphi$ iff $\mathbf {V}, i+1 \models \varphi$.

• 5. $\mathbf {V}, i \models \Box \varphi$ iff $\hbox { for all } j \ge i,\ \mathbf {V}, j \models \varphi$.

• 6. $\mathbf {V}, i \models \Diamond \varphi$ iff $\hbox { there exists } j \ge i,\ \mathbf {V}, j \models \varphi$.

• 7. $\mathbf {V}, i \models \varphi \mathcal{U}\psi$ iff $\exists j \ge i,\ \mathbf {V}, j \models \psi$ and $\forall k \hbox { s.t. } i \le k < j,\ \mathbf {M}, k \models \varphi$.

$\square$

11.5.1 From MIL to LTL

Definition 11.9

(Inertia rule) Let p be an endogenous variable in a signature $\varSigma$. We define inertia(p) as the following formula built on $\hat{\varSigma }$:

$$\begin{aligned} inertia(p) \mathop {=}\limits ^\mathrm{def}\Box \left( \left( \mathbf {Pr}\left( p\right) \vee \left( p \wedge \lnot \mathbf {Cn}\left( p\right) \right) \right) \rightarrow \bigcirc p\right) \end{aligned}$$

(11.3)

$\square$

Thanks to these rules, we can specify how the truth values of biological substances evolve along time. More specifically, this rule means that a protein p might become true if it is the result of a production rule (concept represented by $\mathbf {Pr}\left( p\right)$) or if it is already present and it has not been used to produce other proteins (concept represented by $\mathbf {Cn}\left( p\right)$). By using structural induction we can prove the following proposition:

Proposition 11.1

Let $\varSigma$ be a finite signature. Given a LTL interpretation, $\mathbf {V}$, on $\hat{\varSigma }$. $\mathbf {V},0 \models \bigwedge \limits _{p} inertia(p)$, with p and endogenous variable in $\varSigma$, iff $\mathbf {V}$ satisfies condition (11.1) of Definition 11.5. $\square$

Definition 11.10

(Translation from MIL into LTL) Let F be a pathway formula built on a signature $\varSigma$. We define the formula $tr\left( F\right)$, built on the signature $\widehat{\varSigma }$, as follows:

where both $F_1$ and $F_2$ stand for two arbitrary pathway formulas.$\square$

In order to guarantee that our translation is correct with respect to the MIL semantics presented in Sect. 11.4, we establish the following correspondence between both formalisms:

Lemma 11.1

(Correspondence) Let F be a pathway formula built on a signature $\varSigma$, and $\mathbf {V}$ a LTL interpretation on the extended signature $\hat{\varSigma }$. Then we have the following equivalence:

$$\begin{aligned} \mathbf {V}, 0 \models F \hbox { iff } \mathbf {V}, 0 \models tr\left( F\right) \wedge \bigwedge \limits _{p} inertia(p), \end{aligned}$$

where p is an endogenous variable in F.$\square$

11.6 Temporal Reasoning

As shown in the previous section, we can establish a correspondence between a graph and a temporal formula which describes its behaviour. However, in order to perform temporal reasoning we need to add the supplementary hypothesis of closed world assumption. This concept corresponds to the presumption that a statement that is true is also known to be true. Conversely, what is not currently known to be true, is false. This hypothesis fits perfectly in the biological process, as endogenous proteins appear if and only if a production rule is triggered (except at time 0 for weak endogenous variables) and, moreover, they are consumed only if they are used in a reaction.

11.6.1 Completion Axioms

In order to incorporate this hypothesis we define the Completion axioms [6] for our temporal theories as follows:

Definition 11.11

(Completion axioms) Let $\varSigma$ be a finite signature and let F be a pathway formula built on $\varSigma$. For any pure endogenous propositional variable p in $\varSigma$, COMP(F, p) corresponds to as the following formula built on $\widehat{\varSigma }$:

If p is a weak endogenous variable, COMP(F, p) has the same form as above but omitting the conjunct $\lnot p$. $\square$

Broadly speaking, the meaning of the different components of COMP(F, p) can be explained as follows:

• $\lnot p$: this is a consequence of the type of the substance. If p is pure endogenous (it must be produced before existing), p must not be present at the initial state to that $\lnot p$ must be part of COMP(F, p). For the case of weak endogenous variables, whose truth value at the initial state cannot be deduced, requires that the conjunct $\lnot p$ be omitted from corresponding completion formula.

• $\Box \left( \mathbf {Pr}\left( p\right) \rightarrow \bigvee \limits _{[\alpha ](P^\wedge \multimap p) \in F} P^\wedge \wedge \mathcal{A}(\alpha )\right)$: in any state, the production of a protein p is due to the satisfaction of, at least, one pathway formula.

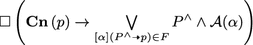• : in any state, if p is consumed then it must be used in a reaction represented by a pathway formula.

• $\Box (\bigcirc p \rightarrow \left( \mathbf {Pr}\left( p\right) \vee \left( p \wedge \lnot \mathbf {Cn}\left( p\right) \right) \right)$: if a substance p is present then it has been produced in the previous state or it was already present and it was not consumed in a reaction.

If we consider now the whole set of propositional variables occurring in F, the resulting completion axioms correspond to the following conjunction

$$\begin{aligned} \bigwedge \limits _{p} COMP(F,p), \hbox {with}~ p~ \hbox {being an endogenous variable}. \end{aligned}$$

11.6.2 Graphs as Splittable Temporal Logic Programs

Completion axioms are used when we want to translate a non-monotonic theory into classical logic. To give an example, in the Answer Set Programming [4] paradigm, the answer sets of a propositional theory can be captured by a classical propositional expression by adding the so called Loop formulas [12, 18] (in the same spirit as Clark’s completion). This result was extended to the case of non-monotonic temporal theories³ in [2] in which it is shown that, regarding a syntactical restricted class of programs, called splittable, loop formulas can be effectively computed. We define such class of programs below:

Definition 11.12

(Splittable temporal logic program) A splittable temporal logic program $\varPi$ for signature $\widehat{\varSigma }$ is said to be splittable if $\varPi$ consists of rules of the form:

$$\begin{aligned} B^\wedge \wedge N^\wedge\rightarrow & {} H \end{aligned}$$

(11.4)

$$\begin{aligned} B^\wedge \wedge \bigcirc B'^\wedge \wedge N^\wedge \wedge \bigcirc N'^\wedge\rightarrow & {} \bigcirc H' \end{aligned}$$

(11.5)

$$\begin{aligned} \Box (B^\wedge \wedge \bigcirc B'^\wedge \wedge N^\wedge \wedge \bigcirc N'^\wedge\rightarrow & {} \bigcirc H') \end{aligned}$$

(11.6)

where B and $B'$ are conjunctions of atoms, N and $N'$ are conjunctions of negative literals like $\lnot p$ with $p \in \widehat{\varSigma }$, and H and $H'$ are disjunctions of atoms.$\square$

Roughly speaking, the idea behind a splittable program is that no past reference depends on the future.

Since the formalism presented in [2], called Temporal Equilibrium Logic (TEL) [1, 5], shares the syntax with LTL we can study our theories under such framework. As a result, we can translate, by using several temporal equivalences, our theories into splittable temporal logic programs, as stated in the following proposition:

Proposition 11.2

Given a conjunction of pathway formulas $F = F_1 \wedge \cdots \wedge F_n$, it can be proved that

$$tr\left( F\right) \wedge \bigwedge \limits _{p} inertia(p),$$

where p corresponds to an endogenous variable in F, is equivalent to a splittable temporal logic program.$\square$

This equivalence allows us to study the relation between our completion axioms and loop formulas, which is considered next.

11.6.2.1 Relation with Loop Formulas

We have already shown that our temporal theories can be translated into splittable temporal logic programs under temporal equilibrium logic semantics. We now show how our completion axioms can be seen as a special case of loop formulas. Before presenting the result, we summarize how loop formulas are computed in [2]. Given a splittable program, $\varPi$, loop formulas are generated from the corresponding (positive) dependency graph of a temporal logic program $\varPi$, denoted by $G(\varPi )$. Nodes of $G(\varPi )$ correspond to the propositional variables in $\varPi$ while edges are defined by the following expression:

$$\begin{aligned} E\!\!=\!\!\lbrace (p,p) \mid p \in \varPi \rbrace \cup \lbrace (p,q) \mid \exists \left( B^\wedge \wedge N^\wedge \rightarrow p\right) \in \varPi \hbox { s.t. } q \in B\rbrace . \end{aligned}$$

(11.7)

for any propositional variable p.

Definition 11.13

(Loop from [12]) A set of atoms L is called a loop of a logic program $\varPi$ iff the sub-graph of $G(\varPi )$ induced by L is strongly connected. Notice that reflexivity of $G(\varPi )$ implies that for any atom p, the singleton $\{p\}$ is also a loop$\square$

When applying this technique to our translation (considering TEL semantics) we must consider the following points:

• 1. Given a conjunction of pathway formulas F, $tr\left( F\right)$ has no positive cycles in the sense of [2]. This means that only unitary cycles must be considered.

• 2. The hypothesis of closed world assumption should not be applied to the exogenous variables, whose presence cannot be justified and whose absence cannot be determined “by default”. They must remain free, specially when querying our representation.

Item 1 means that the computation of the loop formulas, as presented in [2], is equivalent to our completions axioms (see Definition 11.11), while 2 means that completion rules should not be computed in the case of exogenous variables. This result is stated in the following proposition:

Proposition 11.3

Completion axioms of Definition 11.11 are equivalent to loop formulas (under TEL semantics) when they are restricted to endogenous variables (a concept explained in Sect. 11.2). $\square$

This result justifies that our approach can be also considered as non-monotonic temporal logic programs.

11.6.3 Grounding Splittable Temporal Logic Programs

The use of an LTL formalization allows us to consider solutions with infinite length when performing reasoning tasks such as abduction or satisfiability. However, regarding complexity results, it is worth to mention that LTL satisfiability is, in the general case PSpace-complete while, regarding the propositional case, it is NP-complete. In an attempt to reduce the complexity of the problem as well as taking advantage of the tools available for reasoning on propositional logic such as SAT-solvers, abduction algorithms, etc., we consider bounded time, that is, we fix the positive constant max as the maximum time length. This assumption allows us to translate the temporal formulas into a propositional theory, as explained below.

Definition 11.14

Let $\varphi$ a temporal formula built on the language presented in (11.2), $max \ge 0$ and $0 \le i < max$. We define translation of $\varphi$, at instant i, into propositional logic, denoted by ${\langle {\varphi } \rangle }_i$, as follows:

• ${\langle {p} \rangle }_i \mathop {=}\limits ^\mathrm{def}p_i$, with p an atom and $p_i$ a new propositional variable;

• ${\langle {\lnot \varphi } \rangle }_i \mathop {=}\limits ^\mathrm{def}\lnot {\langle {\varphi } \rangle }_{i}$;

• ${\langle {\varphi \odot \psi } \rangle }_i \mathop {=}\limits ^\mathrm{def} {\langle {\varphi } \rangle }_i \odot {\langle {\psi } \rangle }_i$, with $\odot \in \lbrace \wedge , \vee , \rightarrow \rbrace$;

• ${\langle {\bigcirc \varphi } \rangle }_i \mathop {=}\limits ^\mathrm{def} {\langle {\varphi } \rangle }_{i+1}$;

• ${\langle {\Box \varphi } \rangle }_i \mathop {=}\limits ^\mathrm{def}\bigwedge _{i \le j < max} {\langle {\varphi } \rangle }_j$;

• ${\langle {\Diamond \varphi } \rangle }_i \mathop {=}\limits ^\mathrm{def}\bigvee _{i \le j < max} {\langle {\varphi } \rangle }_j$;

• ${\langle {\varphi \mathcal{U}\psi } \rangle }_i \mathop {=}\limits ^\mathrm{def}\bigvee \limits _{i \le j< max} \left( {\langle {\psi } \rangle }_j \wedge \bigwedge \limits _{i \le k < j} {\langle {\varphi } \rangle }_k\right)$.

$\square$

Broadly speaking, this translation simulates the truth value of an LTL propositional variable p along time by a set of n fresh atoms in classical logic, one per time instant. Moreover, the behaviour of modal operators are simulated by (finite) conjunctions and disjunctions, since we are considering bounded time. The following observation shows that, under the assumption of bounded time, we can establish a one-to-one correspondence between temporal and grounded theories.

Observation 11.1

(Model correspondence) Let $\mathbf {V}=V_0,V_1,\ldots$ be an LTL interpretation. Given $max \ge 0$, we define the classical interpretation $I_{max}$ as:

$$I_{max} = \lbrace p_i | p \in V_i \rbrace .$$

It can be proved that $\mathbf {V}$ and $I_{max}$ satisfy the following property:

$$\forall \varphi ,\ \mathbf {V}, i \models \varphi \hbox { iff } I_{max} \models {\langle {\varphi } \rangle }_i.$$

$\square$

11.7 Reasoning and Solving

In the previous section we described the theoretical aspects of the representation of graphs and of the logic used for reasoning on them.

In this section, we are going to show that, after translation, any question can be expressed in classical propositional logic and solved using classical propositional logic tools and that even complex questions, such as the search for a stable state, can be solved by our system.

11.7.1 A Simple Example

We are first going to explain on a simple example how the transformation of a graph into a set of CNF formulas is performed. We are going to work on the graph describing the behaviour of the Lac operon represented on Fig. 11.2 in Sect. 11.2. However we simplify a little this graph into the one represented in Fig. 11.5.

Fig. 11.5

Simplified functional representation of the lac operon

In this example, lacZ and cAMP are exogenous variables. As their value is set once and for all, they don’t have to be grounded in the translation. On the opposite, Galactosidase is a pure endogenous variable, and thus will be grounded. Glucose is a weak endogenous entity: it has to be grounded as its value can change through time, however no completion formula will be computed for the variable describing them at time 0, as they can be present at the start of the process as an initial condition. Here, we will consider Lactose as an exogenous variable (see footnote 2 in Sect. 11.2).

This graph is interesting, because it has a temporal dynamic. For example, if the initial conditions are that lacZ, cAMP and Lactose are present and Glucose is absent then we can simulate informally the evolution of the proteins/conditions as:

Time 0::

lacZ, cAMP, Lactose

Time 1::

lacZ, cAMP, Lactose, Galactosidase

Time 2::

lacZ, cAMP, Lactose, Galactosidase, Glucose

Time 3::

lacZ, cAMP, Lactose, Glucose

Time 3 is a stable state.

Now we are going to see how this informal process can be formalized, and how logical tools can be used to reason about this graph; in a first step, this graph can be represented by:

$$\begin{aligned} Lactose \wedge Galac_t \rightarrow pr(Glucose)_t \end{aligned}$$

(11.8)

$$\begin{aligned} lacZ\wedge Lactose \wedge cAMP \wedge \lnot Glucose_t \rightarrow pr(Galac)_t \end{aligned}$$

(11.9)

$$\begin{aligned} Lactose \wedge Galac_t \rightarrow cn(Galac)_t \end{aligned}$$

(11.10)

$$\begin{aligned} pr(Glucose)_t \rightarrow Glucose_{t+1} \end{aligned}$$

(11.11)

$$\begin{aligned} pr(Galac)_t \rightarrow Galac_{t+1} \end{aligned}$$

(11.12)

$$\begin{aligned} Glucose_t \wedge \lnot cn(Glucose)_t \rightarrow Glucose_{t+1}\end{aligned}$$

(11.13)

$$\begin{aligned} Galac_t \wedge \lnot cn(Galac)_t \rightarrow Galac_{t+1} \end{aligned}$$

(11.14)

Equations 11.8 and 11.9 describe how proteins can be produced: Glucose is produced (at time t) when we have Lactose and Galac at time t (lactose is always present as we suppose that there is always enough lactose in our environment, while galactosidase evolve in time), and Galac is produced at t when we have Glucose at t along with cAMP, Lactose and the lacZ gene.

Equation 11.10 expresses that when we have Lactose and Galac at t then Galac is consumed at t as it is used to produce Glucose according to Eq. 11.8. We have no similar equation for Lactose, as Lactose is exogenous and there will always remain “enough” lactose.

Equations 11.11 and 11.12 express that, when a molecule is produced at time t, then it is present at time $t+1$. This applies here to Glucose and Galac.

Equations 11.13 and 11.14 are inertia rules. If a protein is present at time t and is not consumed at t then it will be present at time $t+1$.

After completing this first representation, the system has to be grounded by time. The number of time steps is chosen by the user. Grounding is trivial and, for one time step, the above set of rules just becomes:

$$\begin{aligned} Lactose \wedge Galac_0 \rightarrow pr(Glucose)_0 \\ lacZ\wedge Lactose \wedge cAMP \wedge \lnot Glucose_0 \rightarrow pr(Galac)_0 \\ Lactose \wedge Galac_0 \rightarrow cn(Galac)_0 \\ pr(Glucose)_0 \rightarrow Glucose_{1} \\ pr(Galac)_0 \rightarrow Galac_{1} \\ Glucose_0 \wedge \lnot cn(Glucose)_0 \rightarrow Glucose_{1}\\ Galac_0 \wedge \lnot cn(Galac)_0 \rightarrow Galac_{1} \end{aligned}$$

Then, we build completion formulas. It is important to notice that completion formulas are always built for pure endogenous variables at all time steps, are never built for exogenous variables, and are built for weak endogenous variables at all time steps except at time 0. This is a consequence of the “closed world” assumption: pure endogenous entities can only be created, produced or consumed internally, and are never present at the start of the process. So, to take a simple example, each time we have multiple paths to produce a pure endogenous variable p, such as $C_1 \rightarrow Pr(p)$ up to $C_n \rightarrow Pr(p)$, then we must add a “completion” formula $Pr(p) \rightarrow C_1\vee \cdots \vee C_n$.

The following completion formulas are respectively associated with the variables: (1) $Galac_0$, (2) $Galac_1$, (3) $Glucose_1$, (4) $cn(Galac)_0$, (5) $pr(Galac)_0$, (6) $pr(Glucose)_0$.

$$\begin{aligned}&\lnot Galac_0\end{aligned}$$

(11.15)

$$\begin{aligned}&Galac_1\rightarrow (Galac_0\wedge \lnot cn(Galac)_0) \vee pr(Galac)_0\end{aligned}$$

(11.16)

$$\begin{aligned}&Glucose_1\rightarrow (Glucose_0\wedge \lnot cn(Glucose)_0)\vee pr(Glucose)_0\end{aligned}$$

(11.17)

$$\begin{aligned}&cn(Galac)_0 \rightarrow (Galac_0 \wedge Lactose)\end{aligned}$$

(11.18)

$$\begin{aligned}&pr(Galac)_0\rightarrow (lacZ \wedge Lactose \wedge cAMP \wedge \lnot Glucose_0)\end{aligned}$$

(11.19)

$$\begin{aligned}&pr(Glucose)_0\rightarrow (Galac_0\wedge Lactose) \end{aligned}$$

(11.20)

Then, all formulas are automatically translated into CNF. With one temporal grounding step, the simple graph considered here is represented by a database of 21 CNF formulas.

11.7.2 From Temporal Reasoning to Classical Propositional Tools

As a graph is now transformed into a database D of propositional CNF formulas, any propositional tool can be used to solve queries.

Some questions Q such as “is molecule p present at time 3” can be expressed by the logical temporal formula $\bigcirc \bigcirc \bigcirc p$, and then easily translated after grounding into the classical $p_3$. Then it can be solved with a SAT solver: $\lnot Q=\lnot p_3$ is added to D and the satisfiability of $D\cup \lnot Q$ is checked. If it is not satisfiable, then Q is of course true.

However, most often, the main problem for biologists is to find the set(s) of conditions/preconditions that will lead to the creation of a protein, or the triggering of a specific condition. For example, many graphs describe how some cellular paths lead to cell death (apoptosis). Then the question is usually “what are the set(s) of condition(s) that lead to cell apoptosis after some time”. Here depending on the complexity of the problem, different tools can be used:

• Abduction is of course the more natural and elegant solution. If we call D the set of CNF formulas after grounding into propositional logic, and Q the question, then we first use a SAT solver to check that $D\cup \{\lnot Q\}$ is consistent (if it is not consistent then Q is already an implicate of D). Now we search for the minimal set H such as Q is an implicate of $T\cup H$. The classical algorithm consists in computing the set $\mathcal{P}(D\cup \{\lnot Q\})$, which is the set of the prime implicates (the strongest clausal consequences) of $D\cup \{\lnot Q\}$, and then checking for each $x \in \mathcal{P}(D\cup \{\lnot Q\})$ that $D\cup \{\lnot x\}$ is consistent. Then each such x is a solution.

  While solutions sets containing only exogenous variables and weak endogenous variables (at step 0) describe the initial conditions leading to Q, abduction is able to find all sets answering a given question, even sets containing pure endogenous variables. This can give valuable information regarding the cell internal dynamic.

• While abduction is the more elegant way to find the set of preconditions answering a given question, the number of prime implicates of a theory can be exponential in the size of the theory and finding only one implicate is an NP-hard problem [13]. Thus the underlying complexity when using large graphs may turn abduction into an impracticable method and an alternative approach has to be used.

  Biologists are mainly interested in solutions that contain only exogenous variables and also initial conditions which are the values of weak endogenous variables at time step 0. As explained before, exogenous proteins are interesting candidates as they usually describe the external conditions that can be set to activate some specific paths inside the graph, and weak endogenous variables at step 0 describe initial conditions. Pure endogenous proteins only depend on the internal dynamic of the cell.

  If we call Ex0 the set of exogenous variables and weak endogenous variables at step 0, an extensive search can be performed with a Sat Solver to check if there is a valuation satisfying $D\cup \{\lnot Q\}$ for a fixed boolean affectation of the set Ex0. If so, then each such affectation is a solution.

  This method is faster than abduction as long as the set of exogenous variables/weak endogenous variables at step 0 remains small. The complexity however grows exponentially with the number of variables in the set, and it can’t provide the solution sets containing pure endogenous variables, nor weak endogenous variables at a time greater than 0.

11.7.3 Expressing Complex Queries

In the previous section we presented the reasoning tools that can be used to answer simple questions. In this section we show how much more complex questions can be expressed and solved.

Any question that can be expressed using the temporal logic described in Sect. 11.5 can be solved using classical propositional reasoning tools, as it can be translated into propositional logic (considering of course bounded time). For example, if we want to know if the introduction of protein p will produce protein q at time 3, we just have to solve the question $Q=p\rightarrow q_3$, i.e. check if $D\cup \{p\}\cup \{\lnot q_{3}\}$ is inconsistent.

More complicated, questions can be asked. For example, if we want to know if a stable state exists, we just write:

$$ Q=\Diamond \Box \bigwedge _{p\in En}(p\leftrightarrow \bigcirc p) $$

where En is the set of endogenous variables (pure and weak). The value of exogenous variables never change, so they are always “stable”. This is grounded and translated into propositional logic as

$$ Q=\bigvee _{0\le i\le n} \bigwedge _{i\le j\le n} \bigwedge _{p\in En}(p_j\leftrightarrow p_{j+1}) $$

where n is the last grounding step. We then add $\lnot Q$ to D and check if $D\cup \{\lnot Q\}$ is inconsistent.

Having the full expressivity of temporal logic to write queries is an important feature of our system. Users are able to build complex queries, and they can be automatically translated and solved by the system. Solving the question can be a “yes/no” answer using a simple consistency check, or a more elaborate answer which will provide the set(s) of conditions which lead to a “yes” answer, using abduction or using the exhaustive search method described in the previous section.

11.8 Implementation

We have already implemented most of the tools necessary for using the system:

• Graphs are built using Pathvisio [20], a public-domain editing software and a well known tool in the biologists community.

• We have developed a parser/translator which reads the XML files generated by Pathvisio, takes as an argument the number of grounding steps, and translates the graphs into a set of classical grounded propositional CNF formulas.

• For consistency check and exhaustive search, we use the Glucose SAT solver [3] which is based on Minisat [11]. To compute prime implicates, we implemented our own version of the Tsiknis, Dean and Johnson algorithm [14, 15, 17]. While our implementation, which is based on machine language operations, seems to be extremely fast, a more exhaustive comparison with other approaches for computing prime implicants,⁴ such as the ones advocated in [7, 13], should be tested.

11.9 Conclusion

We have presented in this paper a method to translate graphs representing biological systems into temporal logic formulas and to solve complex temporal queries regarding these graphs. This method has been almost fully implemented, and the associated tool has now reached a state where it can be tested on large, realistic graphs.

There remains however different points to address:

• Currently the graphs we are using are limited: they can only use elementary relations; while all existing relations can be expressed with this elementary subset, it would be easier (and would keep graphs smaller) if our graph editor and out parser could deal with a larger subset of f these relations.

• graphs are built by hand by biologists, and they very often rely on “common knowledge” among them, so they sometimes “forget” to write some relations or sometimes express some relations between proteins in a non “standard” way. This tool will detect such missing knowledge and will thus help in writing more complete and consistent graphs, but correcting these problems is a mandatory step.

• While translating temporal logic queries into grounded propositional CNF is a technicality, building and understanding the exact meaning of a temporal query is complicated for people who don’t have a training in logic. The goal of our users is to solve problems related to these graphs and we have to be able to describe the reasoning tasks available in a simple way, and give simple tools to write queries that can be solved by our system. A possible solution would be to provide a graphical interface that would help building queries by assembling intuitively variables and connectors as an intermediate between logic and natural language.

• Our system relies on a strong assumption: proteins can either be present or absent, but we are not able to consider partial concentrations. This decision was discussed with the biologists, and they supported it for a simple reason: currently, they are most of the time, if not all of the time, enable to determine the concentration of proteins in a cell. Their understanding of the cell chemical reactions is not precise enough, and they really consider the concepts of “absence”, “presence”, “Production” or “Consumption” when building graphs. However, this does not mean that we will not have to deal with this problem in the future.

The fact that there is now a demand from the biologists we are working with to get the tool and use it by themselves seems to prove that it has reached a certain state of maturity and stability, even if there probably remains work to do before turning it into a fully operational tool.