Abstract
PROPs and Lawvere categories are related notions adapted to the study of algebraic structures borne by an object in a category, but whereas PROPs are symmetric monoidal, Lawvere categories are cartesian. This paper formulates the connection between the two notions using Lack’s technique for composing PROPs via distributive laws. We show Lawvere categories can be seen as resulting from a distributive law of two PROPs — one expressing the algebraic structure in linear form and the other expressing the ability of copying and discarding variables.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
PROPs [28] are symmetric monoidal categories with objects the natural numbers. In the last two decades, they have become increasingly popular as an environment for the study of diagrammatic formalisms from diverse branches of science in a compositional, resource sensitive fashion. Focussing on computer science, they have recently featured in algebraic approaches to Petri nets [11, 35], bigraphs [12], quantum circuits [15], and signal flow graphs [1, 5, 7, 20].
PROPs describe both the syntax and the semantics of diagrams, with the interpretation expressed as a PROP morphism \([\![{\cdot }]\!] :\mathbf {Syntax} \rightarrow \mathbf {Semantics}\). Typically, \(\mathbf {Syntax}\) is freely generated by a signature \(\varSigma \) of operations with arbitrary arity/coarity and can be composed sequentially and in parallel. Thus diagram syntax—which we refer to as \(\varSigma \)-terms—is inherently 2-dimensional: the term structure is that of directed acyclic graphs, rather than trees, as in the familiar case of operations with coarity 1. A crucial aspect is linearity: variables in \(\varSigma \)-terms cannot be copied nor discarded.
It is often useful to axiomatise the equivalence induced by \([\![{\cdot }]\!]\) by means of a set of equations E, and then study the theory \((\varSigma , E)\). For PROPs, completeness proofs typically provide a serious challenge, involving the retrieval of a normal form for \(\varSigma \)-terms modulo E. The difficulty can be drastically reduced by exploiting certain operations on PROPs: an example of this modular methodology is provided by [5, 7], where the PROP operations of sum and composition are crucial for giving a sound and complete axiomatization of signal flow diagrams.
Sum is just the coproduct in the category of PROPs. Whenever two PROPs \(\mathcal {T}_1\) and \(\mathcal {T}_2\) can be presented by the theories \((\varSigma _1, E_1)\) and \((\varSigma _2,E_2)\), then their sum \(\mathcal {T}_1+\mathcal {T}_2\) is presented by the disjoint union \((\varSigma _1\uplus \varSigma _2, E_1\uplus E_2)\).
Composition of PROPs is more subtle, as it requires certain compatibility conditions between the structure of \(\mathcal {T}_1\) and \(\mathcal {T}_2\). Lack [25] describes this operation formally by means of distributive laws, seeing PROPs as monads in the 2-categorical sense of Street [36]. In a nutshell, a distributive law \(\lambda :\mathcal {T}_1 \,;\,\mathcal {T}_2 \rightarrow \mathcal {T}_2 \,;\,\mathcal {T}_1 \) of PROPs is a recipe for moving arrows of \(\mathcal {T}_1\) past those of \(\mathcal {T}_2\). The resulting PROP \(\mathcal {T}_2 \,;\,\mathcal {T}_1\) enjoys a factorisation property: every arrow in \(\mathcal {T}_2\,;\,\mathcal {T}_1\) decomposes as one of \(\mathcal {T}_2\) followed by one of \(\mathcal {T}_1\). The graph of \(\lambda \) can be seen as a set of directed equations \(E_{\lambda } \ :=\ (\xrightarrow {\in \mathcal {T}_1}\xrightarrow {\mathcal {T}_2}) \approx (\xrightarrow {\mathcal {T}_2}\xrightarrow {\mathcal {T}_1})\) and \(\mathcal {T}_2 \,;\,\mathcal {T}_1\) is presented by the theory \((\varSigma _1\uplus \varSigma _2, E_1 \uplus E_2 \uplus E_{\lambda })\).
This work uses distributive laws of PROPs to characterise Lawvere categoriesFootnote 1, a well known class of structures adapted to the study of categorical universal algebra. The essential difference with PROPs is that Lawvere categories express cartesian theories \((\varSigma ,E)\), i.e. where \(\varSigma \) only features operations with coarity 1 and E may include non-linear equations. Our starting observation is that the Lawvere category \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) on a cartesian signature \(\varSigma \) exhibits a factorisation property analogous to the one of composed PROPs: arrows can always be decomposed as \( \xrightarrow { \in \mathsf {Cm}} \xrightarrow { \in \mathcal {T}_{\varSigma }}\), where \(\mathsf {Cm}\) is the PROP of commutative comonoids, generated by a copy \(1\rightarrow 2\) and a discard \(1\rightarrow 0\) operation, and \(\mathcal {T}_{\varSigma }\) is the PROP freely generated by \(\varSigma \). This factorisation represents cartesian \(\varSigma \)-terms by their syntactic tree — the \(\mathcal {T}_{\scriptscriptstyle \varSigma }\)-part — with the possibility of explicitly indicating variable-sharing among sub-terms — the \(\mathsf {Cm}\)-part. This simple observation leads us to the main result of the paper: for any cartesian signature \(\varSigma \), there is a distributive law of PROPs \(\lambda :\mathcal {T}_{\varSigma } \,;\,\mathsf {Cm}\rightarrow \mathsf {Cm}\,;\,\mathcal {T}_{\varSigma }\) which is presented by equations that express the naturality of copier and discarder; the resulting composed PROP \(\mathsf {Cm}\,;\,\mathcal {T}_{\varSigma }\) is the Lawvere category \(\mathcal {L}_{\scriptscriptstyle \varSigma }\).
By a quotient construction on distributive laws, it follows immediately that the above theorem holds more generally for any cartesian theory \((\varSigma , E)\) where the set of axioms E only contains linear equations. For instance the Lawvere category of commutative monoids \(\mathcal {L}_{\scriptscriptstyle \text {Mn}}\) can be obtained by means of PROP composition, while the one \(\mathcal {L}_{\scriptscriptstyle \text {Gr}}\) of abelian groups cannot, because of the non-linear axiom \(x \times x^{-1}=1\). Obviously, one can still formulate \(\mathcal {L}_{\scriptscriptstyle \text {Gr}}\) as the quotient of the composite \(\mathcal {L}_{\scriptscriptstyle \text {Mn}}\) by adding this equation, see Example 4.6 below.
As a side remark, we observe that, by taking the sum \(\mathsf {Cm}+ \mathcal {T}_{\scriptscriptstyle \varSigma }\), rather than the composition, we are able to capture a different, well-known representation for cartesian \(\varSigma \)-terms, namely term graphs, which are acyclic graphs labeled over \(\varSigma \). With respect to the standard tree representation, the benefit of term graphs is that the sharing of any common sub-term can be represented explicitly, making them particularly appealing for efficient rewriting algorithms, see e.g. [34] for a survey on the subject. As shown in [16], \(\varSigma \)-term graphs are in 1-1 correspondence with the arrows of the free gs-monoidal category generated by \(\varSigma \), a concept that actually amounts to forming the sum of PROPs \(\mathsf {Cm}+ \mathcal {T}_{\scriptscriptstyle \varSigma }\). Thus the only difference between term graphs and the representation of terms given by \(\mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle \varSigma }\) is in the validity of naturality of copier and discarder. Intuitively, a term where a resource is explicitly copied is not identified with the term where two copies appear separately: in short, copying is not natural.
Related Works. The motto “cartesian terms = linear terms + copying and discarding” inspired several papers exploiting the role of \(\mathsf {Cm}\) in Lawvere categories, see e.g. [14, 16, 26]. In our work, Lawvere categories feature as a distinguished example of a construction, PROP composition, that is increasingly important in many recent research threads [5, 6, 20, 32]. The significance of this exercise is two-fold. First, it gives a deeper understanding of the nature of Lawvere categories and how they formally relate to PROPs, by showing the provenance of the natural copy-discard structure. Second, our result provides a canonical means of defining a distributive law for freely generated PROPs, showing that the result of composition is a familiar algebraic notion and enjoys a finite axiomatisation.
The following construction, reported by Baez in [2], is close in spirit to our work. There is pseudo-adjunction between symmetric monoidal and categories with finite products

where R is the evident forgetful functor and L adds to any object of \(\mathbb {C}\in \mathsf {SMCat}\) a natural copy-discard structure: natural diagonals and projections. Baez [2] states an equivalence between \(RL(\mathbb {C})\) and \(\mathbb {C}\otimes \mathsf {Cm}\), with the tensor \(\otimes \) defined by \(\mathsf {SMCat}[\mathbb {C}_1 \otimes \mathbb {C}_2, \mathbb {C}_3] \simeq \mathsf {SMCat}[\mathbb {C}_1, \mathsf {SMCat}[\mathbb {C}_2,\mathbb {C}_3]]\). Indeed, our main construction, as well as being a distributive law, is also an instance of a tensor or Kronecker product of symmetric monoidal theories; a concept that has been explored in some detail in the cartesian setting of Lawvere categories, see e.g. [22].
Our work restricts attention to PROPs \(\mathcal {T}_{\scriptscriptstyle \varSigma } \in \mathsf {SMCat}\) freely generated by a cartesian signature \(\varSigma \): in this case, it is enough to add a copy-discard structure for the object 1 and \(RL(\mathcal {T}_{\scriptscriptstyle \varSigma })\) coincides with PROP composition \(\mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle \varSigma }\). Our perspective exploiting distributive laws has the advantage of providing a finite presentation in terms of the naturality axioms.
It is also worth mentioning that the relationship between symmetric monoidal and cartesian structures is central in the categorical semantics of linear logic; in this perspective, the presence of \(\mathsf {Cm}\) allows to interpret the structural rules of contraction and weakening — see e.g. [24, 30].
Prerequisites and Notation. We assume familiarity with the basics of category theory (see e.g. [10, 29]), the definition of symmetric strict monoidal category [29, 33] (often abbreviated as SMC) and of bicategory [3, 10]. We write \(f\,;\,g :a \rightarrow c\) for composition of \(f :a \rightarrow b\) and \(g:b \rightarrow c\) in a category \(\mathbb {C}\), and \(\mathbb {C}[a,b]\) for the hom-set of arrows \(a \rightarrow b\). It will be sometimes convenient to indicate an arrow \(f :a \rightarrow b\) of \(\mathbb {C}\) as \(x\xrightarrow {f \in \mathbb {C}}y\) or also \(\xrightarrow {\in \mathbb {C}}\), if names are immaterial. For \(\mathbb {C}\) an SMC, \(\oplus \) is its monoidal product, with unit object I, and \(\sigma _{a,b} :a \oplus b \rightarrow b \oplus a\) is the symmetry associated with \(a,b \in \mathbb {C}\).
2 PROPs
Our exposition is founded on symmetric monoidal theories: specifications for algebraic structures borne by objects in a symmetric monoidal category.
Definition 2.1
A (one-sorted) symmetric monoidal theory (SMT) is a pair \((\varSigma , E)\) consisting of a signature \(\varSigma \) and a set of equations E. The signature \(\varSigma \) is a set of generators \(o :n\rightarrow m\) with arity n and coarity m. The set of \(\varSigma \) -terms is obtained by composing generators in \(\varSigma \), the unit \( id :1\rightarrow 1\) and the symmetry \(\sigma _{1,1} :2\rightarrow 2\) with; and \(\oplus \). This is a purely formal process: given \(\varSigma \)-terms \(t :k\rightarrow l\), \(u :l\rightarrow m\), \(v :m\rightarrow n\), one constructs new \(\varSigma \)-terms \(t \mathrel {;} u :k\rightarrow m\) and \(t \oplus v :k+n \rightarrow l+n\). The set E of equations contains pairs \((t,t' :n\rightarrow m)\) of \(\varSigma \)-terms with the same arity and coarity.
The categorical concept associated with symmetric monoidal theories is the notion of PROP (product and permutation category [28]).
Definition 2.2
A PROP is a symmetric strict monoidal category with objects the natural numbers, where \(\oplus \) on objects is addition. Morphisms between PROPs are strict symmetric identity-on-objects monoidal functors: PROPs and their morphisms form the category \(\mathbf {PROP}\). We call a sub-PROP a sub-category of a PROP which is also a PROP; i.e. the inclusion functor is a PROP morphism.
The PROP \(\mathcal {T}\) freely generated by an SMT \((\varSigma ,E)\) has as its set of arrows \(n\rightarrow m\) the set of \(\varSigma \)-terms \(n\rightarrow m\) taken modulo the laws of symmetric strict monoidal categories — Fig. 1 — and the smallest congruence (with respect to \(\,;\,\) and \(\oplus \)) containing the equations \(t=t'\) for any \((t,t')\in E\).
There is a natural graphical representation for arrows of a PROP as string diagrams, which we now sketch, referring to [33] for the details. A \(\varSigma \)-term \(n \rightarrow m\) is pictured as a box with n ports on the left and m ports on the right. Composition via \(\,;\,\) and \(\oplus \) are rendered graphically by horizontal and vertical juxtaposition of boxes, respectively.

In any SMT there are specific \(\varSigma \)-terms generating the underlying symmetric monoidal structure: these are \( id _1 :1 \rightarrow 1\), represented as  , the symmetry \(\sigma _{1,1} :1+1 \rightarrow 1+1\), represented as
, the symmetry \(\sigma _{1,1} :1+1 \rightarrow 1+1\), represented as  , and the unit object for
, and the unit object for  , that is, \( id _0 :0 \rightarrow 0\), whose representation is an empty diagram
, that is, \( id _0 :0 \rightarrow 0\), whose representation is an empty diagram  . Graphical representation for arbitrary identities \( id _n\) and symmetries \(\sigma _{n,m}\) are generated according to the pasting rules in (1).
. Graphical representation for arbitrary identities \( id _n\) and symmetries \(\sigma _{n,m}\) are generated according to the pasting rules in (1).
Example 2.3
-
(a)
We write \((\varSigma _M,E_M)\) for the SMT of commutative monoids. The signature \(\varSigma _M\) contains a multiplication
 and a unit
and a unit  . Equations \(E_M\) assert associativity (A1), commutativity (A2) and unitality (A3).
. Equations \(E_M\) assert associativity (A1), commutativity (A2) and unitality (A3). 
We call \(\mathsf {Mn}\) the PROP freely generated by the SMT \((\varSigma _M,E_M)\).
-
(b)
We also introduce the SMT \((\varSigma _C, E_C)\) of cocommutative comonoids. The signature \(\varSigma _C\) consists of a comultiplication
 and a counit
and a counit  . \(E_C\) is the following set of equations.
. \(E_C\) is the following set of equations. 
We call \(\mathsf {Cm}\) the PROP freely generated by \((\varSigma _C, E_C)\). Modulo the white vs. black colouring, string diagrams of \(\mathsf {Cm}\) can be seen as those of \(\mathsf {Mn}\) “reflected about the y-axis”. This observation yields \(\mathsf {Cm}\cong \mathsf {Mn}^{op}\).
-
(c)
The PROP \(\mathsf {B}\) of (commutative/cocommutative) bialgebras is generated by the theory \((\varSigma _M \uplus \varSigma _C, E_M \uplus E_C \uplus B)\), where B is the following set of equations.

Remark 2.4
(Models of a PROP). The assertion that \((\varSigma _M, E_M)\) is the SMT of commutative monoids—and similarly for other SMTs appearing in our exposition—can be made precise using the notion of model (sometimes also called algebra) of a PROP. Given a strict symmetric monoidal category \(\mathbb {C}\), a model of a PROP \(\mathcal {T}\) in \(\mathbb {C}\) is a symmetric strict monoidal functor \(\mathcal {F}:\mathcal {T}\rightarrow \mathbb {C}\). Then \(\mathsf {LinMod}(\mathcal {T},\mathbb {C})\) is the category of models of \(\mathcal {T}\) in \(\mathbb {C}\) and natural transformations between them.
Turning to commutative monoids, there is a category \(\mathsf {Monoid}(\mathbb {C})\) whose objects are the commutative monoids in \(\mathbb {C}\), i.e., objects \(x \in \mathbb {C}\) equipped with arrows \(x \oplus x \rightarrow x\) and \(I \rightarrow x\), satisfying the usual equations. Given any model \(\mathcal {F}:\mathsf {Mn}\rightarrow \mathbb {C}\), it follows that \(\mathcal {F}(1)\) is a commutative monoid in \(\mathbb {C}\): this yields a functor \(\mathsf {LinMod}(\mathsf {Mn}, \mathbb {C}) \rightarrow \mathsf {Monoid}(\mathbb {C})\). Saying that \((\varSigma _M, E_M)\) is the SMT of commutative monoids means that this functor is an equivalence natural in \(\mathbb {C}\). We shall not focus on models as they are not central in our developments and refer the reader to [19, 25] for more information.
Example 2.3 only shows PROPs freely generated from an algebraic specification. However, one can also define PROPs in a more direct manner, without relying on SMTs. Two basic examples will be useful for our exposition:
-
the PROP \(\mathsf {F}\) whose arrows \(n \rightarrow m\) are functions from \(\overline{n}\) to \(\overline{m}\), where \(\overline{n} = \{0,1,\dots ,n-1\}\).
-
the PROP \(\mathsf {P}\) whose arrows \(n \rightarrow m\) exist only if \(n = m\), in which case they are the permutations on \(\overline{n}\).
This kind of definition is often useful as a different, more concrete perspective on PROPs that arise from symmetric monoidal theories. For instance, \(\mathsf {F}\) is presented by the theory of commutative monoids, in the sense that \(\mathsf {F}\) and \(\mathsf {Mn}\) are isomorphic PROPs: once can consider a string diagram \(t \in \mathsf {Mn}[n,m]\) as the graph of a function of type \(\{1,\dots , n\}\rightarrow \{1, \dots , m\}\). For instance,  describes the function \(f :\{1,2\} \rightarrow \{1,2\}\) mapping both elements to 1. By duality, \(\mathsf {Cm}\cong \mathsf {F}^{\scriptstyle op }\), that is, \(\mathsf {F}^{\scriptstyle op }\) is presented by the theory of commutative comonoids.
describes the function \(f :\{1,2\} \rightarrow \{1,2\}\) mapping both elements to 1. By duality, \(\mathsf {Cm}\cong \mathsf {F}^{\scriptstyle op }\), that is, \(\mathsf {F}^{\scriptstyle op }\) is presented by the theory of commutative comonoids.
Similarly, \(\mathsf {P}\) provides a concrete description of the theory \((\emptyset , \emptyset )\) with empty signature and no equations. It is the initial object in the category \(\mathbf {PROP}\).
3 PROP Composition
A basic operation on SMTs \((\varSigma , E)\) and \((\varSigma ', E')\) is to take their sum \((\varSigma \uplus \varSigma ', E\uplus E')\). In \(\mathbf {PROP}\), the PROP generated by \((\varSigma \uplus \varSigma ', E\uplus E')\) is the coproduct \(\mathcal {T}+\mathsf {S}\) of the PROP \(\mathcal {T}\) generated by \((\varSigma , E)\) and \(\mathsf {S}\), generated by \((\varSigma ', E')\).
The sum \(\mathcal {T}+\mathsf {S}\) is the least interesting way of combining theories, because there are no equations that express compatibility between the algebraic structures in \(\mathcal {T}\) and \(\mathsf {S}\). This is a standard pattern in algebra: e.g. a ring is given by a monoid and an abelian group, subject to equations that ensure that the former distributes over the latter. Similarly, the equations of bialgebras (Example 2.3) describe the interplay of a monoid and a comonoid. Ordinary functions, which can always be decomposed as a surjection followed by an injection, are another example.
In [25] Lack shows how these phenomena can be uniformly described as the operation of composing PROPs. The conceptual switch is to understand PROPs as monads, and their composition as a distributive law. These monads live in a certain bicategory [3], as in the classical work by Street [36]Footnote 2.
Definition 3.1
A monad on an object x of a bicategory \(\mathfrak {B}\) is a 1-cell \(\mathcal {F}:x \rightarrow x\) with 2-cells \(\eta ^{\mathcal {F}} : id _x \rightarrow \mathcal {F}\) and \(\mu ^{\mathcal {F}} :\mathcal {F}\,;\,\mathcal {F}\rightarrow \mathcal {F}\) (called the unit and the multiplication respectively) making the following diagrams–in which we suppress the associativity isomorphisms—commute.

A morphism between monads \(x \xrightarrow {\mathcal {F}} x\) and \(x \xrightarrow {\mathcal {G}} x\) is a 2-cell \(\theta :\mathcal {F}\rightarrow \mathcal {G}\) making the following diagrams commuteFootnote 3.

An epimorphic monad morphism is called a monad quotient.
For \(\mathfrak {B}= \mathbf {Cat}\), the above definition yields the standard notion of monad as an endofunctor with a pair of natural transformations. Something interesting happens for the case of the bicategory \(\mathfrak {B}= \mathsf {Span}(\mathbf {Set})\) whose objects are sets, 1-cells are spans of functions (with composition defined by pullback) and 2-cells are span morphisms: monads in \(\mathsf {Span}(\mathbf {Set})\) are precisely the small categories. Indeed, a monad \((\mathcal {F}, \eta ,\mu )\) there consists of a span \( Ob _{\scriptscriptstyle }\xleftarrow { dom _{\scriptscriptstyle }} Ar _{\scriptscriptstyle }\xrightarrow { cod _{\scriptscriptstyle }} Ob _{\scriptscriptstyle }\), which yields a set \( Ob _{\scriptscriptstyle }\) of objects, one \( Ar _{\scriptscriptstyle }\) of arrows and domain/codomain maps \( Ar _{\scriptscriptstyle }\rightrightarrows Ob _{\scriptscriptstyle }\). The unit \(\eta : id \rightarrow \mathcal {F}\) is a span morphism associating an identity arrow to each object (below left). The multiplication \(\mu :\mathcal {F}\,;\,\mathcal {F}\rightarrow \mathcal {F}\) is a span morphism defining composition for any two arrows \(a \xrightarrow {f} b \xrightarrow {g} c\) in \( Ar _{\scriptscriptstyle }\) (below right).

By thinking of categories as monads, one can define the composition of categories with the same set of objects as monad composition by a distributive law in \(\mathsf {Span}(\mathbf {Set})\). This phenomenon is studied in [31].
Definition 3.2
Let \((\mathcal {F}, \eta ^{\mathcal {F}},\mu ^{\mathcal {F}})\), \((\mathcal {G}, \eta ^{\mathcal {G}},\mu ^{\mathcal {G}})\) be monads in a bicategory \(\mathfrak {B}\) on the same object. A distributive law of \(\mathcal {F}\) over \(\mathcal {G}\) is a 2-cell \(\lambda :\mathcal {F}\,;\,\mathcal {G}\rightarrow \mathcal {G}\,;\,\mathcal {F}\) in \(\mathfrak {B}\) making the following diagrams—in which we again omit associativity—commute.

A distributive law \(\lambda :\mathcal {F}\,;\,\mathcal {G}\rightarrow \mathcal {G}\,;\,\mathcal {F}\) yields a monad \(\mathcal {G}\,;\,\mathcal {F}\) with the following unit and multiplication:

Let us verify how the abstract definition works for the case of categories. Pick categories \(\mathbb {C}\) and \(\mathbb {D}\) with the same set \( Ob _{\scriptscriptstyle }\) of objects, seen as monads \( Ob _{\scriptscriptstyle }\xleftarrow { dom _{\scriptscriptstyle \mathbb {C}}} Ar _{\scriptscriptstyle \mathbb {C}}\xrightarrow { cod _{\scriptscriptstyle \mathbb {C}}} Ob _{\scriptscriptstyle }\) and \( Ob _{\scriptscriptstyle }\xleftarrow { dom _{\scriptscriptstyle \mathbb {D}}} Ar _{\scriptscriptstyle \mathbb {D}}\xrightarrow { cod _{\scriptscriptstyle \mathbb {D}}} Ob _{\scriptscriptstyle }\) in \(\mathsf {Span}(\mathbf {Set})\). A distributive law \(\lambda :\mathbb {C}\,;\,\mathbb {D}\rightarrow \mathbb {D}\,;\,\mathbb {C}\) is a span morphism

mapping composable pairs \(a\xrightarrow {\in \mathbb {C}}\xrightarrow {\in \mathbb {D}}b\) to composable pairs \(a\xrightarrow {\in \mathbb {D}}\xrightarrow {\in \mathbb {C}}b\). As described in (7), \(\lambda \) allows to define a monad structure on \(\mathbb {D}\,;\,\mathbb {C}\). That means, \(\lambda \) yields a category \(\mathbb {D}\,;\,\mathbb {C}\) whose arrows \(a\rightarrow b\) are composable pairs \(a\xrightarrow {\in \mathbb {D}}\xrightarrow {\in \mathbb {C}}b\) of arrows of \(\mathbb {D}\), \(\mathbb {C}\) and composition is defined as
PROPs are understood as monads in the same sense that small categories are. The difference is that one needs to refine the bicategory of interest, in order for the composition of PROPs-monads to yield another PROP-monad and not an arbitrary small category. These refinements are in two steps. First, one takes the bicategory \(\mathsf {Span}(\mathbf {Mon})\) whose 1-cells are spans in the category of monoids, instead of sets. This accounts for the monoidal structure — in fact, monads in \(\mathsf {Span}(\mathbf {Mon})\) are small strict monoidal categories. The second refinement has the purpose of correctly account for the symmetry structure of PROPs: one takes the bicategory \(\mathsf {Bimod}(\mathsf {Span}(\mathbf {Mon}))\) whose objects are small strict monoidal categories and 1-cells are the bimodules in \(\mathsf {Span}(\mathbf {Mon})\). PROPs are then monads on the object \(\mathsf {P}\) of \(\mathsf {Bimod}(\mathsf {Span}(\mathbf {Mon}))\).
We shall gloss over further details about the exact formalisation of this observation, as it is out of the scope of this paper — we refer to [25] and [37, § 2.4] for the detailed definitions. The simpler setting of composition of mere categories should provide enough guidance to follow the rest of our exposition.
It is important for our purposes to remark how composition works for PROPs \(\mathcal {T}_1\), \(\mathcal {T}_2\) generated by SMTs, say \((\varSigma _1, E_1)\) and \((\varSigma _2, E_2)\). The PROP \(\mathcal {T}_1 \,;\,\mathcal {T}_2\) induced by a distributive law \(\lambda :\mathcal {T}_2 \,;\,\mathcal {T}_1 \rightarrow \mathcal {T}_1 \,;\,\mathcal {T}_2\) will also enjoy a presentation by generators and equations, consisting of the sum \((\varSigma _1 \uplus \varSigma _2, E_1 \uplus E_2)\) plus the equations \(E_{\lambda }\) arising from the the distributive law. The set \(E_{\lambda }\) is simply the graph of \(\lambda \), now seen as a set of directed equations \((\xrightarrow {\in \mathcal {T}_2}\xrightarrow {\in \mathcal {T}_1}) \approx (\xrightarrow {\in \mathcal {T}_1}\xrightarrow {\in \mathcal {T}_2})\) telling how \(\varSigma _2\)-terms modulo \(E_2\) distribute over \(\varSigma _1\)-terms modulo \(E_1\). In fortunate cases, it is possible to present \(E_{\lambda }\) by a simpler, or even finite, set of equations, thus giving a sensible axiomatisation of the compatibility conditions expressed by \(\lambda \). This is the case for both examples considered below.
Example 3.3
-
(a)
The PROP \(\mathsf {F}\) of functions can be described as the composite of PROPs for surjections and injections. Let \(\mathsf {In}\) be the PROP whose arrows \(n \rightarrow m\) are injective functions from \(\overline{n}\) to \(\overline{m}\). The PROP \(\mathsf {Su}\) of surjective functions is defined analogously. There is a distributive law \(\lambda :\mathsf {In}\,;\,\mathsf {Su}\rightarrow \mathsf {Su}\,;\,\mathsf {In}\) defined by epi-mono factorisation: it maps a composable pair \(\xrightarrow {\in \mathsf {In}}\xrightarrow {\in \mathsf {Su}}\) to a composable pair \(\xrightarrow {\in \mathsf {Su}}\xrightarrow {\in \mathsf {In}}\) [25]. The resulting PROP \(\mathsf {Su}\,;\,\mathsf {In}\) is isomorphic to \(\mathsf {F}\) because any function in \(\mathsf {F}\) can be uniquely factorised (up-to permutation) as a surjection followed by an injection. In more syntactic terms, using the isomorphism \(\mathsf {F}\cong \mathsf {Mn}\), this result says that \(\mathsf {Mn}\) is the composite \(\mathsf {Mu}\,;\,\mathsf {Un}\), where \(\mathsf {Mu}\cong \mathsf {Su}\) is the PROP freely generated by the SMT
 and \(\mathsf {Un}\cong \mathsf {In}\) by the SMT
and \(\mathsf {Un}\cong \mathsf {In}\) by the SMT  . The distributive law \(\lambda :\mathsf {In}\,;\,\mathsf {Su}\rightarrow \mathsf {Su}\,;\,\mathsf {In}\) is then presented by the remaining equation (A3) of \(\mathsf {Mn}\), which indeed describes how the generator
. The distributive law \(\lambda :\mathsf {In}\,;\,\mathsf {Su}\rightarrow \mathsf {Su}\,;\,\mathsf {In}\) is then presented by the remaining equation (A3) of \(\mathsf {Mn}\), which indeed describes how the generator  of \(\mathsf {Un}\) can be moved past the one
of \(\mathsf {Un}\) can be moved past the one  of \(\mathsf {Mu}\).
of \(\mathsf {Mu}\). -
(b)
The composition of \(\mathsf {Cm}\) and \(\mathsf {Mn}\) yields the PROP \(\mathsf {B}\) of commutative bialgebras. First, because \(\mathsf {Mn}\cong \mathsf {F}\) and \(\mathsf {Cm}\cong \mathsf {F}^{\scriptstyle op }\), we can express a distributive law \(\lambda :\mathsf {Mn}\,;\,\mathsf {Cm}\rightarrow \mathsf {Cm}\,;\,\mathsf {Mn}\) as having the type \(\mathsf {F}\,;\,\mathsf {F}^{\scriptstyle op }\rightarrow \mathsf {F}^{\scriptstyle op }\,;\,\mathsf {F}\). This amounts to saying that \(\lambda \) maps cospans \(n \xrightarrow {f\in \mathsf {F}}\xleftarrow {g\in \mathsf {F}} m\) to spans \(n \xleftarrow {p\in \mathsf {F}}\xrightarrow {q\in \mathsf {F}} m\). Defining this mapping via (chosen) pullback in \(\mathsf {F}\) satisfies the conditions of distributive laws [25]. One can now read the equations arising by the distributive law from pullback squares in \(\mathsf {F}\). For instance:

where the second diagram is obtained from the pullback by applying the isomorphisms \(\mathsf {F}\cong \mathsf {Mn}\) and \(\mathsf {F}^{\scriptstyle op }\cong \mathsf {Cm}\). In fact, Lack [25] shows that the equations presenting \(\mathsf {Cm}\,;\,\mathsf {Mn}\) arise from (those of \(\mathsf {Cm}+ \mathsf {Mn}\) and) just four pullback squares, yielding equations (A7)–(A10). Therefore, \(\mathsf {Cm}\,;\,\mathsf {Mn}\) is isomorphic to the PROP \(\mathsf {B}\) of bialgebras encountered in Example 2.3. Furthermore, these PROPs have a “concrete” descriptions as \(\mathsf {F}^{\scriptstyle op }\,;\,\mathsf {F}\). In the terminology of [3], one can see \(\mathsf {F}^{\scriptstyle op }\,;\,\mathsf {F}\) as the classifying category of the bicategory \(\mathsf {Span}(\mathsf {F})\), obtained by identifying the isomorphic 1-cells and forgetting the 2-cells.
There is a tight relationship between distributive laws and factorisation systems. Distributive laws of small categories are in 1-1 correspondence with so-called strict factorisation systems [31], in which factorisations must be specified uniquely on the nose, rather than merely up-to isomorphism. Distributive laws of PROPs correspond instead to a more liberal kind of factorisation system, for which decompositions are up-to permutation. As this perspective will be useful later, we recall the following result from Lack [25].
Proposition 3.4
([25], Theorem 4.6). Let \(\mathsf {S}\) be a PROP and \(\mathcal {T}_1\), \(\mathcal {T}_2\) be sub-PROPs of \(\mathsf {S}\). Suppose that each arrow \(n \xrightarrow {f \in \mathsf {S}} m\) can be factorised as \(n \xrightarrow {g_1 \in \mathcal {T}_1}\xrightarrow {g_2 \in \mathcal {T}_2} m\) uniquely up-to permutation, that is, for any other decomposition \(n \xrightarrow {h_1 \in \mathcal {T}_1}\xrightarrow {h_2 \in \mathcal {T}_2}m\) of f, there exists permutation \(\xrightarrow {p \in \mathsf {P}}\) such that the following diagram commutes.

Then there exists a distributive law \(\lambda :\mathcal {T}_2 \,;\,\mathcal {T}_1 \rightarrow \mathcal {T}_1 \,;\,\mathcal {T}_2\), defined by associating to a composable pair \(\xrightarrow {f\in \mathcal {T}_2}\xrightarrow {g\in \mathcal {T}_1}\) the factorisation of \(f \,;\,g\), yielding \(\mathsf {S}\cong \mathcal {T}_1 \,;\,\mathcal {T}_2\).
Quotient of a Distributive Law. Definition 3.1 introduced the notion of quotient \(\theta :\mathcal {F}\rightarrow \mathcal {G}\) of a monad \(\mathcal {F}\): the idea is that the monad \(\mathcal {G}\) is obtained by imposing additional equations on the algebraic theory described by \(\mathcal {F}\). As one may expect, distributive laws are compatible with monad quotients, provided that the law preserves the newly added equations. This folklore result appears in various forms in the literature: [9] gives it for distributive laws of endofunctors over monads and [4, 8] for distributive laws of monads. All these references concern distributive laws in \(\mathbf {Cat}\). For our purposes, it is useful to state the result for arbitrary bicategories.
Proposition 3.5
Suppose that \(\lambda :\mathcal {F}\,;\,\mathcal {H}\rightarrow \mathcal {H}\,;\,\mathcal {F}\) is a distributive law in a bicategory \(\mathfrak {B}\), \(\theta :\mathcal {F}\rightarrow \mathcal {G}\) a monad quotient and \(\lambda ' :\mathcal {G}\,;\,\mathcal {H}\rightarrow \mathcal {H}\,;\,\mathcal {G}\) another 2-cell of \(\mathfrak {B}\) making the following diagram commute.

Then \(\lambda '\) is a distributive law of monads.
Proof
The diagrams for compatibility of \(\lambda '\) with unit and multiplication of \(\mathcal {G}\) commute because \(\theta \) is a monad morphism and (8) commutes. For compatibility of \(\lambda '\) with unit and multiplication of \(\mathcal {H}\), one needs to use commutativity of (8) and the fact that \(\theta \) is epi.
We remark that Proposition 3.5 holds also in the version in which one quotients the monad \(\mathcal {H}\) instead of \(\mathcal {F}\). It is now useful to instantiate the result to the case of distributive laws of PROPs.
Proposition 3.6
Let \(\mathcal {T}\) be the PROP freely generated by \((\varSigma ,E)\) and \(E' \supseteq E\) be another set of equations on \(\varSigma \)-terms. Suppose that there exists a distributive law \(\lambda \! :\!\mathcal {T}\,;\,\mathsf {S}\! \rightarrow \! \mathsf {S}\,;\,\mathcal {T}\) such that, if \(E'\) implies \(c\! =\! d\), then \(\lambda (\xrightarrow {c \in \mathcal {T}}\xrightarrow {e \in \mathsf {S}})\! =\! \lambda (\!\xrightarrow {d \in \mathcal {T}}\xrightarrow {e \in \mathsf {S}}\!)\). Then there exists a distributive law \(\lambda ' :\mathcal {T}' \,;\,\mathsf {S}\rightarrow \mathsf {S}\,;\,\mathcal {T}'\) presented by the same equations as \(\lambda \), i.e., \(E_{\lambda '} = E_{\lambda }\).
Proof
There is a PROP morphism \(\theta :\mathcal {T}\rightarrow \mathcal {T}'\) defined by quotienting string diagrams in \(\mathcal {T}\) by \(E'\). This is a monad quotient in the bicategory \(\mathsf {Prof}(\mathbf {Mon})\) where PROPs are monads. We now define another 2-cell \(\lambda ' :\mathcal {T}' \,;\,\mathsf {Cm}\rightarrow \mathsf {Cm}\,;\,\mathcal {T}'\) as follows: given \(\xrightarrow {e \in \mathcal {T}'} \xrightarrow {c \in \mathsf {Cm}}\), pick any \(\xrightarrow {d \in \mathcal {T}}\) such that \(\theta (d) = e\) and let \(\xrightarrow {c' \in \mathsf {Cm}}\xrightarrow {d' \in \mathcal {T}}\) be \(\lambda (\xrightarrow {d \in \mathcal {T}}\xrightarrow {c \in \mathsf {Cm}})\). Define \(\lambda '(\xrightarrow {e \in \mathcal {T}'} \xrightarrow {c \in \mathsf {Cm}})\) as \(\xrightarrow {c' \in \mathsf {Cm}}\xrightarrow {\theta (d') \in \mathcal {T}'}\). \(\lambda '\) is well-defined because, by assumption, if \(\theta (d_1) = \theta (d_2)\) then \(E'\) implies that \(d_1 = d_2\) and thus \(\lambda (\xrightarrow {d_1}\xrightarrow {c}) = \lambda (\xrightarrow {d_2}\xrightarrow {c})\).
Now, \(\lambda \), \(\lambda '\) and \(\theta \) satisfy the assumptions of Proposition 3.5. In particular, (8) commutes by definition of \(\lambda '\) in terms of \(\lambda \) and \(\theta \). The conclusion of Proposition 3.5 guarantees that \(\lambda '\) is a distributive law. By construction, \(\lambda '\) is presented by the same equations as \(\lambda \).
We will see an application of Proposition 3.6 in the next section (Lemma 4.8).
4 Lawvere Categories as Composed PROPs
This section introduces and characterises Lawvere categories via a certain class of distributive laws of PROPs. As mentioned in the introduction, Lawvere categories are closely related to PROPs: the essential difference is that, whereas a Lawvere category is required to be a category with finite products — henceforth called a cartesian category, a PROP may carry any symmetric monoidal structure, not necessarily cartesian.
Just as PROPs, Lawvere categories can be also freely obtained by generators and equations. By analogy with symmetric monoidal theories introduced in Sect. 2, we organise this data as a cartesian theory: it simply amounts to the notion of equational theory that one typically finds in universal algebra, see e.g. [13].
Definition 4.1
A (one-sorted) cartesian theory \((\varSigma ,E)\) consists of a signature \(\varSigma =\{o_1 :n_1 \rightarrow 1,\dots ,o_k :n_k \rightarrow 1\}\) and a set E of equations between cartesian \(\varSigma \) -terms, which are defined as follows:
-
for each \(i \in \mathbb {N}\), the variable \(x_i\) is a cartesian term;
-
suppose \(o :n \rightarrow 1\) is a generator in \(\varSigma \) and \(t_1 , \dots , t_n\) are cartesian terms. Then \(o(t_1,\dots ,t_n)\) is a cartesian term.
The Lawvere category \(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)}\) freely generated by \((\varSigma , E)\) is the category whose objects are the natural numbers and arrows \(n \rightarrow m\) are lists \({\langle t_1,\dots ,t_m\rangle }\) of cartesian \(\varSigma \)-terms quotiented by E, such that, for each \(t_i\), only variables among \(x_1,\dots ,x_n\) appear in \(t_i\). Composition is by substitution:
where \(t[t' / x]\) denotes the cartesian term t in which all occurrences of the variable x have been replaced with \(t'\).
\(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)}\) is equipped with a product \(\times \) which is defined on objects by addition and on arrows by list concatenation and suitable renaming of variables:

We use notation \( ovar (t)\) for the list of occurrences of variables appearing (from left to right) in t and, more generally, \( ovar (t_1,\dots ,t_m)\) for the list \( ovar (t_1):\,\!:\dots :\,\!: ovar (t_m)\). Also, \(|l| \in \mathbb {N}\) denotes the length of a list l. We say that a list \({\langle t_1,\dots ,t_m\rangle } :n \rightarrow m\) is linear if each variable among \(x_1,\dots ,x_n\) appears exactly once in \( ovar (t_1,\dots ,t_m)\).
Our first observation is that Lawvere categories are PROPs.
Proposition 4.2
\(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)}\) is a PROP.
Proof
Let \(\times \) act as the monoidal product, 0 as its unit and define the symmetry \(n + m \rightarrow m+n\) as the list \({\langle x_{n+1},\dots ,x_{n+m},x_1,\dots ,x_n\rangle }\). It follows that \(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)}\) equipped with this structure satisfies the laws of symmetric strict monoidal categories, thus it is a PROP.
As a side observation, note that the unique PROP morphism \(\mathsf {P}\rightarrow \mathcal {L}_{\scriptscriptstyle (\varSigma ,E)}\) given by initiality of \(\mathsf {P}\) in \(\mathbf {PROP}\) sends \(p :n \rightarrow n\) to \({\langle x_{p^{-1}(1)},\dots ,x_{p^{-1}(n)}\rangle }\).
Remark 4.3
In spite of Proposition 4.2, cartesian theories are not a subclass of symmetric monoidal theories: in fact, the two concepts are incomparable. On the one hand, a symmetric monoidal theory \((\varSigma , E)\) is cartesian if and only if all generators in \(\varSigma \) have coarity 1 and, for all equations \(t=s\) in E, t and s are \(\varSigma \)-terms with coarity 1. Under these conditions, there is a canonical way to interpret any \(\varSigma \)-term \(n \rightarrow m\) as a list of m cartesian \(\varSigma \)-terms on variables \(x_1,\dots ,x_n\). Below, o ranges over \(\varSigma \):

The inductive cases are defined using the operations \(\,;\,\) and \(\oplus \) on lists given in Definition 4.1. Note that \(\varSigma \)-terms always denote (lists of) linear cartesian terms. This explains why, conversely, not all the cartesian theories are symmetric monoidal: their equations possibly involve non-linear \(\varSigma \)-terms, which are not expressible with (symmetric monoidal) \(\varSigma \)-terms. The subtlety here is that, in a sense, we can still simulate a cartesian theory on signature \(\varSigma \) with a symmetric monoidal theory, which however will be based on a larger signature \(\varSigma '\), recovering the possibility of copying and discarding variables by the use of additional generators. This point will become more clear below, where we will see how copier and discharger, i.e., the cartesian structure, can be mimicked with the use of the PROP \(\mathsf {Cm}\).
Example 4.4
The SMT \((\varSigma _{\scriptscriptstyle M},E_{\scriptscriptstyle M})\) of commutative monoids is cartesian. It generates the Lawvere category \(\mathcal {L}_{\scriptscriptstyle \varSigma _{\scriptscriptstyle M},E_{\scriptscriptstyle M}}\) whose arrows \(n \rightarrow m\) are lists \({\langle t_1,\dots ,t_m\rangle }\) of elements of the free commutative monoid on \(\{x_1,\dots ,x_n\}\).
The example of commutative monoids is particularly instructive for sketching our approach to Lawvere categories as composed PROPs. First, note that the Lawvere category \(\mathcal {L}_{\scriptscriptstyle \varSigma _{\scriptscriptstyle M},E_{\scriptscriptstyle M}}\) includes the PROP \(\mathsf {Mn}\) freely generated by \((\varSigma _{\scriptscriptstyle M},E_{\scriptscriptstyle M})\). Indeed, any string diagram of \(\mathsf {Mn}\) can be interpreted as a list of terms following the recipe of Remark 4.3. For instance,

As we observed above, string diagrams of \(\mathsf {Mn}\) can only express linear terms. What makes \(\mathcal {L}_{\scriptscriptstyle \varSigma _{\scriptscriptstyle M},E_{\scriptscriptstyle M}}\) more general than \(\mathsf {Mn}\) is the ability to copy and discard variables. Indeed, just as any monoidal category in which \(\oplus \) is the cartesian product, \(\mathcal {L}_{\scriptscriptstyle \varSigma _{\scriptscriptstyle M},E_{\scriptscriptstyle M}}\) comes equipped with canonical choices of a “copy” and “discard” operation
natural in n, which satisfy some expected equations: copying is commutative and associative; copying and then discarding is the same as not doing anything — see e.g. [14, 18].
How can we mimic the copy and discard structure in the language of PROPs? First, for each \(n > 1\) one can define \( cpy (n)\) and \( dsc (n)\) in terms of \( cpy (1)\) and \( dsc (1)\), which can therefore be regarded as the only fundamental operationsFootnote 4. Also, the equations that they satisfy can be synthesised as saying that \( cpy (1)\) acts as the comultiplication and \( dsc (1)\) as the counit of a commutative comonoid on 1. Therefore, they are none other than the generators of the PROP \(\mathsf {Cm}\):

Our approach suggests that a copy of \(\mathsf {Mn}\) and of \(\mathsf {Cm}\) “live” inside \(\mathcal {L}_{\scriptscriptstyle \varSigma _{\scriptscriptstyle M},E_{\scriptscriptstyle M}}\). We claim that these two PROPs provide a complete description of \(\mathcal {L}_{\scriptscriptstyle \varSigma _{\scriptscriptstyle M},E_{\scriptscriptstyle M}}\), that means, any arrow of \(\mathcal {L}_{\scriptscriptstyle \varSigma _{\scriptscriptstyle M},E_{\scriptscriptstyle M}}\) can be presented diagrammatically by using \(\mathsf {Mn}\) and \(\mathsf {Cm}\). For instance,

Observe that the diagram is of the factorised form \(\xrightarrow {\in \mathsf {Cm}}\xrightarrow {\in \mathsf {Mn}}\). Intuitively, \(\mathsf {Cm}\) is deputed to model the interplay of variables — in this case, the fact that \(x_1\) is copied and \(x_3\) is deleted — and \(\mathsf {Mn}\) describes the syntactic tree of the terms. Of course, to claim that this factorisation is always possible, we need additional equations to model composition of factorised diagrams. For instance:

The second equality holds if we assume the equation (A8) of the SMT of bialgebras. Thus the example suggests that composition by substitution in \(\mathcal {L}_{\scriptscriptstyle \varSigma _{\scriptscriptstyle M},E_{\scriptscriptstyle M}}\) can be mimicked at the diagrammatic level by allowing the use of bialgebra equations, which as we know from Example 3.3(b) present the composite PROP \(\mathsf {Cm}\,;\,\mathsf {Mn}\). Therefore, the conclusive conjecture of our analysis is that \(\mathcal {L}_{\scriptscriptstyle \varSigma _{\scriptscriptstyle M},E_{\scriptscriptstyle M}}\) must be isomorphic to \(\mathsf {Cm}\,;\,\mathsf {Mn}\) and can be presented by equations (A1)–(A10).
We now generalise and make formal the above approach. Our main result is the following.
Theorem 4.5
Suppose that \((\varSigma ,E)\) is an SMT which is also cartesian and let \(\mathcal {T}_{\scriptscriptstyle (\varSigma ,E)}\) be its freely generated PROP. Then \(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)} \cong \mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle (\varSigma ,E)}\), where distributive law \(\mathcal {T}_{\scriptscriptstyle (\varSigma ,E)} \,;\,\mathsf {Cm}\rightarrow \mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle (\varSigma ,E)}\) yielding \(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)}\) is presented by equations

for each \(o \in \varSigma \).
Before moving to the proof of Theorem 4.5, we show its significance by revisiting some well-known theories in terms of our result.
Example 4.6
-
(a)
If we instantiate Theorem 4.5 to the theory \((\varSigma _M,E_M)\) of commutative monoids (Example 2.3), then (Lw1)–(Lw2) are the bialgebra equations (A7)–(A10). The result that \(\mathsf {B}\cong \mathsf {Cm}\,;\,\mathsf {Mn}\) (Example 3.3(b)) is now an immediate consequence of Theorem 4.5 and tells us that the Lawvere category of commutative monoids can be considered as the PROP of bialgebras.
-
(b)
In the case of monoids, the resulting Lawvere category is precisely a composite PROP, because all the equations only affect the linear part of the theory, that means, the generating cartesian theory is also an SMT. As observed in Remark 4.3, this is not true in general: for instance, the cartesian theory \((\varSigma _G, E_G)\) of abelian groups extends the one \((\varSigma _M,E_M)\) of commutative monoids with an inverse operation
 and a non-linear equation
and a non-linear equation  . In such cases, Theorem 4.5 still yields useful information about the structure of the resulting Lawvere category. For instance, it means that \(\mathcal {L}_{\scriptscriptstyle (\varSigma _G,E_G)}\) is isomorphic to the PROP \(\mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle \varSigma _G,E_M}\) quotiented by the above non-linear equation, which is rendered in string diagrams as:
. In such cases, Theorem 4.5 still yields useful information about the structure of the resulting Lawvere category. For instance, it means that \(\mathcal {L}_{\scriptscriptstyle (\varSigma _G,E_G)}\) is isomorphic to the PROP \(\mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle \varSigma _G,E_M}\) quotiented by the above non-linear equation, which is rendered in string diagrams as: 
Interestingly, the result of this quotient is isomorphic to the PROP of integer matrices, see e.g. [37, §3.5] and its models in a symmetric monoidal category are the Hopf algebras [17], with
 playing the role of the antipode.
playing the role of the antipode. -
(c)
In [21] Fritz presents the category of finite sets and probabilistic maps using generators and equations. The resulting Lawvere category \(\mathcal {L}_{\scriptscriptstyle \text {Prob}}\) can be decomposed following the scheme of Theorem 4.5: there is a linear part \((\varSigma _P,E_P)\) of the theory — given by binary convex combinations
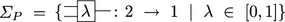 and suitable associativity and commutativity laws in \(E_P\), a commutative comonoid structure, and the two interact according to (Lw1)–(Lw2). This interaction yields a composite PROP \(\mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle (\varSigma _P,E_P)}\) which, quotiented by non-linear equations
and suitable associativity and commutativity laws in \(E_P\), a commutative comonoid structure, and the two interact according to (Lw1)–(Lw2). This interaction yields a composite PROP \(\mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle (\varSigma _P,E_P)}\) which, quotiented by non-linear equations  and
and  , yields \(\mathcal {L}_{\scriptscriptstyle \text {Prob}}\). Footnote 5
, yields \(\mathcal {L}_{\scriptscriptstyle \text {Prob}}\). Footnote 5
Remark 4.7
It is instructive to observe how Theorem 4.5 translates to models of theories. We recalled what is a model for a PROP in Remark 2.4; there is an analogous notion for Lawvere categories. A model for a Lawvere category \(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)}\) is a cartesian category \(\mathbb {C}\) together with a cartesian (i.e., finite-products preserving) functor \(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)} \rightarrow \mathbb {C}\): models of \(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)}\) in \(\mathbb {C}\) and natural transformations between them form a category \(\mathsf {CartMod}(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)},\mathbb {C})\). Now, for \((\varSigma ,E)\) and \(\mathcal {T}_{\scriptscriptstyle (\varSigma ,E)}\) as in Theorem 4.5, we have that models of \(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)}\) in \(\mathbb {C}\) cartesian are the same as models of \(\mathcal {T}_{\scriptscriptstyle (\varSigma ,E)}\) in \(\mathbb {C}\), now seen more abstractly as a symmetric monoidal category. That means, there is an equivalence \(\mathsf {LinMod}(\mathcal {T}_{\scriptscriptstyle (\varSigma ,E)},\mathbb {C}) \simeq \mathsf {CartMod}(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)},\mathbb {C}).\)
The rest of the section is devoted to proving Theorem 4.5. First we observe that, by the following lemma, it actually suffices to check our statement for SMTs with no equations. This reduction has just the purpose of making computations in \(\mathcal {L}_{\scriptscriptstyle (\varSigma ,E)}\) easier, by working with terms instead of equivalence classes.
Lemma 4.8
If the statement of Theorem 4.5 holds in the case \(E = \varnothing \), then it holds for any cartesian SMT \((\varSigma , E)\).
Proof
Let \((\varSigma ,E)\) be a cartesian SMT and \(\mathcal {T}_{\scriptscriptstyle \varSigma }\), \(\mathcal {T}_{\scriptscriptstyle (\varSigma ,E)}\) be the PROPs freely generated, respectively, by \((\varSigma ,\emptyset )\) and \((\varSigma ,E)\). By assumption, Theorem 4.5 holds for \((\varSigma ,\emptyset )\), yielding a distributive law \(\lambda :\mathcal {T}_{\scriptscriptstyle \varSigma } \,;\,\mathsf {Cm}\rightarrow \mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle \varSigma }\). A routine check shows that \(\lambda \) preserves the equations of E, whence Proposition 3.6 gives a distributive law \(\lambda ' :\mathcal {T}_{\scriptscriptstyle (\varSigma ,E)} \,;\,\mathsf {Cm}\rightarrow \mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle (\varSigma ,E)}\) with the required properties.
In the sequel, let us abbreviate \(\mathcal {L}_{\scriptscriptstyle \varSigma ,\emptyset }\) as \(\mathcal {L}_{\scriptscriptstyle \varSigma }\). By virtue of Lemma 4.8, we shall prove Theorem 4.5 for \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) and by letting \(\mathcal {T}_{\scriptscriptstyle \varSigma }\) be the PROP freely generated by \((\varSigma ,\emptyset )\). We shall obtain the distributive law \(\mathcal {T}_{\scriptscriptstyle \varSigma } \,;\,\mathsf {Cm}\rightarrow \mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle \varSigma }\) from the recipe of Proposition 3.4, by showing that any arrow of \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) decomposes as \(\xrightarrow {\in \mathsf {Cm}}\xrightarrow {\in \mathcal {T}_{\scriptscriptstyle \varSigma }}\).
We now give some preliminary lemmas that are instrumental for the definition of the factorisation and the proof of the main result. We begin by showing how string diagrams of \(\mathsf {Cm}\) and \(\mathcal {T}_{\scriptscriptstyle \varSigma }\) are formally interpreted as arrows of \(\mathcal {L}_{\scriptscriptstyle \varSigma }\).
Lemma 4.9
-
\(\mathsf {Cm}\) is the sub-PROP of \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) whose arrows are lists of variables. The inclusion of \(\mathsf {Cm}\) in \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) is the morphism \(\varPhi :\mathsf {Cm}\rightarrow \mathcal {L}_{\scriptscriptstyle \varSigma }\) defined on generators of \(\mathsf {Cm}\) by

-
\(\mathcal {T}_{\scriptscriptstyle \varSigma }\) is the sub-PROP of \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) whose arrows are linear terms. The inclusion of \(\mathcal {T}_{\scriptscriptstyle \varSigma }\) in \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) is the morphism \(\varPsi :\mathcal {T}_{\scriptscriptstyle \varSigma } \rightarrow \mathcal {L}_{\scriptscriptstyle \varSigma }\) defined on generators of \(\mathcal {T}_{\scriptscriptstyle \varSigma }\) by

Proof
First, it is immediate to verify that lists of variables are closed under composition, monoidal product and include all the symmetries of \(\mathcal {L}_{\scriptscriptstyle \varSigma }\): therefore, they form a sub-PROP. The same holds for linear terms.
We now consider the first statement of the lemma. There is a 1-1 correspondence between arrows \(n \xrightarrow {f \in \mathcal {L}_{\scriptscriptstyle \varSigma }}m\) that are lists of variables and functions \(\overline{m} \rightarrow \overline{n}\): the function for f maps k, for \(1 \le k \le m\), to the index l of the variable \(x_l\) appearing in position k in f. This correspondence yields an isomorphism between the sub-PROP of \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) whose arrows are lists of variables and \(\mathsf {F}^{\scriptstyle op }\). Composing this isomorphism with \(\mathsf {Cm}\xrightarrow {\cong } \mathsf {F}^{\scriptstyle op }\) yields \(\varPhi \) as in the statement of the lemma.
For the second statement, faithfulness is immediate by the fact that arrows of \(\mathcal {T}_{\scriptscriptstyle \varSigma }\) are \(\varSigma \)-terms modulo the laws of SMCs, with no additional equations. One can easily verify that \(\varPsi :\mathcal {T}_{\scriptscriptstyle \varSigma } \rightarrow \mathcal {L}_{\scriptscriptstyle \varSigma }\) identifies the linear terms in \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) following the observations in Remark 4.3.
Henceforth, for the sake of readability we shall not distinguish between \(\mathsf {Cm}\) and the isomorphic sub-PROP of \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) identified by the image of \(\varPhi \), and similarly for \(\mathcal {T}_{\scriptscriptstyle \varSigma }\) and \(\varPsi \). Lemma 4.9 allows us to use \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) as an environment where \(\mathsf {Cm}\) and \(\mathcal {T}_{\scriptscriptstyle \varSigma }\) interact. The following statement guarantees the soundness of the interaction described by (LW1)–(Lw2).
Lemma 4.10
Equations (LW1) and (Lw2) are sound in \(\mathcal {L}_{\scriptscriptstyle \varSigma }\).
Proof
We first focus on (Lw1). Following the isomorphisms of Lemma 4.9,  is interpreted as the arrow \({\langle o(x_1,\dots ,x_n)\rangle } \in \mathcal {L}_{\scriptscriptstyle \varSigma }[n,1]\) and
is interpreted as the arrow \({\langle o(x_1,\dots ,x_n)\rangle } \in \mathcal {L}_{\scriptscriptstyle \varSigma }[n,1]\) and  as \({\langle \rangle } \in \mathcal {L}_{\scriptscriptstyle \varSigma }[1,0]\). The left-hand side of (Lw1) is then the composite \({\langle o(x_1,\dots ,x_n)\rangle } \,;\,{\langle \rangle } \in \mathcal {L}_{\scriptscriptstyle \varSigma }[n,0]\), which is equal by definition to \({\langle \rangle } \in \mathcal {L}_{\scriptscriptstyle \varSigma }[n,0]\). Therefore, the left- and right-hand side of (Lw1) are the same arrow of \(\mathcal {L}_{\scriptscriptstyle \varSigma }\).
as \({\langle \rangle } \in \mathcal {L}_{\scriptscriptstyle \varSigma }[1,0]\). The left-hand side of (Lw1) is then the composite \({\langle o(x_1,\dots ,x_n)\rangle } \,;\,{\langle \rangle } \in \mathcal {L}_{\scriptscriptstyle \varSigma }[n,0]\), which is equal by definition to \({\langle \rangle } \in \mathcal {L}_{\scriptscriptstyle \varSigma }[n,0]\). Therefore, the left- and right-hand side of (Lw1) are the same arrow of \(\mathcal {L}_{\scriptscriptstyle \varSigma }\).
It remains to show soundness of (Lw2). Following Lemma 4.9, the left-hand side  is interpreted in \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) as \({\langle o(x_1,\dots ,x_n)\rangle } \,;\,{\langle x_1,x_1\rangle }\) and the right-hand side as \({\langle x_1,\dots ,x_n,x_1,\dots ,x_n\rangle } \,;\,{\langle o(x_1,\dots ,x_n), o(x_{n+1},\dots ,x_{n+n})\rangle }\). By definition, both composites are equal to \({\langle o(x_1,\dots ,x_n), o(x_1,\dots ,x_n)\rangle }\) in \(\mathcal {L}_{\scriptscriptstyle \varSigma }\). Therefore, (Lw2) is also sound in \(\mathcal {L}_{\scriptscriptstyle \varSigma }\).
is interpreted in \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) as \({\langle o(x_1,\dots ,x_n)\rangle } \,;\,{\langle x_1,x_1\rangle }\) and the right-hand side as \({\langle x_1,\dots ,x_n,x_1,\dots ,x_n\rangle } \,;\,{\langle o(x_1,\dots ,x_n), o(x_{n+1},\dots ,x_{n+n})\rangle }\). By definition, both composites are equal to \({\langle o(x_1,\dots ,x_n), o(x_1,\dots ,x_n)\rangle }\) in \(\mathcal {L}_{\scriptscriptstyle \varSigma }\). Therefore, (Lw2) is also sound in \(\mathcal {L}_{\scriptscriptstyle \varSigma }\).
It is useful to observe that (Lw1)–(Lw2) allows us to copy and discard not only the generators but arbitrary string diagrams of \(\mathcal {T}_{\scriptscriptstyle \varSigma }\).
Lemma 4.11
Suppose  is a string diagram of \(\mathcal {T}_{\scriptscriptstyle \varSigma }\). Then the following holds in \(\mathcal {T}_{\scriptscriptstyle \varSigma } + \mathsf {Cm}\) quotiented by (Lw1)–(Lw2).
is a string diagram of \(\mathcal {T}_{\scriptscriptstyle \varSigma }\). Then the following holds in \(\mathcal {T}_{\scriptscriptstyle \varSigma } + \mathsf {Cm}\) quotiented by (Lw1)–(Lw2).

Proof
The proof is by induction on  . For (Lw3), the base cases of
. For (Lw3), the base cases of  and
and  follow by the laws of SMCs (Fig. 1). The base case of
follow by the laws of SMCs (Fig. 1). The base case of  , for o a generator in \(\varSigma \), is given by (Lw2). The inductive cases of composition by \(\,;\,\) and \(\oplus \) immediately follow by induction hypothesis. The proof of (Lw4) is analogous.
, for o a generator in \(\varSigma \), is given by (Lw2). The inductive cases of composition by \(\,;\,\) and \(\oplus \) immediately follow by induction hypothesis. The proof of (Lw4) is analogous.
We can now show the factorisation lemma.
Lemma 4.12
Any arrow \(n\xrightarrow {f \in \mathcal {L}_{\scriptscriptstyle \varSigma }}m\) has a factorisation \(n \xrightarrow {\hat{c}\in \mathsf {Cm}}\xrightarrow {\hat{d}\in \mathcal {T}_{\scriptscriptstyle \varSigma }}m\) which is unique up-to permutation.
Proof
Since the cartesian theory generating \(\mathcal {L}_{\scriptscriptstyle \varSigma }\) has no equations, \(n \xrightarrow {f}m\) is just a list of cartesian \(\varSigma \)-terms \({\langle t_1,\dots ,t_m\rangle }\). The factorisation consists in replacing all variables appearing in \({\langle t_1,\dots ,t_m\rangle }\) with fresh ones \(x_1,\dots ,x_z\), so that no repetition occurs: this gives us the second component of the decomposition as a list of linear terms \(z\xrightarrow {\hat{d}\in \mathcal {T}_{\scriptscriptstyle \varSigma }}m\). The first component \(\hat{c}\) will be the list \(n\xrightarrow { ovar (t_1,\dots ,t_m)\in \mathsf {Cm}}z\) of variables originally occurring in f, so that post-composition with \(\hat{d}\) yields \({\langle t_1,\dots ,t_m\rangle }\). It is simple to verify uniqueness up-to permutation of this factorisation.
We now have all the ingredients to conclude the proof of our main statement.
Proof
(Theorem 4.5). Using the conclusion of Lemma 4.12, Proposition 3.4 gives us a distributive law \(\lambda :\mathcal {T}_{\scriptscriptstyle \varSigma } \,;\,\mathsf {Cm}\rightarrow \mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle \varSigma }\) such that \(\mathcal {L}_{\scriptscriptstyle \varSigma } \cong \mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle \varSigma }\). It remains to show that (Lw1)–(Lw2) allow to prove all the equations arising from \(\lambda \). By Proposition 3.4, \(\lambda \) maps a composable pair \(n\xrightarrow {d \in \mathcal {T}_{\scriptscriptstyle \varSigma }}\xrightarrow {c\in \mathsf {Cm}}m\) to the factorisation \(n\xrightarrow {c' \in \mathsf {Cm}}\xrightarrow {d' \in \mathcal {T}_{\scriptscriptstyle \varSigma }}m\) of \(d \,;\,c\) in \(\mathcal {L}_{\scriptscriptstyle \varSigma }\), calculated according to Lemma 4.12. The corresponding equation generated by \(\lambda \) is \(d \,;\,c = c' \,;\,d'\), with \(d,c,c',d'\) now seen as string diagrams of \(\mathcal {T}_{\scriptscriptstyle \varSigma } + \mathsf {Cm}\). The equational theory of \(\mathcal {L}_{\scriptscriptstyle \varSigma } \cong \mathsf {Cm}\,;\,\mathcal {T}_{\scriptscriptstyle \varSigma }\) consists of all the equations arising in this way plus those of \(\mathcal {T}_{\scriptscriptstyle \varSigma } + \mathsf {Cm}\). What we need to show is that

Since our factorisation is unique up-to permutation, it actually suffices to show a weaker statement, namely that

Statement \((\ddag )\) implies \((\dag )\) because, by uniqueness of the factorisation \(c' \,;\,d'\) up-to permutation, there exists \(\xrightarrow {p \in \mathsf {P}}\) such that \(d' = p \,;\,d''\) and \(c'' = c' \,;\,p\) in \(\mathcal {L}_{\scriptscriptstyle \varSigma }\). Since p is an arrow of both sub-PROPs \(\mathcal {T}_{\scriptscriptstyle \varSigma }\) and \(\mathsf {Cm}\), the first equality also holds in \(\mathcal {T}_{\scriptscriptstyle \varSigma }\) and the second in \(\mathsf {Cm}\). So \(c' \,;\,d' = c' \,;\,p \,;\,d'' = c'' \,;\,d''\) in \(\mathcal {T}_{\scriptscriptstyle \varSigma } + \mathsf {Cm}\).
Therefore, we turn to a proof of \((\ddag )\). We describe a procedure to transform the string diagram \(\xrightarrow {d \in \mathcal {T}_{\scriptscriptstyle \varSigma }}\xrightarrow {c\in \mathsf {Cm}}\) into the form \(\xrightarrow {c''\in \mathsf {Cm}}\xrightarrow {d''\in \mathcal {T}_{\scriptscriptstyle \varSigma }}\) by only using the equations in \(\mathcal {T}_{\scriptscriptstyle \varSigma } + \mathsf {Cm}\) plus (Lw1)-(Lw2). Lemmas 4.9 and 4.10 guarantee that \(d \,;\,c = c''\,;\,d''\) as arrows of \(\mathcal {L}_{\scriptscriptstyle \varSigma }\).
-
1.
First, there is a preparatory step in which we move all symmetries to the outmost part of the string diagram \(d \,;\,c\), to ease the application of (Lw1)–(Lw2). By definition, d only contains components of the kind
 ,
,  and
and  . Using naturality (Fig. 1), we can move all symmetries
. Using naturality (Fig. 1), we can move all symmetries  to the left of components
to the left of components  .
. 
The result is a string diagram \(p \,;\,\bar{d} \,;\,c'\), where p only contains components
 and
and  — i.e., it is a string diagram of \(\mathsf {P}\) — and \(\bar{d}\) is a string diagram of \(\mathcal {T}_{\scriptscriptstyle \varSigma }\) where
— i.e., it is a string diagram of \(\mathsf {P}\) — and \(\bar{d}\) is a string diagram of \(\mathcal {T}_{\scriptscriptstyle \varSigma }\) where  does not appear.
does not appear. 
We then perform a symmetric transformation on the string diagram c. By definition, c contains components
 ,
,  ,
,  and
and  . By naturality, we can move all symmetries
. By naturality, we can move all symmetries  to the right of any component
to the right of any component  and
and  .
. 
The result is a string diagram \(p \,;\,\bar{d} \,;\,\bar{c} \,;\,p'\), where \(\bar{c}\) is a string diagram of \(\mathsf {Cm}\) in which
 does not appear and \(p'\) is a string diagram of \(\mathsf {P}\).
does not appear and \(p'\) is a string diagram of \(\mathsf {P}\). 
-
2.
We now make \(\bar{d}\) and \(\bar{c}\) interact. First note that, since \(\bar{d}\) does not contain
 and all generators \(o \in \varSigma \) have coarity 1, \(\bar{d}\) must the \(\oplus \)-product \(\bar{d_1} \oplus \dots \oplus \bar{d_z}\) of string diagrams \(\bar{d_i} :k_i \rightarrow 1\) of \(\mathcal {T}_{\scriptscriptstyle \varSigma }\).
and all generators \(o \in \varSigma \) have coarity 1, \(\bar{d}\) must the \(\oplus \)-product \(\bar{d_1} \oplus \dots \oplus \bar{d_z}\) of string diagrams \(\bar{d_i} :k_i \rightarrow 1\) of \(\mathcal {T}_{\scriptscriptstyle \varSigma }\). 
For analogous reasons, \(\bar{c}\) is also a \(\oplus \)-product \(\bar{c_1} \oplus \dots \oplus \bar{c_z}\) where, for \(1 \le i \le z\),

We thus can present \(\bar{c}\) as follows:

We are now in position to distribute each \(\bar{d_i}\) over the corresponding \(\bar{c_i}\). Suppose first \(\bar{c_i}\) satisfies the left-hand equality in (9). By assumption, all the equations of \(\mathcal {T}_{\scriptscriptstyle \varSigma } + \mathsf {Cm}\), Lw1 and (Lw2) hold. Thus, by Lemma 4.11, also (Lw3) holds. Starting from \(\bar{d_i}\,;\,\bar{c_i}\), we can iteratively apply (Lw3) to obtain a string diagram of shape \(\xrightarrow {\in \mathsf {Cm}}\xrightarrow {\in \mathcal {T}_{\scriptscriptstyle \varSigma }}\):

In the remaining case, \(\bar{c_i}\) satisfies the right-hand equality in (9). Then, one application of (Lw1) also gives us a string diagram of shape \(\xrightarrow {\in \mathsf {Cm}}\xrightarrow {\in \mathcal {T}_{\scriptscriptstyle \varSigma }}\).

Applying the above transformations for each \(\bar{d_i}\,;\,\bar{c_i}\) yields a string diagram of the desired shape \(\xrightarrow {c''\in \mathsf {Cm}}\xrightarrow {d''\in \mathcal {T}_{\scriptscriptstyle \varSigma }}\).

Observe that all the transformations that we described only used equations in \(\mathcal {T}_{\scriptscriptstyle \varSigma } + \mathsf {Cm}\), (Lw1) and (Lw2). This concludes the proof of \((\ddag )\) and thus of the main theorem.
Notes
- 1.
Usually called Lawvere theories in the literature: i.e. finite product categories with set of objects the natural numbers, where product on objects is addition [23, 27]. In order to keep the exposition uniform, we reserve the word theory for presentations and refer to the presentation \((\varSigma ,E)\) of a Lawvere theory as a cartesian theory.
- 2.
Actually, Street worked in a 2-category, but the same theory can be developed in any bicategory with the obvious, minor modifications [25, §3.1].
- 3.
A notion of morphism can be defined also between monads on different objects, like in [36]. We will not need that level of generality here.
- 4.
For \(n = 0\), both operations are equal to the identity on 0.
- 5.
In fact, the Lawvere category in [21] has finite coproducts, while our \(\mathcal {L}_{\scriptscriptstyle \text {Prob}}\) is based on finite products. This is just a matter of co-/contra-variant presentation of the same data: one can switch between the two by “vertical rotation” of diagrams.
References
Baez, J.C., Erbele, J.: Categories in control (2014). CoRR abs/1405.6881
Baez, J.C.: Universal algebra and diagrammatic reasoning. Lecture (2006). http://math.ucr.edu/home/baez/universal/universal_hyper.pdf
Studer, C.: Introduction. In: Studer, C. (ed.) Numerics of Unilateral Contacts and Friction. LNACM, vol. 47, pp. 1–8. Springer, Heidelberg (2009)
Bonchi, F., Milius, S., Silva, A., Zanasi, F.: Killing epsilons with a dagger – a coalgebraic study of systems with algebraic label structure. Theoret. Comput. Sci. 604, 102–126 (2015)
Bonchi, F., Sobociński, P., Zanasi, F.: A categorical semantics of signal flow graphs. In: Baldan, P., Gorla, D. (eds.) CONCUR 2014. LNCS, vol. 8704, pp. 435–450. Springer, Heidelberg (2014)
Bonchi, F., Sobociński, P., Zanasi, F.: Interacting bialgebras are Frobenius. In: Muscholl, A. (ed.) FOSSACS 2014 (ETAPS). LNCS, vol. 8412, pp. 351–365. Springer, Heidelberg (2014)
Bonchi, F., Sobocinski, P., Zanasi, F.: Full abstraction for signal flow graphs. In: Proceedings of the 42nd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2015, pp. 515–526 (2015)
Bonchi, F., Zanasi, F.: Bialgebraic semantics for logic programming. Log. Methods Comput. Sci. 11(1:14), 1–47 (2015)
Bonsangue, M.M., Hansen, H.H., Kurz, A., Rot, J.: Presenting distributive laws. In: Heckel, R., Milius, S. (eds.) CALCO 2013. LNCS, vol. 8089, pp. 95–109. Springer, Heidelberg (2013)
Borceux, F.: Handbook of Categorical Algebra 1 - Basic Category Theory. Cambridge Univ. Press, Cambridge (1994)
Bruni, R., Melgratti, H., Montanari, U.: A connector algebra for P/T nets interactions. In: Katoen, J.-P., König, B. (eds.) CONCUR 2011. LNCS, vol. 6901, pp. 312–326. Springer, Heidelberg (2011)
Bruni, R., Montanari, U., Plotkin, G.D., Terreni, D.: On hierarchical graphs: reconciling bigraphs, gs-monoidal theories and gs-graphs. Fundam. Inform. 134(3–4), 287–317 (2014)
Burris, S., Sankappanavar, H.P.: A Course in Universal Algebra. Springer, Heidelberg (1981)
Burroni, A.: Higher dimensional word problems with applications to equational logic. Theor. Comput. Sci. 115, 43–62 (1993)
Coecke, B., Duncan, R.: Interacting quantum observables: categorical algebra and diagrammatics. New J. Phys. 13(4), 043016 (2011)
Corradini, A., Gadducci, F.: An algebraic presentation of term graphs, via gs-monoidal categories. Appl. Categorical Struct. 7(4), 299–331 (1999)
Dascalescu, S., Nastasescu, C., Raianu, S.: Hopf Algebras, Pure and Applied Mathematics, vol. 235. Marcel Dekker Inc., New York (2001). An Introduction
Eilenberg, S., Kelly, G.M.: Closed categories. In: Eilenberg, S., Harrison, D.K., MacLane, S., Röhri, H. (eds.) Proceedings of the Conference on Categorical Algebra, pp. 421–562. Springer, Heidelberg (1966)
Fiore, M., Devesas Campos, M.: The algebra of directed acyclic graphs. In: Coecke, B., Ong, L., Panangaden, P. (eds.) Computation, Logic, Games and Quantum Foundations. LNCS, vol. 7860, pp. 37–51. Springer, Heidelberg (2013)
Fong, B., Rapisarda, P., Sobociński, P.: A categorical approach to open and interconnected dynamical systems (2015). CoRR/1510.05076
Fritz, T.: A presentation of the category of stochastic matrices (2009). CoRR abs/0902.2554. http://arxiv.org/abs/0902.2554
Hyland, M., Plotkin, G., Power, J.: Combining effects: sum and tensor. Theor. Comput. Sci. 357(1–3), 70–99 (2006)
Hyland, M., Power, J.: The category theoretic understanding of universal algebra: Lawvere theories and monads. Electron. Notes Theor. Comput. Sci. 172, 437–458 (2007)
Jacobs, B.: Semantics of weakening and contraction. Ann. Pure Appl. Logic 69(1), 73–106 (1994)
Lack, S.: Composing PROPs. Theor. App. Categories 13(9), 147–163 (2004)
Lafont, Y.: Equational reasoning with 2-dimensional diagrams. Term Rewriting. LNCS, vol. 909, pp. 170–195. Springer, Heidelberg (1995)
Lawvere, W.F.: Functorial semantics of algebraic theories. Ph.D. thesis (2004)
Mac Lane, S.: Categorical algebra. Bull. Am. Math. Soc. 71, 40–106 (1965)
Mac Lane, S.: Categories for the Working Mathematician. Springer, Heidelberg (1998)
Melliès, P.A.: Categorical semantics of linear logic. In: Interactive Models of Computation and Program Behaviour, Panoramas et Synthèses 27, Société Mathématique de France 1196 (2009)
Rosebrugh, R., Wood, R.: Distributive laws and factorization. J. Pure Appl. Algebra 175(13), 327–353 (2002). Special Volume celebrating the 70th birthday of Professor Max Kelly
Ross Duncan, K.D.: Interacting Frobenius algebras are Hopf. CoRR abs/1601.04964 (2016). http://arxiv.org/abs/1601.04964
Selinger, P.: A survey of graphical languages for monoidal categories. Springer Lect. Notes Phys. 13(813), 289–355 (2011)
Sleep, M.R., Plasmeijer, M.J., van Eekelen, M.C.J.D. (eds.): Term Graph Rewriting: Theory and Practice. Wiley, Chichester (1993)
Sobociński, P., Stephens, O.: A programming language for spatial distribution of net systems. In: Petri Nets 2014 (2014)
Street, R.: The formal theory of monads. J. Pure Appl. Algebra 2(1), 243–265 (2002)
Zanasi, F.: Interacting Hopf algebras: the theory of linear systems. Ph.D. thesis, Ecole Normale Supérieure de Lyon (2015)
Acknowledgements
The first author acknowledge support by project ANR 12IS02001 PACE. The third author acknowledges support from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013) / ERC grant agreement n\(^{\circ }\) 320571.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Bonchi, F., Sobocinski, P., Zanasi, F. (2016). Lawvere Categories as Composed PROPs. In: Hasuo, I. (eds) Coalgebraic Methods in Computer Science. CMCS 2016. Lecture Notes in Computer Science(), vol 9608. Springer, Cham. https://doi.org/10.1007/978-3-319-40370-0_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-40370-0_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-40369-4
Online ISBN: 978-3-319-40370-0
eBook Packages: Computer ScienceComputer Science (R0)






 and a unit
and a unit  . Equations
. Equations 
 and a counit
and a counit  .
. 

 and
and  . The distributive law
. The distributive law  of
of  of
of 
 and a non-linear equation
and a non-linear equation  . In such cases, Theorem
. In such cases, Theorem 
 playing the role of the antipode.
playing the role of the antipode.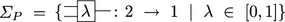 and suitable associativity and commutativity laws in
and suitable associativity and commutativity laws in  and
and  , yields
, yields 

 ,
,  and
and  . Using naturality (Fig.
. Using naturality (Fig.  to the left of components
to the left of components  .
. 
 and
and  — i.e., it is a string diagram of
— i.e., it is a string diagram of  does not appear.
does not appear. 
 ,
,  ,
,  and
and  . By naturality, we can move all symmetries
. By naturality, we can move all symmetries  to the right of any component
to the right of any component  and
and  .
. 
 does not appear and
does not appear and 
 and all generators
and all generators 




