Discontinuous and Enriched Galerkin Methods for Phase-Field Fracture Propagation in Elasticity

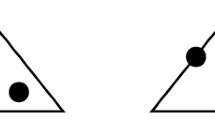
Abstract

In this work, we introduce discontinuous Galerkin and enriched Galerkin formulations for the spatial discretization of phase-field fracture propagation. The nonlinear coupled system is formulated in terms of the Euler-Lagrange equations, which are subject to a crack irreversibility condition. The resulting variational inequality is solved in a quasi-monolithic way in which the irreversibility condition is incorporated with the help of an augmented Lagrangian technique. The relaxed nonlinear system is treated with Newton’s method. Numerical results complete the present study.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Fracture propagation in elasticity, plasticity, and porous media is currently one of the major research topics in mechanical, energy, and environmental engineering. In this paper, we concentrate specifically on fracture propagation in elasticity. We consider a variational approach for brittle fracture introduced in [6], which has been later formulated in terms of a thermodynamically-consistent phase-field technique [8]. In fact, variational and phase-field formulations for fracture are active research areas as attested in recent years, e.g., [1–4, 9, 10]. Our motivations for employing a phase-field model are that fracture nucleation, propagation, kinking, and curvilinear paths are automatically included in the model; post-processing of stress intensity factors and remeshing resolving the crack path are avoided. Furthermore, the underlying equations are based on continuum mechanics principles that can be treated with adaptive Galerkin finite elements.

In this work, we extend existing Galerkin formulations for phase-field fracture with regard to two major aspects:

• Spatial discretization of the displacement field with discontinuous Galerkin (DG) finite elements resulting in NIPG [12] and IIPG methods [5] and an enriched Galerkin (EG) formulation [13];

• Formulation of a quasi-monolithic augmented Lagrangian iteration for the nonlinear coupled displacement-phase-field system.

These frameworks are formulated in Sects. 2, 3 and 4 and are substantiated with numerical tests in Sect. 5.

2 The Phase-Field Fracture Model

We limit our attention to 2-dimensional problems and let $\varOmega \in \mathbb{R}^{2}$, be a smooth, open, connected and bounded set. We denote the L ² scalar product with (⋅ , ⋅ ), and assume that the crack $\mathcal{C}$ is a 1-dimensional set, not necessarily connected, contained in Ω. Using the variational/phase-field approach to fracture [3, 6], the crack $\mathcal{C}$ is represented using a continuous phase-field variable φ: Ω → [0, 1]. This value of the phase-field variable interpolates between the broken (φ = 0) and unbroken (φ = 1) states of the material. The diffusive transition zone between these two states is controlled by a regularization parameter ɛ > 0. Imposing a crack irreversibility condition φ ≤ φ ⁿ⁻¹ (where φ ⁿ⁻¹: = φ(t ⁿ⁻¹) denotes the previous time step solution), and further ingredients for a thermodynamically consistent phase-field framework [8] result in the following Euler-Lagrange formulation:

Formulation 1

For the loading steps n = 1, 2, 3, …: Find vector-valued displacements and a scalar-valued phase-field variable $\{\mathbf{u}^{n},\varphi ^{n}\}:=\{ \mathbf{u},\varphi \}\in \{\bar{\mathbf{u}} + V \} \times W$ such that

$$\displaystyle{ \Big(\big((1-\kappa )\varphi ^{2}+\kappa \big)\sigma (\mathbf{u}),e(\mathbf{w})\Big) = 0\quad \forall \mathbf{w} \in V, }$$

(1)

as well as,

$$\displaystyle\begin{array}{rcl} & & (1-\kappa )(\varphi \sigma (\mathbf{u}): e(\mathbf{u}),\psi -\varphi ) \\ & & \quad + G_{c}\bigg(-\frac{1} {\varepsilon } (1-\varphi,\psi -\varphi ) +\varepsilon (\nabla \varphi,\nabla \psi -\varphi )\bigg) \geq 0\quad \forall \psi \in W_{in} \cap L^{\infty }(\varOmega ),{}\end{array}$$

(2)

where V: = H ₀ ¹(Ω), $W_{in}:=\{ w \in H^{1}(\varOmega )\vert w \leq \varphi ^{n-1} \leq 1\;\text{a.e. on}\;\varOmega \}$ and W: = H ¹(Ω). Furthermore, $\sigma =\sigma (\mathbf{u}) = 2\mu _{s}e +\lambda _{s}tr(e)I$ is the stress tensor with μ _s , λ _s  > 0, and e(u) = 0. 5(∇u + ∇u ^T) is the linearized strain tensor. The critical energy release rate is G _c  > 0. The domain is subject to boundary conditions, and we assume $\varGamma _{D}\neq \emptyset$, with the possibly non-homogeneous and time-dependent Dirichlet boundary conditions $\bar{\mathbf{u}}$. Moreover, κ is a regularization parameter for the elastic energy bounded below by 0, such that κ ≪ ɛ, see e.g., [3].

To treat crack irreversibility, we use the augmented-Lagrangian formulation described in [14]. To apply this method, we begin by approximating the time derivative ∂ _t φ using the backward difference

$$\displaystyle{ \partial _{t}\varphi \approx \partial _{\varDelta t}\varphi = \frac{\varphi -\varphi ^{n-1}} {\varDelta t} \quad \Rightarrow \quad \frac{1} {\varDelta t}\bigg((\lambda +\gamma (\varphi -\varphi ^{n-1}))^{+}\bigg),\quad \varDelta t = t^{n} - t^{n-1}. }$$

Here, λ and γ are a penalization function and parameter, respectively, and φ ⁿ⁻¹ is the phase-field solution at the previous time step. Moreover, (x)⁺: = max{0, x}.

Algorithm 2 Solution algorithm

3 A Quasi-monolithic Incremental Formulation

We choose a quasi-monolithic approach [7] as this reduces algorithmic complexity and has been demonstrated to be numerically robust and efficient when φ is replaced by the extrapolation $\tilde{\varphi }$ in the first term of Formulation 2. The reason for choosing $\tilde{\varphi }$ is the need to circumvent the non-convexity of the underlying energy functional.

Formulation 2

For n = 1, 2, 3, …: Find $U^{n}:= U:=\{ \mathbf{u},\varphi \}\in \{\bar{\mathbf{u}} + V \} \times W$, where V: = H ₀ ¹(Ω) and W: = H ¹(Ω), such that

$$\displaystyle{ A(U)(\varPsi ) = 0\quad \forall \varPsi:=\{ \mathbf{w},\psi \}\in V \times W, }$$

(3)

where A(⋅ )(⋅ ) is the following semi-linear form

$$\displaystyle\begin{array}{rcl} & & A(U)(\varPsi ) =\Big (\big((1-\kappa )\tilde{\varphi }^{2}+\kappa \big)\sigma (\mathbf{u}),e(\mathbf{w})\Big) + (1-\kappa )(\varphi \sigma (\mathbf{u}): e(\mathbf{u}),\psi ) \\ & & +G_{c}\bigg(-\frac{1} {\varepsilon } (1-\varphi,\psi ) +\varepsilon (\nabla \varphi,\nabla \psi )\bigg) + \frac{1} {\varDelta t}\bigg((\lambda +\gamma (\varphi -\varphi ^{n-1}))^{+},\psi \bigg). {}\end{array}$$

(4)

Here $\tilde{\varphi }$ is a linear extrapolation of time-lagged φ, i.e. $\varphi \approx \tilde{\varphi }:=\tilde{\varphi } (\varphi ^{n-1},\varphi ^{n-2})$, with φ ⁿ⁻¹, φ ⁿ⁻² denoting solutions to previous time steps. Solving the nonlinear variational problem (4) is performed with Newton’s method and line search backtracking. The resulting solution algorithm is outlined in Algorithm 2.

4 Spatial Discretization with DG and EG

In this section we establish key notations for DG and EG followed by the mathematical statement of the discrete variational forms. On a conforming subdivision $\mathcal{E}_{h}$ of a polygonal domain Ω subdivided into elements E we define the discontinuous finite element subspace to be

$$\displaystyle{ \mathcal{D}_{k}(\mathcal{E}_{h}) =\{ v \in L^{2}(\varOmega ):\forall E \in \mathcal{E}_{ h},v\vert _{E} \in \mathbb{P}_{k}(E)\}, }$$

(5)

where $\mathbb{P}_{k}(E)$ denotes the space of piecewise polynomials of total degree less than or equal to k on E. We also define the space of CG approximating polynomials enriched with discontinuous piecewise constants

$$\displaystyle{ \mathcal{D}_{k}^{C0}(\mathcal{E}_{ h}):= \mathcal{D}_{k}^{C}(\mathcal{E}_{ h}) \cup \mathcal{D}_{0}(\mathcal{E}_{h}). }$$

(6)

Here $\mathcal{D}_{k}^{C}(\mathcal{E}_{h})$ is the CG approximating space defined as

$$\displaystyle{ \mathcal{D}_{k}^{C}(\mathcal{E}_{ h}) =\{ v \in C(\varOmega ):\forall E \in \mathcal{E}_{h},v\vert _{E} \in \mathbb{P}_{k}^{C}(E),v\vert _{\varGamma _{ D}} = 0\}, }$$

(7)

where $\mathbb{P}_{k}^{C}(E)$ denotes the space of continuous piecewise polynomials of total degree less than or equal to k on E.

Fig. 1

Support points for bilinear and biquadratic basis functions. (a ) CG: all support points in red. (b ) DG: support points for left element in red, for right element in blue. The common edge has two sets of support points – one from each element. (c ) EG: support points from CG approximating space in red, piecewise constants in blue. Only the piecewise constant degree of freedom is discontinuous across the common edge

In order to describe the vector-valued displacements, we consider the spaces of vector functions that generalize (5) and (6): $\boldsymbol{\mathcal{D}}_{k}(\mathcal{E}_{h}) = (\mathcal{D}_{k}(\mathcal{E}_{h}))^{d},\boldsymbol{\mathcal{D}}_{k}^{C0}(\mathcal{E}_{h}) = (\mathcal{D}_{k}^{C0}(\mathcal{E}_{h}))^{d},$ where d is the number of spatial dimensions. We note that the functions in $\boldsymbol{\mathcal{D}}_{k}(\mathcal{E}_{h})$ and $\boldsymbol{\mathcal{D}}_{k}^{C0}(\mathcal{E}_{h})$ are discontinuous along the edges (or faces) of the mesh.

Now, consider two neighboring elements E ₁ ^e and E ₂ ^e that share a common side e. Naturally then, there are two traces of $w \in \boldsymbol{\mathcal{D}}_{k}(\mathcal{E}_{h})$ along e (see Fig. 1). We consider n _e to be the normal vector associated with e to be oriented from E ₁ ^e to E ₂ ^e and define: $\{\mathbf{w}\} = \frac{1} {2}(\mathbf{w}\vert _{E_{1}^{e}}) + \frac{1} {2}(\mathbf{w}\vert _{E_{2}^{e}}),\quad [\mathbf{w}] = (\mathbf{w}\vert _{E_{1}^{e}}) - (\mathbf{w}\vert _{E_{2}^{e}})\quad \forall e = \partial E_{1}^{e} \cap \partial E_{2}^{e}.$ We extend this definition to elements on the boundary ∂ Ω as: $\{\mathbf{w}\} = [\mathbf{w}] = (\mathbf{w}\vert _{E_{1}^{e}})\quad \forall e = \partial E_{1}^{e} \cap \partial \varOmega.$ Further, we denote by | e | the length of an edge e in d = 2. We now state the equations corresponding to a discontinuous spatial discretization directly from inspection of the monolithic formulation (4) and the DG-scheme for pure linear elasticity, e.g., [11]. We pursue a discontinuous representation of the displacement variable u only, recognizing that the regularization in the case of the phase-field variable φ enforces its continuity across the crack.

We augment (4) with the jump and penalization terms to define the discrete incremental semi-linear form

$$\displaystyle{ \begin{array}{rl} &A(U_{h})(\varPsi _{h}) =\sum _{E\in \mathcal{E}_{h}}\int _{E}\Big((1-\kappa )\tilde{\varphi }^{2}+\kappa \big)\sigma (\mathbf{u}),e(\mathbf{w})\Big) \\ & -\sum _{e\in \varGamma _{h}\cup \varGamma _{D}}\int _{e}\big\{((1-\kappa )\tilde{\varphi }^{2}+\kappa \big)\sigma (\mathbf{u}) \cdot \mathbf{n}_{e}\big\}[\mathbf{w}] +\!\eta \sum _{e\in \varGamma _{h}}\int _{e}\big\{((1-\kappa )\tilde{\varphi }^{2}+\!\kappa \big)\sigma (\mathbf{w}) \cdot \mathbf{n}_{e}\big\}[\mathbf{u}] \\ & +\!\eta \sum _{e\in \varGamma _{D}}\int _{e}\Big(((1-\kappa )\tilde{\varphi }^{2}+\kappa \big)\sigma (\mathbf{w}) \cdot \mathbf{n}_{e}\Big)(\mathbf{u} -\mathbf{g}_{D}) +\!\sum _{e\in \varGamma _{h}} \frac{\delta _{e}} {\vert e\vert ^{\beta }}\int _{e}[\mathbf{u}][\mathbf{w}] +\!\sum _{e\in \varGamma _{D}} \frac{\delta _{e}} {\vert e\vert ^{\beta }}\int _{e}(\mathbf{u} -\mathbf{g}_{D})\mathbf{w} \\ &+\!(1-\kappa )(\varphi \sigma (\mathbf{u}): e(\mathbf{u}),\psi )+\!G_{c}\bigg(-\frac{1} {\varepsilon } (1-\varphi,\psi )+\!\varepsilon (\nabla \varphi,\nabla \psi )\bigg)+\!\frac{1} {\varDelta t} \bigg((\lambda +\gamma (\varphi -\varphi ^{n-1}))^{+},\psi \bigg), \end{array} }$$

(8)

where η = 1 (NIPG) or η = 0 (IIPG); and δ _e  > 0 and β > 0 (here β = 1) are the DG-penalization and superpenalization parameters, respectively. The DG-CG variational problem reads: Find $U_{h}:=\{ \mathbf{u},\varphi \}\in \{\bar{\mathbf{u}}_{h} + V _{h}^{DG}\} \times W_{h}^{CG}$ such that

$$\displaystyle{ A(U_{h})(\varPsi _{h}) = 0\quad \forall \varPsi _{h}:=\{ \mathbf{w},\psi \}\in V _{h}^{DG} \times W_{ h}^{CG}. }$$

(9)

The EG-CG variational problem reads: Find $U_{h}:=\{ \mathbf{u},\varphi \}\in \{\bar{\mathbf{u}}_{h} + V _{h}^{EG}\} \times W_{h}^{CG}$ such that

$$\displaystyle{ A(U_{h})(\varPsi _{h}) = 0\quad \forall \varPsi _{h}:=\{ \mathbf{w},\psi \}\in V _{h}^{EG} \times W_{ h}^{CG}. }$$

(10)

The test and trial spaces are $V _{h}^{DG}:= [\mathcal{D}_{k}(\mathcal{E}_{h})]^{2},V _{h}^{EG}:= [\mathcal{D}_{k}^{C0}(\mathcal{E}_{h})]^{2},W_{h}^{CG}:= \mathcal{D}_{k}^{C}(\mathcal{E}_{h}).$ Our formulation enforces both Dirichlet and Neumann boundary conditions weakly. The use of homogeneous Neumann boundary conditions for u and φ results in a formulation exclusively dependent on Γ _D . The directional derivative of (8) needed for the Newton iterations is computed analytically.

5 A Numerical Test: Single Edge Notched Tension

Fig. 2

Schematic of the single-edge-notched tension test (left), the final phase-field crack pattern at T = 6. 6 × 10⁻³ s (middle), and comparison of load-displacement curves from our monolithic scheme with CG, DG-IIPG and EG-IIPG against results reported by Miehe et al. [9] and Heister et al. [7]

The single edge notched tension test is a widely used experimental methodology used to characterize the fracture toughness of various materials in plane-strain.

We consider a square plate with a horizontal notch placed at half-height, running from the right outer surface to the center of the specimen. The plate is subject to zero displacement boundary conditions on the bottom surface, and time-dependent displacement on the top surface. The left and right surfaces are considered to be traction-free. The problem setup is shown in Fig. 2. The material parameters are chosen as λ = 121. 1538 kN/mm², μ = 80. 7692 kN/mm² and G _c  = 2. 7 × 10⁻³ kN/mm. The displacement boundary condition on the top surface is taken to be $\bar{u}_{y}(t) = t\bar{\alpha }$ with $\bar{\alpha }= 1\,\text{mm}/\text{s}.$ The expected response of this test is the build-up of the stress concentration in the vicinity of the crack-tip, followed by unstable, catastrophic crack growth.

Our first objective is to study h-convergence for fixed ɛ. We choose Δ t = 1. 0 × 10⁻⁴ s for the first 50 loading steps, after which Δ t = 1. 0 × 10⁻⁵ s. This adaptivity in the time step is necessary to capture the rapid movement of the crack tip. We choose ɛ = 4. 4 × 10⁻² mm, $\kappa = 1.0 \times 10^{-12}$, and run our code for h ₁ = 4. 4 × 10⁻² mm, $h_{2} = 2.2 \times 10^{-2}\,\mathrm{mm}$, and h ₃ = 1. 1 × 10⁻² mm. We evaluate the surface load vector on the top surface of Ω as $\tau = (F_{x},F_{y}) =\int _{\partial \varOmega _{ \text{top}}}\sigma (\mathbf{u})\mathbf{n}ds.$ In this example, we are particularly interested in F _y . Our findings for the surface load evolution with varying h are shown in Fig. 3 for the IIPG flavors of EG and DG. It is observed that our approach is stable with spatial mesh refinement, and that our solution converges as we use finer meshes. Comparison to literature values are displayed in Fig. 2 at right.

Fig. 3

We fix κ and ɛ on the coarsest mesh level and vary h. Left: CG. Middle: DG-IIPG. Right: EG-IIPG. Spatial convergence is observed for all schemes

Results obtained from DG-NIPG and EG-NIPG are very similar and are therefore not presented here. The SIPG method (η = −1) yields unsatisfactory findings, which are not shown in this work.

With the results of our scheme duly validated, we proceed to study the relative efficiency of the schemes by comparing the number of Newton iterations taken by each of them to converge. We first investigate the variation in the number of Newton steps taken with the penalization parameter δ _e . Note that when we multiply Equations (8) throughout by Δ t, our effective penalization of the jump becomes δ _e Δ t. This is an important detail that cannot be overlooked while using DG/EG for the phase-field equations because for instance, using δ _e  = 10⁵ with $\varDelta t = 1 \times 10^{-5}\,\mathrm{s}$ gives an effective penalization of δ _e Δ t = 1 which is not sufficiently large and produces spurious results. In the case of an adaptive time step size (we usually take Δ t = 1 × 10⁻⁴ s for the first 50 steps, and a smaller time step thereafter), the product δ _e Δ t is reported for the smaller time step. We vary the values of the effective penalization and plot the cumulative number of Newton steps as a function of time for h = 1. 1 × 10⁻² mm, ɛ = 2 h[mm], and κ = 1. 0 × 10⁻¹². The results of this study with IIPG and NIPG are shown in Fig. 4. In Fig. 5, we observe that DG and EG schemes take much fewer Newton iterations to converge than CG especially after the onset of crack growth (approximately t = 0. 0055 s).

Fig. 4

Newton convergence performance with h = 1. 1 × 10⁻² mm, $\varDelta t =\{ 10^{-4},t < 0.005;10^{-5},t \geq 0.005\}$, ɛ = 2 h[mm], and κ = 10⁻¹² and varying penalty δ _e . Left: DG-NIPG. Right: EG-NIPG. Left: DG-IIPG. Right: EG-IIPG. Convergence is faster for higher values of penalization

Fig. 5

Single edge notched tension test results using CG, DG-IIPG and EG-IIPG. Left: load vs. displacement curve. Right: Newton convergence performance for constant Δ t = 10⁻⁵ s

For a better comparison of the efficiency, we run a test with the same physical parameters as above, but with a uniform time step of Δ t = 10⁻⁵ s throughout. The motivation is to suppress the effect of adaptive time stepping on the Newton performance and to give an unbiased comparison. Since the computational burden with such a simulation is significant, we only consider the IIPG case with δ _e Δ t = 10². These results are shown in Fig. 5. As we can see, DG and EG take roughly the same number of Newton iterations (1800) while CG takes significantly more (2520). We also observe that the load-displacement curves for all three methods are in reasonable agreement. Hence, we can conclusively state that the Newton method converges in fewer iterations for the DG and EG schemes than for the CG scheme. Furthermore by inspecting Fig. 1, we see that EG has significantly fewer degrees of freedom than DG.