An Experimental Investigation on the Pancake Problem

Abstract

In this paper, we present an experimental investigation on the pancake problem. Also called sorting by prefix reversals (SBPR), this problem is linked to the genome rearrangement problem also called sorting by reversals (SBR). The pancake problem is a NP-hard problem. Until now, the best theoretical R-approximation was 2 with an algorithm, which gives a 1.22 experimental R-approximation on stacks with a size inferior to 70. In the current work, we used a Monte-Carlo Search (MCS) approach with nested levels and specific domain-dependent simulations. First, in order to sort large stacks of pancakes, we show that MCS is a relevant alternative to Iterative Deepening Depth First Search (IDDFS). Secondly, at a given level and with a given number of polynomial-time domain-dependent simulations, MCS is a polynomial-time algorithm as well. We observed that MCS at level 3 gives a 1.04 experimental R-approximation, which is a breakthrough. At level 1, MCS solves stacks of size 512 with an experimental R-approximation value of 1.20.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

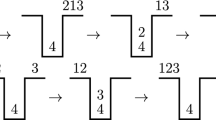
The pancake problem is described as follows. A chef prepares a stack of pancakes that come out all different sizes on a plate. The goal of the server is to order them with decreasing sizes, the largest pancake touching the plate, and the smallest pancake being at the top. The server can insert a spatula below a pancake and flip the substack situated above the spatula. He may repeat this action as many times as necessary. In the particular version, the goal of the server is to sort a particular stack with a minimum number of flips. In the global version, the question is to determine the maximum number of flips f(n) - the diameter - to sort any stack of n pancakes.

This problem is a puzzle, or a one-player game well-known in artificial intelligence and in computer science under the name of sorting by prefix reversals (SBPR). Its importance is caused by its similarity with the sorting by reversals (SBR) problem which is fundamental in biology to understand the proximity between genomes of two different species. For example, the SBR distance between a cabbage and a turnip is three [23]. The SBR problem has been studied in depth [24] for the last twenty years. The SBR problem can be signed when the signs of the genes are considered, or unsigned otherwise. Similarly, the pancakes can be burnt on one side, or not. This brings about four domains: one with unburnt pancakes, one with burnt pancakes, one with unsigned genes and one with signed genes.

In the unburnt pancake problem, Gates and Papadimitriou [22] gave the first bounds of the diameter in 1979, and Bulteau has shown that the problem is NP-hard in 2013 [11]. Very interesting work have been done between 1979 and today. The goal of the current work is to provide an experimental contribution to the unburnt pancake problem. More specifically, we show the pros and cons of two planning algorithms used in computer games: IDDFS [30] and MCS [13]. Besides, we define several domain-dependent algorithms: Efficient Sort (EffSort), Alternate Sort (AltSort), Basic Random EFficient algorithm (BREF), Fixed-Depth Efficient Sort (FDEffSort), and Fixed-Depth Alternate Sort (FDAltSort), and we re-use the Fischer and Ginzinger’s algorithm (FG) [21]. FG was proved to be a 2-approximation algorithm that also reaches a 1.22 approximation experimentally. We show how to use the algorithms above in the MCS framework. We obtain an experimental approximation of 1.04, which is a significant reduction.

The paper is organized as follows. Section 2 defines the SBR and SBPR problems. Section 3 sums up the related work in the four domains. Section 4 presents our work and its experimental results. Section 5 concludes.

2 Definitions

Let N be the size of a permutation $\pi$ and

$$\begin{aligned}{}[\pi (1), \pi (2), ..., \pi (N-1), \pi (N)] \end{aligned}$$

the representation of $\pi$. The problem of sorting a permutation by reversals consists in reaching the identity permutation

$$\begin{aligned}{}[1, 2, ..., N-1, N] \end{aligned}$$

by applying a sequence of reversals. A reversal $\rho (i, j)$ with $i<j$ is an action applied on a permutation. It transforms the permutation

$$\begin{aligned}{}[\pi (1), ..., \pi (i-1), \pi (i), ..., \pi (j), \pi (j+1) ..., \pi (N)] \end{aligned}$$

into

$$\begin{aligned}{}[\pi (1), ..., \pi (i-1), \underline{\pi (j), ..., \pi (i)}, \pi (j+1) ..., \pi (N)]. \end{aligned}$$

The effect of a reversal is reversing the order of the numbers between the two cuts. A cut is located between two numbers of the permutation. In the above example, the first cut is between $i-1$ and i and the second one is between j and $j+1$.

In the pancake problem, each number $\pi (i)$ corresponds to the size of the pancake situated at position i in a stack of pancakes, and the permutation problem is seen as a pancake stack to be sorted by decreasing size. One cut is fixed and corresponds to the top of the stack. The other cut corresponds to the location of a spatula inserted between two pancakes so as to reverse the substack above the spatula. For example, the permutation

$$\begin{aligned}{}[\pi (1), ..., \pi (i), \pi (i+1) ..., \pi (N)] \end{aligned}$$

has its top on the left and its bottom on the right. After a flip $\rho (i)$ between i and $i+1$, the permutation becomes

$$\begin{aligned}{}[\underline{\pi (i), ..., \pi (1)}, \pi (i+1) ..., \pi (N)]. \end{aligned}$$

In addition, a permutation can be signed or not. In the signed case, a sign is associated to each number, i.e. the integers of the permutation can be positive or negative. When performing a reversal, the sign of the changing numbers changes too. For example, after the reversal $\rho (i, j)$,

$$\begin{aligned}{}[\pi (1), ..., \pi (i-1), \pi (i), ..., \pi (j), \pi (j+1) ..., \pi (N)] \end{aligned}$$

becomes

$$\begin{aligned}{}[\pi (1), ..., \pi (i-1), \underline{-\pi (j), ..., -\pi (i)}, \pi (j+1) ..., \pi (N)]. \end{aligned}$$

The burnt pancake problem is the signed version of the pancake problem. In the burnt pancake problem, the pancakes are burnt on one side, and a flip performs the reversal and changes the burnt side. The goal is to reach the sorted stack with all pancakes having their burnt side down.

In the literature, the permutations are often extended with two numbers, $N+1$ after $\pi (N)$, and 0 before $\pi (1)$, and the extended representation of permutation $\pi$ is

$$\begin{aligned}{}[0, \pi (1), ..., \pi (N), N+1]. \end{aligned}$$

The reversal distance of a permutation $\pi$ is the length of the shortest sequence of reversals that sorts the permutation.

A basic and central concept in SBR problems is the breakpoint. For $1\le i \le N+1$, a breakpoint is situated between i and $i-1$ when $|\pi (i)-\pi (i-1)|\ne 1$. In the following, $\#bp$ is the number of breakpoints. Since each breakpoint must be removed to obtain the identity permutation, and since one reversal removes at most one breakpoint, $\#bp$ is a lower bound of the reversal distance. In the planning context, $\#bp$ is a simple and admissible heuristic. In the pancake problem, the possible breakpoint between the top pancake and above is not taken into account. In the signed permutation problem or in the burnt pancake problem a breakpoint is situated between i and $i-1$ when $\pi (i)-\pi (i-1)\ne 1$.

3 Related Work

Since the four domains are closely linked, this section presents them in order: signed permutation, unsigned permutation, unburnt pancakes, and burnt pancakes.

3.1 Signed Permutations

The best overview of the genome rearrangement problem to begin with is by Hayes [24]. Since the genes are signed, the genome rearrangement problem is mainly connected with the signed permutation problem, but also to the unsigned permutation problem. In 1993, Bafna and Pevzner [4] introduced the cycle graph. In 1995, Hannenhalli and Pevzner [23] devised the first polynomial-time algorithm for signed permutations. Its complexity was in $O(n^4)$. The authors introduced the breakpoint graph, and the so called hurdles. This work is the reference. The follow up consists in several refinements.

In 1996, Berman and Hannenhalli [6], and Kaplan et al. [27] in 1998, enhanced the result with an algorithm whose complexity was in $O(n^2)$. The concept of fortress was new. In 2001, Bader and colleagues [3] found out an algorithm that finds the reversal distance in O(n), but without giving the optimal reversal sequence. In 2002, GRIMM [39], a web site, was developed to implement the above theories. In 2003, [28] described efficient data structures to cope with the problem. Then, in 2005, Anne Bergeron [5] introduced a simple and self-contained theory, which does not use the complexities of the previous algorithms, and that solves signed permutation problems in quadratic time as well. In 2006, [37, 38] are subquadratic improvements.

3.2 Unsigned Permutations

The basic work in the unsigned permutation problem is [29] in 1992, by Kececioglu and Sanker. This problem was proved to be NP-hard [12] by Caprara in 1997. In 1998, Christie [16] described the 3/2-approximation algorithm. Reversal corresponding to red nodes are relevant. Furthermore, the Christie’s thesis [17] described many approaches for other classes of permutation problems. In 1999 and 2001, [7, 8] contain complexity results. In 2003, [2, 36] describe evolutionary approaches to the unsigned permutation problem. Particularly, the work of Auyeung and Abraham [2], performed in 2003, consists in finding out the best signature of an unsigned problem, with a genetic algorithm. The best signature is the signature such that the signed permutation reversal distance is minimal. Computing this distance is performed in linear time [3].

3.3 Unburnt Pancakes

The unburnt pancake problem is the most difficult of the four domains [11]. Related work focused on the diameter of the pancake graph. In 2004, a pancake challenge was set up. Tomas Rokicki won the challenge and gave explanations to solve and generate difficult pancake problems [34]. Fischer and Ginzinger published their 2-approximation algorithm [21].

Bounds on the Diameter. A focus is to bound the diameter of the graph of the problem in N the size of the pancake stack. The first bounds on the pancake problem diameter were found by Gates and Papadimitriou in 1979 [22]: $(5n+5)/3$ is the upper bound and (17/16)n is the lower bound. To prove the upper bound, [22] exhibits an algorithm with several cases. They count the number of actions corresponding to each case and obtain inequalities. They formulate a linear program whose solution proves the upper bound. To prove the lower bound, they exhibit a length-8 elementary permutation that can be used to build length-n permutations with solutions of length (18/16)n on average but bounded by below by (17/16)n. The Gates and Papadimitriou’s sequence is

$$\begin{aligned} GP = [1, 7, 5, 3, 6, 4, 2, 8]. \end{aligned}$$

The (15/14)n lower bound was found by Heydari and Sudborough in 1997 [26].

In 2006, the diameter of the 17-pancake graph [1] was computed. In 2009, a new upper bound was found on the diameter: (18/11)n [15]. In 2010, in the planning context, the breakpoint heuristic $\#bp$ was explicitly used in a depth-first-search [25]. In 2011, [18] Josef Cibulka showed that 17n/12 flips were necessary to sort stacks of unburnt pancakes on average over the stacks of size n. Josef Cibulka mentioned a list of interesting concepts: deepness, surfaceness, biggest-well-placed, second-biggest-well-placed, smallest-not-on-top.

The 2004 Pancake Challenge. In 2004, a pancake challenge was organized to focus on the resolution of specific problems. In a first stage, the entrants had to submit pancake problems. In the second stage, the entrants had to solve the submitted problems. The entry of the winner of the pancake challenge was the one of Tomas Rokicki [34]. Its entry is described and gives really interesting ideas.

The Inverse Problem and Backward Solutions. Considering $\pi ^{-1}$ the inverse permutation of the original problem $\pi$ can be helpful. For example, if

$$\begin{aligned} \pi = [ 5, 3, 6, 1, 4, 2] \end{aligned}$$

then

$$\begin{aligned} \pi ^{-1} = [4, 6, 2, 5, 1, 3]. \end{aligned}$$

$\pi ^{-1}$ and $\pi$ correspond to two different problems. The one is the forward problem yielding a forward solution, and the other is the backward problem yielding a backward solution (BS). Because $\pi \pi ^{-1}=Id$, the backward solution is the reverse sequence of the forward solution. The enhancement consists in solving the two problems simultaneously and comparing the lengths of the two solutions, and comparing the times to get them. We call it the BS enhancement. For IDDFS, the two solutions are optimal and share the same length, but the times to solve them can be very different. For MCS or approximate algorithms, the lengths of the two sequences can be different, and the idea consists in keeping the shortest solution. BS works in practice. See Table 3 compared to Table 2.

Difficult Positions. In the diameter estimation context, Tomas Rokicki exhibited two elementary sequences:

$$\begin{aligned} S5 = [1, 3, 5, 2, 4] \end{aligned}$$

and

$$\begin{aligned} L9 = [1, 5, 8, 3, 6, 9, 4, 7, 2]. \end{aligned}$$

Then, he built L9-based (resp. S5-based) permutations by repeating the L9 (resp. S5) permutation shifted by 9 (resp. by 5). For example,

$$\begin{aligned} L9(2) = [1, 5, 8, 3, 6, 9, 4, 7, 2, 10, 14, 17, 12, 15, 18, 13, 16, 11]. \end{aligned}$$

These sequences L9(x) and S5(y) were used to attempt to prove a 11/10 ratio lower bound on the diameter. Unfortunately, this approach did not work. However, these ad hoc sequences are hard to solve, and we consider them as hard problems in the following.

The 2-Approximation Algorithm of Fischer and Ginzinger. Fischer and Ginzinger designed FG, an algorithm that is a 2-approximation polynomial algorithm [21]. It means that the length $L_{FG}$ of the solution found by FG is inferior to two times the length of the optimal solution. Since the best lower bound known today is the number of breakpoints $\#bp$, it means that $L_{FG}$ is proved to be inferior to $2\times \#bp$. In practice, Fischer and Ginzinger mention an approximation ratio $Rapprox=1.22$. The idea is to classify moves in four types. Type 1 moves are the ones that remove a breakpoint in one move. Type 2 and type 3 moves lead a pancake to the top of the stack so as to move it to a correct place at the next move. Type 4 moves correspond to the other cases. Fischer and Ginzinger proves that type 2, 3, 4 moves removes a breakpoint in less than 2 moves, and that type 1 moves remove a breakpoint in one move.

Pancake Flipping Is Hard. In 2012, Laurent Bulteau and his colleagues proved that the pancake flipping problem is NP-hard [10, 11]. He did this by exhibiting a polynomial algorithm that transforms a pancake problem into a SAT problem and vice-versa. He gave an important clue to solve the pancake problem. He considered sequence of type 1 moves only, i.e. moves removing one breakpoint. He defined efficiently sorted permutations, i.e. permutations that can be sorted by type 1 moves, or “efficient” moves. He defined deadlock permutations without type 1 move. A sequence of type 1 moves reaches either the identity permutation and the permutation is efficiently sorted, or deadlock permutations only, and the permutation is not efficiently sorted. To see whether a permutation is efficiently sortable, a binary tree must be developed. Bulteau made a polynomial correspondence between the efficiently sortable permutation problem and the SAT problem, proving by this translation that the former problem is NP-hard.

Miscellaneous. [33] contains results about the genus of pancake network.

3.4 Burnt Pancakes

Here again, the focus was to bound the diameter too. In 1995, the first bounds on the diameter and a conjecture [19] were presented: 3n/2 is a lower bound and $2(n-1)$ a upper bound. The second bounds on the diameter were proved in 1997 [26]. A polynomial-time algorithm on “simple” burnt pancake problems [31] was published in 2011. In 2011, Josef Cibulka showed that 7n/4 flips were necessary to sort stacks of burnt pancakes on average over the stacks of size n [18]. He also disproved the conjecture by Cohen and Blum [19]. Josef Cibulka mentioned interesting concepts: anti-adjacency and clan.

4 Our Work

First, this section presents the domain-independent algorithms used in our work. Secondly, it presents the domain dependent algorithms designed in the purpose of our work. Thirdly, it presents the settings of the experiments. Then, this section yields the results of the experiments in order.

4.1 Domain Independent Algorithms

This section describes the algorithms we used to solve pancake problems as efficiently as possible. There are two basic and general algorithms:

• Iterative Deepening Depth-First Search (IDDFS) [30],

• Monte-Carlo Search (MCS) [13].

We consider IDDFS as an exponential-time algorithm in N [30]. When it completes, the solution found is optimal. However, for N superior to a threshold, IDDFS needs to much time, and becomes useless actually. However, before completion, IDDFS yields a lower bound on the optimal length.

MCS [13] is a simulation-based algorithm that gave very good results in various domains such as general game playing [32], expression discovery [14], morpion solitaire [35], weak Schur numbers [20] and cooperative path-finding [9]. MCS is used with a level L. At any time, MCS stores its best sequence found so far, thus it yields an upper bound on the optimal solution. When used at a given level L, MCS is a polynomial-time algorithm in N. Let assume that the level 0 simulations are polynomial-time algorithms. Let $T_0$ be the time used to perform a complete level 0 simulations. Let us bound $T_1$ the time to complete a level 1 MCS simulation. To move one step ahead in a level 1 simulation, MCS launches at most N level 0 simulations, which costs $N\times T_0$. Since the length of level 0 simulation is bounded by 2N, we have $T_1\le 2N^2 T_0$. If $T_0$ is polynomial in N then $T_1$ is polynomial as well. By induction, a level L MCS is polynomial-time. The higher L, the higher the polynomial degree.

The threshold effect observed for IDDFS does not appear for a polynomial-time algorithm. If you obtain solutions for N in time T, and if d is the degree of the polynomial, you may obtain solutions for $N+1$ in time $T\times (N+1)^d/N^d$ which is just a little bit more expensive than T. Therefore, we get two tools to work with: one is costly but optimal when it completes, IDDFS, and the other one is approximate but its cost is polynomial-time, MCS.

4.2 Domain Dependent Algorithms

We have designed several pancake problem dependent algorithms: Efficient Sort (EffSort), Alternate Sort (AltSort), Basic Random Efficient algorithm (BREF), Fischer and Ginzinger algorithm (FG) [21], Fixed-Depth Efficient Sort (FDEffSort), Fixed-Depth Alternate Sort (FDAltSort). We have implemented each of them and we describe them briefly here.

Since a position has at most two efficient moves, EffSort searches within a binary tree to determine whether a permutation is efficiently sortable [11] or not. If the permutation is efficiently sortable, the sequence of efficient moves is output, and the output permutation is the identity. Otherwise, the longest sequence of efficient moves is output, and the output permutation is a deadlock (i.e. a permutation without efficient move).

When a position is a deadlock, the solver has to perform an inefficient move, i.e. a move that does not lower $\#bp$. A waste move is a move that keeps the $\#bp$ constant. We define two kinds or waste moves: hard or soft. A waste move is hard if it creates a breakpoint while removing another one. A waste move is soft otherwise (the set of breakpoints is unchanged). We define a destroying move as a move that increases $\#bp$.

We designed AltSort. While the output permutation is not sorted, AltSort iteratively calls EffSort and performs a soft waste move if the output permutation is a deadlock. When EffSort is successful, AltSort stops. AltSort and EffSort are inferior to IDDFS. They are exponential time algorithms.

We designed BREF that iteratively chooses and performs an efficient move if possible. A position may have 0, 1 or 2 efficient moves. On a position with one efficient move, this move is selected with probability 1. On a position with two efficient moves, one of them is selected with probability 0.5. Otherwise, BREF chooses and performs a soft waste move defined above. Most of the times, a position without efficient moves has a lot of soft waste moves available. In this case, the move is chosen at random with uniform probability. At the end of a simulation, the reward is the length of the simulation. BREF is a randomized version of AltSort. BREF and FG are polynomial-time algorithms. They can serve as level 0 simulation for MCS.

FDEffSort is the fixed-depth version of EffSort. With depth D, FDEffSort becomes a polynomial-time algorithm. FDAltSort is the version of AltSort using FDEffSort. FDAltSort is a polynomial-time algorithm. It can be used as a level 0 simulation for MCS.

4.3 Experimental Settings

The experiments show the effect of using:

• IDDFS or MCS,

• FG and BREF within MCS,

• backward solutions BS in addition to original solutions,

• FDAltSort within MCS.

There are different classes of test positions: positions randomly generated for a given size, and difficult positions mentioned by related work, mainly [22, 26, 34]. IDDFS may easily solve easy positions of size 60 randomly generated in a few seconds. However, IDDFS cannot solve some hard positions of size 30. Whatever the size and the problem difficulty, MCS always finds a preliminary solution quickly. This solution is refined as time goes on to become near-optimal or optimal.

We mention three indicators to evaluate our algorithms.

• Finding the minimal length Lmin of an optimal solution for a given problem.

• Finding Rapprox as low as possible with a polynomial time algorithm averaged over a set of 100 problems.

• Limiting the running time of an experiment with 100 problems to one or two hours.

Rapprox is the ratio of the length L of the actual solution found over Lmin. Since Lmin is unknown in practice, Lmin is replaced by $\#bp$. $Rapprox=L/\#bp$. The standard deviation of the Rapprox value that we observed for one problem generated at random is roughly 0.05. The two-sigma rule says that the standard deviation over 100 problems is $0.05 \times 2 / 10 = 0.01$. The values of Rapprox given below are 0.01 correct with probability 0.95. On average, the time to solve one problem is inferior to one minute.

Table 1. IDDFS: In practice, how Rapprox varies in N. L is the average length of solutions. T is the average time in seconds to sort one stack.

4.4 MCS and IDDFS

The first experiment consists in assessing IDDFS and MCS under reasonable time constraints: at most one hour. MCS uses BREF as level 0 simulations. When using IDDFS, Table 1 shows how Rapprox varies in N. First, although IDDFS gives an optimal result, Rapprox is not 1. This happens because $\#bp$ is not the length of optimal solutions but a lower bound only. Secondly, Table 1 shows that IDDFS cannot give results in reasonable time for $N>64$. For $N=30$, IDDFS does not solve some difficult positions in less than few hours. Thirdly, Table 2 shows how Rapprox varies in N and in level with MCS. Level 0 simulations can be launched easily with $N=256$. Rapprox is 1.30 for level 0 simulations, 1.28 for level 1 simulations. Then, as the level increases, Rapprox decreases. Level 2 simulations yields $Rapprox=1.22$ which equals the value mentioned in [21]. For higher levels, $Rapprox=1.10$ showing that high levels of MCS give good results in reasonable time, and that MCS is a viable alternative to IDDFS even for difficult positions. When compared to $Rapprox=1.22$ of [21], $Rapprox=1.08$ is a first breakthrough.

Table 2. MCS+BREF: How Rapprox varies in N and Level. L(x) is the average length of solutions at level x. T(x) is the average time in seconds to sort one stack at level x.

Table 3. How Rapprox varies in N and MCS level with the trick of Backward Solutions (BS). L(x) is the average length of solutions at level x. T(x) is the average time in seconds to sort one stack at level x.

4.5 MCS + BREF + BS

Table 3 shows how Rapprox varies in N and in the MCS level when level 0 simulations are the best of one forward simulation and one backward simulation. We call this the BS enhancement. Table 3 must be compared to Table 2. One can observe that the BS enhancement is effective at level 0 indeed, and also at level 1 and level 2. However, its effect is less visible at higher levels of MCS: $Rapprox=1.09$.

4.6 MCS + FG + BS

Table 4 shows how Rapprox varies in N and in the MCS level when level 0 simulations are the forward and the backward FG simulations. So as to see the effect of using FG instead of BREF in MCS, Table 4 must be compared to Table 3. First, the comparison shows that FG is worse than BREF for level 0. FG is on a par with BREF for level 1. For level 2 and higher levels, FG surpasses BREF: $Rapprox=1.05$.

Table 4. How Rapprox varies in N and MCS level with simulations being FG with the trick of Backward Solutions (BS). L(x) is the average length of solutions at level x. T(x) is the average time in seconds to sort one stack at level x.

Table 5. How Rapprox varies in N and MCS level with simulations being randomized FG with the trick of Backward Solutions (BS). L(x) is the average length of solutions at level x. T(x) is the average time in seconds to sort one stack at level x.

Table 5 shows how Rapprox varies in N and in the MCS level when level 0 simulations are the forward and the backward randomized FG. Randomized FG works as follows. If type 1 moves exist, one of them is chosen at random. Otherwise, if type 2 moves exist, one of them is chosen at random and so on. So as to see the effect of using randomized FG instead of FG, Table 5 must be compared to Table 4. As expected and as shown by the R(0) column of Tables 4 and 5, randomized FG yields a worse Rapprox than direct FG. Randomized FG is worse than direct FG for level 1. However, when used in higher levels of MCS, Rapprox with the randomized version is slightly inferior to Rapprox with the direct version. At level 4, MCS gives $Rapprox=1.05$ when using randomized version of FG as basic simulations.

4.7 MCS + FDAltSort

In a preliminary experiment, not reported here, we assessed MCS using AltSort directly as level 0 simulations. This did not work well on hard positions because AltSort is not a polynomial-time algorithm. Consequently some simulations did not complete quickly. We had to limit the depth at which EffSort searches and we had to create FDAltSort. (FDEffSort determines whether a permutation is efficiently sortable at depth D). FDAltSort can be used as a level 0 simulation in MCS. We assessed MCS using FDAltSort at depth $D=10$. For each level, Table 6 displays the variations of Rapprox in N. These results must be compared to the results of Table 5. At level 0, FDAltSort is better than randomized FG and on a par with FG. At level 1, level 2 and level 3, FDAltSort is better than the other algorithms. Launching FDAltSort at level 4 was not interesting. However, Rapprox achieves 1.04 at its minimal value. Furthermore, the good point here is that the results are obtained for pancake stack sizes going up to 512 instead of 256 before, and with $Rapprox=1.20$. This is a significant improvement. FDAltSort as simulations are much more efficient than FG or BREF were. We also tried to incorporate the BS enhancement, but the results were worse.

Table 6. How Rapprox varies in N and MCS level with simulations being FDAltSort at depth $D=10$. L(x) is the average length of solutions at level x. T(x) is the average time in seconds to sort one stack at level x.

5 Conclusion and Future Work

In this work, we summed up the state-of-the-art of the permutation sorting by reversals domain. This domain was studied in depth by researches on the genome. It remains fascinating as underlined by Hayes [24]. The unsigned permutation domain is hard [12] but the signed permutation domain has polynomial-time solver [23]. The pancake problem was less studied. The unburnt pancake problem is difficult [11] while the complexity of the burnt pancake is unknown.

Our contribution is experimental. It shows how MCS extends the results obtained by IDDFS on unburnt pancake stacks. On the one hand, IDDFS can solve some pancake stacks of size 60 [25] in a few minutes but cannot solve some specific hard pancake stacks [34] of size 30 only. On the other hand, MCS can solve pancake stacks of significantly higher sizes and the hard pancake stacks of size 30 not solved by IDDFS. Practically, our MCS solver solves pancake stacks of size up to 512 with a 1.20 R-approximation, under the best configuration. MCS may use BREF, FG or FDAltSort with results that are approximately equal in terms of running time and Rapprox value. Practically, we observed that MCS approximates the best solutions with a Rapprox ratio of 1.04 for size up to 64, which is significantly better than the 1.22 value of [21]. Our MCS solver solves pancake stacks of size 128 or 256 with a R-approximation value roughly situated between 1.10 and 1.25.

In a near future, we want to study the burnt pancake problem. Furthermore, the burnt pancake problem is linked to the unburnt pancake problem. A block of sorted unburnt pancakes can be replaced by one burnt pancake, and the unburnt pancake problem becomes a mixed pancake problem. Solutions to burnt pancake problems could be used to solve ending unburnt pancake problems. We want to investigate in this direction.

To date, the number of breakpoints remains the simplest and the most efficient heuristic to bound the optimal solution length by below. However, this admissible heuristic should be refined to better approximate the optimal solution length. Some hard problems - or stacks - are hard because they contain substacks whose solution lengths are strictly higher than the number of breakpoints. As the permutation problems contain concepts such as hurdles or fortresses [6], and as shown by the work of Josef Cibulka on burnt pancakes, we have to find out the corresponding concepts to design appropriate heuristic functions for the pancake problems.