Comparing Modeling Approaches for the Multi-Level Capacitated Lot-Sizing and Scheduling Problem

Abstract

Determining lot sizes is an essential step during the material requirements planning phase influencing total production cost and total throughput time of a production system. It is well-known that lot-sizing and scheduling decisions are intertwined. Neglecting this relation, as it is done in the classical hierarchical planning approach, leads to inefficient and sometimes infeasible plans. In this work we compare different approaches for integrating the lot-sizing and the scheduling decisions in multi-stage systems. We show their abilities and limitations in describing relevant aspects of a production environment. By applying the models to benchmark instances we analyze their computational behavior. The structural and numerical comparisons show that there are considerable differences between the approaches although all models aim to describe the same planning problem. The results provide a guideline for selecting the right modeling approach for different planning situations.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In the recent years a trend towards integrating multiple levels of the classical hierarchical and sequential planning concept of the production planning and control systems into a single planning step can be observed. This trend results in a demand for new modeling concepts that include lot-sizing as well as capacity planning and scheduling decisions within the material requirements planning. That means planning models are needed which respect the relations between raw materials, intermediate items, subassemblies, and final products (given by the bill-of-materials), capacity restrictions, and timing of production lots simultaneously. Of course, the price to pay for the increased complexity and more detailed models is that (1) the models are usually tailored to a specific situation and they are not general-purpose anymore, and (2) the computational effort to solve these models is increasing despite the technological progress in hardware and software.

In this paper we have a more detailed look on the different model classes discussed in the research literature regarding the aforementioned aspects of tailored models and computational effort. In particular, we investigate models for the capacitated multi-level lot-sizing and scheduling problem and analyze the underlying assumptions and the limitations of those models and their computational properties using a set of benchmark instances.

The main classification of lot-sizing models for dynamic deterministic demand is related to the underlying time structure. The small-bucket models are characterized by a partitioning of the planning horizon into short time buckets (micro-periods) during which only a single setup operation on a machine is allowed. This class of models is solving simultaneously the lot-sizing and the scheduling problem. Big-bucket models use quite long time periods (macro-periods) during which several production lots can be processed on a machine, but each product only once. Here the scheduling aspect is not considered within the basic model concept. Surprisingly, the core of the research literature on multi-level lot-sizing deals with big-bucket formulations (cf. a recent review on big-bucket models by Buschkühl et al. 2010). Nevertheless, there are recent multi-level formulations based on small-bucket models, which we will consider in our study. The goal of this paper is to analyze those different modeling approaches. Hence, the contribution of this paper is twofold:

• We show and compare the limitations of different modeling concepts due to the underlying assumptions. These results will help to select an appropriate modeling approach for a specific situation.

• We provide a numerical comparison of all models in order to underline the limitations and differences discussed in the previous point and to determine more promising model approaches regarding the computational tractability using a standard optimization software.

The paper is organized as follows: in Sect. 2 the relevant literature is discussed. In Sect. 3 the different models are presented and compared regarding their internal structure, whereas in Sect. 4 the computational comparison is provided. Section 5 concludes the paper summarizing the major findings of this study.

2 Literature Review

All basic lot-sizing models for dynamic demand — based on the formulation introduced by Wagner and Whitin (1958) — are driven by the trade-off between the setup and holding costs. Introducing capacity limitations and considering several products simultaneously led to the capacitated lot-sizing problem (CLSP), which Bitran and Yanasse (1982) have shown to be NP-hard. Billington et al. (1983) were among the first researches extending the big-bucket formulation of the CLSP towards the multi-level situation of the material requirements planning which led to the multi-level capacitated lot-sizing problem (MLCLSP). The disregard of the scheduling problem in connection with a multi-level structure in the MLCLSP potentially leads to capacity and inventory problems as shown by Almeder et al. (2015). Therefore, the models have to be extended either considering a one period long delay between the production of a predecessor and a successor item, or allowing a detailed sequencing of lots within a period. The first approach has been used by many researchers (cf. Buschkühl et al. 2010) but it produces unnecessary high work-in-process levels (cf. Almeder et al. 2015). The latter approach is rather complex. A very detailed non-linear model was formulated by Fandel and Stammen-Hegene (2006), but this model is beyond any possibility to be solved. A formulation as a mixed integer linear program by Almeder et al. (2015) is used in this paper.

The continuous setup and lot-sizing problem (CSLP) and the proportional lot-sizing and scheduling problem (PLSP) are the most prominent model approaches in the class of small-bucket problems (cf. Drexl and Kimms 1997). An extension to multi-level systems is straight forward. Nevertheless, not many researchers have been working on this multi-level extension. Stadtler (2011) formulated a multi-level PLSP model which allows the production of a predecessor and a successor product within the same time period. But he restricts his model to the rather simple single-machine case.

Seeanner and Meyr (2013) extended the general lot-sizing and scheduling problem (GLSP) to the multi-level multi-machine case. The GLSP is in some sense a hybrid model concept combining small-bucket and big-bucket ideas. The planning horizon is divided into longer time periods (big buckets), but each such period is subdivided into several smaller periods (small buckets) of variable length. Another approach to the simultaneous lot-sizing and scheduling problem in a multi-level system described in the research literature is a scheduling based one. Kim et al. (2008) proposed an integrated model, where each demand is transformed into production jobs for the requested product and all its predecessors. The resulting scheduling problem is solved using a genetic algorithm. The main criticism might be that this approach does not consider lot-sizing possibilities at their full extent. In fact, lots are formed by combining different (subsequent) demands of the same item, but no demand is split into several lots. Dauzère-Pérès and Lasserre (2002) enhanced a multi-level lot-sizing problem by special scheduling constraints as a substitute for the capacity constraints. They do not consider any setup processes and do not solve the model as an integrated one, but split it into a lot-sizing and a capacity refining step.

3 Model Formulations

3.1 Overview

In this paper, a comparison of three model classes is conducted. The focus lies on the comparison of deterministic capacitated multi-level lot-sizing problems with dynamic demand, a finite planning horizon and a general product structure. The objective is to minimize the sum of setup and inventory costs.

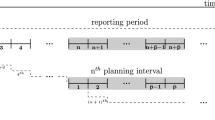
First, the class of small-bucket models is considered. Here the continuous setup lot-sizing problem (MLCSLP) and the proportional lot-sizing problem (MLPLSP) for the multi-level case are analyzed. One of the main disadvantages of these formulations is that they are not adequate for problems where long setup operations occur, as the duration of these operations must not exceed one micro-period. However, enabling multi-period setup operations may cause a substantial increase in model complexity. A recent formulation (MLPLSP _SS ) by Stadtler (2011) is considered in addition, that is built on the MLPLSP and accounts for period overlapping setup times to enable more flexibility in planning. Moreover, Stadtler (2011) assumes a zero lead time offset, whereas for the MLCSLP and the MLPLSP a delay of one micro-period between production of predecessor and successor items is necessary.

The second class reflects the big-bucket models. The basic multi-level capacitated lot-sizing problem (MLCLSP) does not allow to carry over the setup state of a machine from one period to the next one, i.e., in each period a setup is necessary to start production. In order to be consistent and comparable with the small-bucket models, a version with linked lots between periods is used (MLCLSP _L ). Furthermore, two variants presented in Almeder et al. (2015) are considered. One covers the lot-streaming case (referred to as MLCLSP _LS ) and the other allows production in batches (MLCLSP _BS ), where the production of a batch has to be finished before the items can be used as input for the production of successor items.

The third class is the general lot-sizing and scheduling problem for multiple stages (GLSPMS) proposed by Seeanner and Meyr (2013) with their underlying two-stage time structure. The model accounts for both, setup operation and production quantity splitting over consecutive variable micro-periods. Quantity splitting means that the whole production amount of one micro-period is virtually split into two parts, one is available to subsequent processing in the on-going micro-period and the other in the following micro-period at the earliest.

In order to keep this paper comprehensive we refer the reader for detailed model descriptions for MLPLSP _SS , MLCLSP _BS , MLCLSP _LS , and MLGLSP to the respective literature (Stadtler 2011; Almeder et al. 2015; Seeanner and Meyr 2013).

3.2 Basic Notation

Table 1

3.3 Small-Bucket Models

We use the MLCSLP and MLPLSP formulations proposed by Kimms and Drexl (1998) and incorporate setup times. While in the MLCSLP only one setup is allowed to be performed at the beginning of each micro-period, in the MLPLSP this very restrictive assumption is relaxed by allowing the setup to be performed at any time within a period and therefore inducing the possibility to produce two distinct items within one micro-period. Hence, these models implicitly determine also a production schedule. In order to enable a numerical comparison between the micro-period and macro-period structure, a constant number of micro-periods of the same length are embedded into macro-periods. Holding cost and demand will only occur in the last micro-period of a macro-period (if $s \in \Phi ^{t}$). The model formulation for the MLCSLP reads:

$$\displaystyle{ min\sum _{i,s}c_{i} \cdot T_{is} +\sum _{i,s\in \Phi ^{t}}h_{i} \cdot I_{is} }$$

(1)

subject to

$$\displaystyle{ I_{is} = I_{i(s-1)} + X_{is} - E_{is} -\sum _{j\in \Gamma (i)}a_{ij} \cdot X_{js}\qquad \forall \;i,s }$$

(2)

$$\displaystyle{ I_{is} \geq \sum _{j\in \Gamma (i)}\sum _{\tau =s+1}^{min[s+l_{i};S]}a_{ ij} \cdot X_{j\tau }\qquad \forall \;i,s = 0,\ldots,S - 1 }$$

(3)

$$\displaystyle{ \sum _{i\in \phi (m)}\alpha _{is} \leq 1\qquad \forall \;m,s }$$

(4)

$$\displaystyle{ T_{is} \geq \alpha _{is} -\alpha _{i(s-1)}\qquad \forall \;i,s }$$

(5)

$$\displaystyle{ p_{i} \cdot X_{is} + s_{i} \cdot T_{is} \leq L_{ms} \cdot \alpha _{is}\qquad \forall \;i,s }$$

(6)

$$\displaystyle{ I_{is},X_{is},T_{is} \geq 0,\alpha _{is} \in \{ 0,1\}\qquad \forall \;i,s }$$

(7)

The objective to be minimized consists of setup and holding cost (1). External and internal demands have to be fulfilled without delay which is shown by the inventory balance equations (2). Lead times between predecessors and successors are incorporated by constraints (3). Constraints (4) enforce a unique setup state and constraints (5) describe the setup decisions. Either a setup for i takes place in s (T _is  = 1) or a setup state for i is carried over from s − 1 to s. Constraints (6) constitute the capacity restrictions and finally, (7) are the non-negativity constraints and binary variables restrictions. Substituting (6) by constraints (8), describing a setup to be made at any time within a micro-period and new capacity constraints (9) leads to the MLPLSP:

$$\displaystyle{ p_{i} \cdot X_{is} \leq L_{ms} \cdot (\alpha _{i(s-1)} +\alpha _{is})\qquad \forall \;i,s }$$

(8)

$$\displaystyle{ \sum _{i\in \phi (m)}(\,p_{i} \cdot X_{is} + s_{i} \cdot T_{is}) \leq L_{ms}\qquad \forall \;m,s }$$

(9)

A major design decision when employing small-bucket models is the appropriate number of micro-periods for each macro-period. The appropriate number depends on several circumstances: How many distinct items are to be produced, is there a lead time to be considered, of how many stages consists the production process, does the length of the shortest period at least correspond to the length of the longest setup operation? If too few micro-periods are embedded into a macro-period, the detailed planning offered by the model is not exploited and finding a feasible solution may become quite difficult. On the other hand, a very large number of micro-periods leads to very long computational times for real-world instances (cf. Seeanner and Meyr 2013).

The two models above consider a lead time of at least one micro-period. However, situations may occur where even one micro-period lead time is not realistic. Stadtler (2011) extended the single machine PLSP to a multi-level single machine PLSP with zero lead time (MLPLSP _SS ) that accounts for the problem arising in a specific pharmaceutical company. In order to make this model comparable with the other models analyzed, we adapted the original model to the multi-machine case by defining a set of products i ∈ φ(m) assigned to a machine m.

3.4 Big-Bucket Models (MLCLSP)

The second class of lot-sizing models we are discussing are the big-bucket models, where the planning horizon is divided into a few large macro-periods. The MLCLSP by Billington et al. (1983) has some drawbacks compared with the small-bucket models. The scheduling is completely neglected in the MLCLSP. Instead, it is assumed that the production scheduling is carried out in an additional subsequent planning level. This causes serious feasibility problems in multi-level planning when coordination between the production stages is neglected (cf. Almeder et al. 2015). Considering a full macro-period lead time¹ allows to generate feasible production plans, but it leads to overestimated cycle times and huge work-in-process (WIP).

Furthermore, the classical MLCLSP does not preserve the setup state of a machine from one period to the next one, i.e., if the same product is produced at the end of a period and at the beginning of the next period an additional setup is necessary. Hence, a logical extension of the MLCLSP is to introduce so-called linked lots, denoted by MLCLSP _L (cf. Suerie and Stadtler 2003; Haase 1994). We will focus on a formulation by Sahling et al. (2009) that accounts for setup carryovers over multiple periods and lead times.

Since we deal with macro-periods in the MLCLSP, we replace the index s by t for macro-periods. In addition to the variables listed in the basic notation table in Sect. 3.2, a variable for the initial inventory level $\hat{y_{i}}$ and an auxiliary variable v _mt is used in the model formulation.

The objective function of the MLCLSP _L reads:

$$\displaystyle{ min\sum _{i,t}(c_{i} \cdot (\alpha _{it} - T_{it}) + h_{i} \cdot I_{it}) }$$

(10)

subject to:

$$\displaystyle{ I_{i(t-1)} + X_{it} -\sum _{j\in \Gamma (i)}a_{ij} \cdot X_{j(t+1)} - I_{it} = E_{it}\qquad \forall \;i,t = 2,\ldots,T - 1 }$$

(11)

$$\displaystyle{ I_{i(T-1)} + X_{iT} - I_{iT} = E_{iT}\qquad \forall \;i }$$

(12)

$$\displaystyle{ \hat{y}_{i} -\sum _{j\in \Gamma (i)}a_{ij} \cdot X_{j1} - I_{i0} = 0\qquad \forall \;i }$$

(13)

$$\displaystyle{ I_{i0} + X_{i1} -\sum _{j\in \Gamma (i)}a_{ij} \cdot X_{j2} - I_{i1} = E_{i1}\qquad \forall \;i }$$

(14)

$$\displaystyle{ \sum _{i}(\,p_{i} \cdot X_{it} + s_{i} \cdot (\alpha _{it} - T_{it})) \leq L_{mt}\qquad \forall \;m,t }$$

(15)

$$\displaystyle{ X_{it} \leq G \cdot \alpha _{it}\qquad \forall \;i,t }$$

(16)

$$\displaystyle{ \sum _{i\in \phi (m)}T_{it} \leq 1\qquad \forall \;m,t }$$

(17)

$$\displaystyle{ T_{it} \leq \alpha _{i(t-1)}\qquad \forall \;i,t }$$

(18)

$$\displaystyle{ T_{it} \leq \alpha _{it}\qquad \forall \;i,t }$$

(19)

$$\displaystyle{ T_{it} + T_{i(t+1)} \leq 1 + v_{mt}\qquad \forall \;m,i \in \phi (m) }$$

(20)

$$\displaystyle{ (\alpha _{it} - T_{it}) + v_{mt} \leq 1\qquad \forall \;i }$$

(21)

$$\displaystyle{ T_{i1} = 0\qquad \forall \;m,i \in \phi (m) }$$

(22)

$$\displaystyle{ I_{it},X_{it},I_{i}^{0},v_{ mt} \geq 0;\;\alpha _{it},T_{it} \in \{ 0,1\}\qquad \forall \;m,i,t }$$

(23)

Constraints (11)–(14) reflect the inventory balance equations where a one macro-period lead time is incorporated to achieve coordination between the production levels. The initial inventory of item i is denoted by $\hat{y}_{i}$. Constraints (15) are again the capacity restrictions enforcing the capacity limits to be kept. Note, that T _it now has a different meaning from the small bucket models discussed above, as it constitutes the setup carry-over variable, so that T _it  = 0 if there is no setup carryover and thus a setup operation for i takes place. A product can only be produced if a machine is in the appropriate setup state (16). For each period and machine at most one setup carryover is allowed (17). The setup carryover itself is described by (18) and (19) stating that a setup carryover is only possible (T _it  = 1) if the resource is set up for item i in both period t and t − 1 (α _it  = 1 and $\alpha _{i,t-1} = 1$). Constraints (20) and (21) model the multi-period setup carryover characteristic of the formulation.

As mentioned earlier, incorporating a full macro-period lead time may result in long cycle times and huge amounts of WIP. Two extensions of the MLCLSP are proposed by Almeder et al. (2015) dealing with the problem of incorporating lead times in the MLCLSP, one based on batch production and the other on lot-streaming. In contrast to the MLCLSP _L , where scheduling is neglected and the small-bucket models, where sequencing is done implicitly, scheduling is done simultaneously to lot-sizing in these MLCLSP extensions. This can be achieved by using a formulation based on models for sequence-dependent setups. Furthermore, the beginning of production of an item i in period t is captured by a continuous decision variable μ _it .

The first model MLCLSP _BS is based on batch production, where a lot of products can only be further processed when the production of the whole lot is finished. At the start of production of item i the whole amount of predecessor j needed for production of i must be available. The second formulation MLCLSP _LS assumes lot-streaming, meaning that each single item produced may be further processed immediately in the next stage without delay times. Strictly speaking, it allows even simultaneous production of predecessors and successors on different machines. However, one might account for a minimum production lead time τ _i that could be added to the starting time μ _it of product i. For both versions the in-period inventory levels are tracked using the new decision variables μ _it . Additional constraints ensure that this in-period inventory does not become negative.

3.5 Mixed Models (GLSPMS)

The last model considered here is the GLSPMS by Seeanner and Meyr (2013), which is an extension to the single-level GLSP introduced by Fleischmann and Meyr (1997).

The main characteristic of this model is the two-level time structure. The external dynamics within a planning horizon are described by demand data and holding cost and are defined on a fixed discrete time frame of a few macro-periods. Each macro-period t is split into a predetermined number of non-overlapping micro-periods $s \in \Phi ^{t}$. These micro-periods are in contrast to the pure small-bucket models of variable length depending on the lot sizes and the setup operations. Thus, the scheduling problem is solved implicitly by assigning lots to the different micro-periods. In order to enable synchronization over all levels and machines, the GLSPMS enforces the same micro-period structure (i.e. equal starting times and equal length) on all machines. As only one product is allowed to be produced within a micro-period, scheduling is performed by determining the starting times of the variable micro-periods. As in the MLPLSP _SS , in the full variant of GLSPMS, Seeanner and Meyr (2013) split the lot of one micro-period into two parts, one allowed to be further processed in the actual period, the other in the next period at the earliest. In such a way it allows immediate usage of an item for the production of a successor without any delay.

3.6 Comparison of Model Characteristics

In Table 1 some of the major characteristics of the discussed models are summarized. One important distinguishing characteristic of the models regards the way to organize synchronization between production stages. Because of their detailed structure, considering a minimum lead time of one micro-period in the MLCSLP and MLPLSP is a good compromise when lot-streaming is not realizable. The MLPLSP _SS allows going beyond this lead time of one micro-period, because it allows the production of predecessor and successor items in the same micro-period, but only if production is in the first and second campaign, respectively. Furthermore, with none of the small-bucket models it is possible to realize a batching constraint, i.e. starting a successor only after the finishing of the complete batch of the predecessor, because usually a production batch lasts for several micro-periods. For the big-bucket models MLCLSP _{L, BS, LS} the picture is clear. Here we have either synchronization via a lead time of one macro-period, a lot-streaming possibility or a batching constraint. The GLSPMS enables partial lot-streaming (only possible where the production rate of the successor is not higher than of the predecessor) as a result of the variable micro-periods and because of the identical structure of these periods on all machines at all different stages.

Table 1 Comparison of model characteristics ($\mathrm{x}/-$ indicates that a feature is present/missing in the respective model; ≈ indicates that a feature is partially considered.)

Regarding the timing of the setup operations only the MLCSLP is quite restrictive, because it allows only setups at the beginning of the fixed micro-periods. All other models have considerably more flexibility. For the MLPLSP it may be at any time within a micro-period, for the MLPLSP _SS and the GLSPMS it is also possible to split setup operations between micro-periods. All big-bucket models as well as the GLSPMS allow setup operations at any time during a macro-period. (Due to the variable micro-period length also the GLSPMS allows this flexibility.)

Considering the possible number of different products and the possible number of setups within a macro-period, there is a notable difference. All small-bucket models allow a setup each micro-period and in the GLSPMS a micro-period can contain two fractions of different setup operations. Hence, it is possible to produce S∕T ($S/T + 1$ for the MLPLSP and MLPLSP _SS ) different lots within a macro-period. These lots might be of different products or of the same products. The big-bucket models allow only a single setup and a single lot for each product per macro-period.

4 Computational Results

4.1 Test Instances

In order to enable a comparison between the models a subset of the class 1 instances from Tempelmeier and Buschkühl (2009) are used. In total we use 480 instances, each representing a problem with 10 products produced on 3 machines in 3 production stages over a planning horizon of 4 macro-periods. The test instances have the following properties:

Product structure: :

general and assembly

Machine assignment: :

cyclic and acyclic

Coefficient of variation (CV) of the demand: :

0.2, 0.5, 0.8

Capacity utilization (CU): :

50, 70, 90 %, increasing and decreasing from the final to the first production stage.

Time-between-orders (TBO): :

1, 2, 4, and varying.

All instances are capacity feasible considering the MLCLSP _L formulation. Due to the complexity of some of the model formulations, it makes no sense to consider bigger instances. Some pretests on a smaller subset of instances have shown that for small-bucket models 5 micro-periods per macro-period provide a good balance between solution quality and computational tractability. All test instances were solved on a INTEL X5570 processor with 4 GB memory and with a Linux operating system using IBM ILOG CPLEX 12.4.

4.2 Results

Table 2 Computational results of all test instances

All test instances were solved using all seven model variants (MLCSLP, MLPLSP, MLPLSP _SS , MLCLSP _L , MLCLSP _BS , MLCLSP _LS and GLSPMS). A maximum runtime of one hour was applied. In Table 2 we report the obtained results. MAPD denotes the mean average percentage deviation of all instances solved with a specific model to the best solution found. In particular, the model which provides the lowest cost for a certain instance is used as the benchmark. MAPD_sc and MAPD_hc are showing the deviation of holding cost and setup cost, respectively. GAP reports the average gap returned by CPLEX after one hour runtime and the row optimal shows the percentage of instances that could be solved to optimality. The final row RT indicates the average run time.

MLCLSP _LS provides in most cases the solution with the lowest cost. This is not surprising, because this model allows simultaneous production of predecessor and successor items and full scheduling flexibility within a macro-period. The small-bucket models are providing results with slightly higher cost, but the cost are decreasing with the additional flexibility when switching from MLCSLP to MLPLSP and to MLPLSP _SS . The results of the MLCLSP _BS indicate that the batching assumption leads to an average cost increase of 9.2 %. Since the MLCLSP _L includes a lead time of one macro-period a lot of additional inventory is necessary such that the total cost increase by 34.1 %. Surprisingly the quality provided by the GLSPMS is between the MLCSLP and the MLPLSP although it provides more flexibility. But this lower quality might be caused by the extraordinary high average gap of 29.6 %. In particular, the computational behavior regarding gap and average runtime is quite similar with two exceptions. MLCLSP _L can be solved for each instance without any problem and GLSPMS cannot be solved for any instance within the time limit.

Table 3 Resulting average GAP and MAPD for different groups of test instances (Bold numbers indicate the lowest gap in the respective column.)

In Table 3 we disaggregate the gap and the MAPD results for different instances classes. The reported gaps show that for all model variants the instances with a general product structure and an acyclic machine assignment are the easiest to solve. This is surprising because an assembly structure where each item has at most one successor should simplify the scheduling problem. The CV has a clear impact on the solvability—the higher the variation, the easier to solve. An explanation might be that for a uniform demand pattern there exist multiple solutions with similar cost which avoid the early pruning of the branch-and-bound tree. Only the GLSPMS is an exception, where the CV seems to have no effect. The TBO aspect has a different effect on the small- and big-bucket models. For the small-bucket models it is better to have a small TBO, i.e. setup costs are small compared to holding cost. For the GLSPMS this effect is quite dramatic. For the MLCLSP _BS and MLCLSP _LS the picture is contrary. Here it seems that a higher TBO leads to easier problems, which is in contrast to the usual findings for lot-sizing problems. When looking at the CU results, the small-bucket models are not affected by a change of the CU, whereas the big-bucket versions behave like expected, namely, they are easier to solve if the CU is low.

The results for the MAPD show that an increased CV reduces the differences between the model variants, but regarding the TBO and CU we cannot identify a clear picture. The results of the MLCLSP _L indicate that neglecting the scheduling aspect leads to worse results, if the problem instance allows a lot of flexibility in the solution, i.e., a low CV, TBO or CU.

5 Conclusions

We have shown various ways, derived from literature, to model a multi-level capacitated lot-sizing and scheduling problem. Although all the models are aiming to solve the same problem, there are substantial differences. The first aspect is the model structure itself. Here we have seen different ways to represent the scheduling and synchronization aspects in the multi-level product structure. This ranges from allowing simultaneous production of predecessor and successor items (MLCLSP _LS ) to batch production, where a lot has to be completed before it can be used for further processing (MLCLSP _L , MLCLSP _BS ). In between there are models with a relation between successor and predecessor which depends on the internal time structure of the model (MLCSLP, MLPLSP, MLPLSP _SS , GLSPMS). Also the timing of setup operations is an issue in most model variants due to the enforced decomposition of the planning horizon into time buckets.

The numerical results have shown, that all models, which solve the full scheduling problem, demand a high computational effort. Nevertheless, it seems that rather complex big-bucket formulations are worth to consider, because of their additional flexibility regarding the timing and their computational tractability. A surprising result is, that the GLSPMS as a flexible small-bucket model drops behind when solving it. Of course, all models provide different solutions and thus also different objective values. This can be seen as measure of flexibility allowed by the model formulation. Summarizing the results it seems that the MLPLSP _SS , the MLCLSP _LS , and the MLCLSP _BS are the most favorable formulations, regarding flexibility, detailed modeling and computational tractability. But still a significant demand of new and fast solution algorithms is given for these complex models in order to be applied to bigger problem instances and probably sometimes to real-world cases.