Interaction-Based Programming in MGS

Abstract

The modeling and simulation of morphogenetic phenomena require to take into account the coupling between the processes that take place in a space and the modification of that space due to those processes, leading to a chicken-and-egg problem. To cope with this issue, we propose to consider a growing structure as the byproduct of a multitude of interactions between its constitutive elements. An interaction-based model of computation relying on spatial relationships is then developed leading to an original style of programming implemented in the MGS programming language. While MGS seems to be at first glance a domain specific programming language, its underlying interaction-based paradigm is also relevant to support the development of generic programming mechanisms. We show how the specification of space independent computations achieves polytypism and we develop a direct interpretation of well-known differential operators in term of data movements.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

13.1 Introduction

The development of the MGS unconventional programming language was driven by a motto: computations are made of local interactions. This approach was motivated by difficulties encountered in the modeling and simulation of morphogenetic processes [13, 16] where the construction of an organism in the course of time, from a germ cell to a complete organism, is achieved through a multitude of local interactions between its constitutive elements. In this kind of systems, the spatial structure varies over time and must be calculated in conjunction with the state of the system. As an example, consider the diffusion in a growing medium of a morphogen that controls the speed of growth of this medium. The coupling between the processes that take place in a space and the modification of the space due to the processes leads to a chicken-and-egg problem: what comes first?

Recently, a new approach has emerged in theoretical physics to overcome the same difficulty in general relativity where the mass moves along a space-time geodesic while space-time geometry is defined by the distribution of mass. In this approach, space is not seen as a primitive structure but rather as a byproduct of the causal relationships induced by the interaction between the entities of the system.

Contributions

In this chapter, we propose to reconstruct the MGS mechanisms of computation from this point of view. This abstract approach is illustrated in Sect. 13.2 by a down-to-earth example, the bubble sort, and we show how the basic interactions at work (the swap of two adjacent elements) build an explicit spatial structure (a linear space). Our motivation in the development of this example, is to make explicit the basic ingredient of a generic notion of interaction: interactions define a neighborhood and, from neighbor to neighbor, a global shape emerges. This leads naturally to use topological tools to describe computations in MGS.

Section 13.3 presents the notion of topological rewriting and illustrates this notion on various paradigmatic examples of morphogenesis. These examples are only sketched to show the expected relevance of the MGS computational mechanisms in the simulation of physical or biological systems.

In the Sect. 13.4, we show that these computational mechanisms are also relevant to support the development of generic programming mechanisms, not necessarily related to natural computations. Here we address genericity from the point of view of polytypism, a notion initially developed in functional programming.

The MGS approach of polytypism boils down to the specification of patterns of data traversals. In Sect. 13.5, we show these patterns of data movements at work in the interpretation of differential operators. This interpretation gives a computational content to well-known differential operators subsuming discrete and continuous computations. As an illustration, we provide a generic formulation that encompasses discrete and continuous equations of diffusion that can be used in hybrid diffusion. The section ends by sketching how sorting can be achieved by a set of differential equations.

13.2 From Physics to Computation: Interactions

The simulation of morphogenetic systems leads to a chicken-and-egg situation between the processes taking place in a space and the modification of the space due to these processes. This problem has been pointed out by A. Turing in his seminal study of morphogenesis [54].

In general relativity, a similar issue occurs where the mass moves along geodesics while spacial geometry is defined by the distribution of the mass. Physicists achieved to deal with the interdependence between mass and space through the concept of causality in a space-time structure. In this section, we propose to transpose this idea into computations.

13.2.1 Spatial Structure, Causality and Interaction

Space-Time and Causality

To address the interdependence problem, a classical solution consists in considering a space-time as a manifold M endowed with a differentiable structure with respect to which a metric g is defined. Then a causal order is derived from the light cones of g. However, it has been known for some time that one can also go the other way [26, 29]: considering only the events of space-time M and an order relation $\prec$ such that $x \prec y$ if event x may influence what happens at event y, it is possible to recover from $\prec$ the topology of M, its differentiable structure and the metric g up to a scalar factor [5]. Moreover, it can be done in a purely order theoretic manner [30].

The causal relation $\prec$ is regarded as the fundamental ingredient in the description of the system evolution, the topology and geometry being secondary in the description of the dynamics. As advocated by the causal set program developed by Sorkin et al. [40, 41], this approach is compatible with the idea of “becoming”, making possible to see a system more naturally as a “growing being” than as a “static thing”, a mandatory characteristic of genuine morphogenetic processes.

Causality and Interaction

A similar path can be followed for the development of a framework suitable for the computer modeling of morphogenesis. The idea is to describe the evolution of the system as a set of interactions (read: computation). These interactions entail a causal relation. In this way, starting from the set of potential entities in the system and from a set of interactions acting on these entities, one may reconstruct incrementally the spatial structure of the whole system as a byproduct of the causal structure of the system’s interactions (computations).

Focusing on interactions rather than on the spatial background in which the evolution takes place is a solution to the problem of describing morphogenetic processes as dynamical systems. In this view interactions are local by definition. In the manner of the aforementioned causal relation $\prec$, interactions are regarded as the fundamental ingredient in the description of the system evolution, the topology and geometry being secondary.

The study of causality in computations can be traced back at least to the sixties with the development of Petri nets, where an event (i.e., firing of an enabled transition) is a local action and where there is a clear notion of event independence. Since, the subject has been extensively studied, for example with the notion of event structure [56] whose intersection with causal sets in physics has been noticed [35].

13.2.2 Computing with Interactions

To illustrate the previous idea in an algorithmic context, let us revisit a classical algorithm, the bubble sort, by considering first the interactions at work, and then by trying to reconstruct a data structure from them.

Mathematical Notations

The set of functions (resp. total functions) from a domain D to a range R is written $D \rightarrow R$ (resp. $D {{\mathrm{\hookrightarrow }}}R$). If $s \in D \rightarrow R$ and $D' \subseteq D$, then $s|_{D'}$ is the restriction of s to $D'$. The expression $[u_1 \rightarrow a_1, \dots , u_n \rightarrow a_n]$ is an element s of $\{u_1, \dots , u_n\} {{\mathrm{\hookrightarrow }}}\{a_1, \dots , a_n\}$ such that $s(u_i) = a_i$. The expression $s \cdot s'$ denotes a function $s''$ of domain $\text {dom}(s) \cup \text {dom}(s')$ such that $s''(u) = s'(u)$ if $u \in \text {dom}(s')$ else $s''(u) = s(u)$. Given a set $D = \{u_1, u_2, \dots \}$ we form the set of formal elements $\widehat{D} = \{\widehat{u}_1, \widehat{u}_2, \dots \}$. Let e be an expression where the elements of $\widehat{D}$ appear as variables and let s be some function of $D {{\mathrm{\hookrightarrow }}}R$, e[s] denotes the evaluation of expression e where all occurrences of $\widehat{u}$ are replaced by s(u) for all $u \in D$.

The “memory” where the data are stored is specified as a set of places named positions. A position plays the role of the spatial part of an event in physics. By denoting $\mathscr {V}$ the set of values that can be stored, a state of a computation is represented by a total function s from a set of positions to $\mathscr {V}$. Let $\mathscr {P}=\text {dom}(s)$ be the set of positions in some state s, elements of ${\widehat{\mathscr {P}}}$ can be used in some expression e as placeholders replaced by their associated values in e[s].

Interactions as Rules

An interaction is defined by a reciprocal action between positions . The effect of the interaction is to change the values associated with the involved positions. Because the spatial structure can be dynamic, for a given interaction I we consider a set $l_I$ of input positions and a set $r_I$ of output positions. We do not require $l_I \subseteq r_I$ (meaning that some positions may appear during the interaction), nor $r_I \subseteq l_I$ (meaning that some positions may disappear during the interaction). Finally, an interaction is guarded by some condition, that is a Boolean expression $C_I$, which controls the occurrence of the interaction. We will write an interaction I as a rule

$$ l_I \,/\, C_I \longrightarrow R_I $$

where $R_I$ is an expression to be evaluated to a function of $r_I {{\mathrm{\hookrightarrow }}}\mathscr {V}$.

The semantics of an interaction is as follows: an interaction I may occur in a state s if and only if $C_I[s]$ evaluates to true. Then, the result of the interaction is

$$ s|_{\text {dom}(s) \backslash l_I} \,\cdot \, R_I[s] $$

The expression $s|_{\text {dom}(s) \backslash l_I}$ restricts s to the positions that do not take part into the interaction. This partial state is then augmented by the local result $R_I[s]$ of the interaction. After the interaction the set of positions is given by $(\text {dom}(s) \backslash l_i) \cup \text {dom}(R_I)$.

Bubble Sort As a Set of Interactions

For the sake of simplicity, we focus on sorting sequences of three numbers taken in $\mathscr {V}= \{ 1, 2, 3 \}$. Initially, the sequence is encoded using three symbolic positions $p_1$, $p_2$ and $p_3$, so that for instance, the initial sequence [3, 1, 1] is represented by the function:

$$ s_0 = [p_1\rightarrow 3, p_2\rightarrow 1, p_3\rightarrow 1] $$

The elementary instruction at work in the bubble sort consists in swapping two neighbor elements that are not well ordered. The algorithm can then be described by the two following interactions:

$$\begin{aligned} I_1:&\{ p_1, p_2 \} \,/\, (\widehat{p_2}< \widehat{p_1}) \; \longrightarrow [p_1 \rightarrow \widehat{p_2}, p_2 \rightarrow \widehat{p_1}] \\ I_2:&\{ p_2, p_3 \} \,/\, (\widehat{p_3} < \widehat{p_2}) \; \longrightarrow [p_2 \rightarrow \widehat{p_3}, p_3 \rightarrow \widehat{p_2}] \end{aligned}$$

In state $s_0$, only $I_1$ can occur since numbers 3 and 1 are not well ordered on positions $p_1$ and $p_2$. The result of the interaction gives the sequence [1, 3, 1]:

$$\begin{aligned} s_1&= s_0|_{\text {dom}(s_0) \backslash l_{I_1}} \,\cdot \, R_{I_1}[s_0] \\&= [p_3\rightarrow 1]\,\cdot \,[p_1\rightarrow 1, p_2\rightarrow 3] \\&= [p_1\rightarrow 1, p_2\rightarrow 3, p_3\rightarrow 1] \end{aligned}$$

Figure 13.1 gives the state space generated by these interactions where a computation is a trajectory going from bottom to top.

Fig. 13.1

The state space of interactions $\{I_1, I_2\}$ with $\mathscr {V}= \{1, 2, 3\}$ and $\mathscr {P}=\{p_1, p_2, p_3\}$ as set of positions. We write abc for the function $[p_1 \rightarrow a, p_2 \rightarrow b, p_3 \rightarrow c]$. Starting from an initial state $s = a_1a_2a_3$, the final state of the computation must be $s' = a_ia_ja_k$ such that $\{i, j, k\} = \{1, 2, 3\}$ and $a_i \le a_j \le a_k$. There are $|\mathscr {V}^\mathscr {P}| = 3^3 = 27$ states. One goes from one state to another by the application of one interaction (edges are oriented from bottom to top). The branching from 321 shows the possibility to apply either $I_1$ or $I_2$ leading to a non-deterministic behavior

Interactions $I_1$ and $I_2$ alone do not modify the underlying set of positions. To illustrate such a modification, let us consider the removal of duplicate values with some additional interactions which merge neighbor positions sharing the same value:

$$\begin{aligned} I_3&: \{ p_1, p_2 \} \,/\, (\widehat{p_2} = \widehat{p_1}) \; \longrightarrow [p_4 \rightarrow \widehat{p_1}] \\ I_4&: \{ p_2, p_3 \} \,/\, (\widehat{p_3} = \widehat{p_2}) \; \longrightarrow [p_5 \rightarrow \widehat{p_2}] \\ I_5&: \{ p_1, p_5 \} \,/\, (\widehat{p_5}< \widehat{p_1}) \; \longrightarrow [p_1 \rightarrow \widehat{p_5}, p_5 \rightarrow \widehat{p_1}] \\ I_6&: \{ p_4, p_3 \} \,/\, (\widehat{p_3} < \widehat{p_4}) \; \longrightarrow [p_4 \rightarrow \widehat{p_3}, p_3 \rightarrow \widehat{p_4}] \\ I_7&: \{ p_1, p_5 \} \,/\, (\widehat{p_5} = \widehat{p_1}) \; \longrightarrow [p_6 \rightarrow \widehat{p_1}] \\ I_8&: \{ p_4, p_3 \} \,/\, (\widehat{p_3} = \widehat{p_4}) \; \longrightarrow [p_6 \rightarrow \widehat{p_3}] \end{aligned}$$

Interaction $I_3$ (resp. $I_4$) expresses the merge of positions $p_1$ and $p_2$ into $p_4$ (resp. $p_2$ and $p_3$ into $p_5$) when they are labeled with the same value. Interactions $I_5$ and $I_6$ specify the sorting of values when $p_4$ and $p_5$ are labeled. Finally, $I_7$ and $I_8$ describe the merge of positions into a unique position $p_6$.

With these additional interactions, another outcome is possible from state $s_0$ by applying interaction $I_4$:

$$\begin{aligned} s'_1 = s_0|_{\text {dom}(s_0) \backslash l_{I_4}} \,\cdot \, R_{I_4}[s_0] = [p_1\rightarrow 3, p_5\rightarrow 1] \end{aligned}$$

As expected, the set of positions is modified to $\{p_1,p_5\}$. The corresponding state space is of course bigger than the previous one and exhibits more branching (i.e., non-determinism) but remains confluent.

The Spatial Organization of Positions

Although the set of positions comes without any structure, the interactions make a specific use of it so that in general any position is not involved with all the others. As a consequence, the interactions induce a notion of locality leading to a spatial organization of the set of positions. This space can be made explicit by building the minimal structure such that, for any interaction I, the elements of $l_I$ are “neighbors”. Noticing that for an interaction I, the interaction also involves any subset of $l_I$, the neighborhood must be closed by inclusion. It turns out that this property defines a combinatorial spatial structure called an abstract simplicial complex (ASC) [22].

An ASC is a collection $\mathscr {K}$ of non-empty finite sets such that $\sigma \in \mathscr {K}$ and $\tau \subseteq \sigma$ implies $\tau \in \mathscr {K}$. The elements of $\mathscr {K}$ are called simplices. The dimension of a simplex $\sigma \in \mathscr {K}$ is $\text {dim}(\sigma ) = |\sigma | - 1$ and the dimension of a complex is the maximum dimension of any of its simplices when it exists. A simplex of dimension n is called a $n$-simplex. A vertex is a $0$-simplex. The vertex set of an ASC $\mathscr {K}$ is the union of all its simplices, $\text {Vert}(\mathscr {K}) = \cup _{\sigma \in \mathscr {K}}\sigma$. An edge is a $1$-simplex whose border consists of two vertices. A graph is an ASC of dimension 1 built with vertices and edges. An ASC of dimension 2 also contains triangular surfaces bounded by 3 edges. ASCs of dimension 3 contain tetrahedrons bounded by four $2$-simplices. And so on and so forth.

Let $\mathscr {I}$ be a set of interactions. We call the interaction complex of $\mathscr {I}$ , the smallest ASC $\mathscr {K}_\mathscr {I}$ containing all the $l_I$ as simplices for $I \in \mathscr {I}$. For the set of interactions $\{I_1, I_2\}$, the associated interaction complex is:

$$ \mathscr {K}_{\{I_1, I_2\}} = \big \{ \{ p_1 \}, \, \{ p_2 \}, \, \{ p_3 \}, \, \{ p_1, p_2 \}, \, \{ p_2, p_3 \} \big \} $$

The complex is pictured on the left of Fig. 13.2. As expected for a bubble sort, the induced spatial organization is a sequential 1-dimensional structure, here $[p_1,p_2,p_3]$. The bubble sort without duplicate values gives raise to the interaction complex $\mathscr {K}_{\{I_1,\dots ,I_8\}}$ pictured on the right of Fig. 13.2. The complex exhibits the four sequential organizations that the system can take over time: $[p_1,p_2,p_3]$, $[p_4,p_3]$ (after the merge of $p_1$ and $p_2$), $[p_1,p_5]$ (after the merge of $p_2$ and $p_3$), and $[p_6]$ (if the three values were initially the same). Notice that $\mathscr {K}_{\{I_1,I_2\}}$ is a sub-complex of $\mathscr {K}_{\{I_1,\dots ,I_8\}}$ since $\{I_1,\dots ,I_8\}$ contains $I_1$ and $I_2$.

Fig. 13.2

Examples of interaction complex: $\mathscr {K}_{\{I_1,I_2\}}$ on the left and $\mathscr {K}_{\{I_1,\dots ,I_8\}}$ on the right

Asymmetry of Interaction

The interactions involved in the bubble sort are asymmetric. For example, the roles played by $p_1$ and $p_2$ in $I_1$ are not interchangeable so that $I_1$ differs from:

$$\begin{aligned} I'_1: \{ p_2, p_1 \} \,/\, (\widehat{p_1} < \widehat{p_2}) \; \longrightarrow [p_2 \rightarrow \widehat{p_1}, p_1 \rightarrow \widehat{p_2}] \end{aligned}$$

although $l_{I_1} = l_{I'_1}$. In fact, using a set to track the input positions $l_I$ does not catch all the information contained in the interaction. As a consequence, some different sets of interactions may have the same interaction complex. For example, $\mathscr {K}_{\{I'_1,I_2\}}$ is exactly the same as $\mathscr {K}_{\{I_1,I_2\}}$.

We can get round this issue by considering a directed spatial structure rather than an ordinary ASC. The notion of directed graph exists, as well as the notion of directed ASC [21] (direction in ASC differs from the notion of orientation for dimension greater than 2, e.g., there are two orientations for a $2$-simplex but three directions). For the sake of simplicity, let us put aside the asymmetry issue and restrict the formal descriptions to undirected structures.

13.3 An Interaction-Based Programming Language

Following the approach given above, sorting n elements requires n positions and $(n-1)$ interactions, and sorting n elements without duplicate values requires $n(n+1)/2$ positions and $\sum _{i=0}^n 2i(n-i)$ interactions. However, these rules are pretty similar and can be captured by some “meta-rules”. For example, the previous interactions can be represented by the following generic rules:

$$\begin{aligned} \rho _{x, y}:&\{x, y\} \;/\; \widehat{y} < \widehat{x} \; \longrightarrow [x \rightarrow \widehat{y}, y \rightarrow \widehat{x}] \\ \rho '_{x, y, z}:&\{x, y\} \;/\; \widehat{y} = \widehat{x} \; \longrightarrow [z \rightarrow \widehat{x}] \end{aligned}$$

These rules mean to denote a whole family of interactions that are obtained by substituting positions for x, y and z. In fact, x, y and z are position variables instead of actual positions. For example, interaction $I_1$ is got by applying substitution $[x \rightarrow p_1, y \rightarrow p_2]$, that is, $I_1=\rho _{p_1,p_2}$; in the same way, $I_3=\rho '_{p_1,p_2,p_4}$.

However, while some substitutions are desired, a lot of them are not. For example, $\rho _{p_1,p_6}$ is definitively not part of the original specification of the bubble sort. Indeed, the authorized substitutions have to respect some knowledge that was built implicitly in the original interactions. In our example, x and y should stand for two positions so that x is “before” y. As a matter of fact, this knowledge is the one captured by the interaction complex. Thus, a necessary condition for a substitution of $\rho _{x,y}$ (resp. $\rho '_{x,y,z}$) to be accepted is that set $l_{\rho _{x,y}}$ (resp. $l_{\rho '_{x,y,z}}$) corresponds to a simplex of $\mathscr {K}_{\{I_1,\dots ,I_8\}}$.

This approach has been used to design the interaction-based programming language MGS. In MGS, a computation is specified through sets of “meta-rules” called transformations. Such a transformation is to be applied on a topological collection, that is, a set of labeled positions equipped with an interaction complex. The application is done by matching some positions in the collection which respect the inputs and conditions of some rule of the transformation. The instance of the rule gives raise to an interaction which modifies locally the state of the collection and possibly its structure. In this section, the syntax of the language is briefly described and its use is illustrated with a light survey of examples involving dynamic organizations (where the set of positions is not fixed once and for all) and higher dimensional structures (beyond graphs).

13.3.1 A Brief Description of the MGS Language

MGS provides topological collections , an original data structure for representing the state of a system based on the topology of interactions, and transformations, a rule-based definition of functions on collections for specifying the interaction laws of the system.

Topological Collections

Topological collections are the unique data structure available in MGS. They define the interaction structure of a dynamic system. They can also be seen as a field associating a value with each element of a combinatorial structure modeling the topology of a space.

In the previous section, we focused on ASC to model the spatial structure. This structure is the natural choice for the spatial constraint arising from the interactions. However, other combinatorial structures extending the notion of ASC can be used to get more concision and flexibility in the representation. In the MGS language, cell spaces [53] are used to subsume ASC and other kinds of spatial organization, so that a topological collection is a labeled cell space.

Cell Spaces

Formally, cell spaces are made of an assembly of elementary objects called topological cells (cells for short). For the sake of simplicity, let us assume the existence of a set of topological cells $\mathscr {P}$ together with a function $\dim : \mathscr {P}{{\mathrm{\hookrightarrow }}}\mathbb {N}$ associating a dimension with each cell. Cells $\sigma \in \mathscr {P}$ such that $\dim (\sigma ) = n$ are called n -cells. Cells represent elementary pieces of space: $0$-cells are vertices, $1$-cells are edges, $2$-cells are surfaces, $3$-cells are volumes, etc.

A cell space $\mathscr {K}$ is a partially ordered subset of $\mathscr {P}$, that is a couple $\mathscr {K}= \langle S_\mathscr {K},\prec _\mathscr {K}\rangle$ such that $S_\mathscr {K}\subset \mathscr {P}$ and $\prec _\mathscr {K}$ is a strict partial order¹ over S such that the restriction of the dimension function on $S_\mathscr {K}$ is strictly monotonic: for all $\sigma , \tau \in S_\mathscr {K}, \sigma \prec _\mathscr {K}\sigma ' \Rightarrow \dim (\sigma ) < dim(\sigma ')$. If it exists, the dimension of a cell space is the maximal dimension of its cells.

The relation $\prec _\mathscr {K}$ is called the incidence relationship of the cell space $\mathscr {K}$, and if $\sigma \prec _\mathscr {K}\sigma '$, $\sigma$ and $\sigma '$ are said incident. Contrary to ASC, the number of cells in the boundary of a cell is not constrained.

We call closure (resp. star) of a cell $\sigma$ the set $\mathrm {Cl}\,\sigma =\{\,\sigma '\,|\,\sigma '\preceq \sigma \,\}$ (resp. $\mathrm {St}\,\sigma =\{\,\sigma '\,|\,\sigma '\succeq \sigma \,\}$). Operator $\mathrm {Cl}$ is a closure operator that can be used to equip the set of cells $S_\mathscr {K}$ with a topology. Numerous operators can be defined to exploit the induced space. The notions of face and $(p,q)$-neighborhood are especially used in MGS. The faces of a cell $\sigma$ are the cells $\sigma '$ that are immediately incident: $\sigma ' \prec _\mathscr {K}\sigma$ and $\dim (\sigma ')=\dim (\sigma )-1$; $\sigma$ is called a coface of $\sigma '$ and we write $\sigma ' < \sigma$. Two cells are q -neighbor if they are incident to a common $q$-cell. If the two cells are of dimension p, we say that they are (p, q)-neighbor. A $(p,q)$-path is then a sequence where any two consecutive cells are $(p,q)$-neighbor.

Cell spaces are very general objects allowing sometimes unexpected constructions. For example, an edge with three vertices in its border is a regular cell space. Additional properties are often considered leading to particular classes of cell spaces, such as the abstract cell complexes of A. Tucker [52], the CW-complexes of J. H. Whitehead, the combinatorial manifolds of V. Kovalevsky [25], to cite a few. ASCs also form a class of cell spaces. Figure 13.3 shows an example of cell space.

Fig. 13.3

On the left, the Hasse diagram of the incidence relationship of the cell space given in the middle: it is composed of three 0-cells $(c_1, c_2, c_3)$, of three 1-cells $(e_1, e_2, e_3)$ and of a single 2-cell (f). The closure of cell $e_1$ is composed of $e_1$, $c_1$ and $c_2$. The faces of cell f are $e_1$, $e_2$ and $e_3$. The cofaces of cell $c_1$ are $e_1$ and $e_3$. On the right, a topological collection associates data with the cells: positions with vertices, lengths with edges and area with f

Topological Collections

A topological collection C is a function that associates values from an arbitrary set $\mathscr {V}$ with cells of some cell space (see Fig. 13.3). Thus the notation $C(\sigma )$ refers to the value of cell $\sigma$ in collection C. We call support of C and write |C| for the set of cells for which C is defined. Set $\mathscr {V}$ is left arbitrary to allow the association of any kind of information with the topological cells: for instance geometric properties ($\mathscr {V}= \{-1,0,1\}$ for representing orientation or $\mathscr {V}=\mathbb {R}^n$ for Euclidean positions) or arbitrary state of a subsystem (a mass, a concentration of chemicals, a force acting on certain cells, etc).

The collection C can be written as a formal sum

With this notation, the underlying cell space is left implicit but can usually be recovered from the context. By convention, when we write a collection C as a sum

$$ C = v_1\cdot \sigma _1 + \cdots + v_p\cdot \sigma _p $$

we insist that all $c_i$ are distinct.² Notice that this addition is associative and commutative: the specific order of operations used to build a topological collection is irrelevant. Using this notation, a subcollection S of a collection C is defined as a collection forming a subpart of the sum: $C=S+S'$; subcollection $S'$ is then called the complement of S in C and we write $S'=C-S$.

The current implementation of MGS provides the programmer with different types of collections , namely seq, array, set, bag, etc. Actually, the topological collection approach makes possible to unify various data structures as sketched in Sect. 13.4.2.

Transformations

Transformations of topological collections embody the concepts of interaction and interaction complex introduced in Sect. 13.2 with the notion of topological rewriting. A transformation T is a function specified by a set $\{r_1,\dots ,r_n\}$ of rewriting rules of the form $p\;{\texttt {=>}}\;e$ where the left hand side (l.h.s.) p is a pattern and the right hand side (r.h.s.) e is an MGS expression. For example, the bubble sort algorithm is defined in MGS by:

An application of a transformation rule on a collection C selects a subcollection S of C matching with the pattern p that is then substituted by the subcollection resulting from the evaluation of the expression e.

Patterns

Patterns are used to specify subcollections where interactions may occur. They play the exact same role as $l_I$ and $C_I$ in the interaction notation $l_I \,/\, C_I \longrightarrow R_I$ of Sect. 13.2.2. However, the cell space setting used in the definition of topological collections requires a more elaborate tool for this specification instead of a simple set $l_I$ of interacting positions (which is restricted to the simplicies of an ASC). Transformation rule patterns allow the programmer to describe the local spatial organizations (and states) leading to some interactions.

Let us describe the core part of the pattern syntax which is based on three constructions summarized in the following grammar:

$$\begin{aligned} \varPi {\quad }{:}{:}{=}&{\quad } id {\quad }|{\quad }\varPi \;\varOmega \;\varPi {\quad }|{\quad }\varPi \;{\texttt {/}}\;\varLambda \\ \varOmega {\quad }{:}{:}{=}&{\quad }\varepsilon {\quad }|{\quad }{\texttt {<}}{\quad }|{\quad }{\texttt {>}}{\quad }|{\quad }{\texttt {,}} \end{aligned}$$

In this grammar, $\varLambda$ represents an MGS expression, $id$ corresponds to an identifier, and $\varepsilon$ denotes the empty string. The grammar can be described as follows:  

Pattern Variable: :

An identifier x of $id$, called in this context a pattern variable, matches a $n$-cell $\sigma$ labeled by some value $C(\sigma )$ in the collection C to be transformed.

The same pattern variable can be used many times in a pattern; it then always refers to the same matched cell. Moreover, patterns are linear: two distinct variables always refer to two distinct cells.

Incidence: :

A pattern $p_1 \oplus p_2$ of $\varPi \;\varOmega \;\varPi$ specifies a constraint $\oplus \in \varOmega$ on the incidence between the last element matched by pattern $p_1$ and the first element matched by pattern $p_2$. The pattern ${\texttt {x < y}}$ (resp. ${\texttt {x > y}}$) matches two cells $\sigma _{{\texttt {x}}}$ and $\sigma _{{\texttt {y}}}$ such that $\sigma _{{\texttt {x}}}$ is a face (resp. coface) of $\sigma _{{\texttt {y}}}$. The lack of operator ($\varepsilon$) denotes the independence of the cells (there is no constraint between them).

Binary interactions between two elements, say x and z, are frequent in models and can be specified with the pattern ${\texttt {x < y > z}}$. Variable pattern y stands for some $k$-cell making x and z $(k-1,k)$-neighbors, e.g., two vertices linked by an edge in a graph. Often, the naming of y does not matter and the syntactic sugar x, z is used instead.

Although directed structures are out of the scope of this chapter, one may mention that it exists a directed extension of cell spaces that is actually used in MGS. The direction is encoded in the reading so that ${\texttt {x > y}}$ is directed from x to y and will not match the same subcollections than ${\texttt {y < x}}$ in directed collections.

Guard: :

Assuming a pattern p of $\varPi$ and an MGS expression e of $\varLambda$, $p\;{\texttt {/}}\;e$ matches a subcollection complying with p such that the expression e evaluates to true.

We do not detail here the syntax of MGS expressions which is not of main importance but two elements have to be clarified. Firstly, in this chapter,³ function application is expressed using currying as in functional programming: $f\;e_1\;e_2$ means that function f is applied with two arguments $e_1$ and $e_2$. The benefit of this syntax lies in the left associativity of the application so that feeding a binary function with the first argument builds a unary function waiting for the second, like in ${\texttt {(}}f\;e_1{\texttt {)}}\;e_2$. This principle extends to any n-ary functions. Secondly, any pattern variable, say x, can be used in guard expressions (as well as in the r.h.s. expression of a rule) where it denotes the label of the matched $k$-cell. Its faces (resp. cofaces, resp. $(k,k+1)$-neighbor cells) are accessed by faces x (resp. cofaces x, resp. neighbors x).

Since MGS is a dynamically typed language (that is, types are checked at run time), types can be seen as predicates checking if their argument is of the right type. Some syntactic sugar has been introduced to ease the reading of type constraints in patterns so that the pattern x / int(x), matching a cell labeled by some integer, can be written x:int. On the contrary, x:!int matches a cell labeled by something but an integer.

 

For example, the pattern

matches the entire collection of Fig. 13.3 with, for instance, the following association:

$$ \begin{array}{l@{\qquad \qquad }c@{\qquad \qquad }c} {\texttt {v1}}\mapsto (0,4) \cdot c_1 &{} {\texttt {e12}}\mapsto 5 \cdot e_1 &{} {\texttt {f}}\mapsto 12 \cdot f\\ {\texttt {v2}}\mapsto (3,0) \cdot c_2 &{} {\texttt {e23}}\mapsto 6 \cdot e_2 &{} \\ {\texttt {v3}}\mapsto (-3,0) \cdot c_3 &{} {\texttt {e31}}\mapsto 5 \cdot e_3 &{} \end{array} $$

Rule Application

Let $T=\{r_1,\dots ,r_n\}$ be an MGS transformation. Following the interaction-based computation model described in Sect. 13.2.2, the application of a rule $p\;{\texttt {=>}}\;e$ of T on a collection C consists in finding some subcollection S of C matching pattern p then replacing S by the evaluation $S'$ of e in C. One point not discussed earlier is the choice of the rule(s) to be applied when a number of instances exist. This choice is called rule application strategy .

The default rule application strategy in MGS is qualified maximal-parallel. It consists in choosing a maximal set $\{S_1,S_2,\dots \}$ of non-intersecting subcollections of C each matched by some pattern of T. In this context, non-intersecting means that for any two subcollections $S_i$ and $S_j$, their supports check that $|S_i|\cap |S_j|=\emptyset$. The application is then done in parallel as represented by the following diagram:

where each $S'_k$ results from the evaluation of $e_{i_k}$ and $R=C-(S_1+S_2+\cdots )$ consists of the untouched part of C. Since it may exist different ways to decompose collection C w.r.t. transformation T, only one of the possible outcomes (randomly chosen) is returned by the transformation. The formal semantics is given in [47].

On the contrary, the strategy informally used in Sect. 13.2.2 is qualified asynchronous since only one rule application is considered at a time. Its diagram is as follows:

The asynchronism means that two events cannot take place simultaneously. Between the synchronous and the asynchronous strategy, there is considerable room for alternative rule application strategies.

For instance, asynchronism is often assumed for stochastic processes on populations where simultaneous events are unlikely (e.g., in Poisson processes). These kinds of processes are often used for stochastic simulation, for example of chemical or biochemical systems of reactions. In this context, pure asynchronism is not enough: a stochastic constant is attached to each reaction (that is, rule) and expresses “how fast” it is. A continuous-time Markov chain can then be derived from the trajectories generated by the iterations of the transformation. We name the continuous-time extension of the asynchronous rule application strategy with stochastic constants, the Gillespie rule application strategy after the name of D.T. Gillespie. Gillespie proposed in [20] an algorithm for the exact stochastic simulation of well-stirred reaction systems which is implemented in MGS. The MGS Gillespie strategy has been used in different applications in integrative and synthetic biology, see for example [46, 49].

13.3.2 Reviews of Some Applications to Complex Systems

We advocate that MGS is adequate for the modeling and simulation of dynamical systems. In this section, we show various examples that support this assertion. These examples are only sketched to support our claim and the interested reader may refer to the references given for the technical details.

Flocking Birds

In [18] the classical example of a simulation of a flock of birds has been considered. The simulation is the direct implementation of a model of flocking birds proposed by U. Wilensky and by the development of steering behaviors of boids (generic simulated flocking creatures) invented by C. Reynolds [39].

Fig. 13.4

Trajectory of a flock of 50 birds. Left plot the initial state where each bird has a randomly chosen direction. Center plot the configuration after 300 iterations. Right plot after 900 iterations of the transition function

Here, no creation nor destruction of birds happen, but the neighborhood structure changes in time with the movements of the birds. This example uses the Delaunay topological collection [32, 42] where the neighborhood structure is not built explicitly by the programmer but is computed implicitly at run time using the positions of the birds in a Euclidean space represented as labels of $0$-cells in the collection. Figure 13.4 illustrates three iteration steps of the simulation. The transformation corresponding to the dynamics specifies three rules corresponding to the three behaviors described by Wilensky: separation (when a bird is at close range of a neighbor, it changes direction), cohesion (when a bird is too far from all its neighbors, it tries to join the group quickly) and alignment (when the neighbors of a bird are neither too far nor too close, the bird adjusts its direction following the average directions of its neighbors).

Diffusion Limited Aggregation

Diffusion Limited Aggregation, or DLA, is a fractal growth model studied by two physicists, T.A. Witten and L.M. Sander, in the 80s [57]. The principle of the model is simple: a set of particles diffuses randomly on a given spatial domain. Initially one particle, the seed, is fixed. When a mobile particle collides a fixed one, they stick together and stay fixed. For the sake of simplicity, we suppose that they stick together forever and that there is no aggregate formation between two mobile particles. This process leads to a simple CA with an asynchronous update function or a lattice gas automaton with a slightly more elaborated set of rules.

Fig. 13.5

DLA on complex objects (topology and final state). On the left: a sphere with 18 parallels and 24 meridians. On the right: a Klein’s bottle

The MGS approach enables a generic specification of such a DLA process which works on various kinds of space [45]. Figure 13.5 shows applications of the same DLA transformation on two different topologies: it is an example of the polytypic [24] capabilities of MGS.

Declarative Mesh Subdivision

Mesh subdivision algorithms are usually specified informally with the help of graphical schemes defining local mesh refinements. For example, the Loop subdivision scheme [28], working on triangular meshes, is described with the local rule

These specifications are then implemented efficiently in an imperative framework. These implementations are often cumbersome and imply some tricky indices management. Smith et al. [38] asked the question of the declarative programming of such algorithms in an index-free way that has been positively answered in [47] with the MGS specification of some classical subdivision algorithms in terms of transformations (see Fig. 13.6).

Fig. 13.6

Results of the application of subdivision algorithms. From top to bottom: the Loop’s algorithm, the Butterfly algorithm, the Catmull-Clark’s algorithm and the Kobbelt’s algorithm. From the left to the right, the initial state then 3 iteration steps. These pictures have been generated in MGS

Coupling Mechanics and Topological Surgery

Developmental biology investigates highly organized complex systems. One of the main difficulties raised by the modeling of these systems is the handling of their dynamical spatial organization: they are examples of dynamical systems with a dynamical structure.

Fig. 13.7

Simulation of a neurulation-like process in MGS: from the left to the right, a sheet of epithelial cells is curving until the hems sew together to form a tube

In [43] a model of the shape transformation of an epithelial sheet requiring the coupling of a mechanical model with an operation of topological surgery has been considered. This model represents a first step towards the declarative modeling of neurulation. Neurulation is the topological modification of the back region of the embryo when the neural plate folds; then, this folding curves the neural plate until the two borders touch each other and make the plate becomes a neural tube (see Fig. 13.7).

Modeling the Growth of the Shoot Apical Meristem

Understanding the growth of the shoot apical meristem at a cellular level is a fundamental problem in botany. The protein PIN1 has been recognized to play an important role in facilitating the transport of auxin. Auxin maxima give the localization of organ formation. In 2006, Barbier de Reuille et al. investigated in [4] a computational model to study auxin distribution and its relation to organ formation. The model has been implemented in the MGS language using a Delaunay topological collection. Figure 13.8 shows the results of a simulation done in MGS of a model of meristem growth.

Fig. 13.8

Results, at time steps 3, 18, 27, 35, 41 and 59, for the simulation of a virtual meristem done by Barbier de Reuille in [3]. Red dots correspond to auxin and each primordium cell is shown in a different color

Integrative Modeling

Systems biology aims at integrating processes at various time and spatial scales into a single and coherent formal description to allow analysis and computer simulation. Rule-based modeling is well fitted to model biological processes at various levels of description. This approach has been validated through the description of various models of a synthetic bacterium designed in the context of the iGEM competition [48], from a very simple biochemical description of the process to an individual-based model (see Fig. 13.9).

This model, as well as the previous one, aims at the modeling of an entire population (of cells, of bacteria) through an explicit representation of the individuals with mechanical, chemical and biological (i.e., gene expression) behaviors, integrated with the specification of entity/entity interaction and dynamic neighborhood computation.

Fig. 13.9

Results of an integrative model. Germinal cells are in dark gray and somatic cells in light gray. a–c correspond to an initial population and its evolutions at logical time 43 and 62. Refer to [48]

Algorithmic Problems

The use of MGS is not restricted to the modeling and simulation of complex systems. Many other applications not given here have been developed. For example, purely algorithmic applications include the Needham–Schroeder public-key protocol [31], the computation of prime numbers using Eratosthene’s sieve, the normalization of Boolean formulas, the computation of various algorithms on graphs like the computation of the shortest distance between two nodes or the maximal flow, to cite a few. Moreover, any computation described in an unconventional framework can be programmed in MGS since the language unifies many models of computation as we will see in Sect. 13.4.2. Detailed examples can be found on the MGS web page.⁴

13.4 Generic Programming in Interaction-Oriented Programming

While MGS was initially designed as a domain specific programming language dedicated to the modeling of dynamical systems with a dynamical structure, it allows an elegant and concise formulation of classical algorithms (as illustrated with the bubble sort in Sect. 13.2.2). The main difference with other general-purpose programming languages lies in its interaction-based style of programming. In this section, we outline the new perspectives on genericity opened by the interaction-oriented approach.

We advocate that the design of unconventional models of computation has an impact not only in the study of alternative models of computation (with alternative calculability and complexity classes) but may also impact questions raised in “classical programming languages”. This development offers also a link, investigated in the next section, between the notion of data structure/traversal and the notion of differential operators.

13.4.1 Polymorphism, Polytypism and Generic Programming

Genericity in a programming language is the crucial ability to abstract away irrelevant requirement on data types to produce, once and for all, a piece of code that can be reused in many different situations. It is then a central question in software engineering.

Several mechanisms have been proposed to support genericity. In Musser and Stepanov’s approach [34], the fundamental requirements on data structures are formalized as concepts, a notion more general than a type, with generic functions implemented in terms of these concepts. The best known examples are the STL in C++ or the Java Collection interface.

Let us take a look at the Java Collection interface. This interface is implemented by all data containers of the Java standard API. Besides the usual container methods (size, emptiness, membership, etc.), any Java Collection has to implement an iterator over its elements to be compatible with the enhanced for loop syntax. Iterators decouple data structure traversals from data types, which enables the definition of the same algorithm operating on different data type.

This property has been formalized in type theory as polymorphism available in many programming languages. For example, Parametric polymorphism [8 ] allows the definition of functions working uniformly (i.e., the same code) on different types. The uniformity comes from the use of a type variable representing a type to-be-specified-later and instantiated usually at function application. For example, the OCaml type declaration for “lists of something” is as follows:

In this definition (specifying that a list is either empty or built from an element prepended to a list), the type variable can be instantiated by any types: for a list of integers, for a list of strings, for a list of lists of something-abstracted-by-type-variable-$\beta$, etc. Any function acting on the structure of lists independently of the content type has a polymorphic type. For example, the classical map function applying some function f on each element of a list is defined once and for all by:

and is of type . This sole definition works for any instance of type variables and .

We can go further by considering polytypism where the type of the container is also abstracted. For example, consider the following type definition of binary trees:

As for list, a map function can be defined on trees:

of types . Both map functions actually work the same way: they transform all elements of type in the structure by traversing it recursively. This traversal can be specified by associating a combinator with each constructors of the data type (Empty, Leaf, etc).

Generic programming as proposed in [23, 24] generalizes this idea by allowing to program only one map algorithm (in our example, the map function is defined twice). This approach is applicable for a class of types called algebraic data types (ADT). Roughly speaking, ADT are specified inductively using the unit type, type variables, disjoint union of types (operator | in the previous definitions), product of types (operator *), composition of types, and a fixpoint operator. Generic programming uses this uniformity to provide a way to express inductively polytypic algorithms for ADT by associating a combinator with each of these data type constructions. Refer to [23] for a detailed presentation.

13.4.2 From Data Structures to Topological Collections

In MGS, topological collections can be polymorphic in the sense mentioned above since there is no constraint on the set of labels: the same cell space can be labeled by integers, strings, or anything else [9]. In addition, a transformation relies on the (local) notion of neighborhood which is constitutive of the notion of space without constraining a particular (global) shape of space. In other words, the same transformation can be used on any collection providing the programmer with a form of polytypism.

However, the spatial point of view goes beyond polymorphism and polytypism as found in “classical programming languages”. The previous discussion makes apparent that generic programming relies on abstracting away some information on data type to keep the information relevant to data traversal. This can be explicit through the notion of iterators in Java, or implicit through the notion of natural homomorphism (combinator associated to a constructor) in ADT.

This information is alternatively expressed in term of space, where the notion of (data-)movement find a natural setting. The spatial point of view provides both a richer set of data structures than those described by the algebraic approach⁵ and more expressive mechanisms to express elementary movements (e.g., iterators impose an ordering which can be detrimental).

In the following we investigate the idea that a data structure corresponds to a topological collection with a specific kind of topology. The polytypism of MGS transformations is presented together with some examples. In the next section, we introduce a family of generic operators which are finally related with differential operators considered in continuous computation.

Data Structures

In computer science, the notion of data structure is used to organize a collection of data in a well organized manner. The need of structuring data is twofold: firstly, programmers are interested in capturing in a data structure the logical relationship between the data it contains. This is for example one of the primary idea behind database tools like entity–relationship models, UML diagrams, or XML document type definitions when used to specify how the represented objects are ontologically related to each other (e.g., a book has an ISBN, a title, some authors, etc.). The data structure becomes a model of some organization in the world.

Secondly, from a computational perspective, data structures are designed to efficiently access the data. (In this respect, the art of database design consists in modeling consistently reality while being queried efficiently.) Algorithms are often expressed as nested traversals of some structures. The choice of a data structure is then highly coupled to the algorithm to be implemented. For example, the list structure defined above allows a linear traversal of the data in order of appearance in the list, while the tree structure allows the so-called prefix, infix and postfix traversals. In the object-oriented programming paradigm, the iterator design pattern (mandatory for any Java class implementing the Collection interface for example) can be understood as an attempt to catch this notion of traversals.

MGS Collection Types

By confronting the concept of traversal with the concept of topological collection, it is possible to retrieve the conventional notion of data structure in MGS. The main idea consists in extracting from each data structure a specific topology capturing the graph of its traversals: the nodes represent positions for storing the data and the edges are defined so that two elements are neighbor in the collection (i.e., may interact) if they are consecutive in some traversal of the data structure. Let us review some classical data structures and their MGS interpretations. Each of them is associated with a dedicated collection type corresponding to a specific (constrained) topology. Each collection type comes with some syntactic facilities in the current implementation of the language.

Sequences

As already said, such structures are linear, meaning that elements are accessed one after the other. The associated topological structure is then a linear graph as the one obtained in Sect. 13.2. These structures exhibit two natural traversals that we can refer to left-to-right and right-to-left. Considering only one of these two traversals leads to a directed structure similar to a linked list while considering both leads to doubly linked list structures.

In its current implementation, MGS provides the programmer with two linear left-to-right directed collection types: seq and array. They differ by the nature of the underlying space; the former is a Leibnizian collection type where the structure is generated by a specific relationship between the data (here the order of insertion) while the latter is Newtonian ⁶ where the structure is firstly specified (or allocated) and then inhabited. The following example of MGS program illustrates this difference:

Transformation rem removes all labels of positions having an even number on its right. The predicate right can be expressed as a straightforward expression involving the generic comma operator “,”; it takes its specific meaning on sequence from the underlying topology. In the case of a seq collection, the removal modifies the space from a 5-node graph to a 3-node graph. In the case of an array collection, the underlying space remains unchanged but the affected positions are left empty (i.e., without any label).

(Multi-)Sets

The main difference with linear structures is that sets are unordered collections, so that when iterated, no order gets the priority. As a consequence, for any pair of elements there exists at least one iteration making them neighbors. The obtained topological structure is a complete graph.

In the current implementation of MGS, collection types set and bag are available: bag collections allow multiple occurrences of the same element while set collections do not.

Records

A record corresponds to a collection of data aggregated together in a single object. Each data can be referred by a different field name. This is equivalent to a struct construction in the C programming language. The elements of a record are not generally accessed one from the other (they are accessed from the whole record) leading to consider an empty neighborhood between the data. The topological structure of records is then a graph with no edge: each field is represented by an isolated vertex labeled by its associated data.

Group Based Fields (GBF)

Algorithms on matrices often work by traversing data regularly by row and/or by column. Forgetting what happens on the boundary, the induced topological structure exhibits a very regular pattern where each element has four neighbors: its immediate successors and predecessors on its row and column. Of course this reasoning can be extended to any multidimensional arrays.

GBF are the generalization of multidimensional arrays where the regular structure corresponds to the Cayley graph of an abelian group presentation. The abelian group is finitely generated by a set of directions from an element to its neighbors (e.g., north, south, east and west for matrices) together with a set of relations between these directions (e.g., north and south are opposite directions). GBF are a powerful tool that allows the specification in few lines of complicated regular structures. Figure 13.10 illustrates the specification of an infinite hexagonal grid using GBF.

Fig. 13.10

Infinite hexagonal grid generated by 3 directions a, b and c related by $a+b=c$. On the right, a local view of the associated Cayley graph focused on the 4 positions marked in the grid on the left. Each arrow represents the displacement from a position to another following one of the directions or their inverses

Unifying Natural Models of Computation

The previous paragraph shows that the notion of topological collection subsumes a large variety of data structures. As a consequence, it appears that various natural models of computation can be adequately described in the MGS framework simply by choosing the right collection type and the right rule application strategy:

• Artificial Chemistry [2] corresponds to a space where any two entities may interact. We have seen that this corresponds to a complete graph, hence to the set or bag collection types. The application of transformation rules on these structures achieves the same effect as multiset rewriting [10] (rewriting on associative-commutative terms).

• Membrane Computing [14, 36] extends the idea of multiset programming by considering nested multisets (membranes) and transport between them. The corresponding space can be represented as a multiset containing either ordinary values and nested multisets. This example shows the interest to reflect the spatial structure also in the labels, see [19]. The rule application strategy is usually the maximal-parallel one.

• Lindenmayer Grammars [27] correspond to parallel string rewriting and hence to a linear space and a maximal-parallel application strategy.

• Cellular Automata (CA) [55] and Lattice Gas Automata [50] correspond to maximal-parallel rewriting in a regular lattice. Such a lattice can be easily specified as a GBF collection type. For example the classical square grids with von Neuman or Moore neighborhoods are defined in MGS by:

  

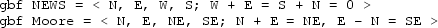
13.4.3 Polytypism in MGS

Transformations allow the programmer to iterate over the neighbors of an element (e.g., with the neighbors, faces and cofaces primitives) or over the pairs of neighbor elements in a topological collection.

Since transformation patterns express interactions in terms of cells incidence in full generality, the same pattern can be applied on any collection of any collection type, so that a transformation can be viewed as a polytypic computation in an interaction-based style.

The following paragraphs present some examples of MGS polytypic transformations.

Map-Reduce in MGS

The MGS counterpart of the aforementioned polytypic map function can be implemented as follows:

In this declaration an extra-parameter f is expected so that map f is a transformation applying f on each element of a collection. For example:

In this example, f is set to the successor function succ so that the elements of the collection are incremented by one.

In functional programming, the map function appears in conjunction with another polytypic function, reduce. This function iterates over the elements of some structure to build up a new value in an accumulator. It is parameterized by the accumulation function. For example, reduce can be used to compute the sum of the elements of a list of integers. The MGS counterpart of this function can be implemented as follows:

This rule collapses two neighbor elements into one unique value computed from the combination function op. Obviously this rule has to be iterated until a fixpoint is reached to finally get the reduction of the whole structure. For example:

sums up all the elements of a sequence. The application of the transformation (reduce add) is annotated by the qualifier fixpoint.

Bio-Inspired Algorithms

Numerous distributed algorithms are inspired by the behavior of living organisms. For instance ant colony optimization algorithms use ants ability to seek the shortest path between the nest and a source of food [12]. Such algorithms are often specified as reactive mutli-agent systems where the individual behavior is defined independently from the spatial organization of the underlying structure. In this respect, these algorithms are polytypic and can be easily specified in MGS. We focus on two toy but representative examples of such computations.

Random Walk

One of the key behaviors of agent-based distributed algorithms is a random walk allowing agents to scatter everywhere in the space so that each place is visited at least once by an agent with high probability. The expression of such a walk in MGS is as follows:

Transformation walk is composed of a simple rule specifying that if an agent has an empty place in its neighborhood, it moves to that place leaving its previous location empty. To get even more genericity the predicates for being an agent or an empty place are given as parameters agent and empty. This rule is not deterministic since a choice as to be done when several empty places surround the agent; in such a case, one of these places is randomly chosen uniformly, ensuring no bias in the walk. This transformation operates on any type of collection.

Propagation

Another fundamental procedure consists in broadcasting some information in space. This mechanism is at work in propagated outbreak of epidemics, in graph flooding in networks or in the spread of fire in a burning forest. A simple MGS transformation can implement this last example as follows:

Two rules are given to (1) set into fire an unburnt place which is neighbor with a burning one (primitive neighbors_exists checks for some neighbor of p where predicate on_fire holds), and to (2) extinguish places in fire. Once again, the genericity of this specification (especially of primitive neighbors_exists which visits all the neighbors of an element whatever the collection type is) makes this transformation polytypic.

The genericity of these specifications allows the development of tools and techniques operable in many different situations. For example, we have developed in [37] the tracking of the spatial activity in such algorithms, leading to a generic optimized simulation procedure usable with any collection type.

13.5 From Computation to Physics: Differential Calculus in MGS

Cell spaces are defined in algebraic topology for a discrete (and algebraic) description of spaces. Therefore, one can expect to find on these spaces the operators mathematicians have imagined on more usual spaces, like differential operators. This is indeed the case and the interested reader may refer to [11] for an introduction.

Topological collections are directly inspired by the notions of topological chain and cochain built upon cell spaces, but with a weaker structure. In the previous sections we have established a direct link between the notion of data structure and the notion of topological collection, it is then tempting to investigate in the context of data structures what a differential operator is. All the mathematical background required to understand this relation is detailed in the Appendix.

In this section, we show how a set of operators can be derived as computation patterns of MGS programs. These operators, which can be seen as movements of data on data structures [15], inherit algebraic properties from differential calculus, providing the programmer with the ability to express a program as a set of differential equations.

13.5.1 Transport of Data

The main motivation of this section is to relate the formal definition of topological collections to the discrete counterpart of differential forms as developed in [11].

As defined in Sect. 13.3.1, a topological collection C is a function associating values from a set $\mathscr {V}$ with the cells of a cell space $\mathscr {K}$. This structure is almost a discrete form: a discrete form further constrains the set $\mathscr {V}$ to be equipped with a structure of abelian group (i.e., with an addition operator $+_\mathscr {V}$) and the cell space $\mathscr {K}$ to be equipped with a structure of chain complex (i.e., with a boundary operator $\partial$). Topological chains are the basic ingredient to define a boundary operator. As a matter of fact, the boundary of a $(n+1)$-cell is a $n$-chain, that is a function associating integers with the $n$-cells of a cell space. These integers are used to represent the multiplicity and the orientation of a cell in the complex. This operator is linearly extended from cells to chains.

From now on, we consider that the set $\mathscr {V}$ of values of a topological collection is an abelian group⁷ written additively $+_\mathscr {V}$, and that a boundary operator $\partial$ is defined on its support cell space. Collections C are then forms. As functions on cells, they can be linearly extended to $n$-chains of $(\mathscr {K},\partial )$, so that:

$$ C(n_1.\sigma _1 + n_2.\sigma _2 + \cdots ) = n_1C(\sigma _1) +_\mathscr {V}n_2C(\sigma _2) +_\mathscr {V}\dots $$

where the $\sigma _i$ are cells of $\mathscr {K}$.

The application of a collection C on a chain c, usually written [C, c], leads to consider a derivative operator $\mathbf d$ as the “adjoint operator” of $\partial$ defined by:

$$ [\mathbf dC, c] = [C, \partial c] $$

By duality, the same can be done to get a dual derivative operator $\star \mathbf d$, called here coderivative, from a dual boundary operator $\star \partial$. Both operators are then related by a correspondence operator $*$ analogous to the Hodge dual. All technical details are given in Appendix.

The point is that the three operators $\mathbf d$, $\star \mathbf d$ and $*$ act on topological collections (forms), and can be defined as transformations parameterized by the group operator $+_\mathscr {V}$ and the boundary operators $\partial$ and $\star \partial$:

• the correspondence operator $*$ behaves like a map function and transforms the value associated with a cell,

• the derivative operator $\mathbf d$ transfers values from cells to their cofaces, and

• the coderivative operator $\star \mathbf d$ transfers values from cells to their faces.

Figure 13.11 illustrates these data movements. From the point of view of data movements, the group operations can be interpreted as follows:

Fig. 13.11

Transport of values under the actions of differential operators: on the left, the derivative operator where only some $1$-cells are labeled; on the right, the dual derivative operator where only the $2$-cells are labeled (the action is represented on the primal mesh)

• Identity: the zero of $\mathscr {V}$ coincides with the absence of label. It can then be used to deal with partially defined collection.

• Addition: is used to combine multiple labels moving to the same cell due to the action of an operator. Examples of such collisions are pictured on Fig. 13.11. The commutativity means that the order of combinations does not matter.

• Negation: this operator is essential to program the relative orientation⁸ between cells and to get the nilpotence of the boundary operator ($\partial \circ \partial = 0$).

The three differential operators can straightforwardly be translated in MGS following the definitions given in Appendix. As an example, the derivative is defined in MGS as follows:

The transformation is parameterized by four arguments. The three first arguments specify the considered abelian group structure⁹ over $\mathscr {V}$, and function inc gives the incidence number of a pair of cells (which defines the boundary operator). Transformation derivative works on each cell $\sigma$ of a collection by summing up (add) all the labels associated with the faces of $\sigma$ (faces_fold) with respect to the relative orientation between incident cells (inc).

13.5.2 Programs and Differential Equations

The previous operators are generic: they are polymorphic because they apply irrespectively of $\mathscr {V}$ (as soon as it is an abelian group) and polytypic because they apply on cell spaces of any shape. We qualify these operators as “discrete differential operators” because they exhibit the same formal properties as their continuous counterparts.

These basic operators can be composed to get more complex data transports. By mimicking their continuous counterparts, they can be used as building blocs to define more elaborated data circulation in the data structures, like gradient, curl, divergence, etc. For example, we have proposed in [15] an MGS implementation of the Laplace–Beltrami operator $\mathrm \Delta$, a general Laplacian operator, defined in our notations by:

$$ \mathrm \Delta = *\star \mathbf d*\mathbf d+ \mathbf d*\star \mathbf d*$$

We have also shown that the straightforward translation of differential equations results in effective MGS programs.

In the rest of this paragraph, we illustrate the approach on the modeling of two classical physical phenomena: diffusion and wave propagation. However, the challenge at stake is not restricted to the generic coding of (the numeric simulation of) physical models. We believe that the abstract spatial approach of computation, based on the notion of interaction, opens the way to a new comprehension of algorithms through the physical modeling of data circulation. To illustrate this idea, we present in the last paragraph of this chapter an analysis of a system of differential equations that exhibits a sorting behavior.

Programming of Differential Equations

Let us consider the modeling of two classical physical systems, the diffusion and the wave propagation, given by the following equations:

$$ \dot{U} = D\mathrm \Delta U \qquad \qquad \ddot{V} = C^2\mathrm \Delta V $$

where D, C are respectively the diffusion coefficient and the wave propagation speed, U, V stand for the collections to be transformed, and $\dot{U}$, $\ddot{V}$ are their first and second temporal derivatives respectively. The behavior of the corresponding MGS programs depends on the parameterization chosen for the differential operators. Figure 13.12 shows simulations where the differential operators are parameterized so that the abelian group of labels corresponds to the real numbers under the usual addition, and the boundary, coboundary and correspondence operators encode a classical square grid with step dx. The temporal derivatives are interpreted using the forward difference (e.g., $\dot{U}(t) = \frac{U(t+dt) - U(t)}{dt}$ for some time t and duration dt).

Fig. 13.12

Simulations of a diffusion and a wave propagation in MGS from the straightforward implementation of the differential equations: diffusion with coefficients $D=10^{-2}$ and $dt=dx=1$ on top line, from left to right at time $t=0$, 1000, 3500 and 10000; wave propagation with coefficients $C=5.10^{-3}$ and $dt=dx=1$ on bottom line, from left to right at time $t=0$, 1500, 3000 and 4500

With these parameters, the MGS programs coincide with the numerical resolution of the equations using a finite difference method. Some applications of Sect. 13.3.2 (neurulation, meristem growth and the integrative model) can also be derived from a model originally described in terms of differential equations.

More complex numerical schemes (equivalent or improved compared to the usual finite element method in terms of error control, convergence and stability) can be expressed in this framework as shown in [11, 51]. All these works rely on the understanding of physical laws with a discrete interpretation of the differential calculus; MGS lends itself to the implementation of these theories.

Furthermore, the genericity of the spatial point of view makes possible to encompass, in the same computational formulation, different physical models of the same phenomena. For example, we can change the nature of the labels in $\mathscr {V}$ from real numbers to multisets of symbols. While the former corresponds to concentrations in the previous setting, the later can be interpreted as individual particles. In this setting, the Laplacian operator $\mathrm \Delta$ expresses the jump of particles from a position to some neighbor in the collection. A multiplication between two collections with same support specifies reactions between particles. We find here the basic ingredients of membrane computing that we have mentioned earlier in Sect. 13.4.2: diffusing between membranes and reacting.

Subsuming different kinds of models is fruitful to get refined models of complex systems. Another application consists in coupling different models relying syntactically on the same differential description. For example, we have been able to simulate a 1D hybrid diffusion system partitioned into subsystems each governed by its own diffusion model, either the Fick’s second law or a random walk of particles both specified by the same generic equation but parameterized by a specific $(\mathscr {V},+_\mathscr {V})$. The interface between two models is simply driven by the conversion laws between the involved parameters (here particles and concentrations). See Fig. 13.13 for an illustration.

Fig. 13.13

Hybrid diffusion in 1D. The initial distribution is given by $\frac{1}{2}(1-\cos (\frac{2\pi x}{L}))$ for $x\in [0,L]$ with $L=100$. The system is divided into 4 parts: on intervals [0, 25] and [50, 75] the diffusion is governed by the Fick’s second law (FL) solved by a finite difference method with space step $\varDelta {x}=5$ and time step $\varDelta {t}=1$; on intervals [25, 50] and [75, 100] the diffusion is governed by a discrete uniform random walk (RW) with space step $\delta {x}=0.5$ and time step $\delta {t}=0.1$. The correspondence between the two models is given by a unit of matter in FL for $10^4$ particles in RW. The figures give the states taken by the system at times $t=0, 10, 20, 30, 40$ and 50 for a diffusion coefficient $D=10$

Programming with Differential Equations

Continuous formalisms are sometimes used to describe the asymptotic behavior of a discrete computation. As an example, we have been able in [44] to provide a differential specification of population protocols, a distributed computing model [1], allowing us to study the asymptotic behavior of such programs.

We further believe that the formulation of classical (combinatorial, discrete) computations through differential operators acting on a data structure, is able to bring new understanding on old problems and to make a bridge with the field of analog computation. In this perspective, a computation is seen as a dynamical system (see [17] for an application in the field of autonomic computing).

To illustrate this point, we elaborate on an example introduced by R.W. Brockett about the computational content of the systems of ordinary differential equations of the form $\dot{H}=[H,[H,N]]$ where H and N are symmetric matrices and $[\cdot ,\cdot ]$ is the commutator operator [6, 7]. It has been shown that by choosing appropriately N and the initial value of H, the system is able to perform many combinatorial algorithms, like sorting sequences, emulating finite automata or clustering sets of data.¹⁰

In the case of sorting, the system corresponds to a non-periodic finite Toda lattice, a simple model for a one-dimensional crystal given by a chain of particles with nearest neighbor interaction. The equations of motion of a particle are given by:

$$ \left\{ \begin{array}{l} \dot{p}_i = e^{(q_{i-1} - q_i)} - e^{(q_i - q_{i+1})} \\ \dot{q}_i = p_i \end{array} \right. \qquad i\in [1..n] $$

where $q_i$ is the displacement of the ith particle from its equilibrium position, and $p_i$ is its momentum. To integrate the system, one uses the following change of variables:

$$ u_i = -\frac{1}{2}p_i \qquad \qquad v_i = \frac{1}{2} e^{(q_i - q_{i+1})/2} $$

giving the following system:

$$ \left\{ \begin{array}{l} \dot{u}_i = v_i^2 - v_{i-1}^2\\ \dot{v}_i = 2 (u_{i+1} - u_i) v_i \end{array} \right. \qquad i\in [1..n] $$

The behavior of this system is as follows: starting from an initial sequence of values $u_i(0)$ (and small non-zero values for the $v_i(0)$), the $u_i(t)$ asymptotically converge to $s_i$ where $s_i$ is the ith value in the sorted sequence of the $u_i(0)$.

This system can be specified in the differential setting of MGS by:

$$ \left\{ \begin{array}{l} \dot{U} = \nabla (V^2)\\ \dot{V} = 2 (\nabla {U}) V \end{array} \right. $$

where U and V are coupled topological collections defined on the same one-dimensional cell space, and $\nabla$ is a gradient-like operator inducing the direction followed by the sort.

From this specification, many applications can be derived. Obviously the original formulation can be retrieved when the underlying cell space is a sequence and labels are real numbers. By understanding literally the specification as a usual system of differential equations, the implementation computes the sorting of a continuous field. In fact, the formulation can be interpreted in n dimensions giving raise to a fully polytypic specification of sorting in several dimensions. By relying on genericity and by switching the labels from numbers to sets of symbols, the system turns to be a distributed sorting algorithm in the artificial chemistry style. See Fig. 13.14 for illustrations.

Fig. 13.14

Different applications of the Brockett’s analog sort in MGS. a presents the results of an MGS simulation of the original system sorting the sequence [1000, 2000, 3000, 4000] into [4000, 3000, 2000, 1000]. Time flows from left to right; each curve in a plot shows the evolution of an element of the sequence. b–d show 3 runs of the same system in the artificial chemistry interpretation. While the original system is deterministic, the chemical version is stochastic (relying on the Gillespie rule application strategy) and exhibits a wide variety of trajectories; however almost all runs converge to the correct sorted sequence (with more or less accuracy). e–f illustrate the sort of continuous fields respectively in 1D (on the left, the space-time diagram of the sort; on the right, states of the system after 0, 100, 1000 and 10000 steps of simulation) and 2D following the x-axis (from left to right, states of the system after 0, 100, 200 and 3000 steps of simulation)

13.5.3 Future Research Directions

The development presented here only scratch the surface of the subject and many works remain to be done to investigate and to understand the contribution of the differential formulation in MGS. For example, while the development of MGS has put emphasis on the spatial structure induced by the interactions, the temporal aspects have been relegated to the choice of the rule application strategy. In differential calculus, time is considered homogeneously with space with the use of a temporal derivative (written $\dot{X}$ in the previous differential equations) revealing the complex and algebraic nature of time in computation. A future work must relate the dot operator with the causal structure mentioned in Sect. 13.2 and revisit the concept of rule application strategy in consequence. In the previous example, the transport of data seems more effective to express patterning rather than structural evolution. The handling of dynamical structures with the sole use of the MGS differential operators remains an open question.

Appendix

This section introduces some elements of algebraic topology and discrete differential calculus used in Sect. 13.5. Algebraic topology (and more especially homology) extends the notion of cell space with an algebraic structure. The key ingredients of this extension are the so-called topological chains and boundary operators.

Topological Chains

Given a cell space $\mathscr {K}$ and a non-negative integer n, topological chains of dimension n (or n-chains) are the elements of the free abelian group $C_n(\mathscr {K})$ finitely generated by the $n$-cells of $\mathscr {K}$. A chain $c \in C_n(\mathscr {K})$ can be understood as a function of $S_\mathscr {K}{{\mathrm{\hookrightarrow }}}\mathbb {Z}$ null everywhere but on a finite set of $n$-cells of $\mathscr {K}$. Consequently they can be represented by finite formal sum of the form:

$$ c = c(\sigma _1).\sigma _1 + \cdots + c(\sigma _p).\sigma _p = \sum _{\sigma \in S_\mathscr {K}} c(\sigma ).\sigma $$

where $\{\sigma _1,\dots ,\sigma _p\}$ is the set of cells of $\mathscr {K}$ where c is not null.

Topological chains can be interpreted in various ways. They provide a mean to count the cells of a cell space; the possibility to count cells negatively allows to consider orientation of cells. Topological chains are sometimes defined with values in an arbitrary group.¹¹ Here we restrict ourselves to the group $\mathbb {Z}$.

Boundary Operators

By definition, cell spaces cannot take into account multi-incidence, that is the number of times a cell is incident to another. A solution [53] consists in considering the incidence numbers $i_\sigma ^\tau$ for any pair of cells $\sigma$ and $\tau$, so that:

$$ \forall \sigma \quad \partial \sigma = \sum _{\tau < \sigma } i_\sigma ^\tau .\tau \quad \Rightarrow \quad \partial {c} = \sum _\sigma c(\sigma ) \partial \sigma $$

Of course, $i_\sigma ^\tau = 0$ if $\sigma$ and $\tau$ are not incident, and $i_\sigma ^\tau$ can be negative to take orientation into account. The operator $\partial$ is linearly extended to any chain of $C_n(\mathscr {K})$.

Homology uses the operator $\partial$ to study holes in a cell space. In such a case, the operator is called a boundary operator and has to respect the nil-potent property: $\partial \circ \partial = 0$, which can be interpreted as “the boundary of a boundary is empty” or “a boundary has no boundary”. Such a boundary operator gives raise to a mathematical structure called a chain complex:

Discrete Forms and Derivative

The discrete counterpart of differential forms coincides with the notion of cochain [11]. The set of discrete forms of dimension n (or n-forms¹²) over a cell-space $\mathscr {K}$ with values in an abelian group G consists of the group homomorphisms of $C^n(\mathscr {K},G) = \mathrm {Hom}(C_n(\mathscr {K}), G)$ from $n$-chains to the group G. This set inherits naturally the group structure of $C_n(\mathscr {K})$ and its elements can be uniquely specified by the value of G they associate with each cell of $\mathscr {K}$. Like chains, forms can be represented by formal sums with a slight difference, the sum can be infinite. For example, the action [F, c] of a $n$-form F on a $n$-chain c works as follows:

$$ [g_1 \cdot \sigma _1 + g_2.\sigma _2 + g_3.\sigma _3,2.\sigma _1-4.\sigma _3] = 2g_1 - 4g_3 $$

where the $g_i$ are elements of G. This application is the discrete analogue of integration of forms on some domain represented by a chain.

The derivative $\mathbf d{F}$ of a $n$-form F is then defined to implement a discrete Stokes’ theorem, that is, $\mathbf d{F}$ is the $(n+1)$-form adjoint of the boundary operator with respect to application:

$$ \forall c\ [\mathbf d{F},c] = [F,\partial {c}] \quad \Rightarrow \quad \mathbf d{F} = \sum _{\sigma } \left( \sum _{\tau < \sigma } i_\sigma ^\tau \,F(\tau )\right) \cdot \sigma $$

Informally the derivative $\mathbf d{F}$ associates with a cell $\sigma$ the sum of the values associated with the incident cells of $\sigma$ in F with respect to the incident numbers. One can show easily that $\mathbf d\circ \mathbf d= 0$ leading to the mathematical structure of cochain complex used in cohomology:

Duality

Since a cell space is a partially ordered set, one may consider its inverse order. With this respect, one associates with any cell space $\mathscr {K}$ a cell space $\star \mathscr {K}$, called the dual of $\mathscr {K}$, as a formal copy of $\mathscr {K}$ where the incidence relationship is reversed. By referring by $\star \sigma$ to the copy of $\sigma$ in $\star \mathscr {K}$, we get

$$ \forall \sigma ,\tau \quad \star \sigma \prec \star \tau \Leftrightarrow \tau \prec \sigma $$

When $\mathscr {K}$ is of dimension n, so does $\star \mathscr {K}$ and $\dim (\star \sigma )=n-\dim (\sigma )$.

Like any cell complex, $\star \mathscr {K}$ can be equipped with a boundary operator $\star \partial$ and its dual derivative operator $\star \mathbf d$, so that, considering a well chosen correspondence operator $*$ between the primal and dual forms, we get the following diagram:

In this presentation, the choice of $\star \partial$ (i.e., of the incidence numbers $i_{\star \tau }^{\star \sigma }$ of $\star \mathscr {K}$) and the correspondence operator $*$ (as well as the group G) are left as parameters since it depends on the application. For example, while [53] chooses $i_{\star \tau }^{\star \sigma }=i_{\sigma }^{\tau }$, [11] uses $i_{\star \tau }^{\star \sigma }=-1^{\dim (\sigma )}i_{\sigma }^{\tau }$. Moreover the correspondence operator takes an important place in the discrete calculus of [11] as it corresponds to the discrete counterpart of the Hodge operator.