Abstract
DNA based nanostructures and devices are becoming ubiquitous in nanotechnology with rapid advancements in theory and experiments in DNA self-assembly which have led to a myriad of DNA nanodevices. However, the modeling methods used by researchers in the field for design and analysis of DNA nanostructures and nanodevices have not progressed at the same rate. Specifically, there does not exist a formal system that can capture the spectrum of the most frequently intended chemical reactions on DNA nanostructures and nanodevices which have branched and pseudo-knotted structures. In this paper we introduce a graph rewriting system for modeling DNA nanodevices. We define pseudo-DNA nanostructures (\(\mathbf {PDN}\)s), which describe the sequence information and secondary structure of DNA nanostructures, but exclude modeling of tertiary structures. We define a class of labeled graphs called DNA graphs, that provide a graph theoretic representation of PDNs. We introduce a set of graph rewrite rules that operate on DNA graphs. Our DNA graphs and graph rewrite rules provide a powerful and expressive way to model DNA nanostructures and their reactions. These rewrite rules model most conventional reactions on DNA nanostructures, which include hybridization, dehybridization, base-stacking, and a large family of enzymatic reactions. A subset of these rewrite rules would likely be used for a basic graph rewrite system modeling most DNA devices, which use just DNA hybridization reactions, whereas other of our rewrite rules could be incorporated as needed for DNA devices for example enzymic reactions. To ensure consistency of our systems, we define a subset of DNA graphs which we call well-formed DNA graphs, whose strands have consistent \(5^\prime \) to \(3^\prime \) polarity. We show that if we start with an input set of well-formed DNA graphs, our rewrite rules produce only well-formed DNA graphs. We give four detailed example applications of our graph rewriting system on (1) Yurke et al. [82] DNA tweezer system, (2) Yurke et al. [77] catalytic hairpin-based triggered branched junctions, (3) Dirks and Pierce [17] HCR, and (4) Qian and Winfree [59] scalable circuit of seesaw gates. Finally, we have a working software prototype (DAGRS) that we have used to generate automatically well-formed DNA graphs using a basic rewriting rule set for some of the examples mentioned.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
15.1 Introduction
15.1.1 Motivation
A DNA nanostructure is a macromolecule composed of DNA strands that are hybridized together and have a predetermined target structure [62]. A DNA nanodevice is a biochemical system composed of DNA nanostructures that undergo dynamic reactions which modify their structure [38]. DNA nanodevices often act as nanoscale machines and are designed to perform specific tasks, including DNA walkers [2, 25, 27, 28, 45, 61, 66–68, 70, 74, 78, 79], tweezers [8, 82], gears [71], and other nanodevices [6, 44, 48, 50].
DNA nanostructures are known to obey structural constraints, which are difficult to model in detail [56]. These include geometric and conformational constraints such as the persistence length, helical pitch, major and minor grooves, supercoiling, conformations under the effect of different hydration levels, and other physical properties [69]. Most commonly intended reactions in structural and dynamic DNA nanotechnology research can be treated on a fundamental level while temporarily discounting these constraints.
We propose a method of coarse-grained modeling that provides a high-level abstraction of DNA nanostructures. Our coarse-grained modeling of DNA nanostructures includes a class of structures which we call pseudo-DNA nanostructures, similar to the conventional cartoon descriptions of DNA nanostructures, and an equivalent class of labeled graphs which we call well-formed DNA graphs.
A general approach to modeling a biophysical structure is to develop a coarse-grained model. The term “coarse-grained modeling” has conventionally been used to refer to models which more concerned with biophysical models [18, 46, 52]. By coarse-grained modeling, we refer to the modeling of the primary and secondary structure, and some other properties that affect hybridization and enzymatic reactions, or transformations, but do not attempt to model or provide specification of tertiary structure. Tertiary structure is not generally of key importance to these reactions on DNA nanostructures with relatively smaller scales of complexity (where steric hindrance does not greatly influence reactions).
15.1.2 Prior and Related Work
The visual representation of DNA nanostructures often termed DNA cartoons is widely used (such as in Fig. 15.1b as a representation of Fig. 15.1a). They provide a visual representation of the secondary structure of DNA nanostructures, including \(5^\prime \) to \(3^\prime \) directionality and hybridizations between single strands of DNA. Their goal is to abstract away individual base-pairings and helical twists to provide a domain-based representation. Though there are many variations on this, most cartoon renderings represent a strand with a line that terminates in an arrow at the \(3^\prime \)-end. When two complementary antiparallel strands hybridize to each other through base pairing, a series of lines between the strands represent the hybridization bonds between each base pair. DNA cartoons are frequently used in practice for describing DNA nanostructures and may also be used by visual GUI software, e.g., for graphical specification and rendering of DNA nanostructures. Alternatives to string-based methods, such as explicit graph structures, are needed in order to model certain DNA nanostructures, especially those with branched or pseudo-knotted regions. Many earlier examples of such graph-based approaches that provide abstractions of DNA nanostructures and their reactions have been developed. Jonoska made early use of graphs for representing DNA-based computations [31]. Reif [60] developed a graph model for representing DNA nanostructures with representation of \(5^\prime \) to \(3^\prime \) directionality and hybridizations between single strands of DNA [60]. In addition, Birac et al. [3] have made use of graph-based data structures for the design and modeling of DNA nanostructures [3]. Other more recent graph models for DNA nanostructures include those of Kawamata et al. [30, 32]. None of these model base-stacking which can be essential for some DNA reactions [76]. There are various prior works on coarse-grained modeling of dynamic DNA nanodevices that transition between distinct DNA nanostructures. Cardelli [5], Phillips and Cardelli [54] and Lakin et al. [40, 42] developed an algebra for representing a restricted set of DNA-based reactions, such as see-saw gates [58]. Yin et al. [77] made use of a graphical representation of biomolecular self-assembly pathways, in which DNA was rendered into an abstract nodal representation, then used to manipulate hybridization self-assembly reaction in constructing nanostructures [77]. Kumara et al. [39] presented analysis of assembly pathways for different types of DX tiles that previously refused to assemble into parallel structures [39]. Ibuki et al. [30] also developed a graph-structure to model basic DNA reactions [30]. Finally, McCaskill and Niemann [49] presented the most relevant example of a DNA graph replacement scheme, which provides a framework for computing intermediary and target DNA and RNA structures, and more specifically enzymatic reactions [49]. Klavins developed graph grammar models for robotic self-assembly, and also adapted this in DNA self-assembly [33–36].
Graph grammars and graph rewriting systems (defined in Sect. 15.2.4) have been described at length in [11, 12, 19, 65]. Graph grammars were introduced as a generalization of formal grammars on strings (Chomsky grammars [9, 10]) to those on graphs [20]. Its use to describe distributed assembly started with [35]. Here, we are attempting to use this same formalism to model commonly intended DNA hybridization reactions. Graph grammars were used by Flamm et al. [22, 22], Andersen et al. [1] and Mann et al. [47] to model chemical reactions, and a Graph Grammar Library (GGL) software developed to that effect.
Related work in the field of DNA nanotechnology includes [26] domain-based DNA reaction enumerator, in which strands and nanostructures are represented as formal structures which produce the most relevant reaction pathway. The method is based on condensing large reaction graphs by excluding a number of transient (fleeting or fast reaction) states and combining strongly connected components in the graph. In Sect. 15.9, we provide an example of how our graph rewriting system can utilize this concept to decrease the number of states. Finally, oxDNA [18, 46, 52] is currently the most advanced coarse-grained modeling systems at the time of writing. However, oxDNA uses a biophysical model that treats each nucleotide as a rigid body, with a plane perpendicular to the base so as to capture its planar orientation, and collinear interacting sites. This paper disregards these physical properties and attempts to abstract them away, since one advantage of this approach is being able to demonstrate lesser-likely reaction pathways.
The behavior of many complex systems can be explicitly rendered into graph transformations. Graph rewriting systems provide a powerful, intuitive and flexible method of analyzing and modeling DNA reactions [15, 55]. Our DNA graph model allows us to model base-stacking interactions between strands in addition to the conventional hybridization bonds in DNA nanostructures. We introduce a graph-theoretic approach that uses graph transformations to represent reactions on DNA nano structures; these graph transformations correspond to DNA reactions, and transform well-formed DNA graphs into modified well-formed DNA graphs that represent the products of these corresponding reactions.
Our DNA graphs and graph rewrite rules provide a powerful and expressive way to model DNA nanostructures and their reactions. These rewrite rules model most conventional reactions on DNA nanostructures, which include hybridization, dehybridization, base-stacking, and a large family of enzymatic reactions. To ensure consistency of our systems, we define a subset of DNA graphs which we call well-formed DNA graphs, whose strands have consistent \(5^\prime \) to \(3^\prime \) polarity. We show that if we start with an input set of well-formed DNA graphs, our rewrite rules produce only well-formed DNA graphs. Initially it was thought that one of the advantages of our approach is that existing rewrite systems which automate the graph rewriting process can be used, but have since realized that they require some modification, which is why we chose to develop our own rewriting systems. Some rule-based systems that were explored included Kappa and KaSim [13, 21], Porgy and Tulip [55], amongst others, but found that they could not easily perform the domain-level modeling that were intended using graph rewriting within these systems. As an example using Kappa, separating out the domains as distinct but connected “agents” while respecting the order in which they occur on a strand, and simultaneous attempting to incorporate branched and pseudo-knotted structures, while accommodating a rule-set that is intended to be generalizable did not seem readily feasible.
15.1.3 Overall Organization
In Sect. 15.2, we define the class of pseudo-DNA nanostructures, with an example, define the class of well-formed DNA graphs, and finally present our graph rewriting systems. Section 15.3 introduces a set of non-enzymatic graph rewrite rules. In Sect. 15.4, we show that every graph generated by our rewriting systems belongs to the class of well-formed DNA graphs, and we show that this class of graphs is equivalent to the class of pseudo-DNA nanostructures. Algorithms 1 and 2 contain algorithms for the construction of members of the classes \(\mathbf {PDN}\) and \(\mathbf {WFDG}\) as part of the proof in Sect. 15.4. In Sect. 15.5, we show an example application of the graph rewriting systems to Yurke et al. [82] DNA tweezer system. Section 15.6 briefly describes our software system for automating our graph rewriting systems. Section 15.7 displays further examples of the application of graph rewriting systems to existing DNA reaction systems, including the catalytic hairpin-based branched junctions [17, 77] HCR [17] and the [59] scalable circuit comprised of seesaw gates [59]. Section 15.8 has an extended (enzymatic) rewrite system that is used in conjunction with the basic system. Section 15.7 Provides further example applications of our graph rewrite rules. Section 15.8 Provides enzymic graph rewrite rules. Sections 15.9, 15.10 and 15.11 discuss further details of the graph rewrite rules and how they can be combined with existing work. Section 15.12 contains a summary of our results as well as a critical analysis of the limitations and advantages of our approach.
15.2 Definitions
15.2.1 Pseudo-DNA Nanostructures
In order to accommodate certain physically feasible structures which may be generated by our rewriting systems, but at the same time maintain a general method of characterizing the most frequently intended DNA reactions, we define a class of structures, pseudo-DNA nanostructures (\(\mathbf {PDN}\)). The class describes only the sequence information and secondary structure of DNA nanostructures, and excludes tertiary structure information. Any pseudo-DNA nanostructure \(p \in \mathbf {PDN}\) is a set of DNA strands in the nanostructure, each described by domains (which can be one nucleobase or a sequence of nucleobases) and the hybridizations between domains.
Formally, we define \(p \in \mathbf {PDN}\) as a quintuple \((\mathscr {D},\mathscr {S}, \delta , \mathscr {H}, \mathscr {B})\), where:
-
1.
\(\mathscr {D}\) is a set of domains \(\{d_1, d_2, \ldots \}\), and their complements \(\{\bar{d_1}, \bar{d_2}, \ldots \}\) (if they exist in the structure). This is necessary because all domains involved in the \(\mathrm {PDN}\) dictate the relationships in the set of hybridizations. If the complementary domains do not exist, then the set of hybridizations is empty.
-
2.
\(\mathscr {S}\) is a set of strands \(\{s_1, s_2, \ldots \}\)
-
3.
\(\delta :\mathscr {S}\rightarrow \mathscr {D}^*\) maps each strand in \(\mathscr {S}\) to a string over the set of domains in \(\mathscr {D}\), and each string’s domains are read in the \(5^\prime \) to \(3^\prime \) direction.
-
4.
\(\mathscr {H}\) is the set that maps the hybridization relationship between domains of strands in \(\mathscr {S}\). \(\mathscr {H}\) is a set of 4-tuples. Each \(h\in \mathscr {H}\) is of the form \((s_1,i,s_2,j)\), indicating that the ith domain of strand \(s_1\) is hybridized to the jth domain of strand \(s_2\). Each domain of any strand can hybridize to no more than one complementary domain of another (or the same) strand.
-
5.
\(\mathscr {B}\) is the set that maps base-stacking interactions, specifically those that involve domains on different strands in \(\mathscr {S}\). That is, the members in \(\mathscr {B}\) define blunt-end, overhang, and frayed-end base-stacking interactions between domains which are located on different strands (whether on the \(3^\prime \) or \(5^\prime \) in the case of blunt-end, or at an unpaired location in the case of frayed-end base-stacking, or both in the case of overhang base-stacking). \(\mathscr {B}\) is a set of 12-tuples. Each \(b\in \mathscr {B}\) is \((s_1,i,e_1,s_2,j,e_2,s_3,k,e_1^\prime ,s_4,\ell ,e_2^\prime )\). This 12-tuple describes the hybridization of two pairs of strands (or two duplexes), (\(s_1,i,s_3,k\)) and (\(s_2,j,s_4,\ell \)). The base stacking exists between \(s_1\)’s ith domain’s \(e_1\)th end with \(s_3\)’s kth domain’s \(e^\prime _1\)th end, and simultaneously between \(s_2\)’s jth domain’s \(e_2\)th end with \(s_4\)’s lth domain’s \(e^\prime _2\)th end. In this case, \(e_1^\prime \) and \(e_2^\prime \) refer to the corresponding domain ends of \(s_1\) and \(s_2\), respectively.
An example is shown in Fig. 15.2, the three-arm branched structure may be represented as a member of \(\mathbf {PDN}\) as follows:
-
1.
\(\mathscr {D}=\{a,b,c,\bar{a},\bar{b},\bar{c}\}\)
-
2.
\(\mathscr {S}=\{s_1,s_2,s_3\}\).
-
3.
\(\delta (s_1)=ab\), \(\delta (s_2)=\bar{b}c\), \(\delta (s_3)=\bar{c}\bar{a}\).
-
4.
\(\mathscr {H}=\{(s_1,1,s_2,2),(s_1,2,s_3,1),(s_3,2,s_2,1)\}\)
-
5.
\(\mathscr {B}\) may be any one of the following sets, depending on the junction’s conformation [43]:
-
a.
\(\emptyset \)
-
b.
\({(s_1, 1, 3^\prime , s_3, 2, 5^\prime , s_2, 2, 5^\prime , s_3, 1, 3^\prime )}\)
-
c.
\({(s_1, 1, 3^\prime , s_3, 2, 5^\prime , s_1, 2, 5^\prime , s_2, 1, 3^\prime )}\)
-
d.
\({(s_2, 1, 3^\prime , s_1, 2, 5^\prime , s_3, 1, 3^\prime , s_1, 2, 5^\prime )}\)
-
a.
15.2.2 DNA Graph Notation
We will define the following notation for DNA graphs in order to facilitate the introduction of our DNA graph rewriting systems (note that we will subsequently show that a subset of DNA graphs, called well-formed DNA graphs, are equivalent to pseudo-DNA nanostructures). A DNA graph is a vertex-labeled and edge-labeled graph formally defined as an 8-tuple \(G=(V,E,L_{V},L_{E},\Sigma ,vl,el,\delta )\) where:
-
1.
V is a finite set of vertices. Each vertex represents an unhybridized DNA strand domain, a hybridized DNA strand domain, a \(3^\prime \)-end or a \(5^\prime \)-end of a DNA strand.
-
2.
E is a finite set of edges. Each edge represents a relationship between two vertices.
-
3.
 is the finite set of vertex labels, where:
is the finite set of vertex labels, where:-
a.
 : unhybridized vertex, where every base in the domain that this vertex is mapped to is unhybridized.
: unhybridized vertex, where every base in the domain that this vertex is mapped to is unhybridized. -
b.
 : hybridized vertex, where every base in the domain that this vertex is mapped to is hybridized.
: hybridized vertex, where every base in the domain that this vertex is mapped to is hybridized. -
c.
\(3^\prime \): 3 prime end.
-
d.
\(5^\prime \): 5 prime end.
-
a.
-
4.
 is the finite set of edge labels, where:
is the finite set of edge labels, where:-
a.
 : base-stacking, where the arrow direction indicates \(5^\prime \) to \(3^\prime \) directionality. Here, we only explicitly represent base-stacking interactions between adjacent bases on different strands, and not the base-stacking interactions between adjacent bases on a single strand.
: base-stacking, where the arrow direction indicates \(5^\prime \) to \(3^\prime \) directionality. Here, we only explicitly represent base-stacking interactions between adjacent bases on different strands, and not the base-stacking interactions between adjacent bases on a single strand. -
b.
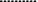 : hybridization.
: hybridization. -
c.
 : covalent bond linking base pairs between two domains, where the arrow direction indicates strand directionality.
: covalent bond linking base pairs between two domains, where the arrow direction indicates strand directionality. -
d.
 : is an edge label that signifies a strand-end, where the vertical bar location indicates strand directionality.
: is an edge label that signifies a strand-end, where the vertical bar location indicates strand directionality.
-
a.
-
5.
\(\Sigma \) is the set of all possible domain names. For each \(d\in \Sigma \), its complement is denoted as \(\bar{d}\), and it represents the reverse-complement base sequence. It is assumed that each \(d\in \Sigma \) has a unique complement \(\bar{d} \in \Sigma \) s.t. no other symbol in \(\Sigma -\{d\}\) can have a complement \(\bar{d}\). Each domain d is mapped to a base sequence, which is a string over the set \(\{A,C,T,G\}\), and the complement of each member is \(\bar{A}=T\), \(\bar{T}=A\), \(\bar{C}=G\), \(\bar{G}=C\).
-
6.
\(vl: V\mapsto L_V\), is a function that assigns a label to each vertex.
-
7.
\(el: E\mapsto L_E\), is a function that assigns a label to each edge.
-
8.
\(m: V \mapsto {\Sigma }\) is a mapping between vertices and domain names.
15.2.3 Well-Formed DNA Graphs
To be concise, we will define a DNA strand graph
here as a maximal subgraph that consists of one or more vertices with a label in the vertex label subset  connected only via edges labeled
connected only via edges labeled  . In other words, it is a graph representing only one strand, with no hybridization or base-stacking labeled edges (as shown in Fig. 15.3).
. In other words, it is a graph representing only one strand, with no hybridization or base-stacking labeled edges (as shown in Fig. 15.3).
There are two types of strands: circular (see Sect. 15.4) and non-circular, where a non-circular strand has an explicit start and end, as opposed to a circular strand, which maintains directionality without having ends.
A well-formed DNA graph (referred to as \(\mathbf {WFDG}\)), is a DNA graph that adheres to the six constraints below. Some of the constraints apply differently to circular strands, which will be made clear as we define the constraints in this section.
The in-degree
of a vertex is the number of edges which are directed into that vertex. The out-degree
of a vertex is the number of edges which are directed out of that vertex. The degree
of a vertex is the sum of its in-degree and out-degree. The direction of an edge is indicated by the edge label’s end marker location. For example, in Fig. 15.3a, the direction of the edge with label  between vertices \(v_1,u_1\) (where label(\(u_1)=3^\prime \), and \(v_1\) is the hybridized vertex, labeled
between vertices \(v_1,u_1\) (where label(\(u_1)=3^\prime \), and \(v_1\) is the hybridized vertex, labeled  and marked with the domain name “\(d_1\)” for ease of reference) is towards \(u_1\).
and marked with the domain name “\(d_1\)” for ease of reference) is towards \(u_1\).
Constraint 1: Strand Ends In circular strands, no ends exist. That is, by definition, \(\not \exists u,v \in V\) s.t. their labels are \(5^\prime \) and \(3^\prime \), respectively.
In a non-circular strand, \(\exists u,v\in V\) s.t. their labels are \(5^\prime \) and \(3^\prime \), respectively, subject to:
-
1.
in-degree(u) \(= 0\) and out-degree(u) \(= 1\), and a directed edge labeled
 from u (i.e. the \(5^\prime \)-end) to some vertex w s.t. label(w)
from u (i.e. the \(5^\prime \)-end) to some vertex w s.t. label(w) .
. -
2.
in-degree(v) \(= 1\) and out-degree(v) \(= 0\), and a directed edge labeled
 to v (i.e. the \(3^\prime \)-end) from some vertex w s.t. label(w)
to v (i.e. the \(3^\prime \)-end) from some vertex w s.t. label(w) .
.
Constraint 2: Unhybridized Vertex Degree \(\forall \) vertices \(v \in V\) s.t.  then in-degree(v) \(= 1\) and out-degree(v) \(= 1\).
then in-degree(v) \(= 1\) and out-degree(v) \(= 1\).
Constraint 3: Hybridized Vertex Degree \(\forall \) vertices \(v \in V\) s.t.  then \(\mathrm {3 \le deg(v) \le 5}\). A discussion of the reasoning behind this can be found in Sect. 15.10 (on P. XXX).
then \(\mathrm {3 \le deg(v) \le 5}\). A discussion of the reasoning behind this can be found in Sect. 15.10 (on P. XXX).
Constraint 4: Vertex Edge Labels For each vertex \(v \in V\) the following conditions apply:
-
1.
If the vertex v has
 , then it has exactly one hybridization-labeled edge
, then it has exactly one hybridization-labeled edge  . This edge is treated as two edges going in both directions, but is represented as one undirected edge. Which means it counts both an an in-degree and out-degree for each participating vertex.
. This edge is treated as two edges going in both directions, but is represented as one undirected edge. Which means it counts both an an in-degree and out-degree for each participating vertex. -
2.
If the vertex v has
 , then \(\exists i\) base-stacking-labeled edges \(e \in E\) connected to v s.t.
, then \(\exists i\) base-stacking-labeled edges \(e \in E\) connected to v s.t.  and i is an integer s.t. \(0\le i \le 2\)
and i is an integer s.t. \(0\le i \le 2\)
-
3.
\(\exists j\) covalently-labeled edges \(e \in E\) connected to v s.t.
 and j is an integer s.t. \(0\le j \le 2\), where there is at most one edge directed towards v and at most one edge directed away from v.
and j is an integer s.t. \(0\le j \le 2\), where there is at most one edge directed towards v and at most one edge directed away from v. -
4.
\(\exists k\) edges labeled with
 connected to v, s.t. \(k=|2-j|\), at most one edge is directed towards v and at most one edge directed away from v.
connected to v, s.t. \(k=|2-j|\), at most one edge is directed towards v and at most one edge directed away from v.
Constraint 5: Complementarity For every vertex v where  , and \(m(v)=d\in \Sigma ^+\) there is a corresponding vertex \(\bar{v}\) s.t.: \(e(v,\bar{v})\in E\),
, and \(m(v)=d\in \Sigma ^+\) there is a corresponding vertex \(\bar{v}\) s.t.: \(e(v,\bar{v})\in E\),  ,
,  and \(m(\bar{v})=\bar{d}\in {\Sigma }^+\), the complement of d.
and \(m(\bar{v})=\bar{d}\in {\Sigma }^+\), the complement of d.
Constraint 6: Directionality If \(\exists w,x,y\in V\) s.t. w is directly connected to x, and x is directly connected to y through edges labelled with  , then exactly one of the following is true:
, then exactly one of the following is true:
-
1.
Either the edge e(w, x) is directed towards x iff the edge e(x, y) is directed towards y, or the edge e(w, x) is directed towards w iff the edge e(x, y) is directed towards x.
-
2.
In non-circular strands (recall Constraint 1), if \(\exists u,v \in V\) s.t. their labels are \(5^\prime \) and \(3^\prime \), then exactly one of the following statements has to be true:
-
a.
There exists a directed path of covalently-labeled edges from u to v that passes through w, x, y, in that order.
-
b.
There exists a directed path of covalently-labeled edges from u to v that passes through y, x, w, in that order.
-
a.
-
3.
In circular strands, this is not applicable (recall Constraint 1). A rendering of the repercussions on circular strands is made in Fig. 15.4.
Directionality is necessary for well-formed DNA graphs to ensure context-free nature of rewriting systems. a A circular duplex structure, where the domain sequences are ordered in the direction of the dotted arrow. b Directionality of the same duplex in a if cut by an enzyme. c Directionality of the same duplex in a if cut by an enzyme, but had the reverse direction of the domain sequences in b
15.2.4 Graph Rewriting Systems
A graph rewriting system is a set of rewrite rules that transforms a graph instance to another, both belonging to the same class of graphs. Each rule in our graph rewriting systems has the form (also known as single pushout) [51] of a triple \(p = \langle L \overset{r}{\rightarrow } R \rangle \), where the left-hand side in each rule, L, undergoes a partial graph morphism r, to a right-hand side R. The rule is applied to a host graph, or the graph to be transformed via the application of a rewrite rule. An occurrence of L in a graph G makes the rule applicable. This occurrence is called a match [64]. In other words, a host graph graph G can be transformed into another graph H, first by finding a matching between the left-hand side L of a rule r within the host graph, and transforming it to the right-hand side R in H. In DAGRS (DNA Graph Rewriting System), a matching is found by applying the subgraph isomorphism algorithm by Ullmann [73] (explained in Sect. 15.6).
15.2.5 Our DNA Graph Rewriting Systems
For the purpose of brevity, we have arranged the set of rewrite rules that define our graph rewriting systems between Sect. 15.3 (non-enzymatic) and Sect. 15.8 (enzymatic): Sect. 15.3 includes only hybridization and base-stacking rules; and Sect. 15.8 lists the extended rewriting rules that accompany the basic set.
Each side of the rewrite rule is a graph that follows the DNA graph notation defined in Sect. 15.2.2; and the well-formedness constraints defined in Sect. 15.2.3. As explained previously, the left-hand side of each rule is a graph that matches a subgraph of a larger, host graph G. This subgraph encodes: the vertices, edges, vertex-labels and edge-labels, and directionality. The host graph G in this case is a DNA state graph, which is some DNA graph G containing one or more DNA strands (as defined in Sect. 15.2.3), which comprise a well-formed DNA graph. These rules are intended for coarse-grained modeling, and are independent of any external parameters like salt concentration and the pH value of the buffer (An extension of this work may involve applying these rules within the confines of reaction rates, which would dramatically decrease the number of possible rules that may be applied at each transformation junction starting from the input species).
15.3 Non-enzymatic DNA Graph Rewriting Rules
The rules are structured as follows:
-
1.
Cartoon Rendering: a DNA cartoon depiction of the DNA strands or complex.
-
2.
Rewrite Rule: the corresponding graph rewrite rule
-
3.
r and l: the direction of rule application. r indicates that the rule transforms the left-hand side L to the right-hand side R. If the rule also has the direction l, then it can be used to transform R to L.
-
4.
L refers to the left-hand side, and R is the right-hand side.
Rule #1: Domain Binding
Cartoon Rendering |
 |
Rewrite Rule |
 |
Rewrite Rule: Two complementary DNA domains d and \(\bar{d}\) hybridize together to form a duplex, or double-stranded DNA. Note, the cartoon represents two strands each made up of one domain, but the strands may be surrounded by other domains (vertices) in either direction, while maintaining their original directionality.
\(\mathbf {L}\): The unhybridized domains d and \(\bar{d}\) are each represented by a circle, with no edge between them.
\(\mathbf {R}\): They are each represented as solid circles (hybridized). The dashed edge represents the hydrogen bond(s) between d and \(\bar{d}\).
Rule #2: Strand Displacement
Cartoon Rendering |
 |
Rewrite Rule |
 |
Rewrite Rule: Five domains are involved in this transformation. The vertex with domain label \(\bar{d_2}\), which corresponds to the domain covalently bound to the complex on the left-hand side, displaces a vertex labeled with the same domain \(\bar{d_2}\), which corresponds to the domain hybridized to \(d_2\).
\(\mathbf {L}\): The upper strand region is composed of domains \(d_1\), \(d_2\). \(d_1\) is hybridized to \(\bar{d_1}\), and \(d_2\) is hybridized to its complement \(\bar{d_2}\).
\(\mathbf {R}\): The hybridization bond between vertex \(\bar{d_2}\) and \(d_2\) has been removed, and \(\bar{d_2}\) has now been relabeled with  . The vertex with domain \(\bar{d_2}\), which is covalently bound to \(\bar{d_1}\), is relabeled as hybridized (
. The vertex with domain \(\bar{d_2}\), which is covalently bound to \(\bar{d_1}\), is relabeled as hybridized ( ), and a hybridization edge has now been added to connect this vertex to vertex \(\bar{d_2}\).
), and a hybridization edge has now been added to connect this vertex to vertex \(\bar{d_2}\).
Rule #3: Base stacking
Cartoon Rendering |
 |
Rewrite Rule |
 |
Rewrite Rule: Two double stranded DNA complexes, each comprised of two vertices with domains \(d_1,\bar{d_1}\) and \(d_2,\bar{d_2}\), respectively, are present. All the vertices are attached to \(5^\prime \) or \(3^\prime \)-labeled vertices, where the vertex labeled \(d_1\) is connected to a vertex labeled with a \(3^\prime \), and \(d_2\) to a vertex labeled \(5^\prime \), etc. A base-stacking bond between them is formed. Since base-stacking may be assumed to be directionally independent [76], the directionality of the domains on each duplex relative to their neighbors do not really matter, so this rule can be extended to include all configurations of antiparallel duplex directionality.
\(\mathbf {L}\): Solid vertices with labels \(d_1\) and \(\bar{d_1}\) are connected by a hybridization edge. The vertex labels \(3^\prime \) and \(5^\prime \) show the directionality of each domain represented by the vertices. Similarly for \(d_2\) and \(\bar{d_2}\).
\(\mathbf {R}\): The two duplexes form a base-stacking bond with each other. This is represented by the edges between vertices labeled \(d_1\) and \(d_2\), and between \(\bar{d_2}\) and \(\bar{d_1}\).
Rule #4: Base stacking with overhangs
Cartoon Rendering |
 |
Rewrite Rule |
 |
Rewrite Rule: Similar to rule #3, however, here one of the double stranded DNA complexes actually has overhangs (domains \(d_3\), \(d_4\)) on both ends.
\(\mathbf {L}\): Vertices with labels \(d_1\) and \(\bar{d_1}\) have covalently-labeled edges with \(d_3\) and \(d_4\), and the edge directions show the strands’ \(5^\prime \) to \(3^\prime \) directionality. The vertices labeled \(d_2\) and \(\bar{d_2}\) explicitly show directionality, through the \(5^\prime \) and \(3^\prime \) labeled vertices connected to them via strand-end edges.
\(\mathbf {R}\): The vertices with \(5^\prime \) and \(3^\prime \) labels are destroyed. Base stacking bonds are formed between \(d_2\) and \(d_1\). Likewise between \(\bar{d_1}\) and \(\bar{d_2}\).
Rule #5: Remote Toehold [23] mediated Strand Displacement
Cartoon Rendering |
 |
Rewrite Rule |
 |
Rewrite Rule: Similar to rule #2, but the double-stranded DNA complex now has an extra unhybridized domain \(d_3\), which separates the domains \(d_1\) and \(d_2\). The overhanging domain \(\bar{d_2}\) has to locate the hybridized domain \(\bar{d_2}\), and then displace it.
\(\mathbf {L}\): Vertex with domain \(d_1\) is hybridized to \(\bar{d_1}\), and \(d_2\) to \(\bar{d_2}\). The vertices labeled \(d_1, d_2, d_3\) are connected via covalent bonds, and the \(d_3\) domain is hollow-labeled to indicate that it is unhybridized.
\(\mathbf {R}\): A vertex labeled \(\bar{d_2}\) replaces another vertex mapped to the same domain. Vertex \(\bar{d_2}\) is relabeled with a hybridization label, and the other vertex labeled \(\bar{d_2}\) is now unhybridized, hence it is relabeled as hollow. Note that variations of rule # 5 exist, where the separator between the two parts of the duplex is not a single-stranded region, but different structures that may act to separate both sides (a hairpin, for example), without preventing the reaction from occurring. In addition, rules # 2 and # 5 are also valid, with reverse directionality of the strands.
15.3.1 Distal Toehold Mediated Strand Displacement
In order to describe reactions in the last step of the example in Sect. 15.7, we need to use conditional graph rewriting rules. A conditional check is performed before the application of this rule, whether the two distal parts participating in this reaction are connected via hybridization and covalent bonds. In other words, the structure connecting the two parts is irrelevant, so long as it connects them (Fig. 15.5).
15.4 Correctness of Our DNA Graph Rewriting Systems
To prove the correctness of our DNA graph rewriting systems, or that every graph generated by the systems is a pseudo-DNA nanostructure, we need to prove two things: (1) the class of structures generated by our graph rewriting systems and the class of well-formed DNA graphs \(\mathbf {WFDG}\) are equivalent and (2) that \(\mathbf {WFDG}\) and the class of pseudo-DNA nanostructures are equivalent.
The first part involves first proving a) that every DNA graph obtained by applying a rewrite rule to a well-formed DNA graph is also well-formed (Theorem 1), and (b) that any member of the class of well-formed DNA graphs can be generated by our graph rewriting systems, by demonstrating that every well-formed DNA graph can be obtained, given a well-formed input set of DNA strand graphs (Lemma 1), thus showing that our graph rewriting systems does not produce DNA graphs that do not belong to the class of well-formed DNA graphs.
Together, these two propositions (Theorem 1 and Lemma 1) show that, given a well-formed DNA graph, any DNA graph produced by our graph rewriting systems is also well-formed, and that every well-formed DNA graph may be produced by our graph rewriting systems, hence, the class of graphs produced by our graph rewriting systems is equivalent to the class of well-formed DNA graphs.
In the second part (Theorem 2), we show that the class of well-formed DNA graphs is equivalent to that of the class of pseudo-DNA nanostructures. This is done by proving (a) every pseudo-DNA nanostructure has a corresponding well-formed DNA graph (Lemma 2) and (b) every well-formed DNA graph represents a pseudo-DNA nanostructure (Lemma 3).
These two theorems demonstrate that the class of pseudo-DNA nanostructures and the class of graphs produced by our graph rewriting systems are equivalent.
Theorem 1
For the rules in Sect. 15.3, any application of a DNA graph rewriting system rule on a well-formed DNA graph produces a well-formed DNA graph.
Proof
Using induction, we consider the following cases:
Single application
Let the initial graph \(G_0\) denote an arbitrary, well-formed, DNA graph. For every rule, given a subgraph \(L\subseteq G_{0}\) that matches the left-hand side, \(r:L\rightarrow R\) transforms the subgraph to \(R\subseteq G_{1}\).
-
Rule #1: Domain Binding If rule #1 is applicable, then a single application of the rule to one pair of vertices transforms the subgraph in \(G_{0}\) that matches the left-hand side of rule #1 to the right-hand side, which rewrites the labels of u, v to
 , and adds an edge between them with the label
, and adds an edge between them with the label  , resulting in a new graph \(G_{1}\). \(G_{1}\), which does not violate any well-formedness constraints:
, resulting in a new graph \(G_{1}\). \(G_{1}\), which does not violate any well-formedness constraints:-
Constraint 1—Strand Ends:
No such vertices are affected, because the rule does not apply to them.
-
Constraint 2—Unhybridized Vertex Degree:
Since these unhybridized vertices have not been transformed, then they remain unhybridized, where their in-degree is 1, and out-degree is 1.
-
Constraint 3—Hybridized Vertex Degree:
For vertices u, v, their degree has changed by adding one edge. Either it has increased from 2 to 3, 3 to 4 (in the case of a pre-existing base-stacking-labeled edge), or 4 to 5 (in the case of two pre-existing base-stacking-labeled edges). For all other hybridized vertices, since they have have not been involved in the transformation, then their degrees remain the same.
-
Constraint 4—Vertex Edge Labels:
For vertices u, v, one new edge has been added which has the label
 . Since prior to the transformation no such edge existed, then exactly one edge
. Since prior to the transformation no such edge existed, then exactly one edge  . No other edges nor labels have been affected.
. No other edges nor labels have been affected. -
Constraint 5—Complementarity:
The rule would only be applied to u, v if \(m(u)=d\in \Sigma ^+\) and \(m(v)=\overline{d} \in \Sigma ^+\), so this rule has not been violated.
-
Constraint 6—Directionality:
If the nanostructure does not allow for circular strands, then the hybridization respects anti-parallel directionality.
-
Constraint 1—Strand Ends:
-
Rule #2: Strand Displacement If rule #2 is applicable, then the subgraph L consists of the vertices \(v_1,v_2,v_3,v_4,v_5 \in V\) (starting from the unhybridized (hollow) vertex \(v_1\) with domain \(d_2\)), and edges such that label(\(e(v_4,v_5)\)) \(=\)
 , and label(\(e(v_1,v_2)\)) \(=\)
, and label(\(e(v_1,v_2)\)) \(=\)  . The rewriting rule destroys the edge \(e(v_4,v_5)\), changes the label of \(v_5\) to
. The rewriting rule destroys the edge \(e(v_4,v_5)\), changes the label of \(v_5\) to  and \(v_1\) to
and \(v_1\) to  , and adds a hybridization edge \(e(v_1,v_4)\), which does not violate any of the well-formedness constraints.
, and adds a hybridization edge \(e(v_1,v_4)\), which does not violate any of the well-formedness constraints.-
Constraint 1—Strand Ends:
No such vertices are affected, because the rule does not apply to them.
-
Constraint 2—Unhybridized Vertex Degree:
Except for \(v_1\) (displacing domain \(d_2\)), unhybridized vertices have not been transformed and remain unhybridized, where their in-degree is 1, and out-degree is 1. \(v_5\) has become unhybridized. An edge between \(v_4,v_5\) has been removed, so the vertex degree has been lessened by 1, which means that its degree has changed from 3 to 2, 4 to 3 (if there is a pre-existing base-stacking-labeled edge), or 5 to 4 (in case of two pre-existing base-stacking labeled edges). In addition, \(v_5\) has been relabeled to
 .
. -
Constraint 3—Hybridized Vertex Degree:
For vertex \(v_1\), which has become hybridized, its degree has changed by adding one edge. Either it has increased from 2 to 3, 3 to 4 (in the case of a pre-existing base-stacking-labeled edge), or 4 to 5 (in the case of two pre-existing base-stacking-labeled edges). For all other hybridized vertices, since they have have not been involved in the transformation, then their degrees remain the same.
-
Constraint 4—Vertex Edge Labels:
For vertices \(v_1,v_4\), one new edge has been added which has the label
 . Since prior to the transformation no such edge existed, then exactly one edge
. Since prior to the transformation no such edge existed, then exactly one edge  . One edge \(e(v_4,v_5)\) with label
. One edge \(e(v_4,v_5)\) with label  has been removed.
has been removed. -
Constraint 5—Complementarity:
The rule would only be applied if \(m(v_1)=m(v_5)=d_2\in \Sigma ^+\) and \(m(v_4)=\overline{d_2} \in \Sigma ^+\), so this rule has not been violated.
-
Constraint 6—Directionality:
If the nanostructure does not allow for circular strands, then the hybridization respects anti-parallel directionality.
-
Constraint 1—Strand Ends:
-
Rule #3: Base Stacking If rule #3 is applicable, then the subgraph \(L\subseteq G_{0}\) consists of the vertices \(v_1,v_2,v_3,v_4 \in V\) labeled
 with domains \(d_1, \bar{d_1}, d_2, \bar{d_2}\), respectively. Each of these vertices are connected to \(u_1,u_2,u_3,u_4\) in the same order, with vertex labels \(3^\prime , 5^\prime , 5^\prime , 3^\prime \), respectively. There are no conditions on the directionality of the strands. The subgraph L undergoes the removal of the edges between each pair \(e(u_i,v_i)\), and the vertices \(u_i\), which violates no well-formedness constraints. Then, \(v_1 \) and \(v_2\) are connected via a base-stacking edge, labeled
with domains \(d_1, \bar{d_1}, d_2, \bar{d_2}\), respectively. Each of these vertices are connected to \(u_1,u_2,u_3,u_4\) in the same order, with vertex labels \(3^\prime , 5^\prime , 5^\prime , 3^\prime \), respectively. There are no conditions on the directionality of the strands. The subgraph L undergoes the removal of the edges between each pair \(e(u_i,v_i)\), and the vertices \(u_i\), which violates no well-formedness constraints. Then, \(v_1 \) and \(v_2\) are connected via a base-stacking edge, labeled  , and likewise for \(v_3\) and \(v_4\). No well-formedness constraints are violated in \(G_{1}\).
, and likewise for \(v_3\) and \(v_4\). No well-formedness constraints are violated in \(G_{1}\).-
Constraint 1—Strand Ends:
The vertices \(u_1,u_2,u_3,u_4\) are destroyed.
-
Constraint 2—Unhybridized Vertex Degree:
These vertices are not affected.
-
Constraint 3—Hybridized Vertex Degree:
Vertices \(v_1,v_6\) have had an edge added with label
 .
. -
Constraint 4—Vertex Edge Labels:
No vertices are relabeled.
-
Constraint 5—Complementarity:
No hybridization reactions have occurred.
-
Constraint 6—Directionality:
The directionality of the strands are maintained in the direction of the base-stacking arrows.
-
Constraint 1—Strand Ends:
-
Rule #4: Base Stacking with Overhangs If rule #4 is applicable, then the subgraph \(L\subseteq G_{0}\) consists of the vertices \(v_1\) through \(v_6\) and \(u_1,u_2\). \(v_1,v_6\) (labeled \(d_1\) and \(\bar{d_1}\)) are labeled
 , which are connected to \(v_2,v_5\) (labeled \(d_3\) and \(d_4\)), respectively. In addition, vertices \(v_3,v_4\) (labeled \(d_2\), \(\bar{d_2}\)) are connected to \(u_1,u_2\), which are \(5^\prime \) and \(3^\prime \) labeled vertices, respectively. It is assumed that there are no conditions on the directionality of the strands. The subgraph L undergoes the destruction of the vertices \(u_1,u_2\), and the edges between each pair \(e(u_i,v_j)\). Then, \(v_1\) and \(v_3\) are connected via a base-stacking edge, labeled
, which are connected to \(v_2,v_5\) (labeled \(d_3\) and \(d_4\)), respectively. In addition, vertices \(v_3,v_4\) (labeled \(d_2\), \(\bar{d_2}\)) are connected to \(u_1,u_2\), which are \(5^\prime \) and \(3^\prime \) labeled vertices, respectively. It is assumed that there are no conditions on the directionality of the strands. The subgraph L undergoes the destruction of the vertices \(u_1,u_2\), and the edges between each pair \(e(u_i,v_j)\). Then, \(v_1\) and \(v_3\) are connected via a base-stacking edge, labeled  , and likewise for \(v_4\) and \(v_6\), which does not violate any well-formedness in \(G_{1}\).
, and likewise for \(v_4\) and \(v_6\), which does not violate any well-formedness in \(G_{1}\).-
Constraint 1—Strand Ends:
Two strand-end vertices (\(u_1,u_2\)) are destroyed.
-
Constraint 2—Unhybridized Vertex Degree:
Since these unhybridized vertices have not been transformed, then they remain unhybridized, where their in-degree is 1, and out-degree is 1.
-
Constraint 3—Hybridized Vertex Degree:
Since these hybridized vertices have not been transformed, then they remain hybridized.
-
Constraint 4—Vertex Edge Labels:
For vertices \(v_1,v_3\) (and \(v_4,v_6\)), one new edge has been added which has the label
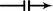 . Since prior to the transformation no such edge existed, then exactly one edge
. Since prior to the transformation no such edge existed, then exactly one edge  .
. -
Constraint 5—Complementarity:
The rule does not affect the hybridization state of any domain, so this constraint remains unviolated.
-
Constraint 6—Directionality:
The rule does not affect the hybridization state of any domain, so directionality is not violated. Directionality of the duplexes relative to each other does not matter [76].
-
Constraint 1—Strand Ends:
-
Rule #5: Remote Toehold mediated Strand Displacement If rule #5 is applicable, then the subgraph \(L\subseteq G_{0}\) consists of the vertices \(v_1,v_3,v_4,v_6 \in V\) labeled
 (with domains \(d_1, d_2, \bar{d_2}, \bar{d_1}\)), and \(v_2, v_5\) are labeled
(with domains \(d_1, d_2, \bar{d_2}, \bar{d_1}\)), and \(v_2, v_5\) are labeled  (with domains \(d_3, \bar{d_2}\), respectively). \(v_5\) is connected covalently to \(v_6\), and \(v_5\) is labeled as unhybridized. Between \(v_1,v_3\), the unhybridized vertex \(v_2\) resides. As the rule is applied, the edge \(e(v_3,v_4)\) is destroyed, and vertex \(v_4\) is relabeled as an unhybridized vertex, and \(v_5\) is then connected to \(v_3\) via a hybridization-labeled edge; these operations violate no well-formedness constraints in \(G_{1}\).
(with domains \(d_3, \bar{d_2}\), respectively). \(v_5\) is connected covalently to \(v_6\), and \(v_5\) is labeled as unhybridized. Between \(v_1,v_3\), the unhybridized vertex \(v_2\) resides. As the rule is applied, the edge \(e(v_3,v_4)\) is destroyed, and vertex \(v_4\) is relabeled as an unhybridized vertex, and \(v_5\) is then connected to \(v_3\) via a hybridization-labeled edge; these operations violate no well-formedness constraints in \(G_{1}\).-
Constraint 1—Strand Ends:
No such vertices are affected, because the rule does not apply to them.
-
Constraint 2—Unhybridized Vertex Degree:
Vertex \(v_6\) (domain \(\bar{d_2})\) has changed from hybridized to unhybridized (and relabeled to
 ). An edge \(e(v_5,v_6)\) was removed, so the degree of \(v_6\) has decreased by 1. All other unhybridized vertices have not been transformed and remain unhybridized, where their in-degree is 1, and out-degree is 1.
). An edge \(e(v_5,v_6)\) was removed, so the degree of \(v_6\) has decreased by 1. All other unhybridized vertices have not been transformed and remain unhybridized, where their in-degree is 1, and out-degree is 1. -
Constraint 3—Hybridized Vertex Degree:
Vertex \(v_1\) (domain \(\bar{d_2}\)) has changed from unhybridized to hybridized. An edge \(e(v_1,v_5)\) has been added. For vertices u, v, their degree has changed by adding one edge. Either it has increased from 2 to 3, 3 to 4 (in the case of a pre-existing base-stacking-labeled edge), or 4 to 5 (in the case of two pre-existing base-stacking-labeled edges). For all other hybridized vertices, since they have have not been involved in the transformation, then their degrees remain the same.
-
Constraint 4—Vertex Edge Labels:
For vertices u, v, one new edge has been added which has the label
 . Since prior to the transformation no such edge existed, then exactly one edge
. Since prior to the transformation no such edge existed, then exactly one edge  . No other edges nor labels have been affected.
. No other edges nor labels have been affected. -
Constraint 5—Complementarity:
The rule would only be applied to u, v if \(m(u)=d\in \Sigma ^+\) and \(m(v)=\overline{d} \in \Sigma ^+\), so this rule has not been violated.
-
Constraint 6—Directionality:
If the nanostructure does not allow for circular strands (which in the current framework we have decided to exclude to ensure this rule’s consistency), then the hybridization respects anti-parallel directionality.
-
Constraint 1—Strand Ends:
Using induction, we have proven that each rewrite rule of our graph rewriting systems generates a well-formed DNA graph, given a well-formed DNA graph as input. We next show that the set of well-formed DNA graphs, has a corresponding member in the set of (tertiary structure-abstracted) DNA nanostructures, or pseudo-DNA Nanostructures. This will be accomplished through Lemmas 1–3, which follow. In Lemma 1, we start by proving that every member W in the class \(\mathbf {WFDG}\) can be generated using the basic set of graph rewriting rules in Sect. 15.3, by starting from the simplest version of W, a DNA strand graph which corresponds to this well-formed DNA strand graph W.
Lemma 1
Every \(W\in \mathbf {WFDG}\) can be produced by a sequence of non-enzymatic rule applications on its corresponding input set of well-formed DNA strand graphs.
Proof
Consider any well-formed DNA graph w. A well-formed DNA graph consists of four types of edge labels, as mentioned in Sect. 15.2.2: base-stacking, hybridization, covalent and strand-ends. Of these, consider only the base-stacking edge set b and the hybridization edge set h. For this \(w \in \mathbf {WFDG}\), construct a graph \(w^\prime \) such that \(w^\prime = w \setminus \{b,h\}\). This results in a set of DNA strands represented by disconnected subgraph components within \(w^\prime \). We consider \(w^\prime \) as the input set of DNA strand graphs. Clearly, \(w^\prime \in \mathbf {WFDG}\). Applying rule # 1 on \(w^\prime \) yields a new graph \(sg_1\). To keep track of states, we can store the graphs in a state graph (called SG), where the root is represented by \(w^\prime \). A child node represents the result of applying a rule to a parent strand graph \(sg_i\in SG\). Subsequent applications of rule # 1, # 3, # 4, which have matching subgraphs in the current \(sg_i\), yields up to two child strand graphs each, until there are no more possible applications. We ignore rules # 2 and # 5, because they result in graphs which are isomorphic to the ones made by the other rules. Let \(w_i^\prime \prime \in SG\) represent a leaf node of SG. Assuming that there are no isomorphic strand graphs, we claim that at least one leaf node w is equivalent to either a \(w_i^\prime \prime \), or any \(sg_i\) in SG. That is because there exists at least one graph \(sg_i\in SG\) which is isomorphic to w. Hence, by some sequence of non-enzymatic rule applications on a set of input DNA strand graphs, we have constructed a well-formed DNA graph. The same holds for any well-formed DNA graph \(\mathbf {WFDG}\).
Lemma 2
Every \(\mathbf {PDN}\) can be represented by a well-formed DNA graph. The algorithm in Algorithm 1 does not violate any \(\mathbf {WFDG}\) constraints.
Proof
Given an input \(\mathbf {PDN}\), \(p = (\mathscr {D},\mathscr {S},\mathscr {H},\mathscr {B})\), we first start by constructing all the strand graphs. For each strand starting from the \(5^\prime \) vertices, an  -labeled vertex is constructed for each domain until no more are encountered, and a \(3^\prime \) vertex is created to terminate the strand. Once all the strand graphs are created, incorporate the hybridization and base-stacking edges (
-labeled vertex is constructed for each domain until no more are encountered, and a \(3^\prime \) vertex is created to terminate the strand. Once all the strand graphs are created, incorporate the hybridization and base-stacking edges ( ), and relabel the hybridized vertices with
), and relabel the hybridized vertices with  .
.
We give an algorithm (Algorithm 1) that constructs a graph W. For each strand, only one \(5^\prime \) and one \(3^\prime \) vertex is created. This ensures constraint 1 is valid. Lines 2–15 ensure constraints 2 and 6 are valid. Lines 19–26 add a single hybridization edge to all hybridized vertices, while lines 28–35 can add at most two base-stacking edges to each vertex. This ensures constraints 3 and 4 are valid. Line 23 ensures constraint 5 is valid.
Lemma 3
Every well-formed DNA graph in \(\mathbf {WFDG}\) has a corresponding \(\mathbf {PDN}\).
Proof
Given an input well-formed DNA graph \(W = (V,E,L_v,L_e,\Sigma ,vl,el,m) \in \mathbf {WFDG}\). We give an algorithm that constructs a \(\mathbf {PDN}\) \(p = (\mathscr {D},\mathscr {S},\mathscr {H},\mathscr {B})\) in Algorithm 2. The pseudocode in Algorithm 2 constructs a valid \(\mathbf {PDN}\) given a well-formed DNA graph. A valid \(\mathbf {PDN}\) contains a set of DNA strands (\(\mathscr {S}\)), the set of domains (\(\mathscr {D}\)) that hybridize (\(\mathscr {H}\)), and the set of domains that base-stack (\(\mathscr {B}\)). Lines 2–15 create a set of domains \(\mathscr {D}\) and strands \(\mathscr {S}\). Each strand can have only one \(5^\prime \) and one \(3^\prime \)-end. Lines 16–20 create a set of hybridizations \(\mathscr {H}\). By constraint 4, there can be at most 1 hybridization per vertex. Lines 21–30 create a set \(\mathscr {B}\) of base stacking tuples. By constraint 4, there can be at most two base-stackings per vertex. The ends of the vertex signify whether the \(5^\prime \) or the \(3^\prime \) end of the vertex base stacks with another edge. Each of the well-formedness constraints ensures that a \(\mathbf {PDN}\) is created.


Theorem 2
Both classes \(\mathbf {WFDG}\) and \(\mathbf {PDN}\) are equivalent: A member of \(\mathbf {PDN}\) exists if and only if it has one corresponding member of \(\mathbf {WFDG}\).
In Lemma 2 we have demonstrated that a pseudo-DNA nanostructure can be transformed into a well-formed DNA graph by constructing vertices and edges for each strand out of the strand domains, and hybridization edges between vertices out of the set of hybridizations, and finally base-stacking edges out of the set of base-stacking interactions, while maintaining the constraints that define the class of well-formed DNA graphs. In Lemma 3, we have demonstrated that every member of \(\mathbf {WFDG}\) has a respective member belonging to \(\mathbf {PDN}\). These three propositions prove that the classes \(\mathbf {WFDG}\) and \(\mathbf {PDN}\) are equivalent. Following that, \(\mathbf {PDN}\) and the class of structures generated by our grammar are equivalent.
15.5 Example: Yurke et al. DNA Tweezer
Table 15.1 illustrates one possible reaction sequence of the DNA tweezer nanomachine, developed by Yurke et al. [82], using DNA graph rewrite rules. In the beginning, the tweezer consists of two duplex DNA arms with toehold domains at both ends (i.e., \(d_2\) and \(d_3\)). \(\bar{d_3}\) and \(\bar{d_2}\) domains from the DNA fuel strand undergo toehold binding (rule # 1) with \({d_3}\) and \({d_2}\) of the tweezer, respectively. As a result of this process, the set strand pinches two arms of the tweezer together and results in the “closed” state with a remaining exposed toehold domain \(d_5\). To open the tweezer, \(\bar{d_5}\) domain of the unset strand \(\bar{d_5}\), \(d_3\), \(d_2\) binds to domain \(d_5\) of the closed-state tweezers. To completely displace the strand \(\bar{d_2}\), \(\bar{d_3}\), \(d_5\) the strand displacement rewrite rule (rule # 2) is applied and results in waste duplex. As a result of this process the original tweezer state is restored. Note this is one path of many possible rule-application sequences. This is also shown in the corresponding states of this path generated by DAGRS in Fig. 15.21.
15.6 Brief Description of Our Prototype Software System
We implemented a prototype that generates all the states possible depending on a subset of the basic rules defined in Sect. 15.3. Choosing a subset of the states, we display one specific sequence of reactions in Table 15.1. The DNA Graph Rewriting System (DAGRS) is a simple prototype implemented in Python 2.7 [57] that uses the graph-tool library [53] to parse, store and apply graph rewriting rules, and uses the [73] subgraph isomorphism algorithm to match the set of left-hand side of the graph rewriting rules to some subgraph in a given host DNA graph G. PyQt5 [63] was used to render the states, which were explored in a breadth-first search manner. This is implemented as follows: a list is maintained of states (E) that have been fully explored (where the given set of rules may no longer be applied to these states), and a queue of states currently being explored Q. The program attempts to find a matching for the first rule supplied by the user on a state removed from the queue (which is some well-formed DNA graph \(s_i\)). If no such matching exists, this is repeated with the next rule in the set. If no matching can be found, the program terminates. If a matching is found, a new state is generated, where the matched subgraph is transformed into the right-hand side of the rule applied. This state is then added to Q, and the next rule is applied to the current state being explored (\(s_i\)). The prototype is able to generate the landscape of states depending on the input species, and the subset of rules supplied. We demonstrated that it is able to accommodate simple systems, including the previous example in Sect. 15.5, as well as further examples mentioned in Sect. 15.7. Depending on the rewrite rules used, all possible applications are considered by using a basic breadth-first exploration of the state-space, starting from an input state. To select the next rule to apply, a subgraph isomorphism test is performed on the current state graph \(G_i\) to check for the existence of some subgraph \(sg_j\) matching the left-hand side of any rewrite rule in a given rule-set. There is the possibility of not generating a large, even exponential, number of structures, if graph rewriting were the only method applied. However, one can restrain the number of generated states depending on other restrictions that are not currently handled, such as domain length (as discussed in the Conclusion section). In essence, the current system does not handle constraining the number of states. However, to show that this graph-centered paradigm can be utilized with at least one alternative way of collapsing the number of states, we applied the results from the work by Grun et al. [26] to an example in Sect. 15.9. Reactions are divided into transient (fast) and non-transient (slow), which has the advantage of decreasing the state-space size.
15.7 Examples of Non-enzymic Devices
15.7.1 Catalytic Hairpin-Based Triggered Branched Junction
Figure 15.7 shows a detailed sequence of graph rewrite rule applications, which can be applied in succession to produce a 3-arm junction. From the cartoon representation of the 3-arm junction in Fig. 15.6, we see the sequence of steps that are involved in the catalytic creation of the DNA complex.
We start with a set of 4 DNA complexes, 3 hairpins A, B, C and an initiator I. Initiator I and hairpin A hybridize via a toehold a, followed by subsequent strand displacement to give complex \(A+I\) (Figs. 15.6 and 15.7). On strand displacement of hairpin A, the stem loop is opened, exposing domain \(\bar{b}\), and allowing it to react with hairpin B. Again, this is followed by stem loop opening of hairpin B, forming complex \(A+B+I\). Domain \(\bar{c}\) is now exposed, which hybridizes with hairpin C and subsequently opens the stem loop.
Note that a region of hairpin C, namely \(\bar{b}\bar{a}\) is complementary to the arm ab of the original hairpin A. By a process of remote-toehold mediated strand displacement [23], the domain \(\bar{b}\bar{a}\) displaces the attached initiator, creating the final 3-arm junction \(A+B+C\), and releasing initiator I, which is free to catalyze the formation of another structure \(A+B+C\) (Figs. 15.9 and 15.10).
15.7.2 Qian and Winfree’s Seesaw Gate
Figure 15.11 shows a sequence of rules that have been applied for the see-saw system, via which [59] developed a circuit that can compute the square root of a fixed integer. We use two graph rewrite rules in the simulation of this complex: domain binding and strand displacement. The rules can also be used to show the leaks, both fuel-gate and gate-gate, if the domains are segmented further to represent shorter sequences.

The set of states generated by the graph rewriting rules given the input species. There are 26 states. Those circled in red (state_0) and blue mark the chosen subset of states in Fig. 15.8
The Qian and Winfree [59] system shown above contains four single-stranded DNA: input (\(S_2 T S_1\)), output (\(S_3 T S_2\)), fuel (\(S_4 T S_2\)), and gate (\(\bar{T} \bar{S_2} \bar{T}\)). We start with a set of three DNA complexes, two single-stranded DNA: input and fuel, and one double-stranded DNA: gate-output complex as shown above. The input and gate-complex hybridize via a toehold (rule #1), followed by strand displacement of the domain \(S_2\) (rule #2). Following this, toehold T dehybridizes, releasing the output strand. A fuel strand reacts with the new input-gate complex, and the same reactions as above take place, only in the reverse order. The input strand is released, and is free to catalyze the release of another output strand.
This shows a sequence of graph rewriting rules that can be applied in succession, for the DNA circuit system based on see-saw gates. The input strand in the above system acts as a catalyst, and helps in releasing the output strand, via help from a fuel strand [59]
The figure shows how to apply our graph rewriting systems to the basic HCR system designed by Dirks and Pierce [17]
15.7.3 Hybridization Chain Reaction
Figure 15.12 shows how to apply the rewrite rules to basic HCR system designed by Dirks and Pierce [17]. We use two graph rewrite rules: toehold binding and strand displacement.
States generated by DAGRS given the subset of rules supplied. Those circled in red (state_0) and blue mark the chosen subset of states in Fig. 15.14
A description of basic HCR system as shown in Fig. 15.13: there are two types of hairpins (H1 and H2) and one type of single strand (I) in this system. The reaction starts with hybridization between \(\overline{a}\) domain of I and a domain of H1 (rule #1). Hairpin H1 is opened by initiator I after toehold binding (rule #1). c domain of \(I*H1\) hybridizes with \(\overline{c}\) domain of hairpin H2 (rule #1). Hairpin H2 is opened by \(I*H1\) after toehold binding (rule #2). The \(\overline{b}\overline{a}\) domain of \(I*H1*H2\) will be the initiator in the next cycle (Fig. 15.15).
15.8 Enzymatic DNA Graph Rewriting Rules
These rules differ from the non-enzymatic ones defined in Sect. 15.3 in that they require a regular expression, which represents a restriction site, to be matched on one or both strands (depending on the enzyme). This is why each rule is separate than its perceived reverse reaction. These rules have not been implemented in DAGRS.
Rule #6: Restriction Enzyme Cutting (Overhang formation)
Cartoon Rendering |
 |
Rewrite Rule |
 |
Rewrite Rule: A double-stranded DNA complex is made up of two strands with domains \(d_1,d_2,d_3\) and \(\bar{d_1},\bar{d_2},\bar{d_3}\). A restriction enzyme recognizes the restriction site \(d_2\), and cuts the strands at different base pair locations. Strand \(d_1,d_2,d_3\) is cut after \(d_2\), and strand \(\bar{d_1},\bar{d_2},\bar{d_3}\) after \(\bar{d_2}\).
\(\mathbf {L}\): Each domain is represented by a hybridization-labeled vertex. The hybridization-labeled edges show hydrogen bonding. The edges between the vertices labeled \(d_1\), \(d_2\), \(d_3\), which have covalent labels, show directionality and covalent bonding between the domains (and likewise for \(\bar{d_3}\), \(\bar{d_2}\), \(\bar{d_1}\)).
\(\mathbf {R}\): The edge between vertices with domains \(d_2\) and \(d_3\) are replaced by base-stacking labeled edges, and likewise for vertices \(\bar{d_2}\) and \(\bar{d_1}\).
Rule #7: Restriction Enzyme Cutting (Blunt-end formation)
Cartoon Rendering |
 |
Rewrite Rule |
 |
Rewrite Rule: A double-stranded DNA complex is made up of two strands with domains \(d_1,d_2\) and \(\bar{d_1},\bar{d_2}\). A restriction enzyme recognizes the restriction site \(d_1\), and cuts the strands at the same base pair location.
\(\mathbf {L}\): Each domain \(d_1,d_2\) is represented by solid vertices. Solid edges show directionality and covalent bonding, while the dotted edges show hydrogen bonding.
\(\mathbf {R}\): The covalently-labeled edges are relabeled to base-stacking edges.
Rule #8: Polymerization
Cartoon Rendering |
 |
Rewrite Rule |
 |
Rewrite Rule: A double-stranded DNA made up of a vertex with domain \(d_1\) hybridized to \(\bar{d_1}\), which is covalently bound to vertex \(\bar{d_2}\) (which is unhybridized). The \(3^\prime \) vertex is connected to \(d_1\) and indicates the end of the strand. A DNA polymerase extends the \(3^\prime \) end that is connected to \(d_1\), and forms a complementary domain to vertex \(\bar{d_2}\).
\(\mathbf {L}\): Hybridized vertices \(d_1\) and \(\bar{d_1}\), and hollow vertex \(\bar{d_2}\). A \(3^\prime \) vertex is connected to \(d_1\).
\(\mathbf {R}\): A new vertex with domain \(d_2\) is created, with domain complementary to \(\bar{d_2}\). It is connected via a covalent edge with \(d_1\), with the same directionality (the edge is pointing towards vertex \(d_1\)). The edge between vertex \(d_1\) and the \(3^\prime \) vertex is removed, and replaced with an edge from vertex \(d_1\).
Rule #9: Strand-displacement via polymerization
Cartoon Rendering |
 |
Rewrite Rule |
 |
Rewrite Rule: A region of double-stranded DNA made up of three strands, comprised of four vertices with domains \(d_1\), \(d_2\) and on the third strand, \(\bar{d_2}\bar{d_1}\). The domains \(d_1\) and \(d_2\) are both hybridized to \(\bar{d_2}\bar{d_1}\). A DNA polymerase extends the \(3^\prime ;\) end of vertex \(v_1\), resulting in the domain \(d_2\) which is complementary to \(\bar{d_2}\). In the process, it displaces the existing vertex \(v_2\) (with domain \(d_2\)).
\(\mathbf {L}\): Hybridized \(v_1\) and \(v_4\), each connected via hybridization edges to \(v_5\) and \(v_3\). In addition, vertices \(v_1\) and \(v_2\) have a base-stacking edge between them.
\(\mathbf {R}\): A new vertex \(v_5\) with domain complementary to vertex \(v_3\) (\(d_2\)) is added. It is connected via a covalently-labeled edge with \(v_1\), and it is connected to vertex \(v_4\) via a hybridization-labeled edge. The existing vertex u now becomes a hollow vertex outside the complex.
Rule #10: Restriction Enzyme Nicking
Cartoon Rendering |
 |
Rewrite Rule |
 |
Rewrite Rule: A double-stranded DNA region made of two strands, with domains \(d_1,d_2\) and \(\bar{d_2},\bar{d_1}\). A restriction enzyme creates a “nick” at the base pair location between domains \(d_1\) and \(d_2\), which is represented by the removal of the edge between domains \(d_1\) and \(d_2\).
\(\mathbf {L}\): The edge between domains \(d_1\), \(d_2\) is a covalently-labeled edge.
\(\mathbf {R}\): The edge between the vertices labeled \(d_1\), \(d_2\) is removed.
Rewrite Rule: A double stranded DNA region made of three strands. These are comprised of four vertices, with domains \(d_1\), \(d_2\) and \(\bar{d_2},\bar{d_1}\). A ligase joins the domains \(d_1\) and \(d_2\), by adding a covalently-labeled edge between the vertices with labels \(d_1\) and \(d_2\).
\(\mathbf {L}\): The edge between vertices labeled \(d_1,d_2\) is removed.
\(\mathbf {R}\): The edge between vertices labeled \(d_1,d_2\) is a covalently-labeled edge.
Rule #11: Single-stranded Ligation
Cartoon Rendering |
 |
Rewrite Rule |
 |
Rule #12: Blunt end Ligation
Cartoon Rendering |
 |
Rewrite Rule |
 |
Rewrite Rule: Two double-stranded DNA regions, made up of four vertices, with domains \(d_1\), \(d_2\), \(\bar{d_2}\), \(\bar{d_1}\). A base-stacking labeled edge exists between the two vertices with domains \(d_1\) and \(d_2\). A ligase creates two covalent bonds at the same location on both strands, connecting the vertices with domains \(d_1\) and \(d_2\) together, and likewise for \(\bar{d_2}\) and \(\bar{d_1}\). This results in a single double-stranded DNA complex.
\(\mathbf {L}\): The edges with domains \(d_1\) and \(d_2\), as well as \(\bar{d_2}\) and \(\bar{d_1}\) are base-stacking labeled edges.
\(\mathbf {R}\): The edges are relabeled as covalent.
Rewrite Rule: A double-stranded DNA region made of 4 strands, which are represented by 6 vertices, with domains \(d_1,d_2,d_3\) and \(\bar{d_3},\bar{d_2},\bar{d_1}\). A ligase creates two covalent bonds, at different locations on both strands. This relabels the edges between vertices with domains \(d_2\) and \(d_3\) together, as well as \(\bar{d_2}\) and \(\bar{d_1}\). This results in a double-stranded DNA region.
\(\mathbf {L}\): The edges between the vertices with domains \(d_2\) and \(d_3\), as well as \(\bar{d_2}\) and \(\bar{d_1}\) are base-stacking labeled edges.
\(\mathbf {R}\): The edges are relabeled to be covalent.
Rule #13: Sticky-end Ligation
Cartoon Rendering |
 |
Rewrite Rule |
 |
15.9 Example Condensed Reaction Graph of Tweezer
Below we show how our graph rewriting systems can be used to supplement the condensed reaction graph introduced by Grun et al. [26], in order to show how the graph rewriting systems can be used to extend it (Figs. 15.16, 15.17 and 15.18).
Under the definitions in [26] States 0, 4, and 7 would be considered resting states and states 1, 2, 3, 5, and 6 would be considered transient
A condensed reaction version of Fig. 15.16
15.10 An Explanation of Constraint 3
We required that \(3\le deg(v) \le 5\) (on P. XXX) because there is a limited number of possible combinations of edges around a hybridized vertex that are accepted in a member of \(\mathbf {WFDG}\). Specifically:
-
1.
\(v_i\) will be connected to another vertex via a hybridization edge (1)
-
2.
If \(v_i\) is a domain on the \(3^\prime \) or \(5^\prime \) ends, then it will connect to either a \(5^\prime \) or \(3^\prime \) vertex via a
 edge. (\(j=0\), \(j=1\) or \(j=2\))
edge. (\(j=0\), \(j=1\) or \(j=2\)) -
3.
If \(v_i\) is a domain that is on the \(3^\prime \) or \(5^\prime \) ends, but base-stacked against another strand’s \(3^\prime \) or \(5^\prime \) end, then instead of the previous edge, it will be connected via a
 edge to this domain (\(k=|2-j|\), so \(k=0\), \(k=1\) or \(k=2\))
edge to this domain (\(k=|2-j|\), so \(k=0\), \(k=1\) or \(k=2\)) -
4.
If \(v_i\) is adjacent to another domain on its strand, then it will be connected via
 (\(i=0\), \(i=1\), or \(i=2\)).
(\(i=0\), \(i=1\), or \(i=2\)).
In Fig. 15.19a, b, we provide an example in vertex \(d_2\), which is connected to other domains using the maximal result of combining all edges while simultaneously maintaining the vertex’s compliance with well-formedness constraints (disregarding the rest of the structure, which does not comply in this case. The example provided is meant to convey how a vertex can be surrounded by 5 edges). Here we see that \(j=2\), \(k=0\) and \(i=2\). A corresponding example is provided in Fig. 15.20a, b for the case of \(d_2\) being unhybridized.
15.11 Software Output for Yurke et. al Tweezer Example
See Fig. 15.21.
The subfigures are a subset of the states generated by DAGRS for the tweezer. This subset was chosen from 18 states, to correspond to the pathway represented in Table 15.1 (the sequence: state_0, state_3, state_8, state_11, state_12, state_15) from the open state (state_0) to the closed. This demonstrates that the software does indeed generate graphs which correspond to the graph rewriting rules provided. The systems do not discriminate between energetically favorable or unfavorable states, and simply generates all the states possible given a specific set of graph rewriting rules. There are states which arise that may or may not occur, depending on the experiment’s conditions, which are currently not taken into account. We think the key advantage of these systems is that it does display all states, intended or not, depending on the set of rewrite rules supplied. a State 0. b State 2. c State 7. d State 14
15.12 Conclusion
In this paper, we have shown that DNA hybridization and enzymatic reactions can be described using a specific set of graph-rewriting rules. We have described a family of DNA graph rewriting systems that can model some well-known DNA mechanisms such as hybridization, dissociation, strand displacement, as well as various enzymic reactions. This technique of using graph rewriting rules is interesting since it can form the basis of a computational tool that can enumerate the transition pathways between complex DNA nanostructures. However, these rules do not take into account tertiary structures, concentrations, or external conditions that can affect their application. In addition, the inclusion of some rules that significantly increases the number of states, however, they do not need to be included unless they must be. A subset of these rewrite rules can likely be used for a basic graph rewrite system modeling most DNA devices, some of which have been demonstrated, which use just DNA hybridization reactions, whereas other of our rewrite rules could be incorporated as needed for DNA devices for example using enzymic reactions. In practice, we would suggest including as few rules as possible to limit to combinatorial explosion of states that can occur if certain of these rewrite rules are included. We aim to model reaction pathways using domain based verification, and we make the same assumptions as commonly made by DNA nanoscience researchers. For instance, in strand displacement, it is assumed that (1) sequences with different domain names are designed to be orthogonal, and that (2) single stranded regions are designed to be secondary-structure free. By keeping these in mind, we can assume that the intermediate states as generated by our grammar are the intermediate states that are intended by the researcher. The goal of this modeling, is to assist researchers in verification of their intended reaction pathway, and to ensure no incorrect pathways exist. If at this coarse-grained modeling step there are design problems, then the researcher can re-design their model. However, following domain level verification, it is possible to take into account tertiary structure information, concentrations, kinetic rates etc., by further modification of the software. One way to take these factors into account is to provide additional information alongside the graph-rewriting rules, that can be mapped onto the vertex, edge and even subgraph levels during the process of applying these graph-rewriting rules. For example, each vertex (domain) can be assigned a length, and each edge (reaction) can be assigned a transition probability. Though non-trivial, these reaction rates can be approximated based on experimental data [7, 83]. In addition, structural checks (steric hindrance check, persistence length check) can be performed after each transition (at intermediate states) to verify no tertiary rules are violated. These graph rewrite rules originate from the commonly known dynamic mechanisms of interaction between DNA strands (strand displacement, base stacking). With accurate kinetic rates for each of these mechanisms being determined [83], the next step would involve the association of kinetic rates with each graph rewrite rule. The rates would be parameterized depending on the properties (e.g., domain lengths, sequence G/C content) of the DNA graph which the rules are applied to.
Current language-based computational tools [40–42, 54, 81] simulate strand displacement between DNA structures, but they lack in one major areas. The language does not allow the modeling of complex DNA nanostructures involving branched or pseudo-knotted structures, even when enzymes are present [80]. Our graph rewrite rule systems attempt to bridge this gap, by using a simple abstract model for each DNA mechanism.
We have implemented a prototype that performs graph rewriting to generate any sequence of states based on a given input species and the set or subset of rules that can be applied. For future work, we envision allowing a user to input a set of DNA nanostructures and their concentrations, and visualize the various transitions that these nanostructures can undergo. These systems would be useful for both the design and verification of large scale DNA computing systems. Verification would allow the user to avoid spurious pathways that the nanostructures could undertake. Additionally, the user would be allowed to selectively choose a set of rules that can operate on an input set. The rules would be plugin based, so that users can design and add in their own rules and their corresponding kinetic rates.
A conditional graph rewrite system is a set of rewrite rules, where each rule is of the form \(p = e | \langle L \overset{r}{\rightarrow } R \rangle \), such that the rule is applicable if and only if all conditions \(c \in e\) hold, and there is a match \(m:L \rightarrow G\) [16, 51]. The application of rules can be driven by the satisfying of conditions such as domain lengths, depending on the kinetic model used [83]. Using existing kinetic models, we can use this property of graph rewriting systems to conditionally apply rules based on the length and sequence information of domains. To model systems such as that of the abstract tile assembly model, one can apply certain restrictions on the application of the rule-set. The results from [24] show that there exists a rule-set that can be consistent with the geometry of a plane, by using planarity constraints. In our case, this can be taken into consideration by only allowing applications of a rule-set that maintain the planarity of the resulting graph, using standard planarity tests [4, 29, 75]. In addition, multiple copies of a tile can be modeled by using a multiset of DNA complexes as input to the system. Furthermore, there would be a combinatorial explosion in the worst case in the number of nanostructures and re-write rules that can be applied as the reaction proceeds. We aim to leverage graph isomorphism heuristics and probabilistic graph rewriting [14, 37, 72] to help reduce this complexity.
References
Andersen, J.L., Flamm, C., Merkle, D.: Inferring chemical reaction patterns using rule composition in graph grammars. J. Syst. Chem. 4(1), 4 (2013)
Bath, J., Green, S., Turberfield, A.: A free-running DNA motor powered by a nicking enzyme. Angew. Chem. Int. Edit. 44(28), 4358–4361 (2005)
Birac, J.J., Sherman, W.B., Kopatsch, J., Constantinou, P.E., Seeman, N.C.: Architecture with GIDEON, a program for design in structural DNA nanotechnology. J. Mol. Gr. Model. 25(4), 470–480 (2006)
Booth, K.S., Lueker, G.S.: Testing for the consecutive ones property, interval graphs, and graph planarity using PQ-tree algorithms. J. Comput. Syst. Sci. 13(3), 335–379 (1976)
Cardelli, L.: Strand algebras for DNA computing. Nat. Comput. 10(1), 407–428 (2011)
Chen, Y., Wang, M., Mao, C.: An autonomous DNA nanomotor powered by a DNA enzyme. Angew. Chem. Int. Edit. 43(27), 3554–3557 (2004)
Chen, Y.-J., Dalchau, N., Srinivas, N., Phillips, A., Cardelli, L., Soloveichik, D., Seelig, G.: Programmable chemical controllers made from DNA. Nat. Nanotechnol. 8(10), 755–762 (2013)
Chhabra, R., Sharma, J., Liu, Y., Yan, H.: Addressable molecular tweezers for DNA-templated coupling reactions. Nano Lett. 6(5), 978–983 (2006)
Chomsky, N.: Three models for the description of language. IRE Trans. Inf. Theory 2(3), 113–124 (1956)
Chomsky, N.: Syntactic Structures, The Hague (1971)
Claus, V., Ehrig, H., Rozenberg, G. (eds.): Graph-Grammars and Their Application to Computer Science and Biology. Lecture Notes in Computer Science, vol. 73. Springer, Berlin (1979)
Courcelle, B.: Graph rewriting: an algebraic and logic approach. Handbook of Theoretical Computer Science, pp. 194–242. Elsevier, Amsterdamm (1990)
Danos, V., Feret, J., Fontana, W., Harmer, R.: Graphs, rewriting and causality in rule-based models (2012)
Danos, V., Harmer, R., Honorato-Zimmer, R.: Thermodynamic Graph-Rewriting. Springer, Berlin (2013)
Danos, V., Laneve, C.: Graphs for Core Molecular Biology. Springer, Berlin (2003)
Dershowitz, N., Jouannaud, J.-P.: Rewrite systems. Handbook of Theoretical Computer Science, vol. B. North-Holland, Amsterdam (1991)
Dirks, R., Pierce, N.: Triggered amplification by hybridization chain reaction. Proc. Natl. Acad. Sci. USA 101(43), 15275–15278 (2004)
Doye, J.P.K., Ouldridge, T.E., Louis, A.A., Romano, F., Šulc, P., Matek, C., Snodin, B.E.K., Rovigatti, L., Schreck, J.S., Harrison, R.M., Smith, W.P.J.: Coarse-graining DNA for simulations of DNA nanotechnology. Phys. Chem. Chem. Phys. 15(47), 20395–20414 (2013)
Ehrig, H.: Introduction to the algebraic theory of graph grammars (a survey). Proceedings of the International Workshop on Graph-Grammars and Their Application to Computer Science and Biology, pp. 1–69. Springer, London (1979)
Ehrig, H., Pfender, M., Schneider, H.J.: Graph-grammars: an algebraic approach. In: Automata Theory, pp. 167–180
Feret, J., Krivine, J.: Kasim: a simulator for kappa (2008–2013)
Flamm, C., Andersen, J.L., Merkle, D., Stadler, P.F.: Inferring chemical reaction patterns using rule composition in graph grammars. arXiv.org (2012)
Genot, A., Zhang, D., Bath, J., Turberfield, A.: Remote toehold: a mechanism for flexible control of DNA hybridization kinetics. J. Am. Chem. Soc. 133(7), 2177–2182 (2011)
Ghrist, R., Lipsky, D.: Grammatical self assembly for planar tiles. In: 2004 International Conference on MEMS, NANO and Smart Systems (ICMENS’04), pp. 205–211. IEEE (2004)
Green, S., Bath, J., Turberfield, A.: Coordinated chemomechanical cycles: a mechanism for autonomous molecular motion. Phys. Rev. Lett. 101, 238101 (2008)
Grun, C., Sarma, K., Wolfe, B., Shin, S.W., Winfree, E.: A domain-level DNA strand displacement reaction enumerator allowing arbitrary non-pseudoknotted secondary structures. http://dna.caltech.edu/Papers/Peppercorn2014-VEMDP.pdf (2014). Accessed 4 Nov 2014
Gu, H., Chao, J., Xiao, S.-J., Seeman, N.: A proximity-based programmable DNA nanoscale assembly line. Nature 465(7295), 202–205 (2010)
He, Y., Liu, D.: Autonomous multistep organic synthesis in a single isothermal solution mediated by a DNA walker. Nat. Nanotechnol. 5(11), 778–782 (2010)
Hopcroft, J.E., Tarjan, R.E.: Efficient planarity testing. J. ACM 21(4), 549–568 (1974)
Ibuki, K., Fumiaki, T., Masami, H.: MPS. Abstraction of DNA graph structures for efficient enumeration and simulation. 2011(12), 1–6 (2011)
Jonoska, N., Karl, S.A., Saito, M.: Graph structures in DNA computing. Computing with Bio-Molecules, Theory and Experiments, pp. 93–110. Springer, Berlin (1998)
Kawamata, I., Aubert, N., Hamano, M., Hagiya, M.: Abstraction of graph-based models of bio-molecular reaction systems for efficient simulation. Computational Methods in Systems Biology, pp. 187–206. Springer, Berlin (2012)
Klavins, E.: Universal self-replication using graph grammars. In: 2004 International Conference on MEMS, NANO and Smart Systems (ICMENS’04), pp. 198–204. IEEE (2004)
Klavins, E.: Programmable self-assembly. IEEE Control Syst. Mag. 27(4), 43–56 (2007)
Klavins, E., Ghrist, R., Lipsky, D.: Graph grammars for self assembling robotic systems. In: Proceedings. ICRA’04. 2004 IEEE International Conference on Robotics and Automation, 2004, vol. 5, pp. 5293–5300 (2004)
Klavins, E., Ghrist, R., Lipsky, D.: A grammatical approach to self-organizing robotic systems. IEEE Trans. Autom. Control 51(6), 949–962 (2006)
Krause, C., Giese, H.: Probabilistic Graph Transformation Systems. New Trends in Image Analysis and Processing—ICIAP 2013, pp. 311–325. Springer, Berlin (2012)
Krishnan, Y., Simmel, F.C.: Nucleic acid based molecular devices. Angew. Chem. Int. Edit. 50(14), 3124–3156 (2011)
Kumara, M.T., Nykypanchuk, D., Sherman, W.B.: Assembly pathway analysis of DNA nanostructures and the construction of parallel motifs. Nano Lett. 8(7), 1971–1977 (2008)
Lakin, M.R., Cardelli, L., Youssef, S., Phillips, A.: Abstractions for DNA circuit design. J. R. Soc. Interface 9(68), 470–486 (2012)
Lakin, M.R., Parker, D., Cardelli, L., Kwiatkowska, M., Phillips, A.: Design and analysis of DNA strand displacement devices using probabilistic model checking. J. R. Soc. Interface R. Soc. 9(72), 1470–1485 (2012)
Lakin, M.R., Youssef, S., Polo, F., Emmott, S., Phillips, A.: Visual DSD: a design and analysis tool for DNA strand displacement systems. Bioinform. (Oxf. Engl.) 27(22), 3211–3213 (2011)
Lilley, D.M.J.: Structures of helical junctions in nucleic acids. Q. Rev. Biophys. 33(02), 109–159 (2000)
Liu, D., Balasubramanian, S.: A proton-fuelled DNA nanomachine. Angew. Chem. Int. Edit. 42(46), 5734–5736 (2003)
Lund, K., Manzo, A.J., Dabby, N., Michelotti, N., Johnson-Buck, A., Nangreave, J., Taylor, S., Pei, R., Stojanovic, M.N., Walter, N.G., Winfree, E., Yan, H.: Molecular robots guided by prescriptive landscapes. Nature 465(7295), 206–210 (2010)
Machinek, R.R.F., Ouldridge, T.E., Haley, N.E.C., Bath, J., Turberfield, A.J.: Programmable energy landscapes for kinetic control of DNA strand displacement. Nat. Communi. 5, 5324 (2014)
Mann, M., Ekker, H., Flamm, C.: The graph grammar library-a generic framework for chemical graph rewrite systems. arXiv.org (2013)
Mao, C., Sun, W., Shen, Z., Seeman, N.: A Nanomechanical device based on the B-Z transition of DNA. Nature 397, 144–146 (1999)
McCaskill, J.S., Niemann, U.: Graph replacement chemistry for DNA processing. DNA Comput. 2054, 103–116 (2001) (Chapter 8)
Modi, S., Krishnan, Y.: A method to map spatiotemporal pH changes inside living cells using a pH-triggered DNA nanoswitch, pp. 61–77 (2011)
Nupponen, K.: The design and implementation of a graph rewrite engine for model transformations. Master’s thesis (2005)
Ouldridge, T.E., Louis, A.A., Šulc, P., Romano, F., Doye, J.P.K.: DNA hybridization kinetics: zippering, internal displacement and sequence dependence. Nucleic Acids Res. 41, 8886–8895 (2013)
Peixoto, T.P.: Graph-tool: efficient network analysis (Version 2.2.31) [Software]. http://graph-tool.skewed.de/ (2014). Accessed 23 June 2014
Phillips, A., Cardelli, L.: A programming language for composable DNA circuits. J. R. Soc. Interface 6(11), 419–436 (2009)
Pinaud, B., Melançon, G., Dubois, J.: PORGY: a visual graph rewriting environment for complex systems. Comput. Gr. Forum 31(3), 1265–1274 (2012)
Potoyan, D.A., Savelyev, A., Papoian, G.A.: Recent successes in coarse-grained modeling of DNA. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 3(1), 69–83 (2012)
Python Software Foundation: Python™. https://www.python.org/download/releases/2.7/ (2001–2014)
Qian, L., Winfree, E.: A simple DNA gate motif for synthesizing large-scale circuits. DNA Computing, pp. 70–89. Springer, Berlin (2009)
Qian, L., Winfree, E.: Scaling up digital circuit computation with DNA strand displacement cascades. Science 332(6034), 1196–1201 (2011)
Reif, J.: Parallel biomolecular computation: models and simulations. Algorithmica 25(2–3), 142–175 (1999)
Reif, J.: The design of autonomous DNA nano-mechanical devices: walking and rolling DNA. DNA Computing, pp. 439–461. Springer, Berlin (2003)
Reif, J., Chandran, H., Gopalkrishnan, N., LaBean, T.: Self-assembled DNA nanostructures and DNA devices, pp. 299–328. Nanofabrication Handbook. CRC Press, Taylor and Francis Group, New York (2012)
Riverbank Computing Limited: PyQt5 (version 5.3.2) [Software]. http://www.riverbankcomputing.com/software/pyqt/download5 (2014)
Rozenberg, G.: Handbook of Graph Grammars and Computing by Graph Transformation: Volume I. Foundations. World Scientific, Singapore (1997)
Rozenberg, G., Ehrig, H.: Handbook of Graph Grammars and Computing by Graph Transformation, vol. 1. World Scientific, Singapore (1999)
Sekiguchi, H., Komiya, K., Kiga, D., Yamamura, M.: A design and feasibility study of reactions comprising DNA molecular machine that walks autonomously by using a restriction enzyme. Nat. Comput. 7(3), 303–315 (2008)
Sherman, W., Seeman, N.: A precisely controlled DNA biped walking device. Nano Lett. 4, 1203–1207 (2004)
Shin, J.-S., Pierce, N.: A synthetic DNA walker for molecular transport. J. Am. Chem. Soc. 126(35), 10834–10835 (2004)
Sinden, R.R.: DNA Structure and Function. Gulf Professional Publishing (1994)
Tian, Y., He, Y., Chen, Y., Yin, P., Mao, C.: A DNAzyme that walks processively and autonomously along a one-dimensional track. Angew. Chem. Int. Edit. 44(28), 4355–4358 (2005)
Tian, Y., Mao, C.: Molecular gears: a pair of DNA circles continuously rolls against each other. J. Am. Chem. Soc. 126(37), 11410–11411 (2004)
Torrini, P., Heckel, R., Ráth, I.: Stochastic simulation of graph transformation systems. Fundamental Approaches to Software Engineering, pp. 154–157. Springer, Berlin (2010)
Ullmann, J.R.: An algorithm for subgraph isomorphism. J. ACM 23(1), 31–42 (1976)
Wang, Z.-G., Elbaz, J., Willner, I.: DNA machines: bipedal walker and stepper. Nano Lett. 11(1), 304–309 (2011)
Wei-Kuan, S., Wen-Lian, H.: A new planarity test. Theor. Comput. Sci. 223(1–2), 179–191 (1999)
Woo, S., Rothemund, P.W.K.: Programmable molecular recognition based on the geometry of DNA nanostructures. Nat. Chem. 3(8), 620–627 (2011)
Yin, P., Choi, H., Calvert, C., Pierce, N.: Programming biomolecular self-assembly pathways. Nature 451(7176), 318–322 (2008)
Yin, P., Turberfield, A., Sahu, S., Reif, J.: Designs for autonomous unidirectional walking DNA devices. DNA Comput. pp. 410–425. Springer, Berlin (2004)
Yin, P., Yan, H., Daniell, X., Turberfield, A., Reif, J.: A unidirectional DNA walker moving autonomously along a linear track. Angew. Chem. Int. Edit. 116(37), 5014–5019 (2004b)
Yordanov, B., Kim, J., Petersen, R.L., Shudy, A., Kulkarni, V.V., Phillips, A.: Computational design of nucleic acid feedback control circuits. ACS Synth. Biol. 3(8), 600–616 (2014)
Yordanov, B., Wintersteiger, C.M., Hamadi, Y., Phillips, A., Kugler, H.: Functional Analysis of Large-Scale DNA Strand Displacement Circuits. Springer International Publishing, Cham (2013)
Yurke, B., Turberfield, A., Mills, A., Simmel, F., Neumann, J.: A DNA-fuelled molecular machine made of DNA. Nature 406(6796), 605–608 (2000)
Zhang, D.Y., Winfree, E.: Control of DNA strand displacement kinetics using toehold exchange. J. Am. Chem. Soc. 131(48), 17303–17314 (2009)
Acknowledgments
This work was supported by the National Science Foundation under NSF CCF 1217457 and NSF CCF 1320360.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Mokhtar, R., Garg, S., Chandran, H., Bui, H., Song, T., Reif, J. (2017). Modeling DNA Nanodevices Using Graph Rewrite Systems. In: Adamatzky, A. (eds) Advances in Unconventional Computing. Emergence, Complexity and Computation, vol 23. Springer, Cham. https://doi.org/10.1007/978-3-319-33921-4_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-33921-4_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-33920-7
Online ISBN: 978-3-319-33921-4
eBook Packages: EngineeringEngineering (R0)







 is the finite set of vertex labels, where:
is the finite set of vertex labels, where: : unhybridized vertex, where every base in the domain that this vertex is mapped to is unhybridized.
: unhybridized vertex, where every base in the domain that this vertex is mapped to is unhybridized. : hybridized vertex, where every base in the domain that this vertex is mapped to is hybridized.
: hybridized vertex, where every base in the domain that this vertex is mapped to is hybridized. is the finite set of edge labels, where:
is the finite set of edge labels, where: : base-stacking, where the arrow direction indicates
: base-stacking, where the arrow direction indicates 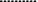 : hybridization.
: hybridization. : covalent bond linking base pairs between two domains, where the arrow direction indicates strand directionality.
: covalent bond linking base pairs between two domains, where the arrow direction indicates strand directionality. : is an edge label that signifies a strand-end, where the vertical bar location indicates strand directionality.
: is an edge label that signifies a strand-end, where the vertical bar location indicates strand directionality.
 from u (i.e. the
from u (i.e. the  .
. to v (i.e. the
to v (i.e. the  .
. , then it has exactly one hybridization-labeled edge
, then it has exactly one hybridization-labeled edge  . This edge is treated as two edges going in both directions, but is represented as one undirected edge. Which means it counts both an an in-degree and out-degree for each participating vertex.
. This edge is treated as two edges going in both directions, but is represented as one undirected edge. Which means it counts both an an in-degree and out-degree for each participating vertex. , then
, then  and i is an integer s.t.
and i is an integer s.t.  and j is an integer s.t.
and j is an integer s.t.  connected to v, s.t.
connected to v, s.t. 

 , and adds an edge between them with the label
, and adds an edge between them with the label  , resulting in a new graph
, resulting in a new graph  . Since prior to the transformation no such edge existed, then exactly one edge
. Since prior to the transformation no such edge existed, then exactly one edge  . No other edges nor labels have been affected.
. No other edges nor labels have been affected. , and label(
, and label( . The rewriting rule destroys the edge
. The rewriting rule destroys the edge  and
and  , and adds a hybridization edge
, and adds a hybridization edge  .
. . Since prior to the transformation no such edge existed, then exactly one edge
. Since prior to the transformation no such edge existed, then exactly one edge  . One edge
. One edge  has been removed.
has been removed. with domains
with domains  , and likewise for
, and likewise for  .
. , which are connected to
, which are connected to  , and likewise for
, and likewise for 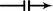 . Since prior to the transformation no such edge existed, then exactly one edge
. Since prior to the transformation no such edge existed, then exactly one edge  .
. (with domains
(with domains  (with domains
(with domains  ). An edge
). An edge  . Since prior to the transformation no such edge existed, then exactly one edge
. Since prior to the transformation no such edge existed, then exactly one edge  . No other edges nor labels have been affected.
. No other edges nor labels have been affected.












 edge. (
edge. ( edge to this domain (
edge to this domain ( (
(

