Atomic Scale Machining of Medical Materials

Abstract

Molecular dynamic simulations of machining at the atomic scale can reveal a significant amount of information regarding the behaviour of machining and grinding processes that cannot be explained easily using classical theory or experimental procedures. This chapter explains how the use of molecular dynamic simulations can be applied to the many problems associated with machining and grinding at the meso-, micro-, and nanoscales. These include: (a) mechanics of nanoscale machining of ferrous and non-ferrous materials; (b) physics of nanoscale grinding of semiconductor materials; (c) effects of simulating a variety of machining parameters in order to minimize subsurface damage; (d) modelling of exit failures experienced during machining such as burr formation and other dynamic instabilities during chip formation; (e) simulation of known defects in microstructures using molecular dynamic simulations, statistical mechanical, and Monte Carlo methods; (f) simulation of machining single crystals of known orientation; (g) extremely high-speed nanometric cutting; (h) tool wear during machining; and (i) the effects of hardness on the wear of tool and workpiece materials. The nature of wear of the material ahead of the machining and grinding process, the variation of machining forces, and the amount of specific energy induced into the workpiece material using molecular dynamic simulations is discussed in this chapter.

1.1 Introduction

Nanotechnology is the creation and utilization of materials, structures, devices, and systems through the control of matter at the nanometre length scale. The essence of nanotechnology is the ability to work at these levels to generate large structures with fundamentally new properties. Although certain applications of nanotechnology, such as giant magnetoresistance (GMR) structures for computer hard disc read head and polymer displays have entered the marketplace, in general nanotechnology is still at a very early stage of development. The barriers between nanotechnology and the marketplace lie in how to reduce the fabrication cost and how to integrate nanoscale assemblies with functional microscale and macro devices . Therefore, reliable mass production of nanostructures is currently one of the most crucial issues in nanotechnology. The commercialization of nanotechnology has to address the underlying necessities of predictability, repeatability, producibility, and productivity in manufacturing at nanometre scale.

Nanometric machining refers to a “top-down” nanofabrication approach. To the authors’ knowledge the concept of nanometric machining is more concerned with precision rather than characteristic size of the product. Therefore, nanometric machining is defined as the material removal process in which the dimensional accuracy of a product can be achieved is 100 nm or less. Nanometric machining can be classified into four categories:

• Deterministic mechanical nanometric machining . This method utilizes fixed and controlled cutting tools, which can specify the profiles of 3D components by a well-defined tool surface. The method can remove materials in amounts as small as tens of nanometres. It includes processes such as diamond turning, micromilling, and nano/micro grinding.

• Loose abrasive nanometric machining . This method uses loose abrasive grits to removal a small amount of material. It consists of polishing, lapping, and honing.

• Non-mechanical nanometric machining comprises processes such as focused ion beam machining, micro-EDM, and excimer laser machining.

• Lithographic method . The method employs masks to specify the shape of the product. 2D shapes are the main outcome; severe limitations occur when 3D products are attempted [19]. Processes include X-ray lithography, LIGA, and electron beam lithography.

The author believes that mechanical nanometric machining has more advantages than other methods since it is capable of machining complex 3D components in a controllable and deterministic way. The machining of complex surface geometries is just one of the future trends in nanometric machining, which is driven by the integration of multiple functions in one product. For instance, the method can be used to machine micro moulds/dies with complex geometric features and high dimensional and form accuracy, and even nanometric surface features. The method is indispensable to manufacturing complex micro and miniature structures, components, and products in a variety of engineering materials. This chapter focuses on nanometric cutting theory, methods, and its implementation and application perspectives.

1.2 Nanomachining

The scientific study of nanometric machining has been undertaken since the late 1990s. Much attention to the study has been paid especially with the advancement of nanotechnology [26]. The scientific study will result in the formation of the theoretical basis of nanometric machining, which enables the better understanding of nanometric machining physics and the development of controllable techniques to meet the requirements for nanotechnology and nanoscience.

1.2.1 Cutting Force and Energy

In nanomanufacturing, the cutting force and cutting energy are important issues. They are important physical parameters for understanding cutting phenomena as they clearly reflect the chip removal process. From the point of view of atomic structures, cutting forces are the superposition of the interactions of forces between workpiece atoms and cutting tool atoms. Specific energy is an intensive quantity that characterizes the cutting resistance offered by a material [73]. Ikawa et al. [26], and Luo et al. [53] have acquired the cutting forces and cutting energy by molecular dynamics (MD) simulations. Ikawa et al. [26] have carried out experiments to measure the cutting forces in nanometric machining. Figure 1.1 shows the simulation and experimental results in nanometric cutting. Figure 1.1a illustrates the linear relationship that exists between the cutting force per width and depth of cut in both simulations and experiments. The cutting forces per width increase with the increment of the depth of cut.

Fig. 1.1

The comparison of results between simulations and experiments: a cutting force per width against depth of cut; b specific energy against depth of cut [26]

The difference in the cutting force between simulations and experiment is caused by the different cutting edge radii applied in the simulations. In nanometric machining the cutting edge radius plays an important role since the depth of cut is similar in scale. Under the same depth of cut higher cutting forces are required for a tool with a large cutting edge radius compared with a tool with a small cutting edge radius. The low cutting force per width is obviously the result of fine cutting conditions, which will decrease the vibration of the cutting system and thus improve machining stability and will also result in better surface roughness.

A linear relationship between the specific energy and the depth of cut can also be observed in Fig. 1.1. The figure shows that the specific energy increases with a decreasing of depth of cut, because the effective rake angle is different under different depths of cut. In small depths of cut the effective rake angle will increase with the decreasing of depth of cut. Large rake angles result in an increase in specific cutting energy. This phenomenon is often called the “size effect”, which can be clearly explained by material data listed in Table 1.1. According to Table 1.1, in nanometric machining only point defects exist in the machining zone in a crystal. Therefore, the material will need more energy to initiate the formation of an atomic crack or the movement of an atomic dislocation. The decreasing of depth of cut will decrease the chance for the cutting tool to meet point defects in the material and will result in increasing the specific cutting energy.

Table 1.1 Material properties under different machining conditions [83]

If the machining unit is reduced to 1 nm, the workpiece material structure at the machining zone may approach atomic perfection; hence more energy will be required to break the atomic bonds. Alternatively, when the machining unit is higher than 0.1 μm, the machining points will fall into the distribution distances of some defects such as dislocations, cracks, and grain boundaries. The pre-existing defects will ease the deformation of workpiece material and result in a comparatively low specific cutting energy.

Nanometric cutting is also characterized by the high ratio of the normal to the tangential component in the cutting force [53, 73], as the depth of cut is very small in nanometric cutting and the workpiece is mainly processed by the cutting edge. The compressive interactions will thus become dominant in the deformation of the workpiece material, which will therefore result in the increase of friction force at the tool–chip interface with a relatively high cutting ratio.

Usually, the cutting force in nanometric machining is very difficult to measure due to its small amplitude compared with the noise generated (mechanical or electronic). A piezoelectric dynamometer, or load cell, is used to measure the cutting forces because of their characteristic high sensitivity and natural frequency. Figure 1.2 shows an experimental force measuring system in micromilling process carried out by Dow et al. [18]. The three-axis load cell, Kistler 9251, is mounted in a specially designed mount on the Y-axis of a Nanoform 600 diamond turning machine. A piece of S-7 steel that has been ground flat on both sides is used as the workpiece and secured through the top of the load cell with a bolt preloaded to 30 N. The tool was moved in the +Z direction to set the depth of cut and the workpiece was fed in the +y direction to cut the groove.

Fig. 1.2

Experimental force measurement system in micromilling process [18]

The milling tool is mounted in a Westwind D1090-01 air bearing turbine spindle capable of speeds up to 60,000 rpm. The spindle is attached to the Z-axis of the Nanoform 600. To determine the rotational speed of the tool and the orientation of each flute, an optical detector (Angstrom resolver) was used to indicate a single rotation of the spindle by reading a tool revolution marker aligned with one flute. The measured 3D cutting forces under depth of cut of 25 μm, feed rate of 18.75 μm/flute, are of the order of several newtons.

1.2.2 Cutting Temperature

In MD simulations, the cutting temperature can be calculated under the assumption that the cutting energy totally transforms into cutting heat and results in increasing the cutting temperature and kinetic energy of system. The lattice vibration is the major form of thermal motion of atoms. Each atom has three degrees of freedom. According to the theorem of equipartition of energy, the average kinetic energy of the system can be expressed as follows:

$$ \overline{E}_{k} = \frac{3}{2}Nk_{B} T = \sum\limits_{i} {\frac{1}{2}m(V_{i}^{2} )} $$

(1.1)

where $\overline{E}_{k}$ is average kinetic energy in equilibrium state, k_B is Boltzmann’s constant, T is absolute temperature, and m_i and V_i are the mass and velocity of an atom, respectively. N is the number of atoms.

The cutting temperature can be calculated using the following equation:

$$ T = \frac{{2\overline{E}_{k} }}{{3Nk_{B} }} $$

(1.2)

Figure 1.3 shows the variation of cutting temperature on the cutting tool in MD simulation of nanometric cutting of single crystal aluminium [10].

Fig. 1.3

Cutting temperature distribution of cutting tool in nanometric cutting (cutting speed = 20 m/s, depth of cut = 1.5 nm, cutting edge radius = 1.57 nm) [10]

The highest temperature is observed at cutting edge although the temperature at the flank face is also higher than that at the rake face. The temperature distribution suggests that a major source of heat exists at the interface between the cutting edge and the workpiece, and that the heat be conducted from there to the rest of the cutting zone. This is because that most of cutting action takes place at the cutting edge of the tool and the resulting dislocation deformation in the workpiece material will transfer their potential energy into kinetic energy and result in the observed temperature rise. The comparatively high temperature exhibited at the flank face is caused by the friction between the flank face and the workpiece. The released energy due to the elastic recovery of the machined surface also contributes to the incremental increase in temperature at flank face. Although there is friction between the rake face and the chip, the heat will be taken away from the rake face by the removal of the chip.

Therefore, the temperature at tool rake face is lower than that at the tool cutting edge and tool flank face. The temperature value shows that the cutting temperature in diamond machining is quite low in comparison with that in conventional cutting, due to low cutting energy in addition to high thermal conductivity of diamond and the workpiece material. The cutting temperature is considered to govern the wear of a diamond tool as shown in the MD simulation study by Cheng et al. [9]. In-depth experimental and theoretical studies are needed to find out the quantitative relationship between cutting temperature and tool wear although there is considerable evidence of chemical damage on the surface of diamond in which increases in temperature tends to plays a significant role [9].

1.2.3 Chip Formation and Surface Generation

Chip formation and surface generation can be simulated by MD simulations. Figure 1.4 shows an MD simulation of a nanometric cutting process on single crystal aluminium [10]. From Fig. 1.4a it is shown that after the initial plough of the cutting edge the workpiece atoms are compressed in the cutting zone near to the rake face and the cutting edge. The disturbed crystal lattices of the workpiece and even the initiation of dislocations can be observed in Fig. 1.4b. Figure 1.4c shows the dislocations have piled up to form a chip. The chip is removed with the unit of an atomic cluster as shown in Fig. 1.4d. Lattice disturbed workpiece material is observed on the machined surface.

Fig. 1.4

MD simulations of the nanometric machining process (Cutting speed = 20 m/s, depth of cut = 1.4 nm, cutting edge radius = 0.35 nm) [10]

Based on the visualization of the nanometric machining process, the mechanism of chip formation and surface generation in nanometric cutting can be explained. Owing to the ploughing of the cutting edge, the attractive force between the workpiece atoms and the diamond tool atoms becomes repulsive. Because the cohesion energy of diamond atoms is much larger than that of Al atoms, the lattice of the workpiece is compressed. When the strain energy stored in the compressed lattice exceeds a specific level, the atoms begin to rearrange so as to release the strain energy. When the energy is not sufficient to perform the rearrangement, some dislocation activity is generated. Repulsive forces between compressed atoms in the upper layer and the atoms in the lower layer are increasing, so the upper atoms move along the cutting edge, and at the same time the repulsive forces from the tool atoms cause the resistance for the upward chip flow to press the atoms under the cutting line. With the movement of the cutting edge, some dislocations move upward and disappear from the free surface as they approach the surface.

This phenomenon corresponds to the process of chip formation. As a result of the successive generation and disappearance of dislocations, the chip seems to be removed steadily. After the passing of the tool, the pressure at the flank face is released. The layers of atoms move upwards and result in elastic recovery, so that the machined surface is generated.

The conclusion can therefore be drawn that chip removal and machined surface generation are, in nature, dislocation slip motion inside the workpiece material grains. In conventional cutting, dislocations are initiated from the existing defects between the crystal grains, which will ease the movement of dislocations and result in smaller specific cutting forces compared with that in nanometric cutting.

The height of the atoms on the surface creates the observed surface roughness. For this, 2D MD simulation roughness average (R_a) can be used to assess the machined surface roughness. The surface integrity parameters can also be calculated based on the simulation results. For example, the residual stress of the machined surface can be estimated by averaging the forces acting on the atoms in a unit area on the upper layer of the machined surface.

MD simulation has been proved to be a useful tool for the theoretical study of nanometric machining [78]. At present, MD simulation studies on nanometric machining are limited by the computing memory size and speed of the computer. It is therefore difficult to enlarge the dimension of the current MD model on a personal computer. In fact, the machined surface topography is produced as a result of the copy of the tool profile on a workpiece surface that has a specific motion relative to the tool. The degree of the surface roughness is governed by both the controllability of machine tool motions (or relative motion between tool and workpiece) and the transfer characteristics (or the fidelity) of tool profile to the workpiece [26]. A multiscale analysis model, which can fully model the machine tool and cutting tool motion, environmental effects and the tool–workpiece interactions, is needed to predict and control the nanometric machining process in a deterministic manner.

1.2.4 Minimum Undeformed Chip Thickness

Minimum undeformed chip thickness is an important issue in nanometric machining because it relates to the ultimate machining accuracy. In principle, the minimum undeformed chip thickness will be determined by the minimum atomic distance within the workpiece. However, in ultra-precision machining practices it depends on the sharpness of the diamond cutting tool, the capability of the ultra-precision machine tool and the machining environment. Diamond turning experiments of non-ferrous work materials carried out at Lawrence Livermore National Laboratory in the United States of America show the minimum undeformed chip thickness, down to 1 nm, is attainable with a specially prepared fine diamond cutting tool on a very stiff ultra-precision machine tool.

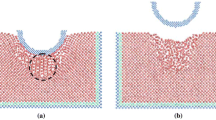
Figure 1.5 illustrates chip formation of single crystal aluminium with the tool cutting edge radius of 1.57 nm [10]. No chip formation is observed when the undeformed chip thickness is 0.25 nm. But the initial stage of chip formation is apparent when the undeformed chip thickness reaches 0.26 nm. In nanometric cutting, as the depth of cut is very small, the chip formation is related to the force conditions on the cutting edge of the tool. Generally, chip formation is mainly a function of tangential cutting force.

Fig. 1.5

Study of minimum undeformed chip thickness by MD simulation. a Undeformed chip thickness = 0.25 nm; b Undeformed chip thickness = 0.26 nm [10]

The normal cutting force makes little contribution to the chip formation since it has the tendency to penetrate the atoms of the surface into the bulk of the workpiece. The chip is formed on condition that the tangential cutting force is larger than the normal cutting force. The relationships between minimum undeformed chip thickness, cutting edge radius, and cutting forces are studied by MD simulations. The results are highlighted in Table 1.2 [10]. The data shows that the minimum undeformed chip thickness is about 1/3–1/6 magnitude of the tool cutting edge radius. Chip formation will be initiated when the ratio of tangential cutting force to normal cutting force is larger than 0.92.

Table 1.2 Minimum undeformed chip thickness against the tool cutting edge radius and cutting forces [10]

1.2.5 Critical Cutting Edge Radius

It is widely accepted that the sharpness of the cutting edge of a diamond cutting tool directly affects the machined surface quality. Previous MD simulations show that the sharper the cutting edge, the smoother the machined surface becomes. But this conclusion is based on zero tool wear. To study the real effects of cutting edge radius, the MD simulations on nanometric cutting of single crystal aluminium are carried out using a tool wear model [78].

In the simulations the cutting edge radius of the diamond cutting tool varies from 1.57 to 3.14 nm with depth of cut of 1.5, 2.2, and 3.1 nm. The cutting distance is fixed at 6 nm. The root-mean-square deviation of the machined surface and mean stress on the cutting edge are listed in Table 1.3.

Table 1.3 The relationship between cutting edge radius and machined surface quality [10]

Figure 1.6 shows the visualization of the simulated data, which clearly indicates that surface roughness increases with the decreasing cutting edge radius when the cutting edge radius is smaller than 2.31 nm. The tendency is caused by the rapid tool wear when a cutting tool with small cutting edge radius is used. But when the cutting edge is larger than 2.31 nm, the cutting edge is under compressive stress and no tool wear happens. Therefore, it shows the same tendency that the surface roughness increases with decreasing the tool cutting edge radius as in the previous MD simulations.

Fig. 1.6

Cutting edge radius against machined surface quality

The MD simulation results also illustrate that it is not true that the sharper the cutting edge, the better the machined surface quality. The cutting edge will wear and results in the degradation of the machined surface quality if its radius is smaller than the critical value for cutting. But when the cutting edge radius is higher than the critical value, the compressive stress will take place at the tool edge and the tool condition is more stable. As a result a high-quality machined surface can be achieved. Therefore, there is a critical cutting edge radius for achieving a high-quality machined surface.

For cutting single crystal aluminium, the critical cutting edge radius is 2.31 nm. The MD simulation approach is applicable for acquiring the critical cutting edge radius for nanometric cutting of other materials.

1.2.6 Properties of Workpiece Materials

In nanometric machining the microstructure of the workpiece material will play an important role in affecting the machining accuracy and machined surface quality. For example, when machining polycrystalline materials, the difference in the elastic coefficients at the grain boundary and interior of the grain causes small steps to be formed on the cut surface since the respective elastic “rebound” will vary. The study by Lee and Chueng [46] shows the shear angle varies with the crystallographic orientation of the materials being cut. This will produce a self-excited vibration between cutting tool and workpiece and result in a local variation of surface roughness of a diamond turned surface [14].

A material’s destructive behaviour can also be affected by nanometric machining. In nanometric machining of brittle materials it is possible to produce plastically deformed chips if the depth of cut is sufficiently small [14]. It has been shown that a “brittle-to-ductile” transition exists when cutting brittle materials at low load and penetration levels. The transition from ductile-to-brittle fracture has been widely reported and is usually described as the “critical depth of cut”, i.e. generally small up to 0.1–0.3 μm. These small depths of cut will result in relatively low material removal rates.

However, it is a cost-effective technique for producing high-quality spherical and non-spherical optical surfaces, with or without the need for lapping and polishing.

The workpiece materials should also have a low affinity with the cutting tool material. If pieces of the workpiece material are deposited onto the tool, this will cause tool wear and will adversely affect the surface in terms of surface roughness and integrity. Therefore, workpiece materials chosen must possess an acceptable machinability on which nanometric surface finishes can thus be achieved.

Diamond tools are widely used in nanometric machining because of their excellent characteristics. The materials currently turned with diamond tools are listed in Table 1.4. Materials that can be processed using ductile mode grinding with diamond wheels are listed in Table 1.5. Table 1.6 summarizes the comparison of nanometric machining and conventional machining in all major aspects of cutting mechanics and physics. The comparison highlighted in the table is by no means comprehensive, but rather provides a starting point for further study on the physics of nanometric machining.

Table 1.4 Diamond turned materials [14]

Table 1.5 Materials that can be processed using ductile mode diamond grinding [14]

Table 1.6 The comparison of nanometric machining with conventional machining [53]

1.3 Material Requirements for the Medical Industry

Corrosion resistance of titanium (Ti) and its alloys is very good when compared to other materials showing 2.0 V breakdown potential while the value for steel is 0.2 V. Even though Ti alloys belong to the group of materials which do not breakdown passivity in the body, mechanical damage can induce the breakdown (metal-on-metal contact or damage caused with a surgical instrument) and if it does, re-passivation time and oxide growth for the Ti6Al4V alloy is 37–41 and 43.4–45.8 ms, respectively. While for steel it is 35–72000 and 6000–72000 ms, respectively [47]. Biocompatibility is a consequence of the ability of a material to form a protective surface layer of semi or non-conductive oxides that somewhat or completely prevent the flow of ions. The dielectric constant of Ti oxides is similar to that of water which makes the human bone or tissue not recognize the implant as a foreign body [47].

Bioadhesion determines the integration of metallic implants through bone and tissue in-growth. When comparing steel to Ti alloy implants, it has been seen that with steel implants the bone formation was low and there was tissue growing between the metallic implant and the bone which was been deprived of blood and has become granulated and unable to withstand high load bearing capabilities causing loosening of the implant. On the other hand, with Ti implants significant bone formation was observed. The detaching moment of the steel implants was much lower than that of Ti implants. The Ti6Al4V alloy shows that there is a biomechanical as well as a biochemical effect to the growth and formation of a strong bond between implants and bone and tissue showing dependence on both time of exposure as well as surface roughness of the implant [47].

When analyzing the necessary mechanical properties of materials used for implants, it is necessary to achieve adequate Young’s modulus, fatigue strength and elongation at fracture. Biofunctionality, which is presented as the ratio of fatigue strength and modulus of elasticity, is superior in Ti alloys when compared with any other materials. Young’s modulus of Ti alloys is very close to the value of the bone and the lower it is, the transmission of the functional load is better therefore stimulating bone growth. However, as Young’s modulus is lower by creating a porous layer of the surface, the value of the fatigue strength decreases giving the best results when using plasma sprayed coatings when the difference from the bone is about 10 %. The amount of material that needs to be porous in Ti alloys is around 20 %, which is much less when compared to Cr–Co alloys that requires almost 50 % and still does not achieve the same results. Apart from the amount of porosity, it is necessary for pores to be in the range of 50–100 μm for the in-growth to occur. This can be achieved by spraying or welding cp T onto a Ti alloy [47]. When analyzing the processes available for processing Ti and its alloys, most processes are applicable and the most common ones include casting, forging and machining. The price of Ti alloys is in the range with stainless steel while the rest of the biocompatible materials have a higher cost.

1.3.1 Properties of Titanium Alloys

Ti is considered to be a non-ferrous, light metal that is heavier than any other light metal although it is only half the specific weight of Ni and Fe. Its excellent specific strength and corrosion resistance have made Ti a popular alloy in industries such as aerospace, medical, chemical, etc. The specific strength of Ti alloys is only matched by carbon-reinforced plastics and only at temperatures below 300 °C. The application of these alloys is very attractive at higher temperatures where their strength peaks. However, depending on the alloying elements oxidation can take place starting at temperatures above 500 °C. Ti alloys with added aluminium can withstand higher temperatures and are in the same range with high temperature steels and Ni alloys.

Ti can have two distinct types of crystal structures. At high temperatures, Ti has a stable body-centred-crystal structure (bcc) known as β-Ti while at the transus temperature of 882 °C it undergoes an allotropic modification where β-Ti changes into a hexagonal close packed (hcp) structure, known as α-Ti, which is stable at lower temperatures. The two crystal structures are the reason for the wide range of properties Ti alloys tend to show that influences both plastic deformation and diffusion rate.

Owing to the type of crystal lattice, the α structure has a very limited deformability while this increases for the β phase. This is a consequence of the fact that hcp crystal system has 3 slip systems, while bcc crystal systems have 12 (Fig. 1.8), thus increasing the number of dislocation glide opportunities by a factor of four. Even though the α phase has a packing density of the slip plane of 91 % compared to 83 % for β phase, the energy needed for the activation of the slip planes is higher having as a result favourable plastic deformation in the β phase. Another issue with the α phase is that it has an hcp structure and has only four independent slip planes instead of five necessary for homogeneous plastic deformation making it extremely hard to form.

Fig. 1.8

Crystal structure of hcp α and bcc β-phases [47]

1.3.2 Classification of Ti Alloys

Alloying elements play an important role when phase diagrams are analyzed. Alloying elements can extend the α region to higher temperatures, extend the β region to lower temperatures or have minimal or no effect on the transus temperature, and are divided into three groups: α stabilizers, β stabilizers and neutral alloying elements. Figure 1.9 shows the effect of alloying elements on the phase diagram of Ti alloys.

Fig. 1.9

Influence of alloying elements on the phase diagram of Ti alloys [47]

α stabilizers are responsible for the development of the two-phase region (α + β) and are divided further into two distinct categories—β isomorphous and β eutectic elements shown in Fig. 1.10. The solubility of β isomorphous elements such as Mo, V and Ta is higher when compared to the β eutectic elements such as Fe, Mn Cr, Co, Ni, Cu, Si, and H which form compounds with titanium. The influence of these alloying elements is on the transus temperature and shape of the phase diagram. However, their influence on the hardness is indifferent and the neutral elements actually play an important role.

Fig. 1.10

α and β stabilizing elements [47]

Ti alloys are classified into several types: α, β, near-α, metastable β and α + β and are presented in Fig. 1.11. α alloys are considered to be pure Ti and Ti with α-stabilizing elements and/or neutral elements. If these alloys have a small fraction of β-stabilizing elements then they are considered to be in the group of near α alloys. If the amount of β phase reaches 5–40 % at room temperature, the alloy is considered to be α + β phase, which is the most commonly used type of Ti alloys. Metastable β alloys are alloys from the two-phase region in which, due to the amount of β-stabilizing elements, the β phase does not undergo a transformation to martensite upon fast quenching. Finishing up, at the end of the phase diagram alloys with a purely β phase, thus stabilizing and/or neutral elements are usually present [47].

Fig. 1.11

3D phase diagram of Ti alloys [47]

α alloys are used for their corrosion resistance, deformability, high specific strength, toughness and weldability. Grade 1 with its lowest strength and excellent formability is used for deep drawing applications for steel reactors. Grade 2 with somewhat higher strength levels is the most widely used cp Ti alloy, while grade 3 is used only for pressure vessels due to its high strength, and grade 4 is used for fittings and mountings due to the highest value of strength of all alloys. When corrosion resistance is of paramount importance, the addition of Pd developed a new grade, grade 7 that allows greatest corrosion resistance. However, it also makes the alloy very high in price causing alloys such as grade 12 to be used as an alternative. All α alloys can be used for cryogenic applications because they have no ductile-to-brittle transformation.

Near α alloys are used for the high temperature applications due to the excellent creep resistance and high strength coming from α and β phases consecutively. α + β alloys are alloys with both the characteristics of α and β regions. The most widely used alloy of all Ti alloys is Ti6Al4V alloy developed by the Illinois institute of Technology. With the great balance of properties and the highest amount of testing that this alloy has undergone due to the interest of the aerospace industry, it has become the most popular Ti alloy in the industry accounting for 50 % of all alloys used. Other α + β alloys are also in use for their application due to high strength and toughness and elevated temperature applications.

Metastable β alloys are characterized by extremely high strength levels achieved by hardening, while high toughness can also be retained due to the complex microstructure of the alloy. Owing to the fact that the specific weight of these alloys is low and oxidation and weldability are a problem these alloys still have a limited usage. β alloys are considered to be extremely formable but prone to ductile–brittle transformation making them unsuitable for low temperature applications. Some of the most common alloys in industrial use are: Ti-10V-2Fe-3Al, Ti-15V-3Cr-3Al-3Sn and Ti-3Al-8V-6Cr-4Mo-4Zr.

When preparing the microstructure for metallography cutting the specimen should be conducted with low cutting velocity and feed while using coolant due to the low thermal conductivity of the alloy. Grinding is performed using SiC paper up to 1200 grit size and polishing is done with a synthetic or cotton cloth with diamonds of 6 or 3 grit, while the last polishing phase can be achieved with a synthetic leather cloth with silicon dioxide of fine grit (0.04 μm) or a short fibre velvet cloth with an Al₂O₃ suspension with saturated hydrous oxalic acid can be used. Liquid soap is used for both versions of the final polishing suspensions. Owing to the fact that Ti develops deformation surface layers that show pseudo microstructure etching is done in several steps where final polishing and etching are alternated approximately three times until the true microstructure is observed. The etchant used is a hydrous solution of 3 ml HF (40 % conc.) + 5 ml HNO₃ (65 % conc.) with 100 ml H₂O.

The observed microstructure transforms from lamellar for cooling from the β region to equiaxial when cooling from the α region. When cooling from the two-phase region, α nucleates at grain boundaries of the β phase. The coarseness of lamellae depends on the cooling rate and is coarsest for the slowest cooling processes. When fast quenching is applied β phase undergoes a martensitic transformation that in contrast to the one in steel shows a moderate influence on the hardness of the alloy. The equiaxial structures are a consequence of recrystallization and require cold working and solution heat treating for acquiring the microstructure.

The amount of α is determined by the solution heat treating temperature and if done close to the β transus temperature results in a bimodal microstructure which is a mix of equiaxial α in the matrix of lamellar α + β. Equiaxed microstructures have good ductility and fatigue strength and are considered to be desirable for the superplasticity. Lamellar structures have good fracture toughness and are resistant to both creep and fatigue cracks. As expected, because bimodal microstructures have both types of structure, the properties they show are a balance of the equiaxial and lamellar structures. The example of the three types of structures is presented in Fig. 1.12. Depending on the coarseness of the microstructure there will be a difference in the strength of the alloy as well as ductility. Apart from having higher strength and ductility, fine microstructures have a good resistance to crack nucleation as well. Coarse microstructures are in comparison lower in strength and ductility but show better resistance to creep and fatigue crack propagation.

Fig. 1.12

Equiaxed microstructure of TI6Al4V. a Fine, b coarse, c bimodal and d bimodal, [47]

1.3.3 Medical Applications of Ti Alloys

As mentioned earlier due to the biocompatibility, corrosion resistance, bioadhesion, modulus of elasticity, fatigue strength and ability to be processed easily, Ti alloys have been one of the main types of alloys used for implants, stents, heart valves, fixtures, bone plates, screws, etc. in the biomedical industry. Of all the types of Ti alloys, CpTi, α + β and β alloys are used for these purposes with CpTi and Ti6Al4V being the most common ones. For example, CpTi alloys are used for bone plates, especially curved ones, where depending on the required strength grades 1–4 can be used. If higher strength plates are required the alloy can be Ti6Al4V or Ti6Al7Nb; however, these alloys cannot achieve much curvature and are mostly used for straight plates. Ti alloys with high fatigue strength are used for stems of hip joints and are mostly chosen to be of Ti6Al4V. The stems can be both forged and investment cast however, while forged stems have stress relieving as the final step, the microstructure is mill annealed or equiaxial while cast stems will have a fully lamellar microstructure with crack nucleation resistance or a bi-lamellar structure after heat treating giving an even higher crack nucleation resistance than forged parts [54].

1.4 Material Models

Manufacturing processes such as machining and forming introduce large deformations with various stress, strain, and temperature levels creating complex deformation states. Apart from the mentioned parameters, the flow stresses in manufacturing processes are also influenced by strain rate, loading history as well as temperature history. The size effect in micromachining is incorporated in the material models by modelling the material strengthening mechanism. Many models have been developed throughout the years. However, no model has been proven to correctly describe the behaviour of all materials used in the vast number of processes in the manufacturing field while incorporating all the influential parameters. A review of current material models has been presented and the model of choice for the modelling of micromachining of Ti6Al4V alloy has been explored.

1.4.1 Johnson–Cook Model (J–C)

J–C model represents a phenomenological material model most often used in literature for finite element analysis (FEA) and modelling of material behaviour [30]. It is most often used with the aim to show the dependence of the flow stress on strain rate and temperature. The mathematical representation of the J–C model is presented with the following equation [23]:

$$ \sigma = (A + B\varepsilon^{n} )\left[ {1 + C\ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right]\left( {1 - T_{h}^{m} } \right) $$

(1.4)

$$ T_{h} = \left( {T - T_{room} } \right)/\left( {T_{melt} - T_{room} } \right) $$

(1.5)

where ε is the equivalent plastic strain, $\dot{\varepsilon }$ is the strain rate, $\dot{\varepsilon }_{0}$ is the reference strain rate, and the constants are: A—yield strength, B and n representing strain hardening, and C is the strain rate constant, T_h is the homologous temperature, T_melt is the melting temperature, and T_room is the room temperature.

There have been several modifications of the J–C model in literature regarding the temperature parameter taking into consideration the effect of temperature before and after the recrystallization temperature has been reached [71], modification with the aim of accounting for the strain softening effect [7], modification using an Arrhenius approach rather than linear dependence of temperature in order to represent adiabatic plasticity [74].

The mathematical formulation of the modified J–C model incorporating the effect of recrystallization temperature is presented as follows [71]:

$$ \sigma = (A + B\varepsilon^{n} )\left[ {1 + C(\ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }})^{m} } \right]\left[ {1 - (T_{h} )^{m} } \right]\frac{{(\sigma_{f} )_{def} }}{{(\sigma_{f} )_{rec} }} $$

(1.6)

σ_fdef and σ_frec represent flow stress prior to and after recrystallization. The ratio of flow stresses before and after reaching the recrystallization temperature has been introduced in order to account for phase transformations that are triggered by increasing temperature above the recrystallization temperature that would undoubtedly influence the material behaviour.

The mathematical formulation of the modified J–C model incorporating the exponential term to more accurately determine Arrhenius-type dependence for adiabatic plasticity is presented as follows [74]:

$$ \tau = \left[ {B\gamma^{n} } \right]\left[ {1 + C\ln (\dot{\gamma }/\dot{\gamma }_{0} )} \right]f\left( {\bar{T}} \right) $$

(1.7)

$$ \bar{T} = T_{m} - T/T_{m} $$

(1.8)

where, B, n, and C are material constants, $\bar{T}$ is a dimensionless temperature, T_m is the melting temperature T₀ is the reference temperature, and γ₀ is the reference strain rate.

The exponential term that more accurately represents the adiabatic plasticity is presented as follows:

$$ f(\bar{T}) = (\tau /\tau_{0} )_{{\gamma ,\dot{\gamma }}} $$

(1.9)

where τ is the shear stress at a given T and τ₀ is the shear stress at a reference temperature.

The mathematical formulation of the modified J–C model incorporating not only the effect of strain rate hardening and thermal softening, but strain softening as well (tanh function), is presented as follows [7]:

$$ \begin{aligned} \sigma & = \left( {A + B\varepsilon^{n} \left( {\frac{1}{{\exp (\varepsilon^{a} )}}} \right)} \right)\left( {1 + C\ln \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right)\left( {1 - \left( {\frac{{T - T_{r} }}{{T_{m} - T_{r} }}} \right)^{m} } \right) \\ & \quad \left( {D + (1 - D)\tanh \left( {\frac{1}{{(\varepsilon + S)^{c} }}} \right)} \right) \\ \end{aligned} $$

(1.10)

$$ \begin{aligned} D & = 1 - \left( {\frac{T}{{T_{m} }}} \right)^{d} \\ S & = \left( {\frac{T}{{T_{m}}}} \right)^{b} \\ \end{aligned} $$

where A, B, C, a, b, c and d are material constants, σ is the equivalent flow stress, ε is the equivalent plastic strain, έ is the strain rate, έ₀ is the reference strain rate, T the workpiece temperature, and T_m and T_r are the material melting and room temperatures, respectively. This model shows a great influence on the chip formation and chip shape because the strain softening effect has an effect on the appearance of shear localization enabling formation of segmented chips. The predictions using this model are not satisfactory when the strain softening level is low.

The J–C model describes the material behaviour relatively well; however, it is a model which does not incorporate the effect of the loading path, strain rate history or temperature history on the overall behaviour. The J–C model uses the determination of constants from experimental data through curve fitting which has no validity if extrapolated beyond the available data, making the model inadequate for application beyond the deformation conditions and microstructures present in the experimental data used. This becomes a serious problem when dealing with machining processes where the deformation is significantly more severe than the deformation achieved in standard tests for material characterization [23].

1.4.2 Mechanical Threshold Model (MTS)

This model has originally been developed by in 1981 [56]. The mathematical representation of this model is shown as [4]:

$$ \sigma \left( {\varepsilon_{p,} \dot{\varepsilon },T} \right) = \sigma_{a} + \left( {S_{i} \sigma_{i} + S_{e} \sigma_{e} } \right)\frac{\mu (p,T)}{{\mu_{0} }} $$

(1.11)

This model is based on the reasoning that the mechanical behaviour of the material is dependent on the change in its microstructure and the dislocation motion. In the model in question σ represents the flow stress, ε_p is the plastic strain, έ is the strain rate, σ_a is the athermal component of the mechanical threshold stress, the variable σ_i represents the intrinsic component of the flow stress and is connected to thermally activated dislocation motion, σ_e is the strain-hardening component of the flow stress, and S_i and S_e are temperature and strain rate dependent terms. μ represents the shear modulus which is temperature and pressure dependent (T, p) and μo is the shear modulus at 0 K and ambient pressure.

1.4.3 Power Law Model

The power law is presented in the following mathematical formulation [23]:

$$ \sigma = K\varepsilon^{n} $$

(1.12)

As it can be seen from the equation, this is a simple model and it is usually used when describing simple deformation models of materials. The power law model uses fitting of parameters in order to determine material constants K and n and does not account for any temperature or strain rate dependence of flow stress σ.

1.4.4 Zerilli and Armstrong Model

The Zerilli and Armstrong model [95] represents a semi-empirical model based on dislocation mechanics with the aim of incorporating strain hardening and thermal softening effects into the material deformation model. This model actually differentiates between fcc and bcc crystals with the reasoning that the dislocation mechanism characteristics in bcc materials are not affected by temperature and strain rates while fcc crystals are [23].

The mathematical formulation of the Zerilli–Armstrong model for bcc and fcc crystals can be presented as follows [95]:

$$ \sigma = {\Delta} \sigma_{G}^{\prime} + C_{1} \exp \left( { - C_{3} T + C_{4} T\ln \dot{\varepsilon }} \right) + C_{5} \varepsilon^{n} + kl^{ - 1/2} $$

(1.13)

$$ \sigma = {\Delta} \sigma_{G}^{\prime} + C_{2} \varepsilon^{0.5} \exp \left( { - C_{3} T + C_{4} T\ln \dot{\varepsilon }} \right) + kl^{ - 1/2} $$

(1.14)

where, ${\Delta} \sigma_{G}^{\prime}$ is the additional component of stress that is a result of the influence solute and original dislocation density on yield stress. σ is the yield stress, ε is the strain, έ is the strain rate, k is the microstructural stress intensity, l is the average grain diameter, and C1–C5 are material constants.

The model incorporates the thermal activation necessary in order for the overcoming obstacles for dislocation motion and dislocation interaction in materials [2]. The dislocation mechanisms are considered to be different for different crystal lattices and are considered to be cutting of dislocation forests in fcc and the overcoming of Peierls–Nabarro barriers in bcc metals and therefore the flow stress which incorporates the effect of temperature and strain rate is the function of the yield stress in bcc materials and hardening stress in fcc materials [2].

1.4.5 Japanese Model

An empirical model that is used by some of the Japanese researchers presents the flow stress as a function of reference stress, strain rate and temperature where the reference stress is a measure of deformation history. Even though the deformation history is incorporated, the temperature or strain rate histories are neglected. This increases the error in the modelling because the flow stress is known to be dependent on the strain path [93]. The mathematical formulation of this model can be presented as follows [23]:

$$\bar{\sigma } = A(10^{ - 3} \dot{\bar{\varepsilon }})^{M} e^{kT} (10^{ - 3} \dot{\bar{\varepsilon }})^{m} \left\{ {\int\limits_{{T, \dot{\bar{\varepsilon }} \equiv h(\dot{\bar{\varepsilon }})}} {e^{ - kT/N} (10^{ - 3} \dot{\bar{\varepsilon }})^{ - m/N} d\bar{\varepsilon }} } \right\}^{N} $$

(1.15)

where, A, m, M, N, and k are material constants.

Just like the J–C model and the power law model this is an empirical model that has no viability outside the measured data. The history effect of temperature, strain rate and load path have been neglected and introduce inaccuracy in modelling material deformation.

1.4.6 Bammann, Chiesa, and Johnson Model (BCJ)

BCJ represents an internal state variable plasticity model. The BCJ model takes into consideration temperature sensitivity, strain rate sensitivity and the damage effect by incorporating hardening and recovery into the model by using the deformation path history effect. The model takes into account the rate of change of internal as well as observable state variables including the creep and plasticity through a deviatoric inelastic flow rule represented as a function of the temperature, the kinematic hardening internal state variable, the isotropic hardening internal state variable, and the functions related to yielding with Arrhenius-type temperature function [23]. The mathematical representation is presented as follows:

$$ \mathop {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }\limits^{ \circ } = \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } } - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{W}^{e} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{W}^{e} = \lambda tr(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{D}^{e} ) \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{I} + 2\mu \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{D}^{e} $$

(1.16)

$$ D^{e} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{D} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{D}^{in} $$

(1.17)

$$ D^{in} = f(T)\sinh \left[ {\frac{{\left\| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha } } \right\| - \left\{ {R + Y(T)} \right\}}}{V(T)}} \right]\frac{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha } }}{{\left\| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha } } \right\|}} $$

(1.18)

$$ \mathop {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha } }\limits^{ \circ } = \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha } } - W^{e} \alpha + \alpha W^{e} = \left\{ {h(T)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{D}^{in} - \left[ {\sqrt {\frac{2}{3}} r_{d} (T)\left\| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{D}^{in} } \right\| + r_{s} (T)} \right]\left\| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha } } \right\|\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha } } \right\} $$

(1.19)

$$ \dot{R} = \left\{ {H(T)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{D}^{in} - \left[ {\sqrt {\frac{2}{3}} r_{d} (T)\left\| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{D}^{in} } \right\| + R_{s} (T)} \right]R^{2} } \right\} $$

(1.20)

where $\mathop {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }\limits^{ \circ }$ and $\alpha$ are objective rates, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{W}^{e}$ is the elastic spin, μ and λ are elastic Lame constants, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{D}^{e}$ is the elastic rate of deformation, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{D}$ is the total rate of deformation, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{D}^{in}$ is the inelastic rate of deformation, f(T) is the strain rate at which yield transition from rate-independent to rate-dependent, h(T) is the anisotropic hardening modulus, H(T) is the isotropic hardening modulus, Rd and rd(T) represent the dynamic recovery, rs(T) and Rs(T) represent diffusion-controlled static or thermal recovery, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\alpha }$ is the kinematic hardening internal state variable. Even though this model incorporates effects that have been neglected in other models, it has 20 constants that need to be determined for calculations. Even though a nonlinear least square program exists for the determination of these constants, the process is still daunting.

1.4.7 The Applied Model

In order to describe the material behaviour, the material model that will be used in the FEA is a power law model. In order to correctly predict the behaviour, strain hardening, strain rate sensitivity, and thermal softening will be included as well as a damage model as follows [84]:

$$ \sigma (\varepsilon^{p} ,\dot{\varepsilon },T) = g(\varepsilon^{p} )*{\Gamma} (\dot{\varepsilon })*\Theta (T) $$

(1.21)

where, $g(\varepsilon^{p} )$ accounts for strain hardening, Г(έ) for strain rate sensitivity and Θ(t) for thermal softening. Strain-hardening function is presented as follows:

$$ g(\varepsilon^{p} ) = \sigma_{0} \left[ {1 + \frac{{\varepsilon^{p} }}{{\varepsilon_{0}^{p} }}} \right]^{{\frac{1}{n}}} \quad {\text{if}}\;\varepsilon^{p} < \varepsilon_{cut}^{p} $$

(1.22)

$$ g(\varepsilon^{p} ) = \sigma_{0} \left[ {1 + \frac{{\varepsilon_{cut}^{p} }}{{\varepsilon_{0}^{p} }}} \right]^{{\frac{1}{n}}} \quad {\text{if}}\;\varepsilon^{p} \ge \varepsilon_{cut}^{p} $$

(1.23)

where, σ₀ the initial yield stress, ε^p is the plastic strain, $\upvarepsilon_{0}^{\text{p}}$ is the reference plastic strain, $\upvarepsilon_{\text{cut}}^{\text{p}}$ is the cutoff strain and n is the strain-hardening exponent.

Strain rate sensitivity function is presented as follows:

$$ \Gamma (\dot{\varepsilon }) = \left( {1 + \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right)^{{\frac{1}{{m_{1} }}}} \quad {\text{if}}\;\dot{\varepsilon } \le \dot{\varepsilon }_{t} $$

(1.24)

$$ \Gamma (\dot{\varepsilon }) = \left( {1 + \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right)^{{\frac{1}{{m_{2} }}}} \left( {1 + \frac{{\dot{\varepsilon }_{t} }}{{\dot{\varepsilon }_{0} }}} \right)^{{\left( {\frac{1}{{m_{1} }} - \frac{1}{{m_{2} }}} \right)}} \quad {\text{if}}\;\dot{\varepsilon } > \dot{\varepsilon }_{t} $$

(1.25)

where, έ is the strain rate, έ₀ is the reference plastic strain rate, and έ_t is the strain rate of the transition between the high and low strain sensitivity. m₁ and m₂ are the low and high strain rate sensitivity indexes, respectively.

Thermal softening function is presented as follows:

$$ {\Theta} (T) = c_{0} + c_{1} T + c_{2} T^{2} + c_{3} T^{3} + c_{4} T^{4} + c_{5} T^{5} \quad {\text{if}}\;{\text{T}} < {\text{T}}_{\text{cut}} $$

(1.26)

$$ {\Theta} (T) = {\Theta} (T_{cut} )\left( {1 - \frac{{T - T_{cut} }}{{T_{melt} - T_{cut} }}} \right)\quad {\text{if}}\;{\text{T}} \ge {\text{T}}_{\text{cut}} $$

(1.27)

where, c₀–c₅ are the coefficients of the polynomial fit, T is the temperature, Tm is the melting temperature, and T_cut is the linear cutoff temperature.

The damage model is presented as follows:

$$ D = \sum\limits_{i} {\frac{{\Delta \varepsilon_{i}^{p} }}{{\varepsilon_{fi}^{p} }}} $$

(1.28)

where D is the dimensionless cumulative damage, $\Delta \varepsilon_{i}^{p}$ is the instantaneous increment of strain, and $\varepsilon_{fi}^{p}$ is the instantaneous strain to failure.

After elaborating on the existing models from the literature, it is necessary to stress that the effectiveness of a model does not lay in capturing the possible behaviour of each and every material in the sense of correctly developing material parameters, but also on the actual ability to apply a certain model in the sense of the ability to determine material constants and develop FEA. With this in mind, it would be necessary to develop a material model which both correctly describes material behaviour by incorporating not only temperature and strain dependence but also the history effect of temperature, strain rates, and load paths while at the same time keeping the number of necessary material constants as low as possible in order to enable realistic FEA. Until such a model is developed, researchers will continue choosing from the pool of existing models, making the decision based on the material type in question and deformation process that the workpiece of choice is being subjected to.

1.5 Machining of Titanium Alloys for Medical Applications

Even though machining Ti alloys produces forces only slightly higher than those developed when machining steel, the specific metallurgical characteristics of these alloys create difficulties and therefore increase the price. Although hard, it is not impossible to achieve excellent surface finish and good production rates when these alloys are machined; however, it is necessary to take into consideration the very unique characteristics which Ti alloys possess such as low heat conduction, reactivity, low Young’s modulus, alloying tendency, surface damage susceptibility, and work-hardening characteristics.

Poor heat conduction of Ti alloys makes the heat linger on the tool cutting edge and tool face effecting tool life. Furthermore, the work-hardening characteristics of the alloy induces the absence of a built-up edge creating localization of heat that in combination with high bearing forces results in rapid tool deterioration. The springback effect in these alloys is high due to the low Young’s modulus and consequently the deflections of the workpiece are significant making precision machining hard. Increasing the systems rigidity, using sharp tools, greater tool clearances are one of the ways to reduce this effect. Surface damage in Ti alloys has an effect when they are used in application where fatigue life is important. To optimize fatigue life it is necessary to maintain sharpness of the tools while machining (mostly grinding) Ti alloys [16].

Main influencing parameters when machining Ti alloys can be considered are as follows:

• Cutting speed

• Feed rate

• Cutting fluid

• Tool sharpness

• Tool–workpiece contact

• Rigidity of the setup.

When setting up the machining parameters for machining Ti alloys, it is necessary to keep the speed low in order to minimize the temperature rise and consequently reduce the influence of heat on the tool tip and edge. Since the tool temperature is affected more by speed and less by feed, then the feed should be kept high while taking into consideration that a work hardened layer is formed after each cut and the consecutive cut needs to be larger than the thickness of this layer. Another influence on the temperature during machining is the amount of cutting fluid used. A generous amount needs to be used to reduce temperatures as well as to clear the work area of chips and reduce cutting forces. The sharpness of the tools used in machining is going to influence the surface finish and if not adequate can cause tearing as well as deflection of the workpiece. The contact of the tool with the workpiece is important because if dwelling of the tool is allowed while tool is in contact with the workpiece it can cause work hardening, smearing, galling, and seizing leading to tool deterioration and eventually breakdown [16].

Most of the efforts made to enhance the machining process of titanium alloys have been focused on decreasing temperature generated at the cutting edge and tool face because it influences tool life and surface characteristics of the workpiece. It has been shown that when machining Ti6Al4V alloys, tool life is increased by decreasing cutting speed and increasing feed. At high cutting speeds, the tool deteriorates rapidly and tool life is dramatically increased by lowering the speed parameter.

The cutting tool material needs to offer abrasion resistance and hot hardness and so far the three most satisfying materials have been proven to be carbide and high speed or highly alloyed steels. Different materials are used for different applications, for example, turning and face milling is mostly done using C2 tungsten carbide grades while HSS tools are used for milling, drilling and tapping of Ti alloys. Productivity is also being influenced by using specific techniques such as specially designed cutters and special cutting techniques [16].

Milling parameter recommendations are given in Tables 1.7, 1.8 and 1.9, for face milling, end milling—slotting, and end milling—peripheral milling, consecutively [16].

Table 1.7 Face milling data

Table 1.8 End milling data—slotting

Table 1.9 End milling data—peripheral milling

The change in cutting speed and/or feed has a significant influence on the chip–tool contact length, chip length, segmentation frequency, segment size, and chip thickness therefore presents the two major parameters for process manipulation. Due to this fact, the effect of machining parameters such as cutting speed and feed on chip formation has been a topic of interest for many researchers.

It has been shown [29] that there is a dependence of the contact length on the cutting speed when machining Ti6Al4V alloys where the contact length is considered to be the contact between the chip and the tool rake face when creating a continuous chip. The dependence presented in Fig. 1.13 shows that there is a maximum contact length that is achieved at the transition in the cutting speed from regular to high speed. They attribute this dependence to the effect of “shear banding”. The contact length is also shown to be dependent on the undeformed chip thickness, where the increase in the undeformed chip thickness yields an increase in the contact length. It has been stated that the chip compression ratio (ratio of the actual and undeformed hip thickness) is hard to comprehend due to the scattered results and they attribute this to the poor machinability of Ti alloys and shear banding as well.

Fig. 1.13

Variation of the contact length with cutting speed for Ti6Al4V [29]

Chip morphology has been researched [82] showing that the saw-chip formation is present and that the chip length is increased while the width decreased with the increase in cutting speed and feed. The segmentation size increases while the frequency of the segmentation decreases with cutting speed. This has also been determined in further work [13] where it has been shown that the segmentation frequency increases linearly with the increase in cutting speed and decreases with increase in feed, Fig. 1.14.

Fig. 1.14

Dependence of chip segmentation frequency on cutting speed [82]

The chip thickness ratio (ratio of undeformed chip thickness and actual chip thickness) has been shown to increase with the decrease in cutting speed and it decreases with the increase in feed when using low speeds [5]—Fig. 1.15.

Fig. 1.15

Chip thickness ratio as a function of cutting speed and feed for Ti6Al4V [5]

The dependence of chip thickness, tool–chip contact length and chip up-curl radius on the tool radius/chip thickness ratio has been presented in Fig. 1.16 [20]. The chip thickness decreases with the increase in the tool radius value as the ratio of the tool radius and undeformed chip thickness is increased. The tool chip contact length follows the same trend as the chip thickness yielding a lower value with the increase of the tool edge radius.

Fig. 1.16

Influence of the tool edge radius [20]

However, the chip thickness is a questionable parameter when Ti alloys are being investigated [36]. The conventional chip thickness ratio for the continuous chip formation models and the parameters such as shear angle which are calculated from the ratio are considered to be incorrect parameters for describing machining characteristics of Ti alloys [36]. This is because that Ti alloy chips become deformed inconsequentially, and are formed by gradual flattening of a softer half wedge by the tool. Consequently, the chip thickness ratio is close to 1. One of the reasons why the machining of Ti alloys cannot be assessed using a conventional formula is that concentrated shear subjects the chip to large strains creating thick chips with low shear angles and low velocity. Energy partition presented in Fig. 1.17 is also different from steel showing

• Energy into the chip U_c = R₁U_s

• Into the tool U_t = (1 − R₁)U_s + R₃U_ff

• Into the workpiece U_w = (1 − R₃)U_ff

(U_ff is the frictional energy per unit volume due to rubbing between the flank and the machined surface and R₃ is the fraction of heat conducted into the tool due to flank friction).

Fig. 1.17

Energy partition when machining Ti alloys [36]

The high temperatures are present when using low values of the depth of undeformed layers due to the rubbing of the flank on the machined surface. When the influence of the rake angle on the chip formation [1] has been investigated, it has been determined that the rake angle has a critical value of −70° when machining zinc, after which there is no chip formation (Fig. 1.18).

Fig. 1.18

Influence of the rake angle on chip formation [1]

This issue has further been addressed [35] where it has been determined that the rake angle at which chip formation ceases is −85°. While elsewhere [68] it has been determined that this value is lower and equals −55°. The mechanism of chip formation when machining Ti6Al4V alloys has been discussed by many researchers and follows two theories. The first theory is the catastrophic thermoplastic shear where thermal softening present in the primary shear zone predominates the strain hardening caused by high strain rates in machining [15, 40, 41, 67, 70]. The second theory is the periodic crack initiation that is considered as a consequence of high stress present during the machining process. This theory is based on the idea that cracks are formed in the primary shear zone and then rewelded through high pressure and heat originating from friction [25, 59, 60, 90]. In the following paper [65] authors show the formation of the chip and its microstructure showing the lack of cracks in Fig. 1.19. The authors have determined that there is no phase transformation taking place classifying the bands to be deformation shear bands and confirming the catastrophic shear model.

Fig. 1.19

Microstructure of the chips and shear bands in Ti6Al4V [65]

Vyas and Shaw on the other hand confirm the crack initiation presented in Fig. 1.20. They show formation of both gross cracks and micro cracks. Gross cracks continue throughout the chip width while micro cracks seem to be discontinuous. The process is based on the idea that the blocks of material which are between the gross cracks glide out with no plastic deformation; while the material surrounding the micro cracks will undergo adiabatic shear in case when the temperature is high enough which may also result in phase transformations [90]. It is obvious from the fact that both theories are present and confirmed in the literature that the chip formation mechanism is not straightforward and must depend on various parameters. Investigation techniques such as X-ray diffraction, energy dispersive X-ray analysis, scanning electron microscopy, and electron backscattering technique can be found useful in determining the causes of the discussed results. It is yet to be determined why these inconsistencies occur and what influences which one of the theories will be observed in the experimental work. Therefore, this can be considered a field with a vast potential for research.

Fig. 1.20

Mechanics of chip formation showing a crack formation, b micro crack formation in Ti6Al4V [90]

1.5.1 Micromachining Medical Materials

Development of modern technology has brought with it the necessity of integrating miniature components into the fields of electronics, telecommunications, defense industry, and biomedical devices. For the longest time, the techniques applied have been a product of the development of the electronics industry and have been based on lithography. These processes have been proven to be limited in the materials that can be processed, achievable geometries, lack cost effectiveness in anything but mass production, etc. The need to overcome these shortcomings and manufacture 3D components with intricate geometries and of various materials has increased the interest in machining processes on the microscale. Many non-conventional processes have been adopted such as laser machining, focused ion beam machining, and electro discharge machining offering the possibility of creating complex geometries, however, still limited in materials they could be applied to as well as limited in productivity. Due to the inefficiencies of the previously mentioned processes, micromechanical processes have been widely investigated. Micromilling applicability has been confirmed [21, 91, 92] showing the flexibility of the process and the microscale.

1.5.1.1 The Size Effect

When analyzing the micromilling process phenomena it is not possible to describe it by simply scaling down the macromilling process itself. The main and critical difference between these two scales of the same process is the fact that the assumption of material homogeneity does not stand any more. The assumption that in macromachining the material acts as a homogeneous body is correct because the tool geometry is significantly larger than the microstructural features. On the other hand, when observing micromachining, the tool geometry is now of the same order of magnitude as the microstructural features making it necessary to take the structure of the material into consideration. As it can be seen from current research [92], the more significant effect of the tool geometry on the cutting process on the microscale is simply a consequence of the limitations in the tool manufacturing industry where the fabrication of miniature tools is extremely hard and it also brings with it a decrease in the structural strength of the tool when compared to macro tools. This means that the inability of fabrication of extremely small edge radii on tools used for micromachining yields the comparable size of tool geometry to feed rate values. All this leads to one of the most important phenomena in micromachining which is defined as size effect. Size effect relates to the significant increase in the specific energy as the uncut chip thickness is decreased.

Many researchers have tackled the problem of identifying causes of the phenomena of the size effect [3, 17, 31, 42, 45] and have connected it to the strengthening mechanism of the material through the decreasing number of crystallographic defects in materials microstructure [3], increasing strain rate at the primary shear zone, decreasing of thermal softening, influence of the tool geometry [33, 37, 52, 69], strain rate sensitivity [45], change in temperature and consequently shear plane angle [42], plastic flow under the workpiece surface [61], and gradient plasticity [49]. Some of the widely accepted causes will be addressed in the following text. Owing to the size effect the phases present in a material show an effect on the machining forces and other parameters. This effect has been shown [11, 12] by developing a simulation model for analyzing multiphase materials. The researchers have shown that there is a change in the chip formation mechanism as well as in the cutting force patterns when changing from a single phase to a multiphase material, Fig. 1.21. The material model used for the simulations was the BCJ model accounting for material behaviour under various stresses, strains, temperatures, damage, etc. Material investigated in the study was ductile iron and therefore to account for machining ferrite pearlite and graphite at different points in time due to the size effect they have been modelled as separate homogenous materials.

Fig. 1.21

Machining forces from cutting pearlite, ferrite and ductile iron respectively [11]

In literature there has been interest in analyzing machining of ductile iron [88]. In order to capture the actual microstructure of ductile iron consisting of graphite, ferrite, and pearlite, the authors have created a map of microstructural constituents using a grid of points with a probability factor of spheres representing the secondary phases while the tertiary phases were assigned to each grid point. Researchers have shown the effect of the multiphase material on the cutting force magnitude and variation showing that there is a higher frequency variation of forces when micromilling a multiphase material where the microstructure effect accounts for over 35 % of the energy in the force signal. They also show the effect of the spacing of the secondary phase and its size on the frequency and magnitude of the cutting force variation. Another significant difference between milling at the two scales is in the function of the dependence of force on the chip thickness. The cutting force increases with the increase in chip thickness when machining on the macroscale; however, when the chip thickness reaches values of the tool edge radius the relationship becomes much more complicated [57]. Many researchers have connected the force function to the chip thickness in their work that will be presented and discussed later in the thesis.

Many researchers have shown the increase in the specific cutting energy with the decrease in the uncut chip thickness [3, 22, 42, 52], Fig. 1.22. The researchers have investigated machining plain carbon steel with ceramic indexable tools.

Fig. 1.22

Specific cutting energy versus uncut chip thickness [49]

It has been accepted in the research community that the machining forces are going to differ if sharp or blunt tools are used in the process. This information has led to research on the topic of the influence of tool geometry on the size effect in machining. It has been concluded by a number of researchers that the size effect is by all means among other things a consequence of tool geometry [33, 37, 52, 69]. Lucca et al. [51] show that when machining germanium the increase in the ratio of thrust force and cutting force is accounted by the decrease in depth of cut and increase in the negative rake angle Fig. 1.23. Tools used in the study were diamond single crystal tools with rake angle of 0°, −15°, −30°, −45°.

Fig. 1.23

Effect of the depth of cut and rake angle on thrust and cutting forces [51]

It has been stated [52] that when the uncut chip is decreased to the value of the radius of the tool, the effective rake angle has the crucial effect on resulting forces. Due to the decreased uncut chip thickness, the direction of the resulting forces is determined by the effective rake angle in this case and not the nominal rake angle.

Research shows that the thrust and cutting forces increase with the increase in tool edge radius up to a certain value where it becomes independent at higher r [37]. The authors argue that at higher values of radii the rake angle is high and the variation is small; while at low values the variation of the angle is significant enough to cause the dependence. Also, the value of the thrust-to-cutting force ratio increases at low values of the radius while stays more constant at higher values of the radius. It has further been determined that there is an increase in the specific cutting energy when increasing the radius size for tools with small radii but no significant effect if the radius is large to begin with.

The effect of the tool edge geometry on machining has further been investigated showing the increase in force with the decrease in tool edge radius and uncut chip thickness [69], Fig. 1.24. This approach has been taken also by other researchers [8] who claim that the tool edge radius has a significant effect on the material deformation process by expanding and widening the plastic deformation zone and changing the material flow around the tool edge as well as increasing the dissipation of energy because of the higher value of the contact length between the chip and the tool.

Fig. 1.24

Effect of the tool edge radius and uncut chip thickness on cutting and thrust forces [69]

In the literature, the size effect has also been attributed to the crystallographic effect [72]. Considering the fact that the tool is extremely small and is approaching the size of the microconstituents in the material, the actual number of defects such as grain boundaries, point defects, etc. is decreasing at the level of machining and the material is considered to be approaching its theoretical strength.

The strain gradient plasticity model has been used to account for the size effect where the material strength is considered to be a function of both strain and strain gradient rather than just strain as it is considered in regular plasticity theory [31]. The authors state that the size effect can be addressed using the geometry and gradient of the strain field because the density of geometrically necessary dislocations increases in comparison to the density of statistically stored dislocations leading to increase in strength even when the scale of deformation is decreased. They evaluate the strain gradient, density of geometrically necessary dislocations, shear strength, and specific shear energy. Authors show that the length of the shear plane decreases with the decrease in the undeformed chip thickness leading to an increase in the shear strength. This model considers the effect of the strain gradient produced in the primary shear zone only.

The effect of the strain gradient has been explored further [49] and the authors came to the conclusions that it contributes to the size effect even more at low cutting speeds and large uncut chip thicknesses. Also the effect is dominant over temperature effect when machining is done at high cutting speeds and large uncut chip thickness. Strain rate sensitivity [45] has also been used as the reasoning behind the size effect. The authors show that the maximum shear strain rate increases with the decrease in the uncut chip thickness that consequently leads to the increase in the flow stress and therefore explains the increase in specific cutting energy.

The temperature influence on the size effect has been adopted by Kopalinsky and Oxley where the drop in temperature affects the shear plane angle and increases the specific cutting force [42]. The size effect has been accounted for through subsurface plastic flow arguing that the amount of energy is not proportional to the uncut chip thickness and shear angle [61].

It is very easy to conclude from the existing research on the origin of size effect that it is not likely that the size effect is a consequence of only one mechanism. It is highly likely that all the mechanisms have an effect at certain points in time depending on the process parameters and/or materials used.

1.5.1.2 Minimum Chip Thickness

The importance of estimating the minimum chip thickness lies in the fact that it is one of the major limiting factors in achieving accuracy at a microscale because a chip thickness smaller than the critical value results in ploughing and rubbing, therefore increasing the achievable surface roughness significantly. Some authors [32] have used estimation of minimum chip thickness using cutting force periodicity in their work. Their reasoning is based on the fact that the tool edge radius/minimum chip thickness is a function of cutting conditions and workpiece–tool material combination making the actual measurement hard. Therefore, they have based their research on the analysis of the periodicity of cutting forces. They have adopted wavelet analysis, which shows that the global wavelet spectrum achieves a maximum at the most significant period of the data and therefore determines the dominant period of the cutting force signatures.

Gurin [24] has used in his thesis the stability of the cutting process as a measure of the transition from ploughing to cutting showing that the change happens when the stresses due to the normal and tangential forces become equal. A criterion has been developed for determining the transition from interfacial sliding to microcutting [43]:

$$ \frac{h}{r} = 0.5\left( {1 - \frac{2\tau }{{\sigma_{T} }}} \right) $$

(1.29)

where, h is the depth of indentation (depth of cut), r is the radius of the indenter (cutting edge radius), τ is the shear strength of the adhesive junction, and σ_T is the yield stress of the workpiece material.

Some researchers [44] argue that there is a neutral point on the tool where all the material above it becomes deformed mainly by the rake face creating a chip; while the material below it, which is the surface layer of the machined part, becomes formed by the rake and clearance faces. The obtained relationship is presented as follows:

$$ a_{\hbox{min} } = r(1 - \cos \theta ) $$

(1.30)

where a_min is the minimum chip thickness, r is the cutting edge radius, and θ is the neutral point angle.

Some researchers have further followed the idea of the neutral point and determined that if the undeformed minimum chip thickness is smaller than the critical value, only ploughing will occur; while it is larger, both ploughing and cutting will be present [6]. Analyzing the energy expended in the chip they analytically determined that the critical value of the angle of the natural point is 37.6° and experimentally determined it is between 28° and 33° when machining lead, soft aluminium and mild steel using HSS tools with the addition of 10 % cobalt. It has been determined that the value of the neutral point angle is independent of the cutting edge radius. Further, it has been determined that there will be influence on the natural point angle from the hardness of the workpiece material, hardness of the tool material, plastic recovery, and friction conditions. Hardness of the material will yield a higher effective edge radius and also higher elastic recovery of the materials; Plastic recovery can be as high as 20 % of the depth of cut for certain materials, which would make it necessary to incorporate into analysis. The friction condition can be various because the process changes from ploughing to cutting while changing along the cutting edge. The authors have shown that if a model developed by other researchers is applied the value of the analytically determined angle is decreased to 30.5°.

The effect of the minimum chip thickness on the surface roughness has experimentally been analyzed [89]. The authors have determined that the value of the minimum chip thickness depends on the material in question and it ranges from 0.2 to 0.35 of the radius from pearlite and ferrite. They have observed that ploughing forces lead to burr formation influencing the surface and subsurface of the workpiece causing potential increase in residual stresses. The relationship between the friction coefficient, tool radius, and minimum chip thickness has been an interesting topic for many researchers [79]. Using analytical methods they have defined the minimum chip thickness as follows:

$$ t_{m} = r\left( {1 - \cos \left( {\frac{\pi }{4} - \frac{\beta }{2}} \right)} \right) $$

(1.31)

where t_m is the minimum chip thickness, r is the tool edge radius, and β is the friction angle between the tool and uncut workpiece passed under the tool. The researchers have proposed a microcutting model and have confirmed the results by experimental work showing that the increase in the friction coefficient and use of a smaller edge radius result in a smaller minimum chip thickness. One of the important facts that has been acknowledged in this work is that the value of the tangential force in simulations and experiments is not the same because there is piling up of the material in front of the tool which cannot be represented in the simulation.

Fang [20] determined the chip thickness using the chip up-curl radius R, angular velocity ω as well as magnitude of chip velocity V.

$$ t = 2\left( {\frac{V}{\omega } - R} \right) $$

(1.32)

By focusing on molecular dynamics simulations for estimating the minimum chip thickness and achievable accuracy it has been shown that this value is material dependent and has a value of 5 % of the cutting edge radius (which had a value of 5–10 nm) when copper and aluminium are machined with diamond [77].

Other researchers have used experimental work to analyze the minimum chip formation when machining aluminium samples using diamond tools showing that the minimum chip thickness reaches a value of 20–40 % of the cutting edge radius when tools with 1–2 µm are used [94]. Instead of using experimental work, some researchers have focused on the analytical determination of the minimum chip thickness developed on the basis of molecular mechanical theory of friction correlating the values to the workpiece and tool thermo mechanical properties [50].

Ikawa et al. [27] have based their investigations on the atomistic modelling of the machining process, Fig. 1.25. They have determined that with a specially prepared diamond tool a thickness of cut of 1 nm can be achieved experimentally which can be seen in Fig. 1.26. The minimum chip thickness remains an open field for research. The values are obviously material dependent as well as process dependent. There is not only the influence of the tool geometry but also the influence of the machine tool rigidity and set up on the process. Therefore, calculating the minimum chip thickness for specific operations and specific combination of tool–workpiece materials remains to be tackled.

Fig. 1.25

Atomistic simulation of machining copper [27]

Fig. 1.26

SEM images of the nominal thickness of cut of 1 nm [27]

1.5.1.3 Computational Analysis

Computational analysis has been used in the last several decades and can be divided into approaches representing the Finite Element Methods (FEM) and Molecular Dynamics simulations (MD) . In the FEM, the material is represented using the continuum mechanics approach where the chemistry, crystal lattice, grain size, etc. are neglected and the material is considered to be a continuum. The nodes and their number are determined arbitrarily and do not represent features of the material. The mesh parameters are set up in such a way that they only determine the sensitivity during the simulation using a finer mesh when using small feeds or depths of cut in order to capture the fine features. On the other hand, in MD simulations the nodes and the mesh are closely related to the workpiece material in question. The mesh actually represents the crystal lattice of the material while the node distance represents the distance between atoms in the crystal lattice [39]. Further, the interatomic bonding is defined using potential energy functions such as Morse, Lennard-Jones, etc. [39].

When analyzing FEM they can be split into three groups: Lagrangian [76, 80], Eulerian [81] and arbitrary Lagrangian–Eulerian methods [58, 63, 66]. Lagrangian FEM is based on the notion that the mesh is attached to the workpiece and it moves with the material. Owing to the fact that the elements change shape it is often necessary to use remeshing to restore distorted elements and adaptive remeshing is often used. Eulerian FEM involves a workpiece material which flows through the pre-set mesh fixed in space. There is no element distortion in this method; however, the chip formation cannot be modelled and only steady state problems can be analyzed. Owing to the advantages and disadvantages of both methods, a combination of the two called arbitrary Lagrangian–Eulerian approach is more frequently used [85].

The effect of the tool edge radius has been an important one throughout the investigations conducted in the machining field. Analysis has been conducted on the effect of edge roundness on stress and temperature when machining AISI 4340 steel using carbide tools using an arbitrary Lagrangian–Eulerian method [64]. Researchers have simulated material flow around the tool edge without re-meshing or using a chip separation criterion and argue that this way of conducting FEA gives better predictions for machining induced stresses. Others [48] have investigated the effect of the cutting edge radius on forces, chip thickness and tool temperature. Due to the less effective cutting with a large radius tool the resulting cutting forces increase with the increase in the tool edge radius. The chip thickness is influenced somewhat by the increase in the tool edge radius showing slight increasing trend.

A decreasing trend for tool temperature is observed with the increase in tool edge radius and explained by the fact that the high temperature is located at the tip of the tool resulting at higher values when the tip is sharper. The results of this study can be observed in Fig. 1.27. The mechanism of chip formation and chip morphology has been investigated by a number of authors who compared the simulated results with the experimentally obtained chips in order to understand the chip formation in various materials. An FEA has been presented of both conventional and high-speed machining of Ti6Al4V alloys incorporating the Johnson–Cook material model [86]. The author has investigated the chip formation and morphology and compared it to the experimentally obtained chips. The comparison was satisfactory as shown in Fig. 1.28.

Fig. 1.27

Influence of the tool edge radius on cutting forces, chip thickness and tool temperature [48]

Fig. 1.28

Comparison of the experimentally obtain chips and chips obtained by FEA for conventional and high-speed machining [86]

Obikawa and Usui have focused their research on implementing a crack growth criterion into finite element modelling to better predict discontinuous chip formation [62]. They have incorporated a fracture strain criterion and obtained results in very close agreement to the experimental findings. The influence of the chosen material model for the FEA has been further investigated [75] and can be seen from Fig. 1.29.

Fig. 1.29

Chips and stress distribution for the Litonski–Batra, power law, Johnson–Cook and Bodner–Partom material models consecutively [75]

It is easy to see that the choice of the model will make a difference when interpreting the chip morphology results and comparing them with the experimentally obtained shapes. The chip curl radius can be observed to be different for the models applied and is argued that the power law gave the values closest to the actual measured ones. The stress patterns seem to be similar in all cases while on the other hand the actual values are somewhat different depending on the model in question. The temperature distribution is also considered to be the same or similar in all cases. However, even though most parameters behave in a similar manner for all models, residual stresses in the workpiece material differ significantly. Machining simulations have been used to investigate the effect of damage and material softening upon reverse loading in heterogeneous materials. The authors compared their work with experimental data from a reverse loading experiment of ductile iron and obtained good agreement, Fig. 1.30 [11].

Fig. 1.30

Chip formation when simulating machining with and without the material softening upon reverse loading [11]

Temperature is considered to be another one of the commonly investigated issued using FEA in the process of machining. Usui et al. [87] investigated the tool edge temperature and its effect on the wear characteristics in machining with ceramic tools. The influence of the cutting speed on the temperature generated in the tool has been investigated showing that there is a significant increase in the tool temperature with a higher value registered for the rake compared to flank face of the tool [34]. The fact that the tool temperature increases with the increase in cutting speed was confirmed [87] and it has been shown that the temperatures are close to the melting temperature of the workpiece material. Kim et al. [33] used finite element modelling to determine temperature and stress distributions in micromachining. The researchers chose oxygen-free copper as the workpiece material while the tool was a diamond cutter. It was presented that the highest temperature occurred within the shear plane at it reaches 562 °C even though the depth of cut is only 2 μm. They determined that if the effect of the temperature is ignored the values obtained for the flow stress are doubled when compared to the experimental one resulting in forces considerably higher than those measured. Cao et al. [8] have concluded in their research that the maximum cutting temperature depends greatly on the tool edge radius and it increases with the increase in the radius itself. It has also been noticed that the effect of the radius in not only on the magnitude of the temperature but also on the temperature field distribution as well. As the ultra-precision machining grew in size, tools for modelling these processes became more sophisticated and in the late 1980s molecular dynamic simulations have been introduced to enhance the research in the field. The research was mainly confined to national laboratories because supercomputers are needed for the memory and processing time required to run these simulations. However, only recently several universities have developed computers with which enable conducting simulations of this scale. Figure 1.31 represents the schematic of the MD simulation.

Fig. 1.31

Schematic of the MD simulation [39]

The influence of friction on the process of nanoscale machining and investigation of the chip formation and the morphology by comparing it to the micromachining results is one of the topics covered in the literature [55]. The researchers show the increase in the bond energy leading to increase in chip thickness and contact length as well as increases in cutting forces and the temperature. Figure 1.32 shows that there is a constant increase in the cutting force and this is due to the fact that the simulation did not include any defects such as vacancies, interstitials, dislocations grain boundaries, etc. and it is predicted that with incorporating those features into the simulations, the results would be different.

Fig. 1.32

Dependence of the cutting force on the ratio of the chip thickness and tool edge radius [55]

A number of researchers [26, 28] investigated the effect of the minimum depth of cut and the ratio of minimum depth of cut and edge radius on chip formation as well as subsurface deformation and specific cutting energy in two dimensional cutting of copper with diamond tools. They have concluded that the influence of the cutting edge on the minimum chip thickness was greater than the influence of the type of work piece material. They have determined that the numerical value of the minimum chip thickness is 0.1 of the tool edge radius.

The effect of the edge radius and depth of cut on nanometric machining has been investigated [37]. The authors have investigated the influence on the forces, specific energy as well as subsurface deformation concluding that the depth of cut 33 has a significant influence on the extent of plastic deformation ahead of the tool as well as subsurface deformation. With the increase in the depth of cut to tool radius ratio, chip generation increases increasing cutting forces and decreasing ploughing. The researchers also conclude that the increase in the tool edge radius yields an increase in the negative rake angle rotating the shear zone towards and into the workpiece material. It has been noted that the increase of forces with the depth of cut is different for the cutting and thrust forces. Cutting force varies linearly while thrust forces have a fast increase at the beginning and saturate at higher depth of cut.

The effect of the rake angle on the cutting and thrust forces has been analyzed by MD simulations [38]. Figure 1.33 shows the results obtained showing that the ratio of the thrust to cutting forces increases from 0.496 to 2.361 when changing the rake angle from 45 to −75 which is also followed by the increase in specific energy from 0.293 to 1.011*E5 N/mm². This change has also been determined at non-nanometric circumstances by the author when investigating depths of cut of 10 µm [35]. The ratio of the thrust force to cutting force was seen to increase to around 5 for the rake angle of −85° after which the chip formation seizes and rubbing and side flow start. The investigators have also shown that the depth of cut has an effect on the forces and specific energy independent of the radius/depth of cut ratio. They show that the cutting force increases with the cut depth and the specific energy decreases with it. Based on the review presented, it can be concluded that applications of the Lagrangian, Eulerian, Lagrangian–Eulerian as well as MD simulations all have their place in the research community and strongly depend on what the intended research findings are. The FEA models that research chip formation and the influence of the size effect in micromachining are still to be improved in order to obtain better understanding of the process. The MD simulations offer immense insight into the field of nanometric cutting simulating the cutting mechanisms on the atomic level.

Fig. 1.33

Influence of the rake angle on the force ratio and specific energy [38]

1.6 Further Developments

The further developments associated with nanometric machining is concerned with two aspects. The first aspect concerns MD simulations of machining different materials with coated and uncoated cutting tool materials, and the simulation of problems that are commonly encountered in machining such as tool wear during machining, thermal deformation of certain engineering alloys during machining, burr formation during machining, and the modelling of exit failures when the cutting tool has completed its task. The second aspect focuses on developing meso-microscale mechanical machine tools that are in the process of being developed. Here, MD simulations of the machining process will contribute to the design of machine tools dedicated to machining at the nanoscale, and will hopefully illuminate the need for better machine tool design at the meso- and macroscales. There is a growing body of work associated with modelling and machining of medical materials. This chapter shows that there is still plenty of research work to be done in machining of medical materials, especially at the micro- and nanoscales.