Semidefinite and Linear Programming Integrality Gaps for Scheduling Identical Machines

Abstract

Sherali-Adams [25] and Lovász-Schrijver [21] developed systematic procedures to strengthen a relaxation known as lift-and-project methods. They have been proven to be a strong tool for developing approximation algorithms, matching the best relaxations known for problems like Max-Cut and Sparsest-Cut. In this work we provide lower bounds for these hierarchies when applied over the configuration LP for the problem of scheduling identical machines to minimize the makespan. First we show that the configuration LP has an integrality gap of at least $1024\text {/}1023$ by providing a family of instances with 15 different job sizes. Then we show that for any integer n there is an instance with n jobs in this family such that after $\varOmega (n)$ rounds of the Sherali-Adams ($\text {SA}$) or the Lovász-Schrijver ($\text {LS}_+$) hierarchy the integrality gap remains at least $1024\text {/}1023$.

Supported by the Swiss National Science Foundation project 200020-144491/1 “Approximation Algorithms for Machine Scheduling Through Theory and Experiments,” by Sciex Project 12.311, by DFG grant MO 2889/1-1, and by CONICYT-PCHA/Doctorado Nacional/2014-21140930.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Scheduling

Machine scheduling is a classical family of problems in combinatorial optimization. In this paper we study the problem, known as $P||C_{\max }$, of scheduling a set J of n jobs on a set M of identical machines to minimize the makespan, i. e., the maximum completion time of a job, where each job $j\in J$ has a processing time $p_{j}$. A job cannot be preempted nor migrated to a different machine, and every job is released at time zero. This problem admits a polynomial-time approximation scheme (PTAS) [16] and even an EPTAS [2], which is the best possible approximation result since the problem is strongly $\mathsf {NP}$-hard [13]. The convex relaxations studied for the problem are weaker than those algorithmic results.

Assignment LP. A straightforward way to model $P||C_{\max }$ with a linear program (LP) is the assignment LP which has a variable $x_{ij}$ for each combination of a machine $i\in M$ and a job $j\in J$, modeling whether job j is assigned to machine i. The goal is to minimize a variable T (modeling the makespan) for which we require that $\sum _{j\in J}x_{ij}\cdot p_{j}\le T$ for each machine i.

Configuration LP. The assignment LP is dominated by the configuration LP which is, to the best of our knowledge, the strongest relaxation for the problem studied in the literature. Suppose we are given a value $T>0$ that is an estimate on the optimal makespan, e. g., given by a binary search framework. A configuration corresponds to a multiset of processing times $C\subseteq \{ p_j: j\in J\}$ such that $\sum _{p\in C}p\le T$, i. e., it is a feasible assignment for a machine when the time availability is equal to T. Let, for given T, $\mathcal {C}$ denotes the set of all feasible configurations. The multiplicity function m(p, C) indicates the number of times that the processing time p appears in the multiset C. For each combination of a machine i and a configuration C the configuration LP has a variable $y_{iC}$ that models whether we want to assign exactly jobs with processing times in configuration C to machine i. Letting $n_p$ denote the number of jobs $j\in J$ with processing time $p_j=p$, we can write:

We remark that in another common definition [26], a configuration is a subset, not of processing times but of jobs. We can solve that LP to a $(1+\epsilon )$-accuracy in polynomial time [26] and similarly our LP above. The definition in terms of multisets makes sense since we are working in a setting of identical machines.

Integrality Gap. The configuration LP $\text {clp}(T)$ does not have an objective function and instead we seek to determine the smallest value T for which it is feasible. In this context, for a convex relaxation K(T) we define the integrality gap to be the supremum value $T_{\text {opt}}(I)/T^{*}(I)$ over all problem instances I, where $T_{\text {opt}}(I)$ is the optimal value and $T^{*}(I)$ is the minimum value T for which K(T) is feasible. With the additional constraint that $T\ge \max _{j\in J}p_{j}$, the Assignment LP relaxation has an integrality gap of 2 (which can be shown using the analysis of the list scheduling algorithm, see e. g., [27]). Here we prove that the configuration LP has an integrality gap of at least $1024\text {/}1023$ (Theorem 1(i)).

Linear Programming and Semi-definite Programming Hierarchies

Hierarchies. An interesting question is whether other convex relaxations have better integrality gaps. Convex hierarchies, parametrized by a number of levels or rounds, are systematic approaches to design improved approximation algorithms by gradually tightening the integrality gap between the integer formulation and corresponding relaxation, at the cost of increased running time. Popular among these methods are the Sherali-Adams (SA) hierarchy [25] (Definition 1), the Lovász-Schrijver ($\text {LS}_+$) semi-definite programming hierarchy [21] (Definition 4) and the Lasserre/Sum-Of-Squares hierarchy [18, 22], which is the strongest of the three. For a comparison between them and their algorithmic implications we refer to [10, 19, 23]. In some settings, for example the Independent Set problem in sparse graphs [4], a mixed SA has also been considered.

Positive Results. For many problems the approximation factors of the best known algorithms match the integrality gap after performing a constant number of rounds of this hierarchies. Examples of such problems are: Max-Cut [1] and Sparsest-Cut [1, 9], dense Max-Cut [11], Knapsack and Set-Cover [8]. In the scheduling context, for minimizing the makespan on two machines in the setting of unit size jobs and precedence constraints, Svensson solves the problem optimally with only one level of the linear LS hierarchy [23] (Sect. 3.1, personal communication between Svensson and the author of [23]). Furthermore, for a constant number of machines, Levey and Rothvoss give a $(1+\varepsilon )$-approximation algorithm using $(\log (n))^{\varTheta (\log \log n)}$ rounds of SA hierarchy [20]. For minimizing weighted completion time on unrelated machines, one round of $\text {LS}_+$ leads to the current best algorithm [5]. Thus, hierarchies are a strong tool for approximation algorithms.

Negative Results. Nevertheless, there are known limitations on these hierarchies. Lower bounds on the integrality gap of $\text {LS}_+$ are known for Independent Set [12], Vertex Cover [3, 7, 14, 24], Max-3-Sat and Hypergraph Vertex Cover [1], and k-Sat [6]. For the Max-Cut problem, there are lower bounds for the SA [11] and $\text {LS}_+$ [24]. For the Min-Sum scheduling problem (i. e., scheduling with job dependent cost functions on one machine) the integrality gap is unbounded even after $O(\sqrt{n})$ rounds of Lasserre [17]. In particular, that holds for the problem of minimizing the number of tardy jobs even though that problem is solvable in polynomial time, thus SDP hierarchies sometimes fail to reduce the integrality gap even on easy problems.

Our Results

Our key question in this paper is: is it possible to obtain a polynomial time $(1+\epsilon )$-approximation algorithm based on applying the SA or the $\text {LS}_+$ hierarchy to one of the known LP-formulations of our problem? This would match the best known (polynomial time) approximation factor we know [2, 16].

We answer this question in the negative. We prove that even after $\varOmega (n)$ rounds of SA or $\text {LS}_+$ to the configuration LP the integrality gap of the resulting relaxation is still at least $1+1{/}1023$. Since the configuration LP dominates¹ the assignment LP, our result also holds if we apply $\varOmega (n)$ rounds of SA or $\text {LS}_+$ to the assignment LP.

Theorem 1

Consider the problem of scheduling identical machines to minimize the makespan, $P||C_{\max }$. For each $n\in \mathbb {N}$ there exists an instance with n jobs such that:

• (i) the configuration LP has an integrality gap of at least $1024\text {/}1023$.

• (ii) after applying $r=\varOmega (n)$ rounds of the SA hierarchy to the configuration LP the obtained relaxation has an integrality gap of at least $1024\text {/}1023$.

• (iii) after applying $r=\varOmega (n)$ rounds of the $\text {LS}_+$ hierarchy to the configuration LP the obtained relaxation has an integrality gap of at least $1024\text {/}1023$.

Since polynomial time approximations schemes are known [2, 16] for $P||C_{\max }$, Theorem 1 implies that the $\text {SA}$ and the $\text {LS}_+$ hierarchies do not yield the best possible approximation algorithms. We remark that for the hierarchies studied in Theorem 1, n rounds suffice to bring the integrality gap down to exactly 1, so results (ii) and (iii) are almost tight in terms of number of levels.

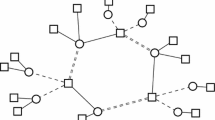
We prove Theorem 1 by defining a family of instances $\{I_{k}\}_{k\in \mathbb {N}}$ constructed from the Petersen graph (see Fig. 1). In Sect. 2 we prove that the configuration LP is feasible for $T=1023$ while the integral optimum has a makespan of at least 1024. In Sect. 3, we show for each instance $I_{k}$ that using the hypergeometric distribution we can define a fractional solution that is feasible for the polytope obtained by applying $\varOmega (k)$ rounds of SA to the configuration LP parametrized by $T=1023$. In Sect. 4 we prove the same for the semidefinite relaxations obtained with the $\text {LS}_+$ hierarchy, and we study the protection matrices used in the lower bound proof. In this part we work with covariances matrices by applying Schur’s complement and a posterior analysis for block-symmetry matrices.

The Hard Instances

To prove the integrality gaps of $1024\text {/}1023$, for each odd $k\in \mathbb {N}$ we define an instance $I_{k}$ that is inspired by the Petersen graph G (see Fig. 1) with vertex set $V=\{ 0,1,\cdots ,9 \}$. For each edge $e=\{u,v\}$ of G, in $I_{k}$ we introduce k copies of a job $j_{\{uv\}}$ of size $2^{u}+2^{v}$. Thus $I_{k}$ has 15k jobs. (If n is not an odd multiple of 15, let $n=15k+\ell$ where k is the greatest odd integer such that $15k<n$. In this case we simply add to the instance $\ell$ jobs that each have processing time equal to zero.) We define the number of machines for $I_k$ to be 3k. For simplicity, in the following we do not distinguish between jobs and their sizes. The graph G has exactly six perfect matchings $\bar{M}_{1},\bar{M}_{2},\cdots ,\bar{M}_{6}$. Since the sum of the job sizes in a perfect matching $\bar{M}_{\ell }$ is

$$\sum _{e\in \bar{M}_{\ell }}p_{j_{e}}=\sum _{0\le u\le 9}2^u=1023,$$

$\bar{M}_{\ell }$ corresponds to a configuration $C_{\ell }$ that contains one job corresponding to each edge in $\bar{M}_{\ell }$ and has makespan 1023. The configurations $C_1,\ldots ,C_6$ are called matching configurations and we denote them by $\mathcal {D}=\{C_1,\ldots ,C_6\}$.

Fig. 1.

The Petersen graph and its six perfect matchings (dashed lines)

2 Integrality Gap of the Configuration LP (Theorem 1(i))

Lemma 1

$\text {clp}[1023]$ is feasible for $I_k$.

Proof

To define the fractional solution, for every machine i and each $\ell \in \{1,2,\cdots ,6\}$ we set $y_{iC_{\ell }}=1/6$. For all other configurations C we set $y_{iC}=0$.

The first set of constraints in clp(T) (for the machines) is clearly satisfied. For the second set of constraints (for the job sizes), let p be such a job size and let e be the corresponding edge in G. The Petersen graph is such that there are exactly two perfect matchings $\bar{M}_{\ell },\bar{M}_{\ell '}$ containing e, thus we get $\sum _{i=1}^{3k} (y_{iC_{\ell }}+y_{iC_{\ell '}})=k$ and y is feasible.    $\square$

Lemma 2

The optimal makespan for $I_k$ is at least 1024.

Proof

Assume, for a contradiction, that $\text {clp}[1023]$ for $I_k$ has an integer solution y. Since the total size of jobs is $k\cdot 3 \cdot 1023$ and there are 3k machines, only configurations C with makespan exacly equal to 1023 may have $y_{iC}\ne 0$.

Consider such a configuration C. Since $1023=\sum _{u=0}^9 2^u$, considering the binary representation of 1023, by induction on u it must be that for every u, configuration C contains an odd number of jobs corresponding to edges adjacent to vertex u in G. Furthermore, since the sum does not exceed 1023, that odd number must be exactly 1. Thus C exactly corresponds to a perfect matching of G, and so the integer solution y corresponds to a 1-factorization of the multigraph $G_{k}$ obtained by taking k copies of each edge in the Petersen graph.

Let $\bar{M}_{1}$ be the perfect matching of the Petersen graph consisting of the five edges $\{0,5\},\{1,6\},\{2,7\},\{3,8\}\{4,9\}$, called spokes. Let $\ell =\sum _i y_{iC_1}$. Since each spoke, which appears in exactly one other perfect matching $\bar{M}_{j}$ ($j>1$), must be contained in k matchings in total, we must have $\sum _i y_{iC_j}=k-\ell$ for each $j\in [2,6]$. Thus $\sum _{i,C}y_{iC}=5(k-\ell )+\ell =5k-4\ell .$ However, that sum equals 3k, the total number of machines, and so $\ell =k/2$. Since k is odd and $\ell$ an integer, the contradiction follows.    $\square$

3 Integrality Gap for $\text {SA}$ (Theorem 1(ii))

We show that for the family of instances $\{I_{k}\}_{k\in \mathbb {N}}$ defined in Sect. 2, if we apply O(k) rounds of SA to the configuration LP for $T=1023$, then the resulting relaxation is feasible. Thus, after $\varOmega (k)$ rounds of SA the configuration LP still has an integrality gap of at least $1024\text {/}1023$ on an instance with O(k) jobs and machines. First, we define the polytope $\text {SA}^{r}(P)$ obtained after r rounds of SA to a polytope P that is defined via equality constraints².

Definition 1

(Polytope $\mathbf{SA}^{r}(P)$ ). Consider a polytope $P\subseteq [0,1]^E$ defined by equality constraints. For every constraint $\sum _{i\in E}a_{i,\ell }y_{i}= b_{\ell }$ and every $H \subseteq E$ such that $|H|\le r$, the constraint $\sum _{i\in E}a_{i, \ell }y_{H\cup \{i\}}=b_{\ell }y_{H}$ is included in $\text {SA}^{r}(P)$, the level r of the Sherali-Adams hierarchy applied to P. The polytope $\text {SA}^{r}(P)$ lives in $\mathbb {R}^{\mathcal {P}_{r+1}(E)}$, where $\mathcal {P}_{r+1}(E)=\{A\subseteq E:|A|\le r+1\}$.

For the configuration LP $\text {clp}(T)$ the variables set is $E=M\times \mathcal {C}$. Since it is defined by equality constraints, the polytope $\text {SA}^{r}(\text {clp}(T))$ corresponds to

Intuitively, the configuration LP computes a set of edges in a complete bipartite graph with vertex sets U, V where U is the set of machines and V is the set of configurations. The edges are selected such that they form a U-matching, i.e., such that each node in U is incident to at most one selected edge.

Definition 2

Given two sets U, V and $F\subseteq U\times V$, the F-degree of $u\in U$ is $\delta _{F}(u)=|\{v:(u,v)\in F\}|$, and $\delta _{F}(v)=|\{u:(u,v)\in F\}|$ if $v\in V$. We say that F is an U-matching if $\delta _{F}(u)\le 1$ for every $u\in U$. An element $u\in U$ is incident to F if $\delta _{F}(u)=1$.

In the following we consider the same family of instances $\{I_{k}:k\in \mathbb {N},k\text { is odd}\}$ as in Sect. 2 and $T=1023$. For any set S we define $\mathcal {P}(S)$ to be the power set of S. We want to define a solution to $\text {SA}^{r}(\text {clp}(T))$ for $T=1023$. To this end, we need to define a value $y_{A}$ for each set $A\in \mathcal {P}_{r+1}(M\times \mathcal {C})$. In particular, for $A\in \mathcal {P}_{r}(M\times \mathcal {D})$, we define this value according to the hypergeometric distribution.

Definition 3

Let $\phi :{\mathcal {P}}(M\times \mathcal {D})\rightarrow \mathbb {R}$ be such that

$$ \phi (A)=\frac{1}{(3k)_{|A|}}\prod _{j\in [6]}(k/2)_{\delta _{A}(C_{j})} $$

if A is an M-matching, and zero otherwise, where $(x)_{a}=x(x-1)\cdots (x-a+1)$, for integer $a \ge 1$, is the lower factorial function.

To get some understanding about how the distribution $\phi$ works, the following lemma intuitively shows the following: suppose that we know that a set A is chosen (i.e., we condition on this), then the conditional probability that also a pair $(i,C_{j})$ is chosen equals $\frac{k/2-\delta _{A}(C_{j})}{3k-|A|}$, assuming that $A\cup \{(i,C_{j})\}$ forms an M-matching.

Lemma 3

Let $A\subseteq M\times \mathcal {D}$ be an M-matching of size at most $3k-1$. If $i\in M$ is not incident to A, then $\phi (A\cup \{(i,C_{j})\})=\phi (A)\frac{k/2-\delta _{A}(C_{j})}{3k-|A|}$.

Proof

Given that i is not incident to A, we have $|A\cup \{(i,C_{j})\}|=|A|+1$. Furthermore, for $\ell \ne j$ we have that $\delta _{A\cup \{(i,C_{j})\}}(C_{\ell })=\delta _{A}(C_{\ell })$ and $\delta _{A\cup \{(i,C_{j})\}}(C_{j})=\delta _{A}(C_{j})+1$. Therefore, $\frac{\phi (A\cup \{(i,C_{j})\})}{\phi (A)}=\frac{k/2-\delta _{A}(C_{j})}{3k-|A|}.$    $\square$

The Feasible Solution. We are ready now to define our solution to $\text {SA}^{r}(\text {clp}(T))$. It is the vector $y^{\phi }\in \mathbb {R}^{\mathcal {P}_{r+1}(E)}$ defined such that $y_A^{\phi }=\phi (A)$ if A is an M-matching in $M\times \mathcal {D}$, and zero otherwise.

Lemma 4

For every odd k, $y^{\phi }$ is a feasible solution for $\text {SA}^{r}(\text {clp}(T))$ for the instance $I_{k}$ when $r=\lfloor k/2\rfloor$ and $T=1023$.

Proof

We first prove that $y^{\phi }\ge 0$. Consider some $H\subseteq E$. Since $y^{\phi }_H=\phi (H)$, using Definition 3, it is easy to check that the lower factorial stays non-negative for $r=\lfloor k/2\rfloor$.

We next prove that $y^{\phi }$ satisfies the machine constraints in $\text {SA}^r(\text {clp})$. If i is a machine incident to H, then all terms in the left-hand summation are 0 except for the unique pair (i, C) that belongs to H, so the sum equals $y^{\phi }_{H}$. If i is not incident to H, then by Lemma 3 we have

$$\begin{aligned} \sum _{C}y^{\phi }_{H\cup \{(i,C)\}}=\frac{\phi (H)}{3k-|H|}\sum _{j\in [6]}(k/2-\delta _H(C_j))=\phi (H)=y^{\phi }_H, \end{aligned}$$

since $6\cdot k/2=3k$ and $\sum _{j\in [6]}\delta _H(C_j)=|H|$.

Finally we prove that $y^{\phi }$ satisfies the set of constraints for every processing time. Fix p and H. Since $y^{\phi }$ is supported by six configurations, we have

$$\sum _{i\in M} \sum _{C\in \mathcal {C}}m(p,C)y^{\phi }_{H\cup \{(i,C)\}}= \sum _{i\in M}\sum _{j\in [6]} m(p,C_j)\phi (H\cup \{(i,C_j)\}).$$

There are exactly two configurations $C_1^p,C_2^p\in \mathcal {D}$ such that $m(p,C_1^p)=m(p,C_2^p)=1$, and for the others it is zero, so

$$\sum _{j\in [6]} m(p,C_j)\phi (H\cup \{(i,C_j)\})=\phi (H\cup \{(i,C_1^p)\})+\phi (H\cup \{(i,C_2^p)\}).$$

Let $\pi _M(H)=\{i\in M:\delta _H(i)=1\}$ be the subset of machines incident to H. We split the sum over $i\in M$ into two parts, $i\in \pi _M(H)$ and $i\notin \pi _M(H)$. For the first part,

$$ \sum _{i\in \pi _M(H)}(\phi (H\cup \{(i,C_1^p)\})+\phi (H\cup \{(i,C_2^p)\})) =\phi (H)(\delta _H(C_1^p)+\delta _H(C_2^p)) $$

since $\phi (H\cup \{(i,C_1^p)\})$ is either $\phi (H)$ or 0 depending on whether $(i,C_1^p)\in H$, and the same holds for $C_2^p$.

For the second part, using Lemma 3 we have that

since $|H\setminus \pi _M(H)|=3k-|H|$. Adding, thanks to cancellations we get precisely what we want:

$$\sum _{i\in M} \sum _{C\in \mathcal {C}} m(p,C)y^{\phi }_{H\cup \{(i,C)\}}=k\phi (H) = n_py_H^{\phi }.$$

   $\square$

Proof

(of Theorem 1 (ii)). Consider instance $I_k$ as defined before, $T=1023$ and $r=\lfloor k/2 \rfloor$. By Lemma 4 the vector $y^{\phi }\in \text {SA}^r(\text {clp}(T))$.    $\square$

We note that in the above proof, the projection of $y^\phi$ onto the space of the configuration LP is the fractional solution from the proof of Lemma 1.

4 Integrality Gap for $\text {LS}_+$ (Theorem 1(iii))

Given a polytope $P\subseteq \mathbb {R}^{d}$, we consider the convex cone $Q=\{(a,x)\in \mathbb {R}^*\times P:x/a\in P\}$. We define an operator $N_+$ on convex cones $R\subseteq \mathbb {R}^{d+1}$ as follows: $y\in N_+(R)$ if and only if there exists a symmetric matrix $Y\subseteq \mathbb {R}^{(d+1)\times (d+1)}$, called the protection matrix of y, such that

• 1. $y=Ye_{\emptyset }=\text {diag}(Y)$,

• 2. for all i, $Ye_i,Y(e_{\emptyset }-e_i)\in R$,

• 3. Y is positive semidefinite,

where $e_i$ denotes the vector with a 1 in the ith coordinate and 0’s elsewhere.

Definition 4

For any $r\ge 0$ and polytope $P\subseteq \mathbb {R}^{d}$, level r of the LS$_+$ hierarchy, $N_+^r(Q)\subseteq \mathbb {R}^{d+1}$, is defined recursively by: $N_+^0(Q)=Q$ and $N_+^r(Q)=N_+(N_+^{r-1}(Q))$.

To prove the integrality gap for $\text {LS}_+$ we follow an inductive argument. We start from $P=\text {clp}(T)$. Along the proof, we use a special type of vectors that are integral in a subset of coordinates and fractional in the others.

The Feasible Solution. Let A be an M-matching in $M\times \mathcal {D}$. The partial schedule $y(A)\in \mathbb {R}^{M\times \mathcal {C}}$ is the vector such that for every $i\in M$ and $j\in \{1,2,\cdots ,6\}$, $y(A)_{iC_j}=\phi (A\cup \{(i,C_j)\})/\phi (A)$, and zero otherwise. Here is the key Lemma.

Lemma 5

Let k be an odd integer and $r\le \lfloor k/2 \rfloor$. Let $Q_k$ be the convex cone of $\text {clp}(T)$ for instance $I_k$ and $T=1023$. Then, for every M-matching A of cardinality $\lfloor k/2 \rfloor -r$ in $M\times \mathcal {D}$, we have $y(A)\in N_+^r(Q_k)$.

Before proving Lemma 5, let us see how it implies the Theorem.

Proof

(of Theorem 1 (iii)). Consider instance $I_k$ defined in Sect. 2, $T=1023$ and $r=\lfloor k/2 \rfloor$. By Lemma 5 for $A=\emptyset$ we have $y(\emptyset )\in N_+^r(Q_k)$.    $\square$

In the following two helper lemmas we describe structural properties of every partial schedule.

Lemma 6

Let A be an M-matching in $M\times \mathcal {D}$, and let i be a machine incident to A. Then, $y(A)_{iC}\in \{0,1\}$ for all configuration C.

Proof

If $C\notin \mathcal {D}$ then $y(A)_{iC}=0$ by definition. If $(i,C_j)\in A$ then $y(A)_{iC_j}=\phi (A\cup \{(i,C_j)\})/\phi (A)=\phi (A)/\phi (A)=1$. For $\ell \ne j$, the set $A\cup \{(i,C_{\ell })\}$ is not an M-matching and thus $y(A)_{iC_k}=0$.   $\square$

Lemma 7

Let A be an M-matching in $M\times \mathcal {D}$ of cardinality at most $\lfloor k/2\rfloor$. Then, $y(A)\in \text {clp}(T)$.

Proof

We note that $y(A)_{iC}=y^{\phi }_{A\cup \{(i,C)\}}/y^{\phi }_A$, and then the feasibility of y(A) in $\text {clp}(T)$ is implied by the feasibility of $y^{\phi }$ in $\text {SA}^r(\text {clp}(T))$, for $r=\lfloor k/2 \rfloor$.    $\square$

Given a partial schedule y(A), let $Y(A)\in \mathbb {R}^{(|M\times \mathcal {C}|+1)\times (|M\times \mathcal {C}|+1)}$ be the matrix such that its principal submatrix indexed by $\{\emptyset \}\cup (M\times \mathcal {D})$ equals

$$\begin{pmatrix}1 &{} y(A)^{\top }\\ y(A) &{} Z(A)\end{pmatrix},$$

where $Z(A)_{iC_j,\ell C_h}=\phi (A\cup \{(i,C_j),(\ell ,C_h)\})/\phi (A)$. All the other entries of the matrix Y(A) have value equal to zero. The matrix Y(A) provides the protection matrix we need in the proof of the key Lemma.

Theorem 2

For every M-matching A in $M\times \mathcal {D}$ such that $|A|\le \lfloor k/2 \rfloor$, the matrix Y(A) is positive semidefinite.

Proof (Sketch)

We prove that Y(A) is positive semidefinite by performing several transformations that preserve this property. First, we remove all those zero columns and rows. Then, Y(A) is positive semidefinite if and only if its principal submatrix indexed by $\{\emptyset \}\cup (M\times \mathcal {D})$ is positive semidefinite. We then construct the covariance matrix $\text {Cov}(A)$ by taking the Schur’s Complement of Y(A) respect to the entry $(\{\emptyset \},\{\emptyset \})$. The resulting matrix is positive semidefinite if and only if Y(A) is positive semidefinite. After removing null rows and columns in $\text {Cov}(A)$ we obtain a new matrix, $\text {Cov}_+(A)$, which can be written using Kronecker products as $I\otimes Q+(J-I)\otimes W$, with $Q,W\in \mathbb {R}^{6\times 6}$, $Q=\alpha W$ for some $\alpha \in (-1,0)$ and I, J being the identity and the all-ones matrix, respectively. By applying a lemma about block matrices in [15], Y(A) is positive semidefinite if and only if W is positive semidefinite. The matrix W is of the form $D_u-uu^{\top }$, with $u\in \mathbb {R}^6$ and $D_u$ is a diagonal matrix such that $\text {diag}(D_u)=u$. By Jensen’s inequality with the function $t(y)=y^2$ it follows that W is positive semidefinite. A complete proof of the theorem can be found in the Appendix.    $\square$

Lemma 8

Let A be an M-matching in $M\times \mathcal {D}$ and i a non-incident machine to A. Then, $\sum _{j\in [6]}Y(A)e_{iC_j}=Y(A)e_{\emptyset }.$

Proof

Let S be the index of a row of Y(A). If $S\notin \{0\}\cup (M\times \mathcal {D})$ then that row is identically zero, so the equality is satisfied. Otherwise,

$$e_S^{\top }\sum _{j\in [6]}Y(A)e_{iC_j}=\sum _{j\in [6]}\frac{\phi (A\cup \{(i,C_j)\}\cup S)}{\phi (A)}.$$

If $A\cup S$ is not an M-matching then $\phi (A\cup S\cup \{i,C_j\})=0$ for all i and $j\in [6]$, and $e_S^{\top }Y(A)e_{\emptyset }=\phi (A\cup S)=0$, so the equality is satisfied. If $A\cup S$ is an M-matching, then

$$\begin{aligned} \sum _{j\in [6]}\frac{\phi (A\cup \{(i,C_j)\}\cup S)}{\phi (A)}= & {} \frac{\phi (A\cup S)}{\phi (A)}\sum _{j\in [6]}\frac{\phi (A\cup S\cup \{(i,C_j)\})}{\phi (A\cup S)} \\= & {} e_S^{\top }Y(A)e_{\emptyset }\sum _{j\in [6]}\frac{y^{\phi }_{A\cup S\cup \{(i,C_j)\}}}{y^{\phi }_{A\cup S}}\\= & {} e_S^{\top }Y(A)e_{\emptyset }, \end{aligned}$$

since $y^{\phi }$ is a feasible solution for the $\text {SA}$ hierarchy.    $\square$

Having previous two results we are ready to prove the key Lemma.

Proof

(of Lemma 5). We proceed by induction in r. The base case $r=0$ is implied by Lemma 7, and now suppose that it is true for $r=t$. Let y(A) be a partial schedule of A of cardinality $\lfloor k/2 \rfloor -t-1$. We prove that the matrix Y(A) is a protection matrix for y(A). It is symmetric by definition, $y(A)e_{\emptyset }=\text {diag}(y(A))=y(A)$ and thanks to Theorem 2 the matrix Y(A) is positive semidefinite. Let (i, C) be such that $y(A)_{iC}\in (0,1)$. In particular, by Lemma 6 we have $(i,C)\notin A$ and $C\in \mathcal {D}$. We claim that $Y(A)e_{iC}/y(A)_{iC}$ is equal to the partial schedule $(1,y(A\cup \{(i,C)\}))$. If S indexes a row not in $M\times \mathcal {D}$ then the respective entry in both vectors is zero, so the equality is satisfied. Otherwise,

$$\frac{e_S^{\top }Y(A)e_{iC}}{y(A)_{iC}}=\frac{\phi (A\cup \{(i,C)\}\cup S)}{\phi (A\cup \{(i,C)\})}=y(A\cup \{(i,C)\})_S.$$

The cardinality of the M-matching $A\cup \{(i,C)\}$ is equal to $|A|+1=\lfloor k/2 \rfloor -t$, and therefore by induction we have that $Y(A)e_{iC}/y(A)_{iC}=(1,y(A\cup \{(i,C)\}))\in N_+^t(Q_k)$. Now we have to prove that the vectors $Y(A)(e_{\emptyset }-e_{iC})/(1-y(A)_{iC})$ are feasible for $N^t_+(Q_k)$. By Lemma 8 we have that for every $\ell \in \{1,2,\cdots ,6\}$,

$$ \frac{Y(A)(e_{\emptyset }-e_{iC_{\ell }})}{1-y(A)_{iC_{\ell }}}=\sum _{j\in [6]\setminus \{\ell \}}\left( \frac{y(A)_{iC_j}}{\sum _{j\in [6]\setminus \{\ell \}}y(A)_{iC_j}}\right) y(A\cup \{(i,C_j)\}), $$

and then $Y(A)(e_{\emptyset }-e_{iC_{\ell }})/(1-y(A)_{iC_{\ell }})$ is a convex combination of the partial schedules $\{y(A\cup \{(i,C_j)\}):j\in \{1,2,\cdots ,6\}\setminus \ell \}\subset N_+^t(Q_k)$, concluding the induction.    $\square$