Synthesis of Distributed Control Laws for Multi-agent Systems Using Delayed Relative Information with LQR Performance

Abstract

In this chapter, a multiagent system composed of linear identical dynamical agents is considered. The agents are assumed to share relative state information over a communication network. This exchange of relative information is assumed to be subject to delays. New methods to synthesize distributed state feedback control laws for the multiagent system, using delayed relative information along with local state information with guaranteed LQR performance, are presented in this chapter. Two types of delays are considered in the relative information exchange: fixed and time-varying. Existing delay-dependent stability criteria are modified to incorporate LQR performance guarantees while retaining convex LMI representations to facilitate the synthesis of the control gains.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Research in consensus and coordination of multiagent systems has received a great deal of attention over the past decade. One problem which is addressed in many of these papers involves ensuring a collection of multiple agents, interconnected over an information network, and operate in agreement or in a synchronized manner. Often the topology of the interconnections is captured as a graph , and in recent years many researchers have obtained novel results by combining graph theory along with systems and control ideas. See [1, 6, 16, 20, 21, 25, 26, 32, 37] and the references therein for further details and examples.

Recently, progress has been made in terms of stabilization and consensus in a network of dynamical systems subject to performance guarantees such as the rate of convergence and LQR/$\mathscr {H}_2$ performance. The rate of convergence can be enhanced by optimizing the weights associated with the consensus algorithm which essentially improves the algebraic connectivity associated with the Laplacian matrix of the graph formed according to the underlying communication topology. In [41], the weights of the Laplacian matrix of the graph are optimized to attain faster convergence to a consensus value: this is posed as a convex optimization problem and solved using LMI tools. The algebraic connectivity, characterized by the second smallest eigenvalue of the Laplacian matrix, is maximized in [18] to improve the convergence performance. An optimal communication topology for multiagent systems is sought in [5] to achieve a faster rate of convergence. A distributed control methodology ensuring LQR performance in the case of a network of linear homogenous systems is presented in [2]. The robust stability of the collective dynamics with respect to the robustness of the local node level controllers and the underlying topology of the interconnections is also established in [2]. A decentralized receding horizon controller with guaranteed LQR performance for coordinated problems is proposed in [17] and the efficacy is demonstrated by an application to attain coordination among a flock of unmanned air vehicles. In [19], the relationship between the interconnection graph and closed-loop performance in the design of distributed control laws is studied using an LQR cost function. In [24], decentralized static output feedback controllers are used to stabilize a homogeneous network comprising a class of dynamical systems with guaranteed $\mathscr {H}_2$ performance, where an upper bound on the collective performance is given, depending only on the node level quadratic performance. LQ optimal control laws for a wide class of systems, known as spatially distributed large scale systems, are developed in [28] by making use of an approximation method. In [4], LQR optimal algorithms for continuous as well as discrete time consensus are developed, where the agent dynamics are restricted to be single integrators. However, interesting relations between the optimality in LQR performance and the Laplacian matrix of the underlying graph are developed. In [23], procedures to design distributed controllers with $\mathscr {H}_2$ and $\mathscr {H}_{\infty }$ performance have been proposed for a certain class of decomposable systems. Although delays are an ubiquitous factor associated with network interconnections as a result of information exchange over a communication medium, in all the above research work [2, 4, 17, 19, 23, 24, 28] no attempt is made to explicitly address or exploit the effects of the measurement delay.

Significant research efforts analyzing the stability and performance of collective dynamics (at network level) in the face of different types of delays have taken place in the recent past: Refs. [3, 22, 29–31, 33, 35, 38, 42] are few examples, although this list is not exhaustive.¹ Necessary and sufficient conditions for average consensus problems in networks of linear agents in the presence of communication delays have been derived in [31]. Stability criteria associated with the consensus dynamics in networks of agents in the presence of communication delays was subsequently developed in [38] using Lyapunov–Krasovskii-based techniques. Moreover, the strong dependency of the magnitude of delay and the initial conditions on the consensus value was also established in [38]. In [29], a network of second-order dynamical systems with heterogeneously delayed exchange of information between agents is considered, where flocking or rendezvous is obtained using decentralized control. This can also be tuned locally, based only on the delays to the local neighbors. Both frequency and time domain approaches are utilized in [29] to establish delay-dependent and delay-independent collective stabilities. Subsequently, the theory was extended in [33] to the case of a network formed from a certain class of nonlinear systems. The robustness of linear consensus algorithms and conditions for convergence subject to node level self delays and relative measurement delays are developed and reported in [30] building on the research described in [29, 33]. ‘Scalable’ delay-dependent synthesis of consensus controllers for linear multiagent networks making use of delay-dependent conditions is proposed in [30]. Reference [42] reports an independent attempt to achieve second-order consensus using delayed position and velocity information. Recently another methodology, based on a cluster treatment of characteristic roots, has been proposed in [3] to study the effect of large and uniform delays in second-order consensus problems with undirected graphs. In [35], the performance of consensus algorithms in terms of providing a fast convergence rate involving communication delays, was studied for second-order multiagent systems. In [22], using methods based on Lyapunov–Krasovskii theory and an integral inequality approach , sufficient conditions for robust $\mathscr {H}_{\infty }$ consensus are developed for the case of directed graphs consisting of linear dynamical systems to account for node level disturbances, uncertainties and time-varying delays.

The main contributions of the present chapter are as follows: While exchanging information among agents over a network, delays are common. Previous efforts to investigate stability and robustness in the face of delays clearly emphasizes the need to account for these delays explicitly. However research in this direction is limited when compared to the available voluminous research in the case of ‘delay free’ consensus algorithms. Motivated by this fact, the idea of designing delay-dependent distributed optimal LQR control laws for homogeneous linear multi agent networks is put forward in this chapter. At a collective network level, a certain level of guaranteed cost is attained, which takes into account the control effort. Fixed, as well as time-varying delays are accounted for in the synthesis process. A Lyapunov–Krasovskii functional approach is used for synthesizing control laws in the presence of fixed delays, whereas a method from [7] is exploited to synthesize distributed control laws in the presence of time-varying delays employing a descriptor system representation. The efficacy of the proposed approaches are demonstrated by considering a homogeneous linear multi agent network (cyclic) where the node level dynamics are represented as double integrators as in [29, 35, 42].

2 Preliminaries

In this chapter, the set of real numbers is denoted by $\mathrm {I\!R}$. Real-valued vectors of length m are denoted as $\mathrm {I\!R}^{m}$. Real-valued matrices of dimension $m\times n$ are denoted as $\mathrm {I\!R}^{m \times n}$. A column vector is denoted by $\mathscr {C}ol(.)$ and a diagonal matrix is denoted by $\mathscr {D}iag(.)$. The notation $P=P^{\text{ T }}>0$ is used to describe a symmetric positive definite(s.p.d) matrix. An identity matrix of dimension $n \times n$ is denoted by $I_{n}$. Finally, the Kronecker product is denoted by the symbol $\otimes$.

Basic concepts from graph theory are described in this section. Standard texts such as [11] can be referred to for further reading on graph theory. An undirected graph $\mathscr {G}$ is described by a set of vertices $\mathscr {V}$ and a set of edges $\mathscr {E} \subset \mathscr {V}^{2}$, where an edge is denoted by $e=(\alpha , \beta ) \in \mathscr {V}^{2}$, i.e., an unordered pair. A finite graph which consists of N vertices along with k edges for a network is represented as ${\mathscr {G}}=({\mathscr {V}},{\mathscr {E}})$. In this chapter, bidirectional communication is assumed and hence the graphs for the network considered are undirected. The graph is assumed to contain no loops and no multiple edges between two nodes. The adjacency matrix, for the graph ${\mathscr {A}}({\mathscr {G}})=[a_{ij}]$, is defined by $a_{ij}=1$ if i and j are adjacent nodes of the graph, and $a_{ij}=0$ otherwise. The adjacency matrix thus defined is symmetric. The degree matrix is represented by the symbol $\varDelta ({\mathscr {G}})=[\delta _{ij}]$. $\varDelta ({\mathscr {G}})$ is a diagonal matrix, and each element $\delta _{ii}$ is the degree of the $i^{th}$ vertex. The difference $\varDelta ({\mathscr {G}})-{\mathscr {A}}({\mathscr {G}})$ defines the Laplacian of ${\mathscr {G}}$, written as ${\mathscr {L}}$. For an undirected graph, ${\mathscr {L}}$ is symmetric positive semidefinite. ${\mathscr {L}}$ has a smallest eigenvalue of zero and the corresponding eigenvector is given by $\mathbf 1 =\mathscr {C}ol(1, \ldots 1)$. ${\mathscr {L}}$ is always rank deficient and the rank of ${\mathscr {L}}$ is $n-1$ if and only if ${\mathscr {G}}$ is connected.

3 Problem Formulation

Consider a network of N identical linear systems given by

$$\begin{aligned} \dot{x}_{i}(t) = Ax_{i}(t) + Bu_{i}(t) \end{aligned}$$

(14.1)

for $i = 1,\ldots ,N$, where $x_i(t) \in \mathrm {I\!R}^n$ and $u_i(t) \in \mathrm {I\!R}^m$ represent the states and the control inputs. The constant matrices $A \in \mathrm {I\!R}^{n \times n}$ and $B \in \mathrm {I\!R}^{n \times m}$ and it is assumed that the pair (A, B) is controllable. Each agent is assumed to have knowledge of its local state information along with delayed relative state information. The relative information communicated to each agent (node) is given by

$$\begin{aligned} z_{i}(t) = \sum _{j \in \mathscr {J}_{i}} (x_{i}(t-\tau ) - x_{j}(t-\tau )), \end{aligned}$$

where $\tau$ is a delay in communication of relative information. The dynamical systems for which the ith dynamical system has information is denoted by $\mathscr {J}_{i} \subset \{1,2, \dots N\} / \{i\}$. Two cases for the delay $\tau$ are considered in this chapter:

• a known fixed delay;

• a bounded time-varying delay with a known maximum bound.

The intention is to design control laws of the form

$$\begin{aligned} u_{i}(t) = -Kx_{i}(t)-Hz_{i}(t-\tau ), \end{aligned}$$

where K $\in \mathrm {I\!R}^{m \times n}$ is designed to achieve consensus and H $\in \mathrm {I\!R}^{m \times n}$, the relative information scaling matrix, is fixed a priori. The closed-loop system at a node level is given by

$$\begin{aligned} \dot{x}_{i}(t) = (A-BK)x_{i}(t) - BHz_{i}(t-\tau ), \end{aligned}$$

(14.2)

and using Kronecker products, the system in (14.1) at a network level is given by

$$\begin{aligned} \dot{X}(t) = (I_{N} \otimes A)X(t) + (I_{N} \otimes B)U(t), \end{aligned}$$

(14.3)

where the augmented states and control inputs are $X(t) = \mathscr {C}ol(x_{1}(t),\ldots ,x_{N}(t))$ and $U(t) = \mathscr {C}ol(u_{1}(t),\ldots ,u_{N}(t))$, respectively. The relative information in (14.3) at a network level can be written as

$$\begin{aligned} Z(t) = (\mathscr {L} \otimes I_{n}) X(t-\tau ), \end{aligned}$$

(14.4)

where $\mathscr {L}$ is the Laplacian matrix associated with the sets $\mathscr {J}_{i}$. Using (14.4) the control law is given by

$$\begin{aligned} U(t) = - (I_{N} \otimes K)X(t) - (\mathscr {L} \otimes BH)X(t-\tau ). \end{aligned}$$

Substituting the previous expression into (14.3), the closed-loop system at a network level is given by

$$\begin{aligned} \dot{X}(t) = (I_{N} \otimes (A-BK))X(t) - (\mathscr {L} \otimes BH)X(t - \tau ). \end{aligned}$$

(14.5)

Since $\mathscr {L}$ is symmetric positive semidefinite, by spectral decomposition $\mathscr {L} = V \varLambda V^T$ where $V \in \mathrm {I\!R}^{N \times N}$ is an orthogonal matrix formed from the eigenvectors of $\mathscr {L}$ and $\varLambda = \textit{diag}(\lambda _{1}, \ldots \lambda _N)$ is the matrix of the eigenvalues of $\mathscr {L}$. Consider an orthogonal state transformation

$$\begin{aligned} X \mapsto (V^{T} \otimes I_{n}) X = \tilde{X}. \end{aligned}$$

The closed-loop system (14.5) in the new coordinates is given by

$$\begin{aligned} \dot{\tilde{X}}(t) = (I_{N} \otimes (A-BK))\tilde{X}(t) - (\varLambda \otimes BH)\tilde{X}(t - \tau ). \end{aligned}$$

(14.6)

Because $\varLambda$ is a diagonal matrix, system (14.6) is equivalent to

$$\begin{aligned} \dot{\tilde{x}}_{i}(t) = A_{0}\tilde{x}_{i}(t)+A_{i}\tilde{x}_{i}(t-\tau ), \end{aligned}$$

(14.7)

for $i=1,\ldots ,N$ where $A_{0} := A-BK$ and $A_{i} := -\lambda _{i}BH$.

In this chapter, it is assumed the initial condition $\tilde{x}(\theta ) = \tilde{x}(0)$ for $-\tau \le \theta \le 0$. The transformed system in (14.7) can be equivalently thought of as

$$\begin{aligned} \dot{\tilde{x}}_{i}(t) = A\tilde{x}_{i}(t)-\lambda _{i}BH\tilde{x}_{i}(t-\tau )+Bu_{i}(t), \end{aligned}$$

(14.8)

where $u_{i}(t) = -K\tilde{x}_{i}(t)$.

Remark 1

The decomposition in (14.8) can be implemented when the delay $\tau$ is identical across all communication links. In reality, the time-delays across the communication links will be unequal. One possible way to overcome this problem is to introduce delay buffers to equalize the delays.

Remark 2

Though the implementation of the controllers is decentralized the computation of the control gains K is obtained from the decomposition of (14.6). This requires the full information of the Laplacian $\mathscr {L}$ and hence the method is not applicable to scale free networks.

The objective is to design the gain matrix K under the following scenarios

• a delay-dependent design for a known fixed delay $\tau$;

• a delay-dependent design for bounded time-varying delays $\tau (t)$.

In both cases, a suboptimal level of LQR performance must be enforced on the overall system.

The stabilization of linear systems with delays, with the structure given in (14.8), has been studied extensively in the control literature. Various stability analysis and control design methods have been proposed. In [7, 8], a descriptor representation along with Lyapunov–Krasovskii functionals are used to obtain stability criteria for linear time-delay systems . In [12] a Lyapunov–Krasovskii functional approach based on the partitioning of the delay is proposed for linear time-delay systems. In [9], bounds on the derivative of delays are considered to derive delay-dependent stability criteria. Most recent methods involve establishing LMI feasibility problems (with varying levels of complexity in terms of the number of decision variables). The reader is referred to [14, 27, 34, 36, 39] for further reading in this area. In this chapter, the systems in (14.8) are to be stabilized simultaneously in the presence of delays while guaranteeing an LQR performance. This is achieved by building on the existing analysis techniques [7, 13]. The techniques in [7, 13], while not necessarily the most recent in the literature, have been found to yield tractable LMI representations under certain mild simplifications. This is important because of the large number of decision variables involved resulting from the multiple agents. The results in [7, 13] are shown to provide a good trade-off between unnecessary conservatism and tractability of LMI formulations.

4 Delay-Dependent Control Design for a Fixed Delay

Prior to stating the objective of delay-dependent control design, anexplicit model transformation from [13] for the system in (14.7) is first performed. For the system given in (14.7), the following observation holds

$$\begin{aligned} \tilde{x}_{i}(t-\tau ) = \tilde{x}_{i}(t)-\int \limits _{t-\tau }^{t}\dot{\tilde{x}}_{i}(\theta )d \theta = \tilde{x}_{i}(t) - \int \limits _{t-\tau }^{t}\left( A_{0}\tilde{x}_{i}(\theta ) + A_{i}\tilde{x}_{i}(\theta -\tau )\right) d \theta , \end{aligned}$$

for $t \ge \tau$. Using the previous expression, the system in (14.7) can be represented as

$$\begin{aligned} \dot{\tilde{x}}_{i}(t) = (A_{0} + A_{i})\tilde{x}_{i}(t) +\int \limits _{t-\tau }^{t}(-A_{i}A_{0}\tilde{x}_{i}(\theta )-A_{i}A_{i}\tilde{x}_{i}(\theta -\tau ))d \theta , \end{aligned}$$

(14.9)

for all $i=1,\ldots ,N$. As argued in [13], system (14.9) can be transformed, by shifting the time axis and lifting the initial conditions, into the system

$$\begin{aligned} \dot{y}_{i}(t) = \bar{A}_{0i}y_{i}(t) + \int \limits _{t-2\tau }^{t}\bar{A}_{i}(\theta )y_{i}(\theta )d \theta , \end{aligned}$$

(14.10)

where

$$\begin{aligned} \bar{A}_{0i}:= & {} A_{0} + A_{i},\\ \bar{A}_{i}(\theta ):= & {} \left\{ \begin{array}{ll} -A_{i}A_{0} &{}\theta \in [t-\tau ,t], \\ -A_{i}A_{i} &{} \theta \in [t-2\tau ,t-\tau ), \end{array} \right. \end{aligned}$$

with the new initial condition $y(\theta ) = \phi (\theta )$ for $-2\tau \le \theta \le 0$. According to [13], stability of (14.10) implies stability of (14.7) but not vice-versa. The control design objective for delay-dependent control design can now be stated as the design of gain matrix K for the systems in (14.10) such that the cost functions

$$\begin{aligned} J_{i} = \int \limits _{0}^{\infty }(y_{i}^{T}(t)Qy_{i}(t)+u^{T}_{i}(t)Ru_{i}(t))dt \end{aligned}$$

(14.11)

are minimized for all $i=1,\ldots ,N$, where

$$\begin{aligned} u_{i}(t) = -K y_{i}(t) \end{aligned}$$

(14.12)

and Q $\in \mathrm {I\!R}^{n \times n}$ and R $\in \mathrm {I\!R}^{m \times m}$ are symmetric positive definite matrices.

Remark 3

In [13] it is shown that the transformed system in (14.10) has all the poles of the original system in (14.8) plus additional poles due to the transformation. Consequently stability of the transformed system implies stability of the original system but not vice-versa, due to the lifting of the initial conditions of the original system. In this chapter, LQR control design has been employed on the transformed system. This will also guarantee a level of performance for the original system in (14.8).

Theorem 1

For a known fixed delay $\tau$, a given scaling matrix H $\in \mathrm {I\!R}^{m \times n}$, selected weighting matrices Q and R and scalars $\alpha _{0}$ and $\alpha _{1}$, the control laws in (14.12) simultaneously stabilize the transformed systems in (14.10) if there exist matrices $Z>0$, W in $\mathrm {I\!R}^{n \times n}$ and Y $\in \mathrm {I\!R}^{m \times n}$ such the following LMI conditions are satisfied

$$\begin{aligned} \left[ \begin{array}{cc} -Z &{} I_{n}\\ *&{} -W \end{array} \right] <0, \end{aligned}$$

(14.13)

$$\begin{aligned} \left[ \begin{array}{ccccc} \bar{\varPhi }_{i} &{} -A_{i}AW + A_{i}BY&{} -A_{i}^{2}W &{} \frac{WQ^{1/2}}{\tau } &{} \frac{Y^{T}}{\tau }\\ *&{} -\alpha _{0}W &{} 0 &{} 0 &{} 0\\ *&{} *&{} -\alpha _{1}W &{} 0 &{} 0\\ *&{} *&{} *&{} -\frac{I}{\tau } &{} 0\\ *&{} *&{} *&{} *&{} -\frac{R^{-1}}{\tau } \end{array} \right] <0 , \end{aligned}$$

(14.14)

where

$$\begin{aligned} \bar{\varPhi }_{i}= & {} \frac{1}{\tau }(((A+A_{i})W-BY)+((A+A_{i})W-BY)^{T}) +(\alpha _{0}+\alpha _{1})W \end{aligned}$$

for all $i=1,\ldots ,N$. The state feedback gain matrix is then given by $K=YW^{-1}$.

Furthermore since the $J_{i}$ from (14.11) satisfy, for $i=1,\dots ,n$

$$ J_{i}< y_{i}^{T}(0)Py(0)(1 + \frac{1}{2}\alpha _{0}\tau ^{2}+ \frac{3}{2}\alpha _{1}\tau ^{2}), $$

minimizing Trace(Z) subject to (14.13)–(14.14) minimizes a bound on the LQR cost.

Proof

This proof uses a restricted Lyapunov–Krasovskii functional as suggested in Proposition 5.16 from [13]. For the system in (14.10) consider a Lyapunov–Krasovskii functional of the form

$$\begin{aligned} V_{i}(y(t)) = y_{i}^{T}(t)Py_{i}(t) + \int \limits _{t-2\tau }^{t}\int \limits _{\theta }^{t}\alpha (\theta )y_{i}^{T}(s)Py_{i}(s)ds d\theta , \end{aligned}$$

(14.15)

where $P>0$ and P $\in \mathrm {I\!R}^{n \times n}$ for all $i=1,\ldots ,N$. In (14.15) $\alpha (\theta )>0$ is a positive scalar function defined over the interval $t-2\tau \le \theta \le t$. Consider the inequality

$$\begin{aligned} y_{i}^{T}(t)&\left( P\bar{A}_{0i} + \bar{A}_{0i}^{T}P + \int \limits ^{t}_{t-2\tau } \alpha (\theta )P d \theta \right) \ y_{i}(t)&+ \int \limits _{t-2\tau }^{t} 2 y_{i}^{T}(t) P\bar{A}_{i}(\theta )y_{i}(\theta )d\theta \end{aligned}$$

$$\begin{aligned} -\int \limits _{t-2\tau }^{t}\alpha (\theta )y_{i}^{T}(\theta )P y_{i}(\theta )d \theta < -y_{i}^{T}(t)Qy_{i}(t) - u_{i}^{T}(t)Ru_{i}(t) . \end{aligned}$$

(14.16)

By adding and subtracting terms involving a symmetric matrix function $M(\theta )$ $\in \mathrm {I\!R}^{n\times n}$, the inequality in (14.16) is equivalent to

$$\begin{aligned} y_{i}^{T}(t)&\left( P\bar{A}_{0i} + A_{0i}^{T}P + Q + K^{T}RK + \int \limits ^{t}_{t-2\tau } M (\theta ) d \theta \right) y_{i}(t) \nonumber \\&+\int \limits ^{t}_{t-2\tau }\bar{y}_{i}^{T}(t,\theta ) \left( \begin{array}{cc} \alpha (\theta )P - M(\theta ) &{} P\bar{A}_{i}(\theta )\\ *&{} -\alpha (\theta )P \end{array} \right) \bar{y}_{i}(t,\theta ) d\theta < 0. \end{aligned}$$

(14.17)

where

$$\begin{aligned} \bar{y}^{T}_{i}(t, \theta ) = \left( \begin{array}{cc} y_{i}^{T}(t)&y_{i}^{T}(\theta ) \end{array} \right) . \end{aligned}$$

Define the symmetric matrix function $M(\theta )$ as

$$ M(\theta ) =\left\{ \begin{array}{lcl} M_{0}, &{}\quad &{} t-\tau \le \theta \le t \\ M_{1}, &{}\quad &{} t-2\tau \le \theta < t-\tau , \end{array}\right. $$

where $M_{0}$ and $M_{1}$ are symmetric matrices $\in \mathrm {I\!R}^{n \times n}$ and the scalar function $\alpha (\theta )$ as

$$ \alpha (\theta ) =\left\{ \begin{array}{lcl} \alpha _{0}, &{}\quad &{} t-\tau \le \theta \le 0 \\ \alpha _{1}, &{}\quad &{} t-2\tau \le \theta < t-\tau , \end{array}\right. $$

where $\alpha _{0}>0$ and $\alpha _{1}>0$. Then as argued in [13] inequality in (14.17) is satisfied for $P>0$ and

$$\begin{aligned} \begin{array}{rcl} P(A_{0}+A_{i}) + (A_{0}+A_{i})^{T}P + Q + K^{T}RK + \tau (M_{0}+M_{1}) &{}<&{} 0 ,\\ \left[ \begin{aligned}{cc} \alpha _{0}P - M_0 &{} -PA_{i}A_{0}\\ *&{} -\alpha _{0}P \end{aligned} \right] &{}<&{} 0 , \\ \left[ \begin{aligned}{cc} \alpha _{1}P - M_{1} &{} -PA_{i}A_{i}\\ *&{} -\alpha _{1}P \end{aligned} \right] &{}<&{} 0. \end{array} \end{aligned}$$

(14.18)

Using the Schur complement and eliminating $M_{0}$ and $M_{1}$ the inequalities in (14.18) are satisfied if

$$\begin{aligned} \left[ \begin{array}{ccc} \varPhi _{i} &{} -PA_{i}A_{0} &{} -PA_{i}A_{i}\\ *&{} -\alpha _{0}P &{} 0\\ *&{} *&{} -\alpha _{1}P \end{array} \right] <0, \end{aligned}$$

(14.19)

where

$$\begin{aligned} \varPhi _{i} = \frac{1}{\tau }(P(A_{0}+A_{i}) + (A_{0}+A_{i})^{T}P + Q + K^{T}RK ) + (\alpha _{0}+\alpha _{1})P, \end{aligned}$$

(14.20)

and $A_{0} = A-BK$ for all $i = 1,\ldots ,N$. To develop a convex representation define $W = P^{-1}$. Pre- and postmultiplying (14.19) by $\textit{diag}(W,W,W)$ means (14.19) is equivalent to

$$\begin{aligned} \left[ \begin{array}{ccc} \hat{\varPhi }_{i} &{} -A_{i}A_{0}W &{} -A_{i}A_{i}W\\ *&{} -\alpha _{0}W &{} 0\\ *&{} *&{} -\alpha _{1}W \end{array} \right] <0, \end{aligned}$$

(14.21)

where

$$\begin{array}{lcl} \hat{\varPhi }_{i}&{} =&{} \frac{1}{\tau }\left( (A_{0}+A_{i})W + W(A_{0}+A_{i})^{T} + WQW\right) \\ &{}&{}+ \frac{1}{\tau }(WK^{T}RKW) + (\alpha _{0}+\alpha _{1})W, \end{array} $$

for all $i = 1,\ldots ,N$. Define an auxiliary symmetric matrix Z $\in \mathrm {I\!R}^{n \times n}$ and employ the change of decision variables $KW = Y$ where Y $\in \mathrm {I\!R}^{m \times n}$. From applying the Schur complement to (14.21), the inequalities in (14.18) become the LMI stated in the theorem statement in (14.14). Inequality (14.16) is equivalent to

$$\begin{aligned} \dot{V}_{i}(y_{i}(t))< -y_{i}^{T}(t)Qy_{i}(t) - u_{i}^{T}(t)Ru_{i}(t). \end{aligned}$$

Integrating both sides the previous equation from 0 to $\infty$ yields

$$\begin{aligned} -y_{i}^{T}(0)Py_{i}(0)-\int \limits _{-2\tau }^{0}\int \limits _{\theta }^{0}\alpha (\theta )y_{i}^{T}(s)Py_{i}(s)ds d\theta <-J_{i}. \end{aligned}$$

(14.22)

Assuming new initial conditions $y_{i}(s)=y_{i}(0)$ for $s<0$, an upper bound for $J_{i}$ is given by

$$\begin{aligned} J_{i}< y_{i}^{T}(0)Py(0)(1 + \frac{1}{2}\alpha _{0}\tau ^{2}+ \frac{3}{2}\alpha _{1}\tau ^{2}), \end{aligned}$$

(14.23)

by explicitly evaluating the integration on the L.H.S of (14.22). Minimization of Trace(P) ensures minimizations of the cost $J_{i}$ for all $i=1,\ldots ,N$. From (14.13), it can be shown by Schur complement that $Z>W^{-1}=P$ and hence minimizing Trace(Z) ensures cost minimization from (14.23). $\blacksquare$

Remark 4

Note that the matrix H and the scalars $\alpha _{0}$ and $\alpha _{1}$ are fixed in (14.14) which renders the matrix $A_{i}$ fixed for all $i=1,\ldots ,N$ and hence (14.14) is an LMI which can be easily solved using modern convex optimization techniques.

5 Delay-Dependent Control Design for Time-Varying Delays

In the previous section, state feedback control laws were designed based on the assumption of relative information having a fixed delay. Assuming fixed delays in a network is somewhat idealistic and hence a need arises for control design involving time-varying delays . In [7], a control design methodology has been presented for time-varying delay where the delay $\tau (t)$ is a bounded continuous function satisfying $0\le \tau (t) \le \tau _{m}$ for $t\ge 0$ where $\tau _{m}$ is known. The equivalent systems to (14.8) with time-varying delays $\tau (t)$ are given by

$$\begin{aligned} \dot{\tilde{x}}_{i}(t) = A\tilde{x}_{i}(t)-\lambda _{i}BH\tilde{x}_{i}(t-\tau (t))+Bu_{i}(t), \end{aligned}$$

(14.24)

for $i=1,\ldots ,N$. Again the objective is to minimize a cost function of the form

$$\begin{aligned} J_{i} = \int \limits _{0}^{\infty }(\tilde{x}_{i}^{T}(t)Q\tilde{x}_{i}(t)+u^{T}_{i}(t)Ru_{i}(t))dt, \end{aligned}$$

where

$$\begin{aligned} u_{i}(t) = -K\tilde{x}_{i}(t), \end{aligned}$$

(14.25)

for all $i=1,\ldots ,N$.

Theorem 2

Assume the bound on the delay $\tau _{m}$ is known, then for a given scaling matrix H from (14.24) and given weighting matrices Q and R, the control laws in (14.25) simultaneously stabilize the systems in (14.8) if there exist matrices $W_{1}>0$, $W_{2}$, $W_{3}$, $Z>0$, $\bar{F}_{1}$, $\bar{F}_{2}$, $\bar{F}_{3}$, $\bar{S}>0$ $\in \mathrm {I\!R}^{n \times n}$ such that the following LMI conditions are satisfied:

$$\begin{aligned} \left[ \begin{array}{cc} -Z &{} I_{n \times n}\\ I_{n \times n} &{} -W_{1} \end{array} \right]< & {} 0, \end{aligned}$$

(14.26)

$$\begin{aligned} \left[ \begin{array}{ccc} \bar{S} &{} 0 &{} \bar{S}A_{i}^{T}\\ *&{} \bar{F}_{1} &{} \bar{F}_{2}\\ *&{}*&{} \bar{F}_{3} \end{array} \right]> & {} 0, \end{aligned}$$

(14.27)

$$\begin{aligned} \left[ \begin{array}{ccccc} \tilde{W}_{2F} &{} \varPhi _{i} &{} \tau _{m}W_{2}^{T} &{} W_{1}Q^{1/2}&{} Y^{T}\\ *&{} \tilde{W}_{3F}&{} \tau _{m}W_{3}^{T}&{} 0 &{} 0\\ *&{}*&{} -\tau _{m}\bar{S}&{} 0 &{} 0\\ *&{} *&{} *&{} -I &{} 0\\ *&{} *&{} *&{} *&{} R^{-1} \end{array} \right] < 0, \end{aligned}$$

(14.28)

where

$$\begin{aligned} \varPhi _{i}= & {} W_{3}-W_{2}^{T} + W_{1}(A+A_{i}) + \tau _{m}\bar{F}_{2} - Y^{T}B^{T}, \\ \tilde{W}_{2F}= & {} W_{2}+W_{2}^{T}+\tau _{m}\bar{F}_{1},\\ \tilde{W}_{3F}= & {} -W_{3}-W_{3}^{T}+\tau _{m}\bar{F}_{3}, \end{aligned}$$

for all $i=1,\ldots ,N$. The state feedback gain matrix is then given by

$$\begin{aligned} K = YW_{1}^{-1}. \end{aligned}$$

Furthermore $J_{i} < \tilde{x}_{i}^{T}(0)P_{1}\tilde{x}_{i}(0)$ and so minimizing Trace(Z) subject to (14.26)–(14.28) minimize a bound on the LQR cost.

Proof

This proof uses concepts from Corollary 3 from [7] to design control laws for the system in (14.8) with a certain level of performance. As in [7] represent the system in (14.7) as a descriptor system given by

$$\begin{aligned} \dot{\tilde{x}}_{i}(t) = \tilde{y}_{i}(t), \qquad 0 = -\tilde{y}_{i}(t) + (A_{0}+A_{i})\tilde{x}(t) - A_{i}\int \limits _{t-\tau (t)}^{t}\tilde{y}_{i}(s)ds, \end{aligned}$$

for $i=1,\ldots ,N$. The previous system can be written as

$$\begin{aligned} E\dot{\bar{x}}_{i}(t)= & {} \left( \begin{array}{c} \dot{\tilde{x}}_{i}(t)\\ 0 \end{array} \right) ~=~ \underbrace{\left( \begin{array}{cc} 0 &{} I\\ (A_{0} + A_{i}) &{} -I \end{array} \right) }_{\tilde{A}_{0i}} \bar{x}_{i}(t) - \left( \begin{array}{c} 0\\ A_{i} \end{array} \right) \int \limits _{t-\tau (t)}^{t}\tilde{y}_{i}(s)ds, \end{aligned}$$

for all $i=1,\ldots ,N$. In the previous equation, $\bar{x}_{i}^{T}(t) = \left( \begin{array}{cc} \tilde{x}_{i}^{T}&\tilde{y}_{i}^{T} \end{array} \right)$ and $E = \textit{diag}(I,0)$. Consider a Lyapunov–Krasovskii functional of the form

$$\begin{aligned} V_{i}(t) = V_{1i}(t) + V_{2i}(t), \end{aligned}$$

where

$$\begin{aligned} V_{1i}(t) = \bar{x}_{i}^{T}EP\bar{x}_{i}, \qquad V_{2i}(t) = \int \limits _{-\tau _{m}}^{0}\int \limits _{t+\theta }^{t} \tilde{y}^{T}_{i}(s)S\tilde{y}_{i}(s)ds d\theta . \end{aligned}$$

For this functional, we assume that the matrix $S\in \mathrm {I\!R}^{n \times n}$ is symmetric positive definite and the matrix P is such that $P = \left[ {\begin{matrix} P_{1} &{} 0\\ P_{2} &{} P_{3} \end{matrix}} \right]$ with $P_{1} > 0$. The cost functions $J_i$, for $i=1,\dots N$, can be represented as

$$\begin{aligned} J_{i} = \int \limits _{0}^{\infty }\bar{x}_{i}^{T}(t)\left[ \begin{array}{cc} Q + K^{T}RK &{} 0\\ 0 &{} 0 \end{array} \right] \bar{x}_{i}(t)dt. \end{aligned}$$

(14.29)

Then, the objective is to ensure the inequality

$$\begin{aligned} \dot{V}_{i}(t)=\dot{V}_{1i}(t) + \dot{V}_{2i}(t) < -\bar{x}_{i}^{T}(t)\left[ \begin{array}{cc} Q + K^{T}RK &{} 0\\ 0 &{} 0 \end{array} \right] \bar{x}_{i}(t) \end{aligned}$$

(14.30)

hold. In the left-hand side of (14.30), we have

$$\begin{aligned} \dot{V}_{1i}(t) = P^{T}\tilde{A}_{0i} + \tilde{A}_{0i}^{T}P -2\int \limits _{t-\tau (t)}^{t}G(\bar{x}_{i}(t),\tilde{y}_{i}(s))ds, \end{aligned}$$

(14.31)

where

$$\begin{aligned} G(\bar{x}_{i}(t),\tilde{y}_{i}(s))=\bar{x}^{T}_{i}(t)P^{T}\left( \begin{array}{c} 0\\ A_{i} \end{array} \right) \tilde{y}_{i}(s), \end{aligned}$$

and

$$\begin{aligned} \dot{V}_{2i}(t) = \tau _{m}\tilde{y}^{T}_{i}(t)S\tilde{y}_{i}(t) - \int \limits ^{t}_{t-\tau _{m}}\tilde{y}^{T}_{i}(s)S\tilde{y}_{i}(s)ds. \end{aligned}$$

(14.32)

Select a matrix F $\in \mathrm {I\!R}^{2n \times 2n}$ such that

$$\begin{aligned} \tilde{S}_{F} = \left[ \begin{array}{cc} S&\left[ \begin{array}{cc}0 &{} A_{i}^{T}\end{array}\right] P\\ P^{T}\left[ \begin{array}{c}0 \\ A_{i}^{T}\end{array}\right]&F \end{array} \right] > 0 \end{aligned}$$

(14.33)

for all $i=1\ldots ,N$. It follows that

$$\begin{aligned} \int \limits ^{t}_{t-\tau }\left[ \begin{array}{c} \tilde{y}_{i}(s)\\ \bar{x}_{i}(t) \end{array} \right] ^{T}\tilde{S}_{F}\left[ \begin{array}{c} \tilde{y}_{i}(s)\\ \bar{x}_{i}(t) \end{array} \right] ds > 0. \end{aligned}$$

(14.34)

By rearranging (14.34), the integral term in (14.31) is

$$\begin{aligned} -2\int \limits _{t-\tau (t)}^{t}G(\bar{x}_{i}(t),\tilde{y}_{i}(s))ds< & {} \int \limits _{t-\tau }^{t}\left( \tilde{y}^{T}_{i}(s)S\tilde{y}_{i}(s) + \bar{x}^{T}_{i}(t)F\bar{x}_{i}(t)\right) ds\nonumber \\= & {} \int \limits _{t-\tau }^{t}(\tilde{y}^{T}_{i}(s)S\tilde{y}_{i}(s))ds + (\bar{x}^{T}_{i}(t)F\bar{x}_{i}(t))\int \limits _{t-\tau }^{t}ds\nonumber \\\le & {} \int \limits _{t-\tau _{m}}^{t}\tilde{y}^{T}_{i}(s)S\tilde{y}_{i}(s)ds + \tau _{m} \bar{x}^{T}_{i}(t)F\bar{x}_{i}(t). \end{aligned}$$

(14.35)

Substituting (14.35) in (14.31) and using (14.32), inequality (14.30) is satisfied if

$$\begin{aligned} \left[ \begin{array}{cc} S &{} [0 \ \ A_{i}^{T}]P\\ *&{} F \end{array} \right]> & {} 0 \end{aligned}$$

(14.36)

and

$$\begin{aligned} P^{T}\tilde{A}_{0i}+ \tilde{A}_{0i}^{T}P + \tau _{m}F +\left[ \begin{array}{cc} Q + K^{T}RK &{} 0\\ 0 &{} \tau _{m}S \end{array} \right] <0 \end{aligned}$$

(14.37)

hold for all $1=1,\ldots ,N$. Define

$$\begin{aligned} P^{-1}=W= \left[ \begin{array}{cc} W_{1} &{} 0\\ W_{2} &{} W_{3} \end{array} \right] . \end{aligned}$$

(14.38)

To create convex LMI representations from the matrix inequalities (14.36) and (14.37) define $Z>0$ $\in \mathrm {I\!R}^{n \times n}$. Pre and post multiply (14.36) by $\textit{diag}(S^{-1},W^{T})$ and $\textit{diag}(S^{-1},W)$ respectively. Also pre and post multiply (14.37) by $W^{T}$ and W respectively. Using the linearizations

$$ W^{T}FW = \bar{F}=\left[ \begin{array}{cc} \bar{F}_{1} &{} \bar{F}_{2}\\ *&{} \bar{F}_{3} \end{array} \right] $$

and $\bar{S} = S^{-1}$, and $KW_{1} = Y$, the inequalities in (14.36) and (14.37) can be represented by the LMIs in (14.27) and (14.28). An expression for the maximum bound on the cost $J_{i}$ can be obtained by integrating (14.30) as

$$\begin{aligned} J_{i} < \tilde{x}_{i}^{T}(0)P_{1}\tilde{x}_{i}(0) + \int \limits _{-\tau _{m}}^{0}\int \limits _{\theta }^{0}\tilde{y}^{T}_{i}(s)S\tilde{y}_{i}(s)ds d\theta ,\end{aligned}$$

for all $i=1,\ldots ,N$. Assuming the initial condition $\tilde{x}(\theta ) = \tilde{x}(0)$ for $-\tau _{m} \le \theta \le 0$, $\tilde{y}_{i}(\theta ) = \dot{\tilde{x}}(\theta ) = 0$ for $-\tau _{m} \le \theta \le 0$. Hence the maximum bound on the cost $J_{i}$ is given by

$$\begin{aligned} J_{i} < \tilde{x}_{i}^{T}(0)P_{1}\tilde{x}_{i}(0). \end{aligned}$$

(14.39)

From (14.26) it can be shown that $Z>W_{1}^{-1}=P_{1}$ and hence minimizing Trace(Z) minimizes the $Trace(P_{1})$ ensuring cost minimization from (14.39). $\blacksquare$

Remark 5

Note that $\tau$ and the matrix H are fixed which renders the matrix $A_{i}$ fixed for all $i=1,\ldots ,N$ and hence (14.27) and (14.28) are LMI representations. Consequently the conditions of Theorem 2 can be easily tested via modern convex optimization solvers

6 Numerical Example

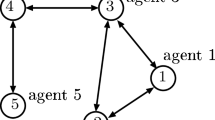
To illustrate the design methodologies, a cyclic nearest neighbor configuration of 5 vehicles moving in a x–y plane, with each vehicle described by two decoupled double integrators is considered. The linear system model is given by

$$\begin{aligned} \dot{\zeta }_{i} = A \zeta _{i} + Bu_{i} \end{aligned}$$

where $\zeta _{i}$ represents the x and y plane positions and velocities which constitute the states of the ith vehicle. The matrices A and B are given by

$$\begin{aligned} A =\left[ \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right] ,\qquad B = \left[ \begin{array}{cc} 0 &{} 0\\ 0 &{} 0\\ 1 &{} 0\\ 0 &{} 1 \end{array} \right] . \end{aligned}$$

The matrix H associated with the relative information exchange in (14.2) is given by

$$\begin{aligned} H =\left[ \begin{array}{cccc} 1 &{} 0 &{}1 &{} 0\\ 0 &{} 1 &{} 0 &{} 1 \end{array} \right] . \end{aligned}$$

For the method proposed in Sect. 14.4, it is assumed that a fixed communication delay of $\tau = 0.1$ s is present in the exchange of relative information. The matrices Q and R for the cost functions given in (14.11) and (14.29) have been chosen as

$$\begin{aligned} Q=\left[ \begin{array}{cccc} 10&{} 0 &{} 0 &{} 0\\ 0 &{}10 &{} 0 &{} 0\\ 0 &{} 0 &{} 10&{} 0\\ 0 &{} 0 &{} 0 &{}10 \end{array} \right] , \qquad R=\left[ \begin{array}{cc} 1&{}0\\ 0&{}1 \end{array} \right] . \end{aligned}$$

For the delay-dependent LMIs in (14.13) and (14.14), the scalars $\alpha _{0}$ and $\alpha _{1}$ have been chosen as $\alpha _{0}=3$ and $\alpha _{1}=3$. For $\tau =0.1$ s, the gain matrix K obtained from this approach is

$$\begin{aligned} K =\left[ \begin{array}{cccc} 2.3931 &{} 0 &{} 2.8428 &{} 0\\ 0 &{} 2.3931 &{} 0 &{} 2.8428 \end{array} \right] . \end{aligned}$$

(14.40)

Figure 14.1 shows that a rendezvous occurs at around $t=5$ s with the gain matrix K obtained in (14.40).

Fig. 14.1

Delay-dependent control with delay of $\tau =0.1$ s

Fig. 14.2

No Rendezvous after $\tau =0.6$ s

In [13], it is stated that the stability criteria of Proposition 5.16 is conservative. Hence the gain matrix K in (14.40) should be able to cope with larger delays. Simulations show that the agents do not attain a rendezvous and diverge once $\tau$ exceeds 0.6s. This is shown in Fig. 14.2.

If there is no communication of relative information, i.e., the control law in (14.2) is replaced by $u_i(t) =-Kx_{i}(t)$, for the system in (14.1), a standard LQR problem results for each agent. With the same set of matrices (A, B, Q, R) using the MATLAB command ’lqr’, the local state feedback gain matrix K obtained is

$$\begin{aligned} K = \left[ \begin{array}{cccc} 3.1623 &{} 0 &{} 4.0404 &{} 0\\ 0 &{} 3.1623 &{} 0 &{} 4.0404 \end{array} \right] . \end{aligned}$$

(14.41)

Figure 14.3 shows 5 disconnected agents attaining a rendezvous at $t=4.8$ s.

Fig. 14.3

Rendezvous of individual agents

Fig. 14.4

Rendezvous with time-varying delay

Comparing the plots in Figs. 14.1 and 14.3, it can be seen that the performance achieved both with and without the relative information is similar. One distinct advantage that can be observed is the reduction of the magnitude of the gains for velocity and position feedback in (14.40) as compared to (14.41).

For the method proposed in Sect. 14.6, the bounded time-varying delay is given by $0\le \tau (t) \le 0.1$ s. The gain matrix obtained from this approach is

$$\begin{aligned} K =\left[ \begin{array}{cccc} 2.9779 &{} 0 &{} 4.4182 &{} 0\\ 0 &{} 2.9779 &{} 0 &{} 4.4182 \end{array} \right] . \end{aligned}$$

(14.42)

Figure 14.4 shows 5 agents attaining a rendezvous at around $t=6$ s for time-varying delay at $\tau (t)=0.07$ s.

7 Conclusions and Future Work

In this chapter a multiagent system composed of linear identical dynamical agents was considered. The agents are assumed to share relative state information over a communication network. This exchange of relative information was assumed to be subject to delays. New methods to synthesize distributed state feedback control laws for the multiagent system, using delayed relative information along with local state information with guaranteed LQR performance, were developed. Two types of delays were considered in the relative information exchange: fixed and time-varying. For the double integrator system considered, the gains with fixed delay in relative information are lower in magnitude as compared to the gains obtained by solving an individual LQR problem for a single agent with no delays with similar performance. Thus the use of relative information maybe advantageous in terms of distributing the control effort. In the case of a time-varying delay, the method which has been proposed guarantees a bound on the LQR performance for delays with a known maximum bound.

The stabilization techniques which were used to incorporate LQR performance, while not necessarily the most recent in terms of the time-delay literature, were shown to yield tractable LMI representations under certain mild simplifications. This is important because of the large number of decision variables involved resulting from the multiple agents. These techniques provided a good trade-off between unnecessary conservatism and tractability of LMI formulations. Ongoing research efforts are attempting to use methods based on discretized Lyapunov–Krasovskii functionals and some of the new delay-dependent stabilization techniques which have been developed to reduce the conservatism.