Distributed Robust Control of Uncertain Multi-agent Systems with Directed Networks

Abstract

This paper investigates the distributed robust control problem of a class of uncertain linear time invariant multi-agent systems with directed networks. It is assumed that the agents have identical nominal dynamics while subject to different norm-bounded parameter uncertainties. Based on relative states information of the neighbor agents and a subset of absolute states of the agents, distributed robust controllers are constructed. Sufficient conditions are proposed based on bounded real lemma and algebraic graph theory. The effectiveness of the theoretical results is illustrated via a numerical simulation.

1 Introduction

Recently, the distributed control problem of multi-agent systems has drawn great attention for its broad potential applications in many areas such as formation control [1–4], flocking control [5], and consensus control [6, 7]. Compared with traditional control systems, agents in the multi-agent systems are coupled through networks which usually are modeled by directed or undirected graphs. The system behavior depends not only on the individual agent dynamic, but also on the structure of the networks [7].

Due to some physical constrains such as limited resources and energy or short communication ranges, individual agent cannot get the global information of the system. Thus, only distributed controllers can be used with local information of neighbor agents. The distributed controllers have many advantages such as flexible scalability, high robustness, and low costs.

The distributed control problem of ideal multi-agent systems without uncertainties has been studied from different perspectives and numerous results have been obtained [1–10]. However, in practical applications, real systems usually have uncertainties or subject to external disturbances such as sensor noise which may destroy the convergence property of the systems. Motivated by this observation, many works have been done. In [11], a decomposition approach was used to study the $H_{\infty }$ control problem of identical dynamically coupled systems subject to external disturbances. Under undirected graphs, based on local relative output information, dynamic $H_{\infty }$ controllers were proposed in [12]. As an extension of consensus regions, the notions of the $H_{\infty }$ and $H_{2}$ performance regions under undirected graphs were introduced and it was proved that the unbounded $H_{\infty }$ performance region was independent of the communication topology as long as it was connected [13]. In [14], a control protocol was introduced to solve the $H_{\infty }$ consensus problem synthesized with transient performance. In [15], under undirected networks, the distributed $H_{\infty }$ robust control problem of linear multi-agent systems with parameter uncertainties was investigated, in which the agents have the same nominal dynamics while subject to different parameter uncertainties. Then the same problem was solved synthesized with transient performance with undirected networks [16].

Note that, the commutations topologies of the existing results relating to the distributed robust control problem of uncertain linear multi-agent systems [15, 16] are restricted to be undirected. However, the communication topologies in real application are usually modeled by directed graphs and the undirected topologies can be seen as a special class of directed topologies in which the edges among the agents are bidirectional.

Motivated by this, in this paper, we investigate the distributed robust control problem of uncertain linear multi-agent systems with directed networks. A directed graph is used to model the communication topology in the networks. It is assumed that the directed graph has a spanning tree and there is at least one root node has a loop. Based on local relative states information of the neighbor agents and a subset of absolute information of the agents, distributed robust controllers are constructed. Sufficient conditions are proposed based on the bounded real lemma and algebraic graph theory. Compared with the existing results in [15, 16] where the communication topologies are assumed to be undirected, a bright feature of this paper is that the networks are assumed to be directed.

The remainder of the paper is organized as follows. In Sect. 2, some necessary concepts and notation are introduced. In Sect. 3, the robust control problem of multi-agent systems is addressed. In Sect. 4, a simulation example is presented. Section 5 is the conclusion.

2 Preliminaries

Please use the “Equation” button for equations and positioned correctly using one tab space before and one after, as below.

In this paper, following notations will be used. ${\mathbf{\mathbb{R}}}^{n \times n}$ and ${\mathbb{C}}^{n \times n}$ denote the set of $n \times n$ real and complex matrices, respectively. ⊗ denotes the Kronecker product. For $\mu \in {\mathbb{C}}$, the real part is $\text{Re} \left( \mu \right)$. $I_{n}$ is the $n \times n$ identity matrix. $\left\| {\begin{array}{*{20}c} \cdot \\ \end{array} } \right\|$ stands for the induced matrix 2-norm. For a square matrix A, $\lambda \left( A \right)$ denotes the eigenvalues of matrix A; $rank\left( A \right)$ denotes its rank. The inertia of a symmetric matrix A is a triplet of nonnegative integers $\left( {m,z,p} \right)$ where m, z and p are respectively the number of negative, zero and positive elements of $\lambda \left( A \right)$. $\hbox{max} \left\{ {\lambda \left( A \right)} \right\}$ ($\hbox{min} \left\{ {\lambda \left( A \right)} \right\}$) denotes the largest (smallest) eigenvalue of the matrix A. $A > B$ ($A \ge B$) means that $A - B$ is positive definite (respectively, positive semidefinite). $\left( {A,B} \right)$ is said to be stabilizable if there exists a real matrix K such that $A + BK$ is Hurwitz.

A directed graph ${\mathcal{G}} = \left( {{\mathcal{V}},{\mathcal{E}},{\mathcal{A}}} \right)$ contains the vertex set ${\mathcal{V}} = \left\{ {1,2, \ldots ,N} \right\}$, the directed edges set ${\mathcal{E}} \, \subseteq \, {\mathcal{V}} \times {\mathcal{V}}$, the weighted adjacency matrix ${\mathcal{A}} = \left[ {a_{ij} } \right]_{N \times N}$ with nonnegative elements $a_{ij}$. $a_{ij} = 1$ if there is a directed edge between vertex i and j, $a_{ij} = 0$ otherwise. The set of neighbors of i is defined as ${\mathcal{N}}_{i} : = \left\{ {j \in {\mathcal{V} }:a_{ij} = 1} \right\}$. A directed path is a sequence of ordered edges of the form $\left( {i_{1} ,i_{2} } \right),\left( {i_{2} ,i_{3} } \right), \ldots$, where $i_{j} \in {\mathcal{V}}$. The Laplacian matrix of the topology ${\mathcal{G}}$ is defined as ${\mathcal{L} } = \left[ {{\mathcal{L}}_{ij} } \right]_{N \times N}$, where ${\mathcal{L} }_{ii} = \sum\nolimits_{j \ne i} {a_{ij} }$ and ${\mathcal{L} }_{ij} = - a_{ij}$. Then 0 is an eigenvalue of ${\mathcal{L}}$ with $1_{N}$ as the eigenvector. A directed graph is called balanced if $\sum\nolimits_{j = 1}^{N} {a_{ij} } = \sum\nolimits_{j = 1}^{N} {a_{ji} }$. A directed graph is said to have a spanning tree if there is a vertex called the root such that there is a directed path from this vertex to every other vertex. A directed graph is said to be strongly connected if there is a directed path between every pair of distinct vertices.

Lemma 1

(Bounded Real Lemma [17]) For a positive scalar $\gamma > 0$ and the transfer function $G\left( s \right) = C\left( {sI - A} \right)^{ - 1} B + D$, then the following are equivalent

• (1) $\text{Re} \left( {\lambda \left( A \right)} \right) < 0$ and $\left\| {G\left( s \right)} \right\|_{\infty } < \gamma$.

• (2) $\bar{\sigma }\left( D \right) < \gamma$ and there exist a positive definite matrix P such that

  $$ A^{T} P + PA + C^{T} C + \left( {PB + C^{T} D} \right)\left( {\gamma^{2} I - D^{T} D} \right)^{ - 1} \left( {B^{T} P + D^{T} C} \right) < 0. $$

Lemma 2

(Schur Complement Lemma [18]) Given a matrix $S = \left[ {\begin{array}{*{20}c} {S_{11} } & {S_{12} } \\ {S_{21} } & {S_{22} } \\ \end{array} } \right]$, where $S \in {\mathbf{\mathbb{R}}}^{n \times n}$, $S_{11} \in {\mathbf{\mathbb{R}}}^{r \times r}$, $S_{21} = S_{12}^{T}$, then the following are equivalent

• (1) $S < 0$.

• (2) $S_{11} < 0 ,$ $S_{22} - S_{21} S_{11}^{ - 1} S_{12} < 0$.

• (3) $S_{22} < 0 ,$ $S_{11} - S_{12} S_{22}^{ - 1} S_{21} < 0$.

3 Main Results

Consider a multi-agent system composed of N agents with following uncertain Lur’e type nonlinear dynamics

$$ \dot{x}_{i} (t) = \left( {A +\Delta A_{i} } \right)x_{i} (t) + Bu_{i} (t),\quad i = 1,2, \ldots ,N, $$

(1)

where $x_{i} (t) \in {\mathbf{\mathbb{R}}}^{n}$ and $u_{i} (t) \in {\mathbf{\mathbb{R}}}^{p}$ are the state and the control input of the $i{\text{-th}}$ agent, respectively. A and B are constant system matrices with compatible dimensions. $\Delta A_{i}$ is an unknown matrix representing the time-varying parameter uncertainty associated with the $i{\text{ - th}}$ agent. Here $\Delta A_{i} = DF_{i} E$, where D and E are known matrices of appropriate dimension which characterize the structure of the uncertainty. $F_{i}$ is an uncertain matrix satisfying $F_{i}^{T} F_{i} \le \rho^{2} I$ and $\rho > 0$ is a given constant.

Here, a directed graph ${\mathcal{G}}$ is used to model the communication topologies. The following assumption is introduced.

Assumption 1

The directed graph ${\mathcal{G}}$ has a directed spanning tree and there is at least one root node has a loop.

Based on this assumption, following distributed static consensus controller is proposed

$$ u_{i} = cK\left( {\sum\limits_{j = 1}^{N} {a_{ij} \left( {x_{j} - x_{i} } \right)} - g_{i} x_{i} } \right), $$

(2)

where $K \in {\mathbf{\mathbb{R}}}^{p \times n}$ is the feedback matrix to be designed, c is the coupling strength to be selected, $a_{ij}$ is the element of the adjacency matrix of the communication topology. $g_{i} = 1$ means that agent i knows its own absolute state information, $g_{i} = 0$, otherwise. Then, according to Assumption 1, $\sum\nolimits_{i = 1}^{N} {g_{i} } \ne 0$.

Then, the closed-loop system dynamics of (1) using the controller (2) is

$$ \begin{array}{*{20}c} \begin{aligned} \dot{x} & = \left( {I_{N} \otimes A - c\left( {{\mathcal{L}} + G} \right) \otimes BK} \right)x + \left( {I_{N} \otimes D} \right)F\left( {I_{N} \otimes E} \right)x \\ & = \left( {I_{N} \otimes A - c\left( {{\mathcal{L}} + G} \right) \otimes BK + \left( {I_{N} \otimes D} \right)F\left( {I_{N} \otimes E} \right)} \right)x \\ \end{aligned} \\ \end{array} , $$

(3)

where $x = [x_{1}^{T} ,x_{2}^{T} , \ldots ,x_{N}^{T} ]^{T}$, $F = diag\left( {F_{1} ,\ldots,F_{N} } \right)$, ${\mathcal{L}} \in {\mathbf{\mathbb{R}}}^{N \times N}$ is the Laplacian matrix of the graph, $G = diag\left\{ {g_{1} ,g_{2} ,\ldots,g_{N} } \right\}$.

Lemma 3

Zero is a simple eigenvalue of ${\mathcal{L}}$ and all the other nonzero eigenvalues have positive real parts if and only if the graph has a directed spanning tree [7]. Furthermore, if there is a root agent i such that $g_{i} \ne 0$, $G = diag\left\{ {g_{1} ,g_{2} ,\ldots,g_{N} } \right\}$, then $\text{Re} \left( {\lambda \left( {{\mathcal{L}} + G} \right)} \right) > 0$.

Lemma 4

Under the Assumption 1, there exist a positive definite matrix Q and a positive scalar α such that

$$ \left( {{\mathcal{L}} + G} \right)^{T} Q + Q\left( {{\mathcal{L}} + G} \right) > \alpha Q, $$

(4)

where $0 < \alpha < 2\hbox{min} \left\{ {\text{Re} \left( {\lambda \left( {{\mathcal{L}} + G} \right)} \right)} \right\}$.

Proof

According to Lemma 3, one can obtain that $\text{Re} \left( {\lambda \left( {{\mathcal{L}} + G} \right)} \right) > 0$. Then $\text{Re} \left( {\lambda \left( {{\mathcal{L}} + G - \frac{1}{2}\alpha I} \right)} \right) > 0$. Thus, there exist a positive definite matrix Q such that $\left( {{\mathcal{L}} + G - \frac{1}{2}\alpha I} \right)^{T} Q + Q\left( {{\mathcal{L}} + G - \frac{1}{2}\alpha I} \right) > 0$. This completes the proof.

Definition 1.

The system (1) with $u_{i} = 0$ is quadratically stable if there exists a common Lyapunov matrix $P > 0$ such that for all admissible uncertainty $\Delta A_{i}$

$$ \left( {A +\Delta A_{i} } \right)^{T} P + P\left( {A +\Delta A_{i} } \right) < 0. $$

Lemma 5

(Small gain theorem) The system (1) with $u_{i} = 0$ is quadratically stable for all admissible uncertainties $F_{i}$ satisfying $F_{i}^{T} F_{i} \le \rho^{2} I$ if and only if A is Hurwitz and $\left\| {E\left( {sI - A} \right)^{ - 1} D} \right\|_{\infty } < \frac{1}{\rho }$.

Based on Lemma 5, following conclusion is introduced.

Theorem 1.

Suppose that the quadratically stable problem of multi-agent system (1) with the controller (2) is solved if there exists a positive definite matrix P such that

$$ \left[ {\begin{array}{*{20}c} {A^{T} P + PA - c\alpha PBB^{T} P} & {PD} & {E^{T} } \\ {D^{T} P} & {\frac{ - 1}{{\rho^{2} \varphi_{1} }}I} & 0 \\ E & 0 & { - \varphi_{2} } \\ \end{array} } \right] < 0, $$

(5)

where $\varphi_{1} = \hbox{max} \left\{ {\lambda \left( Q \right)} \right\}$, $\varphi_{2} = \hbox{min} \left\{ {\lambda \left( Q \right)} \right\}$. Q is a positive definite solution of (4) $0 < \alpha < 2\hbox{min} \left\{ {\text{Re} \left( {\lambda \left( {{\mathcal{L}} + G} \right)} \right)} \right\}$ and the feedback matrix is designed as $K = B^{T} P$.

Proof

According to Lemma 5, system (3) with is quadratically stable if and only if matrix $I_{N} \otimes A - c\left( {{\mathcal{L}} + G} \right) \otimes BK$ is Hurwitz and

$$ \left\| {\left( {I_{N} \otimes E} \right)\left( {sI - \left( {I_{N} \otimes A - c\left( {{\mathcal{L}} + G} \right) \otimes BK} \right)} \right)^{ - 1} \left( {I_{N} \otimes D} \right)} \right\|_{\infty } < \frac{1}{\rho }. $$

According to bounded real lemma, if there exists a positive definite matrix $\bar{P}$ such that

$$ \bar{A}^{T} \bar{P} + \bar{P}\bar{A} + \bar{C}^{T} \bar{C} + \rho^{2} \bar{P}\bar{B}\bar{B}^{T} \bar{P} < 0, $$

(6)

where $\bar{A}{ = }I_{N} \otimes A - c\left( {{\mathcal{L}} + G} \right) \otimes BK$, $\bar{B} = I_{N} \otimes D$, $\bar{C} = I_{N} \otimes E$, system (3) is quadratically stable.

Here, we chose $\bar{P} = Q \otimes P$ and $K = B^{T} P$, where $Q > 0$ is a solution of (4), $P > 0$ is a solution of the LMI (5). Then

$$ \begin{array}{*{20}c} \begin{aligned} & \bar{A}^{T} \bar{P} + \bar{P}\bar{A} + \bar{C}^{T} \bar{C} + \rho^{2} \bar{P}\bar{B}\bar{B}^{T} \bar{P} \\ & = \left( {Q \otimes \left( {A^{T} P + PA} \right)} \right) - c\left( {\left( {{\mathcal{L}} + G} \right)^{T} Q + Q\left( {{\mathcal{L}} + G} \right)} \right) \otimes PBB^{T} P \\ & \quad + I_{N} \otimes E^{T} E + \rho^{2} \left( {Q^{2} \otimes PDD^{T} P} \right) \\ \end{aligned} \\ \end{array} . $$

(7)

From Lemma 4, one has

$$ \left( {\left( {{\mathcal{L}} + G} \right)^{T} Q + Q\left( {{\mathcal{L}} + G} \right)} \right) \otimes PBB^{T} P > \alpha Q \otimes PBB^{T} P, $$

(8)

where $0 < \alpha < 2\hbox{min} \left\{ {\text{Re} \left( {\lambda \left( {{\mathcal{L}} + G} \right)} \right)} \right\}$.

It then follow from (7) using (8), one has

$$ \begin{aligned} & \bar{A}^{T} \bar{P} + \bar{P}\bar{A} + \bar{C}^{T} \bar{C} + \rho^{2} \bar{P}\bar{B}\bar{B}^{T} \bar{P} \\ & < \left( {Q \otimes \left( {A^{T} P + PA} \right)} \right) - c\alpha Q \otimes PBB^{T} P + I_{N} \otimes E^{T} E + \rho^{2} \left( {Q^{2} \otimes PDD^{T} P} \right) \\ \end{aligned} $$

(9)

Since $Q < \varphi_{1} I{}_{N}$ and $Q > \varphi_{2} I{}_{N}$ where $\varphi_{1} = \hbox{max} \left\{ {\lambda \left( Q \right)} \right\}$, $\varphi_{2} = \hbox{min} \left\{ {\lambda \left( Q \right)} \right\}$, one can obtain that

$$ \begin{aligned} & \bar{A}^{T} \bar{P} + \bar{P}\bar{A} + \bar{C}^{T} \bar{C} + \rho^{2} \bar{P}\bar{B}\bar{B}^{T} \bar{P} \\ & < \left( {Q \otimes \left( {A^{T} P + PA} \right)} \right) - c\alpha Q \otimes PBB^{T} P + \frac{1}{{\varphi_{2} }}Q \otimes E^{T} E + \rho^{2} \varphi_{1} \left( {Q \otimes PDD^{T} P} \right) \\ & = Q \otimes \left( {A^{T} P + PA - c\alpha PBB^{T} P + \frac{1}{{\varphi_{2} }}E^{T} E + \rho^{2} \varphi_{1} PDD^{T} P} \right) \\ \end{aligned} $$

According to Schur complement lemma, inequality (5) implies that (6) hold. Thus, the quadratically stable problem for system (1) is solved.

Remark 1

When the topology is undirected, the graph Laplacian matrix ${\mathcal{L}}$ of undirected topology is symmetric positive semidefinite. Thus the matrix ${\mathcal{L}} + G$ is diagonalizable and similarity transformation can be performed. These properties facilitated the derivation greatly. The quadratically stable problem of networked system can be converted into the quadratically stable problems of N individual systems associate with N eigenvalues of ${\mathcal{L}} + G$. As for the directed topology, the Laplacian matrix is not symmetric. Thus, the similarity transformation employed in [15, 16] is not applicable. Here, based on Lemma 4 and the properly designed matrix $\bar{P}$, the quadratically stable problem of networked system is solved using bounded real lemma directly.

4 Examples

In this section, we provide an example to illustrate the effectiveness of the above theoretical results. A multi-agent system consisting four agents is considered. The system matrices are defined as

$$ A = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - 2.8} & 0 \\ \end{array} } \right],B = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right],D = \left[ {\begin{array}{*{20}c} 0 \\ { - 0.4} \\ \end{array} } \right],E = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]. $$

The uncertainty matrices are chosen as $\left| {F_{i} } \right| < 10$.

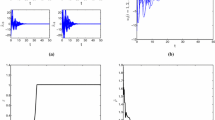
The directed communication topology is given in Fig. 1. Clearly, the communication topology has a directed spanning tree. Agent 1 is the root and agent 1 can obtain its own absolute state information. The Laplacian matrix of communication topology is

Fig. 1

Communication topology

$$ {\mathcal{L}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 \\ { - 1} & 1 & 0 & 0 & 0 \\ 0 & { - 1} & 1 & 0 & 0 \\ 0 & 0 & { - 1} & 1 & 0 \\ { - 1} & 0 & 0 & 0 & 1 \\ \end{array} } \right], $$

and $G = diag\left\{ {1,0,0,0,0} \right\}$. The real part of the smallest eigenvalue of ${\mathcal{L}} + G$ is 1. According to Lemma 5, we set $\alpha = 00 . 5$ and get a feasible solution of (4)

$$ Q = \left[ {\begin{array}{*{20}c} {1.3806} & {0.2799} & { - 0.0717} & { - 0.0920} & {0.2218} \\ {0.2799} & {0.9727} & {0.2399} & { - 0.0612} & { - 0.2111} \\ { - 0.0717} & {0.2399} & {0.8115} & {0.1455} & { - 0.1232} \\ { - 0.0920} & { - 0.0612} & {0.1455} & {0.6511} & { - 0.0498} \\ {0.2218} & { - 0.2111} & { - 0.1232} & { - 0.0498} & {0.7751} \\ \end{array} } \right]. $$

Thus, $\varphi_{1} = 1.5539$, $\varphi_{2} = 0.4402$. Let $c = 80$, solving the inequality (5), we get a feasible solution $P = \left[ {\begin{array}{*{20}c} {0.9436} & { - 1.2799} \\ { - 1.2799} & {4.2009} \\ \end{array} } \right]$. According to Theorem 1, the feedback matrix can be chosen as $K = \left[ {\begin{array}{*{20}c} {0.5503} & {0.4057} \\ \end{array}} \right]$. Fig. 2 show the states trajectories of all the agents. It is shown that states of all the agents converge to zero.

Fig. 2

Trajectories of the states of all agents

5 Conclusions

In this paper, the distributed robust control problem of uncertain multi-agent systems have been investigated under directed communication topologies which have a spanning tree. Distributed robust controller has been constructed based on relative states information of neighbor agents. Sufficient conditions have been obtained using bounded real lemma.