Sub-shock Formation in Reacting Gas Mixtures

Abstract

The shock-wave structure problem is investigated for a gas mixture of four species, undergoing a reversible bimolecular reaction, modelled by a 10 moment Grad closure of reactive Boltzmann equations. The presence of jump discontinuities within the shock structure solution is discussed, the supersonic regime is characterized, and the critical values of Mach number allowing the formation of sub-shocks in the field variables of one or more components of the mixture are pointed out.

1 Introduction

Many recent papers, as among others [2, 5, 6, 12, 17, 18], show that the behaviour of multi-temperature models for gas mixtures exhibits very interesting features in the context of the shock wave structure problems.

For hyperbolic systems of both conservation and balance laws, compatible with an entropy principle, it is well-stated [7, 8, 21] that a continuous solution of the shock wave structure problem, between two equilibrium configurations, can not propagate with a speed, s, greater than the maximum characteristic velocity of the system, evaluated in the unperturbed state. Despite many efforts in this direction, the continuity of wave fronts propagating below this threshold is still an open problem, in the sense that, to authors’ knowledge, no rigorous results are available. Many references on shock waves propagation in a single gas may be found in the literature, among which we mention [1, 9, 22].

For what concerns gaseous mixtures, shock structure solutions have been recently investigated for some specific problems, both from the numerical and the analytical points of view. In [17, 18] numerical examples, compared with experimental data, are shown for inert binary mixtures described in the framework of Extended Thermodynamics [19] at Euler level. On the other hand, in [15, 16, 20], the analysis is developed starting from suitable kinetic models of Boltzmann or BGK type.

For what concerns hydrodynamic closures derived from kinetic Boltzmann equations, a multi-temperature Euler system for an inert binary mixture of monoatomic gases has been rigorously dealt with in [6], in which the role in the continuity of travelling waves played by each singularity manifold related to each component of the mixture is pointed out, and numerical tests show the presence of one or two sub-shocks within the wave front for suitable values of the Mach number. In [5], the steady shock problem is faced for a reactive gas of four monoatomic components undergoing a reversible bimolecular reaction, described by a multi-temperature (and one-velocity) Euler closure of the reactive Boltzmann equations. The existence of discontinuous solutions is shown by numerical simulations in which the variables describing each component may suffer a jump. For the same reacting mixture, but modelled by a 13-moment Grad closure of the reactive Boltzmann equations [3, 4, 14], the discontinuous shock structure solutions are investigated in [12], and it is pointed out that, analogously to the simpler systems studied in [5, 6], each component may generate a sub-shock, on its own variables. Each component, in fact, defines its own singularity sub-manifold in the phase space across which only its own variables suffer a jump discontinuity, if the two (upstream and downstream) equilibria lie on opposite sides with respect to such sub-manifold. The role of the maximum characteristic velocities relevant to each species in the sub-shock formation is also discussed.

In [11], for an inert mixture of multi-velocity, multi-temperature Euler gases in the context of Extended Thermodynamics, the long-time behaviour of the solution of the Riemann problem is studied in order to characterize the corresponding shock structure, and the Rankine–Hugoniot conditions are used to identify each sub-shock within the wave front, confirming the results in [6].

Very recently, in [2], a 10-moment Grad closure of the reactive Boltzmann equations is used to describe a binary mixture of inert monoatomic gases, and the shock wave structure problem is faced within the whole hierarchy of hyperbolic subsystems of balance laws: Grad 10-moments equations, the multi-temperature Euler description recovered assuming vanishing viscous stress tensors (restoring the studies in [6]), and the Euler (single velocity and single temperature) equilibrium sub-system of the hierarchy. The complete description of possible solutions, exhibiting up to two sub-shocks, is given and the explicit expressions of all critical Mach numbers, as well as their admissibility conditions, are deduced in terms of particle masses of the species and of the unperturbed equilibrium state.

The present paper faces the problem of sub-shock formation in 10-moment Grad equations for the more interesting and realistic case of reactive gases, again for the same four-species mixture with the same chemistry considered in [5] and [12], in order to improve the preliminary available results. From the physical point of view, the 10-moment closure suffers the heavy drawback of neglecting the heat flux effects occurring in the evolution. However, with respect to the more realistic 13-moment approximation, it has the advantage of providing explicit expressions for all the involved quantities in terms of a field vector of lower dimension, as well as a wider hyperbolicity region. Therefore, since this paper represents a first attempt of handling chemical processes, the aim of highlighting their effects on the shock wave structure solutions, minimizing at the same time the both analytical and numerical difficulties, may justify the choice of confining again our investigation in the framework of the 10-moment level description adopted in [2], despite the loss of physical consistency. The extensions to the classical 13-moment Grad closure, including the evolution of heat flux vectors, are considered in forthcoming papers. Moreover, from the mathematical point of view, the presence of the reaction (involving exchanges of mass and internal energy in the transient, and imposing the mass action law of chemistry at equilibrium) does not allow to prove all the huge variety of features deduced in [2] for the inert mixture, which is here recovered in the limit of vanishing chemical bond energy. In spite of the drawback of handling the implicit function introduced by the law of mass action defining the chemical equilibrium, we are able to show the effects of the chemistry on the solutions. In order to stress the role of the chemistry, the comparison with the corresponding inert case is carried out. The presence of the reaction modifies the characteristic speeds of the system and of its equilibrium subsystem, which differs from the classical Euler equations establishing the equilibrium subsystem of the inert gas. It will be shown that this situation translates into a change in the supersonic regime, that for the inert gas is characterized by Mach numbers greater than 1, while in the present reactive frame the lower bound of supersonic flows is decreased below 1.

The paper is organized as follows. In Sect. 2 we briefly present the model, its equilibrium subsystem, and all the characteristic speeds involved in our analysis. In Sect. 3 the shock wave structure problem is studied for both inert and reactive gases, and the possible analytical investigation (allowed by the involved implicit function) on the admissible critical Mach numbers is presented. Some results on the existence and uniqueness of a perturbed equilibrium state defined by the unperturbed state are also given. Finally, in Sect. 4, a particular reaction is chosen in order to characterize the different ranges of all possible admitted shock structures, and some concluding remarks are discussed.

2 Governing Equations

Let us consider a 1-D 10-moment approximation of Grad type for a reactive mixture of gases undergoing a reversible bimolecular reaction

$$\begin{aligned} 1+2\rightleftharpoons 3+4. \end{aligned}$$

(1)

Under the hypothesis of negligible heat fluxes, imposed on the 13-moment Grad description proposed in [3, 4], the sixteen macroscopic field variables are species densities $n_i$, mass velocities $u_i$, species temperatures $T_i$ and stress deviators $\sigma _i$, for $i=1,2,3,4$, and they define the global quantities through the relationships

$$\begin{aligned} n&=\sum _{i=1}^4n_i,\qquad \rho =\sum _{i=1}^4\rho _i=\sum _{i=1}^4m_in_i,\qquad \rho u=\sum _{i=1}^4\rho _i u_i,\end{aligned}$$

(2)

$$\begin{aligned} nk_BT&=\sum _{i=1}^4n_ik_BT_i+ \frac{1}{3}\sum _{i=1}^4\rho _i\left( u_i^2-u^2\right) ,\qquad \sigma =\sum _{i=1}^4\sigma _i+ \frac{2}{3}\sum _{i=1}^4\rho _i\left( u_i^2-u^2\right) , \end{aligned}$$

(3)

where $m_i$ is the particle mass for ith species and $k_B$ is the Boltzmann constant.

In the vanishing heat flux limit of 13-moments Grad equations [3, 4], the hyperbolic system of partial differential equations, in conservative form, reads as

$$\begin{aligned}&\partial _t n_i+\partial _x\left( n_iu_i\right) =Q_i,\end{aligned}$$

(4)

$$\begin{aligned}&\partial _t \left( m_in_iu_i\right) +\partial _x\left( m_in_iu_i^2+n_ik_BT_i\right) =R_i+m_iu_iQ_i,\end{aligned}$$

(5)

$$\begin{aligned}&\partial _t\left( \frac{1}{2}m_in_iu_i^2+\frac{3}{2}n_ik_BT_i\right) +\partial _x\left[ \left( \frac{1}{2}m_in_iu_i^2+\frac{5}{2}n_ik_BT_i+\sigma _i\right) u_i\right] =S_i+u_iR_i\nonumber \\&\qquad \ +\left( \frac{1}{2}m_iu_i^2+\frac{3}{2}k_BT_i\right) Q_i,\end{aligned}$$

(6)

$$\begin{aligned}&\partial _t\left( \frac{2}{3}m_in_iu_i^2+\sigma _i\right) +\partial _x\left[ \left( \frac{2}{3}m_in_iu_i^2+\frac{4}{3}n_ik_BT_i+\frac{7}{3}\sigma _i\right) u_i\right] =V_i+\frac{4}{3}u_iR_i\nonumber \\&\qquad \ +\frac{2}{3}m_iu_i^2Q_i, \end{aligned}$$

(7)

where

$$\begin{aligned} Q_i&= \frac{2\nu _{12}^{34}l_i}{\sqrt{\pi }}\left[ n_3n_4\left( \frac{m_{12}}{m_{34}}\right) ^\frac{3}{2} \exp \left( \frac{\Delta E}{k_BT}\right) -n_1n_2\right] \Gamma \left( \frac{3}{2},\frac{\Delta E}{k_BT}\right) \end{aligned}$$

(8)

$$\begin{aligned} R_i&= n_i\sum _{j=1}^4\nu _{1ij}m_{ij}n_j\left( u_j-u_i\right) -m_i\left( u_i-u\right) Q_i\end{aligned}$$

(9)

$$\begin{aligned} S_i&= 2n_i\sum _{j=1}^4\frac{\nu _{1ij}m_{ij}}{m_i+m_j}n_j\left[ \frac{3}{2}k_B\left( T_j-T_i\right) +\frac{1}{2}m_j\left( u_j-u_i\right) ^2\right] \nonumber \\&+\left[ \frac{3}{2}\frac{m_i}{m}k_BT-\frac{3}{2}\left( 1-l_i\right) \Delta E\frac{m-m_i}{m}-\frac{3}{2}k_BT_i+\frac{1}{2}m_i\left( u_i-u\right) ^2\right] Q_i\nonumber \\&+\frac{2\nu _{12}^{34}l_ik_BT}{\sqrt{\pi }}\left[ n_3n_4\left( \frac{m_{12}}{m_{34}}\right) ^\frac{3}{2} \exp \left( \frac{\Delta E}{k_BT}\right) -n_1n_2\right] \frac{m-m_i}{m}\Gamma \left( \frac{5}{2},\frac{\Delta E}{k_BT}\right) \end{aligned}$$

(10)

$$\begin{aligned} V_i&=\frac{2}{3} m_i\left( u_i-u\right) ^2Q_i +\sum _{j=1}^4\frac{2\nu _{1ij}m_{ij}}{m_i+m_j}\left[ \frac{2}{3}m_jn_jn_i\left( u_j-u_i\right) ^2 +n_i\sigma _j-n_j\sigma _i\right] \nonumber \\&-\sum _{j=1}^4\frac{3\nu _{2ij}m_j}{2\left( m_i+m_j\right) ^2}\left[ \frac{2}{3}m_im_jn_in_j\left( u_j-u_i\right) ^2 +m_in_i\sigma _j+m_jn_j\sigma _i\right] \end{aligned}$$

(11)

and $l_1=l_2=-l_3=-l_4=1$, $m=m_1+m_2=m_3+m_4$, $m_{ij}=m_im_j/(m_i + m_j)$, $\Delta E > 0$ is the activation energy for the endothermic reaction $1+2\rightarrow 3+4$, $\nu _{1ij}$ and $\nu _{2ij}$ are suitably weighted elastic collision frequencies and $\nu _{12}^{34}$ is the chemical interaction frequency.

An equilibrium state of the system (4)–(7) is characterized by the so-called mass action law, and by a unique mean velocity and a unique temperature and by vanishing stress deviators

$$\begin{aligned}&n_1n_2=n_3n_4\left( \frac{m_{12}}{m_{34}}\right) ^\frac{3}{2} \exp \left( \frac{\Delta E}{k_BT}\right) ,\end{aligned}$$

(12)

$$\begin{aligned}&u_i=u,\qquad T_i=T, \qquad \sigma _i=\sigma =0,\qquad i=1,2,3,4. \end{aligned}$$

(13)

The conservation equations of total mass, momentum and energy, together with two independent partial conservation equations for number densities through the chemical reaction, represent the equilibrium sub-system, that is

$$\begin{aligned}&\partial _t\left( n_1+n_\ell \right) +\partial _x\left[ \left( n_1+n_\ell \right) u\right] =0,\qquad \ell =3,4,\end{aligned}$$

(14)

$$\begin{aligned}&\partial _t\rho +\partial _x\left( \rho u\right) =0,\end{aligned}$$

(15)

$$\begin{aligned}&\partial _t \left( \rho u\right) +\partial _x\left( \rho u^2+nk_BT\right) =0,\end{aligned}$$

(16)

$$\begin{aligned}&\partial _t\left( \frac{1}{2}\rho u^2+\frac{3}{2}nk_BT-\Delta En_1\right) +\partial _x\left[ \left( \frac{1}{2}\rho u^2+\frac{5}{2}nk_BT-\Delta En_1\right) u\right] =0, \end{aligned}$$

(17)

coupled with the additional constraint due to the chemical equilibrium condition imposed by the mass action law (12).

To conclude this section, let us point out that the characteristic speeds of system (4)–(7) are

$$\begin{aligned} u_i-\sqrt{\frac{3\left( n_ik_BT_i+\sigma _i\right) }{m_in_i}}, \qquad u_i,\qquad u_i+\sqrt{\frac{3\left( n_ik_BT_i+\sigma _i\right) }{m_in_i}}. \end{aligned}$$

(18)

Only the greater ones can be involved in the problem of sub-shock formation, denoted by

$$\begin{aligned} \lambda _i=u_i+\sqrt{\frac{3\left( n_ik_BT_i+\sigma _i\right) }{m_in_i}}, \end{aligned}$$

(19)

together with the highest characteristic velocity of the equilibrium sub-system [10]

$$\begin{aligned} \mu =u+\sqrt{\frac{5nk_BT}{3\rho }\left( 1-\frac{2}{5\mathcal{C}}\right) }, \end{aligned}$$

(20)

where

$$\begin{aligned} \mathcal{C}=1+\frac{3n k_B^2T^2}{2\Delta E^2}\left( \frac{1}{n_1}+\frac{1}{n_2}+\frac{1}{n_3}+\frac{1}{n_4}\right) , \end{aligned}$$

(21)

which, suitably evaluated, represents the lower bound of the wave front speeds in such kind of problem. Moreover, notice that

$$\mu <\mu ^{Euler}=u+\sqrt{\frac{5nk_BT}{3\rho }},$$

meaning that the chemical reaction slows down the maximum characteristic speed of the equilibrium sub-system, which is now smaller than the one for a single Euler gas, $\mu ^{Euler}$, and this means an enlargement of the supersonic regime. Let us finally stress that in the limit as $\Delta E \rightarrow 0$, then $\mathcal{C}\rightarrow \infty$, and $\mu \rightarrow \mu ^{Euler}$.

3 Shock-Wave Structure Solutions

As well-known, a shock-wave structure solution is a function $\mathbf {u}\left( \varphi \right)$ of the variable $\varphi =x-st$, $s > 0$ constant, connecting two equilibrium states, $\mathbf {u}_+$ and $\mathbf {u}_{-}$, of the system

$$\begin{aligned} \lim _{\varphi \rightarrow \pm \infty }\mathbf {u}\left( \varphi \right) =\mathbf {u}_\pm , \qquad \lim _{\varphi \rightarrow \pm \infty }\frac{d\mathbf {u}}{d\varphi }\left( \varphi \right) =0 \end{aligned}$$

(22)

so that the wave propagates, at constant velocity s, into the fixed unperturbed downstream equilibrium $\mathbf {u}_+$. As usual in such kind of problems, let us introduce the relative velocities $v_i$ and Mach number $M_+$ as follows

$$\begin{aligned} v_i=s-u_i,\qquad M_+=\frac{s-u_+}{c_+}, \qquad c_+^2=\frac{5n_+k_BT_+}{3\rho _+}, \end{aligned}$$

(23)

where $c_+$ is the classical Euler unperturbed sound speed and

$$\begin{aligned} v_+=s-u_+=c_+M_+=v_{i+},\qquad \forall \,i=1,2,3,4. \end{aligned}$$

(24)

In the reference frame co-moving with the shock front, the set of balance equations (4)–(7) yields the following system of ODEs

$$\begin{aligned}&\frac{d}{d\varphi }\left( n_iv_i\right) =-Q_i\end{aligned}$$

(25)

$$\begin{aligned}&\frac{d}{d\varphi }\left( m_in_iv_i^2+n_ik_BT_i+\sigma _i\right) =\Sigma _{v_i}\end{aligned}$$

(26)

$$\begin{aligned}&\frac{d}{d\varphi }\left[ \left( \frac{1}{2}m_in_iv_i^2+\frac{5}{2}n_ik_BT_i+\sigma _i\right) v_i\right] =-\Sigma _{T_i}\end{aligned}$$

(27)

$$\begin{aligned}&\frac{d}{d\varphi }\left[ \left( \frac{2}{3}m_in_iv_i^2+\frac{4}{3}n_ik_BT_i+\frac{7}{3}\sigma _i\right) v_i\right] =-\Sigma _{\sigma _i} \end{aligned}$$

(28)

where

$$\begin{aligned} \Sigma _{v_i}= & {} R_i-m_iv_iQ_i,\end{aligned}$$

(29)

$$\begin{aligned} \Sigma _{T_i}= & {} S_i-v_iR_i+\left( \frac{1}{2}m_iv_i^2+\frac{3}{2}k_BT_i\right) Q_i,\end{aligned}$$

(30)

$$\begin{aligned} \Sigma _{\sigma _i}= & {} V_i-\frac{4}{3}v_iR_i+\frac{2}{3}m_iv_i^2Q_i, \end{aligned}$$

(31)

and $Q_i$, $R_i$, $S_i$ and $V_i$ have been properly rewritten in terms of the relative velocities $v_i$.

The equilibrium state $\mathbf {u}_{-}$ is related to the unperturbed state $\mathbf {u}_+$ through the Rankine–Hugoniot conditions applied to the equilibrium sub-system (14)–(17), yielding, besides the trivial case $\mathbf {u}_{-}=\mathbf {u}_+$,

$$\begin{aligned} n_{i-}= & {} n_{i+}\frac{c_+M_+}{v_{-}}+l_iN\left( \mathbf {u}_+,M_+;v_{-}\right) ,\qquad i=1,2,3,4\end{aligned}$$

(32)

$$\begin{aligned} n_{-}= & {} n_+\frac{c_+M_+}{v_{-}},\qquad \rho _{-}=\rho _+\frac{c_+M_+}{v_{-}},\end{aligned}$$

(33)

$$\begin{aligned} T_{-}= & {} T_+\frac{v_{-}}{c_+M_+}\left[ 1+\frac{5M_+}{3c_+}\left( c_+M_+-v_{-}\right) \right] , \end{aligned}$$

(34)

where

$$\begin{aligned} N\left( \mathbf {u}_+,M_+;v_{-}\right) =\frac{\rho _+c_+}{2\Delta E v_{-}}\left( v_{-}-c_+M_+\right) \left[ c_+\left( M_+^2+3\right) -4M_+v_{-}\right] , \end{aligned}$$

(35)

and $v_{-}$ is implicitly defined by the mass action law (12) imposed on $n_{i-}$ and $T_{-}$ provided in (32) and (34).

As pointed out in [12], the presence of a chemical reaction influences the upstream equilibrium, whose existence and uniqueness have now to be verified, since it has to be univocally determined for fixed unperturbed equilibrium and Mach number. It now differs from the one recovered in the inert case [2], coinciding with the classical one of the Euler equations, given by

$$\begin{aligned} n_{i-}^{inert}= & {} n_{i+}\frac{4M_+^2}{M_+^2+3},\qquad n_{-}^{inert}=n_+\frac{4M_+^2}{M_+^2+3},\qquad \rho _{-}^{inert}=\rho _+\frac{4M_+^2}{M_+^2+3},\end{aligned}$$

(36)

$$\begin{aligned} v_{-}^{inert}= & {} c_+\frac{M_+^2+3}{4M_+}, \qquad T_{-}^{inert}=T_+\frac{\left( M_+^2+3\right) \left( 5M_+^2-1\right) }{16M_+^2}. \end{aligned}$$

(37)

Let us observe that relations (32)–(35) coincide with the classical ones (36)–(37), if, and only if, $N\left( \mathbf {u}_+,M_+;v_{-}\right) =0$, which, besides the trivial case $v_{-}=c_+M_+$ corresponding to $\mathbf {u}_{-}=\mathbf {u}_+$, means that $v_{-}$ has to be given by (37).

The physical constraints due to positivity of species number densities and mixture temperature of the upstream equilibrium given by (32)–(35) give some ranges of admissible values for the upstream velocity (different from $v_+=c_+M_+$), that from now on will be denoted as $v_{-}^r$ (and the corresponding upstream state will be set $\mathbf{u}_{-}^r$). To be more precise, the positivity of temperature $T_{-}$ yields the condition $v_{-}^r\in I_T$, with

$$I_T:=\left( 0,c_+\frac{5M_+^2+3}{5M_+}\right) ,$$

whereas, denoting

$$\begin{aligned} \xi _k^\pm= & {} \frac{\rho _+c_+\left( 5M_+^2+3\right) \pm \sqrt{9\rho _+^2c_+^2\left( M_+^2-1\right) ^2+32\Delta E\,n_{k+}\rho _+M_+^2}}{8\rho _+M_+},\qquad k=1,2,\\ \eta _\ell ^\pm= & {} \frac{\rho _+c_+\left( 5M_+^2+3\right) \pm \sqrt{9\rho _+^2c_+^2\left( M_+^2-1\right) ^2-32\Delta E\,n_{\ell +}\rho _+M_+^2}}{8\rho _+M_+},\qquad \ell =3,4, \end{aligned}$$

the positivity of species number densities gives the constraint $v_{-}^r\in I_n$, where, if $\eta _\ell ^\pm \in \mathbb {R}$,

$$\begin{aligned} I_n:=\left( \max \left\{ \xi _1^-,\xi _2^-\right\} ,\min \left\{ \eta _3^-,\eta _4^-\right\} \right) \cup \left( \max \left\{ \eta _3^+,\eta _4^+\right\} ,\min \left\{ \xi _1^+,\xi _2^+\right\} \right) , \end{aligned}$$

which, if $\eta _\ell ^\pm \in \mathbb {C}$, reduces to

$$I_n=\left( \max \left\{ \xi _1^-,\xi _2^-\right\} ,\min \left\{ \xi _1^+,\xi _2^+\right\} \right) .$$

This feature has already been investigated numerically in [12] in the context of an analogous reactive gas mixture described at 13 moment Grad closure, in which the same equilibrium subsystem is obviously admitted.

3.1 Existence and Uniqueness of Upstream Equilibrium State

In order to prove the existence and uniqueness of a physical solution of the mass action law (12) as equation in $v_{-}$, let us denote

$$\begin{aligned} \mathscr {F}\left( v_{-}\right) :=\bar{m}\left( n_{3-}v_{-}\right) \left( n_{4-}v_{-}\right) \exp \left( \frac{\Delta E}{k_BT_{-}}\right) -\left( n_{1-}v_{-}\right) \left( n_{2-}v_{-}\right) =0 \end{aligned}$$

(38)

where $\bar{m}=\left( m_{12}/m_{34}\right) ^{3/2}$ and $n_{i-}$ and $T_{-}$ are given by (32)–(35). Its derivative can be written as

$$\begin{aligned} \mathscr {F}^\prime \left( v_{-}\right)= & {} -\mathscr {M}\left( v_{-}\right) \left[ \bar{m}\exp \left( \frac{\Delta E}{k_BT_{-}}\right) \left( n_{3-}v_{-}+n_{4-}v_{-}\right) +n_{1-}v_{-}+n_{2-}v_{-}\right] \nonumber \\- & {} \bar{m}\left( n_{3-}v_{-}\right) \left( n_{4-}v_{-}\right) \exp \left( \frac{\Delta E}{k_BT_{-}}\right) \frac{\Delta E}{k_BT_{-}^2}\,\mathscr {T}\left( v_{-}\right) \end{aligned}$$

(39)

where

$$\begin{aligned}&\mathscr {M}\left( v_{-}\right) :=l_i\frac{d}{dv_{-}}\left( n_{i-}v_{-}\right) =\frac{\rho _+c_+}{2\Delta E}\left[ c_+\left( 5M_+^2+3\right) -8M_+v_{-}\right] ,\end{aligned}$$

(40)

$$\begin{aligned}&\mathscr {T}\left( v_{-}\right) :=\frac{dT_{-}}{dv_{-}}=\frac{T_+}{3c_+^2M_+}\left[ c_+\left( 5M_+^2+3\right) -10M_+v_{-}\right] . \end{aligned}$$

(41)

It can be immediately noticed that $\mathscr {F}\left( v_{-}\right)$ is decreasing for

$$0<v_{-}<c_+\frac{5M_+^2+3}{10M_+}$$

and $\mathscr {F}\left( v_{-}\right)$ is increasing for

$$\begin{aligned} c_+\frac{5M_+^2+3}{8M_+}<v_{-}<c_+\frac{5M_+^2+3}{5M_+}. \end{aligned}$$

Since $v_+=c_+M_+$, root of (38), satisfies

$$\begin{aligned} c_+\frac{5M_+^2+3}{8M_+}<v_+<c_+\frac{5M_+^2+3}{5M_+}, \end{aligned}$$

(42)

for all $M_+>1$, and in such interval $\mathscr {F}$ is increasing, an admissible root $v_{-}^r$ of (38), different from $v_+$, must be

$$v_{-}^r<c_+\frac{5M_+^2+3}{8M_+}.$$

Let us also point out that for all $M_+>1$

$$\xi _k^-<v_{-}^{inert}<\eta _\ell ^-,\qquad \eta _\ell ^+<v_+<\xi _k^+,$$

and

$$v_{-}^{inert}<c_+\frac{5M_+^2+3}{8M_+}.$$

By noticing that

$$\begin{aligned}&\mathscr {F}\left( \xi _k^\pm \right) =\bar{m}\left( n_{3-}\xi _k^\pm \right) \left( n_{4-}\xi _k^\pm \right) \exp \left( \frac{\Delta E}{k_B T_{-}}\right)>0,\qquad k=1,2,\\&\mathscr {F}\left( v_{-}^{inert}\right) <\bar{m}\left( n_{3+}v_+\right) \left( n_{4+}v_+\right) \exp \left( \frac{\Delta E}{k_BT_+}\right) -\left( n_{1+}v_+\right) \left( n_{2+}v_+\right) =0,\\&\mathscr {F}\left( \frac{3c_+}{5M_+}\right) >\bar{m}\left( n_{3+}v_+\right) \left( n_{4+}v_+\right) \exp \left( \frac{\Delta E}{k_BT_+}\right) -\left( n_{1+}v_+\right) \left( n_{2+}v_+\right) =0 \end{aligned}$$

and by setting $v_1=\max \left( \xi _1^-,\xi _2^-,3c_+/(5M_+)\right)$, one can use the Bolzano’s theorem to conclude about the existence of at least one physical solution $v_{-}^r$ of (38) in $\left( v_1,v_{-}^{inert}\right)$ for $M_+>1$.

It can be numerically checked that the function $\mathscr {F}(v_{-})$ is convex, therefore even uniqueness of a physical solution $v_{-}^r$ is guaranteed. For $M_+>\sqrt{9/5}$, uniqueness may be also proved analytically, by using the monotonicity of $\mathscr {F}\left( v_{-}\right)$ in the interval $\left( 0,c_+\frac{5M_+^2+3}{10M_+}\right)$ and by verifying that

$$\begin{aligned} \mathscr {F}\left( v_{-}\right) <0\quad \quad \forall v_{-}\in \left( c_+\frac{5M_+^2+3}{10M_+},c_+\frac{5M_+^2+3}{8M_+}\right) \cap I_n. \end{aligned}$$

(43)

In fact, under the hypothesis $M_+>\sqrt{9/5}$, one can easily prove that $N\left( \mathbf {u}_+,M_+;v_{-}\right) >0$ and, as consequence,

$$n_{k-}v_{-}>n_{k+}v_+\,, \qquad \,n_{\ell -}v_{-}<n_{\ell +}v_+\,\qquad \quad k=1,2\,, \quad \ell =3,4$$

and also

$$T_{-}>T_+$$

for every $v_{-}\in \left( c_+\frac{5M_+^2+3}{10M_+},c_+\frac{5M_+^2+3}{8M_+}\right) \cap I_n$; therefore

$$\begin{aligned} \mathscr {F}\left( v_{-}\right)&=\bar{m}\left( n_{3-}v_{-}\right) \left( n_{4-}v_{-}\right) \exp \left( \frac{\Delta E}{k_BT_{-}}\right) -\left( n_{1-}v_{-}\right) \left( n_{2-}v_{-}\right) \\&<\bar{m}\left( n_{3+}v_+\right) \left( n_{4+}v_+\right) \exp \left( \frac{\Delta E}{k_BT_+}\right) -\left( n_{1+}v_+\right) \left( n_{2+}v_+\right) =\mathscr {F}\left( v_+\right) =0. \end{aligned}$$

Fig. 1

Plots of $v_+$ (continuous), $v_{-}^r$ (dotted) and $v_{-}^{inert}$ (dot-dashed) (left), and of $u_{-}^r$ (dotted) and $u_{-}^{inert}$ (dot-dashed), with $u_+=0$ (right), versus Mach number $M_+$, the parameters are relevant to the second test for reaction (59) in Sect. 4

Thanks to the previous analysis, it can also be easily shown that

$$\begin{aligned} v_{-}^r<v_{-}^{inert}\le v_+, \end{aligned}$$

(44)

for all $M_+>1$, meaning also that the mean velocity of the upstream equilibrium in presence of the chemical reaction is greater than in the inert case, $u_{-}^r>u_{-}^{inert}$, so that the intensity of the shock structure is increased by the chemical reaction, as confirmed by Fig. 1.

Moreover, it has to be stressed that in the inert case from (36) and (37), observing that $\lim _{M_+\rightarrow 1}v_{-}^{inert}\left( \mathbf {u}_+,M_+\right) =v_+=c_+M_+$, it is easily obtained that $\lim _{M_+\rightarrow 1}$ $\mathbf {u}_{-}^{inert}\left( \mathbf {u}_+,M_+\right) =\mathbf {u}_+$, meaning that in the limit $M_+=1$ the null-shock solution, i.e. the constant solution $\mathbf {u}=\mathbf {u}_{-}=\mathbf {u}_+$, is admitted.

Conversely, in presence of the chemical reaction, by examining the limit as $M_+$ tends to 1 throughout the proof it is easy to prove that

$$\lim _{M_+\rightarrow 1}\mathbf {u}_{-}^r\left( \mathbf {u}_+,M_+\right) =\mathbf {u}_+ \qquad \Leftrightarrow \qquad v_{-}^r=v_+=c_+,$$

meaning that the trivial constant solution $\mathbf {u}=\mathbf {u}_{-}=\mathbf {u}_+$ is still admitted, and obviously coincides with the corresponding one in the inert case. But, as far as non trivial solutions are concerned, in the limit as $M_+$ tends to 1, it is easily shown that

$$\lim _{M_+\rightarrow 1}v_{-}^r\left( \mathbf {u}_+,M_+\right) <v_{-}^{inert}=v_+=c_+M_+,$$

as clearly shown in Fig. 1, where the trend, versus $M_+$, of the perturbed equilibrium relative velocity $v_{-}^r$ is plotted, together with the one in the inert case $v_{-}^{inert}$ corresponding to the same unperturbed value $v_+$. The values of $v_{-}^r$ keep lower than the corresponding ones of $v_{-}^{inert}$, and of $v_+$, for all $M_+>1$. Moreover, it can be checked that both the slopes of $v_{-}^r$ and $v_{-}^{inert}$ have the same asymptotic trend as $M_+$ tends to infinity. Unfortunately, for $M_+^{sonic}<M_+<1$ this analysis can be mainly carried out on the numerical ground.

From Rankine–Hugoniot conditions (32)–(35), it is then easily obtained that

$$\lim _{M_+\rightarrow 1}\mathbf {u}_{-}^r\left( \mathbf {u}_+,M_+\right) \ne \mathbf {u}_+,$$

meaning that in the limit $M_+=1$ the null-shock (constant) solution is not reached. The constraint of the mass action law limits the configurations of the two equilibria in such a way that the shock front speed is increased with respect to the corresponding either inert, or equilibrium cases.

In the Euler or Grad equations for both a single gas or an inert mixture, the supersonic regime is characterized by the condition

$$M_+>1\qquad \Leftrightarrow \qquad s>\mu _+^{Euler}=u_++c_+$$

(which for an inert mixture is the maximum eigenvalue of the equilibrium subsystem), whereas in presence of the reversible bimolecular chemical reaction taken into account it modifies into

$$\begin{aligned} M_+>M_+^{sonic}=\frac{C_+}{c_+}=\sqrt{1-\frac{2}{5\mathcal{C}_+}}\qquad \Leftrightarrow \qquad s>\mu _+=u_++C_+, \end{aligned}$$

(45)

where, recalling (20) and (23),

$$\begin{aligned} C_+^2=c_+^2\left( 1-\frac{2}{5\mathcal{C}_+}\right) ,\qquad \sqrt{\frac{3}{5}}< \frac{C_+}{c_+} < 1, \end{aligned}$$

(46)

(for the details [10] is referred to the reader) and then

$$M_+^{sonic}<1,\qquad \mu _+<\mu _+^{Euler}.$$

Therefore the presence of a chemical reaction with a non-vanishing chemical energy gap $\Delta \!E$ enlarges the supersonic regime. It is worth to be stressed that, as already outlined at the end of Sect. 2, in the limit $\Delta E\rightarrow 0$, the behaviour is analogous to that of the inert mixture, since $M_+^{sonic}\rightarrow 1$, and $\mu _+\rightarrow \mu _+^{Euler}$, even if the mixture is still reacting: in fact, even in the particular case $\Delta \!E = 0$, equilibrium mass action law (12) is still valid, and provides a relation involving the four number densities, that remain non-hydrodynamic variables (not governed by conservation equations).

We can conclude that shock wave structure solutions for this reactive mixture exist for all $M_+>M_+^{sonic}$ and the limit of null-shock solution is reached at the boundary of the sonic regime, i.e.

$$\lim _{M_+\rightarrow \ M_+^{sonic}}\mathbf {u}_{-}^r\left( \mathbf {u}_+,M_+\right) =\mathbf {u}_+.$$

This allows to expect, as shown in Sect. 4, that jump discontinuities may arise even for $M_+<1$, within the supersonic regime, $M_+>M_+^{sonic}$.

3.2 Singular Barriers and Critical Mach Numbers

We now turn our attention to the so-called singular barrier [2, 12, 13]. The ODEs system (25)–(28) can be written in block diagonal matrix form [2], each block being

$$\begin{aligned} \mathbf {B}_i\left( \mathbf {u}_i\right) \cdot \frac{d\mathbf {u}_i}{dx} =\mathbf {g}_i\left( \mathbf {u}\right) , \end{aligned}$$

(47)

where $\mathbf {u}_i=\left( n_i,v_i,T_i,\sigma _i\right) ^T$, and the singular barrier, i.e. the locus of the singularities of the system, is the manifold characterized by the vanishing of the determinant of $\mathbf {B}_i$, whose equation is

$$\begin{aligned} \frac{3}{2}k_B\prod _{i=1}^4 n_iv_i^2B_i\left( \mathbf {u}_i\right) =0, \end{aligned}$$

(48)

where

$$\begin{aligned} B_i\left( \mathbf {u}_i\right) :=m_in_iv_i^2-3\left( n_ik_BT_i+\sigma _i\right) =0,\qquad i=1,2,3,4, \end{aligned}$$

(49)

are the singularities sub-manifolds, each one related to a component within the mixture.

As shown in [12] and [2], the presence of sub-shocks within a shock structure solution is due to the singularities sub-manifolds lying between the equilibrium states $\mathbf {u}_+$ and $\mathbf {u}_{-}^r$.

It is also worth to point out the validity of Lax stability conditions across any sub-shock. In fact, for a fixed $M_+$, if the singular barrier $B_{i^*}\left( \mathbf {u}\right) =0$, relevant to whatever species $i^*$, lies between $\mathbf {u}_+$ and $\mathbf {u}_{-}^r$, and if the signs of $B_{i^*}$ evaluated at $\mathbf {u}_+$ and $\mathbf {u}_{-}^r$ (surely opposite) satisfy the additional requirement $B_{i^*}\left( \mathbf {u}_{-}^r\right)<0<B_{i^*}\left( \mathbf {u}_+\right)$, then the shock front speed s and the characteristic speed $\lambda _{i^*}$ fulfil the relation $\lambda _{i^*}\left( \mathbf {u}_+\right)<s<\lambda _{i^*}\left( \mathbf {u}_{-}^r\right)$. Let us also observe that, denoting by $\varphi _{i^*}$ the value of $\varphi$ at which the relevant sub-shock occurs, and by $\mathbf {u}_R$ and $\mathbf {u}_L$ the two generic limiting states ahead and behind the sub-shock front, $\lim _{\varphi \rightarrow \varphi _{i^{*+}}}\mathbf {u}=\mathbf {u}_R$, $\lim _{\varphi \rightarrow \varphi _{i^{*-}}}\mathbf {u}=\mathbf {u}_L$, then it must be $\mathbf {u}_{i^*R}\ne \mathbf {u}_{i^*L}$ and $\mathbf {u}_{jR}=\mathbf {u}_{jL}$, for all $j\ne i^*$, since only the variables relevant to the component $i^*$ may suffer a jump discontinuity, all the others being continuous. Therefore, smoothness arguments on $B_i\left( \mathbf {u}\right)$ and $\lambda \left( \mathbf {u}\right)$, together with the information on the sign of $B_i\left( \mathbf {u}\right)$ on each of the two half-spaces separated by $B_{i^*}\left( \mathbf {u}\right) =0$, assure that $\lambda _{i^*}\left( \mathbf {u}_R\right)<s<\lambda _{i^*}\left( \mathbf {u}_L\right)$, and hence guaranteeing the stability in the sense of Lax of the sub-shock generated by the species $i^*$. We can conclude that the shock wave structure solution can be either continuous, or discontinuous with at most four (as many as the components in the mixture) different and stable sub-shocks, located in different positions, $\varphi _i$, within the shock front.

As far as the position of $\mathbf {u}_+$ with respect to the barriers $B_i=0$ is concerned, the same results found in the inert case continue to hold [2]. In fact, it is easy to show that

$$\begin{aligned} B_i\left( \mathbf {u}_+\right) =m_in_{i+}c_+^2M_+^2-3n_{i+}k_BT_+\ge 0 \qquad \Leftrightarrow \qquad M_+\ge M_{i+}^{*}:=\sqrt{\frac{9}{5}\xi _{i+}}, \end{aligned}$$

(50)

where

$$\xi _{i+}=\frac{\rho _+}{m_in_+}=\frac{1}{m_i}\sum _{j=1}^4m_j\chi _{j+}, \qquad \chi _{j+}=\frac{n_{j+}}{n_+}.$$

In the inert gas, the quantities $M_{i+}^{*}$ can be possible critical values for Mach number if they are greater than one; otherwise $B_i\left( \mathbf {u}_+\right) > 0$ for all $M_+>1$; moreover,

$$M_{i+}^{*}>1 \qquad \Leftrightarrow \qquad \xi _{i+}>\frac{5}{9}.$$

For the reactive mixture, the admissibility condition becomes $M_{i+}^{*}>M_+^{sonic}$; otherwise, $B_i\left( \mathbf {u}_+\right) > 0$ for any Mach number; moreover,

$$M_{i+}^{*}>M_+^{sonic} \qquad \Leftrightarrow \qquad \xi _{i+}>\frac{5}{9}-\frac{2}{9\mathcal{C}_+}.$$

Because of the implicit form of $v_{-}^r$ due to the presence of the chemical reaction, it is not possible to carry out an explicit analysis concerning the position of $\mathbf {u}_{-}^r$ with respect to the barriers $B_i= 0$, as done in the inert case [2]. In fact, $B_i\left( \mathbf {u}_{-}^r\right)$ can be rewritten in terms of Mach number as follows

$$\begin{aligned} B_i\left( \mathbf {u}_{-}^r\right) =n_{i-}v_{-}^r\left[ \left( m_i+\frac{3\rho _+}{n_+}\right) v_{-}^r -\frac{3\rho _+c_+}{5n_+M_+}\left( 5M_+^2+3\right) \right] \end{aligned}$$

(51)

so, the vanishing of $B_i\left( \mathbf {u}_{-}^r\right)$ can only be explicitly expressed in terms of the relative velocity

$$\begin{aligned} B_i\left( \mathbf {u}_{-}^r\right) \le 0\qquad \Leftrightarrow \qquad 0<v_{-}^r\le v_{i-}^*:=c_+\frac{5M_+^2+3}{5M_+}\frac{3\xi _{i+}}{3\xi _{i+}+1}, \end{aligned}$$

(52)

and the corresponding critical value of the Mach number, say $M_{i-}^{*r}$, can only be evaluated numerically.

However, one can observe that

$$\begin{aligned} M_{i+}^2=\frac{9}{5}\xi _{i+}>1\qquad \Leftrightarrow \qquad \frac{3\xi _{i+}}{3\xi _{i+}+1}>\frac{5}{8} \end{aligned}$$

(53)

and that this last inequality implies that

$$\begin{aligned} v_{i-}^*=c_+\frac{5M_+^2+3}{5M_+}\frac{3\xi _{i+}}{3\xi _{i+}+1}>c_+\frac{5M_+^2+3}{8M_+}>v_{-}^{inert}>v_{-}^r \end{aligned}$$

(54)

for any Mach number $M_+>1$; this allows to conclude that

$$\begin{aligned} M_{i+}^*>1\qquad \Rightarrow \qquad B_i\left( \mathbf {u}_{-}^r\right) <0,\qquad \forall \, M_+>1. \end{aligned}$$

(55)

Moreover, let $i^*$ be the index such that $m_{i^*}=\min _{j=1,\ldots ,4}m_j$; then, since

$$\begin{aligned} m_{i^*}n_+<\rho _+\qquad \Rightarrow \qquad m_{i^*}+3\frac{\rho _+}{n_+}<4\frac{\rho _+}{n_+}, \end{aligned}$$

(56)

hence

$$\begin{aligned} \frac{3\xi _{i^*+}}{3\xi _{i^*+}+1}>\frac{3}{4}>\frac{5}{8}, \end{aligned}$$

(57)

and then, like in the inert case [2], for the lightest species it is always $M_{i^*+}^{*}>1$, and $B_{i^*}\left( \mathbf {u}_{-}^r\right) < 0$. Therefore, the lightest component can always generate a stable sub-shock for $M_+>M_{i^*+}^{*}$, since

$$B_{i^*}\left( \mathbf {u}_{-}^r\right)<0<B_{i^*}\left( \mathbf {u}_+\right) , \qquad \forall \,M_+>M_{i^*+}^{*}.$$

In order to clarify the role of the chemical reaction, it can be interesting to carry out a comparison with the ideal inert mixture case, the unperturbed equilibrium being an arbitrary constant state. As already discussed in [2], in this case the perturbed equilibrium is related to the unperturbed one through the classical Euler Rankine–Hugoniot conditions given by (36) and (37), yielding that

$$\begin{aligned} B_i\left( \mathbf {u}_{-}^{inert}\right) \le 0\qquad \Leftrightarrow \qquad M_+\ge M_{i-}^{*inert}:=\sqrt{\frac{3\left( 3\xi _{i+}+5\right) }{5\left( 9\xi _{i+}-1\right) }}, \end{aligned}$$

(58)

the critical Mach numbers being real and greater than one for $1/9<\xi _{i+}<5/9$.

Therefore, even if in presence of the chemical reaction it is not possible to obtain explicit expressions of the critical Mach numbers related to the upstream equilibrium state, the situation is somehow analogous to that holding for an inert mixture [2].

In fact, as it will be shown by some examples in the next section, it is still true that if the critical Mach number generated by the ith component in one of the two, unperturbed or perturbed, equilibria is admissible, in the sense that it is greater than $M_+^{sonic}$, then the critical Mach number related to the same component in the other equilibrium is certainly not admissible, in the sense that it will be less than $M_+^{sonic}$.

The presence of the chemical reaction modifies, with respect to the inert case, the upstream equilibrium which is now constrained to belong to the sub-manifold of the phase space defined by the additional restriction imposed through the mass action law. In the inert case, any pair of constant states related by the classical Rankine–Hugoniot conditions (36), (37) for an Euler gas, with the additional relations for the species number densities, can represent the boundary values in the problem; in the reactive case, both the equilibria are constrained to lie on the chemical equilibrium manifold, and this obviously influences the signs of the barriers, as well as the critical Mach numbers, and therefore the admitted shock structure solutions.

In order to appreciate the effect of chemistry on the solution, we choose a particular chemical reaction and we analyze, through the sign of the different barriers, the behaviour of the critical Mach numbers in various examples (varying the equilibrium configuration) in both inert and reactive cases.

4 Chemical Reactions and Concluding Remarks

As already said, in presence of the chemical reaction, due to the implicit definition of the upstream equilibrium, it is not possible to carry on the analysis in order to characterize all the possible solutions in all the ranges of Mach number, as in the inert case [2]. Moreover, the presence of more than two components in the mixture does not even allow to deduce general informations on behaviour of solutions with respect to equilibrium concentrations and mass ratios, as it was possible in the case of binary mixtures [2, 6].

Therefore, in order to go deeper into the problem of sub-shock formation, we have to fix particle masses and the internal energy gap, that will be chosen to be

$$m_1=0.018, \quad m_2=0.001, \quad m_3=0.017, \quad m_4=0.002, \quad \Delta E=63300,$$

where $m_2<m_4<m_3<m_1$. These parameters are consistent with the chemical reaction

$$\begin{aligned} H_{2}O+H\quad \rightleftharpoons \quad OH+H_2 \end{aligned}$$

(59)

that however involves even polyatomic species and should be suitably modelled by kinetic (and hydrodynamic) equations with a suitable internal energy variable, which is here neglected.

As a first test, the unperturbed equilibrium configuration $\mathbf {u}_+$ is set to be

$$n_{1+}=0.4, \quad n_{2+}=0.3, \quad n_{3+}=0.2, \quad n_{4+}=0.1, \quad u_+=0,\quad T_+=2772.7,$$

the temperature being determined through the mass action law (12). With this choice, the supersonic regime is bounded by $M_+^{sonic}=0.96$, and the admissible critical Mach numbers are all related to the downstream equilibrium

$$M_{1+}^*=1.05,\qquad M_{2+}^*=4.47,\qquad M_{3+}^*=1.08,\qquad M_{4+}^*=3.16,$$

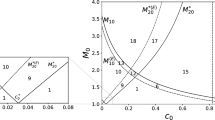
with $M_+^{sonic}<1<M_{1+}^*<M_{3+}^*<M_{4+}^*<M_{2+}^*$, whose order is reverse with respect to that of the corresponding masses. Then, the critical Mach numbers $M_{i-}^{*inert}$, if real, are surely less than $M_+^{sonic}$; in particular,

$$M_{1-}^{*inert}=0.95,\qquad M_{2-}^{*inert}=0.48,\qquad M_{3-}^{*inert}=0.92,\qquad M_{4-}^{*inert}=0.52,$$

and $M_{2-}^{*inert}<M_{4-}^{*inert}<M_{3-}^{*inert}<M_{1-}^{*inert}<M_+^{sonic}<1$.

Figure 2 clearly shows that only the barriers $B_i\left( \mathbf {u}_+\right)$ change their signs for $M_+>M_{i+}^*$, respectively. More precisely, for any $M_+>M_{i+}^*$, it is $B_i\left( \mathbf {u}_{-}\right)<0<B_i\left( \mathbf {u}_+\right)$.

This allows to characterize the five different ranges of possible solutions as follows

• if $M_+^{sonic}<M_+<M_{1+}^*$, only continuous solutions exist, since $B_i\left( \mathbf {u}_+\right) B_i\left( \mathbf {u}_{-}^r\right) > 0$, for all $i=1,2,3,4$;

• if $M_{1+}^*<M_+<M_{3+}^*$, then a sub-shock may appear in the variables relevant to species 1, since $B_1\left( \mathbf {u}_+\right) B_1\left( \mathbf {u}_{-}^r\right) <0$, and $B_i\left( \mathbf {u}_+\right) B_i\left( \mathbf {u}_{-}^r\right) >0$, for all $i=2,3,4$;

• if $M_{3+}^*<M_+<M_{4+}^*$, then two different sub-shocks may appear in the variables relevant to species 1 and 3, since $B_i\left( \mathbf {u}_+\right) B_i\left( \mathbf {u}_{-}^r\right) <0$, for all $i=1,3$, and $B_i\left( \mathbf {u}_+\right) B_i\left( \mathbf {u}_{-}^r\right) >0$, for all $i=2,4$;

• if $M_{4+}^*<M_+<M_{2+}^*$, then three different sub-shocks may appear in the variables relevant to species 1, 3 and 4, since in this case $B_i\left( \mathbf {u}_+\right) B_i\left( \mathbf {u}_{-}^r\right) <0$, for all $i=1,3,4$, and $B_2\left( \mathbf {u}_+\right) B_2\left( \mathbf {u}_{-}^r\right) >0$;

• if $M_+>M_{2+}^*$, then four different sub-shocks, one for each component, may appear, since in this last case $B_i\left( \mathbf {u}_+\right) B_i\left( \mathbf {u}_{-}^r\right) <0$, for all $i=1,2,3,4$.

In the inert case, the only difference in the ranges, with respect to the reactive case, is that $M_+^{sonic}\equiv 1$.

Fig. 2

Plots of $B_i\left( \mathbf {u}_+\right)$ (continuous), $B_i\left( \mathbf {u}_{-}^r\right)$ (dashed) and $B_i\left( \mathbf {u}_{-}^{inert}\right)$ (dot-dashed) versus Mach number $M_+$, for reaction (59), with $n_{1+}=0.4$, $n_{2+}=0.3$, $n_{3+}=0.2$, $n_{4+}=0.1$, $u_+=0$, $T_+=2772.7$

The results become much more interesting in a second test performed by considering the following equilibrium configuration

$$n_{1+}=0.8, \quad n_{2+}=0.9, \quad n_{3+}=0.05, \quad n_{4+}=0.1, \quad u_+=0,\quad T_+=1285.2,$$

in which the concentrations of species 1 and 2, which are the products of the exothermic reaction, are both larger than those of both the other species. As it will be shown, the possible behaviours of the shock wave structure solutions are different in the two cases.

With this choice, in fact, the sonic Mach number is $M_+^{sonic}=0.942$, and the critical Mach numbers due to the unperturbed equilibrium are

$$M_{1+}^*=0.94,\qquad M_{2+}^*=3.99,\qquad M_{3+}^*=0.97,\qquad M_{4+}^*=2.82,$$

with $M_{1+}^*<M_+^{sonic}<M_{3+}^*<1<M_{4+}^*<M_{2+}^*$, and

$$M_{1-}^{*inert}=1.07,\qquad M_{2-}^{*inert}=0.49,\qquad M_{3-}^{*inert}=1.03,\qquad M_{4+}^{*inert}=0.53,$$

with $M_{2-}^{*inert}<M_{4-}^{*inert}<M_+^{sonic}<1<M_{3-}^{*inert}<M_{1-}^{*inert}$.

In this case, as far as the inert case is concerned [2], only $M_{2+}^*$ and $M_{4+}^*$ are greater than one and, as shown in [2], this allows to deduce that $B_{2,4}\left( \mathbf {u}_{-}^{inert}\right) <0$, for all $M_+>1$. This circumstance allows to expect that both species 2 and 4 generate a stable sub-shock, since it will be, analogously to the previous test, $B_i\left( \mathbf {u}_{-}\right)<0<B_i\left( \mathbf {u}_+\right)$, for all $M_+>M_{i+}^*$, with $i=2,4$, both in the inert and reactive case. Figure 3 clearly shows the intersections of $B_2$ and $B_4$ with the horizontal axes at $M_+=M_{2+}^*$ and $M_+=M_{4+}^*$, respectively.

Moreover, the fact that $M_{1+}^*$ and $M_{3+}^*$ are both less than one means that $B_1\left( \mathbf {u}_+\right)$, $B_3\left( \mathbf {u}_+\right) >0$, for all $M_+>1$, as shown in Fig. 3, guaranteeing that $s>\lambda _{1,3}\left( \mathbf {u}_+\right)$, for all $M_+>1$.

Fig. 3

Plots of $B_i\left( \mathbf {u}_+\right)$ (continuous), $B_i\left( \mathbf {u}_{-}^r\right)$ (dashed) and $B_i\left( \mathbf {u}_{-}^{inert}\right)$ (dot-dashed) versus Mach number $M_+$, for reaction (59), with $n_{1+}=0.8$, $n_{2+}=0.9$, $n_{3+}=0.05$, $n_{4+}=0.1$, $u_+=0$, $T_+=1285.2$

As shown in [2], it happens that $M_{1,3+}^*<1$ implies $M_{1,3-}^{*inert}>1$, and then, as in the previous test (except for the nature and the order of the critical Mach numbers), it is $B_{1,3}\left( \mathbf {u}_{-}^{inert}\right)<0<B_{1,3}\left( \mathbf {u}_+\right)$, or equivalently $s<\lambda _{1,3}\left( \mathbf {u}_{-}^{inert}\right)$, for all $M_+>M_{1,3-}^{*inert}$, and each component, for suitable values of $M_+$, can generate a sub-shock. In details, since $1<M_{3-}^{*inert}<M_{1-}^{*inert}<M_{4+}^*<M_{2+}^*$, the possible shock structure solutions are the following

• if $1<M_+<M_{3-}^{*inert}$, only continuous solutions exist, since $B_i\left( \mathbf {u}_+\right) B_i\left( \mathbf {u}_{-}^{inert}\right) >0$, for all $i=1,2,3,4$;

• if $M_{3-}^{*inert}<M_+<M_{1-}^{*inert}$, a sub-shock may appear in the variables relevant to species 3 since $B_3\left( \mathbf {u}_{-}^{inert}\right)<0<B_3\left( \mathbf {u}_+\right)$;

• if $M_{1-}^{*inert}<M_+<M_{4+}^*$, then two different sub-shocks may appear in the variables relevant to species 1 and 3 since $B_{1,3}\left( \mathbf {u}_{-}^{inert}\right)<0<B_{1,3}\left( \mathbf {u}_+\right)$;

• if $M_{4+}^*<M_+<M_{2+}^*$, then three different sub-shocks may arise since in this case $B_{1,3,4}\left( \mathbf {u}_{-}^{inert}\right)<0<B_{1,3,4}\left( \mathbf {u}_+\right)$;

• if $M_+>M_{2+}^*$, then four different sub-shocks, one for each component, may appear since in this case $B_i\left( \mathbf {u}_{-}^{inert}\right)<0<B_i\left( \mathbf {u}_+\right)$, for all $i=1,2,3,4$.

In the reactive case, the situation is different.

Figure 3 clearly shows the intersections of $B_2$, $B_3$ and $B_4$ with the horizontal axes at $M_+=M_{2+}^*$, $M_+=M_{3+}^*$ and $M_+=M_{4+}^*$, respectively. The admissible unperturbed critical Mach numbers are now $M_{2+}^*$, $M_{3+}^*$, and $M_{4+}^*$, since $M_+^{sonic}<M_{3+}^*<1<M_{4+}^*<M_{2+}^*$, and this, through (55) and since species 2 is the lightest, allows to deduce that

$$B_i\left( \mathbf {u}_{-}^r\right) <0,\qquad \forall \,M_+>1,\quad i=2,4.$$

Numerical simulations show that it is also

$$B_{2,3,4}\left( \mathbf {u}_{-}^r\right) <0,\qquad \forall \,M_+>M_+^{sonic}.$$

This circumstance allows to expect that species 2, 3 and 4 generate a stable sub-shock, since it will be, analogously to the previous test,

$$B_i\left( \mathbf {u}_{-}^r\right)<0<B_i\left( \mathbf {u}_+\right) ,\qquad \forall \,M_+>M_{i+}^*,\qquad i=2,3,4.$$

Moreover, the relation $M_{1+}^*<M_+^{sonic}$ again assures that

$$B_1\left( \mathbf {u}_+\right)>0, \qquad \forall M_+>M_+^{sonic},$$

as in the inert case. Differently from the inert case, from the relation $M_{1+}^*<1$, it is not possible to derive analytically any information either on the existence of the critical Mach number $M_{1-}^{*r}$, or on its position with respect to 1.

In Fig. 3 the numerical investigation carried out on $B_1\left( \mathbf {u}_{-}^r\right)$, varying $M_+$, shows that

$$B_1\left( \mathbf {u}_{-}^r\right) <0,\qquad \forall \,M_+>M_{1-}^{*r},$$

with $M_{1-}^{*r}>M_+^{sonic}$, and it should be appreciated that $B_1\left( \mathbf {u}_{-}^r\right)$ intersects the horizontal axis for a Mach which is very close to $M_+^{sonic}$.

So for all $M_+>M_{1-}^{*r}$ the presence of the chemical reaction yields that

$$\lambda _1\left( \mathbf {u}_+\right)<s<\lambda _1\left( \mathbf {u}_{-}^r\right) ,\qquad \forall \,M_+>M_{1-}^{*r},$$

and a stable shock may appear in the variables relevant to constituent 1, even for Mach numbers $M_+$ lower than 1.

The second test also shows how the unperturbed configuration affects the solution. With respect to the first, in the second test, in fact, the unperturbed concentration of one of the heavier (but not the heaviest), component 1, and of the lightest species 2 are increased, and the others are decreased. The effect is that, due to its higher concentration, even if it is not the heaviest, species 1 may generate a sub-shock for Mach numbers, $M_+>M_{1-}^{*r}$, very close to $M_+^{sonic}$, and still lower than those, $M_+>M_{3+}^*$, at which the heaviest species 3 can produce a jump discontinuity.

In presence of the chemical reaction, since $M_+^{sonic}<M_{1-}^{*r}<M_{3+}^*<M_{4+}^*<M_{2+}^*$, the scenario modifies as follows

• if $M_+^{sonic}<M_+<M_{1-}^{*r}$, only continuous solutions exist, since $B_i\left( \mathbf {u}_+\right) B_i\left( \mathbf {u}_{-}^r\right) >0$, for all $i=1,2,3,4$;

• if $M_{1-}^{*r}<M_+<M_{3+}^*$, then a sub-shocks may appear in the variables relevant to species 1 since $B_1\left( \mathbf {u}_{-}^r\right)<0<B_1\left( \mathbf {u}_+\right)$;

• if $M_{3+}^*<M_+<M_{4+}^*$, analogously to the inert case, two different sub-shocks may appear in the variables relevant to species 1 and 3, since $B_{1,3}\left( \mathbf {u}_{-}^r\right)<0<B_{1,3}\left( \mathbf {u}_+\right)$;

• if $M_{4+}^*<M_+<M_{2+}^*$, the situation is analogous to the corresponding one in the inert case: three different sub-shocks may appear in the variables relevant to species 1, 3 and 4, since $B_{1,3,4}\left( \mathbf {u}_{-}^r\right)<0<B_{1,3,4}\left( \mathbf {u}_+\right)$;

• if $M_+>M_{2+}^*$, again the situation is analogous to the corresponding one in the inert case: four different sub-shocks, one for each component, may appear since $B_i\left( \mathbf {u}_{-}^r\right)<0<B_i\left( \mathbf {u}_+\right)$, for all $i=1,2,3,4$.

As already pointed out, in the present reactive frame it is not possible to produce the same general overview of the different solutions, in terms of Mach numbers, mass ratios, and equilibrium concentrations shown in [2] for the inert binary mixture. However, even in presence of a chemical reaction we may deduce that the solution may exhibit up to four different sub-shocks within the shock front, as many as the components are, depending on how many critical Mach numbers are admitted, and on which are exceeded by the fixed value of the Mach number (or of the wave front speed), or, in other words, on which of the singularity sub-manifolds, $B_i=0$, lie between the two equilibria $\mathbf {u}_+$ and $\mathbf {u}_{-}^r$.

The constant solution $\mathbf {u}_{-}^{inert}=\mathbf {u}_+$, which for the inert mixture represents the null shock limit as $M_+\rightarrow 1$, in the reactive case is reached (providing $\mathbf {u}_{-}^r=\mathbf {u}_+$) at sonic threshold $M_+^{sonic}$, which is now lower than 1 due to the chemical processes. The range of Mach numbers allowing only continuous solutions is then a right neighbourhood of $M_+^{sonic}$, and sub-shocks may arise for Mach numbers lower than one, if the minimum of the admissible critical values of Mach number is below one. We can finally stress that the inert case can be recovered in the limit as $\Delta E\rightarrow 0$ of the reactive mixture.