DG Treatment of Non-conforming Interfaces in 3D Curl-Curl Problems

Abstract

We consider 3D Curl-Curl type of problems in the presence of arbitrary, non-conforming mesh-interfaces. The Interior Penalty/Nitsche’s Method (Stenberg, Computational mechanics, 1998) is extended to these problems for edge functions of the first kind. We present an a priori error estimate which indicates that one order of convergence is lost in comparison to conforming meshes due to insufficient approximation properties of edge functions. This estimate is sharp for first order edge functions: In a numerical experiment the method does not converge as the mesh is refined.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The Curl-Curl equation,

$$\displaystyle{ \nabla \times (\mu ^{-1}\nabla \times \mathbf{A}) = \mathbf{j}^{i}, }$$

(1)

can be used to calculate the magnetic field that originates from a stationary current j ⁱ. Herein μ denotes the magnetic permeability, A is the magnetic vector potential and the magnetic field is B = ∇×A. The Magnetostatic model (1) is a special case of the temporally gauged Eddy Current model (note that (2) reduces to (1) in static cases as well as in regions where the electric conductivity $\sigma$ vanishes),

$$\displaystyle{ \sigma \frac{\mathrm{d}\mathbf{A}} {\mathrm{d}t} + \nabla \times (\mu ^{-1}\nabla \times \mathbf{A}) = \mathbf{j}^{i}. }$$

(2)

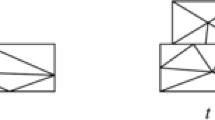
In some applications like the simulation of electric machines or magnetic actuators, magnetic fields have to be computed in the presence of moving, rigid parts. Then one may use separate, moving sub-meshes for them in order to avoid remeshing. However, this leads to so-called “sliding interfaces”, i.e. meshes with hanging nodes (cf. Fig. 1).

Fig. 1

Initially conforming sub-meshes become non-conforming when the upper sub-mesh starts moving

Our aim is to construct a method which solves (1) such that the solution is not affected by the “non-conformity” of the sub-meshes at the common interface. This problem has been studied in depth in the framework of so called Mortar Methods where the continuity requirements are incorporated directly into the trial-space [1] or they are enforced by additional Lagrange Multipliers [2]. These approaches have been proven to be successful, but they require the inversion of a full matrix respectively additional unknowns. A related approach uses a primal/dual formulation and couples the systems in a weak sense across the interface [3].

We pursue a different approach that fits into the framework of Discontinuous Galerkin (DG) methods which support non-conforming meshes naturally. A Locally Discontinuous Galerkin scheme for sliding meshes has already been proposed and analyzed in [4]. We will study a simpler method which has it’s origins in Nitsche’s Method. The idea is to penalize tangential discontinuities along the non-conforming interface, but not in the interior of the subdomains where we use a standard FEM discretization. The method has been analyzed for the Poisson Equation in [5] where it was shown that a symmetric positive definite system matrix results. We aim to extend this idea to (1).

It is important to realize that (1) and (2) (if $\sigma = 0$ anywhere) don’t have a unique solution (in the L ²-norm). In this work, we will therefore study the regularized problem,

$$\displaystyle{ \nabla \times (\mu ^{-1}\nabla \times \mathbf{A}) +\varepsilon \mathbf{A} = \mathbf{j}^{i},\quad \text{in }\varOmega }$$

(3)

$$\displaystyle{ \mathbf{n} \times \mathbf{A} = \mathbf{g}_{D}\quad \text{on }\partial \varOmega. }$$

(4)

Here $\varepsilon > 0$ is the regularization parameter that renders the solution unique. We discuss the influence and necessity of the regularization term in [6]. Finally we want to point out that the boundary condition (4) implies $(\nabla \times \mathbf{A}) \cdot \mathbf{n} = \mathbf{B} \cdot \mathbf{n} = 0$ on ∂ Ω which reflects the decay of the fields away from the source.

We start our discussion by introducing DG notations (Sect. 2) that we need in order to introduce the interior penalty formulation in Sect. 3. Section 3 also analyzes the behavior of the discrete solution as the mesh is refined (h-refinement) and the role of the approximation space is studied. The theoretical results are compared to numerical experiments in Sect. 4. We finish our discussion by a short conclusion and outlook (Sect. 5).

2 Preliminaries

Before we can introduce the Symmetric Weighted Interior penalty (SWIP) formulation of (3)–(4) we introduce some definitions and notations:

Subdomains and Sub Meshes Let us assume that the domain Ω, on which (3)–(4) is posed, is a simply connected polyhedron with Lipschitz boundary. Furthermore we assume Ω to be split into two non-overlapping subdomains $\overline{\varOmega _{1}} \cup \overline{\varOmega _{2}} = \overline{\varOmega }$. On each subdomain we introduce a sequence of shape regular, simplical meshes in the sense of Ciarlet such that the union $\mathcal{T}_{\mathcal{H}} = \mathcal{T}_{\mathcal{H},1} \cup \mathcal{T}_{\mathcal{H},2}$ is quasi-uniform at the non-conforming interface $\varGamma = \overline{\varOmega }_{1} \cap \overline{\varOmega }_{2}$ (cf. [6], Definition 1). It is easy to check that meshes created by the motion of individual sub-meshes (cf. Fig. 1) fit this definition.

Magnetic Permeability We assume there exists a partition $P_{\varOmega } = \left \{\varOmega _{i,\mu }\right \}$ such that each Ω _i, μ is a polyhedron and such that the permeability μ > 0 is constant on each Ω _i, μ . Furthermore the mesh sequence $\mathcal{T}_{\mathcal{H}}$ is compatible with the partition P _Ω : For each $\mathcal{T}_{h} \in \mathcal{T}_{\mathcal{H}}$, each element $T \in \mathcal{T}_{h}$ belongs to exactly one Ω _i, μ  ∈ P _Ω . I.e. the magnetic permeability is allowed to jump over element boundaries, and in particular over the non-conforming interface Γ.

Polynomial Approximation Later on we will seek our discrete solution in the piecewise polynomial space (cf. [7]),

$$\displaystyle{ P_{3}^{k}(\mathcal{T}_{ h}):= \left \{\left.p \in L^{2}(\varOmega )\right \vert \,\forall T \in \mathcal{T}_{ h},\left.p\right \vert _{T} \in P_{3}^{k}(T)\right \} }$$

(5)

where $\mathcal{T}_{h} \in \mathcal{T}_{\mathcal{H}}$ and P ₃ ^k(T) is the usual space of polynomials up to degree k on mesh element T. Note that functions of $P_{3}^{k}(\mathcal{T}_{h})$ are discontinuous across element boundaries.

Mesh Faces, Jump and Average Operators We denote by $\mathcal{F}_{h} = \mathcal{F}_{h}^{b} \cup \mathcal{F}_{h}^{i}$ the set of all boundary and inner faces of a given mesh $\mathcal{T}_{h}$. $\mathcal{F}_{T}$ stands for all faces of the mesh element $T \in \mathcal{T}_{h}$. For each mesh face F, vector valued function $\mathbf{A}_{h} \in P_{3}^{k}(\mathcal{T}_{h})^{3}$, we define

$$\displaystyle{ \begin{array}{rrcl} \text{if }F \in \mathcal{F}_{h}^{i},\;F = \partial T_{i} \cap \partial T_{j}:&&\left [\mathbf{A}_{h}\right ]_{T}& = \mathbf{n}_{F} \times \left (\left.\mathbf{A}_{h}\right \vert _{T_{i}} -\left.\mathbf{A}_{h}\right \vert _{T_{j}}\right ), \\ \text{if }F \in \mathcal{F}_{h}^{b},\;F = \partial T_{i} \cap \partial \varOmega:&&\left [\mathbf{A}_{h}\right ]_{T}& = \mathbf{n}_{F} \times \left.\mathbf{A}_{h}\right \vert _{T_{i}}, \\ \text{if }F \in \mathcal{F}_{h}^{i},\;F = \partial T_{i} \cap \partial T_{j}:&& \left \{\mathbf{A}_{h}\right \}_{\omega } & =\omega _{1}\left.\mathbf{A}_{h}\right \vert _{T_{i}} +\omega _{2}\left.\mathbf{A}_{h}\right \vert _{T_{j}}, \\ \text{if }F \in \mathcal{F}_{h}^{b},\;F = \partial T_{i} \cap \partial \varOmega:&& \left \{\mathbf{A}_{h}\right \}_{\omega } & = \left.\mathbf{A}_{h}\right \vert _{T_{i}}. \end{array} \qquad \begin{array}{l} \text{(jump)} \\[0.8cm] \text{(average)} \end{array} }$$

Here n _F always points from T _i to T _j and ω _i  ∈ [0, 1] such that $\omega _{1} +\omega _{2} = 1$.

3 Symmetric Weighted Interior Penalty (SWIP) Formulation

We chose an arbitrary subspace $V _{h} \subseteq P_{3}^{k}(\mathcal{T}_{h})^{3}$ as discrete test and trial space, and use integration by parts (cf. [7, 8] for details) to arrive at the SWIP formulation of (3): Find A _h  ∈ V _h such that

$$\displaystyle{ a_{h}^{\text{SWIP}}(\mathbf{A}_{ h},\mathbf{A}'_{h}) +\varepsilon \int _{\varOmega }\mathbf{A}_{h} \cdot \mathbf{A}'_{h} =\ell _{h}(\mathbf{A}'_{h})\qquad \forall \mathbf{A}'_{h} \in V _{h} }$$

(6)

with

$$\displaystyle\begin{array}{rcl} a_{h}^{\text{SWIP}}(\mathbf{A}_{ h},\mathbf{A}'_{h})& =& \int _{\varOmega }\left (\mu ^{-1}\nabla \times \mathbf{A}_{ h}\right ) \cdot \left (\nabla \times \mathbf{A}'_{h}\right ) -\sum _{F\in \mathcal{F}_{h}}\int _{F}\left \{\mu ^{-1}\nabla \times \mathbf{A}_{ h}\right \}_{\omega } \cdot \left [\mathbf{A}'_{h}\right ]_{T} \\ & -& \sum _{F\in \mathcal{F}_{h}}\int _{F}\left \{\mu ^{-1}\nabla \times \mathbf{A}'_{ h}\right \}_{\omega } \cdot \left [\mathbf{A}_{h}\right ]_{T} +\sum _{F\in \mathcal{F}_{h}} \frac{\eta \gamma _{\mu,F}} {a_{F}}\int _{F}\left [\mathbf{A}_{h}\right ]_{T} \cdot \left [\mathbf{A}'_{h}\right ]_{T},{}\end{array}$$

(7)

$$\displaystyle\begin{array}{rcl} \ell_{h}(\mathbf{A}'_{h})& =& \int _{\varOmega }\mathbf{j}^{i} \cdot \mathbf{A}'_{ h} -\sum _{F\in \mathcal{F}_{h}^{b}}\int _{F}\left \{\mu ^{-1}\nabla \times \mathbf{A}'_{ h}\right \}_{\omega } \cdot (\mathbf{n} \times \mathbf{g}_{D}) \\ & +& \sum _{F\in \mathcal{F}_{h}^{b}} \frac{\eta \gamma _{\mu,F}} {a_{F}}\int _{F}\left [\mathbf{A}'_{h}\right ]_{T} \cdot (\mathbf{n} \times \mathbf{g}_{D}). {}\end{array}$$

(8)

where $a_{F} = \frac{1} {2}(h_{T_{1}} + h_{T_{2}})$ is the average diameter of the adjacent elements of face F and η is the penalty parameter. The weights are chosen as

$$\displaystyle{ \gamma _{\mu,F}:= \frac{2} {\mu _{1} +\mu _{2}},\qquad \quad \omega _{1}:= \frac{\mu _{1}} {\mu _{1} +\mu _{2}},\qquad \quad \omega _{2}:= \frac{\mu _{2}} {\mu _{1} +\mu _{2}}. }$$

Remark

If $V _{h} \subseteq \mathbf{H}(\mathbf{curl})$, then all inner tangential jumps in (7) will drop out and only jumps at the boundary remain. I.e. we are left with a standard FEM formulation where the inhomogeneous boundary conditions (4) are enforced in a weak sense.

3.1 A Priori Error Estimate

Using the theory of DG Methods one can derive the following error estimate [6]:

Theorem 1

Let $\mathbf{A} \in V ^{{\ast}}:= \mathbf{H}(\mathbf{curl},\varOmega ) \cap H^{2}(P_{\varOmega })^{3}$ be a solution of the strong formulation (3)–(4) (in the sense of distributions) and let $\mathbf{A}_{h} \in V _{h} \subseteq P_{3}^{k}(\mathcal{T}_{h})^{3}$ solve the variational formulation (6). Then there exist constants C > 0, C _η > 0, both independent of h, μ, such that for η > C _η ,

$$\displaystyle{ \|\mathbf{A} -\mathbf{A}_{h}\|_{\text{SWIP}} < C\inf _{\mathbf{v}_{h}\in V _{h}}\|\mathbf{A} -\mathbf{v}_{h}\|_{\text{SWIP},{\ast}}, }$$

(9)

and the discrete problem (6) is well-posed.

The associated function spaces and norms are defined by

$$\displaystyle\begin{array}{rcl} H^{2}(P_{\varOmega })^{3}&:=& \left \{\left.\mathbf{A} \in L^{2}(\varOmega )^{3}\right \vert \forall \varOmega _{ i,\mu } \in P_{\varOmega }:\; \left.\mathbf{A}\right \vert _{\varOmega _{i,\mu }} \in H^{2}(\varOmega _{ i,\mu })^{3}\right \}, \\ \|\mathbf{A}\|_{\text{SWIP}}^{2}&:=& \|\mu ^{-1/2}\nabla \times \mathbf{A}\|_{ L^{2}(\varOmega )}^{2} +\|\varepsilon ^{1/2}\mathbf{A}\|_{ L^{2}(\varOmega )}^{2} +\sum _{ F\in \mathcal{F}_{h}} \frac{\gamma _{\mu,F}} {a_{F}}\|\left [\mathbf{A}\right ]_{T}\|_{L^{2}(F)}^{2}, \\ \|\mathbf{A}\|_{\text{SWIP},{\ast}}^{2}&:=& \|\mathbf{A}\|_{\text{ SWIP}}^{2} +\sum _{ T\in \mathcal{T}_{h}}h_{T}\|\mu ^{-1/2}\left.\nabla \times \mathbf{A}\right \vert _{ T}\|_{L^{2}(\partial T)}^{2}. {}\end{array}$$

(10)

Theorem 1 tells us that the total error is bounded by the best approximation error. In the following we will bound the best approximation error in the $\|\cdot \|_{\text{SWIP},{\ast}}$ norm for two concrete choices of V _h .

Edge Functions of the First Kind In this section we assume $V _{h} = R^{k}(\varOmega _{1}) \oplus R^{k}(\varOmega _{2}) \subset P_{3}^{k}(\mathcal{T}_{h})$, where R ^k is the space of k-th order edge functions (cf. [9], Sect. 5.5) of the first kind. The following polynomial approximation result gives a bound on the right-hand side of (9):

Theorem 2

Assume the exact solution $\mathbf{A} \in V:= \mathbf{H}(\mathbf{curl},\varOmega ) \cap H^{s+1}(\varOmega _{1} \oplus \varOmega _{2})^{3}$ with integer 1 ≤ s ≤ k, then there exists a projector π _h : V ↦ V _h such that

$$\displaystyle{\|\mathbf{A} -\pi _{h}\mathbf{A}\|_{\text{SWIP},{\ast}} < Ch^{s-1}\left (\|\mathbf{A}\|_{ H^{s+1}(\varOmega _{1})^{3}} +\| \mathbf{A}\|_{H^{s+1}(\varOmega _{2})}\right ).}$$

Where C is independent of h.

Sketch of Proof

The approximation space V _h consists of two standard edge element spaces in Ω ₁, Ω ₂. We can thus use the standard projection operator r _h , as it is defined in [9], for edge functions on Ω ₁, Ω ₂ to compose our global projection operator π _h :

$$\displaystyle{\pi _{h}(\mathbf{A}):= \left (r_{h}\left (\left.\mathbf{A}\right \vert _{\varOmega _{1}}\right ),r_{h}\left (\left.\mathbf{A}\right \vert _{\varOmega _{2}}\right )\right ).}$$

Next, we note that all the tangential jumps in (7) and (10) that lie on interior, conforming faces drop out and only jumps over $F \in \mathcal{F}_{h}^{b,\varGamma }:= \mathcal{F}_{h}^{b} \cup \left \{\left.F \in \mathcal{F}_{h}^{i}\right \vert F \subset \right.\left.\overline{\varOmega }_{1} \cap \overline{\varOmega _{2}}\right \}$ remain. Thus,

$$\displaystyle\begin{array}{rcl} & & \|\mathbf{A} -\pi _{h}\mathbf{A}\|_{\text{SWIP},{\ast}}^{2} =\|\mu ^{-1/2}\nabla \times (\mathbf{A} -\pi _{ h}\mathbf{A})\|_{L^{2}(\varOmega )}^{2} +\|\varepsilon ^{1/2}(\mathbf{A} -\pi _{ h}\mathbf{A})\|_{L^{2}(\varOmega )}^{2} {}\\ & & \qquad \qquad +\sum _{F\in \mathcal{F}_{h}^{b,\varGamma }} \frac{\gamma _{\mu,F}} {a_{F}}\|\left [\mathbf{A} -\pi _{h}\mathbf{A}\right ]_{T}\|_{L^{2}(F)}^{2} +\sum _{ T\in \mathcal{T}_{h}}h_{T}\|\mu ^{-1/2}\nabla \times (\mathbf{A} -\pi _{ h}\mathbf{A})\|_{L^{2}(\partial T)}^{2}, {}\\ & & \qquad \qquad \qquad \qquad = T_{1} + T_{2} + T_{3} + T_{4}. {}\\ \end{array}$$

The terms T ₁, T ₂, T ₄ are easily bounded in terms of O(h ^2s) by standard polynomial approximation results (cf. Theorem 5.41 in [9]). However, for T ₃ we have to use Lemma 5.52 in [9] to achieve a rate O(h ^2s−2) which unfortunately dominates the other terms. The fact that the error contribution T ₃ is confined to a neighborhood of the interface, respectively the boundary, does not help, because the solution may be concentrated there as well.

Piecewise Polynomials For the sake of completeness we shortly present an approximation result for the case $V _{h} = P_{3}^{k}(\mathcal{T}_{h})$:

Theorem 3

Assume the exact solution $\mathbf{A} \in V:= \mathbf{H}(\mathbf{curl},\varOmega ) \cap H^{s+1}(P_{\varOmega })^{3}$ with integer 1 ≤ s ≤ k, then there exists a projector π _h ^P : V ↦ V _h such that

$$\displaystyle{\|\mathbf{A} -\pi _{h}^{P}\mathbf{A}\|_{\text{ SWIP},{\ast}} < Ch^{s}\|\mathbf{A}\|_{ H^{s+1}(P_{\varOmega })^{3}}}$$

where C is independent of h.

For the proof of this theorem we refer the reader to the proof of Theorem 3.21 in [8]. The important point is that piecewise polynomials $P_{3}^{k}(\mathcal{T}_{h})$ yield the expected rate of convergence because they span the full polynomial space.

4 Numerical Results

We consider a 3D sphere with radius 1 that is split into two half-spheres which are then meshed individually (Fig. 2). We impose the analytical solution $\mathbf{A} = (\sin y,\cos z,\sin x)$ and choose j ⁱ, g _D correspondingly (μ = 1, $\varepsilon = 10^{-6}$).

Fig. 2

The meshes for the two half spheres. The upper hemi-sphere is turned against the lower hemisphere by $\theta = 2.86$ degrees to create a non-conforming mesh

Figure 3 shows the error for a sequence of quasi-uniform meshes which approximate the boundary linearly. We can see that piecewise polynomials yield always the expected rate of converge, O(h), but this does not hold for edge functions: For V _h  = R ¹(Ω ₁) ⊕ R ¹(Ω ₂) the error fluctuates significantly depending on the angle (see Fig. 4) and for $\theta = 2.86$ (solid line) no convergence is observed. This shows that the estimate in Theorem 2 is sharp for k = 1. For k = 2 we would expect O(h) convergence but for all configurations we observe a rate of order at least O(h ^1. 5) because in this experiment the solution is not concentrated at the interface/boundary: T ₃ decays faster than in the worst case.

Fig. 3

The relative H(curl) error vs. mesh size h for rotation angle $\theta = 2.86$ degrees (solid lines). The dashed gray lines correspond to $\theta = 90n/(50\pi )$ degrees, n ∈ { 0, 1, …, 49}

Finally, Fig. 4 shows the relative error for different rotation angles for a fixed mesh width h. This confirms the previous result in that the error for V _h  = R ¹(Ω ₁) ⊕ R ¹(Ω ₂) depends on the geometry of the overlapping meshes. For $V _{h} = P^{1}(\mathcal{T}_{h})$, respectively V _h  = R ²(Ω ₁) ⊕ R ²(Ω ₂) the error does not depend on $\theta$.

Fig. 4

The relative H(curl) error vs. the rotation angle for h = 0. 261

5 Conclusion and Outlook

We have shown that a straightforward generalization of the Interior Penalty/Nitsche’s Method to 3D Curl-Curl problems does not yield the expected rate of convergence if edge functions of the first kind are used. Generally one order of convergence is lost, i.e. for k-th order edge functions we observe O(h ^k−1) convergence as the mesh is refined. The reason for this is that R ^k doesn’t span the full polynomial space P ^k. Moreover, the result is sharp for k = 1, i.e. the method fails completely for first order edge functions. This problem can be cured by using either the full polynomial space P ¹ or by using second order edge functions R ².

The proposed SWIP scheme leads to a sparse, symmetric positive definite matrix which yields, together with the conjugate gradient method, a fast and robust solution scheme. Furthermore μ can be discontinuous across the non-conforming interface.

Outlook The proof of Theorem 2 suggests that it suffices to use 2nd order edge functions solely in elements adjacent to the non-conforming interface to achieve O(h) convergence. This is easily implemented using hierarchical edge functions [10] and reduces the required number of degrees of freedom drastically. Another open question is whether the problem can still be solved using CG if the regularization term in (3) is dropped because the system matrix then becomes positive semi-definite and the right-hand side is no longer in its range. Also, it is unclear whether the SWIP bilinear form offers a spectrally accurate discretization of the Curl-Curl operator [11] for $\varepsilon = 0$ and thus the convergence rate of CG may deteriorate as h → 0.