Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Methodological approaches for the calculation of quantum transport in non-ideal systems are often compromised by computational restrictions, as complex arithmetics and matrix operations that can involve N 3 processes (where N × N are matrix dimensions) may be necessary. The problem increases when simulations are used for the interpretation of experimental results, as sample dimensions of real devices often range from nanometers to micrometers. It is therefore important to define strategies for the calculation of the conduction characteristics of two-terminal systems with comparable structural characteristics as in real-world experiments. A particular case within this context is the calculation of quantum transport in two-dimensional systems like graphene [1], where disorder is inherently found due to the membrane-like structure of the material, in the form of defects [2] or due to interaction with external parameters like the metallic contacts [3] or the substrate [4]. Additionally, disorder can be engineered through ion-beam processes [5], nano-pattering and nano-lithography [6] or through chemical funtionalization [7]. In all cases, the intrinsic conduction characteristics of the graphene system get significantly altered, with alterations being strongly related to the defect-type or interaction. Such direct relationship between the resulting conduction alteration and its defect origin, make the quantum treatment of transport in graphene-based systems indispensable.

In this paper we discuss strategies for the statistical calculation of quantum transport in disordered graphene systems based on a multiscale approach for the description of the electronic structure and the non-equilibrium Green’s function formalism [8]. We pay particular attention to the computational techniques that can allow for the calculation of the conduction variations when gradually passing from the quasi-one-dimensional limit (graphene nanoribbons) to the two-dimensional case (graphene). We finally discuss localization phenomena, the formation of conduction gaps, transport length scales and conductance characteristics for single-vacancy defected graphene.

2 Methodology

Quantum transport is calculated in two-terminal graphene devices, i.e. devices that comprise of a single graphene channel of finite dimensions in contact with two semi-infinite leads. For the sake of simplicity here we consider ideal contacts, i.e. contacts made of graphene with the same lateral width as the channel material. We start from the single-particle retarded Green’s function matrix

$$\displaystyle{ \mathcal{G}^{r}(\varepsilon ) = [\varepsilon S - H -\varSigma _{ L} -\varSigma _{R}]^{-1}, }$$
(1)

where \(\varepsilon\) is the energy, H the real-space Hamiltonian and S the overlap matrix, which in the case of an orthonormal basis set is identical with the unitary matrix I. \(\varSigma _{L,R}\) are self-energies that account for the effect of ideal semi-infinite contacts, which can be calculated as:

$$\displaystyle{ \varSigma _{L(R)} =\tau _{ L(R)}^{\dag }g_{ L(R)}\tau _{L(R)} }$$
(2)

Here τ L, R are interaction Hamiltonians that describe the coupling between the contacts and the device and g L, R the surface Green functions of the contacts, which can be computed through optimized iterative techniques [9]. The transmission probability of an incident Bloch state with energy \(\varepsilon\) can be thereon computed as the trace of the following matrix product:

$$\displaystyle{ T(\varepsilon ) = Tr\{\varGamma _{L}\mathcal{G}^{r}\varGamma _{ R}[\mathcal{G}^{r}]^{\dag }\}, }$$
(3)

where

$$\displaystyle{ \varGamma _{L(R)} = i\{\varSigma _{L(R)} - [\varSigma _{L(R)}]^{\dag }\} }$$
(4)

are the spectral functions of the two contacts. The reflection coefficient of a single quantum channel can be defined as R = 1 − T. According to the Landauer-Buttiker theory [8], conductance can be calculated as:

$$\displaystyle{ G = \frac{2e^{2}} {h} T, }$$
(5)

where G 0 = 2e 2∕h ≈ 77. 5μ S is the conductance quantum.

The electronic structure of graphene can be easily calculated within a next-neighbor tight-binding (TB) model. Such a description accounts only for the linear combination of π atomic orbitals of graphene, which is however sufficient for the low-energy spectrum of the material. Hence, the next-neighbor TB Hamiltonian can be written as

$$\displaystyle{ H = -t\sum _{<i,j>,\sigma }c_{i,\sigma }^{\dag }c_{ j,\sigma } + H.c., }$$
(6)

where \(c_{i}(c_{i}^{\dag })\) is the annihilation (creation) operator for an electron with spin \(\sigma\) at site i, and t is the hopping integral with a typical value t = 2. 7 eV. As the objective of the study is to calculate the transport properties of disordered graphene, here we consider the presence of a single type of defect, i.e. carbon vacancies. The simplest and most common method to include a vacancy in a site i of the graphene lattice is to remove its π electron from the model by switching to infinite the related on-site energy term \(\varepsilon _{i}\) in the Hamiltonian, or equivalently, by switching to zero the hopping t ij terms between the defected and the neighboring sites. However, a more accurate treatment of the resulting defect states within the electronic spectrum has to take into account the structural reconstruction around the defected site. A method to incorporate such information within the TB model is to perform calculations with methods of higher accuracy (e.g. the density functional theory) and calibrate the TB Hamiltonian in order to reproduce the ab initio results. Here, based on density functional theory calculations of defected graphene quantum dots [10], the tuned values of the on-site energy of the defect site and the hopping integrals between this and neighboring sites have been set to \(\varepsilon _{i} = 10\) eV and t ij  = 1. 9 eV, respectively. This example is a typical paradigm of the multiscale approach often used for conductance calculations in doped and defected graphene systems.

The previous formalism can be considered as the base-formalism for the calculation of quantum transport in laterally confined graphene systems, as the device Hamiltonian H is written in real space. Considering that direct matrix inversions needed for the calculation of the Green function require N 3 operations, it becomes obvious that such an approach can be solely applied for rather short graphene nanoribbons, i.e. laterally confined stripes of graphene. Notwithstanding the computational power offered by modern processing units, it is difficult for this non-optimized approach to reach dimensions higher than the nanoscale. This aspect introduces a non-negligible problem, especially when direct comparisons between theory and experiments are needed, as graphene samples used for electrical measurements often have μm dimensions. It is then obvious that new methodologies as well as optimized numerical approaches are crucial for the calculation of quantum transport in such systems. Scaling as a function of the device length can be achieved by taking advantage of the sparsity in the matrices used within the transport formalism (e.g. Hamiltonian and overlap matrices), in order to reduce the required computations. A linear scaling of matrix operations with the system size can be reached through O(N) techniques [11, 12] by creating tridiagonal blocks within the device Hamiltonian. However, even in this case, scalability is limited to the device length, whereas the lateral confinement remains a problem.

A way to overcome the lateral scalability problem in the quantum transport calculation of disordered graphene structures is to consider systems with lateral periodicity and use the discretization of the wave vector perpendicular to the transport direction in order to define the width of the device. Hence, in this case the electronic structure description starts with the k-space Hamiltonian matrix

$$\displaystyle{ H(\mathbf{k}_{\perp }) =\sum _{m}H_{nm}e^{i\mathbf{k}_{\perp }\cdot (\mathbf{d}_{m}-\mathbf{d}_{n})}, }$$
(7)

where k  ⊥  is the Bloch wave vector within the first Brillouin zone and matrices H nm are written in real space on the previously discussed TB basis set, noting that for n ≠ m, H nm are interaction matrices between neighboring unit cells, whereas in the case of n = m, H nn refers to the Hamiltonian matrix of unit cell n. The single-particle retarded Green’s function matrix then becomes

$$\displaystyle{ \mathcal{G}_{k_{\perp }}^{r}(\varepsilon ) = [\varepsilon S_{ k_{\perp }}- H_{k_{\perp }}-\varSigma _{L,k_{\perp }}-\varSigma _{R,k_{\perp }}]^{-1}, }$$
(8)

whereas all equations of the non-equilibrium Green’s function formalism maintain the same form. The total conductance of the system in this case is the sum of the single conductances calculated at each sampled k-point and the total width of the device is W = T  ⊥ × n k , where T  ⊥  is the translation vector and n k the total number of k-points for the \(\varGamma \rightarrow X\) path of the rectangular Brillouin zone. We note here that the device unit cell can be any rectangular graphene ribbon that can be periodically repeated along the direction which is perpendicular to transport, with the smallest possible cell being adequate for calculations in ideal (non-defected) systems or systems with line defects parallel to the contacts. However, when random defectiveness is the case, the use of rectangular supercells is mandatory. In this case the bigger the periodic supercell used for each k-point calculation, the smaller the error due to periodicity will be. Finally, particular attention has to be paid when performing statistical calculations in disordered graphene systems. Here statistical variations (e.g. the fluctuations of the conductance) can only be correctly evaluated by the real-space formalism, whereas statistical means (e.g. the total conductance) can be correctly evaluated by both real- and momentum space formalisms.

3 Results

3.1 Ideal Graphene

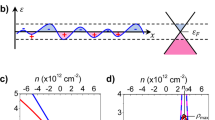
The conductance of ideal graphene systems is characterized by significant qualitative variations when quantum confinement becomes important, i.e. in the case of narrow graphene nanoribbons. In this case the formation of sub-bands in the electronic structure [13] gives rise to integer plateaus in the calculated conductance. Figure 1 shows the ideal conductance of graphene nanoribbons with armchair-type edges and variable widths. It is important to note that within the nearest-neighbor TB picture, narrow armchair ribbons can be either metallic or semiconducting, strictly based on the number of dimer lines that define their width. A simple geometric rule deriving from such calculation shows that \(\forall p \in N\), ribbons with N a  = 3p + 2 dimer lines are metallic while the rest are semiconducting. The main differences observed in the calculated conductance when gradually increasing the lateral width W of the ribbons are: (a) the total conductance proportionally increases with W, as new conduction channels are added to the device, (b) the conductance plateaus progressively become smaller and (c) the band gaps (when they exist) also follow a decreasing trend. From Fig. 1 it is also clear to see that after a transition range when W ≈ 50 − 100 nm, both conductance plateaus and bandgaps become extremely small and the V-shape of two-dimensional graphene conductance appears. A further increase of W only gives rise to quantitative differences whereas the conductivity of the system remains the same.

Fig. 1
figure 1

Ideal conductance of graphene ribbons with armchair-type edges and variable widths

Full size image

Considering calculations in ideal systems, the transport signatures of both one- and two-dimensional graphene should be clearly identifiable in experiments, as in the former case conductance plateaus should appear, whereas in the latter the conductance should reveal a V-shape. In practice, experimentally it is very difficult to demonstrate a quantized graphene conductance even for very narrow graphene ribbons [14]. The origin of this discrepancy is often identified in the presence of disorder, in the form of either structural defects or in the interaction between graphene and its substrate or contacts. It therefore becomes clear that the calculation of quantum transport in graphene considering plausible sources of disorder is fundamental for the correct assessment of the experimental results by the simulations.

3.2 Defected Graphene

Structural defects are very common in graphene samples as they can be generated during the mechanical, chemical or epitaxial growth process. Apart from the local transformation of the hexagonal graphene lattice, such defects give rise to quasi-localized states within the eigenspectrum [15] with resonances that are characteristic of the defect type [16]. The simplest structural defect in graphene is the single vacancy, whose defect states have resonances which impact more heavily on the valence band of the low-energy spectrum rather than on the conduction band, resulting in a conductance asymmetry [17]. Considering a disordered graphene system with just this type of defect, it is very interesting to visualize the alterations of the conductance characteristics as well as the transition of the various localization regimes when altering the geometrical characteristics of the devices.

Figure 2 shows conductance means (solid lines) and fluctuations (points) for a statistical calculation of 100 replicas of a graphene system with fixed W = 9. 88 nm and defect concentration 0.5 %, while scaling the device length L from 20 to 212 nm. Starting from L = 20 nm, the conductance distribution has the following characteristics: (a) the ideal symmetry of the graphene conductance around the charge neutrality point breaks, as a result of the resonances of the single-vacancy states that have a higher density at the valence band of the system rather than the conduction band. In particular a defect state at \(\varepsilon \approx -0.35\,\mathrm{eV}\) gives rise to a local dip of the conductance. (b) Notwithstanding the ideal conductance of this system is characterized by plateaus due to its relatively small width (see Fig. 1), the presence of defects suppresses such feature. It can be therefore argued that even for relatively low defect concentrations it is very difficult to recover quantization features in the conductance. (c) Conductance fluctuations are present throughout the calculated energy spectrum with the conductance variation being \(\delta G \sim 2e^{2}/h\), implying a weak localization regime with universal conductance fluctuations regardless of the number of conduction channels. By gradually increasing the length of the device the following conductance alterations can be seen: (a) the total conductance of the system follows a decreasing trend as a result of the increase of the scattering processes within the device. (b) A transport gap opens at an energy range \(-0.5\,\mathrm{eV} \leq \varepsilon \leq 0\,\mathrm{eV}\) due to the total scattering of the electron waves at such energies from the defect states. It is also very important to see that at this energy region the opening of such a transport gap is accompanied by a strong suppression of the conductance fluctuations δ G, which also defines a change in the localization regime. A method for defining if a disordered system operates within the weak or strong localization regimes is by calculating its characteristic localization length \(\xi\) from:

$$\displaystyle{ < G >\propto e^{-\frac{2L} {\xi } } }$$
(9)

Then, a system with fixed W and defect concentration can be characterized as being in the weak localization regime if the device length \(L \ll \xi\), and similarly, being in the strong localization regime if \(L \gg \xi\). For the case of the ribbon of Fig. 2 the calculated value of \(\xi\) for \(\varepsilon = -0.15\) eV (i.e. an energy value within the transport gap) is found to be 39.24 nm, implying that for the two configurations with L = 105 nm and L = 212 nm, the system is within the strong localization regime at this energy. It is important to note that the localization length strongly depends on the density of defects. Table 1 shows the calculated \(\xi\) for the graphene ribbon of W = 9. 88 nm and single-vacancy concentrations of 0.2, 0.5, 1, and 2 % at energy \(\varepsilon = -0.15\) eV. It is clear that \(\xi\) becomes smaller as the defect concentration increases.

Fig. 2
figure 2

Scaling of the conductance distribution as a function of length for a graphene nanoribbon with W = 9. 88 nm and a fixed vacancy concentration of 0.5 %. Solid lines represent the mean conductance obtained from 100 different configurations of the system (shown as points)

Full size image
Table 1 Localization length \(\xi\) for a graphene nanoribbon with width W = 9. 88 nm and single-vacancy concentrations of 0.2, 0.5, 1, and 2 % at energy \(\varepsilon = -0.15\) eV
Full size table

The influence of the device geometry on the conductance distribution of a disordered graphene system is also important when scaling concerns its lateral width. Figure 3 shows conductance means (solid lines) and fluctuations (points) for a statistical calculation of 100 replicas of a graphene system with fixed L = 20 nm and defect concentration (0.5 %),while varying the device width W from 4.3 to 21 nm. Apart from a gradual increase of the conductance due to the insertion of new conductance channels as the device becomes larger, there are also some qualitative aspects that denote transitions between localization regimes. In particular, it is clear that in the narrower graphene ribbons (W = 4. 3 nm and W = 6. 2 nm) the defect concentration is high enough for the creation of transport gaps at energy resonances relative to single-vacancy defect states, where also the conductance fluctuations are partially suppressed. Such characteristics are typical of the strong localization regime for disordered graphene nanoribbons. On the contrary, the same defect concentration fails in opening a transport gap for wider ribbons, and similarly, the conductance fluctuations recover characteristics which can be attributed to the weak localization regime. The key issue that emerges here is that for the same level of disorder, strong localization can be achieved easier for narrower graphene samples rather than for wider ones. Another important issue regards the conductance fluctuations δ G in the weak localization regime, which appear to be independent from the width of the device, maintaining a fixed value around the conductance mean.

Fig. 3
figure 3

Scaling of the conductance distribution as a function of width for a graphene nanoribbon with L = 20 nm and a fixed vacancy concentration of 0.5 %. Solid lines represent the mean conductance obtained from 100 different configurations of the system (shown as points)

Full size image

A further increase of the width for the disordered graphene ribbon shows that above a certain value of W, differences become only quantitative, as the total conductance increases proportionally with W. Figure 4 shows the mean conductance calculated for a graphene system with L = 20 nm, W = 39. 4 nm and the same defect concentration as before. For this calculation the k-space formalism has been employed, using a rectangular graphene supercell of L = 20 nm and W = 9. 88 nm, while sampling the Brillouin zone \(\varGamma \rightarrow X\) path at n k  = 4 k-points (we note that the k-point sampling is not arbitrary, but considers an equidistant separation of the entire \(\varGamma \rightarrow X \rightarrow \varGamma\) path in [2 × n k + 1] regions). Further increases of the width practically give rise to the same conductivity. This aspect brings to discussion the definition of the transition range between quasi-one-dimensional and two-dimensional transport. Our calculations show that such transition depends on the concentration of the defects, with systems having higher concentrations transiting faster towards the two-dimensional limit. In all cases, the presence of disorder should facilitate the transition of a graphene system to the two-dimensional situation with respect to the ideal case (see Fig. 1).

Fig. 4
figure 4

Mean conductance as a function of energy for a graphene ribbon with W = 39. 4 nm, L = 20 nm and a fixed vacancy concentration of 0.5 %. The mean value has been calculated over 100 replicas of equivalent systems with variable random positions of the defect sites

Full size image

4 Discussion

The objective of this paper has been to discuss the computational strategies for the calculation of quantum transport in disordered graphene systems, in a way that these can be relevant to experimental conductance measurements. To this end, both real- and momentum-space formulations of the non-equilibrium Green’s function formalism have been employed along with acceleration algorithms that can make calculations computationally more affordable. Within this context, the paper has tried to evidence that the dimensions of the graphene channels as well as their level of disorder can be fundamental for the manifestation of different transport features and localization regimes. As a general picture, our results have evidenced that narrow graphene nanoribbons are more influenced by defectiveness with respect to wider ones, as the strong localization regime can be reached easier. We have moreover seen that disorder facilitates the transition of the conduction characteristics from the one-dimensional to the two-dimensional limit.

Although the level of knowledge regarding quantum transport calculations in graphene-based systems is by now well consolidated, there are still plenty of challenges and open issues that have to be affronted in the forthcoming years. A first aspect has to do with the level of complexity in the modeling of defectiveness, as often calculations consider single-type defects, contrary to the intrinsically more complex experimental scenario. A second issue regards the correct assignment of statistical distributions in quantities like the conductance fluctuations [17, 18], especially in the presence of asymmetric disorder (e.g. when defect states are not symmetric with respect to the charge neutrality point). Finally an important issue remains the calculation of disorder effects on the transport characteristics of two-dimensional materials beyond graphene, as in most cases the nearest-neighbor TB Hamiltonian is not adequate for these systems.