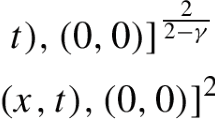Applications

Abstract

In this chapter, we collect many applications of the various ideas that were discussed in the earlier chapters. In the second section, we show how the results for weakly chained diagonally dominant matrices, discussed in Sect. 2.3, have been applied in obtaining bounds for the ℓ ¹ norm for the solutions of certain differential systems and also in deriving bounds for a critical parameter in electric circuit design. In Sect. 8.3, we review how a mapping problem could be reduced to an infinite system of linear equations and then solved. In Sect. 8.4, a similar idea is employed to show how the problem of the flow of fluids in and between two pipes could be handled. In the next section, viz., Sect. 8.5, we recall how some special double points of the Mathieu differential equation could be computed using techniques from infinite matrices. In Sect. 8.6, we discuss how the iterative method described earlier could be applied to obtain good approximate values of Bessel functions in certain intervals. Section 8.7 reviews results for the minimal eigenvalue of the Dirichlet Laplacian in an annulus. In the next section, an approximate solution providing the best match for the hydraulic head in a porous medium is presented. The next section, namely Sect. 8.9, considers eigenvalues of the Laplacian in an elliptic domain. The penultimate section studies the problem of the possibility of “hearing” the shape of a drum. The concluding section, Sect. 8.11, discusses how one could determine the zeros of a Taylor series.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

8.1 Introduction

In this chapter, we collect many applications of the various ideas that were discussed in the earlier chapters. In the second section, we show how the results for weakly chained diagonally dominant matrices, discussed in Sect. 2.3, have been applied in obtaining bounds for the ℓ ¹ norm for the solutions of certain differential systems and also in deriving bounds for a critical parameter in electric circuit design. In Sect. 8.3, we review how a mapping problem could be reduced to an infinite system of linear equations and then solved. In Sect. 8.4, a similar idea is employed to show how the problem of the flow of fluids in and between two pipes could be handled. In the next section, viz., Sect. 8.5, we recall how some special double points of the Mathieu differential equation could be computed using techniques from infinite matrices. In Sect. 8.6, we discuss how the iterative method described earlier could be applied to obtain good approximate values of Bessel functions in certain intervals. Section 8.7 reviews results for the minimal eigenvalue of the Dirichlet Laplacian in an annulus. In the next section, an approximate solution providing the best match for the hydraulic head in a porous medium is presented. The next section, namely Sect. 8.9, considers eigenvalues of the Laplacian in an elliptic domain. The penultimate section studies the problem of the possibility of “hearing” the shape of a drum. The concluding section, Sect. 8.11, discusses how one could determine the zeros of a Taylor series.

8.2 Two Applications of Weakly Chained Diagonally Dominant Matrices

Let us recall that, in Sect. 2.3 the notion of weakly chained diagonal dominance for certain classes of Z-matrices was discussed. Results for upper and lower bounds for the minimal eigenvalue of A, and its corresponding eigenvector, and for the entries of the inverse of A were reviewed there. In what follows, we show how these results have been applied to find meaningful two-sided bounds for both the ℓ ¹-norm and the weighted Perron-norms of the solution x(t) to the linear differential system

$$\displaystyle{\dot{\mathbf{x}} = -A\mathbf{x},\ \mathbf{x}(0) = \mathbf{x}^{0}> 0.}$$

Note that $\mathbf{x}(t) = (x_{1}(t),x_{2}(t),\ldots,x_{n}(t))^{T}$ and $\dot{\mathbf{x}} =\dot{ \mathbf{x}}(t) = (\frac{dx_{1}(t)} {dt},\ldots, \frac{dx_{n}(t)} {dt} )^{T}$. In particular, these systems occur in R-C electrical circuits and a detailed analysis of a model for the transient behavior of digital circuits is studied by Shivakumar, Williams, Ye and Marinov [120].

In order to apply the results of Sect. 2.3, we assume that A is an irreducible weakly chained diagonally dominant Z-matrix with positive diagonal entries. It is proved (Theorem 5.1, [120]) that for all t ≥ 0,

$$\displaystyle{ \sum _{i=1}^{n}z_{ i}\mathbf{x}_{i}(t) = e^{-qt}\sum _{ i=1}^{n}z_{ i}\mathbf{x}_{i}^{0}, }$$

(8.1)

where q = q(A) is the Perron root and $z = (z_{1},z_{2},\ldots,z_{n})^{T}$ is the unique normalized positive eigenvector (the Perron vector) of A ^T corresponding to q.

If bounds for the Perron root are available, viz., $0 <q_{m} \leq q \leq q_{M}$, then one has

$$\displaystyle{ \frac{z_{\min }} {z_{\max }}\|\mathbf{x}_{0}\|e^{-q_{M} } \leq \|\mathbf{x}(t)\| \leq \frac{z_{\max }} {z_{\min }}\|\mathbf{x}_{0}\|e^{-q_{m} }, }$$

(8.2)

where $z_{min} \leq z_{i} \leq z_{max}$ for all $i = 1,2,\ldots,n$ and ∥ . ∥ denotes the 1-norm. References to results of similar nature which motivated the above are given in [120].

Let us turn our attention to a problem in electrical circuits which was also considered by the same authors. It is rather well-known that if $\mathbf{v}(t) = (v_{1}(t),v_{2}(t),\ldots,$ v _n (t))^T denotes the vector of node voltages, then under certain conditions, the transient evolution of an R-C circuit is governed by the differential equation

$$\displaystyle{ C\frac{d\mathbf{v}(t)} {dt} = -G\mathbf{v} + g, }$$

(8.3)

where C is a diagonal matrix with nonzero diagonal entries, g is a given vector, and G is a given matrix of conductances. If $\mathbf{v}^{\infty }$ is the so-called stationary regime voltage vector and if we set $\mathbf{x}(t) = \mathbf{v}(t) -\mathbf{v}^{\infty }$, then the differential equation given above reduces to

$$\displaystyle{ \frac{d\mathbf{x}(t)} {dt} = -C^{-1}G\mathbf{x}(t). }$$

(8.4)

The matrix C ⁻¹ G turns out to be an irreducible Z-matrix with positive diagonal entries with certain further properties. The crucial performance of the digital circuit is the high operating speed that is measured by the quantity

$$\displaystyle{ T(\epsilon ) =\sup \left \{t: \frac{\|\mathbf{x}(t)\|} {\|\mathbf{x}_{0}\|} =\epsilon \right \}, }$$

(8.5)

where again, the norm is the 1-norm and 0 < ε < 1. In practice one takes the value ε = 0. 1. Finding an appropriate value of T(ε) is one of the primary objectives in a design process. Using the inequalities given above, the authors of [120] show that the following inequalities hold (again, the norms below are 1-norms):

$$\displaystyle{ \frac{z_{\min }} {z_{\max }}e^{-q_{M}T_{1}(\epsilon )} \leq \epsilon = \frac{\|\mathbf{x}(T_{1}(\epsilon ))\|} {\|\mathbf{x}_{0}\|} \leq \frac{z_{\max }} {z_{\min }}e^{-q_{m}T_{1}(\epsilon )}, }$$

(8.6)

for a certain delay T ₁(ε) > 0. This implies that

$$\displaystyle{ \frac{1} {q_{M}}\ln \frac{z_{\min }} {\epsilon z_{\max }} \leq T_{1}(\epsilon ) \leq \frac{1} {q_{m}}\ln \frac{z_{\max }} {\epsilon z_{\min }}. }$$

(8.7)

A simple numerical example is given to illustrate how these bounds are reasonably tight. The bounds obtained above are expected to provide useful information in a search for optimal parameters.

8.3 Conformal Mapping of Doubly Connected Regions

Solution of a large number of problems in modern technology, such as leakage of gas in a graphite brick of a gas-cooled nuclear reactor, analysis of stresses in solid propellant rocket grain, simultaneous flow of oil and gas in concentric pipes, and microwave theory, hinges critically on the possibility of conformal transformation of a doubly connected region into a circular annulus.

If D is a doubly connected region of the z-plane, then the frontier of D consists of two disjoint continua C ₀ and C ₁. It is well known [19] that D can be mapped conformally onto a circular annulus, in a one-to-one manner. Moreover, if a and b are the radii of two concentric circles of the annulus, then the modulus of D given by b∕a is a number uniquely determined by D. The difficulties involved in finding such a mapping function and estimating the modulus of D are described by Kantorovich and Krylov [54]. In fact, studies concerning specific regions are very few in the literature. In this section, we review how the mapping problem of the region between a circle and a curvilinear polygon of n sides is reduced to an infinite system of linear algebraic equations, by a direct method. The truncated system of linear algebraic equations turns out to be strictly diagonally dominant.

Let the Jordan curves C ₀ and C ₁ bound externally and internally a doubly connected region D in the z-plane. Then the mapping function

$$\displaystyle{w(z) = e^{[\,\log z+\phi (z)\,]}\;,\;z = x + iy = re^{i\theta },}$$

which is unique except for an arbitrary rotation, maps D + ∂ D onto the annulus $0 \leq a \leq \vert w\vert \leq b <\infty$, where the ratio b∕a is unique and ϕ is regular in D. If ϕ has the form $\phi (z) =\sum _{ -\infty }^{\infty }c_{n}z^{n}$, we then have

$$\displaystyle{\log (z\bar{z})+\phi (z)+\overline{\phi (z)} = \left \{\begin{array}{@{}l@{\quad }l@{}} \log b^{2}\,,\quad &\text{ if }z \in C_{ 0} \\ \log a^{2}\,,\quad &\text{ if }z \in C_{1} \end{array} \right.}$$

The requirement that ϕ satisfies the conditions given above is equivalent to solving the system of infinite linear equations:

$$\displaystyle{\sum _{q=1}^{\infty }a_{ pq}x_{q} = r_{p},\ p = 1,2,\ldots,}$$

for suitable numbers a _pq and r _p (see Eq. (29) and the subsequent values in page 411, [105]). It can be shown that the truncated system of linear equations:

$$\displaystyle{\sum _{q=1}^{n}a_{ pq}x_{q} = r_{p},\ p = 1,2,\ldots,n}$$

has the property that the determinant of the coefficient matrix is nonzero for all n. Thus the system has a unique solution for each n. Let x ⁽ⁿ⁾ be the solution of the truncated system for each n. It then follows from a general principle (see, for instance, [54]) that $\lim \limits _{n\rightarrow \infty }\mathbf{x}^{(n)}$ exists and is a solution of the infinite system. We refer to [105] for the details and numerical examples. We also refer to [102] for a similar procedure for the solution of the Poisson’s equation describing a fluid flow problem.

8.4 Fluid Flow in Pipes

In this section, we consider the problem that arises from the idea that two fluids could be transported with one fluid inside a pipe of cross-section E and the other flowing in an annular domain D in the xy plane bounded internally by C ₂ and externally by C ₁. The flow velocity w(x, y) satisfies the Poisson’s equation:

$$\displaystyle{ w_{xx} + w_{yy} = -P/\mu \text{ in }D, }$$

(8.8)

(P, μ being positive constants), with the boundary conditions:

$$\displaystyle{w = 0\text{ on }C_{1}\text{ and }w = 0\text{ on }C_{2}.}$$

In this problem we are concerned with the rate of flow given by

$$\displaystyle{ R =\int \int w\,dxdy. }$$

(8.9)

It can be shown that using the conformal mapping function

$$\displaystyle{ z = \frac{c} {1-\zeta }\,,\;\zeta =\xi +i\eta, }$$

(8.10)

we get

$$\displaystyle{ w = -\frac{P} {u\mu } \:z\bar{z} +\phi (z) + \overline{\phi (z)}. }$$

(8.11)

We get an infinite series expression for w whose coefficients satisfy an infinite system of algebraic equations. These equations have been shown to have a unique solution. We refer to the work of Shivakumar, Chew, and Ji [102, 106] and [107] for the details. In these the following cases are considered

• (a) C ₀ and C ₁ being eccentric circles.

• (b) C ₀ and C ₁ being confocal ellipses.

• (c) C ₀ being a circle and C ₁ being an ellipse.

• (d) C ₀ and C ₁ being two ellipses.

Calculation of the rate of the flow suggests that the flow is a maximum when the inner boundary has the least perimeter and the outer boundary has the largest perimeter for a given area of flow.

We refer to the work of Luca, Kocabiyik and Shivakumar [68] for an application of the ideas given above in studying fluid flow in a pipe system where the inside of the outer pipe has a lining of porous media. This, in turn, has been shown to have applications in the cholesterol problem in arteries.

8.5 Mathieu Equation

Here we consider a Mathieu equation

$$\displaystyle{ \frac{d^{2}y} {dx^{2}} + (\lambda -2q\cos 2x)y = 0, }$$

(8.12)

for a given q with the boundary conditions: $y(0) = y(\pi /2) = 0$. Our interest is in the case when two consecutive eigenvalues merge and become equal for some values of the parameter q. This pair of merging points is called a double point for that value of q. It is well known that for real double points to occur, the parameter q must attain some pure imaginary value. In [115], Shivakumar and Xue developed an algorithm to compute some special double points. Theoretically, the method can achieve any required accuracy. We refer to [115] for the details. We briefly present the main results, here.

Using a solution of the form

$$\displaystyle{y(x) =\sum \limits _{ r=1}^{\infty }x_{ r}q^{-r}\sin 2rx,}$$

the Mathieu equation is equivalent to the system of infinite linear algebraic equations given by $Bx =\lambda x$, where B = (b _ij ) is an infinite tridiagonal matrix given by

$$\displaystyle{b_{ij} = \left \{\begin{array}{@{}l@{\quad }l@{}} -Q\quad &\mbox{ if $j = i - 1,i \geq 2$} \\ 4i^{2} \quad &\mbox{ if $j = i$} \\ 1 \quad &\mbox{ if $j = i + 1,i \geq 1.$} \end{array} \right.}$$

Here $Q = -q^{2}> 0$. Shivakumar and Xue show (Theorem 3.1, [115]) that there exists a unique double point in the interval [4, 16]. They also show that there is no double point in the interval [16, 36], (Theorem 4.1, [115]). They present an algorithm for computing the double points. In fact, we have $\lambda \approx 11.20$ and Q ≈ 48. 09.

The problem of determining the bounds for the width of the instability intervals in the Mathieu equation has also been studied in the particular case when q = h ², by Shivakumar and Ye [116]. We present the main result here. We consider the following boundary conditions: $y'(0) = y'(\pi /2) = 0$, and $y(0) = y'(\pi /2) = 0$, with the corresponding eigenvalues being denoted by $\{a_{2n}\}_{0}^{\infty }$ and $\{b_{2n}\}_{1}^{\infty }$, respectively. In this connection, the following inequalities are well known: $a_{0} <b_{1} <a_{1} <b_{2} <a_{2} <b_{3} <a_{3} <\ldots$. The next result presents upper and lower bounds for $a_{2n} - b_{2n}$.

Theorem 8.5.1 (Theorem 2, [116]).

For $n \geq \max \,\left \{\,\frac{h^{2} + 1} {2} \,,3\,\right \}$ , set

$$\displaystyle{p_{n} = \frac{8h^{4n}} {4^{2n}[(2n - 1)!]^{2}}.}$$

Then one has

$$\displaystyle{ \frac{p_{n}} {k_{+}}\left [1 - \frac{h^{4}} {8(2n - 1 - h^{2})^{2}}\right ] \leq a_{2n} - b_{2n} \leq \frac{p_{n}} {k_{-}},}$$

for certain constants k ₊ and k ₋ .

8.6 Bessel Functions

An iterative method developed by Shivakumar and Williams [112] was reviewed in Sect. 3.5 of Chap. 3 The authors also present (Example 5.2, [112]) an approximate method for determining the values of the Bessel functions J _n (x) for all values of x lying in an interval. Recall that these functions satisfy the well-known recurrence relation:

$$\displaystyle{J_{n+1}(x) = \frac{2n} {x} J_{n}(x) - J_{n-1}(x),\ n \in \mathbb{N},\ 0 <x <2.}$$

Treating J ₀(x) as given and setting for $J_{n}(x) = x_{n},\ n \in \mathbb{N}$, we get a system of equations whose coefficient matrix satisfies the conditions considered in Sect. 3.5. For instance, choosing x = 0. 6, yields the following system of equations:

$$\displaystyle\begin{array}{rcl} 10x_{1} - 3x_{2}& =& 3J_{0}(0.6), {}\\ -3x_{n-1} + 10nx_{n} - 3x_{n+1}& =& 0,\ n \geq 2, {}\\ \end{array}$$

where $3J_{0}(0.6) \simeq 2.73601459$, [1]. From Corollary 3.5.1, Sect. 3.5, it follows that

$$\displaystyle{\|\mathbf{x} -\mathbf{x}^{(p,n)}\|_{ \infty }\leq \left \{\frac{3} {7}(0.3)^{(p+1)} + \frac{9} {49(n + 1)}\right \}J_{0}(0.6).}$$

Thus for an error of less than 0. 01, we choose n = 16 and p = 6. For the purpose of comparison, if we take p = 16, then, for instance, we have the following: 9. 99555051 E − 07 as against 9. 9956 E − 07 in [1], 9. 99555051 E − 07 as against 9. 9956 E − 07 in [1] for J ₆(0. 6) and 1. 61393490 E − 12 as against 1. 61396824 E − 12 in [1] for J ₁₀(0. 6). We refer to [112] for more details and comparison with known results.

8.7 Vibrating Membrane with a Hole

In this section, we review certain interesting results relating to the behavior of the minimal eigenvalue $\lambda$ of the Dirichlet Laplacian in an annulus. Let D ₁ be a disc on $\mathbb{R}^{2}$, with origin at the center of radius 1, $D_{2} \subset D_{1}$ be a disc of radius a < 1, the center (h, 0) of which is at a distance h from the origin. Let $\lambda (h)$ denote the minimum Dirichlet eigenvalue of the Laplacian in the annulus $D:= D_{h}:= D_{1}\setminus D_{2}$. The following conjecture was proposed in [93]:

Conjecture.

The minimal eigenvalue $\lambda (h)$ is a monotonic decreasing function of h on the interval 0 ≤ h ≤ (1 − a). In particular, $\lambda (0)>\lambda (h),\ h> 0$.

The following results (Lemmas 1 and 2, [93]) were proved as supporting evidence to this conjecture:

Lemma 8.7.1.

We have

$$\displaystyle{ \frac{d\lambda } {dh} =\int _{S}\ u_{N}^{2}N_{ 1}ds,}$$

where N is the unit normal to S = S _h , pointing into the annulus D _h , N ₁ is the projection of N onto x ₁ -axis, u _N is the normal derivative of u, and $u(x) = u(x_{1},x_{2})$ is the normalized L ² (D) eigenfunction corresponding to the first eigenvalue $\lambda$ .

Let D(r) denote the disc | x | ≤ r and μ(r) be the first Dirichlet eigenvalue of the Laplacian in $D_{1}\setminus D_{r}$. Then we have

Lemma 8.7.2.

$\mu (a - h) <\lambda (h) <\mu (a + h),\ 0 <h <1 - a$ .

The conjecture was also substantiated by numerical results [93]. Subsequently, the authors prove the above conjecture in an electronic version of their article (https://www.math.ksu.edu/~ramm/papers/383.pdf). The argument of the proof is presented in the third paragraph in page 4. It is noteworthy to point out that this result has been now shown to be valid in all space dimensions by Kesavan [57].

8.8 Groundwater Flow

Here, we are concerned with the problem of finding the hydraulic head, ϕ in a nonhomogeneous porous medium, the region being bounded between two vertical impermeable boundaries, bounded on top by a sloping sinusoidal curve and unbounded in depth. The hydraulic conductivity K is modelled as K(z) = e ^{β z}, supported by some data available from Atomic Energy of Canada Ltd. Here z is a real variable and β ≥ 0. We recall a method that reduces the problem to that of solving an infinite system of linear equations. This method yields a Grammian matrix which is positive definite, and the truncation of this system yields an approximate solution that provides the best match with the given values on the top boundary. This is the work of Shivakumar, Williams, Ye and Ji [121], where further details are available. We only present a brief outline here.

We require ϕ to satisfy the equation:

$$\displaystyle{\nabla.(e^{\beta z}\nabla \phi (x,z)) = 0,}$$

where ∇ is the vector differential operator

$$\displaystyle{\hat{i} \frac{\partial } {\partial x} + \hat{j} \frac{\partial } {\partial z}.}$$

The domain under consideration is given by

$$\displaystyle{ 0 <x <L,\ \ -\infty <z <g(x) = -\left [\frac{ax} {L} + V \sin (\frac{2\pi nx} {L} )\right ], }$$

(8.13)

where L > 0, a ≥ 0 and V are constants and n is a positive integer. The boundary conditions are given by

$$\displaystyle{ \left. \frac{\partial \phi } {\partial x}\right \vert _{x=0} = \left. \frac{\partial \phi } {\partial x}\right \vert _{x=L} = 0, }$$

(8.14)

ϕ(x, z) is bounded on z ≤ g(x), and ϕ(x, z) = z on z = g(x). The determination of ϕ reduces to the problem of solving the infinite system of linear algebraic equations:

$$\displaystyle{ \sum _{m=0}^{\infty }b_{ km}\alpha _{m} = c_{k},\ \ \ k = 0,1,2,\ldots, }$$

(8.15)

where b _km are given by means of certain integrals. The infinite matrix B = (b _km ) is the Grammian of a set of functions which arise in the study. The numbers b _km become difficult to evaluate for large values of k and m by numerical integration. The authors use an approach using modified Bessel functions, which gives analytical expressions for b _km . They also present numerical approximations and estimates for the error.

8.9 Eigenvalues of the Laplacian on an Elliptic Domain

The importance of eigenvalue problems concerning the Laplacian is well documented in classical and modern literature. Finding the eigenvalues for various geometries of the domains has posed many challenges for which the methods of approach include infinite systems of algebraic equations (as indicated in Sect. 8.5), asymptotic methods, integral equations, and finite element methods. Let us review the work of Shivakumar and Wu [114], where the details of earlier contributions are discussed. The eigenvalue problems of the Laplacian is represented by the Helmholtz equations, Telegraph equations or the equations of the vibrating membrane and is given by:

$$\displaystyle{\frac{\partial ^{2}u} {\partial x^{2}} + \frac{\partial ^{2}u} {\partial y^{2}} +\lambda ^{2}u = 0\text{ in }D,\ \ u = 0\text{ on }\partial D,}$$

where D is a plane region bounded by a smooth curve ∂ D. The eigenvalues k _n and corresponding eigenfunctions u _n describe the natural modes of vibration of the membrane. According to the maximum principle, k _n must be positive (for each n) for a nontrivial solution to exist. Further $k_{n},\ n \in \mathbb{N}$ are ordered such that

$$\displaystyle{0 <k_{1} <k_{2} <\cdots <k_{n} <\cdots \,.}$$

The method described here provides a procedure to numerically calculate the eigenvalues.

Using complex variables $z = x + iy,\bar{z} = x - iy$, the problem becomes

$$\displaystyle{ \frac{\partial ^{2}u} {\partial z\partial \bar{z}} + \frac{\lambda ^{2}} {4}u = 0\mbox{ in }D\mbox{ and }\ \ u = 0\mbox{ on }C }$$

(8.16)

with $u = u(z,\bar{z})$, It is well known that the general solution to (8.16) is given by

$$\displaystyle{ u = \left \{f_{0}(z) -\int _{0}^{z}f_{ 0}(t) \frac{\partial } {\partial t}J_{0}\left (\lambda \sqrt{\bar{z}(z - t)}\right )dt\right \} + \mbox{ conjugate}, }$$

(8.17)

where f ₀ is an arbitrary holomorphic function which can be expressed as

$$\displaystyle{ f_{0}(z) =\sum \limits _{ n=0}^{\infty }a_{ n}z^{n} }$$

(8.18)

and J ₀ is the Bessel function of the first kind of order 0, which is given by a series representation as,

$$\displaystyle{ J_{0}\left (\lambda \sqrt{\bar{z}(z - t)}\right ) =\sum \limits _{ k=0}^{\infty }\left (-\frac{\lambda ^{2}} {4}\right )^{k}\frac{\bar{z}^{k}(z - t)^{k}} {k!\,k!}. }$$

(8.19)

On substituting for f ₀, we obtain the general solution to the Helmholtz equation as

$$\displaystyle\begin{array}{rcl} u& =& 2a_{0}J_{0}(\lambda \sqrt{z\bar{z}}) {}\\ & & +\sum _{n=1}^{\infty }\sum _{ k=0}^{\infty }A_{ n,k}\left ((z +\bar{ z})^{n} +\sum _{ m=1}^{n/2}\alpha _{ m,n}\left (z +\bar{ z}\right )^{n-2m}(z\bar{z})^{m}a_{ n}\right )(z\bar{z})^{k}, {}\\ \end{array}$$

where $\alpha _{m,n} = (-1)^{m} \frac{n} {m}{n - m - 1\choose m - 1}$ and A _n, k are constants determined in terms of certain Beta functions. The expression on the right-hand side demonstrates that the general solution of (8.16) without boundary conditions can be expressed in terms of powers of $z\bar{z}$ and $(z +\bar{ z})$.

In our case, we consider the domain to be bounded by the ellipse represented by

$$\displaystyle{\frac{x^{2}} {\alpha ^{2}} + \frac{y^{2}} {\beta ^{2}} = 1,}$$

which can be expressed correspondingly in the complex plane by

$$\displaystyle{ (z +\bar{ z})^{2} = a + bz\bar{z}, }$$

(8.20)

where $a = \frac{4\alpha ^{2}\beta ^{2}} {\beta ^{2} -\alpha ^{2}}$ and $b = \frac{4\alpha ^{2}} {\alpha ^{2} -\beta ^{2}}$. After considerable manipulation, we get the value of u on the ellipse as,

$$\displaystyle\begin{array}{rcl} u& =& 2a_{0} +\sum \limits _{ n=1}^{\infty }A_{ 2n,0}b_{0,n}a_{n} \\ & +& \sum _{k=1}^{\infty }\left (-\frac{\lambda ^{2}} {4}\right )^{k} \frac{2a_{0}} {k!k!}(z\bar{z})^{k} \\ & +& \sum _{k=1}^{\infty }\left [\sum _{ n=1}^{k}\left (A_{ 2n,k}b_{0,n} +\sum _{ l=1}^{n}A_{ 2n,k-l}b_{l,n}\right )a_{n}\right ](z\bar{z})^{k} \\ & +& \sum _{k=1}^{\infty }\left [\sum _{ n=k+1}^{\infty }\left (A_{ 2n,k}b_{0,n} +\sum _{ l=1}^{k}A_{ 2n,k-l}b_{l,n}\right )a_{n}\right ](z\bar{z})^{k},{}\end{array}$$

(8.21)

for certain constants b _l, n defined in terms of a and b. For u = 0 on the elliptic boundary, we equate the powers of $z\bar{z}$ to zero where we arrive at an infinite system of linear equations of the form

$$\displaystyle{ \sum _{k=0}^{\infty }d_{ kn}a_{n} = 0,\ \ n \in \mathbb{N}, }$$

(8.22)

where d _kn ’s are known polynomials of $\lambda ^{2}$. In [114], the infinite system is truncated to an n × n system and numerical values are calculated and compared to existing results in the literature.

8.10 Shape of a Drum

A drumhead is conceived as a domain D in the plane whose boundary ∂ D is clamped. It is well known that if a membrane D, held fixed along its boundary ∂ D, is set in motion, its displacement obeys the wave equation

$$\displaystyle{\frac{1} {2}\nabla ^{2}U +\lambda ^{2}U = 0,\ U = 0\text{ on }\partial U.}$$

Mark Kac in 1966 [52] published an interesting article on the question: Can one hear the shape of a drum? The phrasing of the title is due to Lipman Bers but the problem itself is older and can be traced back all the way to Hermann Weyl. Similar questions can be asked for the Dirichlet problem for the Laplacian on domains in higher dimensions or on Riemannian manifolds, as well as for other elliptic differential operators such as the Cauchy–Riemann operator or the Dirac operator.

In 1964, John Milnor with the help of a result of Ernst Witt showed that there exist two Riemannian flat tori of dimension 16 with the same eigenvalues but different shapes. However, the problem in two dimensions remained open until 1992, when Gordon, Webb and Wolpert [39] found examples of distinct plane “drums” which “sound” the same. So, the answer to Kac’s question is: for many shapes, one cannot hear the shape of the drum. However, some information can be inferred. Moreover, the answer is known to be “yes” for certain convex planar regions with analytic boundaries. A large number of mathematicians over four decades have contributed to the topic from various approaches, both theoretical and numerical.

In this section, we develop a constructive analytic approach to indicate how a pre-knowledge of the eigenvalues leads to the determination of the parameters of the boundary. This is based on a major contribution of Zelditch in 2000 [140], where a positive answer “yes” is given for certain regions with analytic boundaries. We apply this approach to a general boundary with biaxial symmetry, to a circle boundary, an ellipse boundary, and a square boundary. In the case of a square, we obtain an insight into why the analytical procedure does not, as expected, yield an answer. The work reported here is due to Shivakumar, Wu and Zhang [122].

Let D _L denote the class of bounded simply connected real analytic plain domains with reflection symmetries across two orthogonal axes, of which one has length L. Under generic conditions, if D ₁ and D ₂ are in D _L and if the Dirichlet spectra coincide then D ₁ = D ₂, up to a rigid motion [140].

So, mathematically the problem is, whether a pre-knowledge of the eigenvalues of the Laplacian in a region D leads to the identification of ∂ D, the closed boundary of D. Specifically, we have

$$\displaystyle\begin{array}{rcl} u_{xx} + u_{yy} +\lambda ^{2}u = 0\text{ in }D,& &{}\end{array}$$

(8.23)

$$\displaystyle\begin{array}{rcl} u = 0\text{ on }\partial D.& &{}\end{array}$$

(8.24)

According to the maximum principle for linear elliptic partial differential equations, the infinitely many eigenvalues $\lambda _{n}^{2}$, $n \in \mathbb{N}$, are positive, real, ordered and satisfy

$$\displaystyle{0 <\lambda _{ 1}^{2} <\lambda _{ 2}^{2} <\lambda _{ 3}^{2} <\ldots <\lambda _{ n}^{2} <\ldots <\infty.}$$

Using complex variables $z = x + iy$, $\overline{z} = x - iy$, Eqs. (8.23) and (8.24) become

$$\displaystyle\begin{array}{rcl} u_{z\overline{z}} + \frac{\lambda ^{2}} {4}u = 0\text{ in }D,& &{}\end{array}$$

(8.25)

$$\displaystyle\begin{array}{rcl} u = 0\text{ on }\partial D.& &{}\end{array}$$

(8.26)

By Vekua [134], the completely integrated form of the solutions to the above equations are given by

$$\displaystyle{ u = \left \{f_{0}(z) -\int _{0}^{z}f_{ 0}(t) \frac{\partial } {\partial t}J_{0}\left (\lambda \sqrt{\overline{z } \left (z - t \right )}\right )dt\right \} + \text{conjugate}, }$$

(8.27)

where f ₀(z) is an arbitrary holomorphic function which can be formally expressed as

$$\displaystyle{f_{0}(z) =\sum _{ n=0}^{\infty }a_{ n}z^{n},}$$

and J ₀ represents the Bessel function of first kind and order 0 given by

$$\displaystyle{ J_{0}\left (\lambda \sqrt{\overline{z } \left (z - t \right )}\right ) =\sum _{ q=0}^{\infty }\left (-\frac{\lambda ^{2}} {4}\right )^{q}\frac{\overline{z}^{q}\left (z - t\right )^{q}} {q!q!}. }$$

(8.28)

Now we consider the problem for five types of boundaries: a general boundary with biaxial symmetry, a circular boundary, an elliptic boundary, a square boundary, and an annulus.

Before we study these cases, we recall an identity given in Abramowitz and Stegun [1], viz., when n is an even integer,

$$\displaystyle{ z^{n} + \overline{z}^{n} =\sum _{ m=0}^{\frac{n} {2} }c_{m,n}\left (z + \overline{z}\right )^{(n-2m)}\left (z\overline{z}\right )^{m}, }$$

(8.29)

for certain constants c _m, n . Now we consider the parametrized analytical boundary with biaxial symmetry to be given by

$$\displaystyle{ (z + \overline{z})^{2} =\sum _{ n=0}^{\infty }d_{ n,1}(z\overline{z})^{n} }$$

(8.30)

which yields, on using Cauchy products for infinite series,

$$\displaystyle{ (z + \overline{z})^{2p} =\sum _{ n=0}^{\infty }d_{ n,p}(z\overline{z})^{n} }$$

(8.31)

where

$$\displaystyle{d_{n,p} =\sum _{ l=0}^{n}d_{ l,p-1}d_{n-l,1},\ p = 1,2,\ldots.}$$

For the specific problem at hand, we may assume that

$$\displaystyle{f_{0}(z) =\sum _{ n=0}^{\infty }a_{ 2n}z^{2n}}$$

so that one has

$$\displaystyle{u = 2a_{0}J_{0}\left (\lambda \sqrt{z\overline{z}}\right ) +\sum _{ n=1}^{\infty }a_{ 2n}\sum _{k=0}^{\infty }\left (-\frac{\lambda ^{2}} {4}\right )^{k}A_{ 2n,k}\left (z^{2n} + \overline{z}^{2n}\right )\left (z\overline{z}\right )^{k},}$$

for certain constants A _2n, k . Upon substitution, this yields

$$\displaystyle{u = 2a_{0}J_{0}\left (\lambda \sqrt{z\overline{z}}\right ) +\sum _{ n=1}^{\infty }a_{ 2n}\sum _{k=0}^{\infty }-\left (\frac{\lambda ^{2}} {4}\right )^{k}A_{ 2n,k}\sum _{m=0}^{n}\gamma _{ m,n}(z + \overline{z})^{2(n-m)}(z\overline{z})^{m},}$$

where the constants γ _m, n are given by $\gamma _{m,n} = \left (-1\right )^{m}\frac{2n(2n-m-1)!} {m!(2n-2m)!}$. After a rearrangement of summations, we get

$$\displaystyle{\begin{array}{llll} u& = 2a_{0} +\sum _{ n=1}^{\infty }a_{2n}D_{n,0,0,0} + \left [2a_{0}\left (-\frac{\lambda ^{2}} {4}\right ) +\sum _{ n=1}^{\infty }a_{ 2n}\left \{\sum _{i=0}^{1}\sum _{ p=0}^{1-i}D_{ n,p,1-i-p,i}\right \}\right ]z\overline{z} \\ & + \left \{\right.\sum _{q=2}^{\infty }\left \{\right.2a_{0}\left (-\frac{\lambda ^{2}} {4}\right )^{q} \frac{1} {q!q!} +\sum _{ n=1}^{q-1}a_{ 2n}\left [\sum _{i=0}^{n}\sum _{ p=0}^{q-1}D_{ n,p,q-i-p,i}\right ] \\ & +\sum _{ n=q}^{\infty }a_{2n}\left [\sum _{i=0}^{q}\sum _{p=0}^{q-1}D_{n,p,q-i-p,i}\right ]\left.\left.\right \}\right \}(z\overline{z})^{q}. \end{array} }$$

Here, D _{p, q, r, s} are certain constants. For a circular boundary given by $x^{2} + y^{2} = a^{2}$ we can consider the parametrization $z\overline{z} = a^{2}$. For an elliptic boundary given by

$$\displaystyle{\frac{x^{2}} {\alpha ^{2}} + \frac{y^{2}} {\beta ^{2}} = 1}$$

we can consider

$$\displaystyle{\left (z + \overline{z}\right )^{2} = a + bz\overline{z},\ \alpha>\beta }$$

where

$$\displaystyle{a = \frac{4\alpha ^{2}\beta ^{2}} {\beta ^{2} -\alpha ^{2}},\ b = \frac{4\alpha ^{2}} {\alpha ^{2} -\beta ^{2}}}$$

and

$$\displaystyle{\alpha ^{2} = \frac{a} {4 - b},\ \beta ^{2} = -\frac{a} {b},\ a <0,b> 0.}$$

A square boundary given by $x = \pm a,\ y = \pm a$ can be parametrized as

$$\displaystyle{z^{4} + \overline{z}^{4} = 2(z\overline{z})^{2} - 16a^{2}(z\overline{z}) + 16a^{4}}$$

or

$$\displaystyle{z^{2} + \overline{z}^{2} = 4\left (z\overline{z} - 2a\right )^{2}.}$$

For such a (square) boundary, the authors demonstrate why their analytical approach does not yield information of the boundary with sharp corners from a pre-knowledge of eigenvalues. When the boundary of the drum is an annulus we can hear the shape of the drum if the eigenvalues are known. In other words, for Eqs. (8.23) and (8.24), D is a totally connected region with the boundary conditions

$$\displaystyle{ \begin{array}{rl} &u = 0\text{ on }\pi _{1}: x^{2} + y^{2} = a^{2} \\ & u = 0\text{ on }\pi _{2}: x^{2} + y^{2} = b^{2}\ \ \ \ \ \ a> b,\end{array} }$$

we can show that if the eigenvalues of $\lambda$ are known, then the ratio of the annulus is uniquely determined.

8.11 On Zeros of Taylor Series

We wish to express the zeros z _n , $n \in \mathbb{N}$, of a Taylor series given by

$$\displaystyle{ y(x) =\sum _{ n=0}^{\infty }c_{ n}x^{n} =\prod _{ n=1}^{\infty }(1 + a_{ n}x), }$$

(8.32)

where

$$\displaystyle{ c_{0} = 1,\ c_{1} =\sum _{ k=1}^{\infty }a_{ k}y^{{\prime}}(0), }$$

(8.33)

and $z_{n} = - \frac{1} {a_{n}}$. We assume that the zeros are positive and strictly increasing. Shivakumar and Zhang [117] show that for the second order linear differential equation [110]

$$\displaystyle{ y^{{\prime\prime}}(x) = f(x)y(x) }$$

(8.34)

the formal Taylor series solution about x = 0 is given by

$$\displaystyle{ \begin{array}{rl} y(x)& = y(0) + \frac{1} {2!}f(0)y(0)x^{2} +\sum _{ k=1}^{\infty } \frac{1} {(2k+2)!}\big[\sum _{s_{1}=0}^{1}\sum _{ j=1}^{k+1}P_{ j}(s_{1},2k,0)\big]x^{2k+2} \\ & + y^{{\prime}}(0)x + \frac{1} {3!}[f^{{\prime}}(0)y(0) + f(0)y^{{\prime}}(0)\big]x^{3} +\sum _{ k=1}^{\infty } \frac{1} {(2k+3)!}\big[\sum _{s_{1}=0}^{1}\sum _{ j=1}^{k}P_{ j}(s_{1},2k + 1,0)\big]x^{2k+3} \end{array} }$$

(8.35)

where $P_{q}(s_{1},k,x)$ is given by

$$\displaystyle{ \begin{array}{rl} P_{q}(s_{1},k,x)& =\sum _{ s_{2}=s_{1}}^{k-2(q-1)}\sum _{s_{3}=s_{2}}^{k-2(q-1)}\ldots \sum _{s_{q}=s_{q-1}}^{k-2(q-1)} \\ & {k\choose s_{q} + 2(q - 1)}{s_{q} + 2(q - 2)\choose s_{q-1} + 2(q - 2)}{s_{q-1} + 2(q - 3)\choose s_{q-2} + 2(q - 3)}\ldots {s_{3} + 2\choose s_{2} + 2}{s_{2}\choose s_{1}} \\ & f^{(k-2(q-1)-s_{q})}(x)f^{s_{q}-s_{q-1}}(x)f^{(s_{q-1}-s_{q-2})}(x)\ldots f^{(s_{2}-s_{1})}y^{(s_{1})}(x). \end{array} }$$

(8.36)

We note that

$$\displaystyle{f(x) = \left (\sum _{n=1}^{\infty } \frac{a_{n}} {1 + a_{n}x}\right )^{2} -\sum _{ n=1}^{\infty } \frac{a_{n}^{2}} {(1 + a_{n}x)^{2}}}$$

satisfies (8.34) where y(x) is given by (8.32) and the coefficients c _n of the Taylor series are given in equation (8.35). To facilitate evaluation for c _n we need to find f ^p(0), $p = 0,1,2,\ldots$. Using the notation

$$\displaystyle{Q_{p} =\sum _{ k=1}^{\infty }a_{ k}^{p},\ p = 1,2,3,\ldots,}$$

we get

$$\displaystyle{ \begin{array}{rl} f(0)& = Q_{1}^{2} - Q_{2}, \\ f^{p}(0)& = (-1)^{p+1}p!\left \{\sum _{j=1}^{p+1}Q_{j}Q_{p+2-j} - (p + 1)Q_{p+2}\right \}. \end{array} }$$

(8.37)

Rewrite (8.32) as

$$\displaystyle{y(x) =\sum _{ n=0}^{\infty }\frac{y^{n}(0)} {n!} x^{n}.}$$

From (8.37), we note that Q′s can be expressed in terms of derivatives of f(x) at x = 0 and using derivatives of y(x) in (8.34) and comparing the coefficients of x ⁿ in (8.35), one can obtain

$$\displaystyle{ \begin{array}{rll} Q_{1} & = d_{1}, \\ Q_{2} & = d_{2},\\ &\ldots & \\ Q_{k}& = d_{k}, \end{array} }$$

where d _k ’s are functions of $c_{1},c_{2},\ldots c_{k-1}$. For roots $z_{n} = - \frac{1} {a_{n}}$, a _n ’s satisfy the Vandermonde equation

$$\displaystyle{\sum _{k=1}^{\infty }a_{ k}^{p} = d_{ p}.}$$

Ran and Sereny [94] show that for a large class of infinite Vandermonde matrices the finite section method converges in the l ¹ sense if the right-hand side of the equation is in a suitably weighted l ¹(α) space.