Diving Autopilot Design for Underwater Vehicles Using an Adaptive Neuro-Fuzzy Sliding Mode Controller

Abstract

In general, the diving dynamics of an autonomous underwater vehicle (AUV) has been derived under various assumptions on the motion of the vehicle in vertical plane. Usually, pitch angle of AUV is assumed to be small in maneuvering, so that the nonlinear dynamics in the depth motion of the vehicle could be linearized. However, a small-pitch-angle is a somewhat strong restricting condition and may cause serious modeling inaccuracies of AUV’s dynamics. For this reason, many researchers concentrated their interests on the applications of adaptive control methodology to the motion control of underwater vehicle. In this chapter, we directly resolve the nonlinear equation of the AUV’s diving motion without any restricting assumption on the pitch angle in diving model. The proposed adaptive neuro-fuzzy sliding mode controller (ANFSMC) with a proportional + integral + derivative (PID) sliding surface is derived so that the actual depth position tracks the desired trajectory despite uncertainty, nonlinear dynamics and external disturbances. In the proposed control structure, the corrective term is approximated by a continuous fuzzy logic control and the equivalent control is determined by a feedforward neural network. The weights of the neural network are updated such that the corrective control term of the ANFSMC goes to zero. The adaptive laws are employed to adjust the output scaling factor and to compute PID sliding surface coefficients. Finally, the lyapunov theory is employed to prove the stability of the ANFSMC for trajectory tracking of diving behaviors. Simulation results show that this control strategy can attain excellent control performance.

1 Introduction

Underwater robotic vehicles (URV’s) have experienced remarkable growth in their emerging applications, such as scientific inspection of deep sea, oceanographic mapping, long range survey, underwater structure maintenance, oil and gas exploration, underwater pipelines tracking, rescue operation, underwater precision-guided munitions and so on. The area of URV’s currently falls into two basic categories such as Manned Underwater Vehicles and Unmanned Underwater Vehicles (UUVs). Again, UUVs is classified in to Remotely Operated Underwater Vehicles (ROVs) and Autonomous Underwater Vehicles (AUVs). ROV is a physically linked vehicle via the tether to the surface and are remotely operated by a human pilot. AUV is an unmanned, untethered and underactuated, underwater vehicle that carries its own power source and relies on an on-board computer along with machine intelligence to execute a mission. However, AUV’s dynamics are highly nonlinear, time varying and hydrodynamic coefficients of vehicles are difficult to be accurately estimated a prior, because of the variations of these coefficients with different operating conditions. These types of difficulties cause modeling inaccuracies as parametric uncertainty and unstructured uncertainty in AUV’s dynamics. In order to deal with the uncertainties in the AUV’s dynamics, most control related researchers on URV are mainly focused on the applications of robust control methodology to the motion control of underwater vehicles.

In the existing literatures, several different studies have been done in order to design autopilots for controlling the AUV’s such as PD/PID controllers are designed in [16, 22, 23, 31, 33, 48, 50, 61, 79] as model based controllers most dynamically used in dynamic positioning and motion control. The adaptive control law is developed with estimation of uncertain parameters associated with the hydrodynamic damping co-efficients, which is used to generate appropriate control for the AUV mentioned in [2, 4, 11, 53, 76–78]. Recent progress in the design of robust control schemes has resulted in the linear quadratic gaussian (LQG) methodology with loop transfer recover (LTR), gain scheduling and $H^{\infty }$ control method employed in control of AUV, as described in [15, 40, 47, 51, 54, 56, 57, 59, 60, 64–66]. As compared to robust methods, adaptive control is better for plants with uncertainties because it can improve it’s performance by adaptation with little or no information of the bounds on uncertainties and it is difficult for higher order system.

Sliding mode approach introduced in [9–12, 17, 18, 21, 24, 42, 49, 68, 71, 72] as an effective means of controlling an AUV, mainly due to its ability to tolerate imprecision in the dynamics of undersea robots. A fuzzy logic framework is used for navigation and control of underwater vehicles as discussed in [1, 3, 14, 26, 34, 36, 41, 62, 69]. This control technique dealing with problems characterized by the presence of uncertainty and nonlinearity; in this case the vehicle’s movement and sensing actions depend on a number of environment conditions that are impossible to model. Another intelligent control technique as neural networks (NNs) have an inherent capability of approximating uncertain nonlinear dynamics of the AUV without explicit knowledge of its dynamic structure and it is an attractive tool for steering and diving motion control depicted in [5, 27–30, 44–46, 52, 67, 70, 73–76, 80]. The controllers for AUV should be robust to suppress the uncertain effects from nonlinearity, modeling error and the interferences from complicated external environment.

Usually, it is difficult to derived or identify an accurate dynamic model of a complicated AUV system for designing autopilots. So that, an intelligent control method as fuzzy logic control (FLC) law can be designed based on some knowledge or without any knowledge about the system. In addition, an appropriate FLC can overcome the parameter variation and environmental disturbance during operation. But, there is still lacking of theoretical modeling and analysis for the FLC stability and robustness problems. Hence, the robustness feature of a sliding mode control (SMC) was introduced into the fuzzy controller in current researches. More recently, several studies have been done in order to combine the advantages of SMC and FLC. Kim and Lee [37] proposed a fuzzy controller with fuzzy sliding surface for reducing tracking error and eliminating chattering problem due to that stability and robustness is improved. Song and Smith [63] introduced a sliding mode fuzzy controller that uses pontryagins maximum principle for time optimal switching surface design and uses fuzzy logic to this surface. Guo et al. [19] applied a sliding mode fuzzy controller to motion control and line of sight guidance of an AUV. The parameters of FSMC algorithm are non-adaptive in nature, which could be adapted by intelligent techniques for improving output response. Balasuriya and Cong [6] proposed adaptive fuzzy controller can approximate the unknown system and sliding mode approach provide strong robustness against model uncertainties and external disturbances. Its parameters will be adapted online to utilize control energy more efficiently. Kim and Shin [38] developed autopilot for depth control of an underwater flight vehicle (UFV) based on adaptive fuzzy sliding mode control (AFSMC) with a fuzzy basis function expansion (FBFE) is employed with a proportional integral augmented sliding signal. Afterwards, Kim and Shin [39] proposed an expanded adaptive fuzzy sliding mode controller (EAFSMC), is based on the decomposition method designed by using an expert knowledge and the decoupled sub-controllers and composition method designed by using the FBFE’s. Sebastion et al. (2007) address the kinematic variables controller based on pioneering algorithm, is utilized in control of underactuated snorkel vehicle. In proposed methodology, adaptive capabilities are provided by several fuzzy estimators, while robustness is provided by the SMC law.

In the further development, Bessa et al. [7] presented an adaptive fuzzy control algorithm based on sliding mode for depth control of an ROV, which is employed for uncertainty and disturbance compensation with completely eliminating chattering effect. Later, Bessa et al. [8] applied AFSMC for identification of external disturbances to control the dynamic positioning of underwater vehicles with four controllable degrees of freedom. Javadi-Moghaddam and Bagheri [32] introduced an adaptive neuro-fuzzy sliding-mode-based genetic algorithm (ANFSGA) control system for a ROV with four degrees of freedom (DOF)s. Since, the dynamic of ROVs are highly nonlinear and time varying, an ANFSGA control system is investigated according to direction-based genetic algorithm (GA) with the spirit of sliding mode control and adaptive neuro-fuzzy sliding mode (ANFS) based evolutionary procedure. Guo et al. [20] presented AFSMC to deal with the depth and heading regulation of spherical underwater robots. Furthermore, the designed controller can’t only tolerate actuator stuck faults, but also compensate the disturbances with constant components. Lakhekar and Waghmare [43] designed dynamic fuzzy sliding mode control (DFSMC) for heading angle control in horizontal turn to track desired command, under the influence of disturbances and parameter variations. In this control technique, two fuzzy supervisory systems are employed to determine the value of boundary layer width and hitting gain as the base values of input-output membership functions of FSMC control structure. From the literatures, it can be observed that many approaches in FSMC algorithms have been taken to address the control aspect of the AUV’s.

To accomplish the mentioned motivation in controlling of undersea robots, an ANFSMC designed as diving autopilot for trajectory tracking of AUV’s. This is a cooperative control that is based on the concept of combining NN, FLC and SMC, where the equivalent control is determined by a feed forward NN and the corrective control is approximated by a continuous FLC. At first, we design PID sliding surface and their coefficients are estimated with the help of adaptive control law. In order to reduce the chattering phenomenon, a FLC is used to approximate the corrective control term and the equivalent control is computed by a feed-forward NN. The weights of the NN are adopted by the gradient descent method and adaptive PID sliding surface. This approach can achieve asymptotic stability and converge faster. The rest of this chapter is organized as follows. In Sect. 2, we shall briefly describe diving model of an AUV. The design of ANFSMC applied to AUV for tracking periodic command is described in Sect. 3. Then, Sect. 4 presented, MATLAB/Simulink based numerical simulations for diving motion control for AUV. Finally, conclusions are summarized in Sect. 5.

2 Mathematical Model of AUV

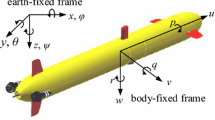
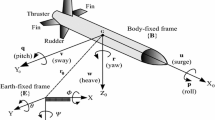
Generally, AUV has a streamlined torpedo-like body propelled by a single thruster and it’s dynamics is highly nonlinear, coupled and time-varying. In addition to these, the hydrodynamic parameters are often poorly known and the vehicle may be subjected to unknown forces due to ocean currents.For vehicle maneuvering, two stern planes and two stern rudder underneath the hull are used. Dynamical behavior of an AUV can be described in a common way through six degree of freedom (DOF) nonlinear equations suggested by Fossen [16], in the two co-ordinate frames such as Body fixed frame and Earth fixed frame as indicated in Fig. 1.

Fig. 1

Body-fixed frame and earth-fixed frame for AUV

The nonlinear underwater vehicle’s motion equation expressed in the Body fixed frame is given as,

$$\begin{aligned} M(\nu )\dot{\nu }+C_{D}(\nu )\nu + g(\eta )+d=\tau , \qquad \dot{\eta }=J(\eta )\nu , \end{aligned}$$

(1)

where, $\eta =[x, y, z, \phi , \theta , \psi ]^{T}$ is the position and orientation vector in earth fixed frame, $\nu =[u, v, w, p, q, r]^{T}$ is the velocity and angular rate vector in body-fixed frame. $M(\nu )\in \mathfrak {R}^{6\times 6}$ the inertia matrix (including added mass), $C_{D}(\nu )\in \mathfrak {R}^{6\times 6}$ denotes the matrix of Coriolis, centripetal and damping term, $g(\eta )\in \mathfrak {R}^{6}$ the gravitational forces and moments vector, d is the disturbances, $\tau$ is the input torque vector and $J(\eta )$ is the transformation matrix. In vertical plane, we can assume that the roll and yaw angular velocities are close to zeros. This can be achieved by properly adjusting the RPM of propeller and the rudders’ angles. Under these assumptions, the heave dynamics of AUVs could be represented as,

$$\begin{aligned} \dot{z}=-u \sin \theta + \nu \cos \theta \sin \phi + \omega \cos \theta \cos \phi \approx -u_{0} \sin \theta \end{aligned}$$

(2)

where $u_{0}> 0$ is a forward constant speed, and the pitch kinematics could be written as

$$\begin{aligned} \dot{\theta }= q \cos \phi - r \sin \phi \approx q \cos \phi \end{aligned}$$

(3)

The roll angle $\phi$ is nearly constant, since $p \approx 0$. Without any loss of generality, we assume that $\phi = 0$. Therefore, above equation could be rewritten as

$$\begin{aligned} \dot{\theta } \approx q \end{aligned}$$

(4)

Consequently, the diving equation of an AUV can be certain modified as

$$\begin{aligned} \dot{z} = -u_{0} \sin \theta \end{aligned}$$

(5)

$$\begin{aligned} \dot{\theta } = q \end{aligned}$$

(6)

$$\begin{aligned} m_{q}\dot{q} = \varPhi ^{T}\varTheta + F_{q} u^{2}_{0} \delta _{q} + d_{q} \end{aligned}$$

(7)

where, $\varPhi =[q, \dot{u}, u, u^{2}, \omega q, r q, \cos \phi \sin \varPsi ]^{T}$, $\varTheta = [\theta _{1}, \theta _{2}, \theta _{3}, \theta _{4}, \theta _{5}, \theta _{6}, \theta _{7}]^{T}$, $m_{q}$ is the inertia term including added mass, $F_{q}$ is the fin moment coefficient and $\delta _{q}$ denotes the stern plane angle and $d_{q}$ is the disturbance term. The main focus of this chapter is taken on an attempt to break a conventional restricting condition, which is typically added to the AUV’s motion behavior while in maneuvering. Mostly, the pitch angle of the vehicle is assumed to be small in maneuvering so that the nonlinear dynamics in the depth motion of the vehicle could be linearized. Here, small-pitch-angle is a strong restricting condition and may cause difficulty in many practical applications. In this work, we directly resolve the nonlinear equation of the vehicle’s depth motion without any restricting assumption on the pitch angle of the vehicle. In fact, robustness has become one of the important aspect related to nonlinear depth control problems, and attention have been taken in to guarantee the stabilities of the proposed control algorithm under various assumptions on the unstructured uncertainties. An ANFSMC was proposed for diving control of an AUV with the nonlinear depth dynamics and their unstructured uncertainties were assumed to be unknown and unbounded.

3 Design of Adaptive Neuro-Fuzzy Sliding Mode Controller

3.1 Proposed Control Structure

The derivation of the proposed ANFSMC scheme for diving control of an AUV is discussed in this section. The control problem is to synthesize an adaptive control law, so that it can provide direct solution to the nonlinear depth dynamics without any restricting assumption on the AUV’s pitch angle, during diving motion behavior. The overall control scheme for motion behavior of undersea robot in vertical plane is depicted in Fig. 2, in which reaching mode control law or switching law means discontinuous control part is approximated by a continuous fuzzy logic control and a feedback control law as equivalent control is to be designed to provide convergence of a system’s trajectory to the sliding surface, within finite time period is computed by a NN. The output of the NN is added with fuzzy logic based corrective control to form the control signal. In the overall control structure, fuzzy logic control is applied to eliminate chattering phenomenon by smoothing the switching signal and the equivalent control effort computed by a feed-forward neural network. The design procedure of the ANFSMC includes the following steps.

• Step(1): Design PID sliding surface with adaptation scheme

• Step(2): Determine corrective control $u_{fe}$ using e or S

• Step(3): Determine equivalent control $u_{eq}$ with the help of NN

• Step(4): Estimate output scaling factor $k_{f}$ of fuzzy logic control

• Step(5): Calculate the overall control signal for diving control

In this work, a NN controller with the learning rule based on sliding mode algorithm, is employed to assure computation of unknown part in the equivalent control under the influence of parametric uncertainties and the second one is chattering free smooth switching law based on fuzzy logic control. The weights of the NN are updated by using iterative gradient algorithm, due to which reaching time is shorten and gain factor of fuzzy inference system along with sliding surface coefficients are computed using adaptive laws.

Fig. 2

The structure of ANFSMC

3.2 PID Sliding Surface

At the first step, let us define a PID sliding surface S(t) in the state space $\mathfrak {R}^{2}$ by the equation $S(q,\theta ,\tilde{z})$ with following equation

$$\begin{aligned} S=K_{p}(z_{(t)}-z_{d})+K_{i}\theta _{(t)}+K_{d} q_{(t)} \end{aligned}$$

(8)

where, $\tilde{z}$ is the tracking error, z is the depth parameter and $z_{d}$ is desired vertical position. An integral term included in the PD type sliding surface expression that resulted in a type of PID sliding surface as hyperbolic function. PID sliding surface coefficients $K_{p}$, $K_{i}$ and $K_{d}$ are designed such that the sliding mode on $S=0$ is stable ie convergence of S to zero in turn guarantees that $\tilde{z}$ converge to zero. The coefficients of PID based sliding surface are strictly positive constant $K_{p}$, $K_{i}$ and $K_{d}$ $\in \mathfrak {R}^{T}$. The coefficients of PID sliding surface can be obtained by adaptive laws as,

$$\begin{aligned} \dot{K}_{p} = -\eta _{1} S e \end{aligned}$$

(9)

$$\begin{aligned} \dot{K}_{i} = -\eta _{2} S \int e dt \end{aligned}$$

(10)

$$\begin{aligned} \dot{K}_{d} = -\eta _{3} S \dot{e} \end{aligned}$$

(11)

where, $\eta _{i}>0$ is the learning rate i = 1, 2, 3, ..., The control law based on a continuous time varying PID sliding surface, here coefficients are systematically obtained according to the adaptive law.

3.3 Corrective Control

An advantage of using fuzzy logic in the controller design is that the dynamics of system need not be fully known. On the other hand, the linguistic expression of the fuzzy controller makes it difficult to guarantee the stability and robustness of the control system. Therefore, their designing based on the sliding mode theory assures performance and stability, while simultaneously reducing the number of fuzzy rules. Sliding mode control (SMC) produces a serious chattering phenomenon, which is avoided by smoothing the switch signal. Therefore, a fuzzy logic controller is used to replace the switching control or discontinuity in the signum function at the reaching phase in the SMC design.

Fig. 3

Membership functions for corrective control as fuzzy logic control

A principal diagram for ANFSMC includes NN module and fuzzy inference system for combined action of equivalent and corrective control algorithm. In fuzzy inference engine, generalized fuzzy sliding mode based rule is designed as follows

$$\begin{aligned} \text {Equivalently,}\, R^{i}\text {: If}\, s \,\text {is}\, F^{'i}_{s}\, \text {then}\, u_{f}\, \text {is}\, F^{'i}_{uf}\text {, i} = 1, 2, \ldots 5. \end{aligned}$$

where, NL is Negative Large, NM is Negative Medium, ZE is Zero, PM is Positive Medium, PL is Positive Large, P is Positive, N is Negative and Z is Zero. NL, NM, ...P, N, Z are labels of fuzzy sets and their corresponding membership functions are depicted in Fig. 3, respectively. Let X and Y are the input and output space of the fuzzy rules, respectively. For any arbitrary fuzzy $F_{x}$ in X, each rule $R_{i}$ can determine a fuzzy set $F_{x}$ * $R_{i}$ in Y. The reduced rule base table for corrective control part in proposed control scheme as stated in Table 1.

Table 1 Rule base for FSMC algorithm

The corrective control part is based on single input single output (SISO) mamdani type fuzzy inference system with minimum If-Then rules. Here, reaching law or corrective control is defined as,

$$\begin{aligned} u_{fe}= k_{f} \,\,u_{fuzzy} \end{aligned}$$

(12)

where, $k_{f}$ is the output scaling factor and $u_{fuzzy}$ is the output of fuzzy inference system, which is determined by the sliding surface S. The fuzzy control rules can be represented as mapping of the input linguistic variable S to the output linguistic variable as $u_{f}$.

According to the following the sup-min compositional rule of inference

$$\begin{aligned} \mu _{\tilde{F_{x}}\circ R^{i}}(u_{f}) = \begin{array}{c} Sup \\ s\in X \\ \end{array} \left[ min \left( \mu _{\tilde{F_{x}}}(s), min\left( \mu _{\tilde{F^{i}_{s}}}(s), \mu _{\tilde{F^{i}_{u_{f}}}}(u_{f}) \right) \right) \right] \end{aligned}$$

(13)

It can be further simplified by supposing $\tilde{F_{x}}$ be a fuzzy singleton, then

$$\begin{aligned} \mu _{F_{x}\circ R^{i}}(u_{f}) = min [\mu _{F^{i}_{s}}(\alpha ),\mu _{F^{i}_{uf}}(u_{f})] \end{aligned}$$

(14)

the deduced MF $F_{u}^{'d}$ of the consequence of all rules is,

$$\begin{aligned} \mu _{\widetilde{F}_{uf}^{d}}^{d}(u_{f}) = max [\mu _{\widetilde{F}_{x}\circ R^{i}}(u_{f}),\ldots \mu _{\widetilde{F}_{x}\circ R^{s}}(u_{f})] \end{aligned}$$

(15)

the output variable in above equation is fuzzified output. For the defuzzifier, the center of area defuzzification method is used to find the crisp output is given as.

$$\begin{aligned} u_{fuzzy} = \frac{\int u_{f} \,\,\, \mu _{\widetilde{F}_{uf}^{d}}^{d}(u_{f})du_{f}}{\int \mu _{\widetilde{F}_{uf}^{d}}^{d}(u_{f}) du_{f}} \end{aligned}$$

(16)

The crisp control signal from extended fuzzy controller is applied to the system model for achieving stabilized diving motion behavior. Other task is to update output scaling factor on line, which depends on sliding surface variable S and its number of fuzzy partitions. The gain updating factor $k_{f}$ is calculated using following relation

$$\begin{aligned} k_{f} = k_{1}[1 /\tilde{p} + |S|] \end{aligned}$$

(17)

Here, $k_{f}$ is nonfuzzy adapted output normalization gain, $\tilde{p}$ is the number of fuzzy partitions of S ie. ($\tilde{p}$ = 5), $k_{1}$ is a positive constant, that will bring appropriate variations in $k_{f}$, which is formulated according to the rule-base of fuzzy inference system with the following strategy: when the state is moving fast towards its set-point, control action needs to be reduced to prevent possible large overshoot and/or undershoot; on the other hand, when the state is rapidly moving away from the set-point, control action needs to be increased to restrict such deviations for a good recovery of the process. In this way, corrective control part is designed to provide smooth switch signal.

3.4 Equivalent Control

The computation of equivalent control is based on fully connected neural network structure, which is consists of an input layer with two neurons (n), one hidden layer with four neurons (h) and a single neuron in output layer (m). The structure of NN presented in control configuration as depicted in Fig. 4 with x is the $n\times 1$ input vector and y is a $m\times 1$ diagonal vector. Here, $\omega$ and $\vartheta$ denotes the input-to-hidden layer and hidden -to-output layer weights respectively in feed forward NN structure.

Fig. 4

NN structure for estimation of equivalent control

In forward propagation, response of NN is expressed as follows:

The input of the $j\mathrm{th}$ hidden layer is specified as

$$\begin{aligned} y_{j} = \sum ^{n}_{k=1} \omega _{jk} \,\, x_{k} \end{aligned}$$

(18)

The output of the $j\mathrm{th}$ hidden unit is represented as

$$\begin{aligned} y_{out_{j}} = f(y_{j}) \end{aligned}$$

(19)

where, f is the sigmoidal transfer function

$$\begin{aligned} f(\sigma )=\frac{2}{1+e^{-\sigma }}-1 \end{aligned}$$

(20)

In above activation function, $\sigma = y_{j}$ is output of first layer in NN. Afterwards, the input to the $i\mathrm{th}$ output unit is

$$\begin{aligned} q_{i} = \sum ^{h}_{j=1} \vartheta _{ij} \,\, y_{out_{j}} \end{aligned}$$

(21)

The output of NN is given as

$$\begin{aligned} q_{out_{i}} = f(q_{i}) \end{aligned}$$

(22)

The estimated value of equivalent control is obtained as

$$\begin{aligned} \hat{u}_{eq} = k_{eq}\,\, q_{out_{i}} \end{aligned}$$

(23)

In backward propagation, the weight adaptation of NN for equivalent control estimation is expressed as follows:

The error back propagation algorithm is derived on the basis of simple gradient principle for minimizing mean square error between the actual output and the desired output. That is, to minimize the cost function selected as the difference between the desired and the estimated equivalent control. Hence, a simple cost function is described as follows

$$\begin{aligned} E = \frac{1}{2}[u_{eq}- \hat{u}_{eq}]^{2} \end{aligned}$$

(24)

The weights are updated by using

$$\begin{aligned} \triangle \vartheta _{ij} = -\alpha \frac{\partial E}{\partial \vartheta _{ij}} \end{aligned}$$

(25)

Similarly, another weights between input and hidden layer is updated as

$$\begin{aligned} \triangle \omega _{jk} = -\alpha \frac{\partial E}{\partial \omega _{jk}} \end{aligned}$$

(26)

Here, $\alpha$ is the learning rate of the back propagation algorithm and it is constant. Moreover, the two factor as $\partial E/ \partial \vartheta _{ij}$ and $\partial E /\partial \omega _{jk}$ can be expressed as follows

$$\begin{aligned} \frac{\partial E}{\partial \vartheta _{ij}} = -\frac{1}{2} k_{eq} (u_{eq}- \hat{u}_{eq}) (1- q_{out_{i}}^{2}) \,\,y_{out_{j}} \end{aligned}$$

(27)

$$\begin{aligned} \frac{\partial E}{\partial \omega _{jk}} = -\frac{1}{4} k_{eq} (u_{eq}-\hat{u}_{eq}) \vartheta _{ij} (1- q_{out_{i}}^{2}) (1- y_{out_{j}}^{2})\,\, x_{k} \end{aligned}$$

(28)

In above equation, $u_{eq}$ is the unknown term. So that, $\partial \vartheta _{ij}$ can not be determined. In order to solve this problem, we have to use the value of adapted PID sliding surface S to replace the $u_{eq}- \hat{u}_{eq}$. The reason is that S is given by the designer and characteristics of $u_{eq}- \hat{u}_{eq}$ and S are similar.

$$\begin{aligned} \frac{\partial E}{\partial \vartheta _{ij}} = -\frac{1}{2} k_{eq} \,\, S (1- q_{out_{i}}^{2}) \,\,y_{out_{j}} \end{aligned}$$

(29)

$$\begin{aligned} \frac{\partial E}{\partial \omega _{jk}} = -\frac{1}{4} k_{eq}\,\, S \,\, \vartheta _{ij} (1- q_{out_{i}}^{2}) (1- y_{out_{j}}^{2})\,\, x_{k} \end{aligned}$$

(30)

The structure of NN that estimate the equivalent control action, is a standard two layer feed-forward NN with the back propagation adaptation algorithm. The error between the desired and estimated equivalent control is adjusted by the PID sliding surface based on adaptive law. The overall output of the neural network structure is given as

$$\begin{aligned} \hat{u}_{eq} = u_{nn} = \varGamma (\vartheta (\varGamma (\omega x_{k}))) \end{aligned}$$

(31)

where, $u_{nn}$ is the output of NN structure, employed to estimate equivalent control and $\varGamma$ is a nonlinear operator. According to the neural network function approximation property, a smooth function $u_{n}$ is a compact set based on hidden layer neurons with weights matrices as $\omega$ and $\vartheta$ such that,

$$\begin{aligned} u_{n}(X)= \vartheta ^{T} g(\omega ^{T}, X) + \varepsilon (X) \end{aligned}$$

(32)

where, $\varepsilon (X)$ represent NN approximation of error satisfying $\Vert \varepsilon (X)\Vert < \varepsilon _{n}$ for some $\varepsilon _{n} > 0$. Then, estimate of $u_{n}$ can be given as

$$\begin{aligned} \hat{u}_{n}(X)= \hat{\vartheta }^{T} g(\hat{\omega }^{T}, X) \end{aligned}$$

(33)

where, $\hat{\vartheta }^{T}$ and $\hat{\omega }^{T}$ are the estimations of $\vartheta$ and $\omega$ respectively obtained by updating weights of NN. The proof of the convergence of E to zero is given

Theorem 1

Using the back propagation algorithm with a proper learning rate, it is guaranteed that E defined in Eq. (24) converges to zero, without bonding to local minimum. Means that, for a bounded disturbance $D_{(t)}$ and unknown dynamics, it is guaranteed that system is stable with zero steady state error.

Proof According to Lyapunov stability criteria, we have to show that $\dot{E}<0$. The derivative of the error function with respect to time is given by

$$\begin{aligned} \frac{dE}{dt}=\frac{\partial E}{\partial \omega }\frac{\partial \omega }{\partial t}+\frac{\partial E}{\partial \vartheta }\frac{\partial \vartheta }{\partial t} \end{aligned}$$

(34)

We know that updated weights in Eqs. (25) and (26) utilized in NN structure and substituted in above Eq. (34),

$$\begin{aligned} \frac{dE}{dt}=-\alpha \left[ \left( \frac{\partial E}{\partial \omega }\right) ^{2}+\left( \frac{\partial E}{\partial \vartheta }\right) ^{2}\right] \end{aligned}$$

(35)

Substituting Eqs. (29) and (30) into Eq. (35),

$$\begin{aligned} \frac{dE}{dt}= & {} -\alpha \bigg \{ \left( -\frac{1}{4} k_{eq} S \vartheta _{ij} (1- q_{out_{i}}^{2}) (1- y_{out_{j}}^{2})\,\, x_{k}\right) ^{2} \nonumber \\&+ \left( -\frac{1}{2} k_{eq} \,\, S \,\, (1- q_{out_{i}}^{2}) \,\,y_{out_{j}}\right) ^{2} \bigg \} \end{aligned}$$

(36)

Due to squaring operation inner terms become positive as $\tilde{H}$ is given as

$$\begin{aligned} \frac{dE}{dt}=-\alpha \left[ H_{1}+ H_{2}\right] = -\alpha \tilde{H} \end{aligned}$$

(37)

Note that Eq. (37) is a negative definite function, which completes the proof.

4 The Parameter Adaptive Method

The ANFSMC structure proposed in the previous section has substantially improved the performance of the fuzzy control (corrective control) by adaptation of dead band width as width of output membership function, while in neural network (equivalent control), learning rate is also adapted by using Lyapunov function.

4.1 Tuning of Output Membership Function in Corrective Control

The response time due to corrective control is minimized, based on the initial condition of system and dead band $\pm d$. These two factors were considered as the tuning parameter to achieve minimum time response. In this work, it is demonstrated that, the settling time can be significantly reduced by on line tuning of the universe of discourse of the output membership function range $\pm a$ with no a prior information of the initial condition is required. Here, problem is that to tune the base value of output membership function defined by three fuzzy sets such as negative, zero and positive with universe of discourse $\{-a,a\}$. In order to accomplish a better performance and devise a systematic method to obtain optimal membership functions. So that, we employ following algorithm for tuning of dead zone parameter as base value of output fuzzy variable, which can significantly minimize settling time of output response.

Determine the universe of discourse $\pm a$ for output fuzzy variable

Initialize dead band d value of output fuzzy variable as d = a/2

Initialize integral absolute function and integral time absolute function

For i = 1 to maximum number of epochs to refinement all d

For j = 1 to minimum number of epochs to refinement one d

Run the experiment and get new values of IAF and ITAF

If ((new IAF $<$ IAF) and (new ITAF $<$ ITAF))

IAF = new IAF;

ITAF = new ITAF;

Save d;

End If

If ((new IAF $\le$ IAF) and (new ITAF $\le$ ITAF))

d = d $\times$ increase ratio

Else

d = d $\times$ decrease ratio

End if

End for

End for

Here, multi variable unconstrained optimization algorithm is employed to determine the minimum state trajectory $\theta$ as function of f(a) of the range $\pm a$ of output membership function in corrective control part. We use decrease ratio and increase ratio as 0.8 and 1.25 respectively. IAF and ITAF are defined as follows:

$$\begin{aligned} IAF: \quad minimize \quad f(a) = \int _{0}^{\infty } |\theta (a)| d\theta \end{aligned}$$

(38)

$$\begin{aligned} ITAF: \quad minimize \quad f(a) = \int _{0}^{\infty } t|\theta (a)| d\theta \end{aligned}$$

(39)

IAF accounts mainly for state at the beginning of the response and to a lesser degree for the steady state duration. ITAF keeps account of state at the beginning but also emphasizes the steady state. Due to this tuning method, response time is significantly reduced with non oscillatory behavior.

4.2 Adaptive Learning Rate

A simple feed-forward NN has a single output with nonlinear activation function for neurons. The network is parameterized in terms of its weights which is represented as a weight vector $\mathbf W \in \mathfrak {R}^{m}$. For a specific function approximation problem, the training data consists of N patterns, $\{x^{p},y^{p}\}$.

Let us consider a specific pattern p for the input vector is $x^{p}$, then the network output is given as,

$$\begin{aligned} y^{p}=f(W,x^{p}) \end{aligned}$$

(40)

In this work, usual quadratic cost function seen in Eq. (24), which is minimized to train the weight vector $W = \{\omega , \vartheta \}$ is mentioned in Eqs. (25) and (26).

We consider a Lyapunov function candidate as

$$\begin{aligned} V = \frac{1}{2} (\tilde{y}^{T},\tilde{y}) \end{aligned}$$

(41)

where, $\tilde{y} = [y^{1}_{d}-y^{1},\ldots ,y^{p}_{d}-y^{p},\ldots , y^{N}_{d}-y^{N}]^{T}$

it’s time derivative is given as

$$\begin{aligned} \dot{V} = - \tilde{y}^{T}\frac{\partial y}{\partial W}\,\, \dot{W} = -\tilde{y}^{T} J \,\, \dot{W} \end{aligned}$$

(42)

where, $J = \partial y/\partial W \in \mathfrak {R}^{N\times m}$

In back propagation algorithm, weights are updated as follows

$$\begin{aligned} W(t+1) = W(t) + \alpha \left( \frac{\partial E}{\partial W}\right) \end{aligned}$$

(43)

Here, $\alpha$ is the fixed learning rate, which is replaced by its adaptive version $\alpha _{a}$ is given by

$$\begin{aligned} \alpha _{a} = \left( \mu \frac{\Vert \tilde{y}\Vert ^{2}}{\Vert J_{p}^{T} \tilde{y}\Vert ^{2}}\right) \end{aligned}$$

(44)

In earliest stage, there have been more contribution concerning the adaptive learning rate and it is the most remarkable factor for determination purpose. However, the computation of adaptive learning rate using the Lyapunov function approach is the key part in neural network based control.

5 Stability Analysis

Lyapunov stability analysis is the most popular approach to prove and to evaluate the stable convergence property of proposed control algorithm as ANFSMC. Here, direct Lyapunov stability approach is employed to investigate the stability property of the proposed controller and to derive the adaptive robust control.

Theorem 2

Let the underwater vehicle represented by Eqs. (5)–(7) in vertical plane. Then subject to required assumptions in diving motion is considered, the proposed controller is combination of corrective control defined by Eq. (12) and equivalent control as in Eq. (23) ensures the convergence of state to the sliding surface S and having desired trajectory tracking response.

Proof Let a Lyapunov function $V_{L}$ be defined as

$$\begin{aligned} V_{L} = \frac{1}{2}S^{2} \end{aligned}$$

(45)

The time derivative of Lyapunov function is,

$$\begin{aligned} \dot{V}_{L} = S \dot{S} \end{aligned}$$

(46)

$$\begin{aligned} \dot{V}_{L} = S \left[ K_{p}(\dot{z} - \dot{z}_{d})+K_{i} \dot{\theta } +K_{d} \dot{q}\right] \end{aligned}$$

(47)

$$\begin{aligned} \dot{V}_{L} = S \left[ K_{p}(-u_{0} \sin \theta ) + K_{i} q + \frac{K_{d}}{m_{q}}(\varPhi ^{T}\varTheta ) + \frac{K_{d} F_{q} u^{2}_{0} \delta _{q}}{m_{q}}- K_{p}\dot{z}_{d}\right] \end{aligned}$$

(48)

Here, control input to the underwater vehicle is u = $\delta _{q}$ as an ANFSMC control signal,

$$\begin{aligned} \dot{V}_{L} = S \left[ f(z, \theta , q) + D_{(t)} + B_{0} u - K_{p}\dot{z}_{d}\right] \end{aligned}$$

(49)

$$\begin{aligned} \dot{V}_{L} = S \left[ f(z, \theta , q) + D_{(t)} + B_{0} (\hat{u}_{eq}+ u_{fe}) - K_{p}\dot{z}_{d}\right] \end{aligned}$$

(50)

$$\begin{aligned} \dot{V}_{L} = S \left[ f(z, \theta , q, D) + B_{0} ((K_{p}\dot{z}_{d}- \hat{f}(z, \theta , q))B^{-1}_{0} + u_{fe}) - K_{p}\dot{z}_{d}\right] \end{aligned}$$

(51)

$$\begin{aligned} \dot{V}_{L} = S \left[ B_{0} u_{fe} + D_{(t)}\right] = S \left[ B_{0} K_{f} fuzz(S)+ D_{(t)}\right] \end{aligned}$$

(52)

$$\begin{aligned} \dot{V}_{L} \le -\left[ B_{0} K_{f} - D_{(t)}\right] |S| \end{aligned}$$

(53)

$$\begin{aligned} \dot{V}_{L} \le -\Vert S\Vert \left[ \Vert B_{0}\Vert \Vert K_{f}\Vert - \Vert D_{(t)}\Vert \right] \end{aligned}$$

(54)

From the above analysis, the global asymptotic stability is guaranteed since the derivative of the Lyapunov function is a negative definite $\dot{V}_{L} = S \dot{S} < 0$.

6 Simulation Results

In order to demonstrate the effectiveness and robustness of the proposed ANFSMC approach for diving motion control of AUV has been simulated using MATLAB/ Simulink. The main focus of this work is to design adaptive diving autopilot for nonlinear depth dynamics control of AUV. In this case, the diving equation of an AUV can be expressed as

$$\begin{aligned} \dot{z}= & {} -u_{0} \sin \theta \end{aligned}$$

(55)

$$\begin{aligned} \dot{\theta }= & {} q \end{aligned}$$

(56)

$$\begin{aligned} \dot{q}= & {} \frac{1}{I_{y}-C_{M_{\dot{q}}}} \left( B_{z_{CB}}\sin \theta + C_{M_{q}}u_{0}q + u^{2}_{0} C_{M_{\delta _{q}}} \delta _{q}\right) \end{aligned}$$

(57)

The parameter values are given as follows:

Length of AUV = 1.8 m

Weight of AUV = $m*g$ = $53*9.81$ = 519.93 $\mathrm{kg.m/s}^{2}$

Density of sea water = $\rho$ = 1025 $\mathrm{kg/m}^{3}$

Forward Speed$\, = u_{0}$ = 1.5 $\mathrm{m/s}$

Vehicle’s mass moment of inertia$\,= I_{y} = 9.921\,\mathrm{kg.m^{2}}$

Vertical distance between center of gravity and center of buoyancy

$B_{z_{CB}}$ = $-(z_{g}-z_{b})*W = -3.5942$

Non-dimensional hydrodynamic coefficient expressed in body frame B

$M_{q} = -0.000641877$

$M_{\dot{q}} = -0.00190690$

$M_{\delta _{s}} = -0.00786620$

Non-dimensional hydrodynamic coefficient = $C_{(.)}$

$C_{M_{q}} = 0.5\rho M_{q} L^{4} = -34.5331$

$C_{M_{\dot{q}}} = 0.5 \rho M_{\dot{q}} L^{5} = -18.4665$

$C_{M_{\delta _{s}}} = 0.5 \rho M_{\delta _{s}} L^{5} = -23.5113$

The performance of the traditional FSMC and ANFSMC has been compared in terms of the set point control, sinusoidal trajectory tracking control, phase portrait and control signal. Moreover, suppose the AUV has some disturbance effect, then tracking capabilities among these controller are also compared for analysis purpose. In order to evaluate the control system performance, three different numerical simulations were performed. In first stage, constant input signal applied to underwater robot, afterwards sinusoidal trajectory tracking of AUV was carried out through simulation and in last simulation disturbance and uncertainties are included in operation of undersea robot.

6.1 Set Point Control

In set point control, the initial conditions of the AUV in diving motion behavior are considered as $\{q_{0}, \theta _{0}, z_{0}\}.$ The simulation response of three parameter with control signal in vertical plane are shown in Fig. 5, which demonstrates that the ANFSMC provides the shortest reaching time, no overshoot and smooth tracking response.

Fig. 5

Set point tracking response of AUV in diving motion behavior

Fig. 6

Sinusoidal trajectory tracking response of AUV

The developed control algorithm employed for regulating diving motion behavior based on combined control action of fuzzy logic control as corrective control and NN control as equivalent control. In this controller design, output fuzzy variable was tuned using multi variable unconstrained optimization method, while learning rate of NN was adopted using Lyapunov function. The weights of NN adapted using back propagation algorithm and adaptive PID sliding surface, while output scaling factor of fuzzy logic control was determined with the help of non fuzzy adaptation technique.

6.2 Sinusoidal Trajectory Tracking Control

In second stage of simulation, sinusoidal reference signal $z_{d}=2\sin (\pi t)$ applied to diving model of AUV gives corresponding results of tracking as seen in Fig. 6, with considering that the initial state coincides with the initial desired state. As observed in sine wave trajectory tracking, ANFSMC is able to provide trajectory tracking with a small associated error and no chattering at all. It can be also verified that proposed method provides a minimum tracking error, when compared with the traditional FSMC. Despite the external disturbance forces and parameter variation with respect to diving model parameters, the ANFSMC allows the underwater robotic vehicle to track the desired trajectory with a less tracking error and undesirable chattering effect was not observed in Fig. 7, the disturbance signal employed in simulation as $d_{(t)} = 0.5\sin (\pi t)$

Fig. 7

Sinusoidal trajectory tracking response under the influence of disturbance effect and parameter variation

As observed phase portrait in Fig. 8, reaching time of proposed control algorithm was better than other control technique such as FSMC, without any chattering effect. Due to the adaptation scheme employed in NN module and fuzzy logic control, reaching time get significantly reduced with smoother response.

Fig. 8

Phase portrait of AUV in vertical plane

Fig. 9

Response of AUV under set point variation

As performance measure for a quantitative comparison, we use integral square of error (ISE) and integral absolute of error (IAE) which are defined as

$$\begin{aligned} ISE=\int _{0}^{t} e^{2}\,\cdot \,dt \end{aligned}$$

(58)

$$\begin{aligned} IAE=\int _{0}^{t} |e|\,\cdot \,dt \end{aligned}$$

(59)

In performance comparison, three conditions are considered as set point tracking and disturbance rejection as shown in Figs. 9 and 10, respectively. Here, a piecewise constant reference positions were employed, which reports that ANFSMC gives better performance than traditional FSMC, due to the adaptation of corrective and equivalent control by selecting parameters like PID sliding surface, output scaling factor, width of output fuzzy variable and learning rate of NN module. In disturbance rejection condition, effect of sampled gaussian noise is less as compared with FSMC on depth parameter regulation by ANFSMC. Time integral performance indices are used such as ISE and IAE for comparison between the controllers. The smaller value of performance measures shows that good controller performance characteristics.

Fig. 10

Response of AUV under influence of sampled gaussian noise

It is observed that, ISE and IAE values for above mentioned conditions are considerably reduced in magnitude than other techniques dealt within this chapter. The values of different errors for various control strategies and under the influences of different conditions are tabulated in Table 2.

The proposed controller is more robust in sense that, under the conditions of set point variation, sinusoidal trajectory tracking, parameter variation and disturbance effects leads to small tracking error and minimum settling time in output response.

Table 2 Performance comparison of controllers

7 Conclusion

In this work, we have presented an ANFSMC for diving motion behavior of AUV in vertical plane. It basically consists of equivalent and corrective control, in which fuzzy logic control is employed for approximating discontinuous control action, while NN module is used to estimate equivalent control, because AUV’s parameters are uncertain in nature. In the adaptation scheme, PID sliding surface coefficients, width of output fuzzy variable, scaling factor, weights and learning rate of NN structure are adapted for improving response of depth parameters of AUV in vertical plane. We found that the performance of the proposed ANFSMC is superior to that of conventional FSMC. The attractive features of the controller are mentioned as follows:

• The exact knowledge of AUV’s diving model and their parameter estimation of upper bounds on uncertainties of the AUV are not required in autopilot design. The necessary information to the design of the diving autopilot is the qualitative knowledge of the system such as operating ranges and the form of its nominal model.

• The fuzzy logic controller is designed to provide smooth control by approximating switching control action. The problem of chattering effect in sliding mode approach is effectively eliminated by given corrective control law

• In fuzzy inference engine, width of output fuzzy variable is tuned by multivariable unconstrained optimization method based on integral absolute function and integral time absolute function for minimizing reaching time.

• In NN module, weights are updated using gradient descent method and their learning rate adopted by Lyapunov function based approach

It is significant to point out that proposed control algorithm assure its validity, effectiveness and its superiority to the conventional FSMC method as demonstrated in simulation results. Further research can be done on adaptation scheme to enhance the output response of AUV in vertical plane by using simplified adaptation algorithm as genetic algorithm, modified particle swarm optimization and other bio-inspired optimization algorithm.