Keywords

1.1 Introduction

Cutting forces are one of the most important quantity in the metal machining process. The cutting forces govern power and torque requirements in the machine tool and drive heat generation which catalyzes tool wear and determines the magnitude and direction of residual stresses in the machined component. Cutting forces also cause deflection of the cutting tool, machine tool and work piece and may have a negative influence on the machined components quality. The cutting forces are therefore important parameters in the evaluation of different cutting tool geometries and concepts. However, dynamic influences from the measurement system affect the result and make it difficult to obtain accurate cutting force data. A commonly used method to remove unwanted dynamic effects from the measured cutting forces is low-pass filtering. Low-pass filtering removes all information above a specified cut-off frequency and may therefore also remove important information related to the true cutting forces contained in frequencies above the cut-off frequency. This is especially evident in milling with transient cutting conditions when the rise times are short and the cutting forces thereby have high frequency content. Therefore, it is difficult to get reliable estimates of the amplitudes and rise times by low-pass filtering transient cutting forces, especially at high cutting speeds.

Accurate estimates of both rise times and force amplitudes are important, e.g., when evaluating and comparing different tools and insert geometries. An alternative approach, to low-pass filtering, that improves the cutting force estimates, i.e. increases the effective frequency range of the force dynamometer, is therefore of great interest.

For example, Tlusty et al. used accelerometers to compensate for the inertia and structural damping of the dynamometer, thereby increasing the effective frequency range [1]. This method has been proven to work under certain conditions, but encounters difficulties around resonance frequencies when the system inertia or damping is large. The method also has problems handling systems with more than one dominating mode [2]. Park and Altintas used a Kalman filtering technique to compensate for unwanted dynamics and process and measurement noise of a spindle integrated force sensor, [3, 4]. The same method has also been applied to cutting force measurements in micro end milling, [5]. Jensen et al., [2], developed a method to obtain an invertible filter of a non-minimum phase frequency response function (FRF) of a force dynamometer. The method was tested on experimental data with promising results. The basic principle of the method is to divide the system’s transfer function into one stable and one unstable causal IIR-filter. The unstable causal IIR-filter is transformed into a non-causal stable FIR-filter. Then, by using these two filters in series a stable inverse filter is obtained. Depending on the location of the non-minimum-phase zeros of the system’s transfer function, the length of the non-causal FIR-filter can become large, introducing long time delays. However, if the method is applied on large data sequences, this will not cause a problem.

In the case when the force dynamometer can be considered linear and the cross-frequency responses between the directions x, y and z are negligible, a minimum-phase inverse filter can be constructed and used to counteract the dynamometer dynamics and thereby increase the usable bandwidth of the dynamometer. A procedure for creating a minimum-phase inverse filter is described in this paper and applied in both simulations and on experimental data from milling under various cutting conditions.

1.2 Inverse Filtering

Consider the FRF H(ω) between the applied force F R (ω) and the force output from the dynamometer F D (ω), Eq. (1.1).

$$ H\left(\omega \right)=\frac{F_D\left(\omega \right)}{F_R\left(\omega \right)} $$
(1.1)

In an ideal case, i.e. when there are no dynamic influences from the dynamometer, the magnitude of H(ω) is equal to unity and the phase equal to zero for all frequencies. However, due to e.g., the mass and shape of the work piece, the stiffness and damping of the force dynamometer and the distance between the actual cutting position and the positions of the force transducers in the dynamometer, the magnitude and phase of the frequency response between applied force and force output will deviate from the ideal values and thus the measured force will differ from the applied force. By applying an inverse filter, describing \( {H}^{-1}\left(\omega \right) \), on the recorded force signal these unwanted dynamic effects can be counteracted. If H(ω) is stable and minimum-phase (all zeros of the system lies within the unit circle in the z-domain) then the system is directly invertible. Usually, mechanical systems are stable and mixed-phase (zeros both inside and outside the unit circle). If the system has zeros outside the unit circle it cannot be directly inverted, since the result will then have unstable poles and the filter output exponentially tends toward infinity. However, a mixed or maximum-phase FRF can be transformed into a minimum-phase FRF while still keeping the amplitude characteristics but changing the phase. An invertible filter describing the characteristics of the minimum-phase FRF can then be estimated as described in this section.

1.2.1 Transformation into Minimum-Phase

A mixed- or maximum-phase transfer function can be transformed into a minimum-phase transfer function by, e.g., using the Hilbert transform [6] or cepstrum [7, 8]. In this paper, real cepstrum is used to transform the FRF of the force dynamometer into minimum-phase.

Let h(n) be a real sequence with H(ω) as its Fourier transform. Its real and complex cepstrum ĉ (n) and ĥ (n) are defined as:

$$ \begin{array}{l}\widehat{C}\left(\omega \right)=\mathrm{\Re}\left(H\left(\omega \right)\right)= \log \left|H\left(\omega \right)\right|\\ {}\kern.5em \widehat{c}(n)={\mathcal{F}}^{-1}\left(\widehat{C}\left(\omega \right)\right)\\ {}\widehat{H}\left(\omega \right)= \log \left(\left(H\left(\omega \right)\right)\right)\\ {}\kern.45em \widehat{h}(n)={\mathcal{F}}^{-1}\left(\widehat{H}\left(\omega \right)\right)\end{array} $$
(1.2)

where \( \log \left|H\left(\omega \right)\right| \) refers to the natural logarithm of \( \left|H\left(\omega \right)\right| \) and \( {\mathcal{F}}^{-1} \) denotes the inverse Fourier transform. Some useful relations between minimum-phase and maximum-phase sequences and their complex cepstrums are, [8]:

  • If h(n) is a minimum-phase sequence, ĥ(n) will be a casual sequence.

  • If h(n) is a maximum-phase sequence, ĥ(n) will be an anti-causal sequence.

Let the minimum-phase counterpart to h(n) be denoted by h min (n) and its complex cepstrum denoted by ĥ min (n). The Kramers–Kronig relations for a causal sequence states that the entire sequence can be described by its even part. The relationship between the even part of ĥ(n) and its Fourier transform is given in [9]:

$$ {\widehat{h}}_e(n)={\mathcal{F}}^{-1}\left(\mathrm{\Re}\left(H\left(\omega \right)\right)\right)=\widehat{c}(n) $$
(1.3)

Since ĥ(n) is a causal sequence when h(n) is minimum-phase, ĥ min (n) can be estimated as:

$$ {\widehat{h}}_{min}(n)=\left\{\begin{array}{c}\hfill 2\widehat{c}(n)\hfill \\ {}\hfill \widehat{c}(n)\hfill \\ {}\hfill 0\hfill \end{array}\kern1.25em \begin{array}{c}\hfill n>0\hfill \\ {}\hfill n=0\hfill \\ {}\hfill n<0\hfill \end{array}\right. $$
(1.4)

According to Equation (1.2), the minimum-phase transfer function H min (ω) can be obtained by:

$$ {H}_{min}\left(\omega \right)={\mathrm{e}}^{\mathcal{F}\left({\widehat{h}}_{min}(n)\right)} $$
(1.5)

1.2.2 Fitting an Invertible Digital Filter to the Minimum Phase FRF

The Steiglitz-McBride iteration algorithm is used to find the filter coefficients describing the given impulse response of the estimated minimum phase FRF, H min (ω), [10]. This method is based on non-parametric frequency response characteristics and describes the identified FRF using a polynomial model. The identification is performed using in-house written Python code, alternatively the MATLAB function invfreqz.m can be used to estimate the coefficents [11]. The identified model is a discrete representation of the minimum-phase transfer function of the force dynamometer, h min (n), and can be represented as:

$$ {H}_{min}(z)=\frac{B(z)}{A(z)}=\frac{b(1)+b(2){z}^{-1}+\dots +b\left(nb+1\right){z}^{-nb}}{a(1)+a(2){z}^{-1}+\dots +a\left(na+1\right){z}^{-na}} $$
(1.6)

The result is an invertible IIR-filter described by the coefficients b and a, where nb and na are the total number of coefficients in the numerator and denominator, respectively. nb and na are selected by visual inspection ensuring a satisfactory fit between the measured and estimated FRFs.

1.3 Simulations

To verify the proposed method and identify usable frequency ranges for the inverse filters, simulations using a model of the force dynamometer obtained from experimental data are performed. The model is based on the FRF matrix of the force dynamometer, with the work piece, mounted in the machine tool. The FRF matrix was estimated using impulse excitation in x- and y-directions, results are shown in Figs 1.1 and 1.2. The cross-frequency response in the region 0 to 3000 Hz is small in both directions. Also, the coherence functions are close to unity up to approximately 3000 Hz, implying linear relationships between inputs and outputs. These results indicate that a linear model, with negligible cross frequency response, of the force dynamometer is valid for frequencies up to approximately 3000 Hz.

Fig. 1.1
figure 1

Measured FRFs of the force dynamometer from impulse excitation. The dynamometer is excited in the x-direction and responses collected in x- and y-directions

Full size image
Fig. 1.2
figure 2

Measured FRFs of the force dynamometer from impulse excitation. The dynamometer is excited in the y-direction and responses collected in y- and x-directions

Full size image

Based on the FRF measurements of the dynamometer, inverse filters in both x and y-directions are estimated and evaluated with respect to both amplitude and phase correction. Comparisons between the measured FRFs and the minimum-phase FRFs are shown in Figs 1.3 and 1.4. To clearly show the amplitude and phase characteristics of the inverse filters, the combined FRFs are also displayed; these are calculated as:

Fig. 1.3
figure 3

Magnitude and phase responses of H xx (ω), H xx(min)(ω) and the combined FRF, \( nb=200 \) and \( na=55. \) The dynamometer’s dominant modes are: 1110 Hz, 1725 Hz, 2700 Hz

Full size image
Fig. 1.4
figure 4

Magnitude and phase responses of H yy (ω), H yy(min)(ω) and the combined FRF, \( nb=200 \) and \( na=55 \). The dynamometer’s dominant modes are: 1120 Hz, 1430 Hz, 1630 Hz, 1750 Hz and 2550 Hz

Full size image
  1. 1.

    Inverse Fourier transform the measured mixed-phase FRF, H(ω), the result is the impulse response.

  2. 2.

    Apply the inverse filter to the obtained impulse response; the result is a unit impulse.

  3. 3.

    The combined FRF is the Fourier transform of the signal obtained from the inverse filter.

If the inverse filter behaves perfectly, the magnitude of the combined FRF should be unity and the phase zero for all frequencies.

The magnitudes of H xx (ω) and H yy (ω) matches well with their respective minimum-phase FRFs H xx(min)(ω) and H yy(min)(ω). The combined FRFs indicate a good amplitude correction over the entire frequency range, even at dominant modes. Due to the minimum-phase transformation, the phase responses of measured and minimum-phase FRFs differ, which is clearly visible in the phase responses of the combined FRFs. However, the phase responses of the combined FRFs are dominated by linear trends which can be related to constant delays in the time domain and will not affect the amplitude responses of the inverse filtered signals. Thus, the phase responses affecting the inverse filtered signals are obtained by removing the linear phase trends from the combined FRFs. As seen in Figs 1.3 and 1.4, the phases of the combined FRFs have deviated approximately 7 degrees from zero at 2500 Hz. Therefore, it is expected that frequencies above 2500 Hz will be out of range for the inverse filter. To avoid influences from the resonances at 2550 Hz in the x-direction and 2700 Hz in the y-direction, the frequency limit of the inverse filters was set to 2400 Hz in both directions; higher frequencies are removed by low-pass filtering. Low-pass filtering also removes any high-frequency noise present in the inverse filtered signal. High frequency noise is common when performing inverse filtering due to the nature of the filter. The reason is that mechanical systems normally act as low-pass filters, attenuating high frequencies. When these systems are inverted they will instead act as high-pass filters and therefore respond badly to high frequency noise. The low-pass filter design used in the simulations is a Butterworth filter of order 3. To remove any phase distortion caused by the low-pass filter, zero-phase filtering is performed by filtering the data in both forward and reverse directions.

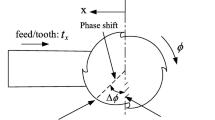
To test the behavior of the inverse filters, simulations are carried out for the cutting speeds and feed rates listed in Table 1.1. Down milling and 50 % radial immersion is used to excite the dynamometer with a high frequency transient signal and thereby clear effects from the dynamometer dynamics appear. The simulations are carried out using both x and y as feed directions. Mechanistic modeled cutting forces are used as input (see Table 1.2), these are filtered through ETFEs of the measured mixed-phase transfer functions, h xx (n), h xy (n) and h yy (n), h yx (n). Each output is then inverse filtered and compared to the reference cutting force (simulated input force), Figs 1.5 and 1.6. The simulated output forces have contributions both from the point FRFs and the cross FRFs. Due to the phase distortion caused by the minimum-phase transformation, superposition of e.g. h xx(min)(n) and h xy(min)(n) does not apply. Therefore only h xx(min)(n) or h yy(min)(n) are used in the inverse filters. Thus, for the results to be accurate, the effect of the cross FRFs have to be negligible.

Table 1.1 Equipment and cutting data used in the cutting force measurements
Full size table
Table 1.2 Estimated cutting force coefficients from milling tests
Full size table
Fig. 1.5
figure 5

Simulation results with feed in x-direction; (a) The isolines of η [%], Eq. (1.7). (b) Comparison between dynamometer output, inverse filtered and reference input forces (Cutting speed, \( {v}_c=2000 \) [m/min]; Feed rate, \( {f}_z=0.25 \) [mm/tooth])

Full size image
Fig. 1.6
figure 6

Simulation results with feed in y-direction; (a) The isolines of η [%], Eq. (1.7). (b) Comparison between dynamometer output, inverse filtered and reference input forces (Cutting speed, \( {v}_c=2000 \) [m/min]; Feed rate, \( {f}_z=0.25 \) [mm/tooth])

Full size image

The similarity between the signals is estimated by calculating the ratio of the energy in the difference between reference and inverse filtered force, \( E\left({f}_R(t)-{f}_I(t)\right) \) and the energy in the reference signal, E(f R (t)), according to:

$$ \eta = \min \left(1+\frac{{\mathrm{R}}_{{\mathrm{f}}_{\mathrm{I}}{\mathrm{f}}_{\mathrm{I}}}(0)-{\overline{\mathrm{f}}}_{\mathrm{I}}^2-2\left({\mathrm{R}}_{{\mathrm{f}}_{\mathrm{R}}{\mathrm{f}}_{\mathrm{I}}}\left(\uptau \right)-{\overline{\mathrm{f}}}_{\mathrm{R}}{\overline{\mathrm{f}}}_{\mathrm{I}}\right)}{{\mathrm{R}}_{{\mathrm{f}}_{\mathrm{R}}{\mathrm{f}}_{\mathrm{R}}}(0)-{\overline{\mathrm{f}}}_{\mathrm{R}}^2}\right) $$
(1.7)

where \( {\mathrm{R}}_{{\mathrm{f}}_{\mathrm{R}}{\mathrm{f}}_{\mathrm{R}}}(0) \) and \( {\mathrm{R}}_{{\mathrm{f}}_{\mathrm{I}}{\mathrm{f}}_{\mathrm{I}}}(0) \) are the autocorrelations at zero time delay between reference and inverse filtered forces, respectively. \( {\mathrm{R}}_{{\mathrm{f}}_{\mathrm{R}}{\mathrm{f}}_{\mathrm{I}}}\left(\uptau \right) \) refers to the cross correlation between reference and inverse filtered forces, where τ is the time delay between the two signals, [12]. \( {\overline{\mathrm{f}}}_{\mathrm{R}} \) and \( {\overline{\mathrm{f}}}_{\mathrm{I}} \) are the average values of the reference and inverse filtered forces, respectively. The best fit between the signals is found at the time delay, τ, where the energy in the difference between the two signals has a minimum. If η = 0 the two signals are identical.

The simulation results show that the inverse filters are able to counteract the dynamic influences and reconstruct the reference cutting forces within a small error margin for all cutting speeds and feed rates listed in Table 1.1. As seen in Figs 1.5a and 1.6a the difference between reference and inverse filtered forces increases as the cutting speed increases. This is expected since the cutting speed affect ramp up times and thereby the frequency content in the reference force signal. Higher cutting speed leads to higher frequencies in the reference force. Thus, the frequency range of the inverse filter may not be enough to fully describe the transient behavior in the force signal at high cutting speeds. Comparisons between reference and inverse filtered forces using maximum feed rate and cutting speed are shown in Figs 1.5b and 1.6b. Additionally, simulations were performed without considering the effect of the cross FRFs on the dynamometer outputs. Neglecting the cross FRFs did not show any significant changes in the results confirming that the cross FRFs are negligible.

1.4 Experimental Tests

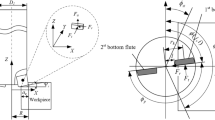
The proposed method was evaluated in experimental cutting tests using different cutting speeds, feed rates and radial immersion. To be able to test the method over a large span of cutting speeds, the tests were performed in aluminum. Forces in both x- and y-directions were recorded and inverse filtered. The results are compared with unfiltered, low-pass filtered and simulated cutting forces. The simulated cutting forces are mechanistic modeled and the cutting coefficients are estimated from milling tests in the work piece used in the experimental tests, see Table 1.2, [13]. The test setup is illustrated in Fig. 1.7. Equipment and cutting data used are listed in Table 1.1.

Fig. 1.7
figure 7

The test setup showing force dynamometer, workpiece and cutter used in the measurements

Full size image

The cut-off frequency used for direct low-pass filtering of the cutting forces was set by visually inspecting the FRFs in Figs 1.1 and 1.2. As seen, the frequency response of the force dynamometer is relatively flat up to 600 Hz. Information contained in the region above 600 Hz is expected to be effected by the force dynamometer dynamics and generate an erroneous output. Thus, the cut-off frequency used for direct low-pass filtering was set to 600 Hz. The cut-off frequency used for low-pass filtering the inverse filtered signals is the same as used in the simulations, 2400 Hz. The filter design and filtering techniques used in the simulations are also used in the experimental tests. Figs 1.8 and 1.9 show results from tests with different radial immersion and cutting speeds.

Fig. 1.8
figure 8

Comparison of unfiltered, simulated, inverse filtered and low-pass filtered cutting forces. Down milling; Cutting speed, \( {v}_c=1200 \) [m/min]; Tooth passing frequency, \( {f}_t=127.3 \) [Hz]; Feed rate, \( {f}_z=0.2 \) [mm/tooth]; Radial immersion \( {a}_e=25 \) [mm]

Full size image
Fig. 1.9
figure 9

Comparison of unfiltered, simulated, inverse filtered and low-pass filtered cutting forces. Down milling; Cutting speed, \( {v}_c=2000 \) [m/min]; Tooth passing frequency, \( {f}_t=212.2 \) [Hz]; Feed rate, \( {f}_z=0.2 \) [mm/tooth]; Radial immersion \( {a}_e=40 \) [mm]

Full size image

The results show that inverse filtered cutting forces are able to predict both amplitude and ramp-up in a reliable manner. Compared with simulated forces the difference in amplitude is small for all cutting conditions tested. Both amplitude and ramp-up prediction is better for inverse filtered compared to low-pass filtered forces. The difference is especially clear for transient cutting conditions and high cutting speeds. Another issue using low-pass filtering is that changes in the estimated cutting forces with respect to cut-off frequency make it difficult to tell if and when the obtained results are accurate. Also, using low-pass filtering the cut-off frequency should be set to the highest possible value in order to preserve as much information as possible. This requires measurements of the dynamometers frequency response for each specific set-up. Thus, to properly select a cut-off frequency for low-pass filtering, the same number of frequency response measurements are needed as are needed to construct an inverse filter. Since the frequency range, in this case, was extended by 400 % using inverse filtering compared to low-pass filtering, the results become more reliable and less sensitive to changes in cutting conditions.

1.5 Conclusions

A method to create an inverse filter for improved cutting force measurements based on minimum-phase FRFs has been presented. The method is based on the assumptions that the force dynamometer can be described by a linear model and that the cross FRFs of the system are negligible. These assumptions were verified by simulations, combining both measured mixed-phase and minimum-phase FRFs of the force dynamometer, confirming the inverse filters validity within the boundaries of the cutting conditions used in the measurements. The method successfully counteracted the dynamometer dynamics in experimental tests with different feed rates, cutting directions and cutting speeds. The results show that a more reliable estimation of the cutting forces can be obtained using the proposed method compared to traditional low-pass filtering, especially under transient cutting conditions and high cutting speeds. Since the dynamic corrections are performed in the time domain, compensation can be performed on both stationary and non-stationary signals, which allows the method to be used under both constant and varying cutting conditions. The method can be used to study detailed force responses such as transient entering and/or exiting forces, which is important, e.g., for cutting tool design.